Abstract
We present a generic computational framework for the simulation of viral capsid assembly which is quantitative and specific. Starting from PDB files containing atomic coordinates, the algorithm builds a coarse-grained description of protein oligomers based on graph rigidity. These reduced protein descriptions are used in an extended Gillespie algorithm to investigate the stochastic kinetics of the assembly process. The association rates are obtained from a diffusive Smoluchowski equation for rapid coagulation, modified to account for water shielding and protein structure. The dissociation rates are derived by interpreting the splitting of oligomers as a process of graph partitioning akin to the escape from a multidimensional well. This modular framework is quantitative yet computationally tractable, with a small number of physically motivated parameters. The methodology is illustrated using two different viruses which are shown to follow quantitatively different assembly pathways. We also show how in this model the quasi-stationary kinetics of assembly can be described as a Markovian cascading process, in which only a few intermediates and a small proportion of pathways are present. The observed pathways and intermediates can be related a posteriori to structural and energetic properties of the capsid oligomers.
INTRODUCTION
Viruses are the cause of some of the deadliest diseases today. In fact, the lethality of viruses emanates from their simplicity; as the ultimate nonautonomous parasites, viruses cannot replicate without a host cell and are therefore immune to standard antibacterial drugs. Basically, a virus consists of two components: genetic material (DNA or RNA) and a protective protein shell, the capsid. In a self-referencing loop, the viral nucleic acids encode the proteins that form the viral capsid. Once the virus penetrates a host cell, it hijacks the cellular machinery of the host and uses it to replicate the viral genome and to express the viral protein(s), which then assemble into capsids. As a result, the infected cell acts as a replicator of new viruses instead of performing its normal tasks (1).
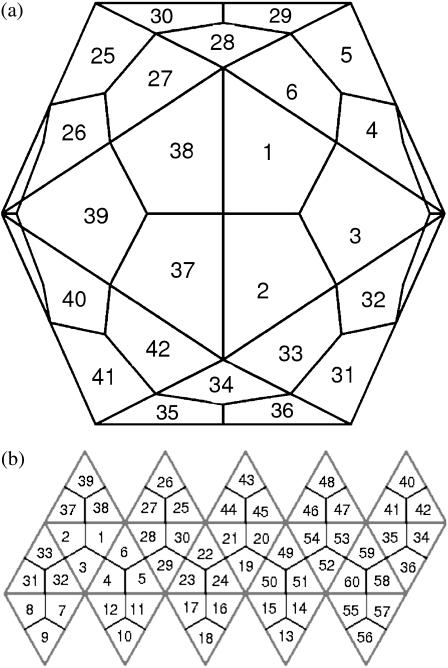
Another remarkable feature of viruses is that capsids are commonly quasi-spherical with icosahedral symmetry (1,2). Although other viral structures, such as cigar-shaped and partial sheets, are possible, we restrict our investigation to icosahedral capsids. Because encoding a large protein to envelop the whole genome is not physically realizable, identical copies of the same protein are used in a symmetric arrangement. Therefore, symmetry is used to economize the number of distinct proteins encoded in the viral genomes. This was formalized beautifully in the classic theory of quasi-equivalence (2,3), which broadly predicts the manner in which identical asymmetric protein units can be used to form a symmetric capsid. Quasi-equivalent viruses are characterized by their T-number, the number of proteins in each asymmetric unit (Fig. 1). This leads to icosahedral capsids with 60 T proteins, where geometrical constraints dictate that T = h2 + hk + k2, with h and k nonnegative integers. Clearly, viral capsids with larger T-values enclose a larger volume while maintaining icosahedral symmetry.
FIGURE 1.
The icosahedral geometry of a T = 1 capsid. (a) There are 60 symmetrically equivalent lattice positions, each one occupied by an asymmetric protein. For the 1stm virus, the protein positioned at 1 has bonds with those positioned at 2, 3, 6, 38, and 37 (but not with 4), with energies as shown in Table 1. (b) A flattened view of the icosahedron above.
The assembly of the capsid, a crucial step in the virus life cycle, could provide an opportunity to interfere with the process of virus replication (4). However, although there is a wealth of structural capsid data from x-ray crystallography and cryo-electron microscopy, the assembly pathways remain largely uncharted. It is known that inside the cell the capsid is assembled around the virus genome (DNA or RNA) with only limited or no assistance from other biomolecules (1). Even more remarkable, for some viruses self-assembly can take place in vitro, in the absence of the genome and outside the cellular environment, and still lead to stable capsids that are indistinguishable from those created in vivo. The role of the genome in the assembly process is not fully clarified and it may well be that in vivo and in vitro assemblies follow different routes (5).
Because detailed experimental data on assembly routes is at present difficult to obtain (5–9), modeling and simulation approaches have come to play an important role in the understanding of this process. In particular, one would like to identify the pathways by which the oligomers combine to form the final capsid and the factors that can influence the process. Previous theoretical work has approached different aspects of the assembly process using a variety of techniques: from dynamic to static models, both microscopic and macroscopic (4,6,10–19).
Ideally, a fully dynamic view of the assembly process could be achieved by performing molecular dynamics (MD) simulations with a full atomic description of the proteins in aqueous solution. However, the computational cost of full MD restricts its applicability to simplistic models of proteins—essentially, balls with sticky pods under Brownian motion. Schwartz et al. and Berger et al. (6,10) performed such a dynamical simulation of capsid formation, where they showed that the assembly can be completed using only local information in the incomplete capsid. Recently, Rapaport (11) has presented more realistic MD results that capture some of the salient features of a generic virus self-assembly process, but still lacking the necessary detail to investigate specific viruses.
Quantitative results for specific viruses can only be obtained through the use of a more detailed protein model. However, it is currently infeasible to simulate explicit dynamics of such a large ensemble of hydrated proteins due to the size and complexity of the units. This has led to microscopic approaches in which the partially completed capsid is investigated as it is assembled quasi-statically. The assumption here is that the relative positions (and thus, the interactions and energies) in the incomplete capsid are identical to those found in the complete capsid. However, this is itself a computationally hard problem due to the combinatorial number of assembly pathways. Horton and Lewis (12) were the first to use combinatorial optimization to find substructures with the most favorable association energies. This scheme was further extended by Reddy et al. (13) with a more refined method for calculating the energies. Beyond purely energetic considerations, structural concepts have been used to characterize protein assemblies: Sitharam and Agbandje-McKenna (14) have used combinatorial and computational algebra to create models based on static geometric and tensegrity constraints, while Hespenheide et al. (15) have investigated rigid protein assemblies as likely candidates to be long-lived.
Alternatively, other theoretical studies have concentrated on more macroscopic approaches. Some studies have focused on the static mechanical structure of the full capsid rather than the dynamics of the assembly (20–22). Recent work of Bruinsma et al. (23,24) (see also (5) for more qualitative ideas) is based on statistical mechanics calculations of free energies that take into account the curvature of the capsid. Finally, the macroscopic kinetic approach pursued by the group led by Zlotnick (4,16–18) (see also (19)) describes capsid assembly through empirical, law-of-mass-action differential equations for the concentration of the different oligomers. However, although the results can be related to bulk concentration measurements, this kinetic approach is still unable to provide information about microscopic pathways. In recent work, Endres et al. (25) have concluded that only a few out of the combinatorially many intermediates play any role and that these cannot be predicted by considering minimal energy configurations alone.
In this article, we develop a modeling framework that incorporates atomic detail of proteins into an explicit implementation of the kinetics of capsid assembly as a stochastic process. Our model starts from atomic descriptions of the protein oligomers, available from databases such as VIPER (26), and simplifies the representation through a reduction of the degrees of freedom based on graph rigidity measures with the aid of the software FIRST (27). These reduced oligomer descriptions are used to simulate stochastically the process of capsid formation, without allowing for malformed structures, through an extended Gillespie algorithm (28). Our scheme includes both diffusive association and dissociation reactions whose reaction rates are derived using the reduced graph representations. Although our algorithm does not implement dynamics explicitly, it provides the stochastic time evolution of the system and the quasi-steady oligomer distribution. This information can be analyzed to infer which pathways are important in the assembly of specific viruses and the role that protein structure and chemical environment play in the assembly process.
Reduced protein descriptions from full atomic models
To incorporate sufficient molecular detail, our computational framework starts from the detailed atomic structure of proteins as determined by crystallographic experiments. An invaluable resource is the database VIPER (26), which provides protein structures, transformation matrices, maps for adjacent proteins, and binding energies for a large number of viruses. This full atom description of the protein oligomers needs to be simplified to make it tractable for computational purposes. The basic physical idea underlying our simplified protein model is the assumption that rigid substructures will effectively move as a block. This implies a reduction in the number of degrees of freedom and, consequently, in the effective size of the problem.
The initial step is the addition of hydrogen atoms to the PDB structure using the software WHAT IF (29). We then characterize the full atom structure of each oligomer with FIRST, a computational tool for the analysis of proteins developed by Jacobs et al. (27). FIRST uses standard potentials to identify covalent and hydrogen bonds, salt bridges, and hydrophobic tethers in the structure, and represents the protein as a bond-bending network. This graph representation, where nodes are atoms and edges indicate constraints introduced by bonds, is then analyzed with a computationally efficient algorithm (the pebble game) to identify flexible (underconstrained) and rigid (overconstrained) regions (30). FIRST also calculates the energies for all the bonds in the protein network.
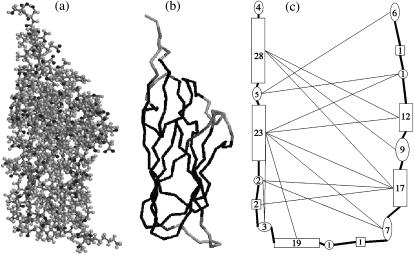
The output from FIRST can be used to produce a flexibility index Fi for each amino acid (27). When Fi ≤ 0, the amino acid is overconstrained, and therefore rigid; when Fi > 0, the amino acid is floppy (underconstrained). We then group adjacent residues with the same binary rigidity into rigid and floppy domains. As shown in Fig. 2, a protein typically consists of long, rigid domains separated by short, floppy hinge segments. It is important to point out that because graph rigidity is a nonlinear property, the rigidity of a protein may change as the aggregation proceeds, even though none of the atoms has moved relative to its neighbors. When two proteins bind, new constraints are added to the graph, usually leading to a more rigid network (see Fig. 3). The procedure outlined in this section amounts to a significant coarse-graining of the model: it starts from a full description (PDB file) with several thousand atomic coordinates for each protein and it outputs a representation consisting of a few rigid blocks (on the order of a few tens per monomer). It is this reduced representation (illustrated in Fig. 2) that we use to implement the stochastic kinetics of self-assembly.
FIGURE 2.
Coarse-grained description of the 1stm coat protein. (a) A view of the 1stm monomer created using RasMol (51). The protein consists of more than 4000 atoms in 157 amino acids. (b) The backbone of the 1stm protein. The gray scale represents rigidity as determined by the software FIRST with Ecut = −0.7 kcal/mol: dark means rigid and light means floppy (27). Adjacent amino acids with equal binary rigidity are grouped into rigid or floppy domains, leading to the typical pattern in capsid proteins: floppy ends and rigid domains separated by short floppy domains at the center. (c) Schematic representation of the domain structure in panel b. Here, rigid domains are drawn as rectangular vertices and floppy domains are drawn as ellipses. The numbers represent the number of amino acids in each domain. The thick lines represent the covalent bonds in the backbone while the thin lines are hydrogen bonds. Note that the domain structure is only needed for the dissociation rates—the association rates can be computed directly from the bond energies.
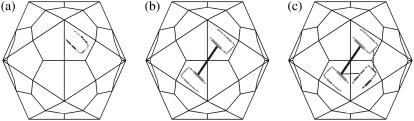
FIGURE 3.
Change of rigidity as the assembly proceeds. (a) In T = 1 viruses, each cell in the icosahedral lattice (Fig. 1) accommodates one protein: here we show a 1stm monomer in its reduced description, as in Fig. 2 c. As the assembly proceeds, the rigidity of every oligomer is recalculated with FIRST from the full atomic data. The existence of intermolecular hydrogen bonds in the 1stm dimer (b) and trimer (c) modifies the rigidity of the constitutive monomeric units.
Stochastic kinetics of capsid assembly
Studying the time evolution of the assembly process by integrating the equations of motion is computationally infeasible even for reduced representations like those described above. There are two main obstacles for the implementation of a fully dynamical approach: first, the combinatorial explosion of the number of intermediates for large aggregates of proteins—a problem that cannot be overcome by sheer computational power and that must be addressed at the modeling stage; and second, the lack of tested and rigorous coarse-grained potentials for explicit dynamics of reduced protein models, especially when diffusion plays a significant role. To circumvent these problems, we consider instead the stochastic kinetics of the assembly process through an extended version of Gillespie's stochastic algorithm in which we consider dissociation and association events modulated by diffusion.
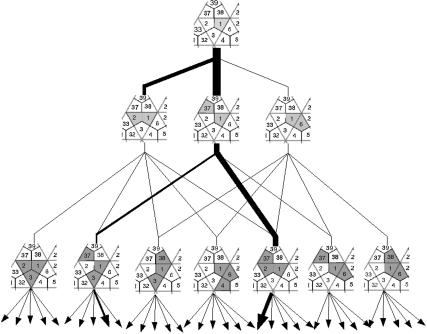
Gillespie's classic algorithm (28,31) was introduced in 1976 as a computational tool for the stochastic simulation of chemical reactions. Recently, Gillespie's algorithm has had a vigorous revival due to its relevance to many biological systems, where only small numbers of molecules are present. The theoretical basis for a stochastic formulation of chemical reactions is the chemical master equation which describes the probability that a given event (or no event) takes place over an infinitesimal time interval (32). Unfortunately, the master equation is not solvable explicitly for systems involving more than a few different molecules and reactions. Gillespie's algorithm addresses this numerically and provides an exact procedure for a Monte Carlo simulation of a system of reacting molecules. As is obvious in Fig. 4, the complexity of the pathways increases combinatorially with the size of the oligomers. The propensity of each reaction is a product of a combinatorial factor, dependent on the number of reactant molecules available for the reaction, and a rate constant, dependent on properties (such as size, velocity, and mass) of the molecules involved in the reaction (33).
FIGURE 4.
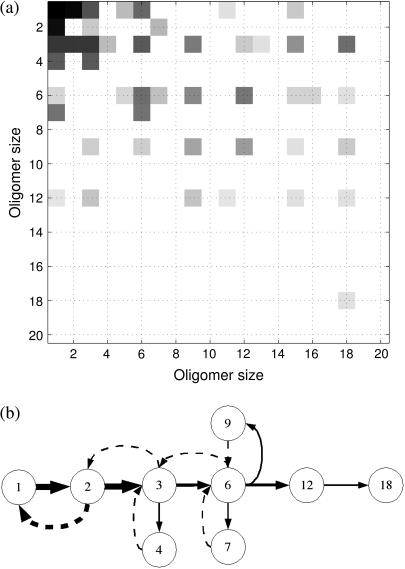
The combinatorial assembly tree of 1stm. A tree representing all the possible monomers, dimers, and trimers in the assembly of 1stm. The thin lines are possible assembly paths by the addition of one monomer at a time. The thick lines represent the pathways that are actually observed in the simulations (compare with Fig. 7). The number of possible pathways explodes combinatorially as the size of the oligomer grows.
Association events
During capsid assembly, there are association and dissociation events. The association events are elementary (bi-molecular) reactions in which two oligomers collide to form a new complex. The association process of structured molecules in solution can be modeled as a succession of two independent processes: first, two oligomers must meet through a diffusive process; next, they must overcome a barrier to aggregate and reach the final bound state (34,35). In its standard form, the Gillespie algorithm assumes that the reactants are dilute, perfectly mixed, structureless molecules in vacuum. This is obviously not a good approximation in our case, and we have extended the algorithm to take into account diffusion, the influence of water, and geometric and entropic factors. Our approach is simpler than the explicit stochastic simulation of the spatiotemporal reaction-diffusion process using computationally intensive voxel models (36,37), yet it captures the relevant physical features.
To account for the diffusive rate, we use concepts from Smoluchowski's theory of rapid coagulation (38). In its simplest form, this theory was developed for spherical colloidal particles and hence needs to be corrected when applied to protein aggregates with specific geometry and binding sites (34,39). It can be shown that the modified Smoluchowski rate is
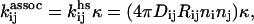 |
(1) |
where 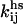 is the Smoluchowski diffusive rate for hard spheres. Here, ni and nj are the unit concentrations of particle types i and j, and the diffusivity
is the Smoluchowski diffusive rate for hard spheres. Here, ni and nj are the unit concentrations of particle types i and j, and the diffusivity 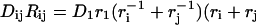 ) is related to D1 and r1, the diffusion coefficient and radius of the monomer, and to ri and rj, the radii of particle types i and j. Based on a simple geometric scaling argument valid for disk-shaped oligomers, it can be assumed that the radius increases as the square root of the number of monomers. The dimensionless parameter κ is a form factor, which reflects the probability that a collision between two oligomers will result in the formation of a complex. It accounts for the fact that the proteins will attach at a lower rate than homogenously sticky particles due to their geometry and specific binding sites. It can also be interpreted as a generic entropic barrier that needs to be surmounted for association (35).
) is related to D1 and r1, the diffusion coefficient and radius of the monomer, and to ri and rj, the radii of particle types i and j. Based on a simple geometric scaling argument valid for disk-shaped oligomers, it can be assumed that the radius increases as the square root of the number of monomers. The dimensionless parameter κ is a form factor, which reflects the probability that a collision between two oligomers will result in the formation of a complex. It accounts for the fact that the proteins will attach at a lower rate than homogenously sticky particles due to their geometry and specific binding sites. It can also be interpreted as a generic entropic barrier that needs to be surmounted for association (35).
The aggregation of oligomers can occur in a number of different ways with different association energies 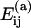 for the specific pairings (see Table 1). When forming a new oligomer we assume the proteins to be at the positions that they attain in the complete capsid. This means that our model does not account for malformed capsids. Neither does it include the maturation or conformational changes that are known to occur in some viruses. To model the fact that oligomers with large negative association energies are more likely to be formed, we multiply the rate in Eq. 1 by a Boltzmann factor exp(
for the specific pairings (see Table 1). When forming a new oligomer we assume the proteins to be at the positions that they attain in the complete capsid. This means that our model does not account for malformed capsids. Neither does it include the maturation or conformational changes that are known to occur in some viruses. To model the fact that oligomers with large negative association energies are more likely to be formed, we multiply the rate in Eq. 1 by a Boltzmann factor exp(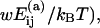 where kB is the Boltzmann constant, T is the temperature, and
where kB is the Boltzmann constant, T is the temperature, and 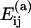 is the association energy. The association energy is modified to include the effect of water shielding. Because the protein is surrounded by water, the effective energy of interprotein hydrogen bonds is reduced, since there exists the alternative of forming bonds with water molecules instead. It is important to note that both the form factor κ and the water-shielding factor w can be estimated from experiments or molecular dynamics simulations (34,40,41).
is the association energy. The association energy is modified to include the effect of water shielding. Because the protein is surrounded by water, the effective energy of interprotein hydrogen bonds is reduced, since there exists the alternative of forming bonds with water molecules instead. It is important to note that both the form factor κ and the water-shielding factor w can be estimated from experiments or molecular dynamics simulations (34,40,41).
TABLE 1.
Association energies from FIRST and VIPER
| Interface | Symmetry |
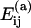 VIPER (kcal/mol) VIPER (kcal/mol) |
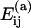 FIRST (kcal/mol) FIRST (kcal/mol) |
|---|---|---|---|
| 1–6 | Quasi-fivefold | −21.0 | −9.0 |
| 1–38 | Quasi-fivefold | −21.0 | −9.0 |
| 1–37 | Quasi-twofold | −29.0 | −48.7 |
| 1–2 | Quasi-threefold | −33.0 | −24.7 |
| 1–3 | Quasi-threefold | −33.0 | −24.7 |
A comparison of the association energies for the Satellite Panicum Mosaic Virus (SPMV, PDB code 1stm) computed using VIPER 26 and with FIRST with Ecut = −0.7 kcal/mol. The interfaces are shown in Fig. 1 a. Note that in the simulations these energies are multiplied by the water shielding factor w = 0.17 to account for protein hydration.
The energies can be obtained from different sources but, for simplicity, we have used throughout this article the energies as calculated by FIRST. We remark, however, that our algorithm is modular and more sophisticated energy calculations could be easily incorporated into our computational framework, e.g., CHARMM energies from VIPER (26,42). For completeness, we have carried out a comparison between the association energies from FIRST and VIPER. We have checked that although the energies can differ significantly in absolute numbers (as shown in Table 1), both the ordering of the bond strengths and the localization of the bonds are broadly consistent between FIRST and VIPER.
Dissociation events
In addition to aggregating, oligomers can also break up into smaller units with a dissociation rate, which is an indication of the longevity of an oligomer. The propensity of a dissociation event depends on the energy required to break the bonds that hold the oligomer together, but is also related to the redistribution of energy into the internal modes of the oligomer. It is in this context that our reduced description of protein oligomers becomes most helpful.
We base our modeling of the dissociation process on transition-state theory as applied to the escape from a multidimensional well. In this framework, the escape rate from a well with N vibrational degrees of freedom is given by (43)
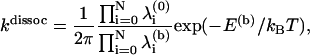 |
(2) |
where 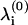 are the eigen-frequencies at the bottom of the well and
are the eigen-frequencies at the bottom of the well and 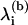 are the eigen-frequencies when the particle is at the point of escape (i.e., at the top of the barrier of height E(b)). The generic Eq. 2 can be related to the reduced protein model introduced in the previous section. If we view the oligomer as a harmonic network, where each domain is treated as a point mass and the bonds connecting domains as linear springs, then the original oligomer represents a local minimum in the energy landscape and escape from this well represents the physical process of splitting the oligomer.
are the eigen-frequencies when the particle is at the point of escape (i.e., at the top of the barrier of height E(b)). The generic Eq. 2 can be related to the reduced protein model introduced in the previous section. If we view the oligomer as a harmonic network, where each domain is treated as a point mass and the bonds connecting domains as linear springs, then the original oligomer represents a local minimum in the energy landscape and escape from this well represents the physical process of splitting the oligomer.
The eigen-frequencies of the system at equilibrium, 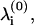 are obtained by diagonalizing the system
are obtained by diagonalizing the system 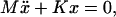 where M is the diagonal matrix of domain masses and K is the weighted Laplacian matrix of the graph. Each weight Kij is the stiffness of the bond-connecting domain i and j obtained from Hooke's law,
where M is the diagonal matrix of domain masses and K is the weighted Laplacian matrix of the graph. Each weight Kij is the stiffness of the bond-connecting domain i and j obtained from Hooke's law, 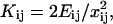 with Eij being the energy of the bond and xij the equilibrium distance of the bond. The diagonal elements of the stiffness matrix, Kii, are given by the condition that the sum of the elements in each row is zero. In our reduced network, there are two types of bonds to be included in the analysis: hydrogen bonds and covalent bonds. The energies are provided by FIRST: hydrogen bonds are of the order of −5 kcal/mol once they have been multiplied by the water-shielding prefactor w, and we assume the covalent bonds to be −74 kcal/mol, a value close to the typical energies of C–N and C–C bonds. (Note that this energy is not multiplied by w, since there is no option for the covalent bonds to form bonds with the surrounding water molecules.) If two domains are linked by both hydrogen bonds and covalent bonds, only covalent bonds are considered since they are an order-of-magnitude stronger.
with Eij being the energy of the bond and xij the equilibrium distance of the bond. The diagonal elements of the stiffness matrix, Kii, are given by the condition that the sum of the elements in each row is zero. In our reduced network, there are two types of bonds to be included in the analysis: hydrogen bonds and covalent bonds. The energies are provided by FIRST: hydrogen bonds are of the order of −5 kcal/mol once they have been multiplied by the water-shielding prefactor w, and we assume the covalent bonds to be −74 kcal/mol, a value close to the typical energies of C–N and C–C bonds. (Note that this energy is not multiplied by w, since there is no option for the covalent bonds to form bonds with the surrounding water molecules.) If two domains are linked by both hydrogen bonds and covalent bonds, only covalent bonds are considered since they are an order-of-magnitude stronger.
To obtain the dissociation rate in Eq. 2 for a given split, we first calculate the eigen-frequencies of the original system 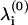 via the generalized eigen-value problem of the unmodified network. The eigen-values of the system at the barrier,
via the generalized eigen-value problem of the unmodified network. The eigen-values of the system at the barrier, 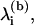 and the barrier height, E(b), are obtained by examining the possible partitions of the graph. A given partition is characterized by the minimal set of edges that is required to split it into two subgraphs. The total energy of the removed edges is equal to E(b) and the
and the barrier height, E(b), are obtained by examining the possible partitions of the graph. A given partition is characterized by the minimal set of edges that is required to split it into two subgraphs. The total energy of the removed edges is equal to E(b) and the 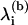 are obtained as the generalized eigen-values of the partitioned graph. Indeed, when the graph is partitioned, one eigen-value becomes zero, which explains why the numerator and denominator do not run over the same indices. For most oligomers, the most favorable splits have an eigen-mode ratio of ∼10−2, although this ratio can be up to five orders-of-magnitude larger in some cases. Similarly to the association events, each split is then considered within our Gillespie algorithm as an independent event with its own characteristic propensity, with rate kdissoc given by Eq. 2.
are obtained as the generalized eigen-values of the partitioned graph. Indeed, when the graph is partitioned, one eigen-value becomes zero, which explains why the numerator and denominator do not run over the same indices. For most oligomers, the most favorable splits have an eigen-mode ratio of ∼10−2, although this ratio can be up to five orders-of-magnitude larger in some cases. Similarly to the association events, each split is then considered within our Gillespie algorithm as an independent event with its own characteristic propensity, with rate kdissoc given by Eq. 2.
Clearly, there are many ways of splitting an oligomer. For example, the trimer in Fig. 3 c can split in three different ways with different propensities. Since the total number of possible splits grows combinatorially with the number of domains in the oligomer, we have reduced the complexity by imposing two constraints on the partitions: only hydrogen bonds are allowed to break, and only bipartitions (i.e., splits into two fragments) are considered. The latter is not an extreme assumption, as splits resulting in more fragments can be composed of a number of subsequent bipartitions. Under these restrictions, and due to the sparsity of the intermonomer connections in the icosahedral lattice, the number of partitions grows subexponentially—the exact rate depending on the topology of the oligomer. The eigen-value calculation for the dissociation events is the most time-consuming step in our simulations. To speed up the calculations, we have devised a data structure that stores the results of known events for use in subsequent runs.
Results of the simulations
Our modeling framework is generic and can be applied to any icosahedral virus. In this section, we illustrate the output of the current version of the program with two small plant viruses: the T = 1 virus, Satellite Panicum Mosaic Virus (SPMV, PDB code: 1stm) and the T = 3 virus, Southern Bean Mosaic Virus (SBMV, PDB code: 4sbv). Interestingly, SBMV is known to be capable of self-assembly in vitro (44), whereas SPMV is not. Before we present some numerics, we make two technical points regarding the simulations.
One advantage of our computational model is that it has relatively few, physically meaningful parameters. Table 2 presents a summary of the parameters:
The temperature and concentration.
The average radius and diffusion coefficient of a monomer in order to calculate the diffusion rate in Eq. 1.
The bond constants used to derive the eigen-frequencies for the dissociation rate in Eq. 2.
TABLE 2.
Parameter values for the simulations
| Parameter | Value | Units |
|---|---|---|
| Temperature, T | 300 | K |
| Initial monomer concentration, C | 5 | μM |
| Monomer diffusion coefficient, D1 | 0.1 | nm2/s |
| Monomer radius, r1 | 1 | nm |
| Covalent bond strength | −74 | kcal/mol |
| Covalent bond length | 1.5 | Å |
| Hydrogen bond length | 3 | Å |
| H-bond effective strength, w | 0.17 | — |
| FIRST cutoff energy, Ecut | −0.7 | kcal/mol |
All these quantities are directly related to physical variables. There are three additional parameters that, although physically motivated, are of a more conceptual nature. First, Ecut is an input parameter for the software FIRST that specifies the cutoff energy for a hydrogen bond to exist. This can be loosely related to temperature and under standard conditions it is ∼−0.7 kcal/mol (27). Second, the fact that proteins are surrounded by water means that the effective strength of the hydrogen bonds is reduced by a factor w, which has been estimated to be 10–25% using detailed MD calculations (41). This parameter is related to pH and to the ionic strength of the solution. Third, the form factor κ used in the modified Smoluchowski equation (Eq. 1) has been estimated to be in the range 10−3–10−5 through computer simulations of diffusing proteins (34, 40). This parameter is related to the specific geometry and docking of the oligomers.
The second technical point refers to size limitations in the software used. Our current implementation uses version 3.1 of the software FIRST, which is limited to analyzing protein structures with a maximum of 75,000 atoms (27). This limitation is not intrinsic to the method (only to version 3.1) and future releases will extend its capabilities. This effectively means that, at present, we do not investigate dissociation paths for oligomers larger than 20 proteins even if the computations are fast. Therefore, our full simulations (including both association and dissociation propensities) are run up to the formation of oligomers of size 20. However, we will also present simulations of the completion of the full capsid obtained from runs with association paths alone, which do not rely on the use of FIRST.
The starting point for the simulations is a state where all proteins are present as monomers. The system then evolves toward aggregation into larger units. There is an initial transient during which a large amount of reactions involving monomers take place. Relatively quickly, the concentration of a few key oligomers builds up and the system then settles into a quasi-steady state, in which the concentration of the different oligomers remains relatively constant—except, of course, for monomers and completed capsids (size larger than 20). Effectively, monomers are transformed into capsids via restricted pathways that do not alter significantly the average concentrations of the intermediates. We explore and characterize this cascading process in what follows.
The quasi-steady solution
We first illustrate some of the results through the analysis of the quasi-steady state in the assembly of the T = 1 SPMV virus (1stm). Each simulation starts with 1000 monomers. To eliminate the transient, we do not collect statistics until the first oligomer of size larger than 20 is formed. At this point, we consider the system past the transient state, we remove the large oligomer and we record the time-weighted concentration average of all oligomers until the next >20-mer is formed. We repeat this procedure 1000 times and average the results, which are presented in Fig. 5. It is important to note that we have also run simulations where, starting from an empty system, we add monomers at a constant rate and remove oligomers larger than size 20. Once this open system reaches a quasi-steady state, we have checked that it behaves in the same way on average as the one starting from a fixed number of monomers.
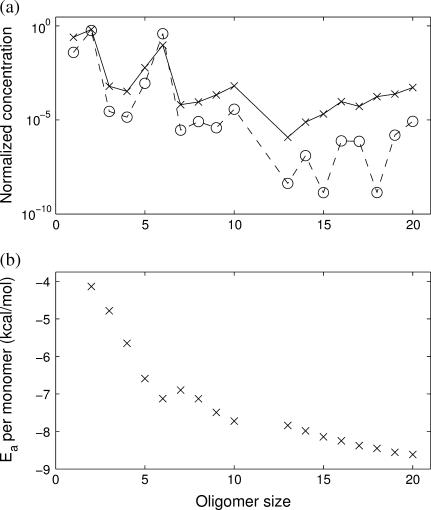
FIGURE 5.
Simulations of the quasi-stationary state of 1stm lumped by oligomer size. (a) Average time-weighted concentration of the different oligomer sizes obtained in the Gillespie simulation (crosses). The solid line is a guide to the eye. Note the high concentration of dimers and hexamers. The circles (and dashed line) show the prediction from the quasi-stationary Markov process (Eq. 3), which shows good agreement with the simulation. (b) Average time-weighted association energy per monomer of the different oligomer sizes. The error bars are hardly visible, indicating that all different conformations of a given size have almost identical association energies. Hexamers lie at a local minimum, a clear signal that they are stable oligomers, relatively more favorable than heptamers and octamers. Note the missing data points for size 11, as no 11-mers are observed in the simulations.
Inspecting the simulations, we find that there are very few distinct oligomers with a significant presence throughout the process (Fig. 5). Only monomers, dimers, and hexamers are present in any significant concentration during the formation of the capsid. The concentrations of all other oligomers are negligible. A similar conclusion was also reached by Endres et al. (25). Interestingly, this is not just the result of the difference in the association energies; Fig. 5 shows that all oligomers have similar association energies (per monomer).
The simulation data also yield information about the processes governing the kinetics of the system. Oligomers larger than hexamers are quite rare and as soon as one is created it tends to participate in a series of rapid reactions leading to a >20-oligomer. This cascading behavior emerges because large intermediates tend to follow from favorable association energies and also tend to be stable with respect to dissociation. This view of the assembly as a cascading process is in good agreement with other dynamical simulations (11,16).
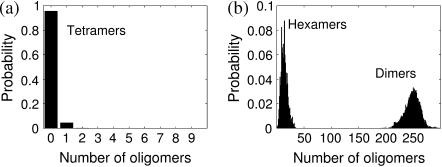
Oligomers with a significant concentration (monomers, dimers, and hexamers) tend to fluctuate around a mean value. On the other hand, oligomers with negligible concentrations are not present most of the time and they react and disappear quickly when present. These two types of behavior are illustrated in Fig. 6 where we plot the average probability distributions of the concentration of dimers, tetramers, and hexamers at quasi-steady state. The distribution of dimers is Gaussian-like around a high concentration, whereas tetramers show the characteristics of a Poisson-like distribution. Hexamers display less clear features. Indeed, although all the underlying elementary stochastic processes of aggregation and dissociation are Markovian, the structure of the kinetic network leads to a variety of quasi-steady distributions for the different intermediates. In Discussion and Conclusions, we provide a simple theoretical argument of how these distinct behaviors emerge.
FIGURE 6.
Different concentration distributions in the simulations of the 1stm assembly. (a) Most oligomers are present at very low concentrations with Poisson-like distributions as exemplified by the 1stm tetramers. This means that low concentration is connected with short persistence. (b) A few oligomers have significant concentrations at all times in the quasi-steady state, such as the 1stm dimers and hexamers shown. Their distributions have Gaussian-like characteristics. Although there are three distinct 1stm dimers, almost all dimers in the simulation are of the most energetically favorable type (the one circled in Fig. 7).
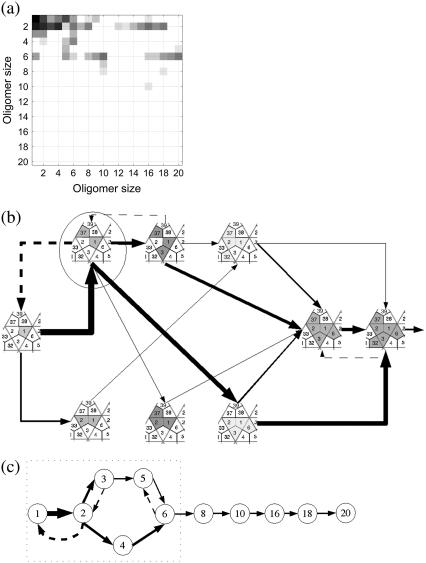
The simulations of the assembly of 1stm can be used to extract further details about the pathways in use in the network of reactions. To make this more explicit, we calculate the average transition probability of association and dissociation events as derived from the numerics. These probabilities form a transition matrix, which we present in Fig. 7 a as a heat map. The upper triangular section of the matrix corresponds to association processes while the lower triangular section corresponds to dissociation reactions. Note that virtually all the dissociation events are confined to the small oligomers. One of the reasons that small oligomers are easier to split is that they have fewer intermonomer bonds per protein. This can be understood from Eq. 2, where the Boltzmann factor has a large impact on the dissociation rate.
FIGURE 7.
Stochastic sampling of the assembly pathways for 1stm with κ = 10−4. (a) The heat map illustrates the observed frequency of the reactions in the assembly: open squares indicate no reactions involving the two sizes, while darker shades indicate many reactions of that type. Reactions above the diagonal represent associations (Mi + Mj → Mk, where k = i + j), while reactions below the diagonal correspond to dissociations (Mk → Mi + Mj, with k = i + j). For example, the (1, 1) square in the top left corner represents a monomer-plus-monomer association reaction, and the square to the right (1, 2) is the association of monomer plus dimer. Meanwhile, the (2, 1) square represents dimers splitting into two monomers. (b) Using the heat map in panel a, we represent the most common oligomers of size 6 or less and the transitions between them. Dashed arrows represent dissociation reactions. Only reactions with a frequency above a given threshold are represented. The thickness of the arrows is proportional to the logarithm of the frequency of the reaction, which means that the vast majority of the reactions involve forming or breaking up oligomers of size 6 or smaller. The majority of reactions in the system merge monomers to form dimers. Most hexamers are formed by merging three dimers. But there is also a second pathway where a trimer and a dimer form a pentamer that later adds a monomer to complete the hexamer. (c) A lumped, schematic representation of the pathways in panel b (inside the dotted rectangle) showing also the higher steps of the cascade.
Using these data, we show in Fig. 7, b and c, that the assembly proceeds via a few pathways that thread through the combinatorially complex association/dissociation tree shown in Fig. 4. These reactions lead to significant quasi-steady concentrations only for monomers, dimers, hexamers, 10-mers, 16-mers, and 20-mers. A mere inspection of the binding energies before the simulations would not lead to this outcome, although it can be understood, a posteriori, in terms of the properties of the oligomers. For instance, almost all the 1stm dimers formed correspond to the dimer circled in Fig. 7 b, which has a bond with twofold icosahedral symmetry in the full capsid (see Fig. 1 and Table 1). Since the other bonds involved in dimers are significantly weaker, there will hardly be any other dimers present. The predominance of this dimer has consequences: the dominant hexamer can, in turn, be viewed as a combination of three of the twofold symmetrical dimers bound by the weaker threefold symmetrical bonds. One of the conclusions of the stochastic simulations is that predicting the prevalent intermediaries cannot be based on energetic considerations alone. It is possible that stable and favorable intermediates, as determined by the static analysis, are never reached because the necessary kinetic steps are not accessible.
A key idea behind our method is to study how chemical properties at the molecular level (as recorded in the protein atomic structure) lead to differences in the assembly path. To illustrate how our computational framework can help explore these connections, we analyze the assembly of the T = 3 virus SBMV (4sbv) in direct comparison to the results obtained above for the T = 1 virus SPMV (1stm): Fig. 8 shows the quasi-steady time-averaged concentrations and association energies for all the oligomer sizes, whereas Fig. 9 presents the heat map of transitions and the relevant pathways of assembly. The results are averaged over 1000 runs of the quasi-steady formation of a >20-mer, as before.
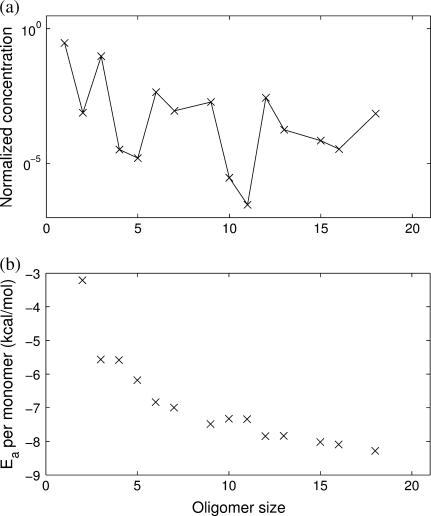
FIGURE 8.
Simulations of the quasi-stationary state of 4sbv lumped by oligomer size. (a) Average time-weighted concentration of the different oligomer sizes. There are peaks for trimers, hexamers, and other multiples of 3, indicating that the trimer is an important building block in the assembly. Compare with 1stm in Fig. 5. (b) Average time-weighted association energy per monomer of the different oligomer sizes. The error bars are hardly visible, because all different conformations of a given size have almost identical association energies. Oligomers formed by multiples of 3 tend to occupy local minima of the energy, a hint of their enhanced stability. Note the missing data points for sizes 8, 14, 17, 19, and 20 since these oligomers are never observed in the simulations.
FIGURE 9.
Stochastic sampling of the assembly pathways for 4sbv with κ = 2 × 10−5 × (a) The heat map shows the frequency of the reactions taking place. Note how the pattern differs from that of 1stm (Figs. 7 and 11). There is a variety of large oligomers present at any given time in the system and the cascading behavior is less pronounced. The checkerboard pattern indicates that reactions involving multiple-trimer oligomers are the most common. (b) A schematic view of the most common reactions for 4sbv deduced from the heat map in panel a. Again, note the differences with the assembly of 1stm (Fig. 7).
The average concentrations, association energies, and heat maps of 4sbv reveal that trimers, hexamers, 9-mers (and, in general, all multiples of three) have local maxima in the concentration plot and corresponding local minima in the association energy plot. This is also visible in the heat map as a checkerboard pattern. In this case, and contrary to 1stm, trimers are the effective units in the assembly of 4sbv, in agreement with Reddy et al. (13) and expected not only for reasons of symmetry, but also from considering the bond energies. Interestingly, Reddy et al. (13) conjecture that the symmetric 15-mer will be the most stable oligomer. Although the analysis with FIRST indicates that this oligomer is favorable both in terms of association energies and of dissociation propensity, we find no evidence of significantly higher concentration than for other large oligomers. This could mean that although stable, this oligomer might not be kinetically easy to access. However, it is also possible that this is a result of our evaluation of the energies with FIRST, as opposed to the use of energies from VIPER.
Comparing the quasi-steady concentrations of 1stm and 4sbv in Figs. 5 and 8, it is clear that the concentration of monomers is significantly higher for 4sbv. Moreover, from the heat map (Fig. 9) it is evident that there are more reactions involving large oligomers. The cascading behavior is therefore less pronounced for 4sbv than for 1stm, as it is less rare to find two large oligomers present at the same time in the solution. This behavior stems from the fact that the bonds in the symmetric 4sbv trimer are significantly stronger than the bonds linking the trimers. Thus, it is less favorable for a large 4sbv oligomer to react than it is for a large 1stm oligomer. This is also reflected in the heat map: since large oligomers react more slowly, there will be more dissociation events (i.e., shaded squares below the diagonal in Fig. 9 a) involving large oligomers for 4sbv.
The formation of the full capsid
Up to now, we have focused on the properties of the quasi-steady state, where we assume that the supply of monomers is constant and the cascading process of assembly leads to a stable output of capsids. We will now examine the kinetics of formation of a full icosahedral capsid from a finite amount of monomers.
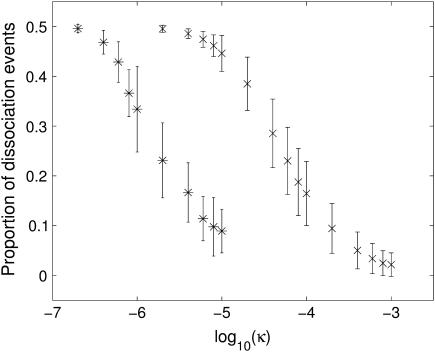
As explained above, our dissociation calculations have an upper limit of 20-mers, due to the use of Vers. 3.1 of the software FIRST. However, the cascading behavior described above for the 1stm virus implies that, once large oligomers are formed, it is unlikely that they will split and thus the dissociation paths might be ignored without much change in the observed behavior. We have explored this idea in more detail by studying the sensitivity of the stochastic kinetics to the form factor κ, which modulates the balance between the association and dissociation pathways. Increasing κ increases all association rates, which implies that the dissociation events will become less likely. Fig. 10 shows the ratio between the number of dissociation events and the total number of events in the assembly of 1stm as a function of κ. For low κ there are almost as many dissociation as association events, and the assembly proceeds very slowly or not at all. In this regime, a dimer will almost immediately be broken up once it has formed and the assembly process is never able to get started. As κ increases, there is a relatively sharp drop in the number of dissociation events. Eventually, the number of dissociation events becomes negligible and the assembly process proceeds almost exclusively by association.
FIGURE 10.
Impact of the form factor κ on the speed of assembly. The figure shows the average proportion of dissociation events for 1stm (×) and 4sbv (*) calculated over 350 independent runs, with the standard deviation indicated by the error bars. As κ increases (making the association more likely), the proportion of dissociation events decays from 0.5 toward zero. Therefore, κ is directly related to the overall speed at which the assembly proceeds. If κ is small, the cascading process is not initiated and the assembly stalls. Clearly, detailed models for the calculation of the form factor κ would be of importance. Note the different κ-values at which both viruses would start to assemble, which is reminiscent of their proclivity to self-assembly in vitro.
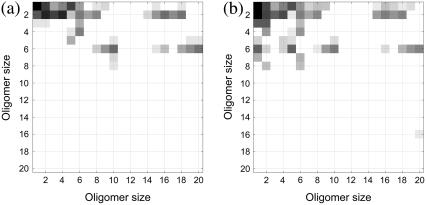
Fig. 11 shows the quasi-steady concentrations and the reaction pathways that appear in the assembly of 1stm for different values of the form factor κ. The key feature of these simulations, however, is that the same types of reactions occur for all values of κ; that is, the main pathways remain unchanged even if there are many dissociation events. Under the current setup for this virus, dissociation appears to slow the progress of aggregation by splitting small oligomers but it does not prompt the assembly to proceed through alternative pathways.
FIGURE 11.
Impact of the form factor κ on the pathways of assembly. Heat maps depicting the pattern of reactions for 1stm with (a) κ = 10−3 and (b) κ = 10−5. As compared to Fig. 7, note that the overall cascading pattern of reactions and pathways remains broadly unchanged. In panel a, larger κ means that there are fewer dissociation events, i.e., fewer dark squares below the diagonal (see Fig. 10). In panel b, smaller κ means more dissociation events, but the pattern of association for the larger oligomers is similar for all three 1stm heat maps.
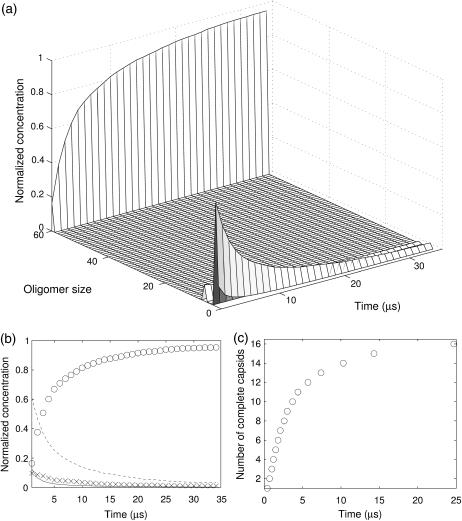
A direct consequence of the particular kinetics of 1stm is that forward (association) reactions are qualitatively similar for a range of values of κ . If the value of κ is relatively high, the rare dissociation events can be neglected. We can then run simulations with association paths alone (no longer capped by the size limit in FIRST) that lead to the explicit formation of complete capsids. In Fig. 12, a and b, we show the concentration of the oligomers over time after the transient has been removed for κ = 10−3. As expected, only monomers, dimers, hexamers, and full capsids have any significant presence, whereas all other intermediate oligomers do not appear in any persistent way. We also show in Fig. 12 c that the rate of capsid formation saturates as the concentration of monomers decreases. The overall shape of this curve is in good agreement with experiments and other theoretical models (16,17). If we consider the almost linear section at the outset, we can derive an approximate capsid formation rate of 1.5 × 10−4 M s−1, which is of the same order of magnitude as the model by Endres and Zlotnick (16).
FIGURE 12.
Kinetics of the completion of the full capsid for 1stm. (a) Average concentration of all oligomer sizes as a function of time. At t = 0 all proteins are monomers and they rapidly react to form larger oligomers. The most conspicuous feature of the distribution is that there are very few oligomers of intermediate sizes. (b) Concentration of the most common oligomers: 1- (solid line), 2- (dashed line), 6- (×), and 60-mers (○) as a function of time. All other oligomers have negligible concentrations. (c) Time for the completion of SPMV capsids with κ = 10−3. For this value of κ, the number of dissociation events is almost negligible, as shown in Fig. 10.
As a final comment, it is interesting to note that 4sbv (SBMV) can form capsids at significantly lower κ-values than 1stm (SPMV), as seen in Fig. 10. This conclusion cannot be drawn easily from the association energies alone: the most favorable 1stm dimer and 4sbv dimer have association energies of −48 and −38 kcal/mol, respectively. However, when a 4sbv dimer is formed, a favorable reaction to form a symmetric trimer tends to follow immediately. On the other hand, despite their higher binding energy, the 1stm dimers have no such favorable aggregation pathway to form a stable large oligomer.
DISCUSSION AND CONCLUSIONS
Understanding the quasi-steady solution as a Markov process
Our Gillespie simulation of the kinetics of the network has shown that although the full assembly tree (Fig. 4) is extremely complex, only a few pathways are crucial for the assembly. In other words, our extended Gillespie algorithm provides us with a stochastic sampling of the reaction network, unknown a priori, which leads to an estimate of the transition probabilities in the system.
We can use the estimated transition matrix (represented in Figs. 7 a and 9 a as heat maps), to investigate the description of the reaction network as a nonhomogeneous Markov process. To check the consistency of the quasi-steady solution obtained numerically in Figs. 5 and 8, we apply the results of Darroch and Seneta (45) for quasi-stationary Markov processes taking the stoichiometry into consideration (46). The system is only quasi-stationary, because ultimately there is an absorbing state where all monomers are part of completed capsids. However, in the transient state, the quasi-stationary distribution (QSD) can be calculated as the fixed point π* of the equation
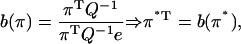 |
(3) |
where π is the distribution of concentrations, e is the vector of ones, and Q is the transition rate matrix as derived from the simulations (47). There are two interpretations of the QSD (45): it can be viewed as a conditional stationary distribution (i.e., the stationary distribution provided that the Markov process is in the transient), or as the expected time spent in each state divided by the total time to absorption. Fig. 5 a shows that the QSD π* is close to the average empirical distribution π from the simulations. The transition rate matrix derived using the stochastic sampling is therefore consistent with the observed quasi-steady distribution under the assumption of a nonhomogeneous semi-Markov process. This description also provides us insight into why some oligomers have a Gaussian-like distribution while others present Poisson-like features. In a system where the total number of monomers is fixed, the (quasi) stationary distribution will be multinomial (48). In the limit of large N and small πi, the distribution of oligomer i can be approximated by a Poisson distribution. For large N and intermediate πi, the Gaussian distribution is a good approximation.
Explaining the probabilistic features of the cascading behavior
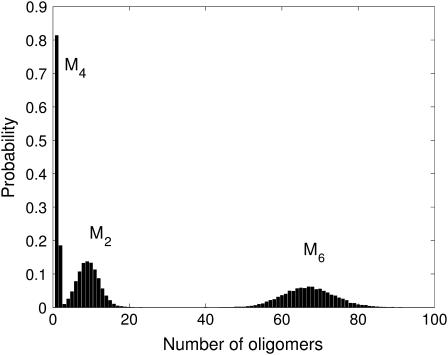
In the cascading process, a few oligomers are relatively long-lived while all other oligomers survive for only very short times before reacting. The existence of Gaussian-like and Poisson-like distributions is related to this cascading process and can be understood through a simplified kinetic model. Consider a toy model of the early stages of aggregation of 1stm consisting of three oligomers (M2, M4, and M6), which can be thought of as analogs of the dimers, tetramers, and hexamers, respectively:
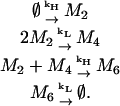 |
(4) |
The first and last reactions correspond to creation from a source and decay to a sink and there are two reaction rates, kH ≫ kL. We simulate this system using the Gillespie algorithm. The resulting stationary distributions, shown in Fig. 13, present similar characteristics to those discussed in the 1stm assembly process (see Fig. 6). This can be understood as follows: the creation rate of the dimers M2 is much higher than the rate at which they are consumed, leading to a Gaussian steady state, as predicted by the linear noise approximation of van Kampen (32,49). On the other hand, the tetramers M4 have a low creation rate and there are always dimers available with which they can react at a high rate. This leads to a Poisson-like distribution for the tetramers. Finally, tetramers disappear quickly to create hexamers M6, which decay at a very low rate and thus have a Gaussian-like distribution.
FIGURE 13.
Different oligomer distributions in a simple cascading system. The simple cascading reaction Eq. 4 involves only three different types of oligomers: dimers (M2), tetramers (M4), and hexamers (M6). In the quasi-steady state, dimers and hexamers have Gaussian-like distributions, while the distribution of tetramers is Poisson-like (compare with Fig. 6).
Summary and future work
This article presents a modular framework for the study of the stochastic kinetics of viral capsid assembly. The calculations are based on structural crystallographic protein data and use rigidity analysis to produce a reduced mechanical description of the protein oligomers. Rates for association and dissociation reactions based on the protein descriptions are then used within an extended Gillespie algorithm to explore the kinetics of capsid assembly.
Because of its biophysical motivation, our model has relatively few parameters and most of them are directly related to physical variables: temperature, concentration, diffusion coefficients, protein radius, covalent bond energies, and bond lengths. We have checked the dependence of our simulations on these physical variables. For instance, if the temperature is increased, dissociation events will become more likely and the overall rate of assembly will drop. In addition, the relative difference in association energies between oligomers decreases. This means that the population of oligomers will become more varied and more reaction pathways will become important; that is, as the temperature increases, the assembly tree will be explored more homogeneously. Similarly, lowering the concentration decreases the association rate. If the concentration is too low, the dissociation events become prevalent and there will be no assembly. However, the characteristics of the assembly pathways are unchanged by concentration.
There are three additional parameters (Ecut, κ, and w) that have physical meaning and motivation, but are not easily related to a single physical variable. We have discussed in depth the effect of the form factor κ in the preceding sections. In addition, we have checked that the results of our analysis do not depend qualitatively on the cutoff energy Ecut or the water-shielding constant w. Increasing the cutoff energy for hydrogen bonds in FIRST reduces the number of hydrogen bonds in the system. This produces the same overall effect as increasing the temperature since all energies in the system are lowered. It also leads to floppier proteins with a higher eigen-ratio in Eq. 2, and thus more dissociation events. Increasing the water-shielding w means stronger hydrogen bonds, which is equivalent to lowering the temperature. The assembly will thus proceed along low energy pathways, with a small variety of oligomers and a reduced number of dissociation events. This discussion indicates that changes in both Ecut and w can be qualitatively understood as an effective change of temperature. Note, however, that the effect of the form factor κ is different. Physically, the increase of κ is equivalent to lowering the barrier for two oligomers to form a larger oligomer with no influence on the dissociation process. Therefore, the likelihood of the dissociation events is reduced and the assembly is sped up.
A key feature of the proposed framework is that it is both modular and extensible, i.e., the algorithms that make up the different components of the model can be exchanged seamlessly at different levels. A number of refinements to the model should be pursued to improve the oversimplifications of this initial work. Indeed, the bond energies could be calculated more precisely using more detailed potentials. This can have far-reaching implications for the pathways and intermediates deduced from the simulations and a variety of energy calculations should be explored carefully when dealing with specific viruses (50). A key ingredient of the protein model is the derivation of a reduced representation from the full PDB data. In this work, we have used FIRST for protein partitioning as a conceptual tool based on ideas from graph rigidity. However, one could use methods based on normal modes (full atom, elastic, or Gaussian models) or principal component analysis to obtain coarse-grained representations of proteins. Another important set of refinements should concentrate on the description of the association process. In particular, a more sophisticated model of the protein docking, including its entropic aspects, would be necessary to improve the physical realism of the form factor κ. Moreover, it would be important to refine the association rates to parallel more closely the kinetics of chemical assembly. The dissociation model itself could also be improved by taking explicitly into account entropic features and incorporating the geometric content of the graph when computing the eigen-frequencies. Finally, it would be important (although nontrivial) to extend our model to allow for nonicosahedral symmetries and for malformed capsids (10,11).
In summary, our work introduces a description of viral capsid formation as a stochastic assembly of protein oligomers. An important aspect is that our framework is data-driven, starting from molecular detail, and exhibits different assembly behaviors for different viruses, as exemplified by the results for 1stm and 4sbv presented here. Importantly, no assumptions are made about specific intermediates through which the assembly has to proceed—all such phenomena emerge from the data. Our methodology bridges the gap between the static and dynamic models of viral assembly by using a stochastic sampling algorithm to investigate the assembly pathways. The sampling is done using an extended version of the Gillespie algorithm, which is derived from fundamental physical principles. This enables a mesoscopic simulation of the kinetics which is less computationally intensive than a microscopic MD simulation. Alternatively, this algorithm provides a physically based sampling of the assembly tree, as opposed to computationally intractable combinatorial optimization techniques (12,13). We are currently in the process of extending and refining our framework in several of the above directions as we pursue a general exploration of other icosahedral viruses in different families.
Acknowledgments
We thank D. J. Jacobs, B. M. Hespenheide, and M. F. Thorpe for permission to use the FIRST software, and for their responsiveness to our queries. We are also grateful to Gert Vriend for access to the WHAT IF software. We gratefully acknowledge helpful discussions with Peter Hänggi, Vijay Reddy, Christina Kyriakidou, and Sophie Scialom.
Research was funded by the Engineering and Physical Sciences Research Council, the Royal Society, and the Institute of Biomedical Engineering at Imperial College London.
References
- 1.Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2002. Molecular Biology of the Cell, 4th Ed. Garland Science, New York.
- 2.Caspar, D. L. D., and A. Klug. 1962. Physical principles in the construction of regular viruses. Cold Spring Harb. Symp. Quant. Biol. 27:1–24. [DOI] [PubMed] [Google Scholar]
- 3.Zlotnick, A. 2004. Viruses and the physics of soft condensed matter. Proc. Natl. Acad. Sci. USA. 101:15549–15550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zlotnick, A. 2003. Are weak protein-protein interactions the general rule in capsid assembly? Virology. 315:269–274. [DOI] [PubMed] [Google Scholar]
- 5.McPherson, A. 2005. Micelle formation and crystallization as paradigms for virus assembly. Bioessays. 27:447–458. [DOI] [PubMed] [Google Scholar]
- 6.Schwartz, R., P. W. Shor, P. E. Prevelige Jr., and B. Berger. 1998. Local rules simulation of the kinetics of virus capsid self-assembly. Biophys. J. 75:2626–2636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Larson, S. B., and A. McPherson. 2001. Satellite Tobacco Mosaic Virus RNA: structure and implications for assembly. Curr. Opin. Struct. Biol. 11:59–65. [DOI] [PubMed] [Google Scholar]
- 8.Fox, J. M., G. Wang, J. A. Speir, N. H. Olson, J. E. Johnson, T. S. Baker, and M. J. Young. 1998. Comparison of the native CCMV virion with in vitro assembled CCMV virions by cryoelectron microscopy and image reconstruction. Virology. 244:212–218. [DOI] [PubMed] [Google Scholar]
- 9.Baker, T. S., N. H. Olson, and S. D. Fuller. 1999. Adding the third dimension to virus life cycles: three-dimensional reconstruction of icosahedral viruses from cryo-electron micrographs. Microbiol. Mol. Biol. Rev. 63:862–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Berger, B., P. W. Shor, L. Tucker-Kellogg, and J. King. 1994. Local rule-based theory of virus shell assembly. Proc. Natl. Acad. Sci. USA. 91:7732–7736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rapaport, D. 2004. Self-assembly of polyhedral shells: a molecular dynamics study. Phys. Rev. E. 70:051905. [DOI] [PubMed] [Google Scholar]
- 12.Horton, N., and M. Lewis. 1992. Calculation of the free energy of association for protein complexes. Protein Sci. 1:169–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Reddy, V. S., H. A. Giesing, R. T. Morton, A. Kumar, C. B. Post, C. L. Brooks III, and J. E. Johnson. 1998. Energetics of quasiequivalence: computational analysis of protein-protein interactions in icosahedral viruses. Biophys. J. 74:546–558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sitharam, M., and M. Agbandje-McKenna. 2006. Modeling virus self-assembly pathways: avoiding dynamics using geometric constraint decomposition. J. Comput. Biol. Accepted for publication. [DOI] [PubMed]
- 15.Hespenheide, B. M., D. J. Jacobs, and M. F. Thorpe. 2004. Structural rigidity in the capsid assembly of Cowpea Chlorotic Mottle Virus. J. Phys. Cond. Matt. 16:5055–5064. [Google Scholar]
- 16.Endres, D., and A. Zlotnick. 2002. Model-based analysis of assembly kinetics for virus capsids or other spherical polymers. Biophys. J. 83:1217–1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zlotnick, A., J. M. Johnson, P. W. Wingfield, S. J. Stahl, and D. Endres. 1999. A theoretical model successfully identifies features of Hepatitis B virus capsid assembly. Biochemistry. 38:14644–14652. [DOI] [PubMed] [Google Scholar]
- 18.Ceres, P., and A. Zlotnick. 2002. Weak protein-protein interactions are sufficient to drive assembly of Hepatitis B virus capsids. Biochemistry. 41:11525–11531. [DOI] [PubMed] [Google Scholar]
- 19.Kegel, W. K., and P. van der Schoot. 2004. Competing hydrophobic and screened-Coulomb interactions in Hepatitis B virus capsid assembly. Biophys. J. 86:3905–3913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lidmar, J., L. Mirny, and D. R. Nelson. 2003. Virus shapes and buckling transitions in spherical shells. Phys. Rev. E. 68:0306741. [DOI] [PubMed] [Google Scholar]
- 21.Marzec, C., and L. Day. 1993. Pattern formation in icosahedral virus capsids: the Papova viruses and Nudaurelia capensis β-virus. Biophys. J. 65:2559–2577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tarnai, T., Z. Gaspar, and L. Szalai. 1995. Pentagon packing models for “all-pentamer” virus structures. Biophys. J. 69:612–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bruinsma, R. F., W. M. Gelbart, D. Reguera, J. Rudnick, and R. Zandi. 2003. Viral self-assembly as a thermodynamic process. Phys. Rev. Lett. 90:248101. [DOI] [PubMed] [Google Scholar]
- 24.Zandi, R., D. Reguera, R. F. Bruinsma, W. M. Gelbart, and J. Rudnick. 2004. Origin of icosahedral symmetry in viruses. Proc. Natl. Acad. Sci. USA. 101:15556–15560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Endres, D., M. Miyahara, P. Moisant, and A. Zlotnick. 2005. A reaction landscape identifies the intermediates critical for self-assembly of virus capsids and other polyhedral structures. Protein Sci. 14:1518–1525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Reddy, V., P. Natarajan, B. Okerberg, K. Li, K. Damodaran, R. Morton, C. L. Brooks III, and J. Johnson. 2001. VIrus Particle ExploreR (VIPER), a website for virus capsid structures and their computational analyses. J. Virol. 75:11943–11947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jacobs, D. J., A. Rader, L. A. Kuhn, and M. Thorpe. 2001. Protein flexibility predictions using graph theory. Proteins Struct. Funct. Gen. 44:150–165. [DOI] [PubMed] [Google Scholar]
- 28.Gillespie, D. T. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81:2340–2361. [Google Scholar]
- 29.Vriend, G. 1990. WHAT IF: a molecular modeling and drug design program. J. Mol. Graph. 8:52–56. [DOI] [PubMed] [Google Scholar]
- 30.Jacobs, D. J. 1998. Generic rigidity in three-dimensional bond-bending networks. J. Phys. A. 31:6653–6668. [Google Scholar]
- 31.Gillespie, D. T. 1976. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22:403–434. [Google Scholar]
- 32.van Kampen, N. G. 1992. Stochastic Processes in Physics and Chemistry, 2nd Ed. Elsevier, New York.
- 33.Turner, T., S. Schnell, and K. Burrage. 2004. Stochastic approaches for modelling in vivo reactions. Comput. Biol. Chem. 28:165–178. [DOI] [PubMed] [Google Scholar]
- 34.Selzer, T., and G. Schreiber. 2001. New insights into the mechanism of protein-protein association. Proteins Struct. Funct. Gen. 45:190–198. [DOI] [PubMed] [Google Scholar]
- 35.Janin, J. 1997. The kinetics of protein-protein recognition. Proteins Struct. Funct. Gen. 28:153–161. [DOI] [PubMed] [Google Scholar]
- 36.Stundzia, A. B., and C. J. Lumsden. 1996. Stochastic simulation of coupled reaction-diffusion processes. J. Comput. Phys. 127:196–207. [Google Scholar]
- 37.Bernstein, D. 2005. Simulating mesoscopic reaction-diffusion systems using the Gillespie algorithm. Phys. Rev. E. 71:041103. [DOI] [PubMed] [Google Scholar]
- 38.Drake, R. L. 1972. Aerosol Physics and Chemistry, Vol. 3, Chapt. 2, 1st Ed. Pergamon Press, Oxford, UK. 201–377.
- 39.Camacho, C. J., Z. Weng, S. Vajda, and C. DeLisi. 1999. Free energy landscapes of encounter complexes in protein-protein association. Biophys. J. 76:1166–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Northrup, S., and H. Erickson. 1992. Kinetics of protein-protein association explained by Brownian dynamics computer simulation. Proc. Natl. Acad. Sci. USA. 89:3338–3342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sheu, S.-Y., D.-Y. Yang, H. L. Selzle, and E. W. Schlag. 2003. Energetics of hydrogen bonds in peptides. Proc. Natl. Acad. Sci. USA. 100:12683–12687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 43.Hänggi, P., P. Talkner, and M. Borkovec. 1990. Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62:251–342. [Google Scholar]
- 44.Savithri, H., and J. Erickson. 1983. The self-assembly of the Cowpea strain of the Southern Bean Mosaic Virus. Virology. 126:328–335. [DOI] [PubMed] [Google Scholar]
- 45.Darroch, J. N., and E. Seneta. 1965. On quasi-stationary distributions in absorbing discrete-time finite Markov chains. J. Appl. Probability. 2:88–100. [Google Scholar]
- 46.Antia, F. D., and S. Lee. 1985. The effect of stoichiometry on Markov chain models for chemical reaction kinetics. Chem. Eng. Sci. 40:1969–1971. [Google Scholar]
- 47.Darroch, J. N., and E. Seneta. 1967. On quasi-stationary distributions in absorbing continuous-time finite Markov chains. J. Appl. Probability. 4:192–196. [Google Scholar]
- 48.Gadgil, C., C.-H. Lee, and H. G. Othmer. 2005. A stochastic analysis of first-order reaction networks. Bull. Math. Biol. 67:901–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hayot, F., and C. Jayaprakash. 2004. The linear noise approximation for molecular fluctuations within the cell. Phys. Biol. 1:205–210. [DOI] [PubMed] [Google Scholar]
- 50.Zhang, T., and R. Schwartz. 2006. Simulation study of the contribution of oligomer/oligomer binding to capsid assembly kinetics. Biophys. J. 90:57–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sayle, R., and E. Milner-White. 1995. RASMOL: biomolecular graphics for all. Trends Biochem. Sci. 20:374–376. [DOI] [PubMed] [Google Scholar]