Abstract
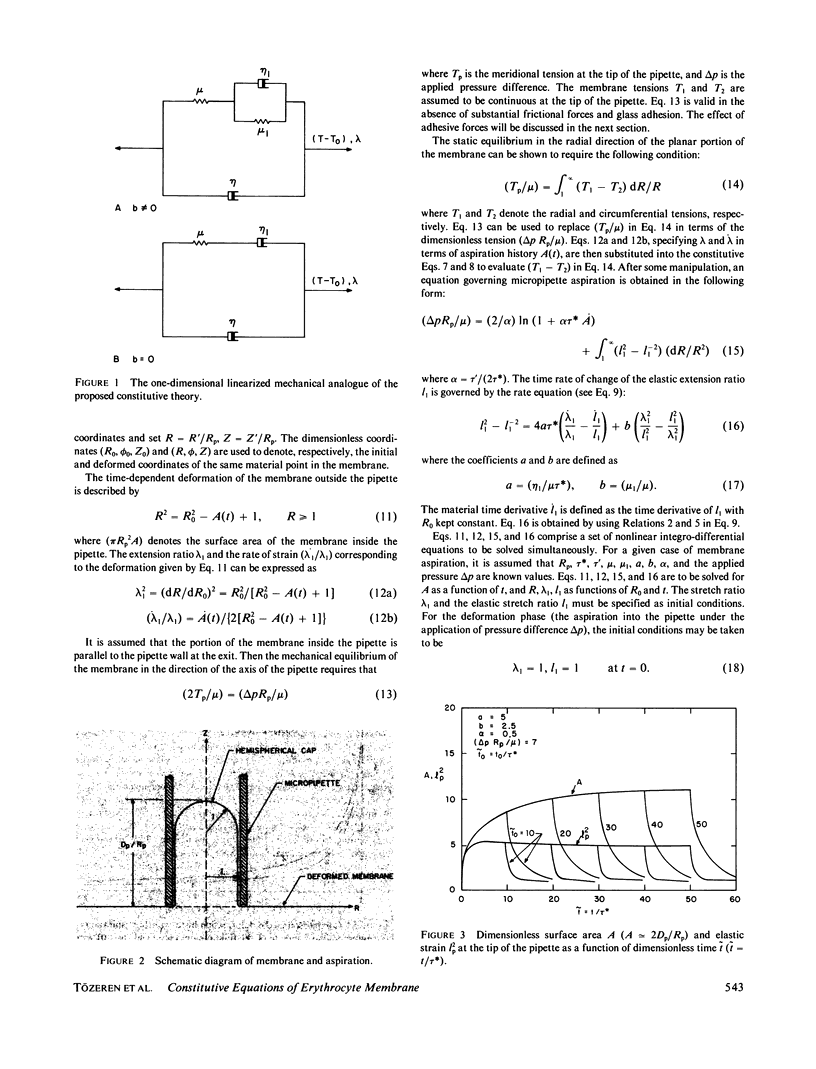
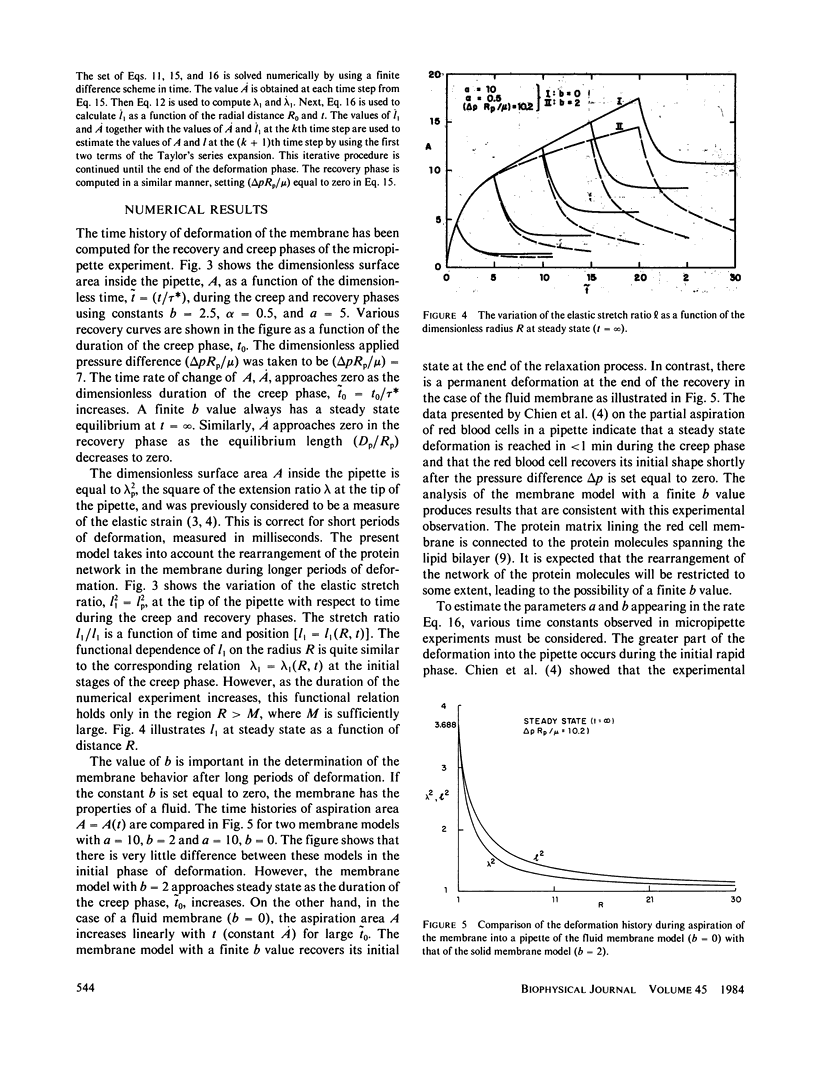
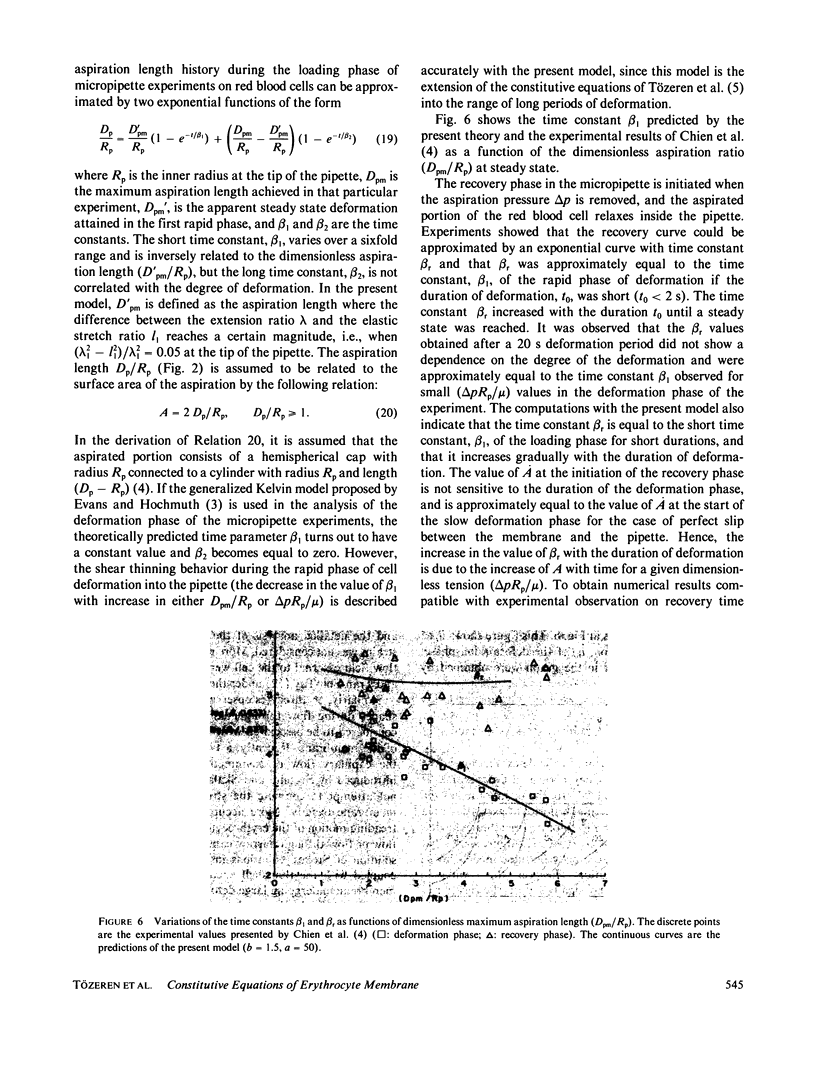
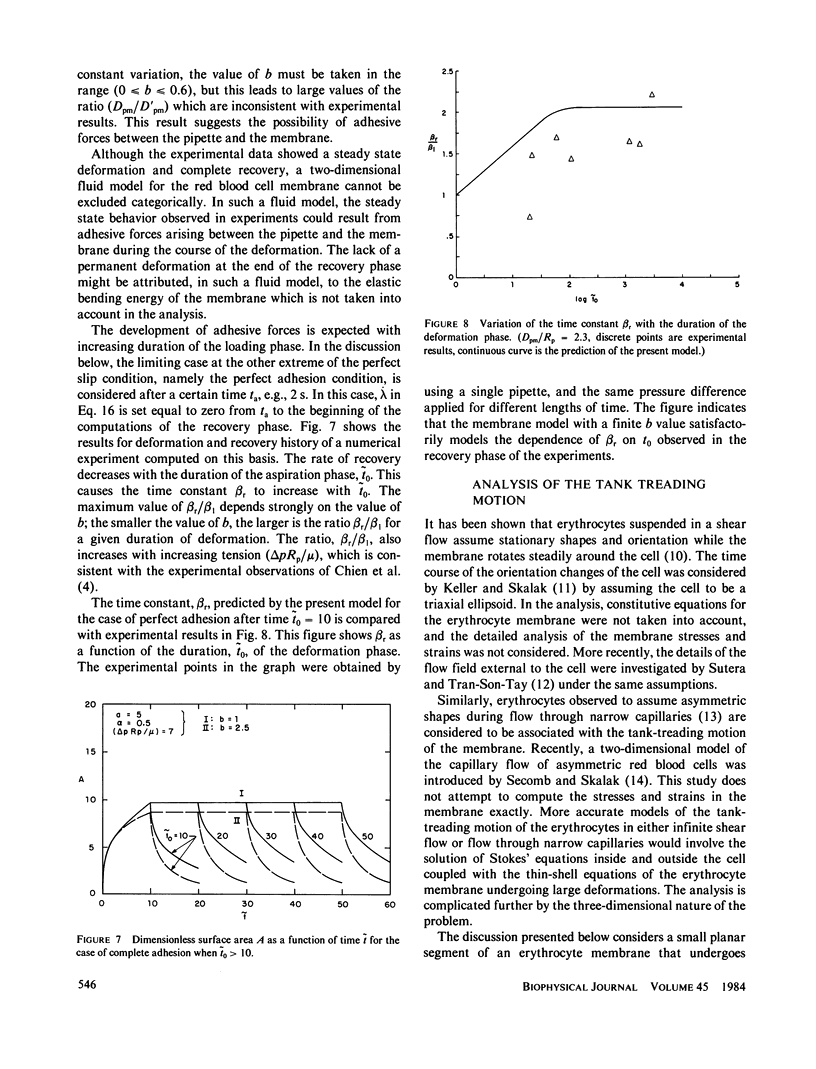
The erythrocyte membrane is modeled as a two-dimensional viscoelastic continuum that evolves under the application of stress. The present analysis of the erythrocyte membrane is motivated by the recent development of knowledge about its molecular structure. The constitutive equations proposed in the present analysis explain in a consistent manner the data on both the deformation and recovery phases of the micropipette experiment. The rheological equations of the present study are applied in a later section to the analysis of a plane membrane deformation that is quantitatively similar to the tank-treading motion of the erythrocytes in a shear field. The computations yield useful information on how the membrane viscosity becomes a more dominant feature in tank-treading motion. The material constants appearing in the proposed constitutive equations may be useful indications of the biochemical state of the membrane in health and disease.
Full text
PDF



Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Chien S., Sung K. L., Skalak R., Usami S., Tözeren A. Theoretical and experimental studies on viscoelastic properties of erythrocyte membrane. Biophys J. 1978 Nov;24(2):463–487. doi: 10.1016/S0006-3495(78)85395-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans E. A. A new material concept for the red cell membrane. Biophys J. 1973 Sep;13(9):926–940. doi: 10.1016/S0006-3495(73)86035-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans E. A., Hochmuth R. M. Membrane viscoelasticity. Biophys J. 1976 Jan;16(1):1–11. doi: 10.1016/S0006-3495(76)85658-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lux S. E. Dissecting the red cell membrane skeleton. Nature. 1979 Oct 11;281(5731):426–429. doi: 10.1038/281426a0. [DOI] [PubMed] [Google Scholar]
- Secomb T. W., Skalak R. A two-dimensional model for capillary flow of an asymmetric cell. Microvasc Res. 1982 Sep;24(2):194–203. doi: 10.1016/0026-2862(82)90056-5. [DOI] [PubMed] [Google Scholar]
- Skalak R., Tozeren A., Zarda R. P., Chien S. Strain energy function of red blood cell membranes. Biophys J. 1973 Mar;13(3):245–264. doi: 10.1016/S0006-3495(73)85983-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tözeren A., Skalak R., Sung K. L., Chien S. Viscoelastic behavior of erythrocyte membrane. Biophys J. 1982 Jul;39(1):23–32. doi: 10.1016/S0006-3495(82)84486-X. [DOI] [PMC free article] [PubMed] [Google Scholar]


