Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1985 Mar;47(3):303–309. doi: 10.1016/S0006-3495(85)83920-5

Continuum rheology of muscle contraction and its application to cardiac contractility.

A Tözeren
PMCID: PMC1435213  PMID: 3978204

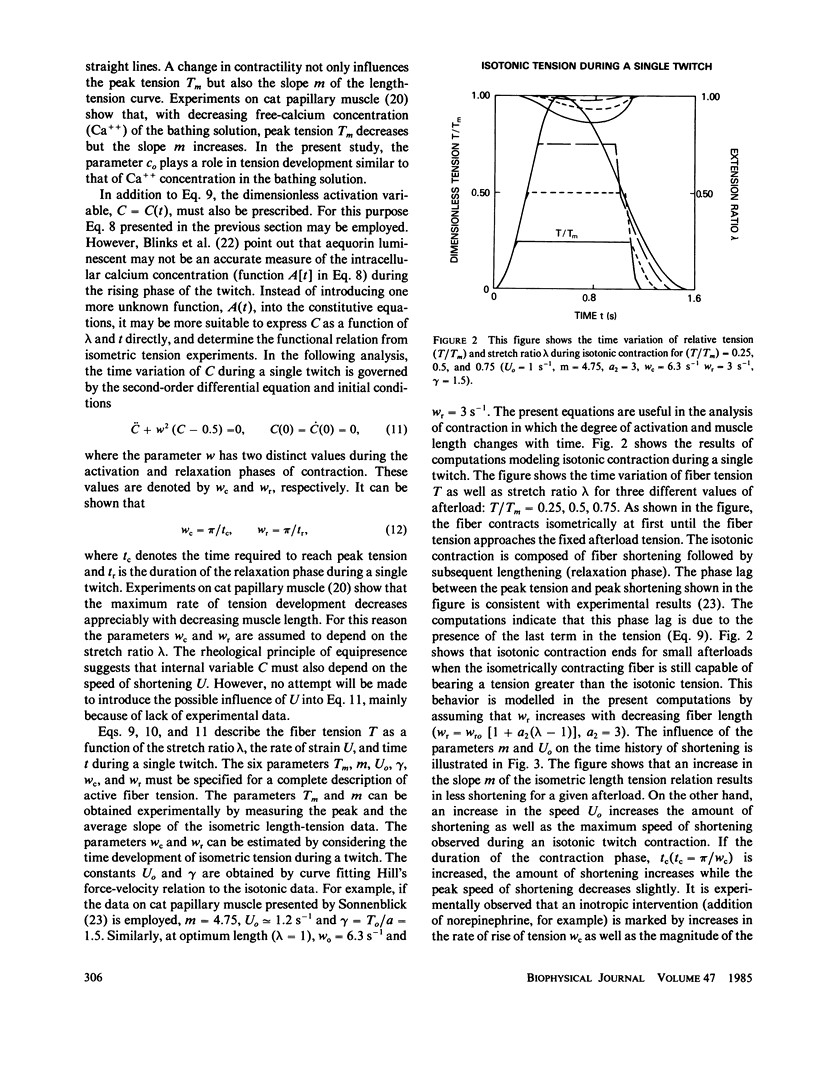
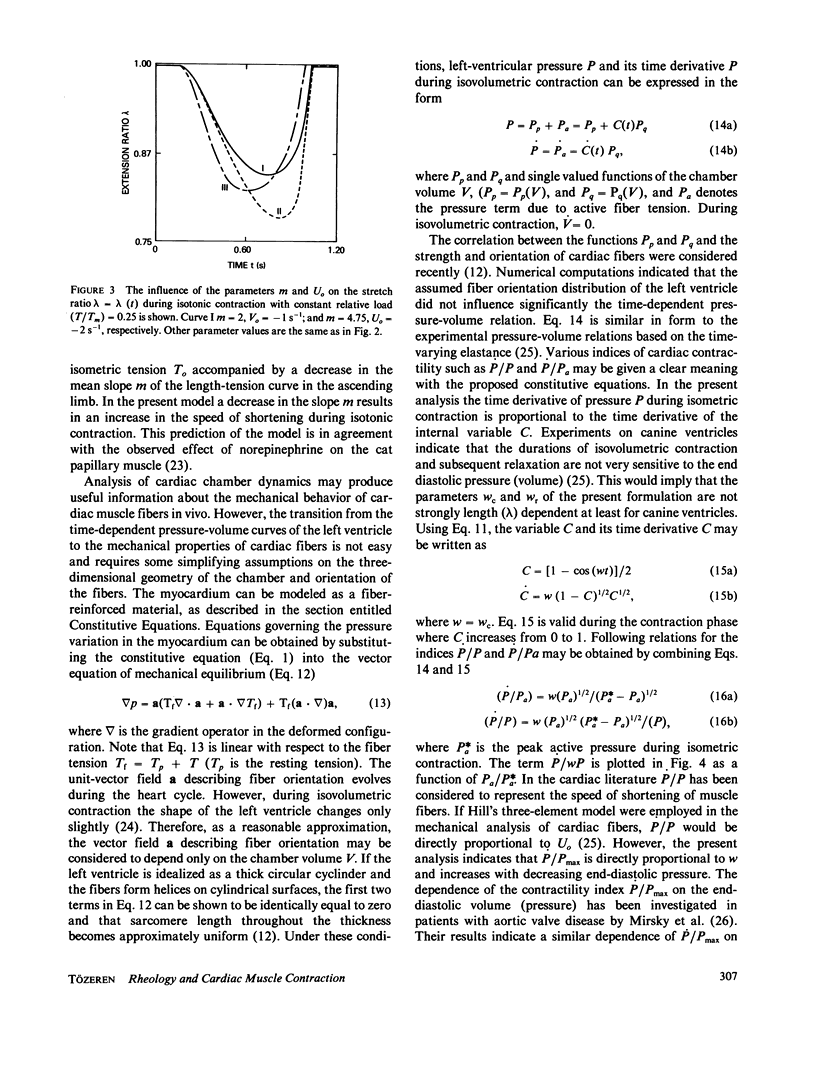
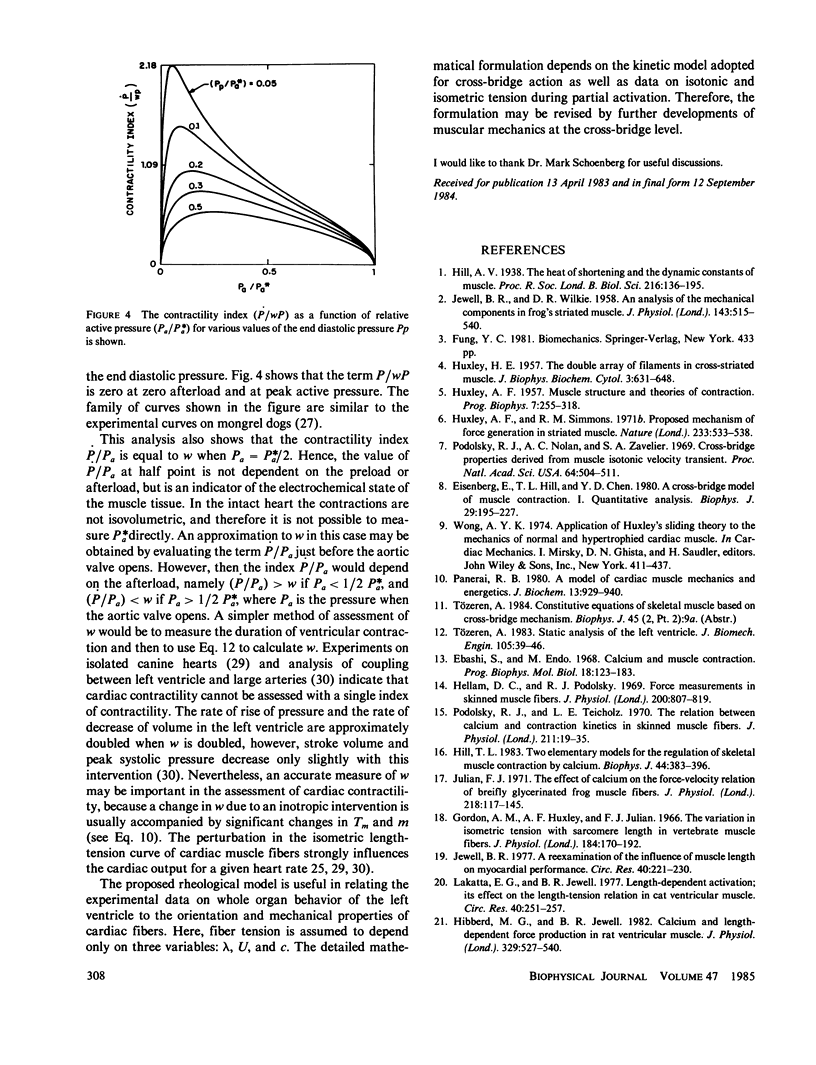
Abstract

A set of constitutive equations is proposed to describe the mechanics of contraction of skeletal and heart muscle. Fiber tension is assumed to depend on the degree of chemical activation, the stretch ratio, and the rate of stretching of the fibers. The time rate of change of activation is governed by a differential equation. The proposed constitutive equations are used to model the time courses of isotonic and isometric twitches during contraction and relaxation phases of the muscle response to stimulation. Various contractility indices of the left ventricle are considered next by using the proposed constitutive equations. The present analysis introduces a new interpretation of the index of contractility (dP/dt)/P used in cardiac literature. It is shown that this index may not be related at all to the maximum speed of shortening and that it may be dependent on both preload and afterload. The development of pressure during isovolumetric contraction of the left ventricle is shown to be governed by a differential equation describing the time rate of change of tension during isometric contraction of myocardium fibers.

Full text

PDF
303

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Blinks J. R., Rüdel R., Taylor S. R. Calcium transients in isolated amphibian skeletal muscle fibres: detection with aequorin. J Physiol. 1978 Apr;277:291–323. doi: 10.1113/jphysiol.1978.sp012273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ebashi S., Endo M. Calcium ion and muscle contraction. Prog Biophys Mol Biol. 1968;18:123–183. doi: 10.1016/0079-6107(68)90023-0. [DOI] [PubMed] [Google Scholar]
  3. Eisenberg E., Hill T. L., Chen Y. Cross-bridge model of muscle contraction. Quantitative analysis. Biophys J. 1980 Feb;29(2):195–227. doi: 10.1016/S0006-3495(80)85126-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Gordon A. M., Huxley A. F., Julian F. J. The variation in isometric tension with sarcomere length in vertebrate muscle fibres. J Physiol. 1966 May;184(1):170–192. doi: 10.1113/jphysiol.1966.sp007909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. HUXLEY A. F. Muscle structure and theories of contraction. Prog Biophys Biophys Chem. 1957;7:255–318. [PubMed] [Google Scholar]
  6. HUXLEY H. E. The double array of filaments in cross-striated muscle. J Biophys Biochem Cytol. 1957 Sep 25;3(5):631–648. doi: 10.1083/jcb.3.5.631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hellam D. C., Podolsky R. J. Force measurements in skinned muscle fibres. J Physiol. 1969 Feb;200(3):807–819. doi: 10.1113/jphysiol.1969.sp008723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hibberd M. G., Jewell B. R. Calcium- and length-dependent force production in rat ventricular muscle. J Physiol. 1982 Aug;329:527–540. doi: 10.1113/jphysiol.1982.sp014317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hill T. L. Two elementary models for the regulation of skeletal muscle contraction by calcium. Biophys J. 1983 Dec;44(3):383–396. doi: 10.1016/S0006-3495(83)84312-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Huxley A. F., Simmons R. M. Proposed mechanism of force generation in striated muscle. Nature. 1971 Oct 22;233(5321):533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
  11. JEWELL B. R., WILKIE D. R. An analysis of the mechanical components in frog's striated muscle. J Physiol. 1958 Oct 31;143(3):515–540. doi: 10.1113/jphysiol.1958.sp006075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Jewell B. R. A reexamination of the influence of muscle length on myocardial performance. Circ Res. 1977 Mar;40(3):221–230. doi: 10.1161/01.res.40.3.221. [DOI] [PubMed] [Google Scholar]
  13. Julian F. J. The effect of calcium on the force-velocity relation of briefly glycerinated frog muscle fibres. J Physiol. 1971 Oct;218(1):117–145. doi: 10.1113/jphysiol.1971.sp009607. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Lakatta E. G., Jewell B. R. Length-dependent activation: its effect on the length-tension relation in cat ventricular muscle. Circ Res. 1977 Mar;40(3):251–257. doi: 10.1161/01.res.40.3.251. [DOI] [PubMed] [Google Scholar]
  15. Mirsky I., Henschke C., Hess O. M., Krayenbuehl H. P. Prediction of postoperative performance in aortic valve disease. Am J Cardiol. 1981 Aug;48(2):295–303. doi: 10.1016/0002-9149(81)90610-x. [DOI] [PubMed] [Google Scholar]
  16. Nejad N. S., Klein M. D., Mirsky I., Lown B. Assessment of myocardial contractility from ventricular pressure recordings. Cardiovasc Res. 1971 Jan;5(1):15–23. doi: 10.1093/cvr/5.1.15. [DOI] [PubMed] [Google Scholar]
  17. Panerai R. B. A model of cardiac muscle mechanics and energetics. J Biomech. 1980;13(11):929–940. doi: 10.1016/0021-9290(80)90163-3. [DOI] [PubMed] [Google Scholar]
  18. Podolsky R. J., Nolan A. C., Zaveler S. A. Cross-bridge properties derived from muscle isotonic velocity transients. Proc Natl Acad Sci U S A. 1969 Oct;64(2):504–511. doi: 10.1073/pnas.64.2.504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Podolsky R. J., Teichholz L. E. The relation between calcium and contraction kinetics in skinned muscle fibres. J Physiol. 1970 Nov;211(1):19–35. doi: 10.1113/jphysiol.1970.sp009263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. SONNENBLICK E. H. Implications of muscle mechanics in the heart. Fed Proc. 1962 Nov-Dec;21:975–990. [PubMed] [Google Scholar]
  21. Sagawa K. The ventricular pressure-volume diagram revisited. Circ Res. 1978 Nov;43(5):677–687. doi: 10.1161/01.res.43.5.677. [DOI] [PubMed] [Google Scholar]
  22. Sunagawa K., Burkhoff D., Lim K. O., Sagawa K. Impedance loading servo pump system for excised canine ventricle. Am J Physiol. 1982 Aug;243(2):H346–H350. doi: 10.1152/ajpheart.1982.243.2.H346. [DOI] [PubMed] [Google Scholar]
  23. Tözeren A. Static analysis of the left ventricle. J Biomech Eng. 1983 Feb;105(1):39–46. [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES