Aspects of large-scale chromatin structures in mouse liver nuclei can be predicted from the DNA sequence

Abstract

The large amount of non-coding DNA present in mammalian genomes suggests that some of it may play a structural or functional role. We provide evidence that it is possible to predict computationally, from the DNA sequence, loci in mouse liver nuclei that possess distinctive nucleosome arrays. We tested the hypothesis that a 100 kb region of DNA possessing a strong, in-phase, dinucleosome period oscillation in the motif period-10 non-T, A/T, G, should generate a nucleosome array with a nucleosome repeat that is one-half of the dinucleosome oscillation period value, as computed by Fourier analysis of the sequence. Ten loci with short repeats, that would be readily distinguishable from the pervasive bulk repeat, were predicted computationally and then tested experimentally. We estimated experimentally that less than 20% of the chromatin in mouse liver nuclei has a nucleosome repeat length that is 15 bp, or more, shorter than the bulk repeat value of 195 ± bp. All 10 computational predictions were confirmed experimentally with high statistical significance. Nucleosome repeats as short as 172 ± 5 bp were observed for the first time in mouse liver chromatin. These findings may be useful for identifying distinctive chromatin structures computationally from the DNA sequence.

INTRODUCTION

One well-studied aspect of chromatin structure is nucleosome positioning. Nucleosome positioning is of interest because it is widespread in yeast (1), and it could, in principle, serve to control the accessibility of regulatory protein binding sites in all eukaryotes. However, the extent of nucleosome positioning in vivo that occurs as a direct consequence of histone-DNA interactions and the mechanisms involved in positioning are not clear. Some regions of DNA can exclude nucleosomes either because they bind to other proteins (2) or because they contain sequences that discourage nucleosome formation (3–5). In either case, the excluded region could then provide a boundary that serves to position adjacent nucleosomes (6). Additionally, both natural and synthetic sequences have been found that possess the ability to position nucleosomes directly through histone-DNA interactions; a variety of DNA sequence motifs have been implicated in nucleosome positioning (7,8).

In addition to the ability of a DNA sequence to control the access of a binding site in its immediate vicinity for a regulatory protein through nucleosome positioning, sequence motifs in genomic DNA, particularly in metazoans, might be involved in other aspects of chromatin structure. For example, a periodic motif in DNA that persists over a large distance might influence nucleosome array formation. For this role, nucleosome positioning need not be precise. It is likely that nucleosome arrays that possess differences in the regularity of nucleosome spacing or differences in the nucleosome repeat length also possess differences in chromatin higher-order structure (9,10), or at least in chromatin fiber flexibility (11). Moreover, these physical chemical differences could be functionally important. With the sequences of human, mouse and other higher organism genomes now available, one can analyze large amounts of sequence computationally and possibly obtain useful information about chromatin structure if one knows what to look for. A goal for the future of genome research is to identify the structural and functional components encoded, perhaps in unexpected ways, in the large amounts of non-coding DNA that is present (12). Little is known about information in DNA that could affect large-scale chromatin structures.

We have previously found that regular oscillations of period-10 non-T, A/T, G (VWG), a periodic motif that is very abundant in vertebrate genomes (13), occurred specifically in regions of DNA that ordered nucleosomes into regular arrays in vitro (14). The period of these oscillations, assessed by Fourier analysis, corresponded almost exactly to a value that was equal to twice the measured nucleosome repeat in all cases studied. Moreover, DNA regions that did not possess a single strong Fourier peak did not order nucleosomes into regular arrays in vitro. These observations suggested the hypothesis that nucleosome ordering by linker histones might be facilitated by a dinucleosome period signal consisting of regular period-10 VWG oscillations. It is not necessary for each nucleosome in an array to have its own positioning signal (8). Linker histone addition to nucleosomes can readily align one nucleosome with respect to another in the absence of signals in the DNA (15). We obtained further support for this hypothesis by making small alterations in the chicken ovalbumin gene sequence which affected nucleosome array formation in vitro in a computationally predictable way (16). We also showed that this oscillating signal appears to work because nucleosomes tend to avoid the DNA regions that have low counts of period-10 VWG; presumably they are less flexible than regions of DNA with high counts. Recently, we have suggested that it might be possible to extend our computational approach to the chromatin in animal tissues if the period-10 VWG oscillations are assessed over a 70–100 kb range (17). Here, we provide evidence for the first time that it is possible to predict computationally, from the DNA sequence, loci that possess distinctive nucleosome arrays in mouse liver nuclei.

MATERIALS AND METHODS

Computational analysis

Sequences were analyzed for long-range periodic oscillations in period-10 VWG content as described previously (14). Briefly, the occurrences of the motif VWG/CWB (complement) with a periodicity from 10.00 to 10.33 were counted in a sliding 102 bp window, ±51 bp from each VWG position. These histogram data were then averaged in a sliding 60 bp window (5 bp increments) to generate a continuous oscillating curve of the average period-10 VWG count versus GenBank nucleotide number. The total number of VWG/CWB occurrences in a sliding 600 bp window was also computed, and used to apply a small correction for the presence of VWG-poor or VWG-rich regions, as described previously. The extent of regularity and the period of the long-range period-10 VWG oscillations were assessed by Fourier analysis using a 100 kb window, unless otherwise stated. Approximately 60 Mb of mouse genomic DNA (NCBI Build 35) from all chromosomes except Y was analyzed to obtain ten 100 kb regions predicted to have strong signals for forming a nucleosome array with a short repeat. These sequences are obtainable by ‘BLASTing’ the reported probe sequences (Supplementary Data), on which they are centered, against the mouse genome. This method, rather than reporting accession numbers, is independent of the NCBI build, which keeps changing over time. A short repeat is operationally defined here as one having a value between 168 and 180 bp, at least 15 bp shorter than the bulk repeat in mouse liver (195 ± 5 bp). The very short yeast-like repeat value of 168 bp is theoretically possible, but may not exist in mouse liver chromatin, whereas the repeat value of 180 bp is closer to the ubiquitous bulk chromatin repeat value, but still readily distinguishable experimentally. The Fourier transform (FT) of the oscillating curve of period-10 VWG counts versus nucleotide number was decomposed into Gaussian peaks within and around the physiological dinucleosome region using the NORMDIST probability mass function of Excel. The mean, peak height and standard deviation of each peak was adjusted by trial and error until the sum of the peaks closely fit the FT curve defined by the computed points, rather than the Excel spline curve through the points. A strong signal is operationally defined as one possessing a nearly symmetrical (Gaussian) Fourier Amplitude peak in the physiological dinucleosome period range (taken to be from 2 × 165 bp to 2 × 200 bp) with a standard deviation between 7.0 and 17 bp, a height (estimated ±5%) that is at least 800 VWG counts for the ∼100 kb window used, and a peak area that is at least 2.0 times the area of the next largest peak in the physiological dinucleosome region. For peaks possessing mean period values that are outside of the physiological dinucleosome region, only the area extending into the physiological region is considered. We also required that the signal was stable with respect to small variations in window size (±10 kb). The above-stated criteria for a strong signal are consistent with what we initially found for the mouse adenosine deaminase gene (17), and it eliminates possible Fourier peaks that are sharp spikes, peaks that have low amplitudes or are very broad, and peaks that are unstable with respect to varying the window size. It does not imply that peaks that do not possess all of the characteristics defined above cannot still be influential. We hypothesize, based on our previous study (17), that the presence of a strong signal in a particular DNA region should result in the formation of an extended nucleosome array in this region with a repeat value that is one-half the value of the dinucleosome period of the signal peak. In the much more common case where no appreciable signal in the DNA sequence exists, we hypothesize that the nucleosome arrays in these regions should possess the bulk chromatin repeat.

Preparation of nuclei, micrococcal nuclease digestion and electrophoresis

Nucleosome arrays in native chromatin were assessed by partial micrococcal nuclease (MNase) digestion of the DNA in the chromatin of mouse liver nuclei. Nuclei were prepared from mouse (strain C57BL/6J, the NCBI reference sequence) liver as described previously (17). Nuclei containing about 1 mg of DNA were gently pelleted and re-suspended in 1 ml of 0.1 M NaCl, 10 mM Tris–HCl (pH 8.0), 1 mM EDTA. After equilibration for 5 min at 37°C, 0.1 M CaCl₂ was added to a final concentration of 2 mM, then 30 U of MNase were added, and the sample was digested for 1.5 or 2 min. After deproteinization, the nucleic acid was treated with RNase A, and prepared for electrophoresis. The same DNA digests were repeatedly run on a 1.5% agarose bridge gel apparatus of dimensions 13.5 by 13.5 cm in TBE buffer for about 4 h, blotted, and the different DNA regions of interest were detected by Southern hybridization. Lambda DNA cut with AflIII (ascending band values in bp: 170, 277, 458, 493, 739, 956, 1268, 1399, 1520, 1712, 1913, 2360, 2691, 4091, 4920, 5733, 6236, 6631) and, in a separate lane, a 100 bp ladder (BioRad), each labeled with [α-³²P]dATP, were used as size markers. Matthiola incana petals (two flower stalks) were minced in a Virtis S 45 homogenizer in 50 ml chilled 400 mM sucrose, 10 mM MgCl₂, 50 mM Tris–HCl (pH 8.0), 10 mM NaCl isolation buffer (IB) to a fine pulp, filtered through four layers of cheesecloth, two layers of miracloth. Triton X-100 to 0.1% final concentration was added drop-wise while stirring on ice. The filtrate was centrifuged in a Sorvall SS34 rotor at 3000 r.p.m. for 5 min at 4°C. The pellet was re-suspend and washed twice with 40 ml chilled IB. Finally, the cream-colored nuclear pellet was re-suspended in 2 ml of chilled IB. MNase digestion was as above.

Southern blots and hybridizations

Probes with sizes ranging from 336 to 820 bp located in the center of each 100 kb region were PCR-amplified from mouse liver genomic DNA. Each probe used is described by the chromosome number, followed by the probe size in base pairs (see Supplementary Data for the DNA sequence of each probe). To purify the PCR-amplified DNA fragments to be used as probes, the DNA was run on an agarose gel, the gel was stained with ethidium bromide to visualize the band of interest, and the DNA fragment was excised from the gel. The DNA was purified from the gel slice using the Qiaex II gel purification kit (Qiagen). The pure denatured DNA probe fragment (25–50 ng) was labeled with [α-³²P]dATP as described previously (17). After stopping the reaction, the labeled DNA was supplemented with about 2 µg of salmon sperm DNA, denatured and chilled on ice. The pre-hybridization and the hybridization solution contained 100 µg/ml denatured salmon sperm DNA. Final probe concentrations in the hybridization buffer were 5 ng/ml. All pre-hybridizations, hybridizations and washes were performed in a Hyb-Aid oven at 65°C using the membrane manufacturer's recommendations, except for the high stringency washes. The high stringency washes were generally done in 0.1× SSC, 0.1% SDS at 63°C, with a room temperature wash in 0.1× SSC. The blots were exposed to Biomax MR film (Kodak) from 1–3 days at −80°C using a Kodak Biomax MS intensifying screen. To assess the specificity of hybridization, purified mouse genomic DNA digested with appropriate restriction enzymes (usually PstI plus HindIII) were included in lanes labeled D. Nearly half of the probes initially prepared failed to hybridize specifically and could not be used; some of these could be rescued by cleaving with a restriction enzyme and re-purifying a sub-fragment of the initial PCR product (see Supplementary Data for restriction sites).

Nucleosome repeat analysis

The midpoint of each of the nucleosome oligomer bands from the 2 min digest was sized based upon the 100 bp ladder, always present in an adjacent lane. The slope of the best-fit straight line in the plot of nucleosome oligomer size versus nucleosome oligomer number gives the nucleosome repeat length (18). Y-intercepts and the standard deviation of the fit, calculated as the square root of the variance of the residuals, are reported for each fit (Supplementary Data, summarized in Table 1). Negative y-intercepts are expected for most genomic DNA regions at the extent of digestion used because of the exonuclease activity associated with MNase, whereas regions that are resistant to digestion and regions with shorter repeats should have y-intercepts that are near zero. A large positive y-intercept would not be consistent with a regular nucleosome array that contained multiples of a unit repeat.

Table 1.

Computational predictions of nucleosome repeats base upon the DNA sequence and the results of the experimental tests of these predictions in mouse liver nuclei

Locus number	Chromosome number-probe size (bp)	Nucleosome repeat		Experiment fit param.		Fourier signal characteristics (Gaussian)
		Theoretical predictiona (bp)	Experimental valueb (±5 bp)	Y-intercept	SD of fit (bp)	Peak SD (bp)	Peak height (VWG count)	Ratioc	Window (kb)	Predicted ranged (kb)
1	4–419	337/2 = (169)e	172	−0.6	11	9.0	1174	2.2	100	90–110
2	7–500	348/2 = 171	172	−1.4	5.8	8.0	773	2.1	100	90–110
3	3–413	347/2 = 174	174	0.7	8.5	7.0	1653	4.5	120	40–500
4	7–474	348/2 = 174	178	−4.6	7.2	15	918	6.6	100	90–200
5	10–336	358/2 = 179	176	−5.4	6.5	9.0	975	3.1	100	70–120
6	2–375	358/2 = 179	180	−0.6	13	17	811	9.3	90	80–100
7	2–450f	357/2 = 179	183	−1.3	12	16	960	7.0	100	90–170
8	12–573	359/2 = 180	179	−14	2.8	7.0	1368	3.4	100	70–130
9	15–407	360/2 = 180	180	−23	11	14	788	5.0	100	90–110
10	3–552	360/2 = 180	181	−2.1	4.9	7.5	931	3.7	90	70–110
Madaf	2–820	370/2 = 185	183	−3.8	9.2	7.5	1011	2.2	110	70–130
	3–342	381/2 = 191	190	−17	9.2	10.5	855	3.8	120	100–130
	19–395	420/2 = (210)	187	−11	5.7	14	1052	2.6	100	90–110
	1–678	bulkg	191	−12	9.2
	9–403	bulkg	192	−7.8	12
	18–735	bulkh	194	−42	8.1
	Et brf	bulk	194	−33	10

^aDinucleosome period mean value (of predominant Gaussian)/2 = predicted nucleosome repeat.

^bAll probes exactly centered on the computation window of best ratio.

^cRatio of the signal peak area to the next largest peak area in the physiological region.

^dRange over which peak area of interest is at least two times greater than the next highest Gaussian in the physiological range.

^eParentheses denote extreme values that might not be physiological for mouse liver chromatin.

^fSee reference (17).

^gNo signal.

^hnon-specific probe.

RESULTS

Specific loci can possess short nucleosome repeats in mouse liver nuclei

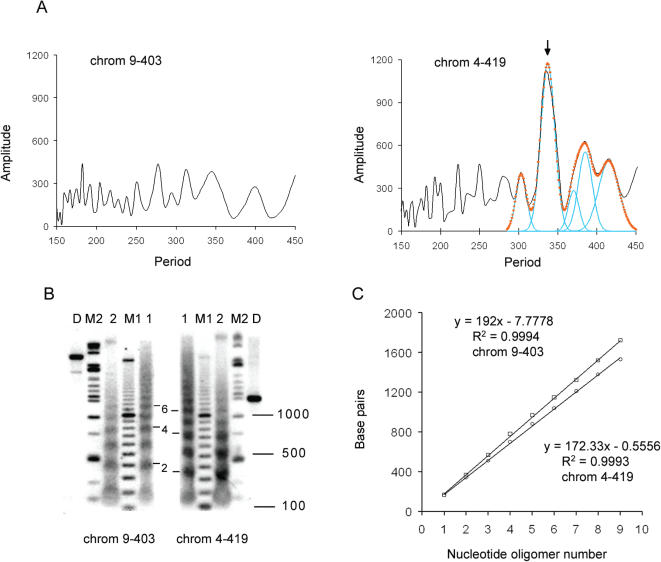
The bulk chromatin nucleosome repeat in mouse liver nuclei is 195 ± 5 bp, as assessed by total DNA staining using ethidium bromide (17,19). Early on it was shown that in mouse liver chromatin transcribed regions, rDNA regions and satellite DNA all have the same nucleosome repeat as the bulk chromatin (19). Thus, the 195 ± 5 bp repeat is representative of most of the chromatin. However, there could be some regions of the genome, possibly having distinctive chromatin structures, which possess nucleosome repeats that differ from the bulk chromatin. A few such regions have been observed in other animal tissues (20–22). In mouse liver nuclei it was recently shown that the ubiquitously expressed adenosine deaminase gene possesses an unusually regular nucleosome array with a repeat length that is about 12 bp shorter than the bulk chromatin value, consistent with the idea that some genomic DNA regions differ from the bulk chromatin (17). To assess whether there are additional genomic DNA regions with perhaps even shorter nucleosome repeats, we attempted to use our computational methods to search ∼60 Mb of DNA to identify ∼100 kb regions predicted to have short nucleosome repeats. After identifying each candidate region computationally, we then prepared a hybridization probe (400–800 bp) by PCR from the center of the 100 kb window, and performed an experiment to test our computational prediction. One such result is shown in Figure 1.

Figure 1.

Predicted and experimentally determined nucleosome arrangements for two loci. (A) FTs of the curves of the oscillations of period-10 VWG with nucleotide number for 100 kb windows. Probe 9–403 (left) was from the center of a locus on chromosome 9 that does not possess a predominant in-phase period-10 VWG oscillation, thus predicting that nucleosome arrays in this locus should have the properties of the bulk chromatin. Probe 4–419 (right) was from the center of a locus on chromosome 4 that exhibits a predominant in-phase period-10 VWG oscillation at a period of 337 bp (arrow), thus predicting a nucleosome array with a very short nucleosome repeat value of 337 bp/2 = 169 bp. The Fourier curve (black points and spline curve) was represented by five Gaussian peaks (blue curves) that summed (orange circles) to fit the computed Fourier points in the physiological dinucleosome region. (B) Southern blots of agarose gel electrophoresis of the DNA fragments obtained from MNase digests of nuclei. Portions of the same digests were probed with probe 9–403 (left) or probe 4–419 (right), and the resultant nucleosome ladders were compared. Lanes 1 were from a 1.5 min digest and lanes 2 were from a 2 min digest. Lanes D were from a HindIII + PstI digestion of purified mouse liver genomic DNA to assess the specificity of the probes, lanes M1 were labeled 100 bp ladders (sizes of selected fragments are indicated on the right) for nucleosome oligomer sizing, and lanes M2 were labeled size markers (see Materials and Methods) for restriction fragment sizing. The nucleosome 2, 4 and 6mers detected by each probe are identified. (C) Analysis of the nucleosome repeat length from the ladders of the 2 min digest detected with each probe. Plots of nucleosome oligomer size (Base pairs) versus nucleosome oligomer number are shown. Probe 9–403, squares; probe 4–419, circles. The equations of the best straight line fits and the R² values are shown. The nucleosome repeat lengths are the slopes of the lines.

Figure 1A (left) shows the FT of the period-10 VWG oscillations in a 90 kb window from a region of chromosome 9. For this DNA region, there is no predominant Fourier peak in the physiological dinucleosome region, and therefore no signal for the formation of a nucleosome array. The prediction in this case is that this region of chromatin should possess the bulk chromatin repeat. In contrast, Figure 1A (right) shows the FT (black points/black spline curve) of the period-10 VWG oscillations in a 100 kb window from a region of chromosome 4, which has a large peak in the physiological dinucleosome region. The curve was decomposed into Gaussian peaks (blue curves) in and around the physiological dinucleosome region (from 330 to 400 bp) such that the black points of the Fourier were well-represented by the curve consisting of the sum of the Gaussian peaks (orange circles). The broad apparent Fourier peak at around 385 bp, possessing a shoulder at ∼370 bp, required two Gaussian peaks to adequately fit it. The predominant Fourier peak at 337 bp has a height of 1174 VWG counts, a standard deviation of 9.0 bp, and is slightly more than twice as large (by area) as the next largest peak area in the physiological dinucleosome region (Table 1). This peak meets all of the criteria that we set (Materials and Methods) for a strong signal for this 100 kb region of DNA, and predicts that the chromatin in this region of the genome should tend to form a nucleosome array with an extremely short repeat (in mouse liver nuclei) of 337 bp/2 = 169 bp.

These predictions were tested experimentally. Hybridization probes were prepared from the center of each ∼100 kb window, and the DNA from a single MNase digest of mouse liver nuclei (with 1.5 or 2 min time points) was examined separately using each probe (Figure 1B). The nucleosome ladder (lane 1) detected by the 9–403 probe closely resembled that of bulk chromatin, whereas a portion of the same sample detected by the 4–419 probe revealed a ladder with a considerably shorter repeat. For example, it can be seen directly from the autoradiograms that for the 9–403 probe the nucleosome 4 and 5mer fragments run close to the 800 and 1000 bp fragments, respectively, of the adjacent 100 bp ladder marker, whereas for the 4–419 probe the nucleosome 4 and 5mer fragments run close to the 700 and 900 bp marker fragments, respectively, of the adjacent 100 bp ladder. A detailed analysis of the ladders is presented in Figure 1C. For each ladder the plot of the nucleosome oligomer size (bp) against nucleosome oligomer number is a straight line with a slightly negative y-intercept and a standard deviation of the fit value of 11–12 bp, indicating that the nucleosome oligomers are close to being multiples of a unit repeat, and therefore that the arrays are periodic. However, the repeat values differ substantially. The nucleosome repeat for the 9–403 region is 192 ± 5 bp, whereas the repeat for the 4–419 region is 172 ± 5 bp, 20 bp shorter. These repeat values are consistent with our computational predictions.

The 172 ± 5 bp nucleosome repeat length is, to our knowledge, the shortest repeat ever observed in mouse liver chromatin. Thus, nucleosome arrays possessing very short repeats exist in mouse liver nuclei. Moreover, our results suggest that it may be possible to predict these regions computationally from the genomic DNA sequence.

Testing our ability to predict regions of the mouse genome that have short nucleosome repeats

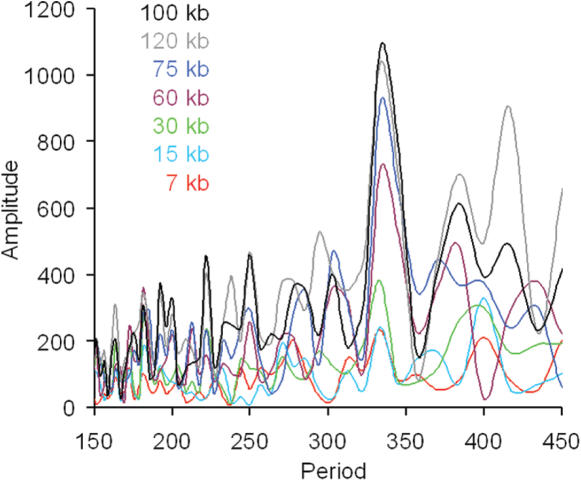
Table 1 shows the results of nine additional experiments similar to the one reported in Figure 1 (probe 4–419) which test the validity of our computational predictions of short repeats. The table entries are arranged in order of increasing predicted repeats. In every case the experiment confirmed the computational prediction for the short nucleosome repeat value within the experimental uncertainty of ±5 bp. The characteristics of each signal are also listed, along with the predicted range of the signal. The range (in kb) over which the signal was strong according to the criteria stated in the Materials and Methods was tested by varying the Fourier window. It was usually fairly narrow and roughly centered on 100 kb. An example is shown in Figure 2 where the window size was varied from 7 to 120 kb for probe 4–419. All of the windows were centered on the 419 bp probe. It can be seen that for the 7 and 15 kb windows, the Amplitude at the Period value of 337 bp (= 2 × 169 bp) is barely above the noise level. For a window of 30 kb, a small peak appears at the Period value of 337 bp, and this peak is only slightly larger than the next largest peak just below 400 bp. The Amplitude at the Period value of 337 bp becomes progressively larger as the window size increases to 60, 75 and 100 kb, respectively. The predominant peak (at 337 bp) meets our criterion of a strong signal by having at least twice the area of any other (Gaussian) peak in the physiological dinucleosome region only between 90 and 110 kb. At 120 kb the Amplitude at the Period value of 337 bp diminishes slightly, and the peaks at 380 and 415 bp increase relative to those in the 100 kb window. Thus, the regular, in-phase oscillations in period-10 VWG are present in large-scale chromatin structures. The Fourier Amplitude reaches maximum strength at 70 kb or greater and remains strong until about 100 kb for most of the loci studied. In two cases the signal reached maximum intensity at 90 kb and remained strong until ∼200 kb. In one case a strong signal was detectable at 40 kb and it persisted until 500 kb.

Figure 2.

Effect of varying the window size on the FT of the period-10 VWG oscillations for locus 1. All windows were centered on the midpoint of probe 4–419. The superimposed curves for windows ranging from 7 to 120 kb can be distinguished from each other by their colors.

In addition to the ten tested predictions, we have included several other entries in Table 1. The fit parameters and signal characteristics are listed for the previously studied mada gene locus (17), a locus predicting a 191 bp repeat, and a locus predicting a 210 bp repeat. The 191 bp prediction was confirmed, but the very high 210 bp prediction was not. Additionally, we included two probes from loci that did not contain a signal; these are representative of most of the genome. These probes detected the bulk repeat, as predicted. We also included the analysis of a ladder that resulted from a probe that did not hybridize specifically, but detected a very large number of loci (detecting a continuum of restriction fragment sizes, instead of the single intended fragment). This probe provided a way of measuring the bulk repeat by Southern blotting, as used in these experiments, instead of by traditional gel staining. The fit parameters obtained by either method were very similar.

Statistical significance of the results confirming our computational predictions

The percentage of mouse liver chromatin possessing nucleosome repeats shorter than 180 bp can not be large because, if it were, the effect of having such repeats present in appreciable amounts should be readily detectable. This point is illustrated in Figure 3 which shows a simulated 195 bp ladder (195) next to a simulated 180 bp ladder (180) and the superposition of these two ladders (merged). It can be seen that the oligomer bands greater than the 5mers become out of phase with each other. This ‘vernier effect’ causes the superimposed ‘ladder’ to lose resolution at about the 6mer where the bands of each individual ladder become maximally out of phase with each other. For short repeat values that are less than 180 bp, the loss of resolution is even more severe (data not shown). Because the bulk chromatin ladder from mouse liver does not lose resolution until beyond the 10mer (17), it can be immediately concluded that the percentage of mouse liver chromatin having repeats shorter than about 180 bp is considerably less than 50% (the percentage in the simulated superimposed ladders of Figure 3).

Figure 3.

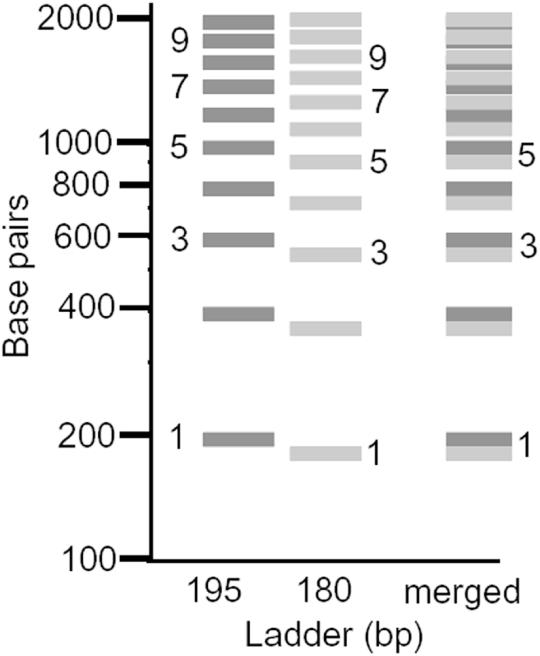
Simulated nucleosome ladders having two different repeats illustrating the vernier effect. A ladder having 195 bp spacing is shown adjacent to a ladder having 180 bp spacing. At least 10 bands can be resolved for each. The superposition of these two ladders (merged) leads to a loss of resolution after the 5mer due to a vernier effect.

The statistical significance of our predictions (Table 1) can be assessed if the percentage of the chromatin in mouse liver nuclei that possesses short nucleosome repeats is known. To estimate this percentage experimentally, we made use of the vernier effect illustrated above. We made mixtures of DNA from MNase-digested mouse liver chromatin (195 ± 5 bp bulk repeat) and M.incana petal chromatin (bulk 183 ± 5 bp repeat) with Matthiola petal: mouse liver weight ratios of: 50:50, 40:60, 30:70, 20:80 and 10:90. We ran these ladder mixtures on an agarose gel along with pure mouse liver chromatin and pure Matthiola petal chromatin nucleosome ladders (Figure 4A). It can be seen that the pure mouse liver (ML) and pure Matthiola petal (MP) nucleosome ladders each extend to the 10mer or beyond, and the ladders begin to go out of phase with each other after the 5mers. As expected, the 50:50-mixture gives a vernier effect similar to the simulation shown in Figure 3. It can also be seen that the vernier effect is detectable at least down to the 20:80 mixture. In Figure 4B the upper regions of the ladders for the 20:80 mixture and for mouse liver chromatin are shown expanded and next to each other. Lane scans are shown in Figure 4C which confirm the visual impression that the peaks for the nucleosome oligomer bands greater than the 5mer are better resolved for the pure mouse liver chromatin than for the 20:80 mixture. Thus, a conservative estimate for the maximum percentage of short repeat chromatin in mouse liver nuclei is about 20%, and therefore the probability of selecting a hybridization probe by chance that detects a short repeat is 0.2. We think that this number is representative of both the repetitive and non-repetitive portions of the genome because ∼20% of the non-specific probes, which hybridized to repetitive DNA, detected repeats that were shorter than the bulk value. The probability of selecting 10 out of 10 probes that detect short repeats (as in Table 1) by chance alone is then about (0.2)¹⁰ = 0.0000001, or one in ten million. Hence, it is highly unlikely that 10 out of 10 probes detecting short nucleosome repeats were selected simply by chance, rather than by following our computational predictions, and the results reported in Table 1 are therefore statistically significant.

Figure 4.

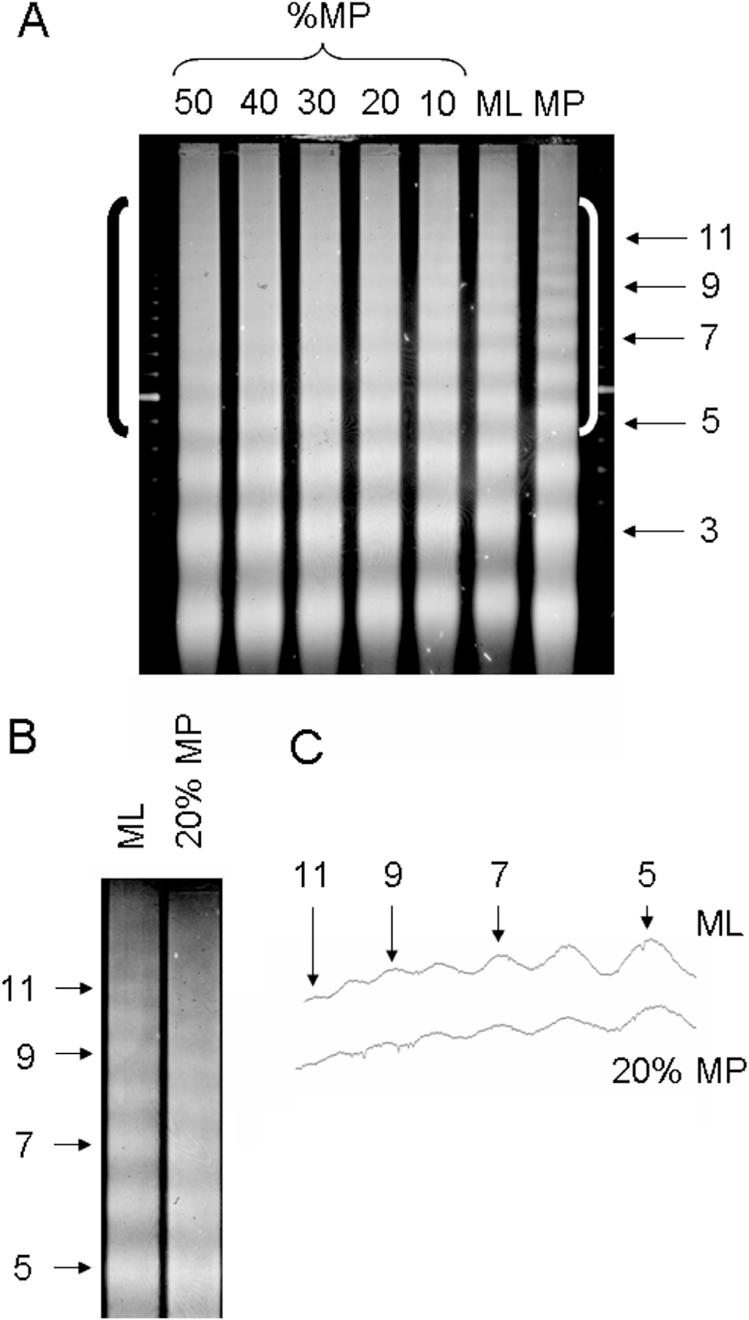
Mixing experiment providing an estimation of the percentage of mouse liver chromatin that possesses a short repeat. (A) Nuclei from mouse liver (ML) or Matthiola petals (MP) were digested with MNase, and the purified DNA fragments were run on an agarose gel which was stained with ethidium bromide to visualize the nucleosome ladders from total genomic DNA for each sample (lanes ML and MP). The shorter nucleosome repeat (183 ± 5 bp) of the MP chromatin compared to the ML chromatin (195 ± 5 bp) is evident. The DNA from the two chromatin samples was mixed together in the proportions indicated (%MP) and analyzed on the same gel. Nucleosome oligomer bands for the MP chromatin are indicated. The brackets denote the upper region of the gel containing the oligomer DNA fragments greater than 5mers. (B) The 20% MP lane is shown adjacent to the ML lane, and the photograph was expanded for comparing the upper region of the gel. The lanes were precisely aligned using the 100 bp ladder markers immediately flanking the gel. (C) Densitometer scan of the ML and 20% MP lanes shown in (B).

DISCUSSION

Our results demonstrate that loci exist in mouse liver chromatin with nucleosome repeats that are well below the bulk chromatin value. Moreover, our results strongly suggest that these loci can be identified from a computational analysis of the DNA sequence. This is the first time that non-repetitive DNA sequence has been used to predict an aspect of large-scale chromatin structure. Experimentally, we have estimated that less than 20% of the chromatin in mouse liver nuclei possesses nucleosome repeats that are ≤180 bp, values at least 15 bp shorter than the bulk chromatin repeat. This estimate is roughly consistent with our computational estimates based upon analysis of ∼60 Mb of DNA sequence. We observed strong unambiguous signals (defined in Materials and Methods), as reported in Table 1, in fewer than 2% of the loci that we analyzed. However, it is likely that signals less strong than those selected here can still be influential. Our computational analysis further suggests that nucleosome repeats with values as short as 175 bp occur very infrequently in mouse liver; signals for such short repeats were observed in less than 1% of the loci analyzed.

In addition to predicting short nucleosome repeats from the DNA sequence, we attempted to define the upper and lower limits for nucleosome repeats that exist in mouse liver chromatin. We have never observed a repeat value longer than the bulk chromatin repeat of 195 ± 5 bp. This was true even when the computational prediction was 210 bp (probe 19–395, Table 1). Thus, nucleosome repeat values longer than the bulk value may not exist in mouse liver chromatin. It is interesting that probe 19–395 detected an 187 ± 5 bp repeat, a value that is slightly shorter than the bulk repeat. For the 100 kb window centered on this probe, a Fourier peak is present at 370 bp = 2 × 185 bp that meets our stated criterion for a strong signal, despite the presence of the larger peak at 420 bp = 2 × 210 bp. Thus, this 370 bp peak could explain the experimentally observed 187 ± 5 bp repeat. The shortest nucleosome repeat that we observed was 172 ± 5 bp (Table 1). This occurred when the computational prediction was 169 bp (Table 1). The observed value of 172 bp in this case was within our experimental uncertainty of ±5 bp of the 169 bp prediction. However, repeats shorter than about 172 bp may not exist in mouse liver chromatin.

From our computational analysis of only 60 Mb of mouse DNA we do not yet know whether there is anything in common among the loci possessing short nucleosome repeats. The number of annotated genes in the ten short-repeat loci identified varied between zero and five for the ∼100 kb windows. This variation is not significantly different from what would be expected from ten randomly selected 100 kb windows. It would be feasible to analyze the whole mouse genome, after the still significant numbers of gaps present are eliminated, and to compare the results with those obtained from the human genome analyzed in the same way. It is interesting that the range over which the signal for the formation of a particular nucleosome repeat extends is close to 100 kb in most cases. It is clear from Figure 2 and Table 1 that DNA windows for analysis with sizes less than about 70 kb would not have good predictive power. Moreover, we have found only one example thus far of a phased period-10 VWG signal that was not evident until a window larger than 100 kb was examined. The DNA length of ∼100 kb could conceivably correspond to some element of large-scale chromatin structure, such as a loop emanating from a scaffold (23–25).

It is plausible that 100 kb regions of DNA with distinctive nucleosome repeats also possess distinctive chromatin structures. Recent work has supported non-solenoid-like models for chromatin structure containing straight internucleosomal (linker) DNA segments (10). Computer modeling studies (9) have suggested that such structures are highly sensitive to linker DNA lengths and their degree of uniformity. Therefore, even if chromatin higher-order structures are dynamic in vivo, different nucleosome arrangements could cause the structures to bend and flex in different ways. Moreover, a genome-wide study of (human) chromatin structure suggested that there is not a simple structural division between heterochromatin and euchromatin, and that there is not a simple correlation between gene expression and chromatin compaction (26). These observations are consistent with the existence of a variety of different higher-order chromatin structures, rather than just open or closed chromatin. The DNA sequence could play a role in the formation of these structures.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.