Forced-Unfolding and Force-Quench Refolding of RNA Hairpins

Abstract

Nanomanipulation of individual RNA molecules, using laser optical tweezers, has made it possible to infer the major features of their energy landscape. Time-dependent mechanical unfolding trajectories, measured at a constant stretching force (f_S) of simple RNA structures (hairpins and three-helix junctions) sandwiched between RNA/DNA hybrid handles show that they unfold in a reversible all-or-none manner. To provide a molecular interpretation of the experiments we use a general coarse-grained off-lattice Gō-like model, in which each nucleotide is represented using three interaction sites. Using the coarse-grained model we have explored forced-unfolding of RNA hairpin as a function of f_S and the loading rate (r_f). The simulations and theoretical analysis have been done both with and without the handles that are explicitly modeled by semiflexible polymer chains. The mechanisms and timescales for denaturation by temperature jump and mechanical unfolding are vastly different. The directed perturbation of the native state by f_S results in a sequential unfolding of the hairpin starting from their ends, whereas thermal denaturation occurs stochastically. From the dependence of the unfolding rates on r_f and f_S we show that the position of the unfolding transition state is not a constant but moves dramatically as either r_f or f_S is changed. The transition-state movements are interpreted by adopting the Hammond postulate for forced-unfolding. Forced-unfolding simulations of RNA, with handles attached to the two ends, show that the value of the unfolding force increases (especially at high pulling speeds) as the length of the handles increases. The pathways for refolding of RNA from stretched initial conformation, upon quenching f_S to the quench force f_Q, are highly heterogeneous. The refolding times, upon force-quench, are at least an order-of-magnitude greater than those obtained by temperature-quench. The long f_Q-dependent refolding times starting from fully stretched states are analyzed using a model that accounts for the microscopic steps in the rate-limiting step, which involves the trans to gauche transitions of the dihedral angles in the GAAA tetraloop. The simulations with explicit molecular model for the handles show that the dynamics of force-quench refolding is strongly dependent on the interplay of their contour length and persistence length and the RNA persistence length. Using the generality of our results, we also make a number of precise experimentally testable predictions.

INTRODUCTION

RNA molecules adopt precisely defined three-dimensional structures to perform specific functions (1). To reveal the folding pathways navigated by RNA en route to their native conformations requires exhaustive exploration of the complex underlying energy landscape over a wide range of external conditions. In recent years, mechanical force has been used to probe the unfolding of a number of RNA molecules (2–4). Force is a novel way of probing regions of the energy landscape that cannot be accessed by conventional methods (temperature changes or variations in counterion concentrations). In addition, response of RNA to force is relevant in a number of cellular processes such as mRNA translocation through the ribosome and the activity of RNA-dependent RNA polymerases. Indeed, many dynamical processes are controlled by deformation of biomolecules by mechanical force.

By exploiting the ability of single molecule laser optical tweezer (LOT) to control the magnitude of the applied force, Bustamante and co-workers have generated mechanical unfolding trajectories for RNA hairpins and the Tetrahymena thermophila ribozyme (5,6). The unfolding of the ribozyme shows multiple routes with great heterogeneity in the unfolding pathways (6). In their first study (5), they showed that simple RNA constructs (P5ab RNA hairpins or a three-helix junction) unfold reversibly at equilibrium. From the time traces of the end-to-end distance (R) of P5ab, for a number of force values, Liphardt et al. (5) showed that the hairpins unfold in a two-state manner. The histograms of time-dependent R (and assuming ergodicity) were used to calculate the free energy difference between the folded and unfolded states. Unfolding kinetics, as a function of the stretching force f_S, was used to identify the position of the transition states (5,7,8). These experiments and subsequent studies have established force as a viable way of quantitatively probing the RNA energy landscape with R serving as a suitable reaction coordinate.

The experiments by Bustamante and co-workers have led to a number of theoretical and computational studies using a variety of different methods (9–14). These studies have provided additional insights into the mechanical unfolding of RNA hairpins and ribozymes. In this article, we build on our previous work (14) and new theoretical analysis to address a number of questions that pertain to mechanical unfolding of RNA hairpins. In addition, we also provide the first report on force-quench refolding of RNA hairpins. This article addresses the following major questions:

1. Are there differences in the mechanism of thermal and mechanical unfolding? We expect these two processes to proceed by different pathways because denaturation induced by temperature jump results in a stochastic perturbation of the native state while destabilization by force is due to a directed perturbation. The molecular model for P5GA gives a microscopic picture of these profound differences.

2. For a given sequence, does the position of the transition state move in response to changes in the loading rate (r_f) or the stretching force f_S? Based on the analysis of experiments over a narrow range of conditions (fixed temperature and loading rate), it has been suggested that the location of the sequence-dependent unfolding transition state (TS) for secondary structure is midway between the folded state while the TS for the ribozyme is close to the native conformation (5). Explicit simulations show that the TS moves dramatically, especially at high values of f_S and r_f. As a consequence, the dependence of the unfolding rate on f_S deviates from the predictions of the Bell model (15).

3. What is the origin of the dramatic differences in refolding by force-quench from stretched conformations and temperature-quench refolding? Experiments by Fernandez and Li (8) on refolding initiated by force-quench on polyubiquitin construct suggest similar differences in the refolding timescales. For RNA hairpins, we show that the incompatibility of the local loop structures in the stretched state and the folded conformations lead to extremely long refolding times upon force-quench.

4. What are the effects of linker dynamics on forced-unfolding and force-quench refolding of RNA hairpins? The manipulation of RNA is done by attaching a handle or linker to the 3′ and 5′ ends of RNA. Linkers in the LOT experiments, which are done under near-equilibrium conditions, are RNA/DNA hybrid handles. These are appropriately modeled as wormlike chains (WLCs). By adopting an explicit polymer model for semiflexible chains we show that, under certain circumstances, nonequilibrium response of the handle (which is not relevant for the LOT experiments) can alter the forced-unfolding dynamics of RNA. We probe the effects of varying the linker characteristics on the dynamics of folding/unfolding of RNA for the model of the handle-RNA-handle construct. In certain ranges of r_f, nonequilibrium effects on the dynamics of linkers can affect the force-extension profiles.

METHODS

Hairpin sequence

To probe the dynamics of unfolding and force-quench refolding we have studied in detail the 22-nucleotide hairpin, P5GA, whose solution structure has been determined by NMR (Protein Data Bank (PDB) id:1eor). In many respects P5GA is similar to P5ab in the P5abc domain of group I intron (16). Both of these structures have GA mismatches, and are characterized by the presence of the GAAA tetraloop. The sequence of P5GA is GGCGAAGUCGAAAGAUGGCGCC (17).

RNA model

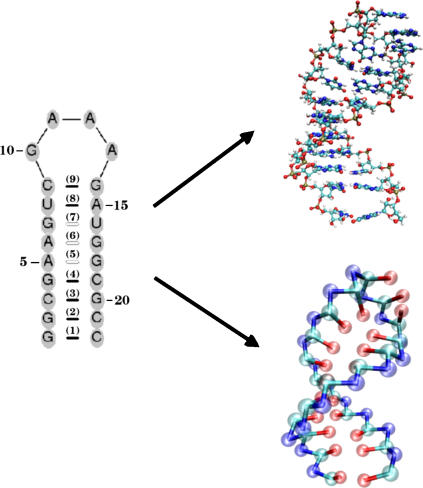
Because it is difficult to explore the unfolding and refolding of RNA hairpins over a wide range of external conditions such as temperature (T), stretching force (f_S), and quench force (f_Q) using all-atom models of biomolecules in explicit water, we have introduced a minimal off-lattice coarse-grained model (14). (Note that throughout the article, while f_S and f_Q each have a specific meaning, we use the notation f for referring to mechanical force in general terms.) In this model, each nucleotide is represented by three beads with interaction sites corresponding to the phosphate (P) group, the ribose (S) group, and the base (B) (14). Thus, the RNA backbone is reduced to the polymeric structure ((P – S)_n) with the base that is covalently attached to the ribose center. In the minimal model, the RNA molecule with N nucleotides corresponds to 3N interaction centers. The secondary structure and the lowest energy structure using the minimal model are shown in Fig. 1.

FIGURE 1.

Coarse-grained representation of a molecule of RNA using three interaction sites per nucleotide—phosphate (P), sugar (S), and base (B). On the left we present the secondary structure of the 22-nt P5GA hairpin, in which the bonds formed between basepairs are labeled from 1 to 9. The PDB structure (17) and the lowest energy structure obtained with the coarse-grained model are shown on the right.

Energy function

The total energy of a RNA conformation, specified by the coordinates of the 3N sites, is written as V_T = V_BL + V_BA + V_DIH + V_STACK + V_NON + V_ELEC. Harmonic potentials are used to enforce structural connectivity and backbone rigidity. The connectivity between two beads (P_iS_i, S_iP_i+1, and B_iS_i) is maintained using

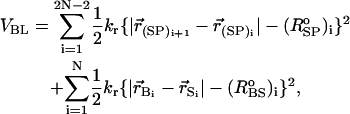(1)

where k_r = 20 kcal/(mol × Å²), and (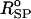)_i and (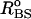)_i are the distances between covalently bonded beads in the PDB structure. The notation (SP)_i, denotes the i^th backbone bead S or P. The angle θ formed between three successive beads (P_i – S_i – P_i+1 or S_i–1 – P_i – S_i) along sugar-phosphate backbone is subject to the bond-angle potential,

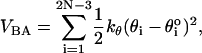(2)

where k_θ = 20 kcal/(mol × rad²), and 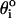is the value in the PDB structure.

Dihedral angle potential

The dihedral angle potential (V_DIH) describes the ease of rotation around the angle formed between four successive beads along the sugar-phosphate backbone (S_i–1P_iS_iP_i+1 or P_iS_iP_i+1S_i+1). The i^th dihedral angle φ_i, which is the angle formed between the two planes defined by four successive beads i to i + 3, is defined by 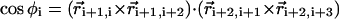. In the coarse-grained model, the right-handed chirality of RNA is realized by appropriate choices of the parameters in the dihedral potential. Based on the angles in the PDB structure (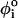), one of the three types of dihedral potentials, trans (t, 0 < 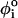< 2π/3), gauche (+) (g⁺, 2π/3 < 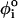< 4π/3), and gauche (–) (g⁻, 4π/3 < 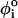< 2π), is assigned to each of the four successive beads along the backbone. The total dihedral potential of the hairpin is

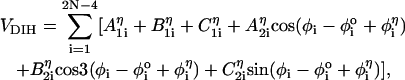(3)

where the parameters (in kcal/mol) defined for t, g⁺, and g⁻ are

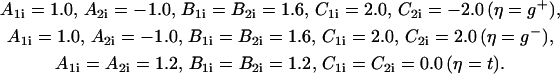To account for the flexibility in the loop region we reduce the dihedral angle barrier by halving the parameter values in 19 ≤ i ≤ 24.

Stacking interactions

Simple RNA secondary structures, such as hairpins, are largely stabilized by stacking interactions whose context-dependent values are known (18–20). The folded P5GA RNA hairpin is stabilized by nine hydrogen bonds between the basepairs (see Fig. 1 B), including two GA mismatch pairs (17). The stacking interactions that stabilize a hairpin can be written as 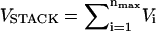(nm_ax = 8 in P5GA). We assume that the orientation-dependent V_i is

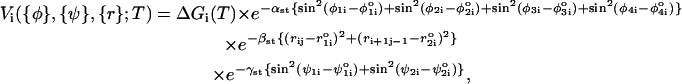(4)

where: ΔG(T) = ΔH – TΔS; the bond angles {φ} are φ_1i ≡ ∠S_iB_iB_j, φ_2i ≡ ∠B_iB_jS_j, φ_3i ≡ ∠S_i+1B_i+1B_j−1, and φ_4i ≡ ∠B_i+1B_j–1S_j–1; the distance between two paired bases is r_ij = |B_i – B_j| and r_i+1j–1 = |B_i+1 – B_j–1|; and ψ_1i and ψ_2i are the dihedral angles formed by the four beads B_iS_iS_i+1B_i+1 and B_j–1S_j–1S_jB_j, respectively. The superscript o refers to angles and distances in the PDB structure. The values of α_st, β_st, and γ_st are 1.0, 0.3 Å⁻², and 1.0, respectively. We take ΔH and ΔS from Turner's thermodynamic data set (18,19). There are no estimates for GA-related stacking interactions. Nucleotides G and A do not typically form a stable bond, and hence GA pairing is considered a mismatch. We use the energy associated with GU for the GA basepair.

Nonbonded interactions

We use the Lennard-Jones interactions between nonbonded interaction centers to account for the hydrophobicity of the purine/pyrimidine groups. The total nonbonded potential is

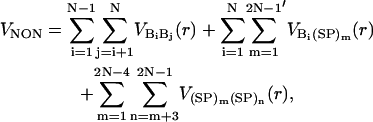(5)

where 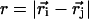. The prime in the second term on the Eq. 5 denotes the condition m ≠ 2i – 1. In our model, a native contact exists between two noncovalently bound beads, provided they are within a cutoff distance r_c (= 7.0 Å). Two beads beyond r_c are considered to be nonnative. For a native contact,

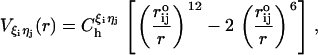(6)

where 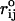is the distance between beads in PDB structure and 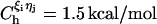for all native contact pairs, except for the B₁₀B₁₃ basepair associated with the formation of the hairpin loop, for which 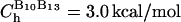. The additional stability for the basepair associated with loop formation is similar to the Turner's thermodynamic rule for the free energy gain in the tetraloop region. For beads beyond r_c the interaction is

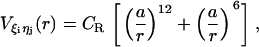(7)

with a = 3.4 Å and C_R = 1 kcal/mol. The value of 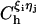(= 1.5 kcal/mol) has been chosen so that the hairpin undergoes a first-order transition from unfolded states. Our results are not sensitive to minor variations in C_h.

Electrostatic interactions

The charges on the phosphate groups are efficiently screened by counterions so that in the folded state the destabilizing contribution of the electrostatic potential is relatively small. However, the nature of the RNA conformation (especially tertiary interactions) can be modulated by changing counterions. For simplicity, we assume that the electrostatic potential between the phosphate groups is pairwise-additive 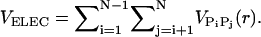For 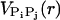we use Debye-Hückel potential, which accounts for screening by condensed counterions and hydration effects, and is given by

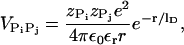(8)

where 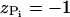is the charge on the phosphate ion, ε_r = ε/ε₀, and the Debye length is 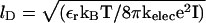with 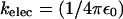= 8.99 × 10⁹ JmC. To calculate the ionic strength 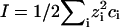, we use the value c_i = 200 mM-NaCl from the header of a PDB file (17). We use ε_r = 10 in the simulation (21). Because of the Debye screening length, 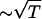, the strength of electrostatic interactions between the phosphate groups are temperature-dependent even when we ignore the variations of ε with T. At room temperature (T ∼ 300 K), the electrostatic repulsion between the phosphate groups at r ∼ 5.8 Å, which is the closest distance between phosphate groups, is 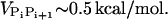Thus, V_ELEC between phosphate groups across the basepairing (r = 16 ∼ 18 Å) is almost negligible. The Debye-Hückel interactions are most appropriate for monovalent counterions like Na⁺.

Models for linker or handle

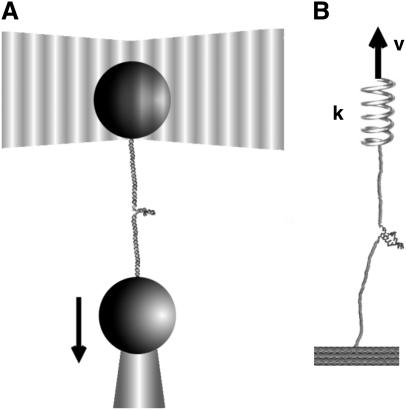
In laser optical tweezer (LOT) experiments, the RNA molecules are attached to the polystyrene beads by an RNA/DNA hybrid handle or linker. A schematic illustration of the pulling simulations that mimic the experimental setups for the LOT (Fig. 2 A) is shown in Fig. 2 B. Globally, the principles involved in atomic force microscopy (AFM) and LOT for mechanical unfolding of biomolecules are essentially the same, except for the difference in the effective spring constant. The spring constant of the nearly harmonic potential of the optical trap is in the range of k = 0.01–0.1 pN/nm, whereas the cantilever spring in AFM experiments (Fig. 2 B) is much stiffer and varies from 1 to 10 pN/nm. To fully characterize the RNA energy landscape, it is necessary to explore a wide range of loading rates (22). To vary r_f we have used different values of k in the simulations.

FIGURE 2.

(A) Schematic illustration of laser optical tweezer (LOT) setup for RNA stretching. A single RNA molecule is held between two polystyrene beads via molecular handles with one of the polystyrene beads being optically trapped in the laser light. The location of the other bead is changed by micropipette manipulation. The extension of the molecule through the molecular handles induces the deviation in the position of the polystyrene bead held in the force-measuring optical trap. (B) Both LOT and AFM can be conceptualized as schematically shown. The RNA molecule is sandwiched between the linkers and one end of the linker is pulled. The spring constant of the harmonic trap in LOT (or the cantilever in AFM experiments) is given by k and v is the pulling speed.

We simulate mechanical unfolding of RNA hairpins either by applying a constant force on the 3′-end with the 5′-end being fixed (unfolding at constant force), or by pulling the 3′-end through a combination of linkers and harmonic spring (Fig. 2 B) at a constant speed in one direction (unfolding at constant loading rate). Comparison of the results allows us to test the role of the linker dynamics on the experimental outcome. If the linker is sufficiently stiff then it should not affect the dynamics of RNA. On the other hand, unfolding at constant loading rate (r_f ≡ k × v, where v is the pulling speed and the stretching force (f_S) is computed using f = k × δz with δz being the displacement of the spring) can be modulated either by changing k or v. Instead of k, an effective spring constant k_eff, with 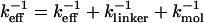, should be used to compute the loading rate. Typically, 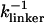and 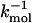(where k_mol is the stiffness associated with the model) are small, and hence, k_eff ≈ k. In this setup, the relevant variables are k, v, and the contour length (L) of the linker and the effective stiffness of the linker. We explore the effects of these factors by probing changes in the force extension curve (FEC). The variations in L are explored only using constant loading rate simulations. Manosas and Ritort (13) used an approximate method to model linker dynamics.

The energy function for the linker molecule is

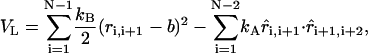(9)

where r_{i, i+1} and 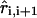are the distance and unit vector connecting i and i + 1 residue, respectively. For the bond potential we set k_B = 20 kcal/(mol · Ų) and b = 5 Å. This form of the energy function describes the wormlike chain (WLC) (23) (appropriate for RNA/DNA hybrid handles used by Liphardt et al. (5)) when k_A is large. The linker becomes more flexible as the parameter describing the bending potential, k_A, is reduced. Thus, by varying k_A the changes in the entropic elasticity of the linker on RNA hairpin dynamics can be examined. We use k_A = 80 kcal/mol or 20 kcal/mol to change the flexibility of the linker. For the purpose of computational efficiency, we did not include excluded volume interactions between linkers or between the linker and RNA. When linkers are under tension, the chains do not cross unless thermal fluctuations are larger than the energies associated with force. To study the linker effect on force extension curves (FEC), we attach two linker polymers, each with the contour length L/2, to the ends of the hairpin and stretch the molecule using the single pulling speed 0.86 × 10² μm/s with spring constant k = 0.7 pN/nm. The total linker length is varied from L = (10–50) nm.

Simulations

We assume that the dynamics of the molecules (RNA hairpins and the linkers) can be described by the Langevin equation. The system of Langevin equations is integrated as described before (14,24). Using typical values for the mass of a bead in a nucleotide (B_i, S_i, or P_i), m = 100 g/mol ∼ 160 g/mol, the average distance between the adjacent beads a = 4.6 Å, the energy scale ε_h = 1 ∼ 2 kcal/mol, the natural time is 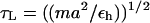= 2.6 ∼ 2.8 ps. We use τ_L = 2.0 ps to convert the simulation times into real times. To estimate the timescale for thermal and mechanical unfolding dynamics, we use a Brownian dynamics algorithm (25,26) for which the natural time for the overdamped motion is 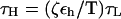. We use ζ = 50 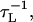which approximately corresponds to friction constant in water, in the overdamped limit. To probe the thermodynamics and kinetics of folding we used a number of physical quantities (end-to-end distance (R), fraction of native contacts (Q), the structural overlap function (χ), number of hydrogen bonds n_bond, etc.) to monitor the structural change in the hairpin.

Computation of free energy profiles

We adopted the multiple histogram technique (27,28) to compute the thermodynamic averages of all the observables at various values of T and f. For example, the thermodynamic average of the fraction of native contact, Q, can be obtained at arbitrary values of T and f if the conformational states are well sampled over a range of T- and f-values. The thermodynamic average of Q is given by

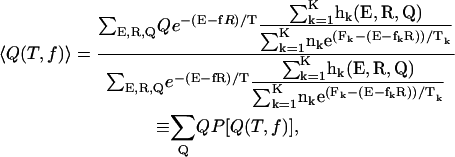(10)

where K is the number of histograms, h_k(E, R, Q) is the number of states between E and E + δE, R and R + δR, Q and Q + δQ in the k^th histogram, 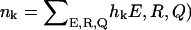, and T_k and f_k are the temperature and the force in the simulations used to generate the k^th histogram, respectively. The free energy, F_k, which is calculated self-consistently, satisfies

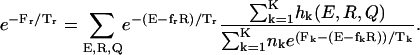(11)

Using the low friction Langevin dynamics, we sampled the conformational states in the (T,f) in the range {0 K < T < 500 K, f = 0.0 pN} and {0.0 pN < f < 20.0 pN, T = 305 K}. Exhaustive samplings around the transition regions at {305 K ≤ T ≤ 356 K, f = 0.0 pN} and {5.0 pN ≤ f ≤ 7.0 pN, T = 305 K} is required to obtain reliable estimates of the thermodynamic quantities. The free energy profile, with Q as an order parameter, is given by

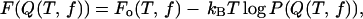(12)

where F_o(T, f) = –k_BT log Z(T, f); 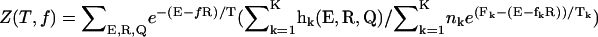; and P(Q(T, f)), as defined in Eq. 10. The free energy profile F(R) with R as a reaction coordinate can be obtained using a similar expression.

RESULTS

Mechanisms of thermal denaturation and forced-unfolding are different

We had previously reported (14) the thermodynamic characteristics of the P5GA hairpin as a function of T and f. The native structure of the hairpin, determined using a combination of multiple slow cooling, simulated annealing, and steepest-descent quench, yielded conformations whose average root mean-square deviation with respect to the PDB structure is ∼0.1 Å (14). The use of a Gō-like model leads to a small value of root mean-square deviation. From the equilibrium (T,f) phase diagram in Hyeon and Thirumalai (14), the melting temperature, T_m ≈ 341 K, at f_S = 0. Just as in thermal denaturation at T_m at zero f, the hairpin unfolds by a weak first-order transition at an equilibrium critical force f_c. Above f_c, which is temperature-dependent, the folded state is unstable.

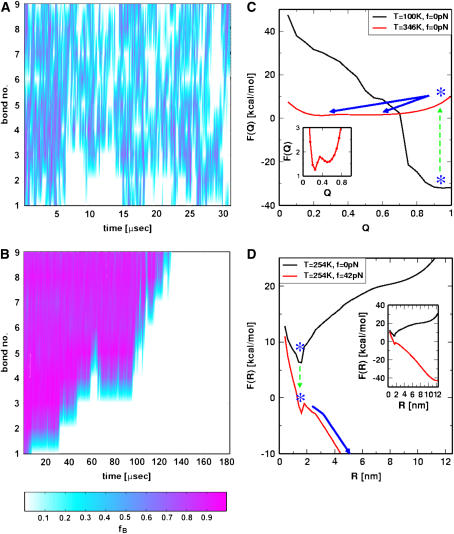
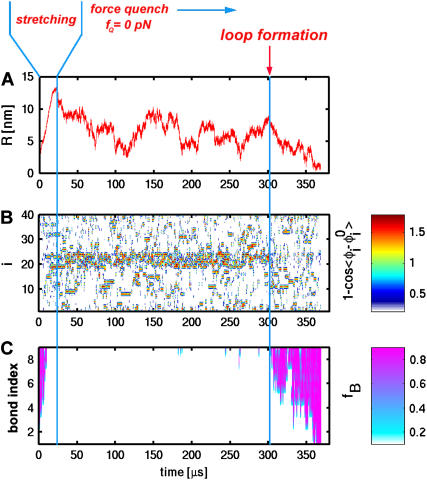
To monitor the pathways explored in the thermal denaturation, we initially equilibrated the conformations at T = 100 K at which the hairpin is stable. Thermal unfolding (f = 0) was initiated by a temperature jump to T = 346 K > T_m. Similarly, forced-unfolding is induced by applying a constant force f_S = 42 pN to thermally equilibrated initial conformation at T = 254 K (14). The value of f_S = 42 pN far exceeds f_c = 15 pN at T = 254 K. Upon thermal denaturation, the nine bonds fluctuate (in time) stochastically, in a manner independent of one another until the hairpin melts (Fig. 3 A). Forced-unfolding, on the other hand, occurs in a directed manner. Mechanical unfolding occurs by sequential unzipping with force unfolding the bond, from the ends of the hairpin (beginning at bond 1) to the loop (Fig. 3 B).

FIGURE 3.

Unfolding pathways upon temperature and force jump. (A) The time-dependence of rupture of the bonds is monitored when the temperature is raised from T = 100 K < T_m ≈ 341 K to T = 346 K > T_m. The nine-bond set is disrupted stochastically. (B) In forced unfolding, bonds rip from the ends to the loop regions in an apparent staircase pattern. For both A and B, the scale indicating the probability of a given bond being intact is given below. (C) Free energy F(Q) as a function of Q. The stable hairpin with Q ≈ 1 at T = 100 K becomes unstable upon rapid temperature jump to T = 346 K (blue asterisks). Subsequent to the T-jump, the hairpin relaxes to the new equilibrium state by crossing a small free energy barrier (≈0.5 kcal/mol) with Q ≈ 0.2. The inset shows the equilibrium free energy profile at T = 346 K and f = 0. (D) Deformation of the free energy profile upon application of force. The R-dependent free energy F(R) = F(R; f_S = 0) – f_S × R favors the stretched state at R = 12 nm when f = 42 pN (see inset). The activation barrier separating the UBA and NBA is ∼ 1–2 kcal/mol.

The differences in the folding pathways are also mirrored in the free energy profiles. Assuming that Q is an adequate reaction coordinate for thermal unfolding (29) we find, by comparing F(Q) at T = 100 K and T = 346 K, that thermal melting occurs by crossing a barrier. The native basin of attraction (NBA) at Q = 0.9 at T = 100 K is unstable at the higher temperature and the new equilibrium at Q ∼ 0.2 is reached in an apparent two-state manner (Fig. 3 C). Upon directed mechanical unfolding, the free energy profile F(R) is tilted from the NBA at R ≈ 1.5 nm to R ≈ 12 nm, at which the stretched states are favored at f = 42 pN. The forced-unfolding transition also occurs abruptly once the activation barrier at R ≈ 1.5 nm (close to the folded state) is crossed (Fig. 3 D).

Free energy profiles and transition state (TS) movements

Based on the proximity of the average transition state location, 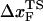, it has been suggested that folded states of RNA (6) and proteins (7) are brittle. If the experiments are performed by stretching at a constant loading rate, then 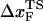is calculated using 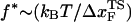log r_f (30), where f* is the most probable unfolding force and r_f, the loading rate, is r_f = df/dt = kv. Substantial curvatures in the dependence of f* on log r_f ((f*, log r_f) plot) have been observed, especially if r_f is varied over a wide range (22). Similarly, in constant force unfolding experiments, 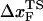is obtained from the Bell equation (15), which relates the unfolding rate to the applied forc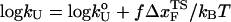e, where 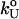is the unfolding rate in the absence of force. In the presence of curvature in the (f*, log r_f) plots or when the Bell relationship is violated (31), it is difficult to extract meaningful values of 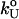or 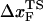by a simple linear extrapolation. By carefully examining the origin of curvature in the (f*, log r_f) plot or in k_U, we show that in the unfolding of hairpin the observed nonlinearities are due to movements in the transition state ensemble, i.e., 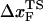depends on f_S and r_f.

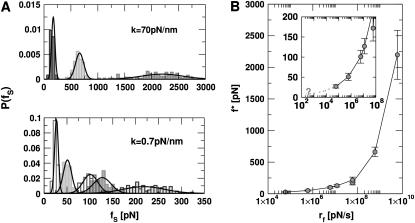
Unfolding at constant loading rate

We performed forced unfolding simulations by varying both the pulling speed v and the spring constant k so that a broad range of loading rates can be covered. The unfolding forces at which all the hydrogen bonds are ruptured are broadly distributed, with the average and the dispersion that increase with growing loading rates (Fig. 4 A). The plot of f* as a function of log r_f (Fig. 4 B) shows marked departure from linearity. The slope of the plot ((f*, log r_f)) increases sharply as r_f increases. There are two possible reasons for the increasing tangent. One is the reduction of 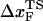, which would lead to an increase in the slope (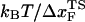) of f* vs. log r_f. The other is the increase of curvature at the transition state region, i.e., the barrier top of the free energy landscape. Regardless of the precise reason, it is clear that the standard way of estimating 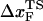using f* at large loading rates results in a very small value of 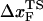. We estimate 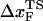from (f*, log r_f) plot to be 4 Å at r_f ≈ 10⁵ pN/s. The estimated value of 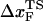is unphysical, because 4 Å is less than the average distance between neighboring P atoms. The minimum pulling speed used in our simulations is nearly five orders-of-magnitude greater than in experiments. The use of large loading rate results in small values of 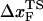. If the simulations can be performed at small values of r_f we expect the slope of f* vs. log r_f to decrease, which would then give rise to physically reasonable values of 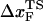at low r_f. Our simulations suggest that the curvature in the plot of f* as a function of log r_f is due to the dependence of 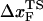on r_f and not due to the presence of multiple transition states (22). As a result, extrapolation to low r_f values can give erroneous results (Fig. 4 B).

FIGURE 4.

Constant loading rate force unfolding. (A) The unfolding force distributions at different pulling speeds with hard (k = 70 pN/nm, top) and soft springs (k = 0.7 pN/nm, bottom). For the hard spring, the pulling speeds from right to left are v = 8.6 × 10⁴, 8.6 × 10³, and 8.6 × 10² μm/s. For the soft spring, the pulling speeds are v = 8.6 × 10⁴, 1.7 × 10⁴, 8.6 × 10³, 8.6 × 10², and 8.6 × 10¹ μm/s from right to left force peaks. The peak in the distributions which are fit to a Gaussian is the most probable force f*. (B) The dependence of f* as a function of the loading rates, r_f. The results from the hard spring and soft spring are combined using the loading rate as the relevant variable. The inset illustrates the potential difficulties in extrapolating from simulations at large r_f to small values of r_f.

Unfolding at constant force

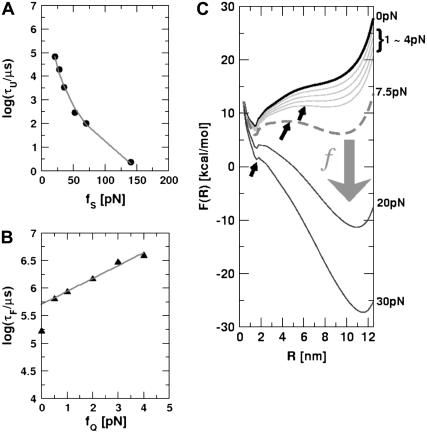
To monitor the transition state movements, we performed a number of unfolding simulations by applying f_S > 20 pN at T = 290 K. The unfolding rates are too slow at f_S < 20 pN to be simulated. Nevertheless, the simulations give strong evidence for force-dependent movement of 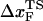. For a number of values of f_S in the range 20 pN < f_S < 150 pN, we computed the distribution of first-passage times for unfolding. The first-passage time for the i^th molecule is reached if R becomes R = 5 nm for the first time. From the distribution of first-passage times (for ∼50–100 molecules at each f_S) we calculated the mean unfolding time. Just as for unfolding at constant r_f, the dependence of log τ_U on f_S shows curvature (Fig. 5 A)—hence deviating from the often-used Bell model (31). By fitting τ_U to the Bell formula (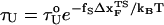), over a narrow range of f_S we obtain 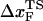≈ 4 Å, which is too small to be physically meaningful at f_S = 0.

FIGURE 5.

Kinetics of forced-unfolding and force-quench refolding. (A) Plot of force-induced unfolding times (τ_U) as a function of the stretching force. Over a narrow range of force τ_U decreases exponentially as f increases. (B) Refolding time τ_F as a function of f_Q. The initial value of the stretching force is 90 pN. By fitting τ_F using 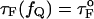exp(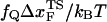), in the range of 0.5 pN < f_Q < 4 pN, we obtain 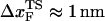and 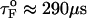. (C) Changes in the equilibrium free energy profiles at T = 290 K F(R) as a function of the variable R. We show F(R) at various f_S values. For emphasis, the free energies at f_S = 0 and at the transition midpoint f_S = 7.5 pN (dashed line) are drawn in thick lines.

Insights into the shift of 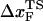as f_S increases can be gleaned from the equilibrium force-dependent free energy F(R) as a function of R. The one-dimensional free energy profiles F(R) show significant movements in 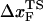as f_S changes (Fig. 5 C). As f_S increases, 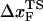decreases sharply, which implies that the unfolding TS is close to the folded state. At smaller values of f_S, the TS moves away from the native state. At the midpoint of the transition, 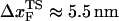, which is approximately half-way to the native state. The result for 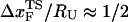(R_U is the average value of R in the unfolded state) is in accord with experiments (5) done at forces that are not too far from the equilibrium unfolding force. Although 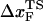is dependent on the RNA sequence, it is likely that, for simple hairpins, 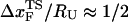. The prediction that 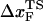is dependent on f_S is amenable to experimental test.

Force-quench refolding times depend (approximately) exponentially on f_Q

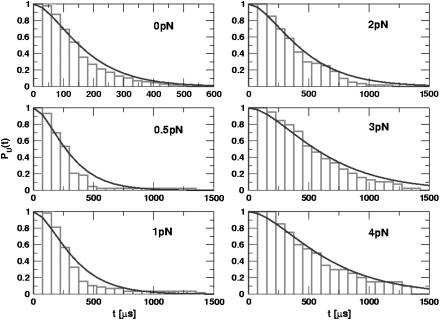
One of the great advantages of force-quench refolding experiments (8) is that the ensemble of conformations with a predetermined value of R can be prepared by suitably adjusting the value of f_S (8). Because force-quench refolding can be initiated from conformations with arbitrary values of R, regions of the energy landscape that are completely inaccessible in conventional experiments can be probed. To initiate refolding by force-quench, we generated extended conformations with R = 13.5 nm, using f_S = 90 pN at T = 290 K. Subsequently, we reduced the force to f_Q in the range 0.5 pN < f_Q < 4 pN. For these values of f_Q, the hairpin conformation is preferentially populated at equilibrium. The probability, P_U(t), that the RNA hairpin remains unfolded at six f_Q values, decays nonexponentially (Fig. 6). The mean refolding times, τ_F(f_Q), upon force-quench, which are computed using P_U(t) (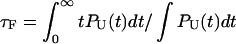), show that in the range 0.5 pN < f_Q < 4 pN (Fig. 5 B),

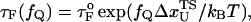(13)

where 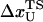is the distance from the unfolded basin of attraction to the refolding transition state, and 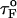is the refolding time in the absence of force. Linear regression gives 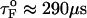and 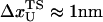. The value of 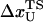, which is obtained from kinetic simulations, is in accord with the location of 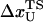obtained directly from the equilibrium free energy profiles F(R) (Fig. 5 C). In the 0.5 pN < f_Q < 4 pN range, the distance from UBA to the TS is ∼1 nm, and is a constant. Thus, kinetic and thermodynamic data lead to a consistent picture of force-quench refolding.

FIGURE 6.

Time-dependence of the probability that RNA is unfolded upon force-quench. In these simulations, T = 290 K, and the initial stretching force, f_S = 90 pN, and f_Q, the quench force, is varied (values are given in each panel). The simulation results are fit using Eq. 14, which is obtained using the kinetic scheme 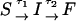. Here, I represents conformations within certain fractions of incorrect dihedral angles. The time constants (τ₁,τ₂), in μs, at each force are: (81.2, 101.3) at f_Q = 0 pN; (159.5, 160.8) at f_Q = 0.5 pN; (180.0, 174.8) at f_Q = 1 pN; (237.6, 240.5) at f_Q = 2 pN; (326.8, 335.6) at f_Q = 3 pN; and (347.7, 329.7) at f_Q = 4 pN.

If the simulations are done with f_Q ≡ 0 pN, then we find that τ_F(f_Q = 0) ≈ 191 μs (Fig. 5 B), which differs from 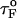obtained using Eq. 13. When f_Q is set to zero, the 3′ end fluctuates, whereas when f_Q ≠ 0, the 3′ end remains fixed. The rate-limiting step in the hairpin formation is the trans→ gauche transitions in the dihedral angles in the GAAA tetraloop region (see below). When one end is free to fluctuate, as is the case when f_Q = 0, the trans→gauche occurs more rapidly than f_Q ≠ 0. The difference between τ_F(f_Q = 0) and 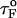is, perhaps, related to the restriction in the conformational search among the compact structures, which occurs when one end of the chain is fixed.

Metastable intermediates lead to a lag phase in the refolding kinetics

The presence of long-lived conformations (see below), with several incorrect dihedral angles in the GAAA tetraloop, is also reflected in the refolding kinetics as monitored by P_U(t). If there are parallel routes to the folded state, then P_U(t) can be described using a sum of exponentials. The lag kinetics, which is more pronounced as f_Q increases (see especially f_Q = 4 pN in Fig. 6), can be rationalized using a kinetic scheme 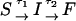where S is the initial stretched state, I is the intermediate state, and F is the folded hairpin. Setting P_U(t) ≡ P_S(t) + P_I(t) = 1 – P_F(t), we obtain

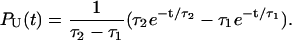(14)

From Fig. 6, which shows the fits of the simulated P_U(t) to Eq. 14, we obtain the parameters (τ₁, τ₂) at each f_Q (see caption to Fig. 6 for the values). If folding is initiated by temperature-quench, τ₁ ≪ τ₂, so that 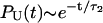. Explicit simulations show that thermal refolding occurs in a two-state manner (data not shown). In force-quench refolding, both τ₁ and τ₂ increase as f_Q increases, and τ₁/τ₂ ∼ O(1) at the higher values of f_Q. There are considerable variations in the structures of the metastable intermediate depending on f_Q. The variations in the conformations are due to the differences in the number of incorrect or nonnative dihedral angles. As a consequence, there are multiple steps in force-quench refolding in contrast to forced-unfolding, which occurs in an all-or-none manner.

Trans→gauche transitions in the GAAA tetraloop dihedral angles lead to long refolding times

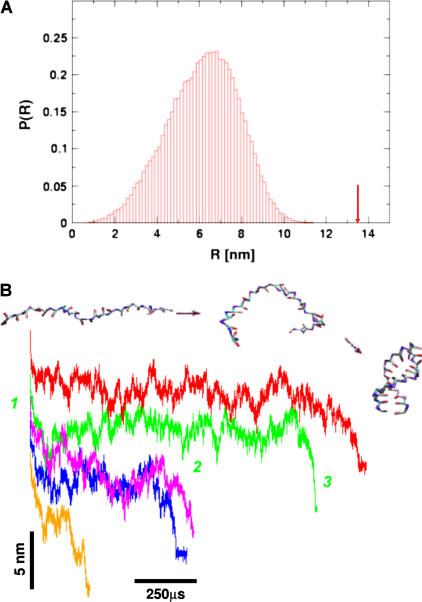
It is of interest to compare the refolding times obtained from stretched ensemble (τ_F(f_Q)) and the refolding time (τ_F(T)) from thermally denatured ensemble. In a previous article (14), we showed that τ_F(f_Q = 0) = 15τ_F(T) (Fig. 5 B). The large difference in refolding times may be because the initial conditions from which folding commences are vastly different upon force and temperature quench (14,32). The fully stretched conformations, with R = 13.5 nm, are very unlikely to occur in an equilibrated ensemble even at elevated temperatures. The canonical distribution of thermally denatured conformations even at T = 1500 K (≫ T_F) shows that the probability of populating conformations with R = 13.5 nm (Fig. 7 A) is practically zero. Thus, folding from thermally denatured ensemble starts from relatively compact conformations. In contrast, the initial condition for force-quench refolding can begin (as in our simulations) from fully stretched conformations upon force-quench. Both R and the radius of gyration (R_g) undergo substantial changes en route to the NBA. Indeed, the refolding trajectories from extended conformations exhibit broad fluctuations in R(t) in the order of 25–75 Å) for long time periods, followed by a cooperative reduction in R at the final stage (Fig. 7 B).

FIGURE 7.

(A) The equilibrium distribution of the end-to-end distance at extremely high temperature (T = 1500 K). Even at this elevated temperature, the fully stretched conformations of R = 13.5 nm (arrow) are not found in the ensemble of thermally denatured conformations. (B) Refolding is initiated by a force-quench from the initial value f_S = 90 pN to f_Q = 4 pN. The five time-traces show great variations in the relaxation to the hairpin conformation. However, in all trajectories, R decreases in at least three distinct stages that are explicitly labeled for the trajectory in green.

The long refolding times upon force-quench starting from fully stretched conformations may be generic for folding of globular proteins as well. Recent experiments on force-quench refolding of poly-ubiquitin (8) show that R(t) for proteins exhibit behavior similar to that shown in Fig. 7 B. The resulting f_Q-dependent refolding times for poly-ubiquitin (0.1–10 s) are considerably larger compared to τ_F (≈ 5 ms (33,34)) in the absence of force. Because the collapse of a single ubiquitin molecule in solution occurs in less than a millisecond, the origin of the long refolding times has drawn considerable attention (32,35). The microscopic model considered here for RNA can be used to shed light on the origin of the generic long refolding times upon force-quench.

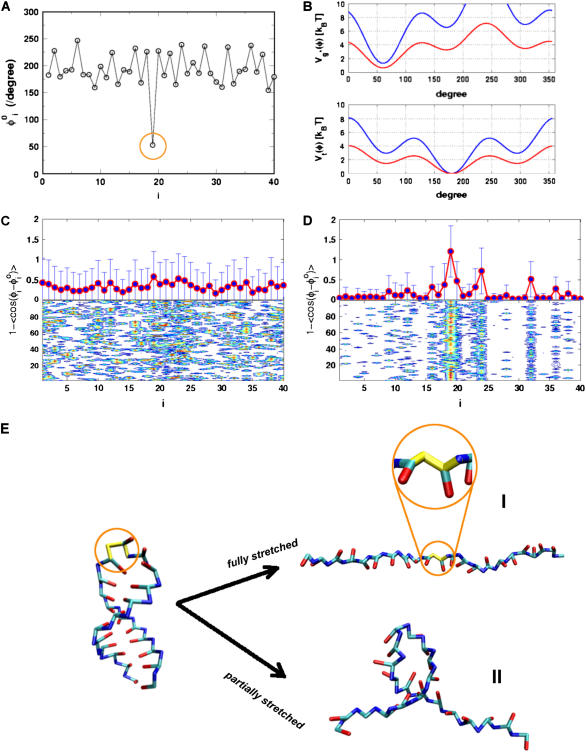
From the phase diagram (see Fig. 2 in (14)), it is clear that the routes navigated by RNA hairpin upon thermal and force-quench have to be distinct. Although the distinct initial conditions do not affect the native state stability (as long as the final values of T and f_Q are the same), they can profoundly alter the rates and pathways of folding. The major reason for the long force-quench refolding times in RNA hairpins is that, in the initial stretched state, there is a severe distortion (compared to its value in the native state) in one of the dihedral angles. The 19th dihedral angle (found in the GAAA loop region) along the sugar-phosphate backbone is in g⁺ conformation in the native state, whereas, in the initial stretched conformation, it is in the t state (Fig. 8 A). Thus, if all the molecules are in the fully stretched conformation, then the 19th dihedral angle in each of them has to, during the force-quench refolding process, undergo the t → g⁺ transition in the GAAA tetraloop region in order to fold. The enthalpic barrier associated with the t → g⁺ transition is ∼1 k_BT (Fig. 8 B). However, this transition is coupled to the dynamics in the other degrees of freedom and such a cooperative event (see Fig. 7 B for examples of trajectories) makes the effective free energy barrier even higher. Although significant fluctuations are found in thermally denatured ensemble at T = 500 K, they are not large enough to produce nonnative dihedral angles in the GAAA tetraloop. The dihedral angles in thermally denatured conformations do not deviate significantly from their values in the native conformation (Fig. 8 C). In contrast, upon fully stretching, P5GA dihedral angles in the GAAA tetraloop adopt nonnative values (Fig. 8 D).

FIGURE 8.

(A) The dihedral angles of the P5GA hairpin in the native state. All the dihedral angles are in the trans form except the 19^th position of the dihedral angle, which is in the gauche (+) conformation (indicated by orange circle). (B) The dihedral angle potentials for trans (top) and gauche (+) forms (bottom) are plotted using Eq. 3. The red lines show the potentials in the loop region. (C and D) The average deviation of the i^th dihedral angle relative to the native state is computed using the 100 different structures generated by high temperature (T = 500 K) (C) and by force (R = 13.5 nm) (D). To express the deviations of the dihedral angles from their native-state values, we used 1 – cos(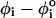) for i^th dihedral angle φ_I, where 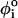is the i^th dihedral angle of the native state. (E) A snapshot of a fully stretched hairpin (I). Note the transition in the 19^th dihedral angle undergoes g⁺→t transition when the hairpin is stretched. This is an example of a partially stretched conformation (II) with the GAAA tetraloop and bond-9 intact. Refolding times starting from these conformations are expected to be shorter than those that start from fully stretched states.

The timescale for the t → g⁺ transitions can be inferred from the individual trajectories. Typically, there are large fluctuations due to g⁺ ↔ t ↔ g⁻ transitions in the dihedral angles in the flexible loop region (i = 19–24). For the trajectory in Fig. 9 B, we observe the persistence of incorrect dihedral angle in the loop region for t ∼ 300 μs. At t > 300 μs, the nativelike dihedral angles form. Subsequently, the formation and propagation of interaction stabilizing the native RNA hairpin takes place. These dynamical transitions are clearly observed in Fig. 9, B and C. The observed mechanism is reminiscent of a nucleation process. We conclude that the formation of the flexible loop with all the dihedral angles achieving near-native values is the rate-limiting step in the refolding kinetics of RNA hairpins upon force-quench starting from the fully stretched state. It should be stressed that the rate-limiting step for thermal refolding of P5GA, or force-quench refolding starting from partially stretched conformations (see below), is different. The observation that the zipping of the hairpin takes place upon synchronous formation of all the nativelike dihedral angles suggests the presence of a high entropic barrier. The crossing of the entropic barrier results in slow refolding if P5GA is fully stretched.

FIGURE 9.

(A) A sample refolding trajectory starting from the stretched state. The hairpin was initially unfolded to a fully stretched state and f_Q was set to zero at t ≈ 20 μs. End-to-end distance monitored as a function of time shows that refolding occurs in steps. (B) The deviation of dihedral angles from their values in native state as a function of time. The large deviation of the dihedral angles in the loop region can be seen in the red strip. Note that this strip disappears around t ≈ 300 μs, which coincides with the formation of bonds shown in C. The value f_B is the fraction of bonds with pink color, indicating that the bond is fully formed.

Linker effects on RNA force-extension curves

In LOT experiments, the force-extension curves (FECs) are measured for the handle(H)-RNA-handle(H) construct (5,6). To unambiguously extract the FEC for RNA alone (from the measured FEC for H-RNA-H construct), the properties of the handle, namely, the contour length L_H and the persistence length 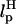, cannot be chosen arbitrarily. In the experiments by Liphardt et al. (5), L_H = 320 nm and 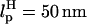for the RNA/DNA hybrid handle. We expect that both 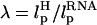and 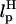will affect the FEC curves of the object of interest, namely, the RNA molecule. To discern the signature for the force-induced transition in the RNA hairpin alone from the FEC for H-RNA-H construct, λ has to be large. If we assume 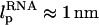, then the experimental value of λ ≈ 50, which is large enough to extract the transitions in the RNA hairpin. If λ ≈ 1, then the entropic fluctuations in the handle can mask the signals in RNA (36). Similarly, the end-to-end distance fluctuation in the handle, δR, should be smaller then the extension in RNA. Because δR grows with L_H (see below), it follows that, if very long L_H is used, even with λ ≫ 1, the signal from RNA can be masked. The square of the fluctuations in the end-to-end distance δR of the linker is given by (δR)² = ∂〈R〉/∂(βf_S), where 〈R〉 is the mean end-to-end distance. For WLC, which describes the linkers, we expect 〈R〉 ∼ (2L_Hl_p)^1/2 for small f_S and 〈R〉 ∼ L_H for large f_S, provided L_H is long. Thus,

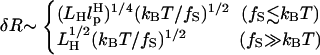(15)

The mean fluctuation in the extension of the spring is, using equipartition theorem, given by

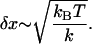(16)

For the signal from RNA to be easily discerned from the experimentally measured FEC, the expansion of end-to-end distance of the molecule at transition should be larger than δR and δx. Since δR grows sublinearly with the linker length (Eq. 15), the attachment of large linker polymer can mask the transition signal. These arguments show that the characteristics of the linker can obscure the signals from RNA.

The FECs in the simulations can also be affected by nonequilibrium effects due to the linker dynamics. In the handle(H)-RNA-handle(H) construct considered here, the force exerted at one of the linkers depends on the angle between f_S and the end of the linker. The initial event in force transmission along the contour of the H-RNA-H construct is the alignment of the molecule along the force direction. The characteristic time for force to reach RNA so that unfolding can occur is f_c/r_f, where f_c is the critical force. Nonequilibrium effects due to linker dynamics become relevant if τ_R, the timescale for alignment of H-RNA-H along the force direction, is τ_R > f_c/r_f. This condition is not relevant in experiments conducted at small values of r_f. However, it is important to consider nonequilibrium effects in simulations performed at high r_f values. The characteristic time depends on L_H and .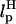

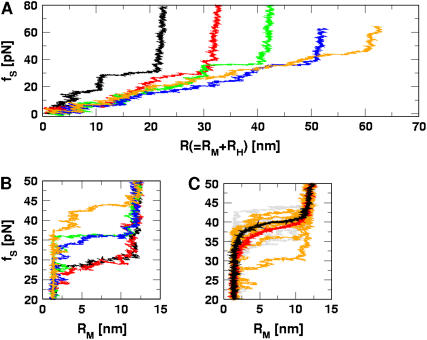
We validate these arguments by obtaining FEC for H-P5GA-H by varying L_H and 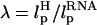. Using the WLC for the linker we calculated FEC where the L_H is varied from 10 to 50 nm. To observe rapid unfolding we have carried out our simulation at the pulling speed v = 0.86 × 10² μm/s and k = 0.7 pN/nm. Under these conditions nonequilibrium effects are relevant for the linker (23), which is not the case in experiments. The FECs show clearly a plateau in the range 20 pN < f_S < 40 pN, which corresponds to the two-state hairpin opening (Fig. 10). For the experimentally relevant plot (Fig. 10 A) showing FEC for H-P5GA-H, the transition plateau is present at all values of L_H. However, when L_H reaches 50 nm, the signal from P5GA is masked. The FEC for P5GA alone (Fig. 10 B) shows modest increase in the unfolding force as L_H increases. Similarly, we find the value of unfolding force also increases as the linker flexibility increases. These observations are due to nonequilibrium effects on the linker dynamics because of the relatively large values of r_f used in the simulations.

FIGURE 10.

The force extension curves (FECs) of RNA hairpin at constant pulling speed and varying linker lengths and flexibilities. Pulling speed is v = 0.86 × 10² μm/s; spring constant is k = 0.7 pN/nm. FECs from different linker lengths are plotted in black (10 nm), red (20 nm), green (30 nm), blue (40 nm), and orange (50 nm). (A) Shows the experimentally relevant plots, namely, FECs for H-RNA-H construct. The signature for the hairpin opening transition region is ambiguous at large L_H values. (B) FECs only, for P5GA corresponding to different L_H values. The FEC for the linker is subtracted from A. The gradual increase of rupture force is observed as L increases. The value of k_A (Eq. 9) of linker polymer used in A and B is 80 kcal/(mol · Å). (C) Comparison between FECs with L_H (= 40 nm) fixed, but at different k_A-values. The red curve is the average of seven individual FECs, which are shown in orange (80 kcal/(mol · Å)). The black curve is the average of nine individual FECs in gray (20 kcal/(mol × Å)). A less-stiff linker leads to a slightly larger unfolding force. It should be stressed that, for both values of k_A, the λ-ratio is large.

Our simulations show that, at high loading rates, the length of the handle is also important. This issue is not relevant in experiments in which loading rates are much smaller. However, they become important in interpreting simulation results. In our case, r_f (= kv) is 6 × 10⁴ times that used in experiments. At such high r_f, nonequilibrium effects control the linker dynamics (23). Thus, to extract unfolding signatures from RNA alone, it is necessary to use a high value of λ and relatively short values of L. In other words: FEC, when r_f is varied, may be a complicated function of 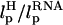and .

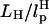Force-quench refolding of P5GA with attached linkers

It is convenient to monitor force-quench refolding of RNA alone using simulations. A similar experiment can only be performed by attaching handles to RNA. In such an experiment, which has not yet been done (however, see Note in Proof added at the end of this article), the H-RNA-H would be stretched by a stretching force f_S > f_c so that RNA unfolds. By a feedback mechanism, the force is quenched to f_Q ≠ 0. 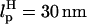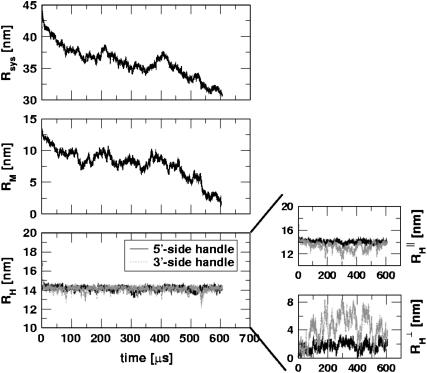We have simulated this situation for the H-P5GA-H construct with L_H = 15 nm, for each handle. We chose very stiff handles (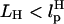) so that the dynamics of RNA can be easily monitored. The end-to-end distance of the H-P5GA-H system as a function of t with f_S = 90 pN and f_Q = 2 pN shows a rapid decrease from R_sys = 44 nm to ∼R_sys = 37 nm in <∼100 μs (Fig. 11). The use of large values of f_S will not affect the results qualitatively. The value of R_sys fluctuates at ∼36 nm for a prolonged period and eventually R_sys attains its equilibrium value at ∼30 nm.

FIGURE 11.

Refolding trajectory of RNA that is attached to the handles. Linkers with 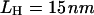and 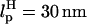are attached to both sides of the RNA hairpin. The initial force (90 pN) stretched P5GA to 14 nm. The value of f_Q = 2 pN. The top panel shows the dynamics of the end-to-end distance, R_sys, of H-P5GA-H. The middle panel corresponds to the end-to-end distance of P5GA. The end-to-end distances, R_H, of the 3′ and 5′-side handles, fluctuate around its equilibrium value of 14 nm after the initial rapid relaxation. The right panels show the decomposition of R_H into the longitudinal and the transverse components. The value of 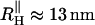agrees well with the equilibrium value obtained by solving 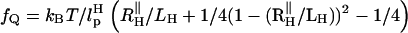with f_Q = 2 pN.

Upon decomposing R_sys into contributions from P5GA and the handle, we find that the major changes in R_sys occur when RNA undergoes the folding transition (compare the top and middle panels in Fig. 11). The time-dependence of R_H, which monitors only the dynamics of the linker, shows that with f_Q = 2 pN after the initial relaxation, R_H fluctuates around its equilibrium value (bottom panel in Fig. 11).

From these simulations and others for different f_Q-values, we can make a few general comments that are relevant for experiments:

1. As long as 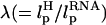is large enough, the qualitative aspect of RNA folding can be obtained from the dynamics of R_sys alone. However, if 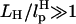, then large transverse fluctuations of the linker can interfere with the signal from RNA molecule.

2. To obtain quantitative results for the dynamics of RNA (i.e., R_M as a function of t), the dynamics of the handle upon force relaxation has to be described accurately. Upon f_S → f_Q quench, the dynamics of the handle cannot be described by the Langevin equation using the equilibrium force. Instead, the relaxation behavior must be determined by solving the Langevin equation for the WLC energy function (37), which is subject to f_S → f_Q quench.

DISCUSSIONS

Transition state movement and Hammond postulate for force

The Hammond postulate (38,39) is widely used to qualitatively predict the nature of transition state in the chemical reactions of organic molecules. In recent years, a number of protein-folding experiments have been interpreted using generalization of the Hammond postulate (40). The Hammond postulate states that if a transition state and an unstable intermediate occur consecutively during a reaction process and have nearly the same energy, their interconversion will involve only a small reorganization of the molecular structure (38). In the context of RNA folding, the Hammond postulate suggests that the position of the transition state along the reaction coordinate is shifted toward the destabilized state, either folded or unfolded, depending on the nature of perturbation. The Hammond behavior is most vividly seen in the free energy profiles F(R) (Fig. 5 C), which pictorially describe mechanical unfolding of RNA hairpins. As f is increased, the unfolded state is preferentially stabilized. From the Hammond postulate we would infer that the major TS should be more nativelike as f increases. The force-dependent F(R) as a function of R indeed confirms (Fig. 5 C) that, as f increases, becomes closer to the native folded hairpin conformation.

RNA hairpins also denature upon heating. To ascertain the variation in the location of the TS as temperature is changed we have calculated the free energy F(Q) as a function of Q at several values of T at f = 0 (Fig. 12 A). Although the location of the TS follows Hammond behavior there is very little change in the TS ensemble over the temperature range examined. Thus, the changes in the TS are very dramatic when unfolding is induced by force compared to thermal denaturation.

FIGURE 12.

(A) Free energy profiles of Q at different temperatures. Note that the positions of the transition states over the temperature variation almost remain constant. (B) The movement of transition state measured in terms of the Leffler parameter (Eq. 17). The structural nature of a transition state is monitored by the free energy difference between NBA and UBA when f is an external variable. The inset shows the variation of α with respect to force; value of T = 290 K.

Hammond behavior can be quantified using the Leffler's proportionality constant α_x which measures the energetic sensitivity of the transition state relative to the native states when the population shift is induced by a perturbation x (39,41). For mechanical unfolding (x = f_S),

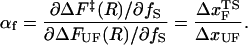(17)

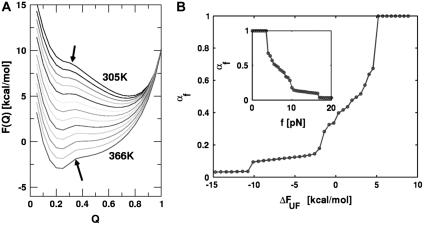
Using the free energy profile, we computed α_f as a function of ΔF_UF or f (Fig. 12 B). The shift in the transition state is quantified by α_f in the range 0 ≤ α_f ≤ 1, and the shift rate (or self-interaction parameter, p_f ≡ ∂α_f/∂ΔF_UF (41)) has its maximum in the force range 4 < f_S < 10 pN. As ΔF_UF decreases (the UBA is stabilized with respect to the NBA), α_f decreases—implying that the TS becomes increasingly nativelike (Fig. 12 B). The inset in Fig. 12 B shows dramatically the changes in α_f with respect to f_S. The largest changes in α_f occur as f_S approaches the T-dependent (T = 290 K) f_c ≈ 7 pN. A similar plot of α_T as a function of T shows practically no change in α_T. From this analysis, we conclude that the nature of the transition-state ensemble is different in mechanical unfolding and thermal denaturation.

The transition state movement with force is very sensitive to the shape of the barrier in the vicinity of the transition state. The free energy profile near the barrier (x ∼ x_ts) can be expanded as 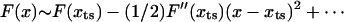. Upon application of the stretching force, F(x) is tilted by –f_S × x. The new barrier position (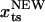) is at 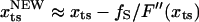. For a sharp transition barrier (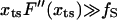), the force will not affect the position of the transition state (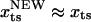). If the transition barrier is broadly distributed as in the unzipping pathway of RNA hairpins, the structure of the transition state progressively changes as the magnitude of the force is varied. Typically, folding transition states are shallow and broad. As a result in biomolecular folding or unbinding, which involve formation or rupture of noncovalent interactions, we predict that the location of the TS depends on f_S and temperature. The assumption of a fixed TS used to interpret (5,42,43) experimental results is not valid. In addition, sequential (22) and/or parallel pathways to the stretched state transition (44,45) are also possible. These observations suggest that a careful inspection of nonlinearity in the Arrhenius plot and α_f will be required to unravel barriers to unfolding.

Entropic barriers and long refolding times from fully stretched state

We have proposed that the long refolding time in P5GA upon force-quench from the initial stretched conformations is due to entropic barriers. The rate-limiting step in the force-quench refolding of P5GA is the t → g⁺ transition in the nucleotides near the GAAA tetraloops. We analyze the simulation results by adopting a model proposed by Zwanzig (46). In this Ising-like model each degree of freedom (in our case the dihedral angle) is presumed to exist in the “correct” state (native) and “incorrect” or nonnative state. Suppose that the energy difference between the incorrect and correct states is ε, and that there are N correct dihedral angles required for forming the hairpin loop. Let the free energy of loop stabilization be ε_loop. The energy, E_n, of a conformation with n-incorrect dihedral angles is E_n = nε – δ_n0ε_loop. If we assume that the dihedral angle is a discrete variable with 1 + ν states (ν is the number of incorrect states), then the partition function is

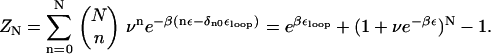(18)

The thermal probability of realizing a conformation with n incorrect dihedral angles is

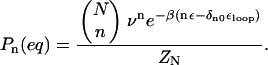(19)

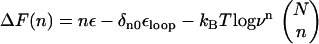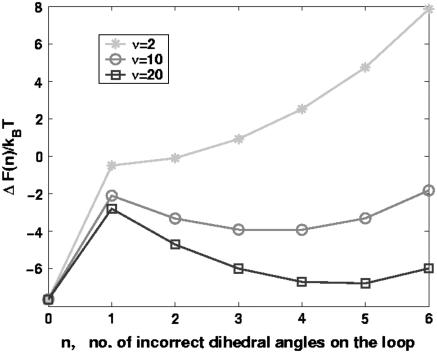
The free energy profile, with n playing the role of a reaction coordinate for dihedral angle transitions, is . For P5GA N = 6, ε ≈ 2 k_BT, and ε_loop ≈ 7.6 k_BT (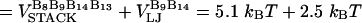). The free energy profile ΔF(n) (Fig. 13) shows that the barrier depends only weakly on ν. Because the dihedral angle is a continuous variable, we use ν as an undetermined parameter. For ν = 13, the free energy barrier (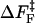) is ∼2.7 k_BT, which leads to the observed increase (τ_F(f_Q = 0) = 15τ_F(T)) in the refolding time by factor of 15 ().

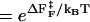FIGURE 13.

The free energy as a function of the number of incorrect dihedral angles calculated using the Zwanzig model (see text for details). As the number of distinct values (ν) that the dihedral angle can take increases the entropic barrier increases. For P5GA, ν = 13 provides the best fit of the model to simulations (see text).

The entropic barrier ∼(5–6) k_BT is significantly larger than the free energy barrier 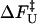in the absence of force. The barrier to the formation of conformations with (tttttt) state in the loop region is large enough that they do not form by thermal fluctuations, and hence are irrelevant when refolding is initiated by temperature quench. However, such conformations are populated with near-unit probability when fully stretched by mechanical force. When folding is initiated by force-quench from extended conformations (like conformation I in Fig. 8 E), metastable conformations with incorrect dihedral angles in the loop regions are formed. These are characterized by plateaus in the dynamics of R (Fig. 9 A). The crossing of the entropic barrier that places the loop dihedral angles in the nativelike gauche state results in the slow refolding of P5GA hairpins. Once the loop is formed, the zipping process quickly stabilizes the hairpin so that barrier crossing in reverse direction is unlikely to occur at low forces.

To further validate the proposed mechanism, we performed simulations in which the value of the initial stretching force f_S is not large enough to fully extend the P5GA hairpin. In these simulations, the ensemble of initial structures is prepared so that they contain the preformed GAAA loop with only a single bond before the intact loop region (see conformation II in Fig. 8 E). The refolding kinetics follows a single exponential decay with a mean refolding time of ∼33 μs, which is only 2–3 times longer than the refolding time of thermally denatured states. This value is much shorter than the refolding time from the fully stretched states (>191 μs, see Fig. 5 B). These simulations also show that τ_F is a function of both f_S and f_Q.

A byproduct of this analysis is that the appropriate reaction coordinate in force-quench refolding of RNA hairpins may be a local variable. In the formation of P5GA hairpin, the local dihedral angles are the relevant reaction coordinates. The local dihedral coordinates, which describe the rate-limiting steps in the UBA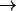NBA transition, are hidden in global coordinates such as Q or R. Indeed, there is no correlation between the formation of native dihedral angles in the GAAA tetraloop and global order parameters. We infer that to describe folding, especially of RNA, multiple reaction coordinates that describe the hierarchical assembly are required.

Difficulties in extracting energy landscape parameters from single molecule force spectroscopy

Several studies (31,42) have pointed out the inherent ambiguities in quantitatively characterizing the energy landscape from measurable quantities in dynamic force spectroscopy. From the plots (f*, log r_f), one cannot unambiguously obtain the location of the transition state(s) or even the number of free energy barriers (42). The significant curvatures in the (f*, log r_f) plots are usually interpreted in terms of multiple transition states (22, 42). In our example, the P5GA hairpin unfolds upon application of force by crossing a single free energy barrier. Explicit equilibrium F(R) profiles (Fig. 5 C) and experiments (5) that have monitored hopping dynamics in P5ab hairpin show that there is only one free energy barrier in these simple structures. Nevertheless, (f*, log r_f) plot is highly nonlinear (Fig. 4 B). In the hairpin case, we have shown that the nonlinearity is due to the dramatic changes in 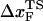as r_f is varied. The standard assumption that Δx_U.^TS is a constant breaks down, and is likely to be an even more of a severe approximation for RNA with tertiary structures.

To further illustrate the importance of transition-state movements, we consider a trivial one-dimensional potential,

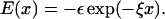(20)

In this barrierless potential, a particle is unbound if |E(x_ts)/k_BT| < 1, where x_ts is the TS location. Upon application of a constant f_S, the potential becomes

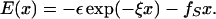(21)

The location of the transition state in the force range 0 < f_S < ξε is

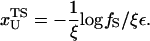(22)

If f_S > ξE, then , and the particle is always unbound (Fig. 14 A). The changes in can lead to significant deviations from the Bell equation even in constant f_S-experiments. The distribution of unbinding forces upon deforming the potential at constant loading rate (f_S(t) = r_ft) can be analytically obtained (see Eq. 8 in (47)). The (f*, log r_f) plot from these calculations show nonlinearities (Fig. 14 B) similar to those found for P5GA (Fig. 4 B). In both instances, the reason for curvature is entirely due to r_f-dependent changes in the TS location.

FIGURE 14.

(A) Sketch of the one-dimensional potential E(x) as a function of x for several values of f_S. The transition-state location is obtained using E′(x_ts) = 0. The boundary separating bound and unbound states is given by |E(x_ts)/k_BT| = 1. (B) Dependence of the most probable unbinding force f* as a function of r_f. The (f*, log r_f) plot for the artificial potential is similar to that shown in Fig. 4 B.

CONCLUSIONS

We have systematically investigated forced-unfolding and force-quench refolding of RNA hairpins. Using a general minimal model for RNA we have obtained a number of new results that give a molecular picture of unfolding and refolding of RNA hairpins triggered by force. Although they were obtained specifically for P5GA, we expect the conclusions to be valid for other RNA sequences as well. The specific predictions of our study, which are amenable to experimental test, are listed below.

1. Besides probing the energy landscape using f as a denaturant, one of the goals of single molecule studies is to extract intrinsic parameters like folding (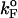) and unfolding rates (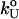) and the nature of the transition state in the absence of force. However, extraction of the kinetic parameters from dynamic force spectroscopy is fraught with difficulties, because several models can produce similar (f*, log r_f) profiles. Here we have shown, for a system that has only a single barrier to unfolding, that 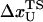depends dramatically on f_S and r_f. The movements in the TS are intrinsic to properties of RNA hairpins and are clearly reflected in the free energy profiles. Combining the present results and our previous study (14) we surmise that 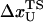is dependent on T and f. Thus, extrapolations to zero force to obtain reliable estimates of unfolding rates requires not only accounting for free energy barriers (31) but also on the dependence of 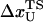on T and f. Only by performing multiple experiments (or simulations) over a range of f_S and T can the free energy landscape be fully characterized.

2. An important prediction of our work is that refolding times upon force-quench τ_F(f_Q) from stretched states are much greater than those obtained by temperature quench. More generally, τ_F(f_Q) depends, sensitively, on the initial value of the stretching force. The microscopic origin of the long force-quench refolding times in P5GA has been traced to the time needed for the trans→gauche transition in the GAAA tetraloop region. From this observation we predict that refolding time τ_F(f_Q) should be very long compared to thermal refolding times for P5ab, which also has the GAAA tetraloop. Because the refolding times for RNA hairpins are determined by the local structural features in the initial stretched states we suggest that, at a fixed temperature, τ_F(f_Q) might depend upon only weakly on the helix length or the precise sequence (percentage of GC for example).

3. Dissecting the folding mechanism of RNA is difficult because of an interplay of a number of factors (48). We predict that refolding mechanisms (pathways and the nature of the transition state ensemble) by temperature (or by increasing cation concentration) and force-quench have to be drastically different. In the former, the transition to the low entropic NBA proceeds from a high entropy relatively compact state, whereas in the latter it occurs from a low-entropy stretched state (49). The predicted dramatic differences in the folding mechanisms can be established by probing force-quench refolding at fixed T and counterion concentration.

The present model has a number of limitations. The use of the Gō model for force-unfolding may not be a serious approximation because unfolding pathway are largely determined by the native topology (50). However, the neglect of nonnative interactions will have dramatic effect on refolding. At a minimum, the roughness (δε) of the energy landscape is underestimated by the Gō model. The importance of δε can be assessed by doing forced-unfolding experiments over a range of temperature (47,51). Finally, the electrostatic interactions in RNA have been modeled in the simplest manner that is only appropriate for monovalent cation (52). To address the effect of counterion (Mg²⁺ or polyanions) explicit modeling of the cations will be required.

APPENDIX 1

In this Appendix we describe the procedure for determining the persistence length of the linkers used in our simulations. For the linker molecules, whose energy function is given by Eq. 9, we calculated the persistence length by fitting the wormlike chain end-to-end (R) distribution function (P_WLC(R)) (53) to the simulated P(R). We adopted Monte Carlo simulation with Pivot algorithm (54) to generate a large number of equilibrium conformations of the linker molecule. Given k_B(= 20 kcal/(mol · Ų)), k_A = 20 kcal/mol or 80 kcal/mol, and varying N the number of monomers in the WLC linker, we obtained the unknown parameters, namely, the contour length (L) and the persistence length (l_p) by fitting P(R) to

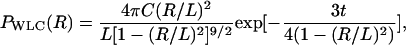(23)

where t ≡ L/l_p. The normalization constant C = 1/(π^3/2e^−αα^−3/2(1 + 3α⁻¹ + 15/4α⁻²)) with α = 3t/4, satisfies . The dependence of the persistence length of the linkers, as a function of N is displayed in Fig. 15. The quality of the fit improves as N becomes larger (data not shown). We also computed the persistence length and the contour length of P5GA at T > T_m using the same fitting procedure, which gives and L = 12.5 nm (Fig. 15, inset on the bottom). In our simulations 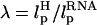ranges from 10 < λ < 70. The experimental value of λ ≈ 50 (5).

FIGURE 15.

Persistence length l_p as a function of contour length L for linkers at 290 K. The number of monomers N (Eq. 9) is also shown. The values of l_p and L are obtained by fitting the end-to-end distance distribution function P(R) generated by simulations to the theoretical expression based on a mean field model (Eq. 23). An example of such a fit for a linker with N = 50, using two different values of k_A (see Eq. 9), is shown in the top inset. For large N, l_p converges to a constant value. The fit of simulated P(R) for P5GA computed at T = 500 K > T_m is shown in the bottom inset. From the WLC fit, we obtain l_p ≈ 1.5 nm and L = 12.5 nm for P5GA.