Sub-Angstrom Conformational Changes of a Single Molecule Captured by AFM Variance Analysis

Abstract

A system's equilibrium variance can be analyzed to probe its underlying dynamics at higher resolution. Here, using single-molecule atomic-force microscope techniques, we show how the variance in the length of a single dextran molecule can be used to establish thermodynamic equilibrium and to detect conformational changes not directly observable with other methods. Dextran is comprised of a chain of pyranose rings that each undergoes an Angstrom-scale transition from a chair to boat conformation under a stretching force. Our analysis of the variance of the molecule's fluctuations verifies equilibrium throughout the force-extension curve, consistent with the expected thermodynamic ensemble. This validates further analysis of the variance in the transition region, which reveals an intermediate conformation between the chair and the boat on the sub-Angstrom scale. Our test of thermal equilibrium as well as our variance analysis can be readily extended to a wide variety of molecules, including proteins.

INTRODUCTION

Recent single-molecule force-spectroscopy experiments have provided insight into the mechanical stability and conformational changes of molecules such as proteins, polysaccharides, DNA, and RNA (1–4). However, the resolution of these experiments has been limited to several nanometers. Sub-Angstrom resolution can be reached with nuclear magnetic resonance (NMR) spectroscopy (5), x-ray crystallography (6), and scanning transmission electron microscopy (7). However, these techniques require large ensembles of molecules that are all in the same configuration. It is therefore difficult to observe conformations of a molecule that are transient, dynamic, and only occupied by a fraction of the ensemble. Einstein's 1905 work on Brownian motion famously demonstrated how a system's equilibrium variance can reveal its underlying dynamics at higher resolution (8). A prominent example of this principle used in biology was the estimation of single ion-channel conductance from the variance of the macroscopic membrane current (9) before the era of patch-clamp methods. This type of analysis has never before been used in force-spectroscopy experiments even though fluctuations have previously been quantified (10–14). Here, we demonstrate a fundamental thermodynamic test of equilibrium using variance. This is a prerequisite for further variance analysis of a single dextran molecule stretched with an atomic force microscope (AFM) to observe the dynamic conformational changes of its ring subunits with sub-Angstrom resolution. The method we describe here represents the most sensitive approach for capturing dynamic conformations in a single molecule to date.

For the measured variance to be a useful quantity, equilibrium must first be established. Although in the past few years, numerous researchers have investigated the appropriate statistical mechanics relevant to force-spectroscopy experiments (15–21), their theories concerning the establishment of thermal equilibrium have not yet been applied in experiments. In previous experiments, the existence of thermal equilibrium has been primarily determined by the absence or presence of hysteresis in the force-extension relation. However, the absence of hysteresis does not necessarily imply equilibrium with the bath (e.g., the parameter range may not be large enough to observe hysteresis). Additionally, interpretation of the measured molecular variance must also proceed with caution. This is especially true for measurement systems employing active feedback. The response time of the feedback must be fast enough to track the molecule's thermal motion. These considerations have not been fully appreciated in previous experiments, where it was crucial to know the thermodynamic state of the system (22,23).

Here, we report a variance analysis of the stretching of single dextran molecules with an AFM. First, the variance in length of dextran is used to prove thermal equilibrium of the molecule with the bath. Because the system is in equilibrium, we can then confidently use the variance to probe the conformational changes that occur when dextran's subunits, single pyranose rings, flip from the chair to the boat conformation under force (24,25). These conformational changes occur on length changes smaller than one Angstrom.

MATERIALS AND METHODS

Single-molecule atomic force microscopy

We used a custom-made AFM under constant-velocity and force-clamp conditions (26,27). Each cantilever (Si₃N₄ from Digital Instruments, Santa Barbara, CA) was calibrated in solution by applying the equipartition theorem (28). The spring constant was typically found to be ∼50 pN nm⁻¹.

Dextran molecules were manually picked up by pushing the cantilever onto the coverslip for up to several minutes. The piezo was then retracted while force and extension were observed in real-time on the oscilloscope. Once the user was confident that a single molecule was attached, a program was started to stretch and relax the molecule up to several hundred times before it detached. All experiments were performed at room temperature.

For the force-clamp experiments, the force was linearly changed at a rate of 1000 pN s⁻¹ from a minimum to a maximum force and back, encompassing the transition region. We verified that this pulling rate results in the same force-extension relation as slower pulling rates (29). Furthermore, this pulling rate results in smaller piezo velocities than the maximum velocity for near-equilibrium conditions (34).

For the constant-velocity experiments, the extension of the piezo was manually adjusted depending on the length of the molecule to capture the transition region. The pulling rate was typically 250 nm s⁻¹. To rule out any effect of the pulling rate on the variance, one molecule was pulled at both 150 nm s⁻¹ and 250 nm s⁻¹. The sampling rate was set around 12.5 kHz to acquire 10,000 data points over a period of ∼0.8 s, depending on the length of the dextran molecule. The anti-aliasing filter (eight-pole Bessel) was set to a fraction of the Nyquist frequency (6.25 kHz). Varying this cutoff frequency between 50 and 90% of the Nyquist frequency had no effect on the measured variance. However, at 7% of the Nyquist frequency, the variance was reduced by a factor of 2 and no increase in the transition region was observed.

Constant-velocity experiments do not involve any feedback that may interfere with the molecule's thermal equilibrium; however, instrumental noise could potentially still be a problem. The presence of electronic noise in the piezoelectric actuator should create fluctuations independent of the conformational state of the molecule, adding a roughly constant value to the variance independent of the molecule's extension. Based on the actual variance of the pulls alone, this value is small enough that we can still observe a change in the variance with respect to the extension of the molecule. More significantly, the striking accord between the actual variance and the predicted variance assuming thermodynamic equilibrium implies that any instrumental noise is completely negligible. We are therefore confident that there was no impact of the instrumentation on our measurements of the variance.

Data analysis

Calculation of the variance from all traces for a particular molecule was carried out in the following manner. Inherent drift in the piezo position and force over the time of the experiment required shifting all traces such that the transition regions overlapped. Each individual trace was smoothed to obtain the mean, which was then subtracted from the original trace, leaving only the fluctuations. These fluctuations were then squared, organized into bins of an appropriate size, and averaged over all traces for one molecule to obtain the variance in the length of the molecule (force-clamp experiments) or in the force on the molecule (constant-velocity experiments). For the latter case, the variance in the force was converted to the length variance using the spring constant of the cantilever (15).

Force-extension curves were fit using the modified freely jointed chain (FJC) model, which is based on the Langevin equation but includes segment elasticity. The fits were performed simultaneously to the low-force (chair conformation) and the high-force (boat conformation) regime using the Levenberg-Marquardt method (30). In the fits, the length of the pyranose ring in each conformation is fixed to the value obtained from ab initio calculations: l_{k, chair} = 4.412 Å and l_{k, boat} = 5.696 Å (25). This leaves N, S_{e, chair}, and S_{e, boat} to be determined by the fit. The resulting N is rounded to the closest integer because it represents an integer quantity (number of rings in the dextran molecule). The standard deviation for N is at most five rings, and depends on how accurately the segment elasticity of the boat could be determined from the force-extension curve. This uncertainty in N does not significantly affect the results of the fits to the variance.

The variance was fit using our two- and three-state models. Contributions to the variance from the FJC elasticity are taken into account by a straight line connecting the value of the variance at the beginning and at the end of the transition region. Based on this straight line, we estimate the elasticity due to the FJC and add this to the elasticity due to the transitions between the chair and the boat conformations. In the fit, the number of rings, N, is fixed to the value obtained from the fit to the force-extension curve. This leaves Δl_bi, Δl_bc, and B to be determined by the fit to the variance.

Dextran

We used dextran T500 (Pharmacia Biotech, Uppsala, Sweden), which is a >95% linear homopolymer consisting of α-(1 → 6) D-glucopyranose rings.

The sample was prepared by dissolving dextran in water at a concentration of 0.1–1% (wt/vol). It was then applied onto a clean glass coverslip and dried overnight. By rinsing extensively with water, excessive dextran was washed off so that only a thin layer of molecules tightly adsorbed to the surface remained. All experiments were carried out in phosphate-buffered saline solution or in water.

RESULTS AND DISCUSSION

Force-clamp experiments

In typical single-molecule stretching experiments, either the distance between the cantilever and coverslip is externally controlled (constant-velocity) (25), or the force on the molecule (force-clamp) (27). In thermal equilibrium, these methods respectively yield the Helmholtz or the Gibbs ensemble. Below, we discuss two sets of stretching experiments that employ force-clamp and constant-velocity conditions.

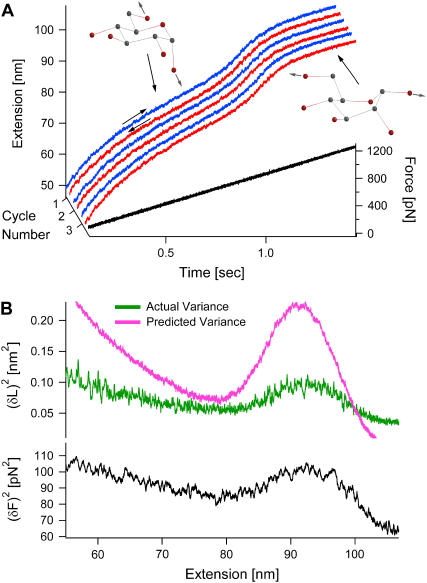
We first describe our force-clamp experiments, in which the force on the molecule is externally controlled. Fig. 1 A shows a typical recording of a single dextran molecule (comprised of many pyranose rings) as it is stretched (blue) and relaxed (red) throughout the chair-boat transition region by ramping the force while applying an electronic feedback (27,29). At low forces, the pyranose rings are in their ground-state chair conformation, and the molecule's elasticity is well described by a modified FJC model (31). The accelerated increase in length between 800 and 1000 pN characterizes the transition region as the pyranose rings flip from the chair to the boat conformation. This change results in an elongation of the pyranose rings by 20% (25).

FIGURE 1.

Variance reveals that force-clamp experiments are not in thermal equilibrium in the Gibbs ensemble. (A) A single dextran molecule was stretched (blue) and relaxed (red) consecutively by linearly varying the force. The figure shows the first three out of 108 cycles. In the transition region, between 800 and 1000 pN, the pyranose rings in dextran are thought to flip from a chair to a boat conformation, corresponding to a 20% increase in length (25). The noise in the length increases markedly in the transition region. (B) The experimental (green) and predicted (pink) length variances are highly discrepant, indicating that the molecule is not in thermal equilibrium in the Gibbs ensemble.

The fluctuations in the length of the molecule are given by the difference between the measured extension and its mean. The variance is then calculated by squaring the fluctuations and averaging over all traces for one molecule. The resulting variance for the molecule from Fig. 1 A is shown as the green curve in Fig. 1 B.

If the system is in thermal equilibrium in the Gibbs ensemble, the variance can also be obtained from the equipartition theorem, using the slope of the force versus extension curve (15),

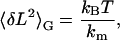(1)

where 〈…〉 indicates an average, k_B is the Boltzmann constant, and T is the temperature of the bath, and where an effective spring constant, k_m = d〈F〉/d〈L〉, describes the macroscopic elasticity of the molecule (see Appendix A). This predicted variance is shown as the pink curve in Fig. 1 B. The experimental and predicted variances are highly discrepant. In addition, the force variance increases in the transition region (black curve in Fig. 1 B). In the derivation of the variance, we assume perfect force feedback where the force is held constant with infinite time resolution. However, the molecule is clearly fluctuating on timescales faster than the response time of the electronic feedback, which has a bandwidth at ∼600 Hz. To fully account for the effect of the feedback we would need to know its complete transfer function, including the cantilever, the electronic feedback, the piezoelectric actuator, and the molecule, in order to predict the measured variance. This evaluation is most difficult and would have to be done for each individual cantilever-molecule combination.

Therefore, we cannot confirm that the molecule is in equilibrium despite the reversibility of its force-extension relation. For these reasons, further information cannot be obtained from the variance under these conditions.

We note that the finite response time of the force-feedback has been discussed in previous publications (4). However, for proteins, typical unfolding and folding time-series extend over several seconds. In this case, the millisecond response time of the feedback is trivial in comparison and therefore does not interfere with those previous measurements.

Constant-velocity experiments

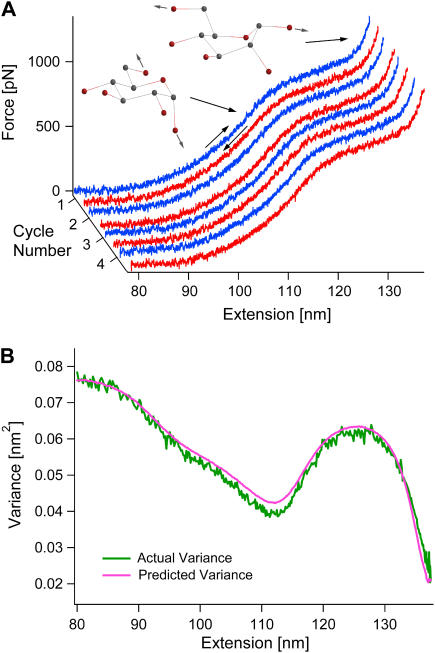
Since thermal equilibrium cannot be confirmed in our force-clamp experiments, we consequently repeat the experiment under constant-velocity conditions where feedback is not employed. Fig. 2 A shows a typical recording of a single dextran molecule. The variance is calculated from the fluctuations in the measured force from all pulls of the molecule. This force variance is then converted into the variance in the length of the molecule using the spring constant of the cantilever. The resulting variance is shown as the green curve in Fig. 2 B.

FIGURE 2.

Variance reveals that constant-velocity experiments are in thermal equilibrium in the Helmholtz ensemble. (A) A single dextran molecule was stretched (blue) and relaxed (red) consecutively at a rate of 250 nm s⁻¹. The figure shows the first four out of 667 cycles. (B) The experimental (green) and predicted (pink) length variances are in very good agreement, indicating that the molecule is indeed in thermal equilibrium in the Helmholtz ensemble.

Applying a similar analysis as for the Gibbs ensemble above, the predicted variance of the coupled cantilever-molecule system in equilibrium in the Helmholtz ensemble is (15)

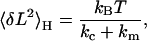(2)

with k_c as the spring constant of the cantilever and k_m = d〈F〉/d〈L〉 (see Appendix A). This predicted variance is shown as the pink curve in Fig. 2 B. The exceptional agreement between the experimental and the predicted variance confirms that the system is indeed in equilibrium in the Helmholtz ensemble.

Two-state model fails to describe chair-boat transition

Because equilibrium has been established, the molecule's variance enables us to further investigate its conformational changes. Previously, the chair-boat transition in dextran was assumed to be a two-state process (25,29). We now examine whether this assumption is indeed appropriate. The mean extension of the molecule is 〈L〉=N(1−p_c)Δl_bc, where L is measured relative to the beginning of the transition region, N is the total number of pyranose rings in the dextran molecule, p_c is the probability that a ring is in the chair conformation, and Δl_bc = l_boat−l_chair is the difference in length between the boat and the chair conformation. From the binomial distribution, the variance is 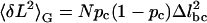in the Gibbs ensemble. Eliminating p_c from these two equations provides a functional relationship between the variance and the mean extension of the molecule, in analogy to standard ion channel variance analysis (9):

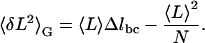(3)

The theory assumes that each ring is statistically independent of all other rings.

The expression for the variance given by Eq. 3 is valid for the Gibbs ensemble, but our experiments were carried out in the Helmholtz ensemble. Fortunately, there exists a simple relationship between the variances in both ensembles. The stiffness of the molecule, k_m, is the same in each case, allowing us to combine Eqs. 1 and 2 to obtain

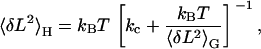(4)

where 〈δL²〉_G is given by Eq. 3.

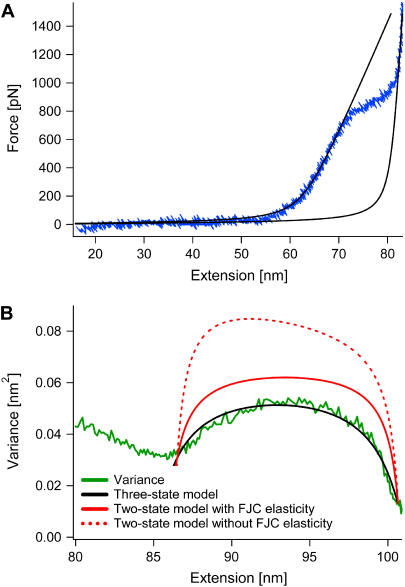
The resulting variance for a two-state system in the Helmholtz ensemble is shown as the red curve in Fig. 3 B. The number of rings for this molecule was determined to be N = 142 (rounded to an integer) from simultaneously fitting the low-force (chair) and the high-force (boat) regime of the force-extension curve with the FJC model (Fig. 3 A) using respective chair and boat lengths of 4.412 and 5.696 Å (Δl_{bc, ai} = 1.284 Å) from ab initio calculations (25) (see Materials and Methods). Fixing N at this value, the fit of the two-state variance without (red dashed curve) and with (red solid curve) taking into account the FJC elasticity (see Materials and Methods) to the experimental variance (green curve) resulted in a value of 0.99 Å for the length difference between boat and chair, Δl_bc, when the widths of the two variances corresponded to each other. The magnitude of the variance of the two-state model in either case clearly disagrees with the experimental variance. This deviation was similar for all nine molecules that we observed. We therefore conclude that the chair-boat transition in dextran is not a two-state process.

FIGURE 3.

Two-state versus three-state model. (A) The force-extension curve (blue) from one molecule is fit in the low-force (chair) and high-force (boat) regime simultaneously with the modified FJC. In the fit (black), the Kuhn segment lengths of the chair and the boat, l_k,chair and l_k,boat, were fixed to 4.412 and 5.696 Å, as given by ab initio calculations (25). The number of rings, N = 142, and the segment elasticities, S_{e, chair} = 11, 519 pN nm⁻¹ and S_{e, boat} = 90, 230 pN nm⁻¹ (all values rounded to closest integer), are the results of the fit. (B) The magnitude of the predicted variance from the two-state model (red) clearly disagrees with the experimental variance (green) (fixing N = 142 from the FJC fit). A simple three-state model (black), however, results in good agreement with the experimental variance (again fixing N = 142). The results of the fit are Δl_bi = 0.488 ± 0.005 Å, Δl_bc = 0.994 ± 0.004 Å, and B = 0.617 ± 0.010.

Variance reveals sub-Angstrom intermediate

We find, however, that a three-state model fits the experimental variance very well. This model introduces an intermediate state between the chair and the boat. The variance in the Gibbs ensemble using the trinomial distribution is (see Appendix B):

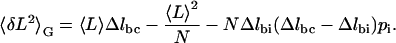(5)

Here, p_i is the probability that a given ring is in the intermediate conformation, Δl_bc = l_boat − l_chair is again the difference in length between boat and chair, and Δl_bi = l_boat − l_intermediate is the difference in length between boat and intermediate. We then assumed the following functional form for p_i based on known constraints about its shape (see Appendix B),

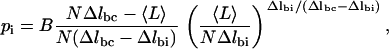(6)

where B is the maximum value of the probability.

Our fit of this model to the molecule shown in Fig. 3 is executed similarly to the previous fit of the two-state model (see Materials and Methods). We again take the number of rings to be N = 142 from fits of the FJC to the force-extension curve. From the variance, we obtain the following values for the three fitting parameters (black curve): Δl_bi = 0.488 ± 0.005 Å, Δl_bc = 0.994 ± 0.004 Å, and B = 0.617 ± 0.010. Note that the fitted value for B is indeed <1 as required for a probability. In general, we find that the width of the transition region and the number of rings, N, essentially determine Δl_bc, the slope of the variance at the end of the transition region determines Δl_bi, and the maximum value of the variance determines B.

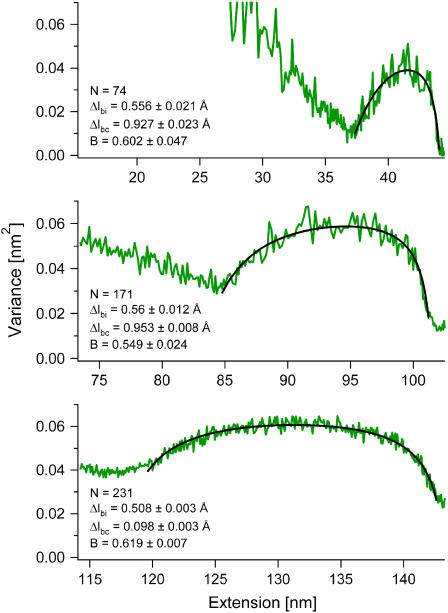
We analyzed a total of nine molecules, including the one shown in Fig. 3 and the three shown in Fig. 4. From the FJC fits to their force-extension curves, we find that these molecules had widely different lengths, ranging from N = 74–289. Despite their different lengths, we obtained fairly narrow distributions for the three fitting parameters (see Table 1) with average values 〈Δl_bi〉 = 0.518 ± 0.018 Å, 〈Δl_bc〉 = 0.988 ± 0.020 Å, and 〈B〉 = 0.626 ± 0.037.

FIGURE 4.

Fits using our three-state model (black) result in good agreements with the variances (green) of molecules of very different lengths. For each molecule, N is fixed to the value obtained from fitting the force-extension curves using the FJC model, while Δl_bi, Δl_bc, and B are left free to vary. The values obtained for the fitting parameters are very similar even though the molecules vary in length by more than a factor of 3.

TABLE 1.

Results from fits with three-state model

Molecule #	N	Δlbi(Å)	Δlbc(Å)	B
1	74	0.556 ± 0.021	0.927 ± 0.023	0.602 ± 0.047
2	128	0.604 ± 0.008	1.095 ± 0.011	0.714 ± 0.013
3	142	0.488 ± 0.005	0.994 ± 0.004	0.617 ± 0.010
4	171	0.560 ± 0.012	0.953 ± 0.008	0.549 ± 0.024
5	173	0.436 ± 0.014	0.933 ± 0.011	0.533 ± 0.034
6	189	0.561 ± 0.049	1.074 ± 0.084	0.836 ± 0.046
7	231	0.508 ± 0.003	0.983 ± 0.003	0.619 ± 0.007
8	233	0.464 ± 0.002	0.946 ± 0.002	0.697 ± 0.005
9	289	0.489 ± 0.031	0.990 ± 0.022	0.466 ± 0.063
Average		0.518 ± 0.018	0.988 ± 0.020	0.626 ± 0.037

The force-extension curve for each molecule is fit with the FJC model to obtain the number of pyranose rings, N. Fixing N at this value, the variance for each molecule is fit with our three-state model. The values of the fitting parameters, Δl_bi, Δl_bc, and B, for each molecule as well as the overall averages are listed above. For each parameter, the uncertainty of its average value is determined from 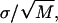where 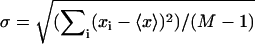with x_i and 〈x〉, respectively, denoting each molecule's fit value and the average value and where M is the total number of molecules. All uncertainties are 1 σ.

Note that 〈Δl_bc〉 = 0.988 Å is significantly smaller than the value from ab initio calculations, Δl_{cb, ai} = 1.284 Å, used to fit the force-extension curves (see above). This is likely because the ab initio calculations considered the pyranose ring in equilibrium under no external force, whereas our molecule was under a stretching force in the transition region. From the slope of the force-extension curves, we know that the molecule's elasticity coefficient is smaller in the chair than in the boat conformation (i.e., the boat is stiffer than the chair). Therefore, the length difference between boat and chair should decrease under force, as observed.

Our results indicate an intermediate state that lies approximately half-way between the chair and the boat. Interestingly, recent SMD simulations of dextran suggest the existence of an intermediate conformation corresponding to simultaneous rotation of the protruding carbon-oxygen bond and transition of the pyranose ring to a boat structure distinct from the final one (32).

CONCLUSION

We have demonstrated for the first time the use of variance analysis to capture dynamic molecular conformations of a single molecule mechanically stretched by an AFM. The fluctuations that we have detected occur at the sub-Angstrom level and are invisible to any other type of spectroscopy, including NMR and x-ray crystallography, as those techniques require large ensembles of molecules that are all in the same configuration. It is therefore difficult to observe conformations of a molecule that are transient, rapidly fluctuating, and only occupied by a fraction of the ensemble. By contrast, our single molecule force spectroscopy analysis of the variance in the length of a stretched dextran molecule readily captures transient conformations on the sub-Angstrom scale. Furthermore, we developed a rigorous test for the applicability of our variance analysis based on establishing that the molecule under study was in thermodynamic equilibrium.

This analysis should be equally applicable to any stretching experiment in order to probe the thermodynamic state of the system as well as equilibration timescales. In particular, future tests of fundamental thermodynamic theories such as the Jarzynski's equality should always start with a robust verification of nonequilibrium conditions, as suggested previously (2,23).

Finally, our analysis should allow for the investigation of conformational changes in a wide variety of molecules at significantly higher resolution than is now possible. These include simple molecules with a ring structure similar to dextran (1) as well as more complex molecules like DNA (33), RNA (2), and proteins (26) that undergo discrete conformational changes under a stretching force.

APPENDIX A: MACROSCOPIC ELASTICITY OF THE MOLECULE

In Eq. 2 we assume k_m is constant over the fluctuation range at each point in the force-extension curve, which is correct to first order. The exact expression for k_m can be written as a Taylor expansion, as

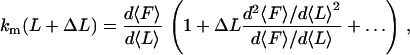(7)

where 〈…〉 indicates an average. Substituting 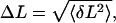we find that the second term in the series is at most 7% of the leading order term for all molecules, thereby validating our assumption.

APPENDIX B: VARIANCE FOR THREE-STATE MODEL

Our three-state model introduces an intermediate between the chair and the boat conformation. The probability density function is given by the trinomial distribution

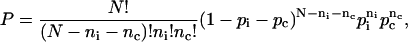(8)

with a variance, in the Gibbs ensemble, of

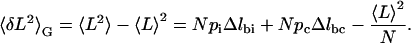(9)

Here, n_i and n_c are the number of monomers in the intermediate and chair conformation, p_i and p_c are the probabilities that a given ring is in the intermediate or chair, and Δl_bi and Δl_bc, respectively, are the differences in length between boat-intermediate and boat-chair.

In contrast to the two-state theory, it is not possible to eliminate both probabilities from the variance. We can, however, choose which probability to keep in Eq. 9. We decided to keep the probability of the intermediate, p_i, which yields the relation given by Eq. 5. We chose p_i because there are some constraints on its shape as a function of the average length of the molecule:

1. Its magnitude has to be ≤1.

2. It has to be 0 outside the transition region.

3. Its maximum has to occur at NΔl_bi.

A simple function fulfilling these conditions is Ax^c(1 − x) with x in the interval [0, 1]. In our particular case, this becomes Eq. 6, given in the main text.