Identification of a Locus Under Complex Positive Selection in Drosophila simulans by Haplotype Mapping and Composite-Likelihood Estimation

Abstract

The recent action of positive selection is expected to influence patterns of intraspecific DNA sequence variation in chromosomal regions linked to the selected locus. These effects include decreased polymorphism, increased linkage disequilibrium, and an increased frequency of derived variants. These effects are all expected to dissipate with distance from the selected locus due to recombination. Therefore, in regions of high recombination, it should be possible to localize a target of selection to a relatively small interval. Previously described patterns of intraspecific variation in three tandemly arranged, testes-expressed genes (janusA, janusB, and ocnus) in Drosophila simulans included all three of these features. Here we expand the original sample and also survey nucleotide polymorphism at three neighboring loci. On the basis of recombination events between derived and ancestral alleles, we localize the target of selection to a 1.5-kb region surrounding janusB. A composite-likelihood-ratio test based on the spatial distribution and frequency of derived polymorphic variants corroborates this result and provides an estimate of the strength of selection. However, the data are difficult to reconcile with the simplest model of positive selection, whereas a new composite-likelihood method suggests that the data are better described by a model in which the selected allele has not yet gone to fixation.

THE recent action of positive selection is expected to leave a footprint on patterns of intraspecific DNA sequence variation. This footprint results from the effects that selection imposes on the genealogy of genomic segments linked to the selected variant and the spatial localization of these effects due to recombination. Because all sequences with complete linkage to the beneficial mutation must coalesce before the mutation event (going backward in time), these sequences will form a star-like tree of relationships with very short branch lengths relative to the neutral coalescent expectation (Kaplan et al. 1989). The star phylogeny results in a decrease in heterozygosity associated with the rapid increase in frequency of the beneficial mutation, which has been called genetic hitchhiking (Maynard Smith and Haigh 1974) or selective sweep. The extent of the region affected by a sweep is determined by the strength of selection and the local rate of recombination (Maynard Smith and Haigh 1974; Kaplan et al. 1988, 1989). As neutral mutations accumulate on a postsweep genealogy, most of those present in samples of reasonable size will be singletons or of low frequency, producing a skew in the site-frequency spectrum (Aguadé et al. 1989; Braverman et al. 1995). However, both the reduction in polymorphism and the site-frequency skew are expected to dissipate with distance along the chromosome from the selected site because of recombination. This dissipation should produce a valley of minimal heterozygosity in the region containing the selected site, with decay on either side of the valley to neutral levels of heterozygosity (Maynard Smith and Haigh 1974; Kim and Stephan 2002).

The combination of positive selection and recombination produces distinctive patterns at sites that are linked to the selected mutation, but distant enough that at least one sequence in the sample has undergone a recombination event between the neutral and selected sites. In such a region, the genealogy will resemble a star phylogeny connected by a long branch to other lineages with a more neutral-looking set of coalescent relationships (Fay and Wu 2000). This particular topology results in an excess of rare polymorphic variants due to the long branches between the swept lineages and the recombined lineages. Furthermore, because of the relatively long branch connecting the swept alleles with the most recent common ancestor of the sample, many of these polymorphisms will be in the derived state as determined by comparison to an outgroup sequence. The excess of high-frequency-derived variants should therefore be diagnostic of a region with partial linkage to a swept site.

These genealogical relationships will also affect the haplotype structure among sampled chromosomes. The relatively long branches between swept and recombined alleles should produce an excess of linkage disequilibrium, due to the large number of polymorphic variants that are fixed between the haplotype groups (Przeworski 2002). Furthermore, when a recombination event occurs early in the sweep, then two or more chromosomes, each with its own distinctive set of polymorphisms, may rapidly move to high frequency, producing multiple haplotype groups with little or no variation within each, but an excess of variants fixed between them. As with the patterns of heterozygosity and polymorphism frequencies, this pattern of haplotype structure is also expected to decay with distance from the selected site, and the observation of such blocks of linkage disequilibrium has been proposed as a method for mapping the recent action of positive selection from genome sequence data (Sabeti et al. 2002).

A region located within polytene band 99D on chromosome arm 3R in Drosophila simulans was recently shown to contain a pattern of nucleotide polymorphism consistent with the recent action of positive selection by the criteria outlined above (Parsch et al. 2001a). This region contains three paralogous, testes-expressed genes, janusA (janA), janusB (janB), and ocnus (ocn; Yanicostas et al. 1989; Parsch et al. 2001b). A comparison of DNA sequences sampled from a worldwide collection of eight D. simulans lines revealed that this region contains low levels of DNA polymorphism and an excess of high-frequency-derived alleles. In addition, this region showed strong haplotype structure, with a high-frequency haplotype group containing very little heterozygosity and a low-frequency haplotype group with levels of variation that are more typical for D. simulans. The previous study revealed a break in the haplotype structure located between janB and ocn; however, recombination events that could define the proximal limit of the haplotype structure were not observed, leaving the extent of the selected region in question. To further characterize the geographic and chromosomal extent of this haplotype structure, we report here a survey of DNA sequence polymorphism in a worldwide sample of haplotypes from D. simulans at the jan-ocn region and in the three serendipity (sry) genes, sryδ, sryα, and sryβ, which are located just proximal to janA. The results indicate distinct recombination events disrupting the haplotype structure on either side of janB, suggesting that the target of positive selection lies in or near this gene. Application of a likelihood-ratio test for a selective sweep also localizes the selected site to janB. Because the presence of low-frequency, ancestral alleles throughout the putative selected region is inconsistent with a single, completed sweep, we have elaborated previously developed methods for detecting selective sweeps (Kim and Stephan 2002) to allow discrimination between the hypotheses of complete and incomplete sweeps. The results indicate that a partial-sweep model fits the data significantly better than a completed sweep and suggest the historical or current action of more complex evolutionary forces, such as balancing or epistatic selection, in this region of the genome.

MATERIALS AND METHODS

Fly stocks:

D. simulans lines were provided by P. Capy and Y. Tao. All lines were derived from a single female and maintained by full-sib matings for >50 generations. The majority of lines were initially collected by Rama Singh in 1983, and a number of others are described in Atlan et al. (1997). This worldwide collection of isofemale lines reflects the history of collection by researchers more than any aspect of D. simulans population structure. All flies were raised on standard cornmeal agar medium at 25°.

DNA sequencing:

Genomic DNA was extracted from a single male of each line as described previously (Parsch et al. 2001b). The janA-ocn region was PCR amplified as a single 2.4-kb fragment from genomic DNA using primers and conditions described previously (Parsch et al. 2001a). Four primer pairs designed using the published D. melanogaster genome sequence (Adams et al. 2000) were used to amplify a ∼700-bp fragment from sryα, a ∼900-bp fragment from sryβ, and two overlapping fragments totaling ∼1200 bp from sryδ. PCR products were used as sequencing templates following purification with the QIAquick PCR purification kit (QIAGEN, Valencia, CA) or after treatment with the SAP/EXO reagent (United States Biochemical, Cleveland). Gene-specific internal primers and the original amplification primers were used for sequencing with the BigDye 2.0 cycle sequencing kit (Applied Biosystems, Foster City, CA) following the manufacturer's protocol. Sequences were run on an ABI 3100 automated sequencer, and each fragment was sequenced at least once on both strands. DNA sequences have been submitted to GenBank under the accession numbers AY663111, AY663284.

DNA polymorphism and haplotype analysis:

Nucleotide sequence data were extracted in Sequencher 4.1 (Gene Codes, Ann Arbor, MI) and aligned in Clustal X (Thompson et al. 1997). Nucleotide polymorphism, haplotype and recombination statistics, and tests of neutrality were calculated using DnaSP 3.99 (Rozas et al. 2003) and SITES (Hey and Wakeley 1997). The probabilities associated with Tajima's D (Tajima 1989), haplotype diversity, and Fu and Li's D and F statistics (Fu and Li 1993) were calculated using DnaSP 3.99. Fay and Wu's H statistic (Fay and Wu 2000) and associated probabilities were calculated using a program available from J. Fay, assuming no recombination and a probability of back-mutation of 0.03 (using D. melanogaster as the outgroup) or 0.05 (using D. yakuba as the outgroup). The haplotype test of Hudson et al. (1994) was calculated using a program provided by J. Braverman. This test compares the observed configuration of segregating sites among haplotypes with that expected under neutrality. This comparison is done by partitioning the data into two groups of sequences and determining the probability of observing i sequences with j or fewer segregating sites. Partitions that maximized i and minimized j were chosen and corrected for the a posteriori choice of i and j by including the probability of all possible configurations more extreme than that observed. Probabilities of summary statistics and of configurations of the haplotype test were determined from 10,000 random coalescent simulations with no recombination, conditioned on the observed number of segregating sites. Heterogeneity in the ratio of polymorphism and divergence was assessed using the DNA Slider program (McDonald 1998) with the published D. melanogaster sequence as an outgroup. Following the logic outlined by McDonald (1996), 100 neutral simulations were run with the per-locus scaled population recombination parameter (R) set to 1, 2, 4, 8, 16, 32, and 64. The value(s) of R that maximized the probability of the data were then chosen, and the probability was recalculated with 10,000 simulations.

Composite-likelihood analysis:

Kim and Stephan (2002) proposed a composite-likelihood method to detect the diagnostic features of a selective sweep from DNA sequence data. However, this method assumed that the population from which the sequences have been sampled is fixed for the putative beneficial mutation (i.e., a complete sweep). Because we suspected that the pattern in the jan-ocn region was caused by the hitchhiking effect of a beneficial mutation that has not yet fixed (Parsch et al. 2001a), we modified the method of Kim and Stephan (2002) to allow the frequency of the beneficial mutation at the time of sampling, β, to be less than one (i.e., an incomplete sweep). The modified method proposes a new composite likelihood in which β is an additional parameter (appendix).

For a given sample of DNA sequences, the maximum composite likelihood is obtained under three different models: the neutral model (L₀), the complete-sweep model (L₁), and the incomplete-sweep model (L₂). All three models assume that θ (the population mutation parameter 4Nμ) and R_n (the scaled per-nucleotide recombination rate 4Nρ) are known. L₁ is the maximum composite likelihood found by varying the location of the beneficial mutation, X, and the strength of selection, 2Ns = α, while setting β = 1. L₂ is obtained by allowing β to vary between 0 and 1, producing joint estimates of X, α, and β. These different hypotheses are tested using the likelihood ratios LR₁ = log(L₁/L₀) and LR₂ = log(L₂/L₁). To evaluate these likelihood ratios and examine the performance of the parameter estimation, maximum composite likelihoods were calculated for data sets simulated under various models. Simulations were conducted according to Kim and Stephan (2002) with the following modifications: if β < 1.0 in the selective sweep model, simulations were started with nβ sequences carrying the beneficial mutation and n(1 − β) sequences carrying the ancestral allele. In other words, the ancestral recombination graph is constructed starting in the middle of the selective phase, with k_B = nβ and k_b = n(1 − β) (the number of “B” and “b” edges, respectively; see Kim and Stephan 2002).

All simulations were conducted with the same structure as the sampled sequences in this study (n = 36 and six sequenced segments over a 7.8-kb region, as shown in Figure 1). For both simulation and composite-likelihood analyses, the sequence was divided into noncoding and coding regions, and the per-nucleotide mutation rate for each region was given as θ and 0.3θ, respectively, where θ is Watterson's estimator of the population mutation parameter calculated from the data (Watterson 1975). This approach is conservative for the likelihood-ratio test (Kim and Stephan 2002). Nonsynonymous and insertion/deletion polymorphisms were excluded from the analysis. Ancestral and derived alleles at polymorphic sites were identified by comparison with the published D. melanogaster sequence (Adams et al. 2000). The scaled per-nucleotide recombination parameter R_n was estimated as 0.065. This number was obtained from seven alleles of haplotype group II (Parsch et al. 2001a) using the method of Hudson (1987). We also estimated R_n using γ, a coalescent estimator of the population recombination rate (Hey and Wakeley 1997), which gives values ranging from 0.009 (using all of the sequenced sites and all 36 lines) to 0.027 (using sites in the janA-ocn region with the same seven alleles as above). These are likely to be lower bounds on the true population recombination parameter, as γ under most circumstances underestimates the true R_n (Wall 2000). Estimates from the genetic map, using data from True et al. (1996) and following the method of Andolfatto and Przeworski (2000), give an R_n of 0.037 for interval 99D in D. simulans. We therefore included simulations and tests with R_n = 0.005, 0.03, and 0.1 to examine the effect of R_n on the composite-likelihood analysis, as these values represent a reasonable range of values for the true R_n in this region of the genome.

Figure 1.—

Diagram of the portion of chromosomal band 99D studied here. Solid bars represent exons and intervening lines represent introns. Bars above represent sequenced regions.

RESULTS

Reduced polymorphism and skewed site frequencies at 99D:

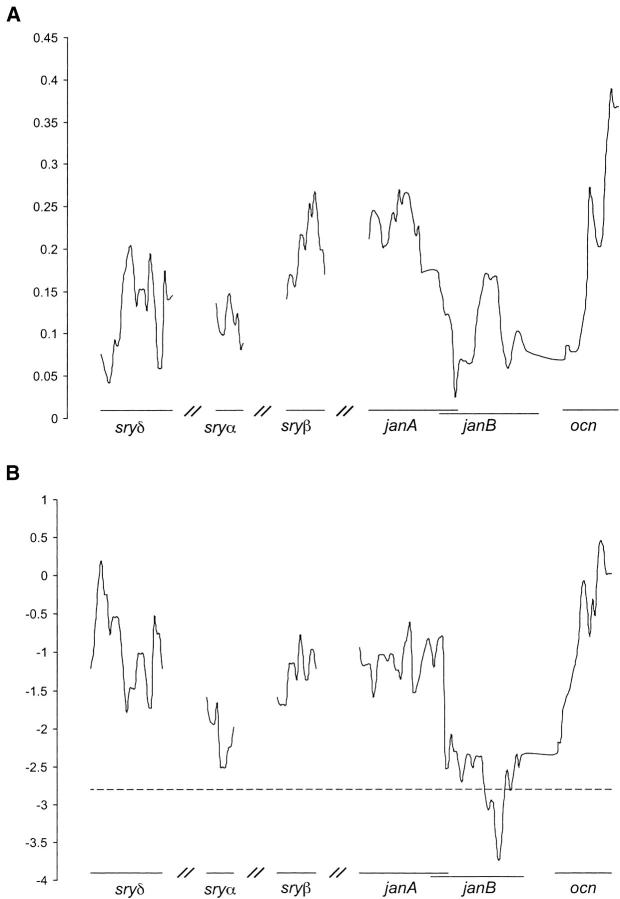
We sequenced ∼5 kb of a 7.5-kb region located within cytological band 99D on chromosome arm 3R from 36 lines of D. simulans (Figure 1). The configuration of segregating sites in this sample is shown in Figure 2. Polymorphism in this region is low relative to other loci that have been sequenced from chromosome arm 3R in D. simulans (Begun and Whitley 2000) and the other autosomes (Moriyama and Powell 1996). Figure 3A depicts polymorphism scaled by divergence (π/K) calculated within a sliding window of 400 bp over the sampled region. Scaled polymorphism in this region is lowest at the 5′ end of janB. The ratio of polymorphism to divergence appears to be unusually heterogeneous across this region, as determined by a sliding window test that compares runs of consecutive polymorphic and fixed mutations with neutral coalescent simulations (McDonald 1998). The number of runs of consecutive polymorphic or fixed sites across the 7.5 kb surveyed is significantly lower than expected under neutrality (P = 0.0061) and remains so (P = 0.037) following a Bonferroni correction for the multiple statistics that can be used to describe this heterogeneity (McDonald 1998).

Figure 2.—

Sequence data for six genes in region 99D. The D. melanogaster (mel) sequence is from Adams et al. (2000); the D. yakuba (yak) sequences are from Parsch et al. (2001b)(janA-ocn) and Caccone et al. (1996)(sryα). Asterisks below the sequences indicate nonsynonymous polymorphisms; vertical lines indicate noncoding polymorphisms. Boxed sites indicate that the rare D. simulans allele matches D. melanogaster and the common D. simulans allele matches D. yakuba; shaded sites indicate that the rare D. simulans allele matches D. yakuba and the common D. simulans allele matches D. melanogaster. Abbreviations for the location of origin of the D. simulans lines are: SA, South Africa; SM, St. Martin; JA, Japan; FR, France; TU, Tunisia; AU, Australia; HA, Haiti; US, United States; SE, Seychelles; PE, Peru; KE, Kenya; CO, Congo; PO, Polynesia; and ZI, Zimbabwe.

Figure 3.—

Low polymorphism and excess of singletons at janB. Graphs were generated using DnaSP 3.99 (Rozas et al. 2003) with a sliding window of 400 nucleotides and a step size of 25 nucleotides. (A) Average pairwise differences (Tajima 1983) divided by divergence. (B) Fu and Li's D (Fu and Li 1993). The horizontal line indicates values of D that are significantly different from 0 at P < 0.05.

Departures from neutral genealogies will distort the spectrum of site frequencies found in DNA sequence data. Tajima's D-statistic (Tajima 1989) tests for deviations of this sort, with negative values indicating an excess of rare polymorphic variants, and positive values resulting from an excess of intermediate frequency variants. Tajima's D is significantly negative at janB and is negative, although not statistically significant, for five of the six genes and for all of the data combined (Table 1), indicating a deficiency of polymorphisms at intermediate frequency. Fu and Li have proposed tests of neutrality that compare the proportion of mutations found on the internal and external branches of a genealogy with the proportion expected under neutrality (Fu and Li 1993). Their D-statistic produces a significantly negative value at janB (Table 1), which results from the large number of singletons present in 10 of the 36 sequences (Figure 2). Figure 3B shows the values for Fu and Li's D calculated for a sliding window of 400 bp over the entire region. A localized segment with significantly negative values can be seen toward the 3′ end of janB, and similar results are obtained with Fu and Li's F (not shown). The remaining genes in this region show no significant departures from neutrality by these tests (Table 1). Thus, while the pattern of DNA sequence polymorphism and segregating site frequencies is unusual across the sampled region, these deviations from neutrality are strongest in the vicinity of janB.

TABLE 1.

Summary statistics for six genes in 99D

Gene	Sitesa	πa	θa	Tajima's D	Fu and Li's D	Fay and Wu's Hb	hdiv	sub(i, j)
sryδ	1088 (317)	4.13 (13.1)	5.51 (17.6)	−0.86	−1.70	−0.64	0.687*	(21, 0)*
sryα	637 (155)	3.79 (8.16)	6.44 (15.6)	−1.36	−2.08	−1.29 (−1.64)	0.878	(21, 2)
sryβ	740 (210)	5.01 (17.6)	5.87 (20.6)	−0.49	−1.23	−1.57	0.646*	(21, 0)*
janA	744 (410)	12.5 (21.7)	15.7 (27.0)	−0.60	−0.68	−5.49 (−9.37)	0.683**	(19, 0)**
janB	1027 (619)	6.67 (10.1)	13.2 (20.1)	−1.72*	−2.86**	−7.13 (−15.6*)	0.765**	(24, 1)**
ocn	573 (238)	10.8 (25.8)	10.2 (24.2)	0.23	−0.07	−4.72 (−6.78*)	0.633*	(21, 0)*
All	4809 (1949)	6.82 (15.0)	9.36 (20.8)	−0.97	−1.84	−20.90 (−31.74*)c	0.94*	(8, 0)*

π, average number of pairwise differences (Tajima 1983); θ, estimator of 4Nμ (Watterson 1975); hdiv, haplotype diversity (Nei 1987); sub(i, j), the most extreme subset of the sample, where i and j are the number of alleles and number of segregating sites in the subsample, respectively (Hudson et al. 1994). Significance levels were determined by 10,000 random coalescent simulations conditioned on the observed number of alleles and segregating sites and assuming no recombination. janB includes the region labeled “intergenic” in Figure 2. *P < 0.05; **P < 0.01.

^aValues of π and θ were multiplied by 10³; values in parentheses are for synonymous and noncoding sites only.

^bValues in parentheses were determined using the D. yakuba sequence as an outgroup.

^cjanA, janB, and ocn only.

Comparison with the D. melanogaster sequence reveals that, at a large fraction of the nonsingleton segregating polymorphic sites, the common allele is in the derived state (Figure 2). The presence of a high-frequency, derived haplotype with low levels of polymorphism was previously observed in the janA-ocn region in a subsample of the data presented here (Parsch et al. 2001a) and is a hallmark of a selective sweep (Fay and Wu 2000). When the D. melanogaster sequence is used as an outgroup, the H-test of Fay and Wu (2000) does not produce a value inconsistent with neutrality for any of the six genes or for the region as a whole (Table 1). This is due to the retention of relatively high amounts of genetic variation present in a minority of chromosomes (s18–s36 in Figure 2). However, if the more distantly related D. yakuba sequence is used to polarize the D. simulans polymorphisms as ancestral or derived, a significant H-statistic is obtained for all of the genes for which D. yakuba sequence data is available (Table 1). This is due to a number of sites where a rare polymorphism in D. simulans matches D. yakuba but not D. melanogaster (Figure 2, shaded sites). It is not clear whether this homoplasy can be attributed to multiple hits at these sites or to the retention of ancestral polymorphisms in the D. simulans and D. melanogaster lineages. Excluding all sites with conflicting outgroup information produces H-test results qualitatively similar to those obtained using the D. melanogaster sequence (not shown).

Composite-likelihood test of a selective sweep:

To examine the ability of the new composite-likelihood method to detect partial sweeps, we applied the method to data sets simulated under an incomplete sweep model. Table 2 and Figure 4 show the results of parameter estimation for simulations where the frequency of the selected allele at the time of sampling was β = 0.7. The method performs fairly well when estimating X and is more precise when X = 6.3 than when X = 5. This is due to the location of the gaps in the sequenced region (Figure 1). When a sweep occurs, it creates a valley of heterozygosity and skew in the site frequencies centered on the site of the beneficial mutation (Maynard Smith and Haigh 1974; Kim and Stephan 2002). The power to detect a sweep is dependent on the ability to observe sites that have experienced some recombination with the selected site, as these will produce the maximal skew in the site frequency spectrum. Detecting both “edges” of the valley of reduced heterozygosity should be more powerful than detecting only one edge. The sequenced regions from sryB, janA, janB, and ocn form an almost continuous stretch of sequences, with X = 6.3 near the center of this block (Figure 1). In contrast, X = 5 is located within the sryB sequence, and a simulated sweep located on X = 5 may contain an edge in a gap (i.e., it may miss a recombination event).

TABLE 2.

Composite-maximum-likelihood estimation of parameters applied to simulated data

α	X (kb)	α̂	X̂ (kb)	β̂
100	5	73 (21, 266)	5.02 (2.97, 6.81)	0.993 (0.766, 1)
500	5	381 (77, 1090)	5.11 (4.06, 6.26)	0.857 (0.694, 1)
2000	5	1754 (463, 5831)	5.24 (3.59, 6.89)	0.761 (0.666, 0.906)
100	6.3	82 (26, 257)	6.26 (4.86, 6.89)	0.918 (0.720, 1)
500	6.3	465 (117, 1190)	6.34 (5.71, 6.95)	0.796 (0.692, 0.983)
2000	6.3	1793 (318, 5960)	6.34 (5.03, 7.52)	0.758 (0.682, 0.853)
500a	5	447 (182, 853)	5.00 (4.71, 5.62)	—
500a	6.3	447 (119, 796)	6.30 (5.94, 6.73)	—
2000a	6.3	1359 (525, 2628)	6.29 (5.71, 6.99)	—

Median and (10%, 90%) values for each estimate are shown; β = 0.7. Results are based on 1000 simulations for each parameter set.

^aParameter values were estimated under the complete-sweep CLR method using subsets of chromosomes carrying a beneficial allele generated under incomplete-sweep simulations.

Figure 4.—

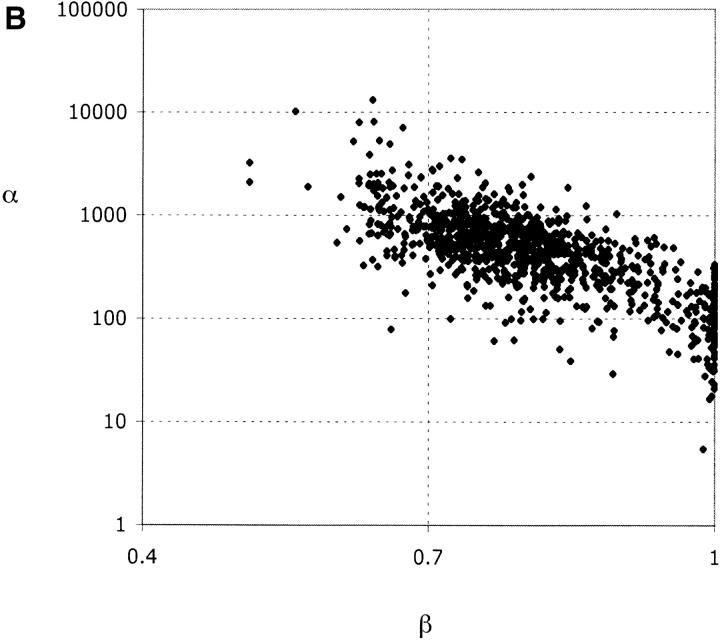
Parameter estimation for data sets simulated under incomplete sweep with α = 500, X = 6300, β = 0.7. (A) Joint distribution of X̂ and β̂. (B) Joint distribution of β̂ and α̂.

However, the method produces poorer estimates of α and β. Mean estimates of α are upwardly biased due to a small fraction of simulated data sets that generate very large estimates, and the median α̂ seems to underestimate the true α (Figure 4B; Table 2). For many data sets, the maximization of L₂ leads to β̂ = 1.0, which therefore yields LR₂ = 0. From the joint distribution of α̂ and β̂, it appears that a better fit is frequently given to a model of a complete sweep causing a reduction in variation over a small region, i.e., an overestimate of β and an underestimate of α (Figure 4B). However, even excluding those simulations where β̂ = 1.0, β̂ still overestimates β. Estimates of these parameters from data must therefore be interpreted cautiously.

We evaluated the power of this method to detect incomplete sweeps by comparing the distribution of LR₂ obtained from data sets simulated under the neutral, complete-sweep, and incomplete-sweep models (Table 3). To evaluate the ability of the method to distinguish partial sweeps from both neutral genealogies and complete-sweep simulations, null distributions of LR₂ were generated under complete sweeps as well as neutral equilibrium. In all cases, the cutoff for statistical significance was chosen to be the value of LR₂ generated under a null-distribution model (neutrality or a complete sweep) below which 95% of the null-distribution mass was contained. With R_n = 0.065 and across a range of values of α and X, the maximum 95% cutoff for LR₂ was <2.5 for neutral null distributions and <3.5 for completed-sweep null distributions (Table 3). Therefore, if the data produce an LR₂ > 3.5, we may reject either a neutral or a complete-sweep model in favor of an incomplete sweep. Using this threshold, the power to detect an incomplete sweep from simulated data (with β = 0.7) ranges from 0.013 to 0.855 depending the location and strength of selection (Table 3, cases 16–22) and increases with the strength of selection. Inspection of Table 3 reveals that the power to detect a sweep (partial or complete) is greater for beneficial sites located at X = 6.3 than at X = 5. This is a result of the influence of the structure of the sequenced regions on the likelihood method described above.

TABLE 3.

Distributions of LR₂ obtained from simulations

Case	Rn	α	X (kb)	β	Q0.05a	Q0.2	Q0.5	Q0.8	Q0.95
1	0.005	0b	—	—	0c	0.27	1.55	4.40	9.22
2	0.03	0b	—	—	0	0	0.26	1.32	3.76
3	0.065	0b	—	—	0	0	0.12	0.86	2.36
4	0.1	0b	—	—	0	0	0.06	0.71	1.79
5	0.065	50	2	1.0	0	0	0.08	0.66	1.82
6	0.065	100	2	1.0	0	0	0.07	0.72	1.97
7	0.065	500	2	1.0	0	0	0	0.34	1.45
8	0.065	1,000	2	1.0	0	0	0.01	0.81	2.73
9	0.065	50	7	1.0	0	0	0.17	1.39	3.28
10	0.065	100	7	1.0	0	0	0.09	0.99	2.86
11	0.005	500	7	1.0	0	0	0.62	2.40	5.67
12	0.03	500	7	1.0	0	0	0.01	0.92	4.11
13	0.065	500	7	1.0	0	0	0.01	0.61	3.09
14	0.1	500	7	1.0	0	0	0.01	0.39	2.51
15	0.065	1,000	7	1.0	0	0	0	0.29	2.71
16	0.065	100	5	0.7	0	0	0.11	0.74	1.99
17	0.065	500	5	0.7	0	0.01	0.73	3.18	7.00
18	0.065	2,000	5	0.7	0.01	1.59	5.90	11.2	16.7
19	0.065	100	6.3	0.7	0	0.01	0.63	2.45	4.89
20	0.065	500	6.3	0.7	0.02	0.99	4.21	8.07	12.6
21	0.065	1,000	6.3	0.7	0.29	2.52	6.53	11.4	16.5
22	0.065	2,000	6.3	0.7	1.68	4.63	9.10	13.8	19.0
23	0.065	10,000	5	1.0	0	0	0	0.36	2.78
24	0.065	10,000	7	1.0	0	0	0	0.99	6.12
25	0.065	14,000	6.3	1.0	0	0	0	0.31	2.05

All simulations were done with θ = 0.02.

^aQ_x is the xth percentile of LR₂ from 1000 simulations.

^bSimulation under the neutral model.

^c“0” means <0.01.

Applying the complete-sweep composite-likelihood method to the data shown in Figure 2, and assuming R_n = 0.065, we obtain LR₁ = 16.08 (α̂ = 90.1 and X̂ = 7.01 × 10³). Because the 99th percentile of LR₁ from the neutral simulations is 10.3, the neutral model is clearly rejected in favor of the complete sweep. However, the estimated strength of selection (α̂ = 90.1) is too small to explain the unusual haplotype structure spanning the entire 7.8-kb region surveyed. A sweep is expected to influence variation only at linked neutral loci where the recombination fraction with the beneficial locus is <s/2 (Maynard Smith and Haigh 1974; Stephan et al. 1992). With R_n = 0.065, the region influenced by directional selection of this magnitude is not expected to extend beyond 1.4 kb in either direction from the selected site, and this expectation ranges from 1.2 to 1.6 kb over the values of R_n considered here. The complete linkage between sites as far apart as 4.6 kb (i.e., sites 3167 and 7735) therefore suggests a stronger selective benefit associated with the favored site. This inference, as well as inconsistencies in the data with the predictions following a complete sweep, provide the impetus for a composite-likelihood-ratio (CLR) test of a partial sweep.

Applying the partial-sweep test to the data and again assuming R_n = 0.065, we obtain LR₂ = 10.20 (α̂ = 2.94 × 10⁴, X̂ = 7.20 × 10³, and β̂ = 0.60). Because LR₂ = 10.2 ≫ Q_0.95 derived from simulations of a complete sweep with a number of parameter values (Table 3), we can reject the complete sweep in favor of the incomplete-sweep model. In this case, α̂ is overestimated, as an incomplete sweep of this strength would completely wipe out variation on affected chromosomes over a region >400 kb. This overestimation can likely be attributed to the ignorance of the correlation between polymorphic sites in the calculation of the composite likelihood. This likelihood is obtained by multiplying the probability of the observed frequency of derived alleles across sites, ignoring the correlation between polymorphic sites. An overestimation of α will then result from homogeneity in the frequency of derived alleles. If similar frequencies of derived alleles are present throughout the data, as seen in Figure 2, a model of a partial sweep driven by very strong selection is favored by the composite likelihood. In other words, the data in Figure 2 do not show a sufficient decay in the frequency spectrum skew in either direction to be compatible with a moderate α. This conclusion is supported by the profile of LR₂ as a function of X. Although there is a peak at X = 7.10 kb, the plot of LR₂ is almost flat over the entire region (the difference between multiple local optima is <0.5; data not shown). A much more limited footprint of a selective sweep is inferred from the changes of haplotype structure over this region (see below).

To examine the sensitivity of these results to our estimate of R_n, we repeated the analysis with R_n = 0.005, 0.03, and 0.1. Table 4 shows that the null distribution of LR₂ increases with decreasing R_n, and the same trend can be observed in the values of LR₂ obtained from the data. However, the empirical LR₂ is still >Q_0.95 for all values of R_n (Table 4). The profiles of LR₂ as a function of X for different recombination rates are also similar (data not shown). Therefore, the support for a partial-sweep model over a complete-sweep model and the inference of the location of the beneficial allele is largely insensitive to assumptions regarding R_n. The minimum estimated value of α (1.15 × 10⁴) still appears to be greater than expected, on the basis of the observed extent of nucleotide variation.

TABLE 4.

Influence ofR_n on composite-likelihood methods

	Complete-sweep model				Incomplete-sweep model
Rn	Q0.95a	LR1	α̂	X̂c	Q0.95b	LR2	α̂c	X̂c	β̂
0.005	9.22	14.88	5.81	6.45	5.67	11.4	14.3	7.07	0.60
0.030	3.76	14.69	47.2	7.02	4.11	11.62	11.5	7.09	0.59
0.065	2.36	16.08	90.1	7.01	3.09	10.20	29.4	7.20	0.60
0.100	1.79	16.14	129	7.02	2.51	10.13	29.3	7.09	0.60

^aNeutral simulations.

^bComplete-sweep simulations; α = 500.

^cValues were multiplied by 10⁻³.

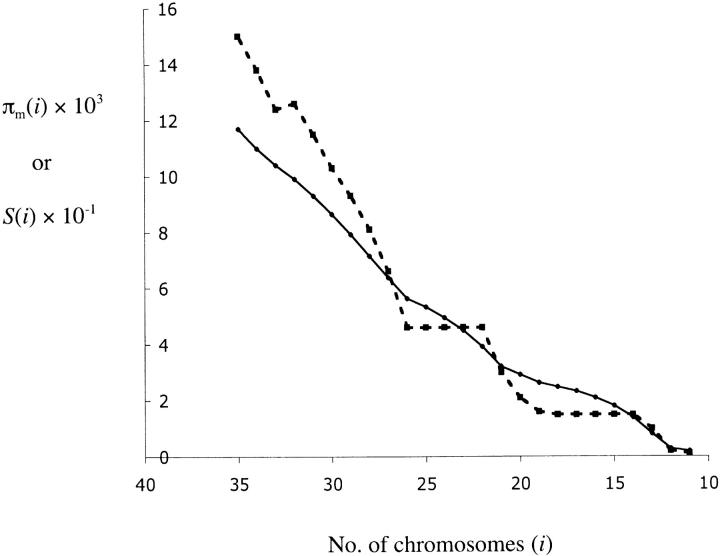
While the composite-likelihood approach clearly supports the hypothesis of an incomplete sweep, it cannot identify which chromosomes carry the putative beneficial mutation. Because the sequences carrying the beneficial mutations are descendants of a recent common ancestor, we may infer the haplotypes that have experienced the sweep by identifying a group of chromosomes within which diversity is greatly reduced. To identify this group, we selected a subsample of i chromosomes such that the estimated heterozygosity (π) within this group of chromosomes is minimized. This minimum is denoted π_m(i). We then calculated the number of segregating sites for this subsample (S(i)) and graphed both S(i) and π_m(i) as a function of i (Figure 5). Figure 5 shows that π_m(i) gradually decreases with decreasing i, as expected. On the other hand, S(i) decreases rapidly and then reaches a plateau at S(i) = 46 from i = 26 to i = 22. This indicates that the 26 chromosomes chosen to minimize π(i) contain a few sets of identical haplotypes, and this group of chromosomes is a good candidate for the one homogenized by the putative incomplete sweep. These 26 chromosomes are s21 to s26 in Figure 2, and we designate them as haplotype group I and the remaining 10 alleles as haplotype group II (Figure 2, s35 to s18). The second plateau in Figure 5 [S(i) = 16 from i = 19 to i = 14] contains the first 20 sequences in Figure 2, excluding s15. This subset is contained within the haplotype group I sequences, and so we designate it as haplotype group Ia. The haplotype group I sequences also maximize the linkage disequilibrium and the frequency of derived alleles (Figure 2), which are clear signatures of a selective sweep (Fay and Wu 2000; Kim and Stephan 2002; Przeworski 2002).

Figure 5.—

Average number of pairwise differences (π, solid line) and number of segregating sites (S, dashed line) for subsets of chromosomes that minimize π (π_m(i)), graphed against the number of chromosomes in each subset. See text for details.

Given the wide confidence intervals associated with α̂ and β̂ and the lack of resolution regarding the location of the selected site under the partial-sweep model, we reasoned that a complete-sweep CLR test using only those chromosomes likely to have been involved in the sweep might provide more accurate estimates of α and X. Theoretical work indicates that the frequency of a neutral allele conditional on its linkage to a beneficial mutation changes only slightly during the period when the frequency of the beneficial mutation increases from 0.5 to 1 (Stephan et al. 1992). In other words, the hitchhiking effect on neutral loci is mainly determined when the frequency of the beneficial mutation is low. The frequency of the putative beneficial mutation is likely to be >0.5, considering that the likelihood estimate of β = 0.6, and the frequencies of haplotype groups I and Ia are 0.72 and 0.53, respectively. This means that the skew in site frequencies among swept chromosomes under a partial sweep should be similar to that among all chromosomes following a complete sweep (see materials and methods) and justifies the application of a CLR test of a complete sweep to a subsample that is assumed to be in complete association with the beneficial mutation.

This reasoning is borne out by applying the complete-sweep CLR method to the subset of chromosomes carrying the beneficial allele in data sets simulated under an incomplete-sweep model (Table 2). Although the median α̂ sometimes more severely underestimates the true value, the median X̂ is closer to the actual location of the selected site in all cases. In addition, the 10–90% range of estimated parameters is on average twofold narrower when using only the swept chromosomes than when using all of the sequences.

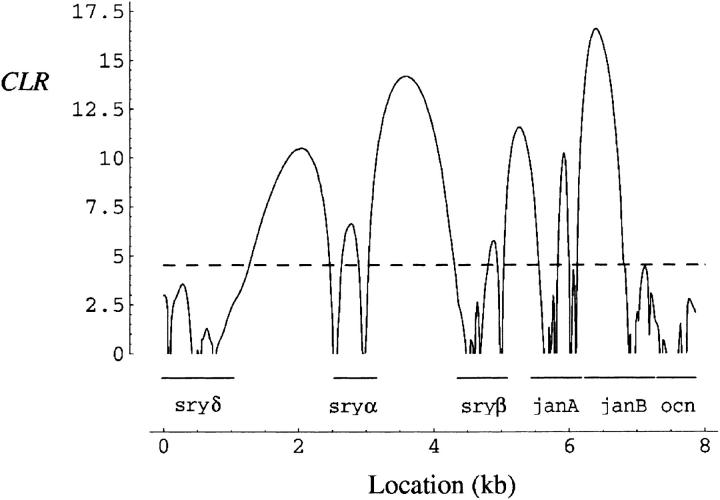
When the CLR test of a complete sweep is applied to the 19 haplotype group Ia sequences, a nonsignificant result is obtained (R_n = 0.065, θ̂_W = 0.00196; LR₁ = 3.54, P < 0.057). However, a significant CLR is obtained for the 26 haplotype group I sequences (R_n = 0.065, θ̂_W = 0.0052; LR₁ = 16.6, P < 0.001). We propose, therefore, that all of the haplotype group I chromosomes, rather than just haplotype group Ia, represent the best candidates for the partially swept haplotype. Under this model, the beneficial mutation is estimated to be located near the 5′ end of janB (Figure 6; X̂ = 6.39 kb) and its estimated strength is α̂ = 455. Figure 6 shows that there are many local optima along the sequence. The difference between the highest and the second highest (located between sryα and sryβ) peaks is ∼2.4 CLR units. Therefore one may argue that the putative beneficial mutation is ∼11 (≅e^2.4) times more likely to be in or near the janB gene than between sryα and sryβ.

Figure 6.—

The composite-likelihood ratio (CLR) as a function of the position of the putative beneficial mutation. Sequenced segments corresponding to six genes in this region are indicated by horizontal lines above the x-axis. The CLR was obtained from 26 chromosomes corresponding to haplotype group I. The dashed line represents the 95th percentile of CLR (4.52) determined by neutral simulations.

Inferring the location of the selected region from haplotype structure:

The inference of a selected site at janB is further supported by the pattern of linkage disequilibrium (LD), which the composite-likelihood analysis does not take into account. DNA polymorphism across this region is clearly grouped into distinct haplotypes. A number of alleles are identical (or nearly so) in their combination of polymorphic variants across the entire region (e.g., s9, s13, s14, s16, and s26), and the majority of the low-frequency and singleton variants are contained entirely within the 10 haplotype group II chromosomes. There is a significant reduction in haplotype diversity as compared with a neutral genealogy at all genes except sryα and across the region as a whole (Table 1). The same result is found with a haplotype test (Hudson et al. 1994) that partitions the data into two groups and compares the number of segregating sites in each group with that expected under neutrality (Table 1). Consistent with the polymorphism data and the composite-likelihood results, the most extreme haplotype structure is also found at janB.

Because the duration of a sweep is expected to be very short, there should be limited opportunities for recombination events during the selective phase. Because recombination breakpoints on either side of the beneficial mutation should occur independently, observing a stretch of LD that extends across the site of the beneficial mutation is very improbable. Simulations confirm that an excess of LD is observed on both sides of a selected site but that the association is broken between the two sides (Kim and Nielsen 2004). The extent of a genomic region affected by positive selection may also be inferred from the location of recombination events between derived (selected) and ancestral alleles. Derived polymorphisms are expected to be at their highest frequency near to the selected variant, and their frequency should decrease due to recombination as one moves away from the selected site in either direction (Fay and Wu 2000; Kim and Stephan 2002). Note, however, that a region in complete linkage with a selected site that has recently gone to fixation should have no high-frequency-derived variants, as all polymorphism will be the result of new mutations.

Within subsets of sequences in haplotype group I, there are two stretches of ancestral polymorphic sites in complete LD (Figure 2). Alleles s9, s13, s14, s16, and s26 match the ancestral (D. melanogaster) haplotype at 15 sites ranging from position 79 in sryδ to position 6022 in janA, but then match the derived haplotype over the entire janB-ocn region. Similarly, alleles s7, s10, s11, s22, s29, and s30 match the derived haplotype at all but 2 sites over the sryδ-janB region, but then match the ancestral haplotype at 9 sites in the ocn gene. These two inferred recombination events both disrupt haplotype associations across janB and decrease the frequency of derived alleles on either side. The sequence of strain s5 is of particular interest in this context, as it shows evidence of recombination events on both sides of janB (i.e., sites 536 and 7379 in Figure 2) that bring the derived sequence onto an ancestral haplotype both proximal and distal to janB. The localization of the maximal frequency of derived variants and the disruption of LD to the same region are further evidence for a partial, rather than a complete, selective sweep in this region. On the basis of the observed recombinants, the selected site is postulated to lie between position 6022 in janA and position 7379 in ocn, which is consistent with the estimates of X̂ = 6390, 7010, and 7200 from the partial- and complete-sweep likelihoods. It is noteworthy that, following recombination, a number of ancestral segments that became linked to the derived allele in the putative selected region appear to have increased in frequency themselves. For the proximally recombined alleles, the recombinants are in a frequency of 5/36; for the distally recombined alleles, the recombinants are in a frequency of 7/36. This could be the result of hitchhiking of ancestral segments that recombined early in the sweep onto a positively selected chromosome.

Estimation of the age of haplotype group I:

The age of a recently derived haplotype group can be estimated on the basis of the number of new mutations that have occurred among the alleles since they last shared a common ancestor (Rozas et al. 2001). In the case of janB, there are 26 haplotype group I alleles with three new mutations (sites 6791, 6936, and 7204). Assuming a star phylogeny (as is expected following a selective sweep or population bottleneck), there are 26 branches of length t on which mutations can occur. If the number of mutations follows a Poisson distribution, then the expected number of mutations in the janB sample is 26tμ, where μ is the mutation rate per sequence per year. On the basis of the observed silent site divergence (synonymous and noncoding sites) at janB of 0.14 between D. melanogaster and D. simulans, and assuming a divergence time of 2.5 million years for these two species (Lachaise et al. 1988; Hey and Kliman 1993), μ is estimated to be 1.73 × 10⁻⁵. The probability of observing three mutations is then

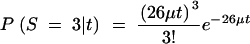and the maximum-likelihood estimate of t is 6667 years. Ninety-five percent confidence intervals for this age can be calculated by finding t_max and t_min such that P(S ≤ 3|t_max) = 0.025 and P(S ≥ 3|t_min) = 0.025. This produces the values t_min = 1375 and t_max = 19,481 years. The estimate of t should be taken as an approximate lower bound, as the 26 sequences in haplotype group I do not conform to the assumption of a star phylogeny.

An excess of nonsynonymous fixed differences:

Recurrent positive selection on amino acid substitutions at a locus should result in an excessively low ratio of nonsynonymous intraspecific polymorphisms to nonsynonymous fixed interspecific differences, relative to the analogous ratio of synonymous substitutions (McDonald and Kreitman 1991). The number of each type of substitution for each gene and for the region as a whole is presented in Table 5, along with the neutrality index (Rand and Kann 1996), which is a ratio of the two ratios described above. A neutrality index less than one indicates a relative paucity of nonsynonymous polymorphisms. Five of the six genes in this region have an excess of fixed replacement substitutions between D. simulans and D. melanogaster, and this excess is statistically significant at janB and sryδ, as well as for the region as a whole. This result does not appear to be the result of an excess of unpreferred synonymous substitutions segregating within D. simulans, as there is no detectable difference in the frequency distribution of preferred to unpreferred vs. unpreferred to preferred changes (Akashi 1997; sites were pooled across all six loci, Mann-Whitney U-test, z = 0.907, P > 0.05). Using the D. yakuba sequence to polarize fixed differences to the D. simulans or D. melanogaster lineages results in nonsignificant McDonald-Krietman tests for janA, janB, and ocn individually due to small sample sizes (not shown). However, pooling data across these three loci gives a significant excess of replacement fixations along the D. simulans lineage (Table 5). These results suggest that one (or more) of these genes has been a target of positive selection along the D. simulans lineage since its divergence from D. melanogaster.

TABLE 5.

McDonald-Kreitman tests

Gene	DS	PS	DN	PN	N.I.	P-value
sryδ	15	16	8	1	0.12	0.021
sryα	18	10	3	7	4.2	0.060
sryβ	12	13	4	1	0.23	0.176
janA	5	15	3	1	0.11	0.059
janB	11	11	7	0	0.00	0.026
ocn	6	10	2	0	0.00	0.183
All	67	75	31	10	0.29	0.001
janA-ocna	8	36	6	1	0.04	<0.001

D_S, number of fixed synonymous substitutions; P_S, number of polymorphic synonymous substitutions; D_N, number of fixed nonsynonymous substitutions; P_N, number of polymorphic nonsynonymous substitutions; N.I., neutrality index (Rand and Kann 1996). P-values were calculated by a G-test except for janB and ocn, which were calculated by Fisher's exact test.

^aMutations were polarized to the D. simulans lineage using the D. yakuba sequence as an outgroup.

DISCUSSION

Theoretical studies have explored the effects of positive selection on heterozygosity (Maynard Smith and Haigh 1974; Kaplan et al. 1988, 1989), the distribution of segregating site frequencies (Braverman et al. 1995; Kim and Stephan 2002), the fraction of sites that are singletons (Fu and Li 1993), and the haplotype structure of linked neutral variation (Przeworski 2002; Wall et al. 2002). An excess of rare polymorphisms following a sweep is expected either due to the recovery of genetic variation on the star-like genealogy that results from the abrupt coalescence of all lineages during the sweep (Aguadé et al. 1989) or due to the persistence of ancestral mutations segregating on a limited number of recombined lineages some distance from the selected site (Fay and Wu 2000). In the data presented here, the rare variants are a combination of ancestral and derived polymorphisms retained in the haplotype group II sequences. Despite the presence of high-frequency-derived polymorphisms that are consistent with a sweep, nonsignificant values of Fay and Wu's H are obtained when D. melanogaster is used as an outgroup (Table 1). We infer this to be due to the presence of many low-frequency, derived variants among the haplotype group II alleles. These variants counteract the high-frequency, derived variants of haplotype group I, resulting in a nonsignificant value of H. Our interpretation is that this retention of a few haplotypes with relatively high heterozygosity is the result of linkage to a beneficial mutation bringing one or a few alleles to high frequency, but not to fixation (i.e., an incomplete sweep).

This interpretation is supported by the CLR analysis, which clearly indicates that the pattern of site frequencies across this region is better explained by a model of a complete sweep than by a neutral model and better explained by a model of a partial sweep than by one of a complete sweep. This result is robust to mis-estimation of the true recombination rate (Table 4). However, we are much less confident in our estimation of the parameters associated with this putative partial sweep. The parameter that is probably most accurately estimated is X, which shows the lowest bias and narrowest range in simulations (Table 2). X ranges from 6.39 to 7.20 kb across the various analyses, and this is consistent with the observed pattern of haplotype structure. Given the performance of the composite likelihood in estimating α, the sensitivity of these parameter estimates to R_n (Table 4), and the inconsistency between some of these estimates and the observed haplotype structure, it is difficult to say anything definitive about the strength of selection. Similarly, consistent overestimation of β and covariation between α̂ and β̂ (Table 2, Figure 4) indicates that we cannot say much about the current frequency of the selected allele, except that β is most likely >0.5. Uncertainty regarding β also results from the discrepancy between the assumption of a single population used in the CLR analysis and the worldwide sample of lines used here.

As mentioned above, the presence of the haplotype group II chromosomes suggests either that the favored allele has not been fixed in a number of populations or that there is another explanation for the observed pattern of DNA sequence variation. It should be noted that the influence of a selective sweep on the site frequency spectrum is highly stochastic (for example, Figure 3 in Kim and Stephan 2002), and that this may be exacerbated by the nonrandom sampling of isofemale lines from various locations around the world. As a result, the gaps between the sequenced regions at the sry loci, or a locus outside of the sequenced region, could potentially harbor the selected site and show a pattern of nucleotide polymorphism more consistent with a completed sweep. However, none of these gaps is >1.5 kb, and the largest gap is the most proximal one (between sryδ and sryα). sryδ and sryα have the highest-frequency of haplotype group II sequences (40–50% for each). Given that a region more strongly affected would presumably be entirely (or almost so) haplotype group I sequences, this would require an extremely localized segment with this signature. A different study of nucleotide polymorphism in this region of the genome in D. simulans (Quesada et al. 2003) provides some evidence against these possibilities (see below). Another alternate explanation could be population structure—demographic history combined with restricted gene flow can produce large blocks of linkage disequilibrium and may be the cause of a genome-wide reduction from expected levels of recombination in Drosophila (Wall et al. 2002). However, three observations make it unlikely that demographic forces could have produced the pattern observed here. First, there is no obvious geographic pattern to the presence or frequency of the rarer haplotype group II sequences. Of the six geographic regions with more than two representative lines, at least three contain alleles of both haplotype groups. Second, a very similar pattern consisting of a single haplotype with low polymorphism has been observed at the rp49 gene (which is immediately proximal to sryδ) in an independent sample of D. simulans (Rozas et al. 2001). In this study, a haplotype with very low heterozygosity (referred to here as haplotype group I for consistency) was observed at intermediate frequency within populations sampled from Spain and Mozambique. Estimation of the age of the haplotype group I alleles in these samples produced an estimate of ∼6000 years (Rozas et al. 2001), which is consistent with our results. The persistence of haplotype group II alleles at similar frequencies in populations from two continents and in locations as geographically diverse as South Africa, Australia, and Japan is difficult to reconcile with a simple model of gene flow.

Third, there is strong evidence that this haplotype structure is restricted to this region of the genome. In a subsequent study, sequences from the Spanish and Mozambique D. simulans lines were sampled at intervals up to 35 kb away on either side of the jan-ocn/rp49 region (Quesada et al. 2003). These data show convincingly that the reduction in polymorphism and unusual haplotype structure decay with increasing distance in either direction from jan-ocn/rp49. Furthermore, the observation of a reduction in haplotype structure from sryβ to sryδ and beyond is similar to the one presented here and is additional evidence against a selected site located in a gap or outside the sry-ocn region. The observation of a valley of minimal heterozygosity and maximal haplotype structure, coupled with the retention of haplotype group II lineages (with normal levels of variation and linkage disequilibrium) throughout, led these authors to similarly conclude that a partial selective sweep was a plausible explanation for their observations (Quesada et al. 2003).

The CLR analysis indicates that the selected site is most likely somewhere in the vicinity of janB. However, there is not an obvious candidate for the selected mutation within this region. All of the polymorphic sites in janA, janB, and ocn are silent (with the exception of the singleton polymorphism in s2 at the 5′ end of janA), indicating that any selected site in this region must be regulatory in nature. One candidate region that might harbor important regulatory variants is the portion of the janA 3′-UTR that overlaps with the janB 5′-UTR and has been shown to be sufficient to regulate transcription of janB and restrict translation to postmeiotic spermatids (Yanicostas and Lepesant 1990). However, none of the intermediate-frequency polymorphisms in the janA 3′-UTR (e.g., those at positions 6081–6104 in Figure 2) lie in this region, and the most 5′ segregating site within the janB transcript that is fixed between the two haplotype groups is in the second exon (Figure 2, site 6623). If the selected site lies within the janA 3′-UTR, this would highlight the stretch of ancestral polymorphisms present in an otherwise haplotype group I chromosome, s15, which is likely the result of a gene conversion event. Such a gene conversion event between haplotype I and II sequences would be more likely to have occurred after the swept chromosomes reached an equilibrium frequency.

If this is indeed a partial selective sweep, what is maintaining the presence of the haplotype group II sequences? One possible explanation is that the sweep is ongoing, and that the new haplotype is destined for fixation. Assuming an effective population size for D. simulans of 2 × 10⁶ and 10 generations per year, the transit time to fixation for an allele with a selective benefit 2Ns = 455 could be between 10,000 and 20,000 years (Stephan et al. 1992), so catching this allele in flagrante delicto is not inconceivable and is consistent with the estimate of ∼7000 years for the age of haplotype group I. However, if the sweep were ongoing, one might expect it to have gone to fixation in geographical regions closer to the origin of the selected mutation, rather than the consistently intermediate frequencies observed here across the world and in geographically disparate populations (Rozas et al. 2001).

An alternate explanation is that the fixation of the selected allele is inhibited by the presence of another beneficial mutation segregating nearby on a haplotype group II background, and both mutations must wait to fix until recombination can bring them together (Kirby and Stephan 1996). Given the high density of genes and the evidence for a history of positive selection in this region (Table 5), this might seem a plausible explanation. However, the patterns of variation at this locus and further away on chromosome arm 3R do not support this hypothesis. There is no evidence, for example, for a recently selected mutation in any of the three sry genes, or rp49 (Rozas et al. 2001), as determined by haplotype structure and recombination breakpoints. Additionally, such a “traffic” model predicts that at some distance from janB, haplotype group II alleles would display a region of low polymorphism and strong haplotype structure in the neighborhood of the other selected site. None of the sequences sampled in either direction from janB show evidence for another recently derived haplotype that could be competing with haplotype group I (Quesada et al. 2003).

Finally, consider the possibility that the swept allele is not destined for fixation, but rather that it is nearing or has reached an equilibrium frequency determined by balancing selection at janB or epistatic selection between janB and an allele at another locus. The evidence for positive selection having acted on the genes in this study (Parsch et al. 2001b); and the expression of janA, janB, and ocn in testes (Yanicostas et al. 1989; Parsch et al. 2001b); is consistent with the observation of elevated rates of sequence evolution among genes associated with sex and reproduction in a wide range of taxa (Civetta and Singh 1998; Swanson and Vacquier 2002). A number of phenomena associated with male reproduction can also lead to stable polymorphisms, such as meiotic drive (Charlesworth and Hartl 1978), sperm competition (Clark et al. 1999), and sexually antagonistic pleiotropy (Rice 1984). Further functional analysis of the phenotypic differences between the genetic variants at these loci will be required to discriminate between these and other selective hypotheses.

The number of reports in the literature that invoke positive selection from DNA sequence data has become impressive of late (see Andolfatto and Przeworski 2001 and Przeworski 2002 for references). This alternative to the neutral (Kimura 1968) and mildly deleterious (Ohta and Kimura 1971) theories of molecular evolution is further supported by recent multilocus analyses suggesting that the fraction of interspecific substitutions driven by positive selection may be substantial (Fay et al. 2002; Smith and Eyre-Walker 2002), at least among Drosophila nuclear loci (Weinreich and Rand 2000; Bustamante et al. 2002). The large number of reported sweeps has prompted the reevaluation of the ability of current methods to discriminate positive selection from other forces shaping nucleotide variation; these studies suggest that migration and complex demographic history may explain part of the pattern (Przeworski 2002; Wall et al. 2002). However, more complex models of selection may also be necessary. While there are reports compatible with a recently completed selective sweep (e.g., Nachman and Crowell 2000; Schlenke and Begun 2004), a significant number of studies that infer positive selection have found haplotype patterns suggestive of positive selection in conjunction with balancing or epistatic selection (Hudson et al. 1994; Kirby and Stephan 1996; Cirera and Aguadé 1997; Andolfatto et al. 1999; Benassi et al. 1999—but see Andolfatto et al. 1999 for possible reinterpretations of the statistical significance of some of the haplotype structures in these studies). This may indicate an important role for positive selection in shaping patterns of genetic divergence and also a significant contribution of epistatic and balancing selective forces to the maintainence of natural genetic variation (Lewontin 1974; Zapata et al. 2002). Systematic studies of nucleotide sequence data collected from natural populations without the biases associated with the studies of single loci will be instrumental in resolving this question.

APPENDIX

Assume that a beneficial mutation arises at a site located near a neutral locus. Let y be the frequency of alleles at the neutral locus whose ancestry traces back to the chromosome on which the beneficial mutation occurred (Gillespie 2000). At the moment that the beneficial mutation arises, y = 1/2N. With little recombination between the two loci, y increases along with the frequency of the beneficial allele (0 < y ≤ β). When the beneficial allele is fixed, y ∼ ε^r/s (Kim and Stephan 2002), where r is the recombination rate between the selected and the neutral sites and s and ε are the selection coefficient and the frequency of the beneficial mutation at the beginning of the sweep, respectively. Therefore, y represents the fraction of the population that becomes identical by descent due to hitchhiking. With strong selection (α = 2Ns ≫ 1), the reduction of variation and the skew of the allele frequency distribution depend on the parameter y (Fay and Wu 2000; Gillespie 2000; Kim and Stephan 2002). Because of this, the hitchhiking effect on a neutral locus should be identical for a fixed value of y regardless of the final frequency of the beneficial mutation.

In the middle of the selective phase, y can be decomposed as βy₁ + (1 − β)y₂, where y₁ and y₂ are the frequency of the neutral allele originally linked to the first copy of the beneficial mutation, on chromosomes carrying the beneficial and the ancestral alleles, respectively. At t generations after the occurrence of the beneficial mutation, the expectation of y₁ is given approximately by

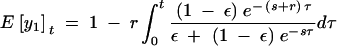A1

(Stephan et al. 1992; Kim and Stephan 2002). Using the approximations given by Stephan et al. (1992), Equation A1 can be simplified to (ε(1 − β)/β(1 − ε))^r/s if ε ≤ β < 0.5 and ε^r/s if 0.5 ≤ β ≤ 1. A corresponding equation for y₂ can be solved to prove that y₂ is negligible compared to y₁ unless the recombination rate is high. We therefore obtain

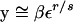A2

[for ε ≤ β < 0.5, β(ε(1 − β)/β(1 − ε))^r/s ≅ βε^r/s if r ≪ s]. Then, the frequency distribution of the derived allele at a neutral locus under the model of incomplete sweep is approximately

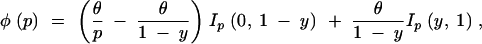A3

where I_p(a, b) is 1 if a < p < b and 0 otherwise (Fay and Wu 2000; Kim and Stephan 2002). From this distribution the probability of observing k derived alleles at a site in a sample of n chromosomes is obtained, and this probability is used to calculate the composite likelihood under the model of an incomplete sweep. Because the deterministic change of the frequency of the beneficial allele from 1/(2N) to 1 − 1/(2N) is very different from the actual trajectory, which is influenced by genetic drift at the early stage (Barton 1998; R. Durrett, personal communication), choosing ε = 1/(2N) underestimates this initial rate of increase. Barton (1998) showed that, conditional on fixation, the early increase in the frequency of a beneficial allele is accelerated by a factor 1/(2s) relative to the deterministic increase from 1/(2N). Then, the true trajectory might be approximated by a deterministic one that starts from 1/(4Ns). We therefore use ε = 1/(4Ns) = 1/(2α). As y ≅ βε^r/s = β(2α)^−R/(2α), the composite likelihood under the selective-sweep model is now a function of scaled parameters α and R (R = |X − m|R_n, where X and m are the nucleotide positions of the selected and the neutral loci and R_n is the scaled recombination rate per nucleotide). Source code written in C for implementing this method is available from the authors upon request.