The Role of Natural Selection in Genetic Differentiation of Worldwide Populations of Drosophila ananassae

Abstract

The main evolutionary forces leading to genetic differentiation between populations are generally considered to be natural selection, random genetic drift, and limited migration. However, little empirical evidence exists to help explain the extent, mechanism, and relative role of these forces. In this study, we make use of the differential migration behavior of genes located in regions of low and high recombination to infer the role and demographic distribution of natural selection in Drosophila ananassae. Sequence data were obtained from 13 populations, representing almost the entire range of cosmopolitan D. ananassae. The pattern of variation at a 5.1-kb fragment of the furrowed gene, located in a region of very low recombination, appears strikingly different from that of 10 noncoding DNA fragments (introns) in regions of normal to high recombination. Most interestingly, two main haplotypes are present at furrowed, one being fixed in northern populations and the other being fixed or in high frequency in more southern populations. A cline in the frequency of one of these haplotypes occurs in parallel latitudinal transects. Taken together, significant clinal variation and a test against alternative models of natural selection provide evidence of two independent selective sweeps restricted to specific regions of the species range.

RECENT large-scale studies of genetic variation are beginning to confirm that species range expansion and the colonization of previously uninhabited territories are accompanied by genetic adaptation to changes in environmental conditions, the signature of which may be detected at the molecular level (Harr et al. 2002; Glinka et al. 2003; Kauer et al. 2003). In the case of Drosophila melanogaster, such an expansion is believed to have started from Africa ∼10,000–15,000 years ago (David and Capy 1988; Lachaise et al. 1988). D. ananassae, another cosmopolitan species in the melanogaster group, is thought to have its origin in Southeast (SE) Asia (Tobari 1993). A recent multilocus study of worldwide populations of D. ananassae substantiates this claim, defining the ancestral range of this species to be a region of SE Asia that existed as a single landmass (Sundaland) during the late Pleistocene (∼18,000 years ago), while other populations including those in more temperate regions appear to be more recent colonizations (Das et al. 2004, accompanying article in this issue). Thus, a similar scenario is emerging for this species, with the invasion of new climatic zones providing a priori expectation that local populations have adapted to their new environments. However, in contrast to D. melanogaster, D. ananassae is a species displaying significant population structure, enabling the footprints of natural selection at the DNA level to be analyzed in a subdivided population.

Previous studies of four D. ananassae populations (Nepal, Myanmar, India, and Sri Lanka) found compelling evidence for the action of natural selection at loci in regions of low recombination (Stephan et al. 1998; Chen et al. 2000). At both the vermilion (v) and furrowed (fw) loci, a pattern of homogenization of allele frequencies within, but differentiation between geographic regions [i.e., North (Nepal, Myanmar) vs. South (India, Sri Lanka)] was found. In both studies, this homogenization of allele frequencies in the northern populations rejected a model of background selection against deleterious mutations (Charlesworth et al. 1993), instead favoring a model of the spreading of a beneficial allele (the selective sweep model; Maynard Smith and Haigh 1974; Kaplan et al. 1989; Stephan et al. 1992). At the fw locus, the background selection model was rejected for the southern populations as well (Chen et al. 2000), raising several important questions about the mode of selective sweeps in this subdivided species. Namely, is this pattern best explained by a single sweep (Slatkin and Wiehe 1998), or have two independent sweeps occurred? Furthermore, the geographic distribution of the sweep(s) is unknown, as is whether it is associated with adaptation to novel environments. Given that D. ananassae is highly structured and occupies a wide range of climatic zones, answers to these questions would also shed light on the role of natural selection in genetic differentiation.

For these reasons, we have expanded the study of nucleotide variation at the fw locus to include 13 populations, spanning a majority of the species range of D. ananassae. In contrast to previous studies, polymorphism data were collected by PCR and direct sequencing rather than by single-strand conformation polymorphism (SSCP) and stratified sequencing. The migration behavior of this selected locus is compared to that of 10 independent neutrally evolving loci (Das et al. 2004), which alleviates the potential stochasticity of single-locus estimates of the migration rate. The pattern of differentiation between pairs of populations is tested against alternative models of selection by the F_ST test of background selection (Stephan et al. 1998; Chen et al. 2000). To further understand the nature of the selective forces shaping variation at fw, the distribution of fw haplotypes is analyzed with respect to population latitude.

MATERIALS AND METHODS

Population samples:

A total of 126 isofemale lines were sampled from 13 locations in India, SE Asia, Australia, and Japan. The location, abbreviation, number of sampled lines, and date of collection are listed for each population in Table 1.

TABLE 1.

Population samples ofD. ananassae used in this study

Sampling location	Country	Abbreviation	No. of isofemale lines	Collection date
Chennai	India	CH	9	2000
Puri	India	PUR	8	2000
Bhubaneswar	India	BBS	9	2000
Kathmandu	Nepal	KATH	10	2000
Mandalay	Myanmar	MAN	10	1994
Chiang Mai	Thailand	CNX	10	2002
Bangkok	Thailand	BKK	8	2002
Kota Kinabalu, Borneo	Malaysia	KK	8	2002
Bogor, Java	Indonesia	BOG	16	2001
Darwin and Kakadu	Australia	DAR	9	1995
Cebu	Philippines	CEB	9	2002
Manila	Philippines	MNL	10	2002
Kumejima, Okinawa	Japan	KMJ	10	2000

DNA extraction, PCR amplification, and direct sequencing of individual fw alleles:

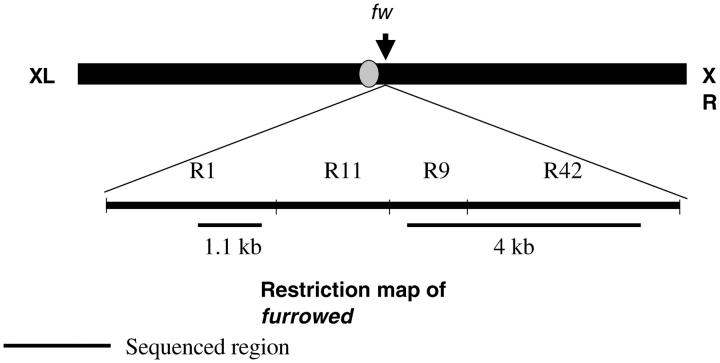
To obtain sequence data from individual X chromosomes, genomic DNA was extracted from individual male flies using the PUREGENE DNA isolation kit (Gentra Systems, Minneapolis, MN). Oligonucleotides for amplification and direct sequencing were designed on the basis of previously published D. ananassae fw sequence of the R1 (AF185289) and R9 and R42 (combined; AF185290) EcoRI restriction fragments described by Chen et al. (2000). The R1 fragment covers part of the 5′-untranslated region (UTR) and exons 1–9; R9/R42 covers exon 12, the 3′-UTR, and 3′ flanking region. A 5.1-kb region (1.1 kb of R1 and 4 kb of R9 and R42) corresponding to the 5.7-kb fw fragment of Chen et al. (2000)(minus 600 bp of 5′ sequence) was amplified in three separate PCR reactions (Figure 1). The sequence data of the R1 and R9/R42 fragments are entered as population data sets under the accession numbers AY686940–AY687065 and AY687066–AY687191, respectively. Due to the presence of stretches of repetitive sequence, the R11 fragment was not sequenced (Chen et al. 2000). Products were purified with QIA-quick columns (QIAGEN, Valencia, CA), and both strands were subsequently sequenced using primers spaced ∼400–500 bp apart. Sequencing was performed on a Megabace 1000 automated DNA sequencer (Amersham Biosciences, Buckinghamshire, UK). The primer sequences and cycling conditions for both PCR and sequencing reactions are available from the authors upon request.

Figure 1.—

Restriction map of furrowed and location of the region sequenced in this study. R1–R42 are EcoRI restriction fragments described by Chen et al. (2000). The R1 fragment covers part of the 5′-untranslated region (UTR) and exons 1–9; R9/R42 covers exon 12, the 3′-UTR, and 3′ flanking region. A 5.1-kb region (1.2 kb of R1 and 3.9 kb of R9 and R42) corresponding to the 5.7-kb fw fragment of Chen et al. (2000)(−600 bp of 5′ sequence) was amplified in three separate PCR reactions and subjected to direct sequencing.

Sequence analysis:

Sequences were edited with SeqMan and aligned with MegAlign (DNAStar, Madison, WI). The DnaSP program version 3.51 (Rozas and Rozas 1999) was used for most intraspecific analyses. Nucleotide diversity, θ̂, was estimated according to Watterson (1975) and π̂ according to Nei (1987).

Pairwise HKA tests:

The HKA test (Hudson et al. 1987) was performed for all pairwise comparisons between loci [11 loci (fw + 10 neutral loci) → 55 comparisons], for each of the 13 sampled populations using a program kindly provided by Lino Ometto. For each population, the probability of observing at least i significant tests at the fw locus given that n paired tests were performed and k were significant between the l loci was calculated by

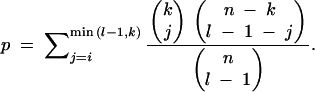1

F_ST test of the background selection model:

The original development of this test is described in Stephan et al. (1998) and was modified by Chen et al. (2000). In summary, this test takes into account the effect of background selection and recombination on the effective population size of the locus of interest, enabling the effect of background selection on neutral variation in a subdivided population to be approximated by simulating the neutral coalescent under a model of population structure. In these simulations, the finite island model (Crow 1986, Chap. 3.4) is used. The per-locus nucleotide diversity θ_S, the migration rate M_S, and the recombination rate R_S at the locus putatively under selection are specified along with the number of subpopulations, k.

The migration rate at the locus putatively under selection, M_S, is estimated from the data

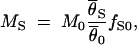2

where M₀ is the migration rate at neutrally evolving reference loci. M₀ is estimated for each pair of populations as in Chen et al. (2000), but is now obtained by taking the average over 10 neutrally evolving loci (introns). 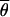_S and 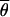₀ are the arithmetic means of the per-site nucleotide diversities in the two subpopulations at the locus putatively under selection and the average of 10 neutral loci, respectively. The factor f_S0 takes differences in the neutral mutation rate between loci into account (Chen et al. 2000).

Analysis of clinal variation:

To assess the association of allele frequency with population sample latitude, a linear regression analysis was performed. If selection affecting the observed distribution of fw haplotypes is attributable to an environmental gradient covarying with latitude, allele frequencies at fw may be expected to display a latitudinal cline. This analysis was performed on both a haplotype and a site-by-site basis following the design of Berry and Kreitman (1993). To distinguish between the effects of selection and population history, clinal variation at fw was compared to that observed at 10 neutrally evolving loci.

To assess the statistical significance of clinal variation, haplotype and SNP frequencies were first arcsine-transformed and then regressed on population latitude (measured as distance from the equator). The significance of the observed squared correlation coefficient, r², was then estimated by generating 10,000 randomized data sets by binomial sampling under the expected frequency (the overall mean in the entire sample) of a SNP or haplotype. This generates 10,000 new frequencies for each subpopulation, for which 10,000 r² values are then computed to determine the significance of the observed r².

In addition, we performed an analysis to investigate the extent to which clinal variation at one site can be explained by the amount of linkage disequilibrium to another site as described by Berry and Kreitman (1993). In this approach, each site in turn is considered as the “governing” site, for which the clinal variation of every other “affected” site within a given locus may be explained by linkage to this site. For example, consider site X as the governing site and an affected site Y. For the entire pooled sample, the nucleotide T at site Y is present in 50% of the chromosomes in which the nucleotide A is present at site X and in 25% of the chromosomes that lack A at site X. If A is present at site X in 8 out of 12 chromosomes in a given subpopulation, the expected frequency of T at site Y in this subpopulation is (0.5 × 8) + (0.25 × 4) = 5/12. The expected frequency is computed in this manner for each individual subpopulation, from which 10,000 simulated frequencies are generated for each subpopulation. The significance is then determined by performing regressions on each of the 10,000 simulated sets of frequencies as described above. Thus, if the r² falls within the 95% confidence interval of the simulated r² values, the clinal variation of T at site Y may be explained by linkage with A at site X.

RESULTS

DNA polymorphism at fw:

A region totaling 5.1 kb including most of the 3′ half of the fw transcriptional unit and a large portion of the 3′ flanking region was subjected to PCR and direct sequencing (Figure 1). On average, 10 lines per population were sequenced for 13 populations, giving a total of 126 sequenced lines (Table 1). A total of 54 nucleotide and 11 length polymorphisms were detected in this sample. An insertion of ∼1 kb in intron 6 occurring twice in the sample (line 8 from KK and line 27 from CH) was partially sequenced. Representative polymorphism data are shown in Figure 2. Of the three nucleotide polymorphisms in the coding region, only one changes the amino acid sequence (Glu to Gln at position 1113 of the R1 fragment), and this occurs only once in the sample (line 95 from BOG). The estimates of average nucleotide diversity, π̂ and θ̂, at silent sites are low for each population (Table 2), on average >10-fold lower than estimates at 10 neutral loci in regions of normal to high recombination (π̂_fw = 0.00066; π̂_neutral = 0.0079; Das et al. 2004). Notably, populations from the northernmost range of the sampled locations (Nepal, Myanmar, and Japan) show the lowest levels of diversity, the most extreme being Nepal, which is monomorphic at fw. The values of Tajima's (1989) D-statistic are negative in a majority of the populations, with the exception of those populations of more intermediate latitude, which show positive values. The D-value of the population from Java (BOG) significantly deviates from zero, although this may represent a genome-wide effect in this population as the values of D from the 10 neutral loci also significantly deviate from zero in this population (Das et al. 2004). This interpretation is supported by the observation that three of the four populations from Sundaland surveyed show strongly negative D-values at fw, consistent with the observation at the 10 neutral reference loci.

Figure 2.—

Representative polymorphism at fw. Length polymorphisms are not shown. The standard sequence is based on the inferred ancestral sequence as determined by D. pallidosa. All nucleotides shown as letters represent the derived state of the polymorphism. Polymorphisms distinguishing the northern haplotype class (sites 1504 of R1 and 687, 969, 3994, and 4106 of R9/R42) are highlighted in blue. Note that site 1004 of R1 is not diagnostic of this haplotype class because it is not completely linked to these sites (see CH population). Polymorphisms distinguishing the southern haplotype class (sites 1854 and 2961 of R9/R42) are highlighted in red. Coordinates of the R1, and R9 and R42 (combined), fragments correspond to those given by the accession nos. AF185289 and AF185290, respectively.

TABLE 2.

Summary of polymorphism atfw

Population	Diversity, π̂	Diversity, θ̂	Tajima's D	Divergence
CH	0.00140	0.00132	0.32	0.00563
PUR	0.00068	0.00065	0.26	0.00556
BBS	0.00049	0.00070	−1.36	0.00574
KATH	0	0	—	0.00591
MAN	0.00023	0.00022	0.10	0.00585
CNX	0.00110	0.00089	1.04	0.00563
BKK	0.00132	0.00114	0.80	0.00541
KK	0.00077	0.00098	−1.07	0.00507
BOG	0.00034	0.00082	−2.28**	0.00502
DAR	0.00077	0.00093	−0.80	0.00530
CEB	0.00053	0.00077	−1.49	0.00511
MNL	0.00077	0.00112	−1.44	0.00585
KMJ	0.00013	0.00022	−1.56	0.00592

Nucleotide diversity π̂ was estimated accordting to Nei (1987), and θ̂ according to Watterson (1975). The value of D was obtained by Tajima's (1989) method.

^**P < 0.01.

Polymorphism and divergence:

The average silent divergence between D. ananassae and its sibling species D. pallidosa at fw was 0.0055, while the average value of the 10 neutral loci was 0.0148 (Das et al. 2004). Under a constant-rate, neutral model of molecular evolution, levels of polymorphism and divergence should be correlated. To test this hypothesis, the method of Hudson, Kreitman, and Aguadé (the HKA test; Hudson et al. 1987) was performed for all pairwise comparisons between loci [11 loci (fw + 10 neutral loci) → 55 comparisons], for each of the 13 sampled populations. For each population, the probability of observing at least i significant tests at the fw locus given that n paired tests were performed and k were significant between the l loci was calculated using Equation 1 (see materials and methods). The number of comparisons deviating from the neutral expectation was significantly higher than expected for all northernmost populations (PUR, BBS, KATH, MAN, and KMJ), as well as several populations in the South (KK, DAR, and CEB). Thus, a constant-rate, neutral model of molecular evolution is rejected for these populations. These results are summarized in Table 3.

TABLE 3.

Results of pairwise HKA tests betweenfw and 10 neutral loci

Population	Significant comparisons with fw	Total significant comparisons	P
CH	0	4	1
PUR	5	5	7.2E-05
BBS	4	4	0.00062
KATH	10	10	3.4E-11
MAN	9	16	1.6E-05
CNX	1	1	0.18
BKK	2	3	0.08
KK	2	2	0.0303
BOG	0	0	1
DAR	3	3	0.00457
CEB	4	4	0.00062
MNL	1	1	0.18
KMJ	7	9	1.9E-05

The HKA test was performed for all pairwise comparisons between loci [11 loci (fw + 10 neutral loci) → 55 comparisons], for each of the 13 sampled populations. For each population, the probability of observing at least i significant tests at the fw locus given that n paired tests were performed and k were significant between the l loci was calculated using Equation 1 (see materials and methods). Populations in italics indicate that the number of comparisons deviating from the neutral expectation was significantly higher than expected for this population.

Haplotype structure:

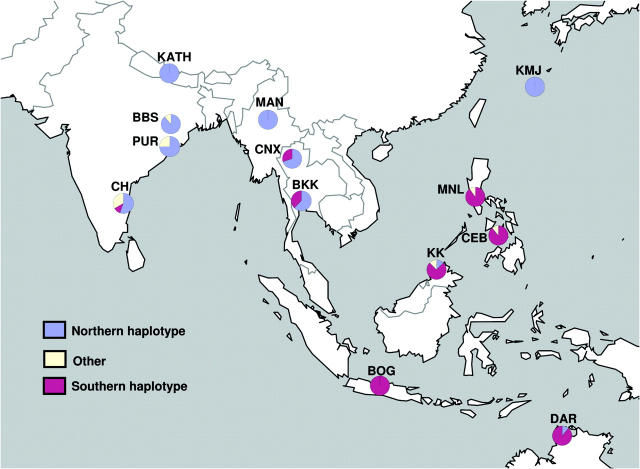
Of the 37 haplotypes observed in our data set, two major haplotype classes are apparent and are distinguishable by unique, high-frequency-derived polymorphisms in complete linkage disequilibrium with one another. The “northern” haplotype class, which is in high frequency or fixed within the northern range of the sampled locations (overall frequency = 49.2%), is distinguished from all other haplotypes by a “T” at position 1504 of the R1 fragment and “A,” T, A, and T at positions 687, 969, 3994, and 4106 of the R9/R42 fragment, respectively (Figure 2). Likewise, the “southern” haplotype class is in high frequency or fixed within the South (overall frequency = 43.7%) and is distinguished from all other haplotypes by A and T at positions 1854 and 2961 of the R9/R42 fragment, respectively (Figure 2). The remaining haplotypes constitute 7.1% of the sample and do not contain any of these diagnostic derived polymorphisms. These are collectively more variable than the northern or southern haplotype classes and are likely representative of ancestral polymorphism at fw (π̂_other = 0.00078). The haplotype classes in high frequency, in particular the northern class, harbor less variation (π̂_northern = 0.00024; π̂_southern = 0.00045). The geographic distribution of northern, southern, and other haplotypes is shown in Figure 3.

Figure 3.—

Geographic distribution of fw haplotype frequencies.

Analysis of clinal variation:

The relationship of allele frequency with population latitude is plotted for each haplotype class in Figure 4. A significant correlation (r²) between transformed haplotype frequency and population latitude was found for both the northern (r² = 0.841; P < 0.0001) and southern (r² = 0.669; P < 0.001) haplotype classes.

Figure 4.—

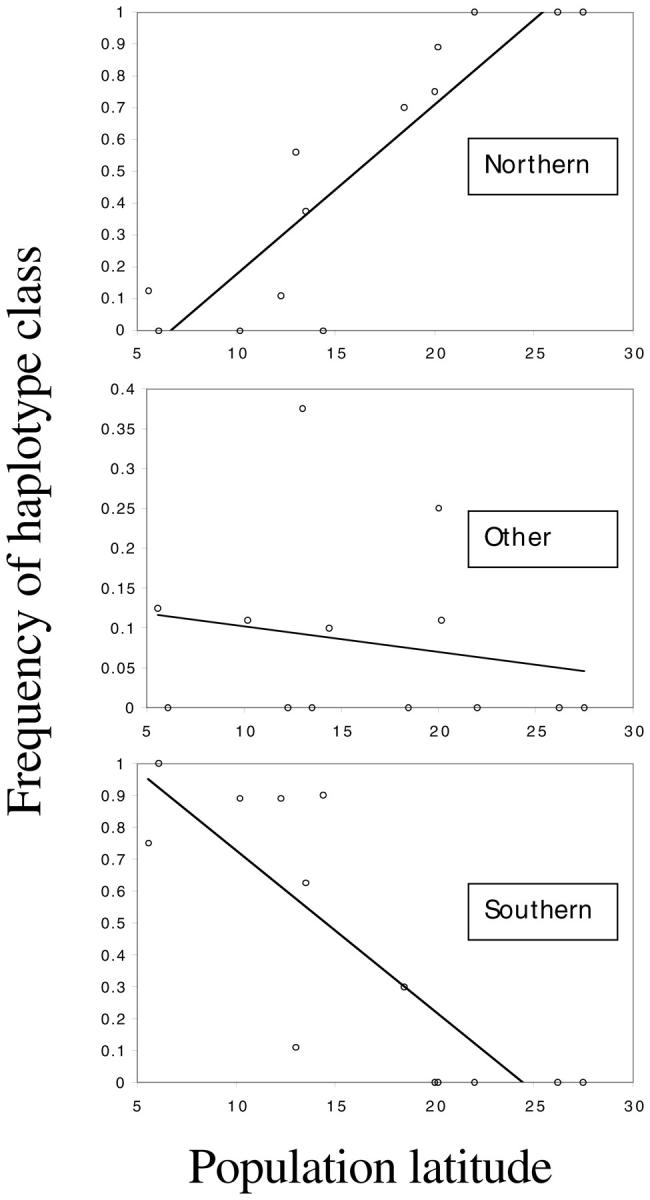
Relationship of nontransformed haplotype frequency and population latitude (measured as distance from the equator). Regressions (r²) and slopes (m) are based on transformed frequencies: northern r² = 0.841 (P < 0.0001), m = 10.224; southern r² = 0.669 (P < 0.001), m = −10.115.

To investigate the observed clinal variation at fw in more detail and distinguish between the effects of natural selection vs. population structure and/or history, a linear regression analysis was performed on a site-by-site basis for both fw and 10 neutrally evolving loci, following the design of Berry and Kreitman (1993). If selection acting on a site(s) linked to fw is responsible for the observed cline, the expectation is to observe clines only at fw or other sites linked to the target(s) of selection. In contrast, if population history is responsible, clines may be observed at loci across the entire genome. Thus, we compared the clinal variation of polymorphic sites at fw with that found at 10 unlinked, neutrally evolving loci. Of the 25 polymorphic sites (singletons were eliminated) subjected to regression analysis at fw, 9 were significantly correlated with latitude with an average correlation of r² = 0.751. In comparison, of a total of 326 polymorphic sites tested at the neutral loci, 19 were significantly correlated with latitude with an average correlation of r² = 0.324. The results of the regression of polymorphic site frequency with population latitude for these 11 loci are summarized in Table 4.

TABLE 4.

Summary of clinal variation of polymorphic sites atfw and 10 neutral loci

				r2
Locus	Site	Frequency	Slope	All populations	India	SE Asia	Easternmost
fw	834	0.07	9.79	NS	—	—	0.821*
(25)	1004	0.53	8.84	0.782***	NS	0.886*	0.812*
1504	0.49	10.46	0.857***	0.929*	0.886*	0.812*
687	0.49	10.46	0.857***	0.929*	0.886*	0.812*
969	0.49	10.46	0.857***	0.929*	0.886*	0.812*
1069	0.19	8.9	0.305*	NS	NS	—
1854	0.44	−10.57	0.693***	—	0.987**	NS
2292	0.06	−6.05	NS	0.589*	—	—
2961	0.44	−10.57	0.693***	—	0.987**	NS
3994	0.49	10.46	0.857***	0.929*	0.886*	0.812*
4023	0.05	−11.8	NS	0.948*	—	—
4106	0.49	10.46	0.857***	0.929*	0.886*	0.812*
1	4	0.07	−22.65	NS	NS	NS	0.808*
(35)	10	0.14	6.81	NS	NS	NS	0.850*
14	0.19	5.74	NS	NS	NS	0.825*
53	0.14	−20.91	0.335*	NS	NS	NS
2	28	0.05	21.56	NS	—	—	0.890*
(63)	47	0.12	−23.67	0.283*	NS	NS	NS
48	0.10	−48.77	0.424*	—	NS	NS
80	0.78	5.46	NS	—	0.933**	NS
83	0.88	10.27	0.290*	—	0.857*	NS
89	0.02	−94.96	0.270*	—	0.852*	—
90	0.05	−5.48	NS	—	0.852*	NS
94	0.02	77.84	0.308*	NS	—	—
3	3	0.31	5.35	NS	0.928*	NS	NS
(60)	8	0.01	114.99	0.280*	—	—	—
9	0.01	104.11	0.251*	—	—	—
11	0.15	3.96	NS	0.994*	NS	NS
13	0.05	10.80	NS	—	0.840*	NS
18	0.01	114.99	0.280*	—	—	—
47	0.01	114.99	0.280*	—	—	—
52	0.81	−1.16	NS	NS	NS	0.802*
53	0.80	−2.78	NS	NS	NS	0.802*
4	72	0.07	23.81	NS	—	NS	0.795*
(34)
5	2	0.18	−18.56	NS	0.936*	NS	NS
(27)	13	0.05	−57.94	0.343*	—	NS	NS
6	7	0.18	28.16	0.398*	NS	NS	NS
(10)
7	10	0.10	8.36	NS	NS	NS	0.821*
(19)	20	0.01	−126.33	0.370**	—	—	—
8	8	0.03	−50.13	0.305*	—	NS	—
(15)
9	22	0.91	18.28	0.454**	—	NS	0.959**
(29)	25	0.33	−4.82	NS	0.931*	NS	NS
10	7	0.01	−129.66	0.356*	—	0.852*	—
(34)	21	0.25	12.62	0.315*	0.943*	NS	NS
23	0.86	4.74	NS	0.935*	NS	NS
39	0.27	13.13	0.303*	NS	NS	NS
46	0.16	10.41	NS	NS	NS	0.874*
	58	0.37	−10.48	0.313*	NS	NS	NS

The numbers of polymorphic sites analyzed for clinal variation (singletons were eliminated) at each locus are indicated in parentheses in column 1. Only sites displaying significant clinal variation in one or more subsets (see below) are shown. The frequency of individual sites is calculated for the entire pooled sample, on the basis of the derived state of the polymorphism as determined by the outgroup D. pallidosa. The slopes are computed from transformed data based on the entire pooled sample. Regressions (r²) of transformed allele frequencies on latitude were performed for all the populations combined, as well as the following subsets: India (KATH, BBS, PUR, and CH), SE Asia (MAN, CNX, BKK, and BOG), and Easternmost (KMJ, MNL, CEB, KK, BOG, and DAR). Polymorphic sites monomorphic or occurring only once in individual subsets are indicated by dashes. NS, no significant clinal variation.

^*P < 0.05;

^**P < 0.01;

^***P < 0.001.

In addition, we analyzed the relationship between allele frequency and latitude in various subsets of the sampled populations. If selection is responding to environmental factors covarying with latitude, the same linear relationship of allele frequency with latitude should be observable in multiple latitudinal transects (i.e., parallel clines), as seen with the F/S polymorphism of D. melanogaster Adh (Oakeshott et al. 1982). We divided the population samples into subsets labeled India (KATH, BBS, PUR, and CH), SE Asia (MAN, CNX, BKK, and BOG), and “easternmost” (KMJ, MNL, CEB, KK, and DAR). The five sites diagnostic of the northern haplotype class (R1, 1504; and R9R/42, 687, 969, 3994, and 4106) remain significant in all three subsets. The two sites diagnostic of the southern haplotypes (R9/R42, 1854 and 2961) are significant in SE Asia, although not in the easternmost or India subsets. Indeed, the above tests of correlation between haplotype class frequency and latitude (Figure 4) are not independent, and it seems likely that the northern haplotype is largely responsible for the observed pattern. Furthermore, of the 36 polymorphic sites at the neutral loci displaying significant clinal variation in at least one set of populations (entire sample or one of the three subsets), 31 are significant in only one set, while the remaining five are significant in only two sets (Table 4). Thus, while polymorphic sites associated with the northern haplotype class display significant clinal variation for the entire data set as well as independent subsets, the clinal variation observed at the neutral loci is inconsistent across the data set and more likely caused by chance on a more local scale. To our knowledge, this is the first example of a cline in a region of low recombination.

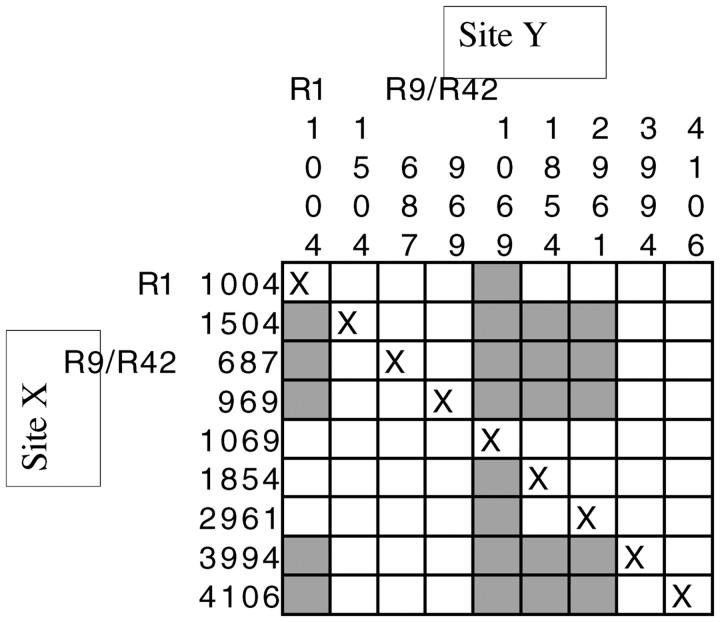
Although the overall scheme and rationale of our analysis of clinal variation at fw follows that of Berry and Kreitman (1993), our data set differs in an important way. Previous studies applying this design (Berry and Kreitman 1993; Verrelli and Eanes 2000) have focused on distinguishing and identifying the target(s) of clinal selection (e.g., sites such as amino acid polymorphisms displaying significant clinal variation that could not be explained by linkage to other sites were identified as putative targets). Although linkage disequilibrium should technically be calculated only for individual populations, extensive nonindependence between polymorphic sites exists across the entire surveyed region. In particular, the derived polymorphisms characterizing the northern and southern haplotypes are in complete linkage disequilibrium. This is not surprising, given that fw resides in a region of very low recombination (Stephan and Mitchell 1992); the size of the region in which linked neutral variation is affected by selection may be very large. Given that 53 of 54 segregating mutations in this data set are silent and the single nonsynonymous mutation occurs only once in the sample, the target(s) of selection is unlikely to reside within the region sequenced in this survey. However, the analysis of clinal variation with respect to linkage disequilibrium to other sites applied to this data set is informative nonetheless, as it reaffirms that sites distinguishing the northern haplotype are responding to clinal selection in a nonindependent manner (Figure 5), most likely due to being linked to a target(s) outside of the sequenced region.

Figure 5.—

Summary of clinal variation at fw for all populations. Only sites with significant clinal variation are shown (see Table 4). Shaded boxes refer to significant clinal variation at site Y that cannot be explained by linkage to site X.

Finally, although a clear relationship between frequency and population latitude is present with the northern haplotype in particular, visual inspection of Figure 3 suggests other factors such as population longitude. To further investigate this, the relationship between haplotype class frequency and population longitude was analyzed for the entire data set as well as subsets labeled North (BBS, PUR, KATH, MAN, CNX, MNL, and KMJ) and South (CH, BKK, BOG, KK, CEB, and DAR). A weak correlation was found for the southern haplotype in the entire data set (r² = 0.383; P < 0.05), though in neither of the subsets, while the northern haplotype displayed a correlation only in the South subset (r² = 0.685; P < 0.05). While an apparent small longitudinal effect is present, other important factors should be kept in mind in interpreting the distribution of these haplotypes. First, the sampling of populations is subject to geographical constraint (e.g., one can sample only on land); and second, environmental factors covarying with latitude may not be completely consistent across the entire sampling range (see discussion).

Test of the background selection model:

The above results of the HKA test indicate that for several populations, the level of polymorphism at fw is too low to be explained by a constant-rate, neutral model. Two alternative models proposed to explain the reduction of variability in regions of low recombination are the hitchhiking (Maynard Smith and Haigh 1974; Kaplan et al. 1989; Stephan et al. 1992) and background selection (Charlesworth et al. 1993; Hudson and Kaplan 1995; Charlesworth 1996) models. The hitchhiking model describes the effect of rare, strongly selected beneficial mutations on linked neutral polymorphism, while the background selection model considers the effects of frequent, strongly deleterious mutation onlinked neutral variants. In the following, we applied the method of Stephan et al. (1998), which utilizes the unique prediction of background selection operating in a subdivided population to distinguish between these two alternative models. Because the effective size of local demes is reduced in regions of low recombination relative to that in regions of normal to high recombination, a smaller number of effective migrants is expected to increase F_ST (Charlesworth et al. 1997).

To test the null hypothesis that background selection is responsible for the observed pattern of differentiation between pairs of populations throughout the D. ananassae species range, we generated a probablity density of F_ST values under the finite island model for k demes and a migration rate M_S, mutation parameter θ_S, and per locus recombination rate R_S at the locus putatively under selection (fw). A range of values was chosen for the unknown parameters k and R_S, while M_S and θ_S were estimated from the data (see materials and methods). The probability of obtaining a value of F_ST less than or equal to the observed F_ST under background selection is given for representative pairwise comparisons between populations in Table 5. For several comparisons among populations in the North and among populations in the South, F_ST values are too low to be explained by the background selection model for various values of k and R_S, whereas almost all remaining values within these regions approached significance. Although less conservative, higher values of k are likely more realistic for D. ananassae (Das et al. 2004) and produced lower P-values. In addition, in contrast to the previous study of fw, evidence of intragenic recombination was found by the four-gamete rule (Hudson and Kaplan 1985) in this data set, indicating that a nonzero level of recombination may be appropriate, which also produces lower P-values. Thus, the low level of differentiation among populations within each of these two geographic regions may be indicative of the spread of positively selected alleles.

TABLE 5.

Probability of obtaining the observed or lower values ofF_ST under the background selection model

			k = 100		k = 500
Population 1	Population 2	Region of comparison	R = 0	R = 0.1	R = 0	R = 0.1
KATH	MAN	N-N	0.068	0.057	0.070	0.032
KATH	BBS	N-N	0.039	0.027	0.039	0.012
KATH	KMJ	N-N	0.080	0.077	0.080	0.078
MAN	BBS	N-N	0.025	0.029	0.025	0.005
MAN	KMJ	N-N	0.051	0.035	0.050	0.019
KATH	BOG	N-S	0.522	0.536	0.525	0.556
MAN	DAR	N-S	0.456	0.458	0.461	0.437
BBS	DAR	N-S	0.516	0.498	0.509	0.473
BBS	BOG	N-S	0.747	0.766	0.737	0.770
KMJ	KK	N-S	0.342	0.322	0.332	0.299
DAR	BOG	S-S	0.107	0.074	0.107	0.030
DAR	CEB	S-S	0.048	0.034	0.045	0.017
DAR	KK	S-S	0.065	0.046	0.065	0.019
BOG	CEB	S-S	0.056	0.038	0.057	0.013
BOG	KK	S-S	0.064	0.039	0.069	0.012

Significant comparisons are shown in italics. N, North; S, South.

DISCUSSION

Overview:

In this study, we have reexamined the pattern of nucleotide variation at fw on a much larger scale, using PCR and direct sequencing as opposed to SSCP and stratified sequencing. Although in most cases new population samples were used (only the Myanmar sample was also used by Chen et al. 2000), the overall level of polymorphism at fw was found to agree between these two methods. In addition, the added advantage of a detailed knowledge of population history from 10 neutrally evolving loci was available (Das et al. 2004). The major goals of this study were to elucidate the pattern and distribution of selective sweeps at this locus and help establish the role of natural selection in differentiation between populations. In the following, we discuss several lines of evidence for natural selection playing a significant role, in particular with respect to recent range expansions and potential adaptation to new environments.

Selection vs. demography:

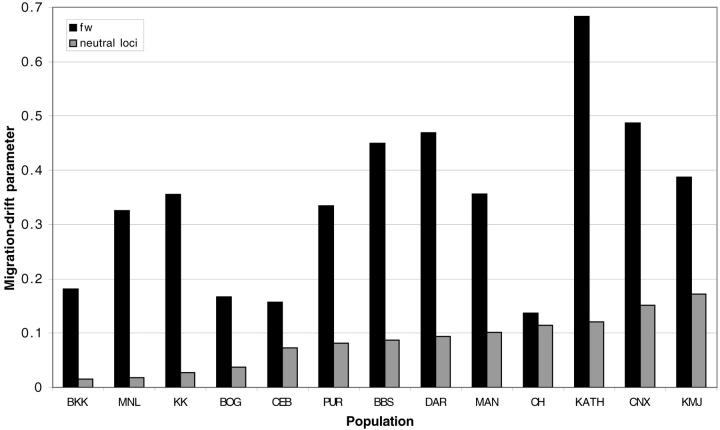
In addition to providing a control for nonadaptive processes in the analysis of clinal variation, detailed analysis of population structure based on10 neutral loci has revealed other interesting aspects of the population history of D. ananassae that shed light on the pattern of variation observed at fw (Das et al. 2004). First, the method of Vogl et al. (2003) applied to these loci has enabled these populations to be characterized as either central or peripheral by the inference of the migration-drift parameter, Θ_P. In short, this is the probability that two sequences randomly drawn from a population coalesce before migration. High values of Θ_P are indicative of populations being highly differentiated due to drift (and thus peripheral), while low values indicate the population is closer to the central, ancestral species distribution (Vogl et al. 2003). The populations from five SE Asian localities [BKK, KL (Kuala Lumpur, not included in the fw survey), BOG, KK, and MNL] display high variability and low estimates of Θ_P and are inferred to be central populations likely representative of an ancestral population of D. ananassae (Das et al. 2004). The other populations showed lower variability and higher estimates of Θ_P, indicating that these populations are more peripheral. Due to the consistent ∼10-fold lower variation at fw in comparison to the neutral loci, estimates of Θ_P are systematically higher at fw. However, the relative difference in these estimates between populations differs at fw and the 10 neutral loci in several cases (Figure 6). In particular, the CH population has one of the highest estimates of Θ_P at the neutral loci, in contrast to the lowest at fw. Thus, although CH appears to be one of the most peripheral of all the populations based on the neutral loci, a higher diversity of haplotypes is present at fw relative to the other populations. A peripheral status in combination with intermediate latitude may have left this population less subject to the effects of selection observed in other populations. The presence of the highest frequency (33%) of non-sweep-associated haplotypes in this population is consistent with this hypothesis.

Figure 6.—

Comparison of the migration-drift parameter, Θ_P (Vogl et al. 2003), at fw and 10 neutral loci.

Second, analysis of the ancestry of these populations is suggestive of selection influencing the distribution of haplotypes at fw. On the basis of both the model-based clustering algorithm of the program Structure (Pritchard et al. 2000) and a neighbor-joining population tree (based on F_ST), the 10 neutral loci reveal a close relationship between the Indian populations (BBS, PUR, and CH), KATH, and MAN and the sample from Australia (DAR). Similarly, the samples from Java (BOG) and Japan (KMJ) are closely related, suggesting a common ancestral origin for these pairs of populations (see Das et al. 2004, accompanying article, this issue, Figure 3). In contrast, these pairs of populations are highly differentiated at fw, being fixed or nearly fixed for the northern and southern haplotypes in these respective regions. Thus, the composition of the ancestral populations from which current peripheral populations are sampled does not appear to have solely determined the current pattern observed at fw.

Selective sweeps in a subdivided population:

Previous analysis of polymorphism at fw in four populations (Nepal, Myanmar, India, and Sri Lanka) considered several possible scenarios of a selective sweep in a subdivided population (Chen et al. 2000). One possibility is that the pattern of homogenization of allele frequencies within, but differentiation between geographic regions [North (Nepal, Myanmar) and South (India, Sri Lanka)], was caused by independent selective sweeps in each region (the two-sweep model). Alternatively, if more than one haplotype became associated with the selected allele via recombination, differential migration of these two haplotypes could result in a similar pattern (the single-sweep model; Slatkin and Wiehe 1998). A third scenario not mutually exclusive of the above two models is that of local adaptation, where a selective sweep may be restricted to certain regions of a species range.

The significantly expanded sampling of this current survey greatly facilitates distinguishing between alternative models. Similar to the study of Chen et al. (2000), a pattern of homogenization within, but differentiation between geographic regions is observed. However, two important differences are the scale on which this is observed and the cline of allele frequencies between these two regions. The northern haplotype is fixed or in high frequency in all populations of higher latitude, and a cline of decreasing frequency is found throughout the entire sample. A similar pattern is observed with the southern haplotype, although the pattern of clinal variation is not as strong: the northern haplotype also decreases in frequency in the absence of high frequencies of the southern haplotype (e.g., in India); thus, the cline of southern haplotype frequency in the opposite direction may be a secondary effect (see Analysis of clinal variation and below). The model of Slatkin and Wiehe (1998) predicts that differential migration of two different haplotypes linked to the same selected allele will lead to the fixation of only one of these haplotypes in any given population. In addition, should this single-sweep model be invoked, the selective advantage of the beneficial allele should also be necessarily unconditional. Thus, under this model, given that populations in the North and South are fixed or nearly fixed for their respective haplotypes, populations located in intermediate locations (e.g., CH, CNX, and BKK) should also be fixed for one haplotype or the other. In contrast to this prediction, the northern haplotype coexists with other haplotypes, the degree to which being determined by latitude. For this reason, the single-sweep model is unlikely to explain the data. Thus, it is most plausible that two independent sweeps have occurred in the northern and southern regions.

Given the strong evidence for clinal variation of the northern haplotype, it seems that minimally this sweep is a candidate for a locally favored substitution. We hypothesize that the regional high frequency of the southern haplotype is more likely due to the spread of an unconditionally favorable allele [i.e., some populations showing evidence of this sweep are part of the ancestral range of D. ananassae (Das et al. 2004)], although this has not spread throughout the species range because a second, independent sweep associated with a locally favored allele has occurred in the North. Partial inconsistencies in the distribution of the northern haplotype (e.g., the Indian and the Philippine samples have similar latitudes but different composition of fw haplotypes) may at least in part be due to inconsistencies in environmental variables that correlate with latitude. For example, the central and southern Phillipine islands remain hot and humid all year round, while the Indian subcontinent experiences seasonal variation in temperature.

Target(s) of selection:

Traits such as cold tolerance are known to vary with latitude in several species, including D. ananassae (Gilbert and Huey 2001), and it was recently shown that high-altitude Himalayan strains of this species have evolved a temperature dependency to the rhythmicity of eclosion (Khare et al. 2002). Although the pattern of differentiation at fw suggests that positively selected mutations have occurred at linked sites, the size of the fragment displaying reduced variation may be quite large due to the low recombination of the region containing fw. Although numerous chromosomal rearrangements have occurred since D. ananassae and D. melanogaster last shared a common ancestor, gene order on a more local scale is more likely to be preserved. In D. melanogaster, fw lies in a region of normal to high recombination that is relatively gene rich (∼10 genes in a 100-kb window around fw). Thus, it is reasonable to expect that many potential targets of selection are linked to fw. The availability of the genome sequence of D. ananassae in the near future will greatly facilitate the identification of mutation(s) involved in this sweep(s), as well as provide the necessary background for studying adaptation at the genome level in another species. The parallels between the recent evolutionary history of the two cosmopolitan species D. melanogaster and D. ananassae (e.g., the invasion of temperate regions from an ancestral tropical environment) provide an exciting opportunity for comparative studies of adaptation at the genome level.