Experimental Adaptation of Salmonella typhimurium to Mice

Abstract

Experimental evolution is a powerful approach to study the dynamics and mechanisms of bacterial niche specialization. By serial passage in mice, we evolved 18 independent lineages of Salmonella typhimurium LT2 and examined the rate and extent of adaptation to a mainly reticuloendothelial host environment. Bacterial mutation rates and population sizes were varied by using wild-type and DNA repair-defective mutator (mutS) strains with normal and high mutation rates, respectively, and by varying the number of bacteria intraperitoneally injected into mice. After <200 generations of adaptation all lineages showed an increased fitness as measured by a faster growth rate in mice (selection coefficients 0.11–0.58). Using a generally applicable mathematical model we calculated the adaptive mutation rate for the wild-type bacterium to be >10⁻⁶/cell/generation, suggesting that the majority of adaptive mutations are not simple point mutations. For the mutator lineages, adaptation to mice was associated with a loss of fitness in secondary environments as seen by a reduced metabolic capability. During adaptation there was no indication that a high mutation rate was counterselected. These data show that S. typhimurium can rapidly and extensively increase its fitness in mice but this niche specialization is, at least in mutators, associated with a cost.

HOW rapidly and to what extent bacteria can genetically adapt to novel environments has been examined mostly in evolution experiments under apparently homogenous and constant laboratory conditions. These studies show that considerable potential to increase niche-specific fitness often exists (Lenski and Travisano 1994; Rosenzweig et al. 1994; Rainey and Travisano 1998; Rainey et al. 2000; Rozen and Lenski 2000; Buckling et al. 2003; Elena and Lenski 2003). A landmark study of such experimental adaptation was performed by Lenski and coworkers who propagated 12 lineages of Escherichia coli by serial passage in batch cultures of glucose-limited minimal medium for >20,000 generations. Adaptation was associated with a substantial fitness increase, changed cell size, and altered pattern of gene expression (Lenski and Travisano 1994; Travisano and Lenski 1996; Lenski et al. 1998; Cooper et al. 2003; Lenski et al. 2003). Most of the fitness increase occurred during the first 1000 generations and appeared to be conferred by a limited number of mutations, at least some of which increased fitness by allowing a more efficient scavenging of glucose (Lenski and Travisano 1994; Travisano and Lenski 1996; Cooper et al. 2001).

Less is known about the rates and mechanisms by which pathogenic bacteria adapt to the complex and variable natural environment of a host. For example, the gram-negative pathogen Salmonella typhimurium can adhere to and invade gut epithelial cells, disseminate to systemic sites (e.g., liver, spleen) via blood and lymph, and survive and replicate within a variety of host cells, including macrophages (Richter-Dahlfors et al. 1997; Cooper et al. 2001; Salcedo et al. 2001; Santos et al. 2003). To successfully adapt to these different niches the bacterium regulates expression of an extensive repertoire of virulence factors that confer an appropiate physiological response (Clements et al. 2001). In addition, during growth within a host there might be selection for bacterial mutants, which, due to specific regulatory/physiological changes, are better adapted to one or more of the specific host niches (Eriksson et al. 2000; Clements et al. 2002).

In this context the role of mutator alleles and the influence of an increased mutation rate on bacterial short- and long-term adaptation is of interest. Bacteria with increased mutation rates (mutators) have been found among several bacterial species at frequencies varying from 0.1 to 36% depending on the species and the site of isolation (LeClerc et al. 1996; Boe et al. 2000; Oliver et al. 2000; Bjorkholm et al. 2001; Denamur et al. 2002; de Visser 2002). Whether an increased mutation rate confers mainly a cost or a benefit depends on several factors, including environmental stability, how well adapted a bacterium is to a particular niche, and the population structure. As shown by both theoretical analyses (Tenaillon et al. 1999) and experimental studies in laboratory media (Mao et al. 1997; Sniegowski et al. 1997; Tanabe et al. 1999; Schaaff et al. 2002) and animals (Giraud et al. 2001, 2002), high mutation rates might initially confer a benefit because of a faster generation of adaptive mutations. However, once adaptation has been achieved mutator alleles are often counterselected, probably because they generate deleterious mutations at a higher rate (Trobner and Piechocki 1984; Funchain et al. 2000; Giraud et al. 2001).

A related question is whether trade-offs exist between adaptations to different niches. For example, it has been shown that E. coli adapted to a mouse intestine shows lower fitness in a laboratory environment (Giraud et al. 2001). Conversely, it is well known that propagation of pathogens under laboratory conditions often results in a loss of virulence (Siebers et al. 1999; Somerville et al. 2002; Vandenberg and Cantone 2004). The reasons for these trade-offs are unclear but one proposal is that they result from the random accumulation of deleterious mutations in genes that are not under selection in the primary environment. An alternative explanation, the antagonistic pleiotropy hypothesis of niche specialization, suggests that there are genetic or physiological trade-offs such that adaptive mutations that increase fitness in particular niches will inevitably cause a loss of fitness in a dissimilar secondary environment (Levins 1968; Lynch and Gabriel 1987; Turner and Elena 2000; Caley and Munday 2003). It has been difficult in several experimental systems to distinguish between these hypotheses but a convincing illustration of antagonistic pleiotropy was recently provided in Pseudomonas fluorescens by MacLean et al. (2004).

Here we examined how the mutation rate and the population size of S. typhimurium affect the rate and extent of adaptation to mice and whether mouse adaptation resulted in lowered fitness in dissimilar secondary environments. In addition, we used a generally applicable mathematical model to analyze the kinetics of fixation of adaptive mutations during growth in mice.

MATERIALS AND METHODS

Bacterial strains and media used:

All strains used in the experiments were S. enterica Var. typhimurium LT2 (referred to as S. typhimurium in the text). In the evolution experiment strain JB124 (wild type) and strain JB2152 (Tn10dTet 95% linked to a nonsynonomous mutS⁻ base-pair substitution), with a low and high mutation rate, respectively, were used. For all competition experiments strain JB1660 [cobI-24::MudJ(kanR)] was used as the reference competitor. The MudJ insertion is selectively neutral both in mice and under laboratory conditions as indicated by competition experiments against the untagged wild-type strain (data not shown). Media [Luria-Bertani broth (LB), glucose minimal medium, Luria-Bertani agar (LA) plates, and PBS] and antibiotics were prepared and used as described (Davis et al. 1980).

Evolution experiments:

All mouse experiments were performed at the animal facility at the Tumor and Microbiology Center, Karolinska Institute (Stockholm) in accordance with institutional and national guidelines (ethical permit N38/00). Populations of S. typhimurium were serially passaged in BALB/c mice for up to 130 generations of growth. Four different passage conditions were used: (i) low mutation rate (u) and small population bottleneck size (N), (ii) high u and small N, (iii) low u and large N, and (iv) high u and large N. To vary the mutation rate two different strains, a wild-type strain (JB124) and a mutS mutator strain (JB2152), were used and by introducing either 10⁴ or 10⁶ cells into mice in each passage different population bottleneck sizes were obtained. Since the number of viable bacteria decreases ∼10-fold soon after injection of this strain into mice (Bjorkman et al. 2000) the actual bottlenecks were 10³ and 10⁵, respectively. For each of the four different conditions described above, four to five independent lineages were serially passaged. For each passage 6- to 8-week-old female BALB/c mice were infected with either 10⁴ or 10⁶ cells in a 100-μl volume of phosphate-buffered saline (PBS) by intraperitoneal injection. The mice were killed after 3–5 days and the spleens were removed and homogenized in 2% sodium deoxycholate. The homogenate was washed once in PBS and appropriate dilutions were plated on Luria agar plates and incubated overnight to determine the number of viable cells recovered from the spleen. From the viable count determination, the inoculum for the next passage was adjusted to 10⁴ or 10⁶ cells by using a suitable dilution of the homogenate. Samples of the evolving populations were frozen at −80° at regular intervals.

Competition experiments in mice:

Fitness of the evolved populations was estimated after 66 and 132 generations of growth by performing competition experiments in mice. Each population sample to be tested was thawed and 20 μl of the sample was inoculated into 200 μl LB and incubated at 37° overnight. The population sample was then mixed with a genetically tagged competitor reference strain (JB1660) at a 1:1 ratio and 2 × 10⁴ cells of the mix diluted in PBS were used as an inoculum to infect five mice. After 3–5 days, mice were sacrificed and the spleens removed and homogenized in PBS. To determine the ratio of the reference competitor to the population samples, different dilutions of the homogenates were plated on LA and LA plates supplemented with kanamycin. The competition index (CI) was calculated after one cycle of growth in a mouse (∼10 generations) as the ratio of the tested population divided by the reference strain. From this value an approximate intracellular doubling time was calculated using the formula described in Table 1 and the previously determined 5-hr doubling time for the wild-type strain (Bjorkman et al. 2000).

TABLE 1.

Characteristics of parental strains and lineages evolved for 132 generations in mice

Strain/population	Mutation rate	Population bottleneck (cells)	CI after 10 generations	Estimated generation time, tgen (hr)	Estimated s-values
Parent
JB124	Low (MutS+)	1	5 (Bjorkman et al. 2000)
JB2152	High (MutS−)	1	5 (Bjorkman et al. 2000)
Evolved
DA5772	High	105	34	3.3	0.51
DA5778	High	105	19	3.5	0.42
DA5785	High	105	21	3.5	0.44
DA5791	High	105	11	3.7	0.35
DA5797	High	105	13	3.6	0.37
DA5836	High	103	20	3.5	0.43
DA5846	High	103	18	3.5	0.42
DA5857	High	103	17	3.5	0.41
DA5867	High	103	18	3.5	0.42
DA5803	Low	105	19	3.5	0.42
DA5810	Low	105	57	3.2	0.58
DA5816	Low	105	25	3.4	0.46
DA5822	Low	105	5.2	4.0	0.24
DA5828	Low	105	14	3.6	0.38
DA5884	Low	103	2.9	4.3	0.15
DA5894	Low	103	2.1	4.5	0.11
DA5915	Low	103	2.7	4.4	0.14

One lineage was contaminated and was excluded from this analysis. Competition indexes (CI) were calculated as the ratio of the evolved population per parent after 10 generations of growth in mice and the equations used to calculate t_gen and s were s = ln(CI)/10 ln(2) and t_gen = 5/(1 + s).

Competition experiments in LB medium:

Fitness in secondary environments was estimated by performing competition experiments of the evolved populations against the parental reference strain in LB medium at different temperatures. Population samples from all lineages were tested after 132 generations of growth in mice for fitness in LB at 30°, 37°, and 42°. Each population sample to be tested was thawed and 20 μl of the sample was inoculated into 200 μl LB and incubated at 37° overnight. For competition experiments at 37° the population sample was then mixed with strain JB1660 at a 1:1 ratio and serially passaged in LB for 60 generations of growth. The serial passage was performed by transferring 2 μl (2 × 10⁶ bacteria) of overnight culture to 3 ml of LB medium. This culture was grown overnight to a density of 2 × 10⁹ bacteria/ml (corresponding to 10 generations of growth) and the passage was repeated. For competition experiments at 30° and 42° each population and the reference competitor were allowed to grow for one cycle at the temperature used for the competition before mixing. For each passage 2 × 10⁶ cells were transferred to 3 ml fresh LB. Ratio of the population tested to the reference competitor was determined by selective plating in the same way as for the competition experiments in mice.

Mutation rate determinations:

The mutation rate of the evolved populations was determined after 132 generations of growth in mice. Each population sample was thawed and 5 μl of each sample was inoculated into 200 μl LB. After pregrowth at 37° overnight, for each population, 20 independent 1.5-ml cultures were inoculated with 5 μl from a 10⁻⁵ dilution (∼200 cells) of the pregrowth culture. The cultures were then allowed to grow to saturation and suitable dilutions of the cultures were spread on LA plates without and with 50 mg/liter nalidixic acid to determine the total number of viable cells and nalidixic acid-resistant mutants, respectively. The number of colonies appearing after growth for 24 hr at 37° was scored and the mutation rate for each population was estimated as previously described (Rosche and Foster 2000).

Auxotrophy frequency determinations:

The frequency of auxotrophs in the evolved population was determined by spreading suitable dilutions of the evolved populations on LA plates. After incubation at 37° overnight the colonies were replica printed to both glucose minimal medium and LA plates. Auxotrophs were scored as cells forming colonies on the LA plates but not on the minimal medium plates after incubation at 37° overnight. Approximately 200 (mutators) or 1200 (wild-type) colonies were tested.

Metabolic capacity of evolved strains:

The ability to metabolize 46 different carbohydrates was tested for one random single clone from each evolved population using PhP48 plates according to the manufacturer's instructions (PhPlate AB, Stockholm). Briefly, bacteria were suspended in a growth medium containing a pH-sensitive indicator dye. The bacterial suspension was then added to a microtiter plate where each well contains a unique carbohydrate. The color change was measured at three time points and the data were analyzed using the PhPWin software. Each clone was tested twice and the results were compared to the respective parental strain.

RESULTS

Experimental design:

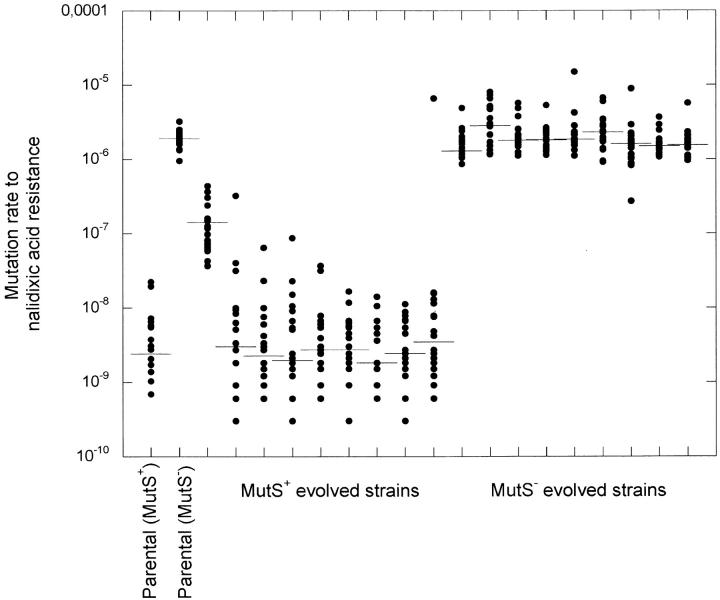
To perform the evolution experiments, we used S. typhimurium LT2 because this bacterium is genetically well defined, the LD₅₀ dose is large (∼10³–10⁴ cells after intraperitoneal injection), and the course of infection is well characterized (Santos et al. 2003). Mice were inoculated intraperitoneally with bacteria and after 3–4 days bacterial cells were harvested from the spleen and used to inoculate new mice. After intraperitoneal injection, the bacteria were rapidly taken up by macrophages at peripheral lymph nodes and transported via blood and lymph to the liver and spleen. In the interpretation of our results we have made the simplifying assumption that both the parental strain and the adapted derivatives have similar transit times from the site of injection to the spleen and liver. The major part of the bacterial growth then occurs within the phagosomes of organ-specific macrophages (Richter-Dahlfors et al. 1997; Salcedo et al. 2001). This cycling was repeated for 8–10 cycles, corresponding to between 66 and 132 generations. Four different conditions were examined: low mutation rate-small N, low mutation rate-large N, high mutation rate-small N, and high mutation rate-large N. The population bottleneck size was varied by changing the number of bacteria that was injected intraperitoneally and the mutation rate was varied by using either a wild-type or a mutS strain that is defective in DNA-directed methyl mismatch repair. Compared to the wild type the mutS strain had a 500- to 800-fold increase in its point mutation rate as measured by nalidixic acid (Figure 1) and rifampicin (not shown) resistance, respectively. For each condition four or five independent lineages were serially passaged. At two different time points, 66 and 132 generations, the fitness of the evolved lineages (as a population) was determined by competition experiments against the parental strains tagged with a neutral MudJ insertion encoding kanamycin resistance.

Figure 1.—

Mutation rates to nalidixic acid resistance of parental strains and evolved lineages. Mutation rates were measured as previously described (Rosche and Foster 2000). Each data point represents one culture and the horizontal line shows the median of all 20 cultures. Note that many points are overlapping.

Rate and extent of adaptation:

The evolved populations were competed against the respective parental strain to determine their extent of adaptation. The evolved populations and the parental strains were mixed at a 1:1 ratio, inoculated intraperitoneally into four to five mice, and after 3–4 days bacteria were harvested and plated on LA and LA-kan plates to determine the number of total and parental reference bacteria, respectively. In Figure 2, the competition indexes are shown. All lineages appeared to show increased fitness after 66 and 132 generations. After 66 generations, the competition indexes varied between 2.5 and 8 where the lower value was for the low N and low u lineages and the higher values were for the large N and high u lineages. After 132 generations the geometric mean CI was ∼20 except for the low N and low mutation rate lineages.

Figure 2.—

Fitness of lineages evolved by serial passage in mice with different population bottleneck sizes and mutation rates. The competition index represents the ratio of evolved lineages per parental reference strain after one growth cycle in mice (∼10 generations of growth) when the parental strain and evolved lineages were injected at a 1:1 ratio. Each data point represents one lineage and the horizontal line shows the geometric mean of all lineages. Open and solid triangles represent lineages evolved for 66 and 132 generations, respectively.

Calculations of relative fitness and adaptive mutation rate:

In previous experiments, we determined the generation time for S. typhimurium in BALB/c mice to be ∼5 hr (Bjorkman et al. 2000). Using this value and the number of generations of growth in the competition experiment we calculated the generation times and selection coefficients (s-values) of the evolved lineages (Table 1). The s-values varied between 0.11 and 0.58, showing that the evolved lineages had considerably increased their fitness in the reticuloendothelial system of mice (Richter-Dahlfors et al. 1997; Salcedo et al. 2001). Adaptation was faster for the mutS lineages at both population sizes but after 132 generations of evolution the mean adaptation was similar for the wild-type and mutS lineages (t_gen ∼ 3.5 hr and s ∼ 0.4), at least when adaptation occurred with the larger population size. As expected, the wild-type lineages with a small population size were least adapted (t_gen ∼ 4.5 hr and s ∼ 0.1).

Beneficial mutations can appear any time during the growth cycles. Before they can increase in number and become fixed in the population the mutants must become established and survive the sampling (bottleneck). Thereafter they will outgrow the original variant and eventually take over. For high mutation rates, the growth advantage is limiting for the fixation time whereas for low mutation rates and/or a small bottleneck, the time for first establishment is crucial (see Equation A15 and Figures A1 and A2 in the appendix). From the s-values, the population sizes during cycling, and the number of generations of adaptation we calculated the apparent mutation rates for the beneficial mutations for the wild-type and mutator strains (see the appendix for the detailed model). It appears that adaptation took place in at least two steps through fixation of two successive mutations, each with an s-value of ∼0.2 (Figure 2). For the mutator strain, the size of the bottleneck seems to be of little consequence. This suggests that the fixation time is limited by the growth advantage and that the mutation rate is >10⁻⁵ (Figure A2 in appendix). This is also consistent with the fixation of a mutation with s = 0.2 in 66 generations (Figure 2). Mutations with s = 0.2 can be fixed within ∼100 generations with a bottleneck of 10⁵ for mutation rates down to ∼10⁻⁶ (Figure A2 in appendix); this may be the case for the wild type. However, also with the 10³ bottleneck, there seems to be some adaptation in the wild type. There was one adaptive mutant after 66 generations with s = 0.25. If u = 10⁻⁷ for the beneficial mutations, the expected fixation time would be 5000 generations, and with u = 10⁻⁶ it would be 600. However, with the small bottleneck and not very large mutation rate, the outcome is very stochastic; if by chance the mutant survives the first sampling, it can be fixed within 60 generations. When s = 0.2, this will happen with probability 0.03 for u = 10⁻⁶ and 0.003 for u = 10⁻⁷ (Figure A1 in appendix). Thus, if there is one adapted line in this set, we expect u > 10⁻⁶ for the wild type. Assuming that the adaptive mutations are point mutations that occur with a mutation rate of 10⁻¹⁰/replication/base pair for the wild-type strain (Hudson et al. 2002), the target size for the adaptive mutations may be as large as 10⁴ bp or more.

Fitness in unselected secondary environments:

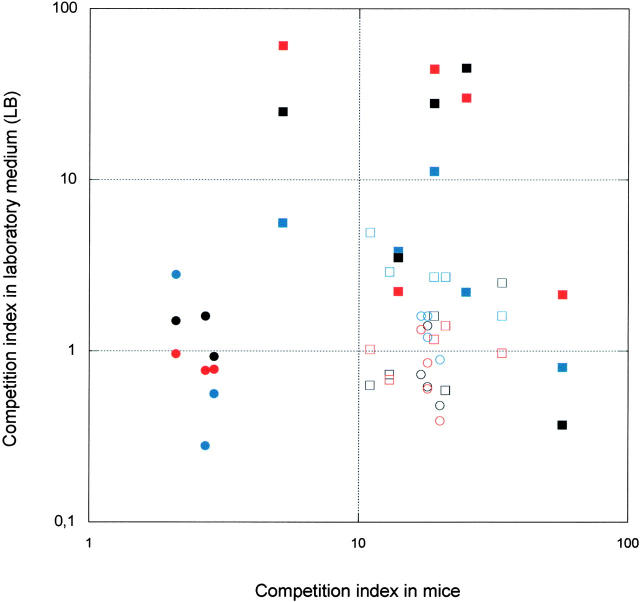
To examine if adaptation in mice resulted in loss of fitness in secondary, presumably dissimilar, environments we determined if the evolved lineages showed reduced fitness in LB at 30°, 37°, and 42°. Competition experiments were performed by mixing parental and evolved lineages in a 1:1 ratio and then growing them for 60 generations. Samples were taken at different time points and plated on agar plates to determine the number of parental and evolved bacteria. In Figure 3, we have plotted the CI values of the evolved lineages in LB as a function of the CI values in mice after 60 and 10 generations of competition, respectively. The mouse-evolved strains showed no general loss of fitness under laboratory conditions. Instead most strains were unchanged in fitness (less than twofold change in CI) at all three temperatures. One class (three lineages) had significantly increased its fitness also in LB at all three temperatures (Figure 3).

Figure 3.—

Fitness in laboratory medium (LB) and mice of evolved lineages as compared to parental strains. Fitness was measured as competition indexes after 60 and 10 generations of growth in LB and mice, respectively. CIs in LB were measured at 30° (blue), 37° (black), and 42° (red). Solid circles, low mutation rate-small N; solid squares, low mutation rate-large N; open circles, high mutation rate-small N; and open squares, high mutation rate-large N.

It was unexpected that no fitness loss was observed in the secondary environment and one potential explanation for this finding is that growth in a rich medium and in a host might place similar selective demands on bacterial physiology. That is, some mutations that are beneficial for growth in mice might also be beneficial in rich laboratory medium. Support for this idea comes from the fact that three mouse-adapted lineages also showed increased fitness in the LB medium. To test for loss of other functions that are likely to be less selected in mice, we used two methods to examine the metabolic capacity of the evolved strains. First, we determined the frequency of auxotrophs in the evolved wild-type and mutS lineages (Table 2). Colonies were replica printed from LB plates onto minimal medium and glucose plates and the frequency of nongrowers on the minimal plate was calculated. In all mutS lineages auxotrophs were found (0.7–39% of the total population depending on the lineage) whereas for the wild-type lineages no auxotrophs were identified (<0.08%). Second, we examined the evolved strains for their capability to utilize various carbon sources. One randomly picked colony from each lineage was tested in the PhP test system where the rate of utilization of 46 different carbon sources can be examined (Hojberg et al. 2003; Kuhn et al. 2003). None of the eight wild-type lineages had lost any metabolic functions whereas all nine mutS lineages had one or more defects (Table 2).

TABLE 2.

Auxotrophy and carbon source utilization ofMutS⁺ andMutS⁻ parental and evolved lineages

Strain	Auxotrophs (%)	Manlacton	Maltose	Inositol	Tagatose	Melbionate	Galactone	Ornithine	Other carbon sources
Parental strains
JB124 (MutS+)	<0.08	+	+	+	+	+	+	+	+
JB2152 (MutS−)	<0.08	+	+	+	+	+	+	+	+
Evolved lineages
MutS−
DA6006	1	+	+	+	−	−	+	+	+
DA6011	3.5	+	+	−	+	−	+	−	+
DA6016	1.8	−	+	+	+	+	+	+	+
DA6021	2.4	+	−	−	+	−	+	+	+
DA7287	1.6	+	+	+	+	−	+	+	+
DA7292	0.7	+	+	+	+	−	−	+	+
DA7297	1.3	+	+	+	+	−	+	+	+
DA7302	0.9	+	+	+	+	+	+	+	+
DA7307	39	+	+	+	+	−	−	+	+
MutS+ (eight   lineages)	<0.08	+	+	+	+	+	+	+	+

Auxotrophy was measured as no growth on glucose, minimal agar plates. Auxotrophies found were histidine, threonine, isoleucine, tryptophan, arginine, pyridoxine, phenylalanine, glycine, and thiamine. Other carbon sources are l-arabinose, d-xylose, galactose, cellobiose, trehalose, palatinose, sucrose, lactose, melibiose, lactulose, gentobiose, melezitose, raffinose, inosine, adonitol, d-rabitol, glycerol, maltitol, sorbitol, dulcitol, sorbose, deoxyglucose, deoxyribose, rhamnose, d-fucose, l-fucose, amygdalin, arbutin, b-me-gluc, 5-ketogluc, gluconate, salicine, citrate, fumarate, malinate, malonate, pyruvate, l-tartarate, and urea.

From the mathematical theory (see appendix), we calculated if the higher frequency of auxotrophs found in the mutS lineages as compared to the wild type could be accounted for by the increased mutation rate. In the mutator lineages there were on average 2% auxotrophs after 132 generations with a bottleneck of 10⁵. Assuming that this accumulation of auxotrophs is due to neutral mutation accumulation and has taken place during approximately six growth cycles (half of the total), the mutation rate would be u = 5 × 10⁻⁴ (Equation A17 in appendix). With an estimated target size for auxotrophy of 2 × 10⁵ bp (Hughes and Andersson 1997), the mutation rate per base pair per replication would be 2 × 10⁻⁹. However, assuming a more reasonable mutation rate for the mutator, 10⁻⁷/base pair/generation (∼1000-fold over the wild type; this article; LeClerc et al. 1996; Boe et al. 2000; Denamur et al. 2002; de Visser 2002), the expected fraction of auxotrophs after a single generation would be 0.02. At this rate nearly all lineages are expected to be auxotrophs after 66 generations. This calculation cannot be reconciled with the 2% observed mean fraction and it suggests that auxotrophy is under negative selection in the mutator background (Curtiss et al. 1993). For the wild type, no auxotrophs were found among the 1200 cells examined for each lineage and this result requires that either the mutation rate is smaller than expected (<5 × 10⁻¹²/base pair/generation) or there is counterselection against the auxotrophs also in the wild-type strain. In view of the results for the mutators we find the latter explanation more likely.

Mutation rates in evolved lineages:

It is conceivable that a mutator allele is counterselected after adaptation to a novel environment has occurred due to the cost of deleterious mutations associated with a high mutation rate. To examine if counterselection had occurred during the experiment, we determined if the mutation rate in the evolved mutator lineages had decreased as compared to the parental strain. In Figure 1 the mutation rate to nalidixic acid resistance is shown for the parental and evolved populations. No change was seen except for one of the wild-type lineages that appeared to have evolved into a mutator with an ∼50-fold increase in mutation rate. Analysis of this population showed that it was a mixed population comprising ∼93% wild-type bacteria and 7% mutators with an 800-fold increase in mutation rate. We conclude from these results that the mutation rates in the evolved mutator populations have not decreased during this experiment.

How rapidly mutators are counterselected depends on the cost conferred by an increased mutation rate and the rate of formation of any reversion or modifier mutations that could reduce the mutation rate. We calculated the rate of such counterselection (see appendix) on the basis of the previous experimental estimate of an ∼1% cost (s = 0.01) of a mutS mutation during growth in laboratory medium (Boe et al. 2000). With these assumptions it is not expected that the mutators would be lost. Thus, even if reversion/modifier mutations occurred at high rates (up to 10⁻⁵), it would take in excess of 1000 generations before a nonmutator would become fixed (Equation A15 and Figure A2 in appendix). Obviously, if the mutator cost was much higher in mice than in laboratory medium nonmutators would become fixed more rapidly. However, competition experiments in mice between wild-type and mutS strains of S. typhimurium indicate that the cost associated with a mutS defect is also low in a host environment (Zahrt et al. 1999; A. I. Nilsson and D. I. Andersson, unpublished data).

DISCUSSION

As shown by this work, S. typhimurium has a considerable potential to increase its mouse-specific fitness. Thus, 18 independent lineages with different population size and mutation rate all showed a significant increase in fitness after <200 generations of adaptation. As expected, the population size and the mutation rate had a strong impact on the rate of adaptation where lineages with low mutation rate and small population bottleneck size showed the slowest adaptation. The mutation rate for the adaptive mutations in the wild type was calculated to >10⁻⁶. Since the mutation rate per base pair per generation is typically 10⁻¹¹–10⁻¹⁰ (Hudson et al. 2002) this finding implies that the adaptive mutations are not specific point mutations. Which other types of mutations could occur with this high rate? One possibility is loss-of-function mutations in single genes that commonly occur with a rate of ∼10⁻⁶ (Slechta et al. 2003). S. typhimurium mainly resides and replicates in the reticuloendothelial system and it is likely that the adaptive mutations promote growth within the phagosomes of macrophages of the liver and spleen (Richter-Dahlfors et al. 1997; Salcedo et al. 2001). For example, the mutations could increase resistance to or interfere with the production of bacterial growth suppressors such as antibacterial peptides (Boman 2003; Ganz 2003), reactive oxygen species (Janssen et al. 2003; Linehan and Holden 2003), nitric oxid compounds (Roy and Malo 2002; Linehan and Holden 2003), or acids (Rathman et al. 1996). Previous work has resulted in the identification of several genes in Salmonella, which when inactivated cause an increased growth rate or virulence or both. Thus, inactivation of the pcgL (Mouslim et al. 2002), phoN (Miller et al. 1989), grvA (Ho and Slauch 2001), and pnp (Clements et al. 2002) genes increases the bacterial growth rate/virulence in mice. It is not fully clear how these mutations confer their effect but pcgL mutations cause accumulation of D-ala-D-ala, which might interfere with innate immunity, and grvA mutations appear to increase resistance to toxic oxygen species. Similar observations of host growth-suppressing genes have also been made in P. aeruginosa (Chugani et al. 2001), Streptococcus pyogenes (Engleberg et al. 2001), Cryptococcus neoformans (D'Souza et al. 2001), and Leishmania major (Cunningham et al. 2001). An alternative explanation for the high adaptive mutation rate might be gene amplification. It is known that gene duplications occur spontaneously at a high frequency in bacteria (e.g., 10⁻⁶–10⁻² in S. typhimurium depending on the chromosomal region; Anderson and Roth 1981) and that cells with increased gene dosage can be selected under particular conditions (Andersson et al. 1998; Hendrickson et al. 2002; Slechta et al. 2003). Thus, adaptation to mice could occur by gene amplification of a function that is limiting for bacterial survival and replication within a mouse.

This study shows that trade-offs exist between adaptations to different environments, at least in lineages with a high mutation rate. Thus, during their adaptation to mice all mutator lineages had lost some fitness, measured as impaired anabolic and/or catabolic ability. Such accumulation of mutations that limit the niche may mirror the accumulation of pseudogenes in host-restricted microbes (Frank et al. 2002). Although this study was not intended to distinguish between potential mechanisms for the observed trade-off, our results suggest that a substantial part of the fitness loss seen in the secondary environment is due to mutation accumulation. The mutator lineages showed several metabolic defects but the wild-type lineages were not impaired in spite of the fact that they, at least with the larger bottleneck, were as well adapted to mice as the mutators. However, this finding does not exclude the possibility that some adaptive mutations decrease fitness in the secondary environment due to antagonistic pleiotropy. In conclusion, deleterious mutation accumulation is, especially for an organism with a high mutation rate, expected to be a recurrent problem during specialization whereas antagonistic pleiotropy is probably more niche and organism specific (Cooper and Lenski 2000).

Finally, the mutS mutator allele was not counterselected strongly enough to result in the selection of low-mutation-rate variants. This experimental finding was supported by our calculations, which showed that even if potential mutations that reduced the mutation rate occurred at rates up to 10⁻⁵ it would still require >1000 generations before a nonmutator would become fixed when the mutator-associated s-value is ∼ −0.01 (Boe et al. 2000). This result is in contrast to the findings of Giraud et al. (2001) who observed that mutators were counterselected in mice after an initial adaptation phase. However, their experiment was performed over a longer time period and with an intestinal infection model where counterselection against the mutator could be stronger.

APPENDIX

Fixation of adaptive mutations:

The population cycles between exponential growth and sampling (bottlenecks). Assuming that each growth phase starts with N_B cells, growth is allowed by a factor G (G ≫ 1) to a total N_T = GN_B cells, when a new sample of N_B cells are taken and allowed to grow again. How many cycles of growth and sampling are required before an adaptive mutation can be fixed? The effective population size, N_e, of such a fluctuating population can be calculated as the harmonic average; i.e., 1/N_e equals the time average of 1/N(t), which for exponential growth gives

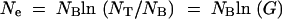A1

Deterministic appearance and growth:

Growth starts from a sample containing N₀ cells of an original variant and n₀ (N_B = N₀ + n₀) of a mutant with selective advantage s. The original variant is assumed to have growth rate constant k₀ = 1, corresponding to a doubling time (generation time) equal to ln(2). This determines the units of the timescale used. During growth, the mutation can appear with probability u in each replication event, i.e., with rate u ln(2) per generation. The original variant grows to N(t) = N₀e^t individuals at time t. If the growth phase lasts for time T, the total growth factor is

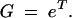A2

Mutants grow with a rate that is a factor 1 + s faster than the original variant. The deterministic appearance and growth of the mutants at time t is determined from the differential equation for their mean number :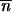

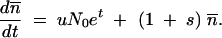A3

The first term describes the appearance of new mutants from the N₀e^t nonmutants that are present at time t. The second term describes the continued growth of the mutant cells. The solution to Equation A3 is 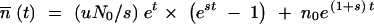. This gives the expected ratio of mutants to nonmutants at the end of growth at time t = T:

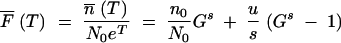A4

The population growth of the mutant will appear deterministic as described above if n₀ > 0 or uN₀ > 1. When this condition is not satisfied, the appearance of the first mutation will be a strongly stochastic event. If, with low probability, it appears early (jackpot mutation), there will be many descendants. As a consequence, there can be a broad distribution of possible outcomes at the end of growth.

Quasi-deterministic appearance and growth:

To account for the largest effect of the jackpot mutations, we can assume that the growth is deterministic only after the first appearance of a mutant. Thus if n₀ > 0, mutant growth is assumed to follow Equation A4. If there are no mutants at the start, n₀ = 0, they will appear with rate

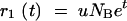A5

as given by the first term of Equation A3. The probability, P₀(t), that no mutation has appeared before time t can be determined from the equation

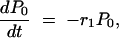A6

which can be integrated to give

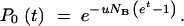A7

The rate, R₁, of the first mutation appearance is given by −dP₀/dt (Equation A6). Thus the probability that the first occurrence is in the time interval t′, t′ + dt′ is given by

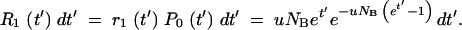A8

Assume that after the first appearance at time t′, mutants continue to appear and grow deterministically; i.e., Equation A3 is assumed valid for t > t′ with the initial condition 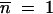at t = t′. Then integration of Equation A3 gives the ratio of mutants to nonmutants at the end of growth at time T, conditional on a first appearance at time t′, as

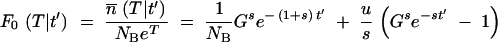A9

The first term gives the growth in numbers of the descendants of the first mutant that appeared at time t′. The second term describes the deterministic appearance and subsequent growth of all later mutants. Equation A9 with t′ = 0 is the same as Equation A4 with n₀ = 1, when deterministic growth starts from a single mutant at time zero.

Ultimate fixation probability:

To take over a population, adaptive mutants must appear, grow in number, and survive the sampling at the end of each growth cycle. Sampling N_B cells from a large (N_T ≫ N_B) population where the fraction of mutants is F/(1 + F) gives n₁ mutants with the binomial probability

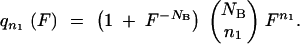A10a

The probability that no mutant survives the sampling is

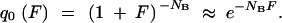A10b

If a cycle starts with n₁ mutants, the probability that one of them eventually will take over is given by Kimura (1962),

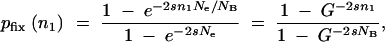A11

where in the last equality the effective population size from Equation A1 has been introduced. Although derived for a slightly different situation, simulations show that Equation A11 works well also for the cycles of growth and sampling employed here. Thus the probability that at least one mutation survives the sampling(s) and goes on to fixation is the sum over all possible n₁ values weighted by their probabilities:

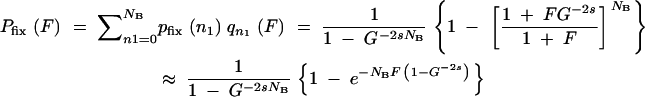A12

The last approximation is valid for F ≪ 1, which is usually the case as F is the ratio of mutants to nonmutants at the end of the preceding growth cycle that started with no mutants. In the deterministic description, F in Equation A12 can be replaced by its average 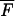T from Equation A4 with n₀ = 0. For large s (s > 0.2), the quasi-deterministic description gives a better estimate. In this limit, F in Equation A12 is identified with F₀(T|t′) from Equation A9, and the expectation value for P_fix over all possible appearance times t′ can be calculated from their probability density R₁ (Equation A8) as

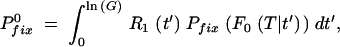A13a

where ln(G) = T from Equation A2 is the total length of a growth cycle. After replacing the integration variable as y = e^t′/G, this gives

A13b

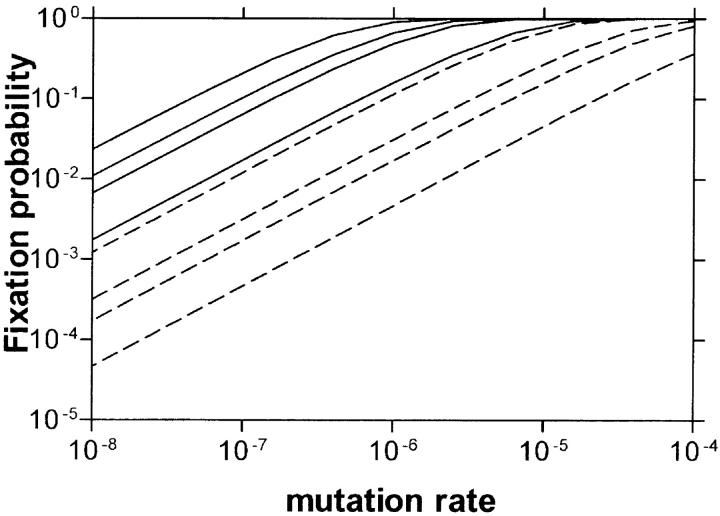
This is the probability that in a cycle starting with no mutants, a mutation appears that survives the first sampling and goes on to fixation. The fixation probability from Equation A13b has been plotted in Figure A1

Figure A1.—

Fixation probability per growth cycle for adaptive mutations (from Equation A13b). Solid lines are for N_B = 10⁵ and dashed lines are for N_B = 10³. For both sets, the s-values are (from top to bottom) s = 0.5, 0.2, 0.1, and 0.02. Each growth cycle was ended at N_T = 10⁸.

as a function of the mutation rate for some values of N_B and s.

Equation A13 expresses the probability that the first surviving mutant appears in a cycle. Thus the mean number of cycles required before a mutant appears that will go on to fixation is 1/P⁰_fix. Once a surviving mutant has appeared, deterministic growth will make it reach 50% after time T₅₀. This can be calculated by setting in Equation A4 and solving for T, which gives

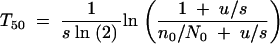A14

The division by ln(2) is to get the time in units of generations. n₀ is the number of mutants that first survive a sampling. In general, n₀ is a very small number and we use n₀ = 1 and N₀ = N_B in the following. As the number of generations per cycle is ln(G)/ln(2), the total number of generations required before the mutation has reached at least 50% presence is

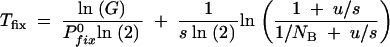A15

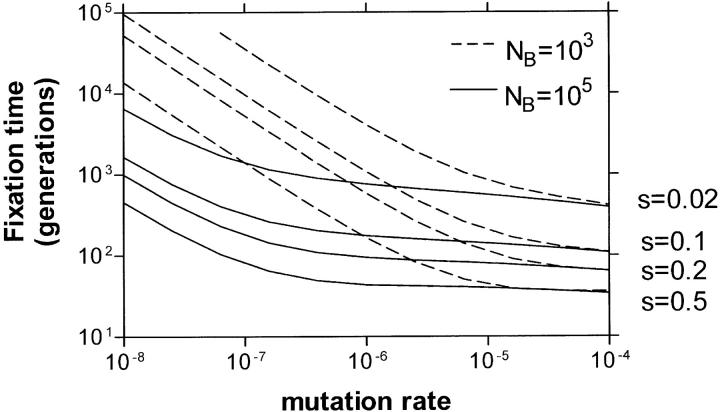
The expected fixation time from Equation A15 has been plotted in Figure A2

Figure A2.—

The expected fixation time for adaptive mutations (from Equation A15) with bottleneck sizes and growth advantage as indicated. Each growth cycle was ended at N_T = 10⁸.

as a function of the mutation rate at different bottlenecks (N_B) and selection coefficients (s). To the right in this figure, at high mutation rates, the fixation time is dominated by the deterministic growth given by the second term in Equation A15 and is very weakly dependent on u and N_B.

The probability Q₀₀ that no mutants survive the sampling, if there were none present at the start of the cycle, can be calculated as the expectation value over all possible appearance times t′ and the probability that none survives the sampling (Equation A10b):

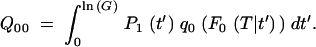A16a

Previously (Maisnier-Patin et al. 2002) we calculated 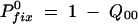on the assumption that once a mutation has survived one sampling, it will grow to sufficient numbers during the next cycle so it will also not be lost in the subsequent samplings. Then Equation A16a can be rewritten as

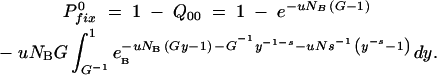A16b

This is true for sufficiently large values for s and/or G, i.e., for G^−2s ≪ 1 or, equivalently, for s > 1/ln(G) when p_fix(n₁ = 1) from Equation A11 is nearly 1. In this limit the results from Equation A16 are virtually indistinguishable from those of Equation A13. Here we have used Equation A13b in all calculations and Equation A16b has been used primarily as a control. Note that Equation A16b corrects two misprints that appeared in the corresponding equation presented in Maisnier-Patin et al. (2002).

Accumulation of neutral mutations:

Neutral mutations have no growth advantage and will accumulate linearly in time,

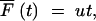A17

from Equation A4 with s = 0 and n₀ = 0. If u and N_B are sufficiently large, this accumulation will continue uninterrupted so that the fraction expected after S cycles would be 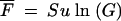. If N_Bu ln(G) < 1, the probability that the neutral mutants are lost (Equation A10b) in the first sampling becomes significant and, with large probability, the linear accumulation would take place only during the last of the growth cycles considered. Another complication is the appearance of adaptive mutations that will either interrupt the neutral accumulation or, by hitchhiking, carry it to dominance. If there is no hitchhiking, the neutral mutation would accumulate only at the end of the rise to dominance of the last adaptive variant; this would lead to a relatively small fraction. If hitchhiking has occurred we would expect a large fraction of the neutral mutation at the end of the adaptation experiment. Numerical calculations based on the equations above were carried out with Mathcad from MathSoft.