The Influence of Genes on the Aging Process of Mice

Abstract

Genetic interventions that accelerate or retard aging in mice are crucial in advancing our knowledge over mammalian aging. Yet determining if a given intervention affects the aging process is not straightforward since, for instance, many disease-causing mutations may decrease life span without affecting aging. In this work, we employed the Gompertz model to determine whether several published interventions previously claimed to affect aging in mice do indeed alter the aging process. First, we constructed age-specific mortality tables for a number of mouse cohorts used in longevity experiments and calculated the rate at which mortality increases with age. Estimates of age-independent mortality were also calculated. We found no statistical evidence that GHRHR, IGF1R, INSR, PROP1, or TRX delay or that ATM + TERC, BubR1, klotho, LMNA, PRDX1, p53, WRN + TERC, or TOP3B accelerate mouse aging. Often, changes in the expression of these genes affected age-independent mortality and so they may prove useful to other aspects of medicine. We found statistical evidence that C/EBP, MSRA, SHC1, growth hormone, GHR, PIT1, and PolgA may influence aging in mice. These results were interpreted together with age-related physiological and pathological changes and provide novel insights regarding the role of several genes in the mammalian aging process.

ALTHOUGH aging is a major biological problem, the mechanisms involved are largely a mystery. One essential tool in understanding the biological basis of aging is the manipulation of the aging process in animal models. Namely, genetic interventions that accelerate or retard aging in mice are crucial in advancing our knowledge over the genetic and molecular mechanisms of mammalian aging (Liang et al. 2003; Hasty and Vijg 2004; Quarrie and Riabowol 2004). Several interventions, including mutations, have been reported to increase or decrease life span when compared to wild-type controls (Table 1). Yet determining if these interventions accelerate or delay aging is not straightforward since, for instance, many disease-causing mutations may decrease life span without affecting aging. Therefore, for genetic interventions to enhance our knowledge over aging it is crucial to discriminate between interventions affecting the aging process and interventions affecting health, as proposed by many others (Williams 1999; Hayflick 2000; Pletcher et al. 2000).

TABLE 1.

Mortality parameters for different rodent populations with altered life span

Gene/intervention	Type	Strain	n	t50	tmax	Reference
ATM + TERC	−/−, −/−	C57BL/6 + WW6	51	0.93	NR	Wong et al. (2003)
bGH-Tg	WT	C3H + C57BL/6 (males)	16	2.16	3.20	Bartke (2003)
Tg	9	1.23	1.57
BubR1	H/H	C57BL/6	212	0.50	1.25	Baker et al. (2004)
Cancer prone	NZB/W	22	0.71	1.05	Conde et al. (1998)
C/EBP	WT	C57BL/6J	30	1.92	2.5	Chiu et al. (2004)
β/β	30	2.33	NR
Lepob/ob	40	1.5	2
CR	WT	Fisher 344 (male rats)	115	1.96	2.62	Yu et al. (1982)
EXP	115	2.87	3.91
Fish oil	WT	NZB	30	0.67	0.91	Jolly et al. (2001)
EXP	+NZW	30	0.96	1.28
GHR	WT	Ola-BALB/cJ	15	1.88	2.59	Coschigano et al. (2003)
−/−	(Males)	11	2.41	3.31
GHRHR	WT	C57BL/6J	31	1.96	2.62	Flurkey et al. (2001)
−/−	35	2.87	3.91
IGF1R	WT	129/J (females)	17	1.34	2.24	Holzenberger et al. (2003)
±	20	1.75	2.67
INSR	WT	C57BL/6	67	2.32	2.94	Bluher et al. (2003)
−/−	+ 129/Sv	60	2.68	3.42
KL (klotho)	−/−	C57BL/6J + C3H/J	29	0.15	0.25	Kuro-o et al. (1997)
LMNA	−/−	C57BL/6	25	0.08	0.11	Mounkes et al. (2003)
MSRA	WT	C57BL/6J	14	1.91	2.25	Moskovitz et al. (2001)
−/−	17	1.10	1.37
p53	WT	129/Sv	56	2.30	3.00	Tyner et al. (2002)
±	+ C57BL/6	217	1.42	3.00
+/m	35	1.89	2.64
p66 (SHC1)	WT	129/Sv	14	2.08	2.33	Migliaccio et al. (1999)
−/−	15	2.67	2.98
PIT1	WT	C3H/HeJ	34	2.28	2.90	Flurkey et al. (2001)
−/−	+ DW/J	25	3.23	3.98
PolgA	mt/mt	129 + C57BL/6	38	0.92	1.17	Trifunovic et al. (2004)
PRDX1	−/−	B6	64	1.85	NR	Neumann et al. (2003)
PROP1	WT	Ames stock (females)	13	1.80	2.74	Brown-Borg et al. (1996)
−/−	16	3.42	4.03
SAM	WT	AKT	377	1.07	2.27	Takeda et al. (1981)
EXP	493	0.85	1.58
TOP3B	−/−	C57BL/6J + 129/svEv	30	1.22	NR	Kwan and Wang (2001)
TRX	WT	C57BL	82	1.42	2.25	Mitsui et al. (2002)
TG	94	1.84	2.75
WRN + TERC	−/−, −/−	129 + C57BL/6	39	0.54	NR	Chang et al. (2004)

n, number of animals in cohort; t50, time, in years, at which 50% of animals had died; t_max, maximum life span for cohort in years. NR, not reported.

To ascertain whether aging changed or not due to a given intervention, one approach is to determine whether the pace of age-related changes and/or the onset of age-related pathologies has shifted (e.g., Kuro-o et al. 1997; Miller 2001). Another approach is to calculate the rate at which mortality increases with age, which is a normal outcome of aging in most species (Pletcher et al. 2000). Using the Gompertz equation it is possible to calculate the mortality rate doubling time (MRDT; Finch 1990, pp. 22–24; Mueller et al. 1995). Caloric restriction (CR) in rodents, for example, fulfills both these criteria since it roughly doubles the MRDT and delays age-related debilitation (Weindruch and Walford 1988). Unfortunately, details of age-related changes and MRDT calculations are rarely available in genetic interventions affecting longevity in mice and so researchers often assume that a change in longevity is representative of a change in the aging process when such may not be the case. Instead, changes in aging-independent mortality may be the cause of a shortened or lengthened life span (Finch 1990, pp. 22–25). For example, cancer-promoting genes may decrease life span in mice by increasing cancer rates without affecting aging (Donehower et al. 1992).

In this work, we first wanted to evaluate the Gompertz model to study aging in mice, particularly since such experiments often involve small cohorts. Afterward, we wanted to determine whether several published genetic interventions affecting longevity in mice that have hinted to influence aging do indeed affect the aging process. We calculated the MRDT for the mouse cohorts used in these experiments and tested whether the changes in the MRDT derived from genetic interventions are statistically significant. If available, the description of age-related changes and pathology was also taken into consideration when interpreting the results. Our ultimate goal was to identify those genes that may be related to mammalian aging by determining which ones affect aging rather than health and thus allow research on the biology of aging to focus on the mechanisms that indeed influence aging and not merely health.

MATERIALS AND METHODS

Mortality data were obtained from a number of published experiments that might alter the rate of aging in rodents (Table 1). As described (Finch 1990, pp. 22–23, 123), data on mortality rate as a function of age were obtained from mortality schedule data, where available, or extracted from survivorship graphs. If necessary, the digital imaging software Paint Shop Pro 7 (Jasc, Eden Prairie, MN) was used to capture from graphs the exact number of animals dying at each constant time interval. In experiments where individual deaths were reported, discrete time intervals were set and the number of animals dying at each interval counted. Even though other methodologies may use individual day of death to infer the Gompertz parameters (Pletcher et al. 2000), frequently such data were unavailable and so we based our method on regular time intervals. The length of the time interval for each cohort was chosen to maximize the number of consecutive mortality estimates during the exponential increase in mortality. For each time interval, the age-specific mortality (q_x) was estimated as the number of animals alive at the end of the interval over the number of animals at the start of the interval. The hazard rate (hz) was estimated by hz = 2q_x/(2 − q_x).

The Gompertz equation was used to model the aging process: R_m = R₀e^αt, where R_m is the chance of dying—i.e., the hz function—at age t, R₀ is the nonexponential factor in mortality, and α is the exponential parameter (Finch 1990, pp. 13–22; Strehler 1999, pp. 111–113). Although other mathematical models may be more accurate, given the limitations in sample size, the Gompertz model is the most appropriate choice for this analysis since it is accurate while being simple enough to fit most data (Wilson 1994; Pletcher et al. 2000; Pletcher 2002). The weighted linear regression was obtained from: ln(R_m) = ln(R₀) + αt and the MRDT given by: MRDT = 0.693/α. Maximum-likelihood estimates of the Gompertz parameters were also obtained through an R script by David Steinsaltz (http://www.demog.berkeley.edu/dstein/agingpage.html).

Larger data sets were also fit by the logistic model, which maintains the α-parameter while accounting for hazard-rate deceleration at old ages (Pletcher et al. 2000): R_m = R₀e^αt/(1 + s(R₀/α)(e^αt − 1)). Importantly, our aim in this work was not to find the best model to fit the whole mortality data but rather to determine whether the exponential increase of mortality—i.e., the α-parameter—was affected by a number of genetic perturbations. Consequently, we preferred the simpler, nested Gompertz model (with s = 0) and, in the larger data sets, frequently excluded data prior to the onset of senescence and when hazard rates decelerated at very old ages, as detailed below; even so, we never excluded >10% of animals.

The time when the exponential increase in mortality occurred was selected, as previously done (Flurkey et al. 2001), and the initial mortality rate (IMR) was calculated from the Gompertz equation on the basis of the mortality rate prior to the age-related increase in mortality. If data were available for the entire life span of animals, then frequently a value of t = 0.25 years was used, as previously described (Finch 1990, pp. 22–23, 123). Alternatively, if data were available only after a given age t, then this value was used to estimate the IMR. Given the short life span of many mutant cohorts, these values were, at times, adjusted. Moreover, if the increase in hazard rates decelerated at very old ages, these values were not considered. When the logistic model was used, the entire mortality trajectory was analyzed.

To reduce the noise in the data, the T4253H smoothing algorithm from the SPSS package (SPSS, Chicago) was applied to obtain the mortality curves. The smoothed values were used to interpret the visual representations of the data, not to fit the Gompertz parametric model.

We tested for differences in the regression coefficient α to calculate whether the MRDT differed among cohorts of the same experiment. Through a “dummy variables” test, we compared the slopes of the experimental and wild-type hazard functions obtained by linear regression, as previously described (Keppel 1991, pp. 317–320; Guimarães and Cabral 1997, pp. 535–538). The P-value was then obtained through a one-tailed t-test since our aim was to find differences in one specific direction.

For each set of experiments we always used the same methodology in calculating the Gompertz parameters, so that despite different approximations and different genetic backgrounds and housing conditions used across experiments, we could compare the Gompertz parameters for each experiment. The complete results are available as supplementary material at http://www.genetics.org/supplemental/. Data analysis was performed using the SPSS package version 11.5 and regression analysis was obtained using SigmaPlot 7 (SPSS).

RESULTS

The Gompertz mortality model:

Given the large number of experimental settings used in the studied cohorts, our first step was to create coherent mortality curves permitting an analysis of Gompertz parameters. Unfortunately, many published interventions affecting longevity in mice provide data in different forms, such as mortality schedule data and survivorship graphs. Therefore, we built mortality tables using discrete time intervals and estimating the age-specific mortality at each time interval. These results are available as supplementary material at http://www.genetics.org/supplemental/ and may serve as the basis for other similar studies attempting to compare the mortality curves of different mouse cohorts.

We attempted to fit the Gompertz model to these data sets. Since most experiments involved a small number of animals, the Gompertz model was deemed the most appropriate (Wilson 1994; Pletcher 2002). Although we also derived Gompertz parameters using a maximum-likelihood estimation (MLE) approach, the results using linear regression yielded less MRDT variation in control cohorts: 46%, while using MLE the relative standard deviation was 62%. Gompertz curves obtained using an MLE approach were also less accurate in predicting t50 (age when 50% of animals have died): 60% vs. 11% using linear regression in relative variation between the predicted and the observed t50. As such, and given the small size of the cohorts under study, the Gompertz parameters estimated through linear regression were preferred. Moreover, in 14/15 experiments comparing the MRDT of wild-type and experimental cohorts, similar results were obtained using linear regression and MLE. Both sets of results are available as supplementary material at http://www.genetics.org/supplemental/.

Through linear regression, we calculated the MRDT for a number of experiments previously claimed to alter aging in mice. Estimates of the IMR, which is expected to be independent of the rate of aging, were also calculated (Tables 2 and 3). Since the MRDT is expected to be species specific and not affected by housing conditions, it is not surprising that the relative standard deviation of the IMR was over threefold higher than that for the MRDT in the wild-type cohorts: 110% vs. 34%, respectively. As also expected, the inverse correlation between ln(IMR) and t50 was highly significant across cohorts for which we were able to fit the Gompertz model (P < 0.001), as was the correlation between ln(IMR) and the maximum life span or t_max (P < 0.001). Interestingly, the correlation between MRDT and t50 was not as statistically significant as the correlation between MRDT and t_max: P = 0.103 vs. P = 0.007, respectively. This is clearly in support of the commonly cited notion that changes in t_max are a better predictor of changes in the rate of aging than are changes in t50. As predicted by the Strehler-Midvan theory (Strehler 1999, pp. 111–113; 119–124), we found an inverse correlation between log(R₀) and α (P < 0.001) but not between ln(IMR) and α (P = 0.13).

TABLE 2.

Gompertz parameters for cohorts used in life-extending experiments

Gene/intervention	Type	Strain	α	ln(R0)	r2	MRDT (yr)	IMR	Δ age changes
C/EBP	WT	C57BL/6J	2.53	−5.70	0.86	0.27	0.52
β/β	1.54	−5.00	0.84	0.45	0.38	NR
Lepob/ob	3.26	−5.70	0.94	0.21	0.19	NR
CR	AL	Fisher 344	4.13	−8.61	0.84	0.17	0.031
CR	(Male rats)	1.85	−6.68	0.97	0.37	0.034	Delayed
FO	AL	NZB	9.10	−6.26	0.92	0.08	0.73
FO	+NZW	4.92	−5.34	0.79	0.14	0.56	NR
GHR	WT	Ola-BALB/cJ	1.94	−4.34	0.81	0.36	0.52
KO	(Males)	1.51	−4.18	0.77	0.46	0.59	Delayed
GHRHR	WT	C57BL/6J	2.38	−6.56	0.91	0.29	0.19
KO	2.50	−7.31	0.84	0.28	0.15	NR
IGF1R	WT	129/J	1.79	−2.80	0.97	0.39	0.30
KO	(Females)	2.20	−4.26	0.97	0.32	0.06	NR
INSR	WT	C57BL/6	1.95	−4.97	0.83	0.36	0.078
KO	+129/Sv	2.43	−6.61	0.81	0.29	0.035	NR
p66	WT	129/Sv	6.22	−13.37	0.92	0.11	1.7
KO	2.81	−7.05	0.77	0.25	0.29	NR
PIT1	WT	C3H/HeJ	3.05	−7.63	0.90	0.23	0.020
KO	+DW/J	2.28	−8.35	0.92	0.30	0.0035	Delayed
PROP1	WT	Ames stock	0.92	−2.06	0.45	0.75	1.29
KO	(Females)	1.98	−6.86	0.76	0.35	0.74	Unclear
TRX	WT	C57BL	1.71	−3.27	0.64	0.41	1.13
	TG		1.84	−3.93	0.89	0.38	0.69	NR

α, Gompertz slope or exponential parameter; ln(R₀), nonexponential factor in mortality; r², sum of squares; Δ age changes, shift in pace of age-related changes; IMR, initial mortality rate in probability of dying per year; NR, none reported.

TABLE 3.

Gompertz parameters for cohorts used in life-reducing experiments

Gene/intervention	Type	Strain	α	ln(R0)	r2	MRDT (yr)	IMR	Δ age changes
ATM + TERC	−/−, −/−	C57BL/6 + WW6	0.52	−1.76	0.16	ND	0.60	Accelerated
bGH-Tg	WT	C3H +	2.03	−4.83	0.90	0.34	0.17
Tg	C57BL/6 (males)	3.73	−5.08	0.87	0.19	1.28	Accelerated
BubR1	KO	C57BL/6	2.34	−2.69	0.879	0.30	1.0	Accelerated
klotho	KO	C57BL/6J + C3H/J	17.90	−3.47	0.75	ND	7.8	Accelerated
LMNA	KO	C57BL/6	43.30	−3.77	0.69	0.016	13	NR
MSRA	WT	C57BL/J6	1.39	−2.25	0.99	0.50	0.41
KO	3.39	−2.75	0.96	0.20	0.24	NR
NZW/B	WT	NZB/W	4.26	−3.69	0.68	0.16	1.7	NR
p53	WT	129/Sv	2.76	−7.55	0.80	0.25	0.48
KO	+ C57BL/6	1.97	−4.12	0.83	0.35	0.95	NR
TG	2.16	−5.27	0.74	0.32	0.92	Accelerated
PolgA	mut	129 + C57BL/6	8.84	−8.90	0.87	0.078	1.2	Accelerated
PRXD1	KO	B6	1.00	−2.97	0.34	0.70	0.64	NR
SAM	WT	AKT	1.85	−3.86	0.80	0.37	0.63
SAM	3.27	−4.06	0.89	0.21	0.77	Accelerated
TOP3B	KO	C57BL/6J + 129/svEv	0.45	−2.42	0.27	ND	1.2	NR
WRN + TERC	−/−, −/−	129 + C57BL/6	0.36	−2.50	1.64	ND	1.17	Accelerated

α, Gompertz slope or exponential parameter; ln(R₀), nonexponential factor in mortality; r², sum of squares; Δ age changes, shift in pace of age-related changes; IMR, initial mortality rate in probability of dying per year; NR, none reported; ND, not determined.

In addition to the Gompertz parameters, we also derived mortality plots as a data exploration technique (Figures 1–3). Given the limitations in the Gompertz calculations (see discussion), plots with smoothed data may be used as a complementary approach to the computed Gompertz parameters. Since the choice of onset of senescence and outliers is partly subjective, different plots can be obtained for the same mortality data and different interpretations are possible, as detailed below.

Figure 1.—

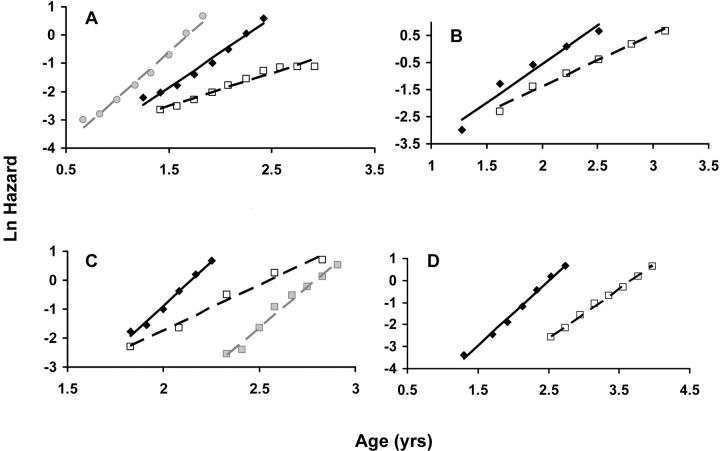
Natural logarithm of mortality rates fitted using the T4253H smoothing algorithm. Lines represent estimated adult mortality trajectories based on Gompertz parameters for wild-type (straight lines) and experimental (dashed lines) conditions. (A) C/EBP wild type (solid diamond), β/β (open square), and β/− Lep^op/op (shaded circle). (B) GHR wild type (solid diamond) and −/− KO (open square). (C) p66^shc wild type (solid diamond) and −/− KO (open square); the shaded line represents an alternative for the −/− KO cohort (shaded square) that excludes the first three points and uses a smaller time scale. (D) PIT1 wild type (solid diamond) and −/− KO (open square).

Figure 3.—

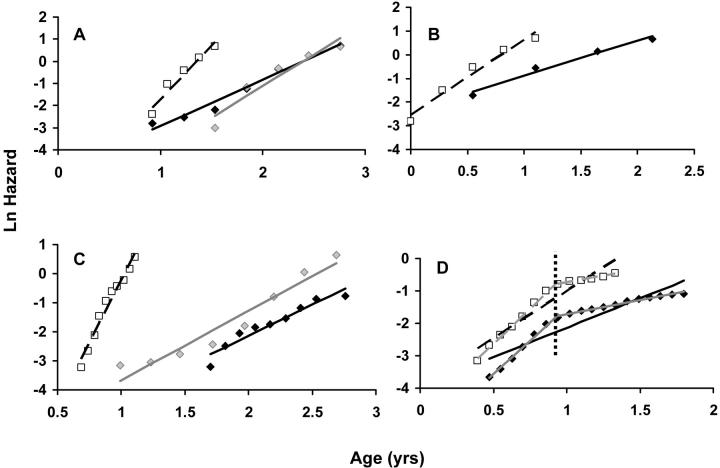
Natural logarithm of mortality rates fitted using the T4253H smoothing algorithm. Lines represent estimated adult mortality trajectories based on Gompertz parameters for wild-type (straight lines) and experimental (dashed lines) conditions. (A) Bovine GH wild-type (solid diamond) and transgenic (open square) mice; straight shaded line represents an alternative for the control cohort (shaded diamond) that excludes the first two points as outliers. (B) MSRA wild type (solid diamond) and −/− KO (open square). (C) PolgA mut/mut (open square), p53 wild type (solid diamond), and INSR WT (shaded diamond). (D) SAM wild type (solid diamond) and SAM (open square); shaded lines represent alternatives dividing each cohort in two at 0.94 years of age; the vertical dashed line represents the point in time at which the mortality curve was changed in both cohorts used in the SAM experiment (t = 0.94 years).

Genes deemed as delaying aging:

Contrary to the suggestion that they delay aging, manipulations in the GHRHR, IGF1R, INSR, PROP1, and TRX loci failed to increase the MRDT when compared to the corresponding control cohorts (Table 2). The MRDT increased in C/EBP, GHR, p66^shc, and PIT1 mutants and so we decided to further evaluate the significance of these results.

We found evidence that C/EBP influences the rate of aging. Mice homozygous for the C/EBPβ protein had a 67% higher MRDT, suggesting that aging is influenced by C/EBP. The shift in MRDT was statistically significant (P = 0.002) and the Gompertz curve appeared affected (Figure 1A). On the other hand, it is not clear from a physiological perspective that C/EBPβ delays aging (Chiu et al. 2004). In the same experiment, mice carrying the Lep^ob/ob gene, which become obese due to an excessive food intake, lived shorter lives than did controls and the MRDT decreased 22%, but the change in MRDT was not statistically significant (P = 0.060).

The MRDT increased almost 28% in mice mutant for GHR. Even though a slight shift in the slope of the Gompertz curve was visible (Figure 1B), this was not statistically significant (P = 0.300). From a physiological perspective it is arguable that GHR delays the onset of age-related pathology (Coschigano et al. 2000, 2003; Bartke 2003). Given the small number of animals used in the experiment (n = 26), however, further studies are necessary.

An over twofold increase in MRDT was found in p66^shc −/− mice when compared to controls, which was apparently a result of a delayed aging process (P = 0.007). Given the small number of animals used in the experiment, however, the assumption that p66^shc influences the rate of aging is premature. We did not remove any values from our calculations, given the small sample size, and so the Gompertz slope appeared to decrease in the double-mutant mice (Figure 1C). In contrast, when we removed the outliers of the curve and adjusted the time when the mortality began to climb, the shift in the slope of the Gompertz curve was no longer statistically significant (P = 0.110).

Mice double mutant for PIT1 had a higher MRDT (30% increase) and a significantly different Gompertz slope (P < 0.001), which hints that PIT1 may influence the rate of aging (Figure 1D). Given that a delay in age-related changes has been reported in PIT1 knockouts (Flurkey et al. 2001, 2002), it appears that the PIT1 locus may influence mammalian aging, even though we did not find similar evidence for PROP1 (Table 2), which sits upstream of PIT1.

Nutrition and aging:

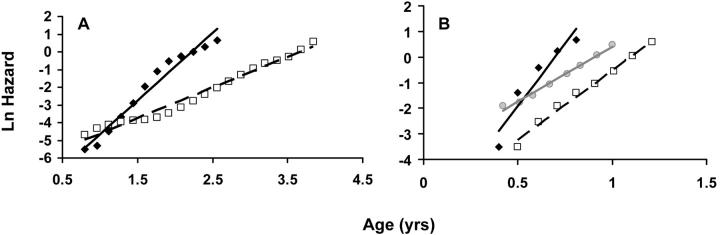
Since CR had previously been shown to delay aging in rodents (Weindruch and Walford 1988), we calculated the MRDT and IMR for caloric-restricted rats as a control (Table 2). Despite a decrease in IMR, the MRDT in CR rats more than doubled when compared to ad libitum controls (0.37 vs. 0.17 year), confirming that CR delays the rate of aging. These results are in line with previous calculations (Finch 1990, p. 508; Pletcher et al. 2000), even though a variation in the Gompertz parameters is expected due to differences in the methodologies (see discussion). The notable (Figure 2A) change in the slope of the Gompertz curve in CR animals was statistically significant (P < 0.001). When the logistic model was fit to controls (r² = 0.90), the MRDT was even lower: 0.07 year with the IMR at 0.00016/year.

Figure 2.—

Natural logarithm of mortality rates fitted using the T4253H smoothing algorithm. Lines represent estimated adult mortality trajectories based on Gompertz parameters for wild-type (straight lines) and experimental (dashed lines) conditions. (A) Rats fed ad libitum (solid diamond) and food restricted (open square). (B) NZB/W mice fed corn oil (solid diamond) or fish oil (open square) and NZB/W control (shaded circle) from another experiment.

We also calculated the Gompertz parameters for the NZB/W strain, which has a significantly shorter life span due to spontaneous cancer but for which accelerated aging has not been described. The MRDT for the cancer-prone NZB/W mice was 0.16 year (Table 2), which is slightly lower than that for other populations of NZB/W mice, even though the NZB/W has a relatively low MRDT when compared to other strains (Finch 1990, pp. 322–323; 508). Not surprisingly, the IMR was very high in the NZB/W strain (1.7/year).

One surprising finding was that fish oil could shift the Gompertz slope in NZB/W mice. The MRDT increased almost twofold in animals fed fish oil (Table 2) and fish oil appeared to affect the Gompertz slope (Figure 2B). These results were statistically significant (P < 0.001). On the other hand, the control value for MRDT (0.08 years) was lower than that reported for this strain, so we cannot exclude some sort of artifact as an explanation (Figure 2B).

Genes deemed as accelerating aging:

As for genes hinted to accelerate aging, we were unable to calculate the MRDT for ATM + TERC and WRN + TERC knockouts, TOP3B −/−, and klotho −/− mice because we could not fit the Gompertz model to these experiments (see discussion). Although we calculated the MRDT for BubR1 and PRDX1 mutants, the obtained values, 0.30 and 0.70 years, respectively, do not suggest a decrease in MRDT even though control values are absent (Table 3). Given the large (n = 212) number of animals used in the BubR1 experiment, we also fit the logistic model (r² = 0.92) but, again, found no indication that aging was accelerated in these animals: IMR = 1.4/year and MRDT = 0.82 years.

The MRDT decreased for LMNA-deficient mice (0.016 years), but the IMR also increased dramatically (13/year or 1.1/month). Although the decrease in MRDT suggests that aging was accelerated in these animals, that is not the interpretation we derive from the physiological observations (Mounkes et al. 2003). The reported accelerated disease progression in these animals (Nikolova et al. 2004) and the high IMR raise doubts about whether we are dealing with accelerated aging or accelerated pathology (see discussion).

Overexpression of transgenic growth hormone in mice reduces longevity (Bartke 2003). Interestingly, it appears that mice overexpressing bovine growth hormone (bGH) have a lower MRDT: 0.19 vs. 0.34 years in controls (Figure 3A). Even though the IMR was increased in transgenic mice (1.28 vs. 0.17/year), it appears that growth hormone (GH) may indeed affect the rate of aging (P = 0.015). A more careful analysis, however, warns caution. The number of animals used in the experiment is small (n = 25). Moreover, if the first three points in the controls were excluded, judging that the onset of senescence occurs only afterward, then the MRDT for controls dropped to 0.25 years and the shift in MRDT was no longer statistically significant (P = 0.101). Finally, the logistic model appeared to give a better fit to the control data: r² = 0.93 with IMR = 0.066/year and MRDT = 0.24 years, arguing that larger data sets are needed to fully understand the mortality patterns of these animals.

In MSRA −/− mice, we found a decrease of 60% in the MRDT (Table 3), consistent with a shift in the slope of the Gompertz curve (Figure 3B) and in the rate of aging (P < 0.001). Although an accelerated aging phenotype has not been described in MSRA −/− mice, our results suggest that MSRA could influence mammalian aging. Since there was a >30% discrepancy between the observed t50 and the t50 predicted from the Gompertz parameters, further studies using a larger data set are needed.

Recently, mice with a disrupted DNA mitochondrial polymerase (PolgA) have been reported to age faster than controls (Trifunovic et al. 2004). Our results clearly support this view (Table 3). Even though survival curves are not available for the controls, comparisons with controls of the same strain—129 + C57BL/6—taken from other experiments suggest an accelerated aging phenotype (Figure 3C).

The senescence-accelerated mouse (SAM) has been claimed as a model of accelerated aging (Takeda et al. 1981). In line with previous reports, the MRDT decreased by over 40% and the Gompertz slope appeared to be affected (P < 0.001). Although these results indicate that the selection of SAM did indeed provide a model of accelerated aging, the erratic Gompertz curve is worthy of a more careful evaluation (Figure 3D). Prior to age 1, the difference in the Gompertz slope between control and SAM mice is not significant (P = 0.99), but afterwards it becomes highly significant (P < 0.001). Therefore, environmental conditions could play a role and thus bias the results (see discussion). Another possibility is that given the large number of animals used in the experiment, the Gompertz model does not capture the real mortality trajectory. We also fit the logistic model to the data from the SAM experiment: for controls the IMR was 0.089/year (R₀ = −4.95) and the MRDT 0.18 years (r² = 0.96) while for the SAM the IMR was 0.42/year (R₀ = −7.04) with an MRDT of 0.08 years (r² = 0.96), arguing in favor of seeing SAM as animals with accelerated aging.

DISCUSSION

The Gompertz equation as a tool for the study of mammalian aging:

Most studies based on the Gompertz equation have been conducted in large experimental sets, such as those involving invertebrates (Wilson 1994; Mueller et al. 1995; Pletcher 2002). Thus one potential caveat of our work is the use of small cohorts, particularly since most of the described experiments have not been replicated. Yet our aim was not to study the entire mortality trajectory but rather to assert whether a number of genetic interventions affected aging or not. Assuming that each experimental cohort featured the same mouse strain and was subjected to similar environmental conditions as the control cohort, our rationale was that the genetic perturbation under study was responsible for the change in longevity by altering the rate of aging, aging-independent mortality, or both. By focusing on individual experiments, we were then able to compare the Gompertz parameters between the cohorts and, in most cases, determine whether the rate of aging was indeed altered. Although large amounts of animals—in the order of several hundred individuals—are needed to study the entire mortality trajectory of a given species (e.g., Wilson 1994; Pletcher 2002), our results show that the Gompertz model is suitable to evaluate the rate of aging in rodent experiments. It is possible to use our approach to derive meaningful conclusions even from experiments using a small number of animals, provided some precautions are taken (discussed below).

The analysis of mouse longevity studies faces several potential artifacts and great care is necessary to analyze the results. For instance, researchers often report incomplete mortality curves, excluding deaths occurring prior to the onset of senescence or accidental deaths, which may be misleading in calculating the Gompertz parameters. In addition, housing conditions and other experimental variables may cause an increase in mortality that biases the results. The large variation in IMR among controls supports this view: a relative standard deviation of 110% when compared to 34% in MRDT. In fact, 10-fold differences in IMR estimates have been observed for the same cohort when different methodologies are used (Finch 1990, p. 507). Consequently, comparisons between different experimental settings must be done with care due to differences in the genetic background of the animals used, housing conditions, and methodology. This rationale also implies that adequate controls are necessary, which is not the case in a number of experiments (Table 1).

We employed the nested Gompertz model not taking into account parameters such as the degree of heterogeneity or the Makeham constant. In some cases, more complex models may fit the data better: for example, in the CR experiment the Gompertz model fits the CR group but the logistic-Makeham model offers a better fit to the control group (Pletcher et al. 2000). Even though the MRDT always increases in CR animals, a significant variation in MRDT is observed among methodologies. The MRDT that we obtained for the control group was 0.17 years, compared to the 0.30 years in the work of Finch (1990, p. 508) and the 0.10 years using the logistic-Makeham model (Pletcher et al. 2000). Using the logistic model, we obtained an MRDT of 0.07 years. Therefore, we preferred to be consistent and use the simpler Gompertz model, in line with other works (Finch 1990, pp. 507–510; Flurkey et al. 2001). By eliminating deaths prior to the onset of senescence and deaths at very late ages and by creating visual displays of the data (see materials and methods), we obviated common problems in analyzing mortality data, such as the deceleration of mortality at high ages. While other models may fit the entire mortality trajectory better, our calculations provide a simple but effective way to estimate whether the aging process differs between cohorts of the same experimental background. Overall, it is the combination of Gompertz parameters, visual representations, and age-related physiological changes that may help us to infer whether a given intervention has or has not affected the aging process.

Although it has already been argued by others (Finch 1990, pp. 24–29; Williams 1999; Hayflick 2000), our work demonstrates that changes in average and/or maximal longevity are not reliable indicators of alterations in the aging process. Even though t_max may in some cases be an indicator of shifts in the rate of aging, we advise caution in future such studies. It is important that researchers reporting interventions affecting life span also calculate the Gompertz parameters and describe age-related changes in biochemical and physiological indicators. Finally, since some interventions may mimic caloric restriction by, for instance, reducing food intake, it is important to have body weight information and developmental schedules for life-extending experiments. This is exemplified by the C/EBPβ +/+ cohort, which lived longer and had a higher MRDT, but also had a much lower average body weight than controls (Chiu et al. 2004).

A measure of the genetics of mammalian aging:

We failed to find statistical evidence that IGF1R, INSR, PROP1, GHRHR, or TRX retard the rate of aging. The results for PROP1, despite the possible need for larger data sets, are in accordance with previous reports suggesting that these double-mutant mice do not age more slowly (Quarrie and Riabowol 2004). Since there is little or no published information that these loci affect the progression of age-related changes and/or pathologies, we suggest that these genes do not influence aging in mice. Changes in the expression of these genes appear to decrease the IMR and so they may be useful to other aspects of medicine. Alternatively, it is possible that we were unable to detect changes in rate of aging either because of errors in the experiments or because the samples were not large enough. For instance, the IMR for TRX controls was much higher than that usually reported for the C57BL strain, and their longevity was considerably lower (Liang et al. 2003). As acknowledged by the authors of the experiment, environmental conditions may be to blame for increasing mortality and thus a bias in the results. Fortunately, similar experiments are being conducted at another facility to confirm the role, if any, of TRX in aging (Mitsui et al. 2002).

On the other hand, we found some statistical evidence that C/EBP, GHR, PIT1, and p66^shc could influence aging in mice. Similarly, transgenic mice overexpressing bovine GH appeared to age faster, which provides evidence that the growth hormone pathway is involved in mammalian aging. In fact, cognitive decline has been delayed in GHR −/− mice and accelerated in bGH transgenic mice (Bartke 2003; Quarrie and Riabowol 2004). The way in which the GH pathway appears to impact on aging may be interpreted as a side effect of its stimulatory effects on development: growth, maturation, and reproduction, as argued before (Bartke 2003). On the other hand, although a shift in the Gompertz slope was visible in GHR mutant animals (Figure 3A), removing outliers and adjusting the age at which mortality begins to climb affected the results, making the shift in the Gompertz slope no longer statistically significant (P = 0.101). Therefore, further studies are necessary.

Clearly, the p66^shc experiment deserves further attention since the number of animals used was relatively small (n = 29). In fact, it is frustrating to analyze the experiment on p66^shc, one of the splice variants of the SHC1 locus. Despite the intriguing increase in longevity (Migliaccio et al. 1999) and the increased MRDT, suggesting that the SHC1 locus could indeed affect aging, little information is available on the p66^shc double-knockout strain: there is barely any information on age-related changes, cancer incidence, morbidity, or developmental schedules. In addition, it has been argued that the p66^shc controls lived a shorter time than in other experiments using the 129/Sv strain and so it is possible that the increased longevity of p66^shc −/− mice is due to increased resistance to an adverse environment (Liang et al. 2003). Indeed, the MRDT that we obtained for the wild-type cohort (0.11 years) was the lowest among controls (Tables 2 and 3). Further studies of this gene and these double-knockout mice are necessary to address these questions.

The C/EBP proteins are involved in fat metabolism with C/EBPβ preventing lipid accumulation. If indeed the aging process is influenced by C/EBPβ, as suggested by our results, one possible mechanism is an alteration in metabolism, similar to what occurs in CR. In fact, as mentioned earlier, body weight is significantly decreased throughout life in C/EBPβ +/+ animals and increased in the Lep^op/op cohort (Chiu et al. 2004).

It remains to be seen whether klotho and TOP3B affect aging and whether ATM + TERC and WRN + TERC knockouts age faster. We failed to calculate the MRDT for these cohorts, presumably because the IMR is so high and the pathologies affecting these animals so severe that animals die before the onset of aging. Alternatively, the high IMR masks aging-related mortality. Interestingly, we found similar problems in calculating the MRDT for strains with mutations at the LMNA and PRDX1 loci and for the NZB/W strain, although to a lower degree. Our suggestion is that disease rather than aging is fostered in these animals, causing an increase in aging-independent mortality and thus a shorter life span. The surprisingly high values in the MRDT obtained for PRDX1 mutant mice are probably a result of the increased pathologies affecting these animals and masking the calculations, in line with the Strehler-Midvan theory in which high age-independent mortality increases the MRDT (Strehler 1999, pp. 111–113, 119–124). Indeed, the correlation coefficient for the PRDX1 mutant mice was 0.34.

Despite the low MRDT for LMNA −/− mice, our interpretation is that these results represent a limitation of the Gompertz model rather than a case of accelerated aging. As pointed out by others (Finch 1990, pp. 24–25; Miller 2001), specific diseases affecting a given strain can alter the MRDT and thus mask the real impact of genetic interventions on aging. The incidence and rapid progress of cardiomyopathy in these animals (Nikolova et al. 2004) leads us to think they are not suffering from premature senescence but rather from premature lethality, or a form of mechanical senescence. In fact, although rare, there are cases of disease-prone mouse strains having a very low MRDT. For instance, the MRDT for the D2SM females has been reported as 0.04 years with an IMR of 0.2/year (Finch 1990, p. 322). Similarly, one could argue that the relatively small MRDT for the NZW/B strain results from increased cancer incidence. Perhaps the increase in cancer incidence leads to an increase in IMR and a decrease in MRDT even though the aging process has not been changed (Miller 2001). That is, however, not observed in the p53 experiment, where despite large variations in cancer incidence, longevity, and IMR, the MRDT remains fairly constant (Table 3). As such, we think the Gompertz model is best used in comparing cohorts of the same experiment. In addition, it appears that the Gompertz model is better suited to investigate life-extending rather than life-reducing experiments due to the extreme pathologies that can affect animals in the latter experiments.

We also found statistical evidence that SAM are indeed senescence accelerated, in line with what was originally reported (Takeda et al. 1981). Even so, at about 1 year of age there is a bizarre shift in the Gompertz slope (Figure 3D). Since the logistic model provided a good fit for the SAM experiment, it can be argued that the deceleration of hazard rates at later ages is responsible for this phenomenon. Yet t50 was very different between both cohorts at the time the shift in mortality was observed, which suggests that this phenomenon may not be related to aging. A number of environmental conditions—such as housing conditions—could have increased the mortality prior to age 1. The fact that only after age 1 does the Gompertz slope change is an indication that only under optimum conditions could the shift in the Gompertz slope be detected. On the other hand, it can be argued that since <50% of SAM animals were alive after age 1, comparing the mortality curves after this point is not representative of the real mortality trajectory.

Two novel findings were that the PolgA and MSRA loci may influence mammalian aging. Interestingly, MSRA was shown to affect not only longevity but also the rate of aging in Drosophila (Ruan et al. 2002). Our results suggest that the MSRA gene merits further attention. Finally, PolgA appears to affect mammalian aging, even though control cohorts were not from the same experimental setting.

Concluding remarks:

Unfortunately, many researchers publishing mortality data do not make the distinction between interventions affecting aging and interventions affecting longevity. In this work, we addressed this problem and redefined the role of several loci in the aging process of mice with multiple implications for future research on aging conducted in genetically modified mice and for understanding the genetics of human aging. Our work also provides a refined but simple method to evaluate the influence of genetic interventions in murine aging that should be implemented by researchers conducting longevity studies.