Estimation of Long-Term Effective Population Sizes Through the History of Durum Wheat Using Microsatellite Data

Abstract

Estimation of long-term effective population size (N_e) from polymorphism data alone requires an independent knowledge of mutation rate. Microsatellites provide the opportunity to estimate N_e because their high mutation rate can be estimated from observed mutations. We used this property to estimate N_e in allotetraploid wheat Triticum turgidum at four stages of its history since its domestication. We estimated the mutation rate of 30 microsatellite loci. Allele-specific mutation rates μ were predicted from the number of repeats of the alleles. Effective population sizes were calculated from the diversity parameter θ = 4N_eμ. We demonstrated from simulations that the unbiased estimator of θ based on Nei's heterozygosity is the most appropriate for estimating N_e because of a small variance and a relative robustness to variations in the mutation model compared to other estimators. We found a N_e of 32,500 individuals with a 95% confidence interval of [20,739; 45,991] in the wild ancestor of wheat, 12,000 ([5790; 19,300]) in the domesticated form, 6000 ([2831; 9556]) in landraces, and 1300 ([689; 2031]) in recent improved varieties. This decrease illustrates the successive bottlenecks in durum wheat. No selective effect was detected on our loci, despite a complete loss of polymorphism for two of them.

THE effective population size (N_e) is defined as the size of an ideal population that would present the same amount of genetic drift as the population under study. Effective size determines the rate at which populations lose alleles through random genetic drift and, together with the mutation rate, it determines the number of alleles expected in populations. This parameter is therefore a measure of the genetic diversity that can be maintained in populations. Demographic events (expansions or reductions) can have dramatic effects on the long-term effective size of a population. Domestication and subsequent agronomic improvement of crop species are usually accompanied by such changes in population size. Population size reductions, typically referred to as genetic bottlenecks, have usually led to decreased levels of diversity in cultivated crops relative to that observed in their wild progenitors (see Buckler et al. 2001 for a review of grasses). The management of genetic resources for cultivated plant species would benefit from a better understanding of how genetic diversity has changed throughout their evolutionary history. In this context, knowledge of how effective population sizes have changed in crop species is of special interest, in that N_e is expected to reflect the reduction of genetic diversity that has occurred at different stages in the history of crop domestication.

The section of allotetraploid wheats with AB genomes (Triticum turgidum 2n = 4x = 28) is an appropriate model to study the impact of demographic events on effective population size since the history of wheat domestication is well documented and the different gene pools (e.g., wild and domesticated) are still available as accessions conserved in seed banks. Durum wheat (T. turgidum ssp. durum) is traditionally grown around the Mediterranean Sea and is currently the most common cultivated form of allotetraploid wheat. Wheat domestication took place ∼12,000 years ago in the Near East, with the wild ancestor (T. turgidum ssp. dicoccoides) giving rise to the first domesticated form (emmer wheat, T. turgidum ssp. dicoccum; Zohary and Hopf 2000). About 2000 years after this event, the spread of agriculture from this region led to the expansion of T. turgidum ssp. dicoccum (mainly through Europe). During the same period, durum wheat (T. turgidum ssp. durum), which is characterized by free threshing, appeared in the Near East and replaced its ancestor T. turgidum ssp. dicoccum to become the major cultivated form of allotetraploid wheat by the second millennium BC (Maier 1996; Nesbitt and Samuel 1996; Zohary and Hopf 2000). The most recent history of durum wheat has been marked by modern genetic improvement, involving the replacement of landraces by inbred varieties and the introduction of dwarfing genes (second part of the 20th century). These historical events are likely to have altered the genetic diversity of wheat through two mechanisms: first, a genome-wide loss of diversity is expected due to the sampling of a few individuals at each historical transition (a bottleneck effect); second, in genomic regions harboring genes coding for favorable traits, even more severe losses of diversity would be expected as a consequence of direct selection on these genes (see, for instance, Wang et al. 1999 for a striking example on the domestication of maize and its effects on the diversity of the tb1 locus).

Here we seek to estimate the long-term effective population size of gene pools representing several key stages of the history of durum wheat, using contemporary samples. Estimates of N_e are notoriously difficult to obtain from samples at a single point in time and usually only the product N_eμ is estimable, where N_e is the effective population size and μ the mutation rate of the locus used for surveying diversity in the sample. However, if independent knowledge of the mutation rate is available, it is possible to estimate N_e from observed polymorphism (Nei and Graur 1984). Microsatellite markers present high mutation rates that can therefore be estimated from direct observation of mutation events (Ellegren 2000a; Xu et al. 2000; Thuillet et al. 2002). Estimates of N_e based on these markers have been obtained for several species (Lehmann et al. 1998; Spong et al. 2000; Pascual et al. 2001; Vigouroux et al. 2002). Over the last decade, a large collection of data has been generated concerning microsatellite mutation rates and their pattern of evolution. In particular, microsatellite allele length has been shown to be positively correlated with the rate of mutation (Brinkmann et al. 1998; Schlötterer et al. 1998; Vigouroux et al. 2002; Brodehe et al. 2004). Making use of this information should allow one to obtain increased accuracy of estimating N_e values using these markers (Ellegren 2000b; Schlötterer 2000; Xu et al. 2000).

In this article, we first provide direct estimates of mutation rates for a set of microsatellite loci in T. t. durum and develop a calibration allowing the prediction of allele-specific mutation rates from their allele length. Second, using these calibrated microsatellites to survey diversity, we estimate absolute values of the effective population sizes in four taxonomic groups representative of key stages in the evolution of T. t. durum. This allows us to quantify the impact of demographic events on the genetic diversity through the history of durum wheat since its domestication. We also examine severe losses of genetic diversity at several loci in the context of selection for agronomic traits.

MATERIALS AND METHODS

Plant material:

Mutation-accumulation design:

Five hundred inbred lines diverged for 8 or 10 generations of controlled selfing from a single doubled haploid of the variety Sham I were genotyped to obtain microsatellite loci mutation rate estimates. This variety belongs to the subspecies T. t. durum. Plant material is reported in detail in Thuillet et al. (2002).

Plant material used for the diversity survey:

Three hundred fourteen genotypes were sampled to examine diversity at four main stages of the history of the allotetraploid wheat T. turgidum. The four groups were defined as follows: 59 accessions originating from the Near East represented the wild emmer wheat (T. turgidum ssp. dicoccoides); 94 individuals coming from the Near East, Turkey, the Balkans, eastern Europe, Italy, Spain, Russia, and Morocco (accessions were kindly provided by the U.S. Department of Agriculture, International Center for Agricultural Research in the Dry Areas, and International Maize and Wheat Improvement Center) constituted the sample of domesticated emmer wheat (T. turgidum ssp. dicoccum); 40 accessions, conserved at INRA (Montpellier) were old varieties of durum wheat that were cultivated in the first part of the 20th century; and 121 accessions were French modern varieties of durum wheat registered after 1960, the date corresponding to the introduction of dwarfing genes to produce elite varieties (provided by the Group of Study and Control of Varieties and Seeds, France). We further refer to these four groups as the wild group, domesticated emmer, old durum varieties, and elite durum varieties, respectively.

DNA extraction and microsatellite genotyping:

DNA of the mutation-accumulation lines and of inbred lines comprising the four diversity groups was extracted from fresh leaves following a protocol adapted from Tai and Tanksley (1990). Amplification reactions for microsatellite genotyping were performed in a final volume of 20 μl in the presence of 20 ng of template DNA, 1 pmol of the reverse primer, and 4 pmol of the forward primer; 0.2 mm of each deoxynucleotide; 1.5 mm MgCl₂; and 1 unit Taq polymerase (Sigma, St. Louis). The forward primer was 5′-labeled with one of the three fluorophores (6FAM, NED, or HEX). PCR was carried out using a PTC 100 thermocycler (MJ Research, Watertown, MA). After 5 min at 94°, 30 cycles were performed for 30 sec at 94°; 30 sec at 50, 55, or 60° (depending on the locus); and 30 sec at 72°, followed by a final extension step of 5 min at 72°. Amplified products were detected on an ABI (Columbia, MD) prism 3100 Genetic Analyzer. Samples were prepared by adding 3 μl of diluted PCR products to 6.875 μl formamide and 0.125 μl GenSize 500 Rox. Analysis was performed using the Gene Scan 3.1 and Genotyper 2.5 software (Applied Biosystems, Foster City, CA).

Direct estimation of the mutation rates:

Mutation rates for 30 microsatellite loci, mapped on the A and B genomes of the bread wheat T. aestivum (Röder et al. 1998a), were estimated directly in the mutation-accumulation lines derived from the variety Sham I. Seven loci were scored after 8 generations (Thuillet et al. 2002) and 23 loci were scored after 10 generations (3 loci reported in Thuillet et al. 2002; 20 loci in this study; see Table 1). Being allotetraploid, segregation of alleles at a given locus is disomic. Therefore, at each locus, the mutation rate was estimated as the number of mutant alleles observed in the 500 mutation-accumulation lines divided by the number (n) of possible mutation events scored (n = L(2 − 2^1−g + g), where L is the number of lines screened and g the number of generations considered, n = 4996 for 500 lines and 8 generations, and n = 5999 for 500 lines and 10 generations; see Thuillet et al. (2002) for details. Exact confidence intervals around these estimates were computed by assuming that the total number of mutation events detected at a given locus is Poisson distributed (Casella and Berger 1990).

TABLE 1.

Direct estimation of mutation rates for 30 microsatellite loci

		Motif
Locus	Ch	Chinese spring	Sham I	Mutation rate	C.I. 95%	+2	+1	−1	−2	−4	−5	−6
Xgwm164	1A	(GA)16	(GA)20	0	0; 5.2 × 10−4	.	.	.	.	.	.	.
Xgwm99a	1A	(GT)20	(GT)29	0	0; 5.3 × 10−4	.	.	.	.	.	.	.
Xgwm413	1B	(GA)18	(GA)20	3.5 × 10−4	1.1 × 10−4; 1.3 × 10−3	.	.	2	.	.	.	.
Xgwm153a	1B	(GA)18	(GA)>34	10−3	4.7 × 10−4; 2.5 × 10−3	.	4	1	.	.	.	.
Xgwm339	2A	(GA)22	(GA)25	5.3 × 10−4	1.9 × 10−4; 1.6 × 10−3	.	3	.	.	.	.	.
Xgwm372a	2A	(GA)>51	(GA)26	0	0; 6.4 × 10−4	.	.	.	.	.	.	.
Xgwm312a	2A	(GA)37	(GA)30	6.4 × 10−4	2.3 × 10−4; 1.9 × 10−3	.	3	.	.	.	.	.
Xgwm257a	2B	(GT)30	(GT)6GC(GT)5	0	0; 6.4 × 10−4	.	.	.	.	.	.	.
Xgwm374a	2B	(GT)17	(GT)10	0	0; 6.4 × 10−4	.	.	.	.	.	.	.
Xgwm148a	2B	(GT)22	(GT)11	0	0; 6.4 × 10−4	.	.	.	.	.	.	.
Xgwm526a	2B	(GA)16	(GA)18	0	0; 6.4 × 10−4	.	.	.	.	.	.	.
Xgwm2	3A	(GT)18	(GT)5GA(GT)5	3.6 × 10−4	1.1 × 10−4; 1.3 × 10−3	.	2	.	.	.	.	.
Xgwm247	3B	(GA)24	(GA)14	1.7 × 10−4	4.2 × 10−5; 9.6 × 10−4	.	1	.	.	.	.	.
Xgwm285	3B	(GA)27	(GA)19	0	0; 5.2 × 10−4	.	.	.	.	.	.	.
Xgwm160a	4A	—	(GA)12GG(GA)7	0	0; 5.3 × 10−4	.	.	.	.	.	.	.
Xgwm160b	4A	—	(GA)4+14+7+2	0	0; 5.2 × 10−4	.	.	.	.	.	.	.
Xgwm601	4A	(GA)17	(GA)18	0	0; 5.2 × 10−4	.	.	.	.	.	.	.
Xgwm6a	4B	—	(GA)22AA(GA)10	2.1 × 10−3	1.2 × 10−3; 3.6 × 10−3	1	10	.	.	1	.	.
Xgwm6b	4B	—	(GA)53	1.6 × 10−3	8.3 × 10−4; 2.9 × 10−3	.	5	2	.	.	1	1
Xgwm495a	4B	(GA)20	(GA)12A(GA)12	0	0; 5.3 × 10−4	.	.	.	.	.	.	.
Xgwm126	5A	(GT)15	(GT)12	—	—	.	.	.	.	.	.	.
Xgwm156	5A	(GT)14	(GT)17	0	0; 5.2 × 10−4	.	.	.	.	.	.	.
Xgwm604	5B	(GA)29	(GA)28	5.2 × 10−4	1.9 × 10−4; 1.5 × 10−3	.	3	.	.	.	.	.
Xgwm234	5B	(GA)16(GT)20	(GT)8(GA)3GG	0	0; 5.2 × 10−4	.	.	.	.	.	.	.
(GA)15
Xgwm213	5B	(GA)35	(GA)38	0	0; 5.2 × 10−4	.	.	.	.	.	.	.
Xgwm494	6A	(GT)13	(GT)3CG(GT)8	0	0; 5.2 × 10−4	.	.	.	.	.	.	.
Xgwm334	6A	(GA)19	(GA)16	1.8 × 10−4	4.3 × 10−5; 9.8 × 10−4	.	1	.	.	.	.	.
Xgwm260	7A	(GA)20	(GA)11	3.7 × 10−4	1.1 × 10−4; 1.3 × 10−3	.	1	.	1	.	.	.
Xgwm297	7B	(GT)12(GA)18	(GA)18(GT)20	3.4 × 10−4	10−4; 1.2 × 10−3	.	.	1	1	.	.	.
Xgwm537a	7B	(GT)18(TA)13	(GT)28	7 × 10−4	2.8 × 10−4; 1.8 × 10−3	.	1	3	.	.	.	.

The last seven columns give the distribution of the mutation events at each locus, +x (respectively −x) representing a mutation causing the gain (respectively loss) of x repeats. (—) Missing data. (·) No mutation of the corresponding size was observed. Ch, chromosome location in the variety Chinese spring; C.I. 95%, 95% confidence interval.

^aLoci for which the mutation rate has been estimated in a previous study (Thuillet et al. 2002).

Influence of the allele length on the mutation rate of microsatellite alleles:

The number of repeats of the initial allele was obtained after cloning and sequencing PCR products obtained on Sham I (see Thuillet et al. 2002). The relationship between the mutation rate of an allele (μ̂) and its number of repeats (R) was investigated by a regression analysis in the Sham I mutation-accumulation design. For imperfect loci, we considered each uninterrupted part of the sequence as an independent perfect repeated array. Thus, R was set as the arithmetic mean of all uninterrupted parts of the repeated sequence, and the observed corresponding mutation rate at the locus was divided by the number of uninterrupted parts of the sequence. This aims to take into account the fact that interrupted microsatellites seem to present lower mutation rates than perfect microsatellites for a similar total length (Brinkmann et al. 1998). Loci for which no mutant allele was observed were not used in the regression since no estimate of the mutation rate was available in this case. Indeed, single estimates are needed for every locus to build the regression and using zero as an estimate for these loci would bias the equation of the regression line. Therefore we discarded from our regression analysis loci for which no estimate of the mutation rate is available. These loci were used instead to cross-validate the equation obtained from the regression analysis μ̂ = f(R). If the prediction of their mutation rate based on their number of repeats is valid, the predicted value should lie within the 95% confidence interval obtained for these loci (based on zero mutation observed).

Estimation of locus-specific mutation rates in each group of T. turgidum:

The four groups of T. turgidum were genotyped for a subset of 15 loci among the 30 loci analyzed on the mutation-accumulation lines. The equation μ̂ = f(R) deduced from the regression analysis (see results below) was used to infer allele-specific mutation rates, at each locus in each group. The number of repeats of each individual allele was deduced from its length in base pairs compared to the length of the (sequenced) reference allele in Sham I. As differences in allele size among alleles consisted of even numbers of bases, we assumed that the flanking sequence did not vary among alleles and that all the differences in size we detected were due to variations in the number of motifs in the repeated array. Mutation rates were calculated for each allele and we tested the homogeneity of the predicted mutation rates between loci and among groups through an analysis of variance (SAS 1999–2000).

Estimation of θ in the groups of T. turgidum:

θ = 4N_eμ can be estimated (i) from Nei's heterozygosity (H_e; Nei 1987) or from the variance of allele size under a stepwise mutation model (SMM, where mutation events involve a single repeat) and (ii) from H_e or from the number of alleles under an infinite allele model (IAM, where each mutation event creates a new allele not present in the population). Most of our loci are compatible with a SMM assumption (see below), which is moreover reasonable for microsatellites as for these loci alleles can mutate to a state that is already preexistent in the population. The estimator of θ based on the variance of allele size has a high sampling variance (Kimmel and Chakraborty 1996) and is sensitive to mutation events involving more than one repeat, since these events would increase the variance in allele size dramatically. We consequently focus here on Nei's heterozygosity under a SMM. H_e was calculated at the 15 loci in the four groups. Under the assumptions of a SMM and of mutation-drift equilibrium, the parameter θ = 4N_eμ is estimated from H_e as θ̂_He = 1/2[(1 − H_e)⁻² − 1] (Ohta and Kimura 1973). This estimator being biased (Zouros 1979), we used the correction proposed by Xu and Fu (2004) and refer to the bias-corrected estimator of θ as θ̂_F . We estimated the effective population size of group i and at locus j (N̂_eij) by dividing θ̂_Fij by four times the average predicted mutation rate at locus j in group i, μ̂_ij, i.e., 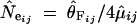. For each group i, we averaged over the j loci the values of N̂_eij. A bootstrap (10,000 resampling) over loci was performed to obtain an ∼95% confidence interval around the effective population size in each group. Loci departing significantly from neutrality and from the SMM were not used in the estimation of N_e (see the following sections).

Computer simulations:

Under a SMM and under the mutation-drift equilibrium assumption, θ̂_F is better than other existing estimators of θ for microsatellite data, since it is unbiased and has the smallest variance among currently available estimators (Xu and Fu 2004). However, Xu and Fu (2004) also showed that this estimator can be dramatically misleading when mutation events involve more than one repeat. Moreover, in our case populations have been sampled to represent postbottleneck stages: if populations have not recovered an equilibrium state, this might also affect the value of θ̂_F. Therefore we performed computer simulations to investigate the behavior of θ̂_F under a two-phase model (TPM), where mutation events involving more than one repeat gain/loss can occur, (Di Rienzo et al. 1994) and after a bottleneck. In addition, we tested (i) loci for a deviation from the SMM and (ii) groups for signature of strong demographic nonequilibrium (see the following section).

Simulations were based on the coalescent process following the algorithm proposed by Hudson (1990) to simulate population samples. Under each mutation model, assuming constant population size, we simulated 1000 samples consisting of 50 genes for 10 values of θ ranging from 1 to 40. The parameters for the TPM were a proportion p = 0.20 of multistep mutations where the number of steps was sampled in a geometric distribution of parameter α = 0.85, corresponding to a variance σ² = 38. The values chosen here for p and α are consistent with values proposed in the literature to fit actual microsatellite polymorphism data (Di Rienzo et al. 1994). The bottleneck was simulated with a sudden reduction of the effective population size as suggested by Hudson (1990). Through the simulated bottleneck the population size was reduced to one-twentieth of its initial value 10,000 generations before present. After a bottleneck, values of θ ranged from 0.2 to 16.

Detection of loci departing from the SMM:

At a microsatellite locus presenting a given number of alleles, some values of the variance of allele size are unlikely under a SMM whereas they are still plausible under a TPM (Thuillet et al. 2004). Simulations of a large number of data sets under a broad range of θ (from 1 to 50; Thuillet et al. 2004) were used to obtain the joint distribution of the number of alleles (k) and the variance of allele size (V) under a SMM. Ninety-nine percent of the simulated data sets were kept to define a threshold beyond which values of V at a given locus are highly unlikely under the SMM assumption. This test is described in more detail in Thuillet et al. (2004) and was applied here in each group of wheat to discard loci likely to evolve in a TPM manner.

Detection of the signature of a past bottleneck in each group:

Except for the wild ancestor, the different groups have been sampled to represent the diversity of groups that are likely to have undergone a bottleneck during their history. The assumption underlying our estimation of N_e in each group is that a mutation-drift equilibrium state has been recovered by the population since the bottleneck. If it is not the case, the estimation of θ can be affected. We tested if the signature of a bottleneck was still detectable in each population, including the wild ancestor, since a demographic decrease might have occurred after the domestication event. The test relies on the fact that in a recently bottlenecked population, the number of alleles is reduced faster than the gene diversity (Nei et al. 1975). The software Bottleneck was used (Cornuet and Luikart 1996). A Wilcoxon signed-rank test was used to test if a significantly high number of loci showed a heterozygosity excess or deficiency relative to the expected heterozygosity computed under the equilibrium hypothesis from the number of alleles. Loci suspected to follow a TPM were excluded. Note, however, that among the remaining loci, some might still evolve under a TPM but may be compatible with a SMM if the population has experienced a recent bottleneck (Thuillet et al. 2004). Both the SMM and the TPM hypotheses have been considered to compute expected heterozygosities in the different groups at the different loci given the observed number of alleles. The parameters of the TPM were set as previously for simulations (p = 0.2, σ² = 38).

Detection of loci departing from the neutral expectation:

To avoid a selective bias in the estimation of effective sizes due to outlier loci and to detect a signature of selection in our data set, we tested each locus used in the diversity survey for a departure from neutral evolution. At a given microsatellite locus, assuming that the mutation rate is identical in two populations, the expectation of the ratio of θ = 4N_eμ for a pair of populations estimates the ratio of N_e between both populations. The logarithm of this ratio, using θ̂_He to estimate θ, has been shown to follow a normal distribution under neutral evolution (Schlötterer 2002; Kauer et al. 2003). As it appeared from simulation results that the estimation of the ratio calculated from θ̂_F presented a larger variance than that calculated from θ̂_He (data not shown), we kept θ̂_He for the calculation of the ratio. The normality of the distribution of the ratio holds when the pattern of evolution does not vary for a given locus from one population to the other, but the distribution of the estimated ratio can depart from normality when a bottleneck occurs, especially for TPM loci (Kauer et al. 2003). To account for possible differences in the mutation rates in the different populations, we corrected each ratio by the corresponding group mutation rates in each population. This new ratio, noted ln(R[θ/μ]), was calculated for each locus and for three pairs of wheat groups: (a) the wild group and the domesticated group, (b) the domesticated group and the old varieties, and (c) the old varieties and modern varieties. To test departure from neutrality, the expected distribution of the statistic ln(R[θ/μ]) was obtained by computer simulations.

The average ratio of N_e between two populations (excluding TPM loci) provided an estimate of the expected reduction of N_e between each pair of populations, which was used to parameterize coalescence simulations and obtain the expected distribution of ln(R[θ/μ]) from 1000 coalescent simulations. For each pairwise comparison, loci outside the interval spanning 95% of the expected distribution of ln(R[θ/μ]) were considered as outliers potentially affected by selection.

RESULTS

Direct estimation of mutation rates:

Loci properties are summarized in Table 1. All loci were dinucleotide repeats, 21 were perfect (i.e., presented an uninterrupted repetition of the microsatellite motif), and 9 were imperfect (i.e., presented an interruption in the repetition of the microsatellite motif). Sequences are available from GenBank under accession nos. AF275895, AF275896, AF275897, AF275898, AF275899, AF275900, AF275901 and AY579587, AY579588, AY579589, AY579590, AY579591, AY579592, AY579593, AY579594, AY579595, AY579596, AY579597, AY579598, AY579599, AY579600, AY579601, AY579602, AY579603, AY579604, AY579605, AY579606, AY579607 for 28 loci. For the two last loci (Xgwm537 and Xgwm99) we could not obtain a clean sequence after several attempts because of technical problems. However, in these two cases, the number of repeats could be deduced approximately, with an uncertainty of plus or minus one repeat. Primers used to amplify loci Xgwm160 and Xgwm6 provided two amplicons in Sham I (the amplified loci are noted hereafter loci Xgwm160a, Xgwm160b, Xgwm6a, and Xgwm6b). The number of repeats (CA or GA) was variable across loci. The mean mutation rate over the 30 loci was 3.1 × 10⁻⁴ when a value of zero was considered for loci presenting no mutation. A total of 49 mutation events were observed among 13 loci and the highest observed mutation rate was 2.1 × 10⁻³ (Table 1). A great majority of gains of one repeat occurred (26 gains against five losses; χ² = 14.5, d.f. = 1, P < 0.0005). Multistep mutations of two, four, five, or six repeated units also occurred and consisted in losses of repeats except for one gain of two repeats (Xgwm6a). The number of repeats deduced from the sequence in Sham I was compared to the number of repeats of the sequence at the same locus in the genotype of hexaploid wheat Chinese spring (Table 1): no difference of structure was detected for 20 loci among 26 for which the comparison was possible (i.e., perfect or imperfect loci in both species). The conservation of structure of the loci seems consequently a safe assumption within the species T. turgidum.

Prediction of mutation rates from the number of repeats:

The correlation between the mutation rate (μ) and the number of repeats of the allele (R) was based on the 13 loci for which mutations were observed. When all 13 loci were considered, variation in R explained only 34% of the variation in μ (P < 0.04). However, this low value seemed to be due to one particular locus (Xgwm6a) that exhibited a particularly high mutation rate despite a low number of repeats. Removing this locus from the analysis resulted in a dramatic increase of the regression coefficient (R² = 0.83, P < 0.0001) and the relationship between allele length (R) and mutation rate (μ) was

1

This regression was based on 10 perfect and 2 imperfect loci. Considering the 10 perfect microsatellites alone, the correlation was slightly improved, with a better coefficient of determination (R² = 0.91, P < 0.0001). Equation 1 was kept for further prediction of mutation rates.

At all 6 imperfect loci, and at 7 of 10 perfect loci for which no mutation events were detected in the mutation-accumulation design, the predicted mutation rates in Sham I were compatible with the probability of observing zero mutation at the 95% confidence level. Three perfect loci (Xgwm213, Xgwm99, and Xgwm372) had higher predicted mutation rates than the maximum rate expected at the 95% confidence level given zero mutation observed.

Equation 1 was considered robust enough to predict mutation rates in the different groups of wheat. Among the 15 loci that were used to survey microsatellite diversity, 6 were part of the 12 loci used to build the regression analysis. For those 6 loci, the mutation rate predicted by Equation 1 is by construction in agreement with the observed mutation rate in the mutation-accumulation design. Among the remaining 9 loci used in the diversity analysis, no mutation was observed for 8 of them, but only the locus Xgwm213 showed a discrepancy between its observed and predicted mutation rate from Equation 1 in the mutation-accumulation design. For locus Xgwm126, no direct estimation of the mutation rate was available. The predicted mutation rates at the 15 loci were significantly different among the four T. turgidum groups (ANOVA, P < 0.0001) and among loci in a given group (ANOVA, P < 0.0001). The estimated mutation rates at the 15 loci within each group are given in Table 2.

TABLE 2.

Predicted mutation rates at each locus in each group (×10⁻⁴)

Locus	Wild	Domesticated	Old varieties	Elite varieties
Xgwm164	5.9	4.4	5.3	4.7
Xgwm413	4.4	5.9	4.7	5
Xgwm312	6.8	6.8	6.5	7.4
Xgwm257	0.8	0.8	0.8	0.8
Xgwm374	4.7	3.8	2	2
Xgwm2	2.3	0.8	1.4	0.5
Xgwm285	6.2	11.3	6.5	5.6
Xgwm601	4.7	5	5.6	4.4
Xgwm6b	6.2	8	11.3	9.8
Xgwm495	2	2	2	1.7
Xgwm126	3.2	3.2	3.8	3.2
Xgwm234	4.4	4.7	5.3	4.1
Xgwm213	5.3	5.6	5.3	7.4
Xgwm297	5	4.1	4.7	4.7
Xgwm537	7.1	7.4	5.9	6.5
Mean	4.6	4.9	4.74	4.52

Estimation of θ:

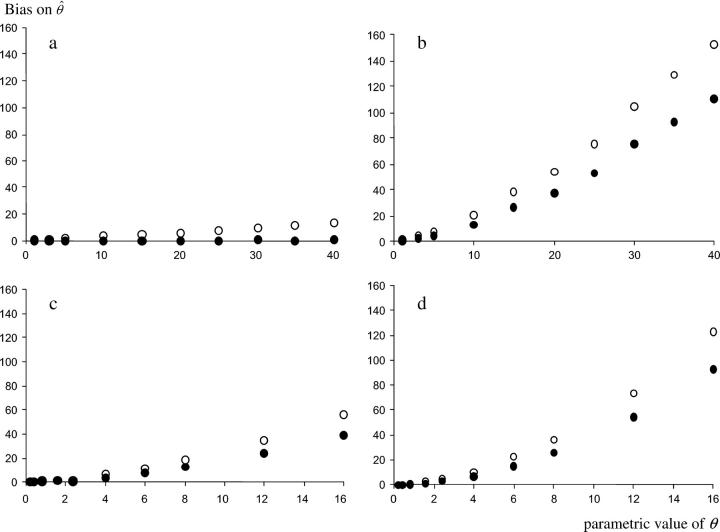
At equilibrium and under a SMM, both estimators θ̂_He and θ̂_F behaved as expected: the bias on θ̂_He was removed by the correction on θ̂_F (Figure 1a) and the variance of θ̂_F was smaller than the variance of θ̂_He. At equilibrium and under a TPM, the decrease in homoplasy resulted in an increase of H_e compared to a SMM and led to an overestimation of θ by both estimators (Figure 1b). When a bottleneck occurred, its effect on the estimation of θ was less dramatic under a SMM than under a TPM, but in both cases θ was overestimated (Figure 1, c and d). For any departure from the SMM at equilibrium, a smaller bias and a smaller variance were observed for θ̂_F than for θ̂_He. We examined the relative efficiency of both estimators, defined as the ratio of their variances. On average, θ̂_F was ∼1.5–2 times more efficient than θ̂_He. However, the efficiency of θ̂_F compared to θ̂_He decreased when θ increased, and the overestimation of θ by θ̂_F was very important when a departure from a SMM or demographic equilibrium occurred. θ̂_F was consequently chosen to estimate effective population sizes.

Figure 1.—

Magnitude of the bias on θ̂_F (solid circles) and on θ̂_He (open circles) for different values of θ. The x-axis represents the parametric value of θ used for the simulations. Each point represents the average bias estimated on the basis of 1000 simulated data sets. Simulations were realized assuming either a constant population size and (a) a SMM or (b) a TPM or a bottlenecked population and (c) a SMM or (d) a TPM.

Departures from the SMM, demographic equilibrium, and neutrality:

The locus Xgwm213 presented a variance in allele size that was not compatible with a SMM given the number of alleles observed at this locus. This departure was observed in all four groups. Loci Xgwm312 and Xgwm285 were also unlikely to fit a SMM hypothesis in all groups but the wild one. Locus Xgwm6b was not compatible with a SMM in two groups (domesticated emmer and elite durum varieties) among the four.

No evidence for a recent bottleneck was detected under the SMM hypothesis for any of the four groups (Table 3). Although a TPM assumption for all loci revealed a possible trace of a recent bottleneck in the wild group, this conclusion was dependent on the parameters chosen for the TPM and did not hold under a weaker TPM (P = 0.1 and σ² = 30), which does not provide a strong support for the existence of a recent bottleneck in this group. A deficiency in heterozygosity given the number of alleles was detected under the SMM hypothesis for both groups of durum wheat (old and elite durum varieties). Only the deficiency of heterozygosity detected in the elite durum varieties was robust to a change of model. A recent expansion of population is unlikely for this group, but this observation can be explained by a recent event of migration from a different gene pool, which could have increased the number of rare alleles without affecting the heterozygosity, thus mimicking an increase in the population size (Cornuet and Luikart 1996). Such a scenario is indeed expected for elite durum varieties as the introduction of dwarfism genes has been realized from varieties of bread wheat (T. t. aestivum).

TABLE 3.

Test for mutation-drift equilibrium using the method of Cornuet and Luikart (1996)

	SMM		TPM
	E/D	P-value	E/D	P-value
Wild	9/4	0.59	10/3	0.04
Domesticated	4/7	0.91	6/5	0.90
Old varieties	3/7	0.03	4/6	0.85
Elite varieties	0/10	<0.001	0/10	<0.001

E/D, number of loci showing an excess/deficiency heterozygosity given the observed number of alleles. The associated P-value for a Wilcoxon signed-rank test (two tails) is given.

No evidence for indirect selective effect was detected using the statistic ln(R[θ/μ]) when comparing the wild group and the domesticated emmer or when comparing old and elite durum varieties. This suggests that none of the 15 loci studied was affected by a selective sweep either during the domestication or during more recent selection on elite durum varieties. Alternatively, all loci may have mutation rates that are high enough to erase the signature of such events. But loci Xgwm257 and Xgwm374 were found completely monomorphic in old durum varieties, while their heterozygosities were ∼0.5 and 0.8, respectively, in the domesticated emmer. They could consequently not be included in the distributions of ln(R[θ/μ]) for the two comparisons including the group of old varieties. A selective effect during the creation of the first durum wheat varieties could have led to complete loss of polymorphism at these loci, although this observation alone is not conclusive. We note that Xgwm257 was also monomorphic in the group of elite varieties. Among the 13 remaining loci, 1 locus (Xgwm285) exhibited a departure from neutrality when comparing domesticated emmer and old varieties. This effect corresponds, however, to a particularly high estimated effective population size at this locus in domesticated emmer, compared to the N_e at the other loci in this group. This locus is likely to evolve under a TPM in both groups. The detected departure from neutrality could then instead be explained by a departure from the SMM, with a greater overestimation of θ̂_He in domesticated emmer than in old varieties because of a higher diversity level in domesticated emmer.

Estimation of effective population sizes:

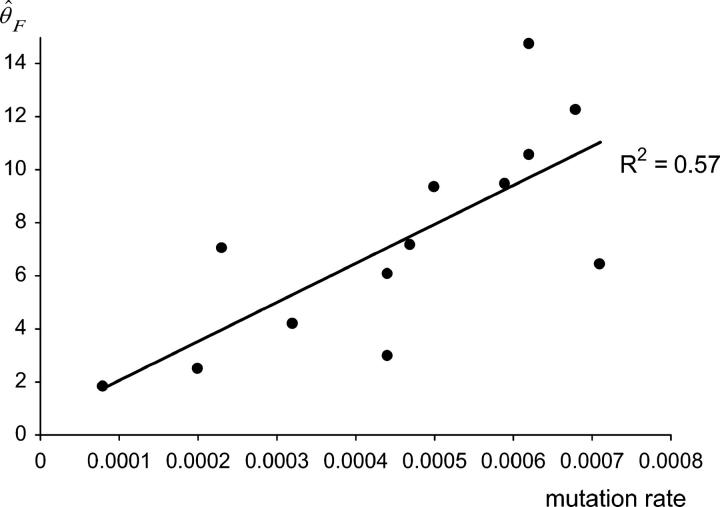
Besides loci likely to evolve under a TPM and monomorphic loci, Xgwm601 was discarded from the estimation of N_e in the wild group because of a very high proportion of null alleles (46 individuals among 59 did not amplify). Excluding this locus and locus Xgwm213 (TPM) from the wild group, θ̂_F was highly correlated to the mutation rate in that group (R² = 0.57, P < 0.003, Figure 2). The same trend was observed in the three other groups (R² = 0.37 in domesticated emmer, R² = 0.40 in old durum varieties, and R² = 0.44 in elite durum varieties; P < 0.05). This observation supports that effective population size is rather homogenous among the remaining loci (i.e., non-TPM or nonmonomorphic) and illustrates the importance of taking into account the variability of mutation rates between loci. Estimates of the mean effective population sizes per group and per locus along with an ∼95% confidence interval are shown in Table 4. Average N_e in the wild group was ∼32,000 individuals. Only ∼37% of this effective population size has then been retained in the first domesticated form, where N_e dropped dramatically to ∼12,000 individuals in the domesticated emmer. The trend was similar between domesticated emmer and old varieties, as only ∼50% of N_e is retained from the domesticated emmer to old varieties (N_e = 6000). The least polymorphic group of allotetraploid wheats was the elite varieties group with a mean N_e value of 1300 corresponding to 22% of the N_e of old durum varieties and representing only 4% of the N_e of its wild ancestor. Differences in the estimated N_e in the different groups were large and significant despite the wide confidence intervals (Table 4).

Figure 2.—

Correlation between θ̂_F and the predicted mutation rate in the wild group of wheat (R² = 0.56, P < 0.003).

TABLE 4.

Estimates of effective population sizes (N_e)

Locus	Wild	Domesticated	Old varieties	Elite varieties
Xgwm164	38272	2557	679	748
Xgwm413	5022	4208	1328	943
Xgwm312	55155	22735	1684	244
Xgwm257	10236	2945	0	0
Xgwm374	27159	6469	0	13
Xgwm2	53596	10005	213	51
Xgwm285	45268	69613	832	267
Xgwm601	249	16171	1357	532
Xgwm6b	87630	27839	9391	7241
Xgwm495	7653	23797	18216	2880
Xgwm126	13900	1311	3510	2360
Xgwm234	20871	2410	11730	3280
Xgwm213	120565	13391	844	1992
Xgwm297	43536	36041	7256	1086
Xgwm537	14579	26456	5973	1367
Mean	32529	12034	5965	1326
95% C.I.	[20739; 45991]	[5790; 19300]	[2831; 9556]	[689; 2031]

Underlined values were not included in the calculation of the mean effective population size of a group. Values in boldface type represent loci detected as evolving in a TPM manner. Values in italics represent loci displaying a high frequency of null alleles, and when a locus is fixed in a group, the value zero is given to N_e.

DISCUSSION

The use of microsatellites individually calibrated for their mutation rate provides a new way to obtain estimates of long-term effective population sizes. Focusing directly on the estimation of N_e allowed us to quantify the effect of the successive bottlenecks that have affected durum wheat since its domestication. We discuss below the accuracy of our method and the values we obtained in the light of the history of durum wheat.

Mutation rate estimates:

Direct observation of mutation events in durum wheat is consistent with previous observations concerning microsatellite loci that typically range from 10⁻⁶ to 10⁻² (Weber and Wong 1993; Schug et al. 1997). The main conclusions were: (1) a majority of single-step mutation events affected these loci, (2) rare mutation events involving several steps could be detected, and (3) the mutation rate was length dependent and allele specific rather than locus specific. The strong correlation obtained between the length of the repeated array and the mutation rate has been also observed in several other organisms (Wierdl et al. 1997; Brinkmann et al. 1998; Schlötterer et al. 1998; Ellegren 2000a; Vigouroux et al. 2002).

As the allele length appeared to be a crucial factor for the variation of the mutation rate in our set of loci, we used this property to predict mutation rates in the different populations. This can be inaccurate if other factors have an impact on the mutation rate as well (i.e., repeated motif, chromosomal position; Thuillet et al. 2004). The size of the repeated motif and the structure of the alleles (perfect or imperfect) have both been shown to have a substantial effect on the mutation rate of microsatellites (Chakraborty et al. 1997; Brinkmann et al. 1998). In our case, we used only dinucleotide loci. Although perfect microsatellites yielded a stronger correlation between mutation rate and length of the repeated array than when both perfect and imperfect loci were included, we kept the two imperfect loci to build Equation 1 since this did not prevent observing a correlation between θ̂_F and predicted mutation rate. As 83% of the variation in μ in the accumulation design was explained by the number of repeats and the equation relied on loci also used in the diversity survey, we believe that our prediction for μ is likely to be fairly accurate. Miscellaneous and unidentified factors are possible, however, as suggested by the existence of three outlier loci. Two of them were not used for the diversity analysis, and the last one, Xgwm213, was discarded from the estimation of N_e in all groups since it was suspected to mutate under a TPM. Another source of error in the prediction of the mutation rate is a bad estimation of the number of repeats of the alleles. For example, in maize some microsatellites have been shown to present a continuous variation of their size due to a high proportion of insertions or deletions (Matsuoka et al. 2002). This kind of situation would make it difficult to deduce the number of repeats from the size of the alleles. In our case, the structure of the loci was considered to be conserved between individuals as it appeared to be mostly conserved between the genomes of the bread wheat genotype Chinese spring and the durum wheat genotype Sham I. Furthermore, the allelic distributions presented either even or odd sizes but not both at the same locus, suggesting an evolution by steps rather than by insertions/deletions.

Effective population size estimates:

Significant differences existed in the predicted mutation rates between groups and between loci. Therefore, the estimation of effective population sizes was realized using predicted mutation rates per locus and for each group. Apart from the error due to the prediction of μ, here assumed to be relatively low, an important source of error in the estimation of N_e comes from the estimation of the parameter θ. The corrected estimator θ̂_F appeared to be more efficient than θ̂_He even when a departure from the SMM and demographic equilibrium assumption occurs and was consequently chosen to estimate θ in our diversity study. The use of θ̂_F, however, can be extremely misleading when such a departure from the assumptions occurs (especially when the diversity level is high). In that case, our values of N_e would be overestimated.

We detected four loci that are likely to follow a TPM in at least one group. The tests used to discriminate between SMM and TPM were realized under a demographic equilibrium hypothesis. If the tested populations have actually experienced a recent bottleneck, we might have missed loci for which the TPM hypothesis is likely (Thuillet et al. 2004). Our conclusion concerning the four TPM loci would still hold in that case. These loci exhibited a particularly high value of θ̂_F (data not shown), supporting the existence of multistep mutation events during their evolution. Note that multisteps have been observed in the mutation-accumulation design for the locus Xgwm6b. These four loci were excluded from the N_e estimation in groups where the SMM was unlikely. The remaining loci were assumed to have evolved under a SMM. This does not exclude the existence of a minor departure from the SMM, but it should also have a less dramatic effect on the estimation of θ.

The existence of a bottleneck in the studied populations is also likely to lead to an overestimation of θ by θ̂_F. No strong evidence for the existence of a bottleneck in any group was detected when using Bottleneck software (Cornuet and Luikart 1996). However, the deficiency in Nei's heterozygosity given the number of alleles in the elite varieties of durum wheat was highly significant and robust to the assumed pattern of evolution (SMM or TPM). The proposed scenario of a recent introduction of alleles from bread wheat is plausible and in that case we probably underestimated θ compared to what it would be if the population was at equilibrium state. The magnitude of this effect is difficult to measure, but it should be noted that the number of varieties of bread wheat that are known to have been used to introduce dwarfism genes is small. Thus, the impact of this introduction may be small.

Demographic bottlenecks in durum wheat:

A continuous decrease of effective population sizes was observed from the wild form of wheat to the current cultivated subspecies of allotetraploid wheat. The effective population size of each group is the harmonic mean of the effective population sizes realized throughout the history of each subspecies. A subspecies with a smaller effective population size is considered to have experienced a stronger or a more intense bottleneck. T. t. dicoccoides is considered as the current lineage originating from the wild ancestor of AB allotetraploid wheats. The fact that we detected no strong evidence for the existence of a past reduction of population size in this group does not mean that the effective population size has remained constant for 12,000 years. If a strong reduction of size occurred a long time ago and demographic size subsequently stayed constant, this group might have recovered an equilibrium state and could exhibit no footprint of bottleneck. This could have happened if a reduction of the natural geographic area of the wild subspecies has occurred, due, for instance, to an expansion of cultivated surfaces. In that case, it is possible that the effective size estimated in T. t. dicoccoides represents a minimum estimate of the diversity in the wild ancestor at the time of domestication.

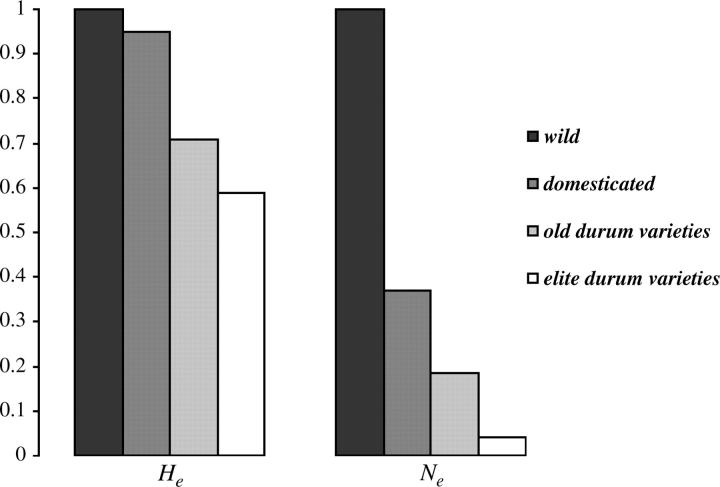
The current effective size of T. t. dicoccum, which was the first domesticated wheat derived from the wild form, was only 37% of that of its ancestor T. t. dicoccoides. In terms of Nei's heterozygosity, 95% of the diversity present in T. t. dicoccoides was retained in T. t. dicoccum (Figure 3). Compared to other species, this value was very high as ∼60–70% of genetic diversity was retained through domestication in maize, sorghum, rice, oats, or pearl millet (Buckler et al. 2001). This discrepancy between the decrease in H_e and the decrease in N_e may be due to the high mutation rates of microsatellites that can recover diversity much quicker than gene nucleotide sequences, on which these other studies were based. This is also true for subsequent reductions and shows that the bottleneck effect may be largely underestimated when one focuses only on summary statistics of diversity especially when (new) mutation accounts for a substantial portion of the observed polymorphism (Figure 3). After the domestication event, T. t. dicoccum spread out of the Fertile Crescent and was then replaced by T. t. durum populations (Nesbitt and Samuel 1996; Zohary and Hopf 2000). So, most of the populations of T. t. dicoccum that were present after the domestication have disappeared. The current diversity and N_e values of this group are then more difficult to interpret as they likely result from the succession of several demographic events. However, the current value of N_e in this group is likely to be smaller than what it was after the domestication. Therefore the reduction of N_e imposed by the free-threshing acquisition could be underestimated.

Figure 3.—

Reductions of heterozygosity (H_e) and effective population size (N_e) from the wild form, T. t. dicoccoides, to the elite varieties of durum wheat. Values are shown relative to the value in the wild form that is retained in the subsequent population.

On the other hand, N_e in old durum varieties could also be underestimated since a number of landraces might have disappeared. Elite varieties of our study come mostly from the French variety catalog but are expected to sample adequately the diversity in modern worldwide material due to a low number of founders of short stature at the international level and subsequent intense exchange between countries (P. Grignac, personal communication). The reduction of the effective population size in that group (−78% relative to old varieties) was dramatic. This value is representative of the bottleneck associated with the selection for semidwarf stature and to intensive cultivation practices.

Footprints of selection in durum wheat?

None of the polymorphic loci showed obvious departure from neutrality. However, two loci (Xgwm257 and Xgwm374) were completely monomorphic in old varieties of durum wheat. Both are located on the short arm of chromosome 2B. The gene Tg2 (tenacious glumes), also located on the same chromosomal arm, is a candidate gene for a QTL involved in the acquisition of free threshing during the transition from T. t. dicoccum to T. t. durum (Simonetti et al. 1999).

A first explanation for the absence of polymorphism at loci Xgwm257 and Xgwm314 could be that these loci experienced a reduction of diversity that is comparable to the rest of the genome (through a demographic bottleneck) but exhibit a low mutation rate and therefore did not recover any diversity. Under this assumption, estimates of their mutation rate should be low as well as their level of diversity in T. t. dicoccoides. Locus Xgwm257 presented indeed a low heterozygosity in the wild group (0.69, whereas the average for the group is 0.85) and had a low predicted mutation rate (0.8 × 10⁻⁴) with no mutation detected in the mutation-accumulation design. Locus Xgwm374, on the other hand, had a high mutation rate (2 × 10⁻⁴–4.7 × 10⁻⁴) and high heterozygosity (H_e = 0.91) in T. t. dicoccoides. Thus a mere demographic effect appears unlikely to explain patterns of microsatellite variation observed at this locus.

The marker Xrsq805, located on the distal region of chromosome 2B, is reported by Simonetti et al. (1999) as strongly associated with threshability in tetraploid wheat and as marking a QTL corresponding to locus Tg2. By comparison of different existing maps of wheat (Röder et al. 1998a; Simonetti et al. 1999; Paillard et al. 2003), we inferred the genetic position of Xgwm374 and Xgwm257 loci relative to Xrsq805. Xgwm257 should be ∼37 cM more proximal than the putative position of Tg2, and Xgwm374 was itself located 35 cM more proximal than Xgwm257 (72 cM from Xrsq805). By comparison with physical maps of wheat, it appears that Xgwm257 and Tg2 belong to the same physical bin (between 84 and 100% of the distal part of the short arm; Sourdille et al. 2004), whereas Xgwm374 belongs to the adjacent proximal physical bin. The genetic distance between both microsatellite markers covers ∼40% of the estimated physical length of the chromosomal arm (Röder et al. 1998b; Sourdille et al. 2004). Consequently, the marker Xgwm374 is actually located relatively far from the Tg2 gene. A direct effect of the gene Tg2 on this marker would require a strong selective effect spanning a very large region of the genome. On the other hand, if Tg2 is not involved in the selection process that seems necessary to explain the loss of polymorphism at Xgwm374, another candidate gene could be located closer to the microsatellite marker. It would then be interesting to investigate patterns of polymorphism in the surrounding region of this marker.

No trace of selection attributable directly to domestication was detected in our data set. We also did not detect genomic regions with a marked decrease of effective sizes due to selection during key stages of modern breeding. The main explanation is probably the low number of markers used in this study. Even with strong linkage drag, as expected in a selfing species, a greater number of markers are required to cover the 14 chromosomes of allotetraploid wheats.