Abstract
Based on the crystal structure of the cross-β spine formed by the peptide NNQQNY, we have developed a computational approach for identifying those segments of amyloidogenic proteins that themselves can form amyloid-like fibrils. The approach builds on experiments showing that hexapeptides are sufficient for forming amyloid-like fibrils. Each six-residue peptide of a protein of interest is mapped onto an ensemble of templates, or 3D profile, generated from the crystal structure of the peptide NNQQNY by small displacements of one of the two intermeshed β-sheets relative to the other. The energy of each mapping of a sequence to the profile is evaluated by using rosettadesign, and the lowest energy match for a given peptide to the template library is taken as the putative prediction. If the energy of the putative prediction is lower than a threshold value, a prediction of fibril formation is made. This method can reach an accuracy of ≈80% with a P value of ≈10−12 when a conservative energy threshold is used to separate peptides that form fibrils from those that do not. We see enrichment for positive predictions in a set of fibril-forming segments of amyloid proteins, and we illustrate the method with applications to proteins of interest in amyloid research.
Keywords: amyloid, prediction, rosettadesign, lysozyme, myoglobin
Amyloid-like fibrils of protein are common to deposition diseases such as Alzheimer’s, the spongiform encephalopathies including Creutzfeldt-Jakob disease and bovine spongiform encephalopathy, and the protein-based heredity of [PSI+] and other prions in yeast. Thus understanding the range of protein sequences that can undergo fibrillization and the basis for stability of fibrils could have wide significance. We address these problems with a computational method for predicting which segments of a given protein might form the cross-β spine in the fibrillar form.
The ability to form amyloid fibers is not restricted to those proteins associated with amyloid or prion disease. Otherwise innocuous proteins can be fibrillized by altering the pH, temperature, or composition of their native solvent (1–3). In addition, numerous short peptides (e.g., four to seven residues) are found to form amyloid-like fibrils in isolation from the rest of the protein (4–11). De novo-designed synthetic peptides have also been shown to form fibers (12–14).
The question of how both full proteins and short peptides can form fibrils was illuminated by the crystal structures (11) of NNQQNY and GNNQQNY, which showed that the fundamental structure of the protofibril is a pair of β-sheets, which mate at a dry interface where their side chains tightly interdigitate in a “steric zipper.” To form this steric zipper, the strands in the sheets need be only four to six residues in length. Therefore, we would expect that short peptides with a tendency to fibrillize can do so, either when cleaved from the rest of the protein chain, as for the β-amyloid (Abeta) peptide of Alzheimer’s disease, or when they are unmasked from an inaccessible position in a native protein. In this article we demonstrate a method that identifies which hexameric peptides have this tendency to fibrillize.
This method for predicting which peptides will fibrillize is enabled by a growing body of examples of proteins and peptides that either form fibrils or do not form fibrils, providing a library of positive and negative examples for method development. The diversity in sequence of these examples makes difficult work for traditional sequence-based approaches (e.g., regular expressions, motifs, hidden Markov models, etc.) to predict fibril formation. For example, a regular expression or “sequence pattern” was derived by Lopez de la Paz and Serrano (14), by recording the positive and negative results of fibrillization assays of all 19 point mutations for all positions of the amyloidogenic peptide STVIIE. This straightforward approach relies on the assumption that residue preferences at a given position in the sequence are independent of the residue types at other positions. This assumption likely generates large numbers of false positives because of its lack of restrictions on interacting residue types. Also the pattern fails to recognize known fibril-forming hexapeptides (e.g., NFGAIL, NNQQNY, and VQIVYK). Taking a different direction, Pawar et al. (15) developed a property-based method for identifying “aggregation-prone” segments of proteins based on a linear function of hydrophobicity, charge, and helical and β-sheet propensity derived from entire proteins. The values of these properties are summed, again assuming that positions in the sequence are independent. The primary contributor to this function is hydrophobicity, so this approach will overpredict amyloid in hydrophobic segments of proteins and miss some polar amyloidogenic segments such as NNQQNY (11). An indirect structure-based approach was developed by Yoon and Welsh (16, 17) for predicting the β-sheet propensity of a span of residues conditioned on its tertiary structure context. Sequences with a strong propensity for β-strand structure contingent on a tightly packed environment were taken to be likely fibril formers.
A direct structure-based approach to prediction of fibril formation is possible, starting from the crystal structure of the fibril-forming peptide NNQQNY (and its isomorphic variant GNNQQNY) from the sup35 prion protein of Saccharomyces cerevisiae (11). To the extent that this structure is representative of cross-β spines, we can explore the energetic space of peptides capable of adopting this structure. There is no need to equate amyloidogenicity with hydrophobicity or to assume that sequence positions in a protein are independent of one another. To scan protein sequences and identify those segments that might be capable of fibrillization, we use an approach similar to 3D profiling (18) by mutating the side chains in the cross-β spine of NNQQNY to those of the sequence of interest and evaluating the energetic fit by using rosettadesign (19). We provide a quantitative assessment of the predictive utility of this method in addition to several examples of its application to proteins of interest in amyloid research.
Results
Prediction of Fibril-Forming Hexapeptides.
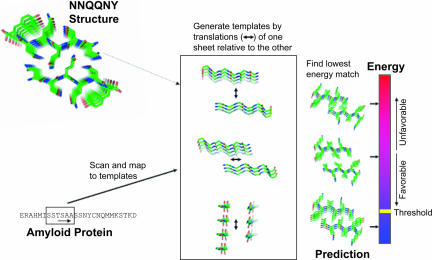
The computational method for predicting amyloid-forming hexapeptides from amino acid sequences of amyloid-forming proteins is illustrated in Fig. 1 and discussed at greater length in Methods.
Fig. 1.
Schematic representation of the 3D profile method with rosettadesign energy for detecting fibril-forming segments. From the crystal structure of the NNQQNY peptide (Upper Left), a set of near-native templates is generated by translations of one of the two β-sheets relative to the other, along three orthogonal directions, as shown (Center). A sequence of interest (Lower Left) is scanned by sliding a window of six residues and mapping each peptide onto the templates in the ensemble. Each mapping of sequence to template is evaluated energetically with rosettadesign. Finally, a putative prediction is made by taking the best-scoring (lowest energy) fit between peptide and template (Right). The putative prediction is accepted as a prediction if its energy is lower than the threshold energy.
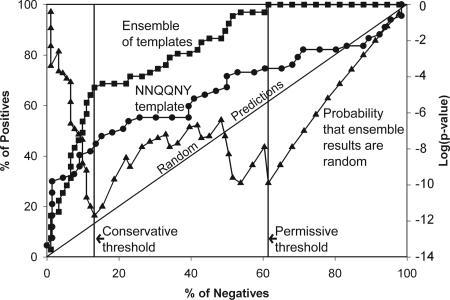
Results from applying the method to the AmylHex data set of hexapeptides known either to form fibrils or not to form fibrils (see Methods) are shown in Fig. 2 in the form of a receiver-operator characteristic plot. We can see from Fig. 2 that simply using a single template of the native structure of NNQQNY and the rosettadesign energy function does a fair job of separating peptides that form fibrils from those that do not. This is largely because of the favorable energetic fit of the STVIIE-derived peptides (14) within the cross-β spine. A random predictor would follow the diagonal in the plot. We also see that the use of the near-native template ensemble provides a substantial improvement in prediction performance, because changes in side-chain volumes and alternative packing arrangements are allowed. For the predictions made with the template ensemble, the probability of obtaining the results at each energy threshold at random was computed by using the hypergeometic distribution. The logarithm of this P value is also plotted in Fig. 2 (read off the y axis on the right) where we see that it has two minima. We will use these minima as energy thresholds in our discussion of specific applications to full-length amyloid proteins in the following sections. The right-hand vertical line corresponds to an energy threshold of −19.0 kcal/mol on the rosettadesign energy scale. The P value for the prediction results obtained by using this “permissive” threshold is 10−10, where 100% of the positives have been recovered and 60% of the negatives have accumulated, giving a false-positive error rate of 45%. The black vertical line in Fig. 2 corresponds to an energy threshold of −25.5 kcal/mol. The P value for the predictions obtained by using this “conservative” threshold is 10−12 where 69% of the positives have been recovered and 14% of the negatives have accumulated, giving a false-positive error rate of 22%.
Fig. 2.
Prediction performance of the 3D profile method with rosettadesign energy for predicting fibril-forming sequences from the AmylHex database, shown as receiver-operator characteristic curves. The percentage of correct predictions is shown as a function of percentage of wrong predictions, as the energy threshold is raised from a very low value (good energetic fit) to a very high (poor energetic fit). The curve with circles shows the fit of hexapeptides to the NNQQNY crystal structure; the curve with squares shows the fit by using the entire near-native ensemble (variations of the NNQQNY structure). The diagonal line shows how a random predictor would perform. The curve plotted with triangles (read off the right y axis) traces the probability that the results at each point on the curve plotted with squares could have been obtained by chance. The two minima of the probability curve are indicated by the black and gray lines.
Enrichment for Predictions in Amyloidogenic Segments of Proteins.
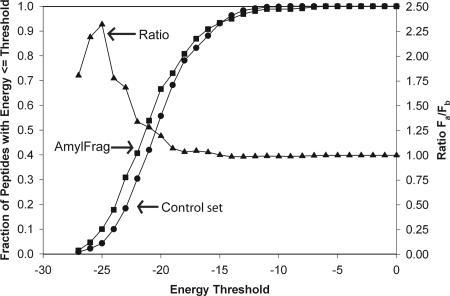
One would expect that an accurate method for identifying fibril-forming segments of proteins would make more positive predictions in the set of experimentally determined, fibril-forming segments of amyloid proteins (our AmylFrag data set; see Methods), than in a control set of sequences not known to form fibrils. We took this challenge of predicting fibril-forming segments from amyloid-forming proteins as a second quantitative test of our approach, and the results are displayed in Fig. 3. First, for a given energy threshold for declaring a hexamer as a fibril-forming positive hit we computed the fraction of positive hits in the AmylFrag data set. Each unique hexameric peptide was counted only once in the event that it occurred in more than one fragment found in AmylFrag. To represent a control set (or background) of predictions, we computed the fraction of positive hits in a set of full-length proteins (lysozyme, myoglobin, ribonuclease, tau, calcitonin, β2-microglobulin, and amylin), excluding those peptides that occurred in AmylFrag or AmylHex. There were a total of 359 unique peptides in AmylFrag and 648 unique peptides in the control set.
Fig. 3.
Enrichment of fibril-forming sequences predicted in the AmylFrag database of sequences compared with a reference set of sequences. The curves plotted with squares and circles show the fractions of predictions with energies below the threshold energy on the x axis obtained for the AmylFrag and control sets of peptides, respectively. The triangle curve (read off the right y axis) gives the ratio of these two fractions, Fa for AmylFrag and Fb for background, as a measure of enrichment. Energy thresholds <−19.5 do not provide enrichment, whereas an energy threshold of −25.5 provides substantial enrichment.
Results are shown in Fig. 3; the circles and squares give, respectively, the fractions of peptides with energies less than or equal to the thresholds for the background and AmylFrag sets of peptides. Notice that the AmylFrag curve is shifted to lower threshold energies than the control (background) curve. The significance of this shift is evident when the ratio of the fraction of AmylFrag peptides to the fraction of background peptides is plotted as the curve with triangles in Fig. 3. We see that for most of the range of energy thresholds, the ratio of the two curves is one; that is, the predictions appear random. Below the permissive energy threshold of −19.0 kcal/mol, we see a rise in the ratio, indicating enrichment of predictions in the AmylFrag set at lower energies. The curve peaks around our conservative threshold of −25.5 kcal/mol with an enrichment factor of >2-fold. That is, peptides found to match a template with energy less than the conservative threshold are twice as likely to be fibril formers as are random peptides.
Examples.
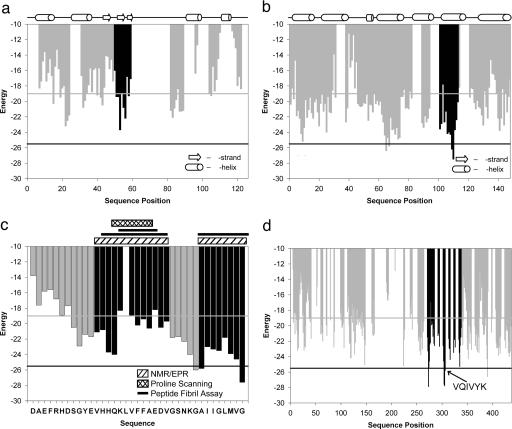
Having quantified the predictive utility of our approach, we now examine specific examples of known amyloid proteins in more detail. The bar graphs of Fig. 4 depict the lowest energy matches (on the ensemble of templates) for each six-residue peptide in each protein. The energy is plotted at the position of the initial residue of each peptide. The potential disulfide bond of cysteine might present problems in a cross-β spine, and proline residues are penalized heavily at all positions except the first because of their inability to donate a backbone H bond. Thus, to avoid energy calculations likely to yield ambiguous results in the following examples, we ignored all peptides containing cysteine or proline residues. This accounts for some residue positions where an energy bar is missing in Fig. 4. Where the structure of the protein is known, the sequence positions of β-strand and α-helical secondary structure elements are shown in Fig. 4.
Fig. 4.
Application of the 3D profile method with rosettadesign energy for detecting fibril-forming segments of proteins known to form fibrils. (a) Lysozyme. The vertical bars represent the lowest energy template matches for each hexapeptide, with the black bars indicating a known fibril-forming segment of the protein (21). Notice that the hexamer predicted to have the lowest energy is within the known fibril-forming segment. Gray and black horizontal lines indicate the permissive and conservative thresholds, respectively, taken from Fig. 1. (b) Myoglobin. The gray vertical bars represent the lowest energy template matches for segments of the protein where there are no experimental data. The black bars indicate the segment of the protein that forms fibrils in isolation (23), and these include the segments with the lowest energies. Gray and black horizontal lines indicate the permissive and conservative thresholds, respectively. (c) Abeta(1–42). The vertical bars represent the lowest energy template matches for each hexapeptide with those colored gray representing residue positions for which there is no experimental data. Black and gray horizontal lines indicate the permissive and conservative thresholds, respectively. Black vertical bars indicate those segments of the peptide for which there is experimental evidence of fibril formation or ordered β-structure. The experimental evidence for fibril formation of various segments is shown above the plot with the hatched boxes representing NMR/EPR (6, 27, 28), the cross-hatched box representing proline-scanning mutagenesis (29), and the solid lines representing positive fibrillization assays (26, 30). Notice that the lowest energy segment is the C-terminal segment known to be important for fibril formation. (d) Tau. The vertical bars represent the lowest energy predictions for each hexapeptide. Gray bars represent positions where there is no experimental data. Black bars indicate the segment of the protein (PHF43) implicated in aggregation, including the position of the known amyloidogenic peptide VQIVYK (4). Notice that this segment is one of the lowest energy segments. Gray and black horizontal lines indicate the permissive and conservative thresholds, respectively.
Lysozyme.
Lysozyme is the amyloid-forming protein in patients with non-neuropathic systemic amyloidosis (20). Fig. 4a shows a scan of the lysozyme sequence by our 3D profile method evaluated with rosettadesign, where we see relatively few predictions passing even the permissive threshold. The black bars correspond to a segment of the protein experimentally identified as fibril-forming (21). The strongest predictions are localized to this segment, including the peptide IFQINS where the initial isoleucine, if mutated to threonine, is known to enhance the fibrillization of this protein (20). Additionally, this peptide is located in spatial proximity to the active site in the 3D structure of the protein (22). It is known that enzymatic activity is lost upon fibrillization. Thus, our predictions agree with what is currently known about the fibrillization of lysozyme. Notice, also, that the lower energy matches occur in various types of secondary structure, indicating the method is not merely identifying β-strands as putative fibril-forming segments of the protein.
Myoglobin.
Muscle myoglobin is not associated with an amyloid pathology, but it can be induced to form amyloid-like fibrils (3). In Fig. 4b, the black bars correspond to an experimentally verified fibril-forming segment (23). Nearly all of the six-residue peptides in this segment score well, with a couple of them surpassing the conservative threshold. Thus our method identifies experimentally established fibril-forming segments of a protein with precision. As the myoglobin structure is predominantly helical, the ability of the method to identify fibril-forming segments in helical proteins is borne out in this example.
Abeta(1–42).
Abeta(1–42) is the primary component of the extracellular fibrillar aggregates of protein found in the brains of patients with Alzheimer’s disease (24). A scan of this peptide is shown in Fig. 4c. The black bars are those segments of the peptide that have been found to be important in fibril formation or the formation of β structure either by proline scanning mutagenesis, solid-state NMR, site-directed spin labeling, or fibril assays of smaller peptides in those segments (6, 25–29). The lowest energy matches are found in the C terminus of this 42-residue peptide with the best-scoring predicting at the C-terminal six residues (GGVVIA). This finding is consistent with kinetic data showing that the 42-residue peptide fibrillizes faster than the truncated Abeta(1–40) (30).
Tau.
The microtubule-associated tau protein localizes to the neurofibrillary tangles of Alzheimer’s disease (31). A scan of the tau protein is shown in Fig. 4d where light gray bars are predictions for which we do not have experimental data. The black bars correspond to a segment of the protein (PHF43) implicated in the aggregation of tau (4). There are several predictions in this segment below the conservative energy threshold. One of these peptides, VQIVYK (indicated by the black bar), is known to form fibrils (4). In this example, our approach was able to identify a known fibril-forming segment of a large protein with precision.
Discussion
Our structure-based, computational approach to identifying fibril-forming segments of proteins is based on two experimental findings. The first is that short peptides of four to seven residues can themselves form amyloid-like fibrils (4–14). Therefore the capacity for self-complementation of proteins that leads to fibrilization of the amyloid type must somehow be encoded in even short sequences. The second finding is the atomic structure (11) of NNQQNY, which reveals one pattern of interpeptide bonding in which the cross-β spine of amyloid-like fibrils can be realized.
By using a 3D profile consisting of an ensemble of templates derived from the structure of NNQQNY by small perturbations, we have been able to identify other hexapeptide segments that fit well into the template, as judged by the rosettadesign energy function. This function includes contributions from apolar interactions, hydrogen bonds, and steric overlaps. Because it includes these various contributions, it can accept sequences that form fibrils, but would not be selected on the basis of simple properties, such as hydrophobicity or β-strand propensity. In fact, segments that form fibrils, such as NNQQNY, are recognized by our template method, but are not by simple residue properties. Also fibril-forming segments are found in α-helical and coil segments of native proteins, as well as in β-sheets, as is evident in Fig. 4. In short, our template method is capable of detecting amyloid-forming segments that property-based methods may miss.
The present approach shows promise in discriminating between segments of proteins that form fibrils and those that do not. Its performance is easily quantified and is based on nonarbitrary thresholds using P value calculations. The utility of the method is demonstrated by its enrichment of hits in the set of fibril-forming fragments of amyloid proteins over those in a control set of background proteins. Moreover, the positive predictions made for the full-length proteins in the examples tend to localize with precision to experimentally established fibril-forming segments and are not restricted to β secondary structure.
The 3D profile algorithm will improve as more template structures become known. In the case of the tau protein and myoglobin, we saw that the template method was able to localize predictions to experimentally determined fibril-forming segments. A likely interpretation of our positive predictions is that these segments form cross-β cores that share certain features with the structure of the NNQQNY peptide such as two parallel β-sheets with like-faces packed tightly together. The structures of other fibril-forming peptides will soon be available, and their addition to our ensemble of templates will likely improve the prediction performance of our template approach. For instance, if the core structure of some of the fibrils was composed of antiparallel β-sheets, we would likely miss them with our current ensemble of parallel β-sheet templates. With additional templates and analysis of individual predictions, we can also consider adjusting the energy function to cater to the problem of fibril prediction.
Methods
Data Sets.
A data set of six-residue peptides including positive and negative examples of fibril formation was compiled from the literature. From the point mutations of the peptide STVIIE, we gleaned 56 true positives and 38 true negatives after peptides with chemically protected termini were excluded (13, 14). From the Islet amyloid protein (amylin) and the cytoskeletal tau protein we obtained three true positives and two true negatives (4, 5, 32). An additional 51 true negatives and 8 true positives were obtained from 59 hexameric peptides from insulin and β2-microglobulin (33). Thus in total we have a set of 158 peptides of which 67 have been shown to form fibrils and 91 have yielded negative results in fibril-forming assays. We term this data set AmylHex and use it to quantify the performance of our method. This data set is listed in Table 1, which is published as supporting information on the PNAS web site.
From the literature, we also compiled a set of 45 amyloidogenic fragments of proteins identified by various researchers, although roughly half of these are slight variants of one another or overlap substantially (e.g., NFGAIL and AFGAILSS). The lengths of these fragments vary considerably and peptides with lengths <6 residues were excluded. We term this data set AmylFrag, and it is found in Table 2, which is published as supporting information on the PNAS web site.
Near-Native Template Ensemble.
Using the structure of the NNQQNY peptide, we created a profile or ensemble of 2,511 near-native templates. Each template comprises two β-sheets, one with three strands and one with four strands. We consider the three-stranded sheet to be fixed in space, whereas the four-stranded sheet is shifted translationally with respect to the fixed sheet. In this way, the central strand of the three-stranded sheet, to be used for energy scoring, is always buried, and its environment is completely defined. The distance between β-sheets varies from 5 to 11.5 Å in 0.25-Å increments, the shift along the strand axis covers 7.5 Å in 0.25-Å steps, and the shift along the fibril axis spans 2.4 Å at 1.2-Å increments (Fig. 1, where the three double-headed arrows indicate translations along one of the fiber axes). The templates retain the basic topology of two parallel β-sheets oriented antiparallel to one another with the interface formed by the like-sides of each sheet.
Scoring.
Each six-residue peptide is threaded onto each of the near-native templates, and the energetic fit is evaluated by using the rosettadesign program. The fibril is treated as an infinite periodic system, by computing energy terms using a peptide chain in the center of the template, and then applying these energies to symmetric positions in each of the other chains.
The terms used in the energy function are the Lennard-Jones potential, an orientation-dependent hydrogen-bonding potential, an amino acid-dependent backbone and side-chain torsional potential, a solvation energy based on the generalized Born model (34), and amino acid-specific reference energies representing averaged interactions in the unfolded state. Each of the terms has an associated weight (19). The rosettadesign program is freely available for academic use (www.rosettacommons.org).
Supplementary Material
Acknowledgments
We thank Shilpa Sambashivan and Michael Sawaya for discussions and Duilio Cascio, Alex Lisker, and Tom Holton for computational assistance. This work was supported by the National Science Foundation, the National Institutes of Health, and the Howard Hughes Medical Institute. J.K. was supported by the Damon Runyon Cancer Research Foundation, and S.A.S. was supported by a University of California, Los Angeles, Integrative Graduate Education and Research Traineeship.
Abbreviation
- Abeta
β-amyloid.
Footnotes
Conflict of interest statement: No conflicts declared.
References
- 1.Guijarro J. I., Sunde M., Jones J. A., Campbell I. D., Dobson C. M. Proc. Natl. Acad. Sci. USA. 1998;95:4224–4228. doi: 10.1073/pnas.95.8.4224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chiti F., Webster P., Taddei N., Clark A., Stefani M., Ramponi G., Dobson C. M. Proc. Natl. Acad. Sci. USA. 1999;96:3590–3594. doi: 10.1073/pnas.96.7.3590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fandrich M., Fletcher M. A., Dobson C. M. Nature. 2001;410:165–166. doi: 10.1038/35065514. [DOI] [PubMed] [Google Scholar]
- 4.von Bergen M., Friedhoff P., Biernat J., Heberle J., Mandelkow E. M., Mandelkow E. Proc. Natl. Acad. Sci. USA. 2000;97:5129–5134. doi: 10.1073/pnas.97.10.5129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tenidis K., Waldner M., Bernhagen J., Fischle W., Bergmann M., Weber M., Merkle M. L., Voelter W., Brunner H., Kapurniotu A. J. Mol. Biol. 2000;295:1055–1071. doi: 10.1006/jmbi.1999.3422. [DOI] [PubMed] [Google Scholar]
- 6.Balbach J. J., Ishii Y., Antzutkin O. N., Leapman R. D., Rizzo N. W., Dyda F., Reed J., Tycko R. Biochemistry. 2000;39:13748–13759. doi: 10.1021/bi0011330. [DOI] [PubMed] [Google Scholar]
- 7.Azriel R., Gazit E. J. Biol. Chem. 2001;276:34156–34161. doi: 10.1074/jbc.M102883200. [DOI] [PubMed] [Google Scholar]
- 8.Balbirnie M., Grothe R., Eisenberg D. S. Proc. Natl. Acad. Sci. USA. 2001;98:2375–2380. doi: 10.1073/pnas.041617698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Reches M., Porat Y., Gazit E. J. Biol. Chem. 2002;277:35475–35480. doi: 10.1074/jbc.M206039200. [DOI] [PubMed] [Google Scholar]
- 10.Ivanova M. I., Sawaya M. R., Gingery M., Attinger A., Eisenberg D. Proc. Natl. Acad. Sci. USA. 2004;101:10584–10589. doi: 10.1073/pnas.0403756101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nelson R., Sawaya M. R., Balbirnie M., Madsen A. O., Riekel C., Grothe R., Eisenberg D. Nature. 2005;435:773–778. doi: 10.1038/nature03680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Orpiszewski J., Benson M. D. J. Mol. Biol. 1999;289:413–428. doi: 10.1006/jmbi.1999.2768. [DOI] [PubMed] [Google Scholar]
- 13.Lopez De La Paz M., Goldie K., Zurdo J., Lacroix E., Dobson C. M., Hoenger A., Serrano L. Proc. Natl. Acad. Sci. USA. 2002;99:16052–16057. doi: 10.1073/pnas.252340199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lopez de la Paz M., Serrano L. Proc. Natl. Acad. Sci. USA. 2004;101:87–92. doi: 10.1073/pnas.2634884100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pawar A. P., Dubay K. F., Zurdo J., Chiti F., Vendruscolo M., Dobson C. M. J. Mol. Biol. 2005;350:379–392. doi: 10.1016/j.jmb.2005.04.016. [DOI] [PubMed] [Google Scholar]
- 16.Yoon S., Welsh W. J. Protein Sci. 2004;13:2149–2160. doi: 10.1110/ps.04790604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yoon S., Welsh W. J. Proteins. 2005;60:110–117. doi: 10.1002/prot.20477. [DOI] [PubMed] [Google Scholar]
- 18.Bowie J. U., Luthy R., Eisenberg D. Science. 1991;253:164–170. doi: 10.1126/science.1853201. [DOI] [PubMed] [Google Scholar]
- 19.Kuhlman B., Baker D. Proc. Natl. Acad. Sci. USA. 2000;97:10383–10388. doi: 10.1073/pnas.97.19.10383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pepys M. B., Hawkins P. N., Booth D. R., Vigushin D. M., Tennent G. A., Soutar A. K., Totty N., Nguyen O., Blake C. C., Terry C. J., et al. Nature. 1993;362:553–557. doi: 10.1038/362553a0. [DOI] [PubMed] [Google Scholar]
- 21.Krebs M. R., Wilkins D. K., Chung E. W., Pitkeathly M. C., Chamberlain A. K., Zurdo J., Robinson C. V., Dobson C. M. J. Mol. Biol. 2000;300:541–549. doi: 10.1006/jmbi.2000.3862. [DOI] [PubMed] [Google Scholar]
- 22.Muraki M., Harata K., Jigami Y. Biochemistry. 1992;31:9212–9219. doi: 10.1021/bi00153a014. [DOI] [PubMed] [Google Scholar]
- 23.Fandrich M., Forge V., Buder K., Kittler M., Dobson C. M., Diekmann S. Proc. Natl. Acad. Sci. USA. 2003;100:15463–15468. doi: 10.1073/pnas.0303758100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sipe J. D. Annu. Rev. Biochem. 1992;61:947–975. doi: 10.1146/annurev.bi.61.070192.004503. [DOI] [PubMed] [Google Scholar]
- 25.Lansbury P. T., Jr., Costa P. R., Griffiths J. M., Simon E. J., Auger M., Halverson K. J., Kocisko D. A., Hendsch Z. S., Ashburn T. T., Spencer R. G., et al. Nat. Struct. Biol. 1995;2:990–998. doi: 10.1038/nsb1195-990. [DOI] [PubMed] [Google Scholar]
- 26.Tjernberg L. O., Callaway D. J., Tjernberg A., Hahne S., Lilliehook C., Terenius L., Thyberg J., Nordstedt C. J. Biol. Chem. 1999;274:12619–12625. doi: 10.1074/jbc.274.18.12619. [DOI] [PubMed] [Google Scholar]
- 27.Petkova A. T., Ishii Y., Balbach J. J., Antzutkin O. N., Leapman R. D., Delaglio F., Tycko R. Proc. Natl. Acad. Sci. USA. 2002;99:16742–16747. doi: 10.1073/pnas.262663499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Torok M., Milton S., Kayed R., Wu P., McIntire T., Glabe C. G., Langen R. J. Biol. Chem. 2002;277:40810–40815. doi: 10.1074/jbc.M205659200. [DOI] [PubMed] [Google Scholar]
- 29.Williams A. D., Portelius E., Kheterpal I., Guo J. T., Cook K. D., Xu Y., Wetzel R. J. Mol. Biol. 2004;335:833–842. doi: 10.1016/j.jmb.2003.11.008. [DOI] [PubMed] [Google Scholar]
- 30.Jarrett J. T., Berger E. P., Lansbury P. T., Jr. Biochemistry. 1993;32:4693–4697. doi: 10.1021/bi00069a001. [DOI] [PubMed] [Google Scholar]
- 31.Goedert M., Spillantini M. G., Jakes R., Rutherford D., Crowther R. A. Neuron. 1989;3:519–526. doi: 10.1016/0896-6273(89)90210-9. [DOI] [PubMed] [Google Scholar]
- 32.Mazor Y., Gilead S., Benhar I., Gazit E. J. Mol. Biol. 2002;322:1013–1024. doi: 10.1016/s0022-2836(02)00887-2. [DOI] [PubMed] [Google Scholar]
- 33.Ivanova M. I., Thompson M. J., Eisenberg D. Proc. Natl. Acad. Sci. USA. 2006;103:4079–4082. doi: 10.1073/pnas.0511298103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schaefer M., Bartels C., Leclerc F., Karplus M. J. Comput. Chem. 2001;22:1857–1879. doi: 10.1002/jcc.1137. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.