The molecular elasticity of the insect flight muscle proteins projectin and kettin

Abstract

Projectin and kettin are titin-like proteins mainly responsible for the high passive stiffness of insect indirect flight muscles, which is needed to generate oscillatory work during flight. Here we report the mechanical properties of kettin and projectin by single-molecule force spectroscopy. Force–extension and force-clamp curves obtained from Lethocerus projectin and Drosophila recombinant projectin or kettin fragments revealed that fibronectin type III domains in projectin are mechanically weaker (unfolding force, F_u ≈ 50–150 pN) than Ig-domains (F_u ≈ 150–250 pN). Among Ig domains in Sls/kettin, the domains near the N terminus are less stable than those near the C terminus. Projectin domains refolded very fast [85% at 15 s⁻¹ (25°C)] and even under high forces (15–30 pN). Temperature affected the unfolding forces with a Q₁₀ of 1.3, whereas the refolding speed had a Q₁₀ of 2–3, probably reflecting the cooperative nature of the folding mechanism. High bending rigidities of projectin and kettin indicated that straightening the proteins requires low forces. Our results suggest that titin-like proteins in indirect flight muscles could function according to a folding-based-spring mechanism.

The success of insects as a major animal group may be attributed in part to the evolution of asynchronous flight muscles (1). In asynchronous muscles there is asynchrony between muscle electrical and mechanical activity in that a single muscle action potential can trigger a series of contraction–relaxation cycles. In the indirect flight muscle (IFM), these oscillatory contractions are produced by delayed activation in response to stretch combined with the resonant properties of the thorax (2). For example, some insect flight muscles can operate at very high frequencies (100–1,000 Hz) (1). This rapid oscillatory contraction requires that the sarcomeres are stiff. This stiffness coupled with a stretch activation response allows insects' wings to beat hundreds of times per second. The molecular basis for this mechanism is not well understood but many proteins are emerging as contributing factors. Projectin and kettin form a mechanical link between the Z-discs and the ends of the thick filaments and are responsible for a large part of the passive elasticity of insect muscles (3–5) and may be responsible for the high relaxed stiffness as a prerequisite for the stretch activation response (6).

Projectin and kettin are high-molecular-weight members of the titin protein superfamily (7) and are found in invertebrate muscles. Kettin is in the I-band, and projectin is in the A-band, except in IFM, in which a large part of the molecule is in the short I-band. Projectin is an 800- to 1,000-kDa protein consisting of long sections of repeated Ig and fibronectin type III (FnIII) domains. There is also a kinase domain near the C terminus and a region rich in proline, glutamate, valine, and lysine (PEVK) near the N terminus. Immunofluorescence data indicate that, in the IFM, projectin molecules are anchored at the Z-disk, extend over the I-band region, and associate with myosin at the A-band edge (8, 9). Mutant forms of projectin have been shown to alter insect flight dynamics (10). Kettin is an alternatively spliced product of the Drosophila sls gene. In contrast to projectin, kettin is an ≈540-kDa protein and is made up of 35 repeating Ig domains. In the IFM, the molecule is anchored to the Z-disk, extends over the I-band running along the actin filament, and then attaches to the thick filaments (11, 12). Kettin may have an essential function for sarcomere formation because adult fruit flies heterozygous for a kettin mutation cannot fly (13). Experiments using laser tweezers suggest that kettin may have roles consistent with a provider of passive tension based on entropic elasticity and folding of Ig domains (14).

The structure and location of projectin and kettin suggest that they may have regions that are exposed to mechanical forces and hence contribute to the passive stiffness of the IFM sarcomere. Here we used single-molecule atomic force microscopy (AFM) techniques (15–17) to examine the molecular elasticity of single projectin and kettin molecules. The results show that projectin and kettin Ig/FnIII domains refold much faster than titin domains, even under appreciable forces, which hints at the potential for a previously uncharacterized folding-based spring mechanism.

Results

The Flexibility of Projectin and Kettin Molecules Measured by EM Techniques.

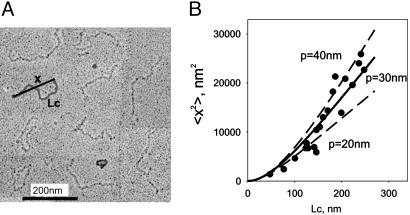
Projectin and kettin molecules are thought to function as elastic filaments in IFM fibers (18). This elasticity may result from the flexibility of their tandemly arranged domains, the stretching of the PEVK region and also from the unfolding and refolding of individual Ig and FnIII domains (19). We estimated the flexibility of intact projectin molecules by using rotary shadow EM techniques (5). EM images of Lethocerus projectin molecules show worm-like structures that appear to be flexible throughout their length (Fig. 1A). We found that the contour length, L_c (gray line in Fig. 1A), varied between ≈50 and ≈250 nm. The upper limit value is similar to the predicted length of a protein with 78 Ig and FnIII domains [ref. 20; assuming 4 nm per domain (21)]. The shorter molecules are degradation products and are useful here because they facilitate the estimation of the persistence length. According to models of polymer elasticity (22), the expected value of the end-to-end length, x, is related to the contour length of the polymer chain, L_c, and the flexibility of the polymer, measured by its persistence length, p:

Fig. 1.

Flexibility of single projectin molecules. (A) Rotary-shadowed EM showing individual projectin proteins (micrograph courtesy of Kevin Leonard, European Molecular Biology Laboratory, Heidelberg, Germany). The gray line shows the measured contour length, L_c, and the black line shows the measured end-to-end distance, x. (B) Plot of the square of the average x as a function of the contour length (filled circles) (data obtained from 20 molecules). The solid line is a nonlinear fit of Eq. 1, giving a value of P=30 nm. The dashed lines correspond to fits of P=20 and 40 nm.

From these images we extracted the persistence length value by plotting x (black line in Fig. 1A) vs. L_c. The lines in Fig. 1B correspond to the prediction of Eq. 1 at three different values of p: 20, 30, and 40 nm. We found that a value of p=30 nm best describes the experimental data. Similar analysis done for kettin molecules revealed a p=45 nm (data not shown). The higher p value observed for kettin suggests that the Ig domain chains are less flexible than the Ig/FnIII domain chains in projectin. These values are higher than those for native skeletal titin and recombinant titin molecules estimated by EM (p=13 and 9.8 nm, respectively; refs. 23 and 24) but similar to those measured for titin by using immunofluorescence microscopy and myofibril mechanics (p=20–40 nm; ref. 25). Structural and modeling techniques have shown that titin predicted to have an extended and relatively stiff conformation (26–28). The high p values in projectin and kettin suggest that at least 6–8 domains must be directionally correlated in these molecules; this long-range order resulted in a relatively high stiffness. Thus, straightening of projectin or kettin Ig/FnIII domain chains during sarcomere extension would require little force.

Force–Extension Relationships of Projectin Molecules.

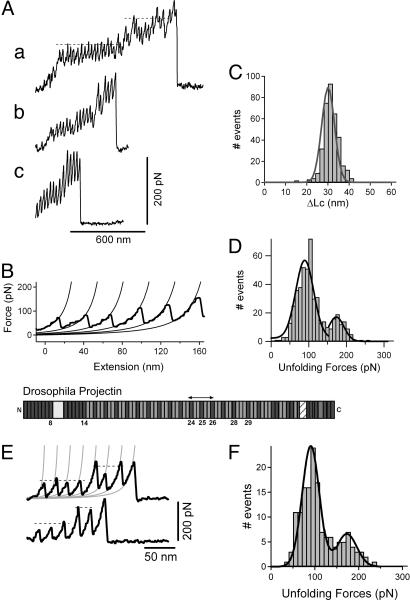
To measure the elastic properties of projectin, we used single-molecule AFM techniques. Random segments of projectin were picked up by the AFM tip and then stretched with a pulling speed of ≈0.5 nm/ms. The resulting force–extension curves (Fig. 2A and B) showed sawtooth patterns that are characteristic of the unfolding of FnIII and Ig domains (15–17, 29). One striking feature of these sawtooth patterns is the presence of distinct levels of unfolding forces (dotted lines in Fig. 2A, curve a). Fig. 2D shows a histogram of unfolding forces measured for 36 projectin molecules. There are two prominent peaks, one centered at ≈90 pN and a second at ≈170 pN (n=478 force peaks). Most of the projectin protein is arranged in a repeating pattern of Ig–FnIII–FnIII domains (Fig. 2). One simple explanation is that FnIII and Ig domains have a different mechanical stability that would account for the two levels of unfolding forces observed in the sawtooth patterns.

Fig. 2.

Force–extension relationships of projectin molecules. (A) Several examples of force–extension curves obtained after stretching single projectin molecules. (B) To analyze the spacing between peaks in the sawtooth patterns we used the wormlike chain model. The lines were generated by using P=0.4 nm and ΔL_c=29 nm. (C) Histogram of contour length increments observed upon unfolding, ΔL_c (Gaussian fit: 30.1 ± 4.3 nm, n=362). (D) Histogram of force peaks shows two main peaks (Gaussian fits: 89.1 pN and 172.3 pN; mean force peak value: 109.4 ± 41 pN, n=479). (E) (Lower) Mechanical properties of a projectin recombinant fragment containing three Ig and four FnIII domains (PIg24–PIg26). (Upper) Domain structure of Drosophila projectin. (F) Histogram of unfolding forces for PIg24–PIg26 shows two peaks, one at ≈83 pN and the other at ≈171pN (n=142).

We tested this hypothesis by analyzing the mechanical properties of a recombinant protein containing a small number of Ig and FnIII domains. Fig. 2E shows force–extension curves for a recombinant protein with three Ig and four FnIII domains (Ig24–FnIII–FnIII–Ig25–FnIII–FnIII–Ig26; Fig. 2E, upper curve). Stretching this protein resulted in force–extension curves (Fig. 2E) with equally spaced force peaks but with two distinct levels of unfolding forces, one at ≈80 pN and the second at ≈170 pN (Fig. 2F). We attribute the low force peaks to the unfolding of FnIII domains and the high force peaks to the unfolding of the Ig domains. Hence, these data show that in the PIg24–PIg26 protein, the FnIII and Ig domains are unfolding in a hierarchical pattern in which the mechanically weaker FnIII domains unfold before the Ig domains.

Force–Extension Relationships of Kettin and Upstream Sls Ig Domains.

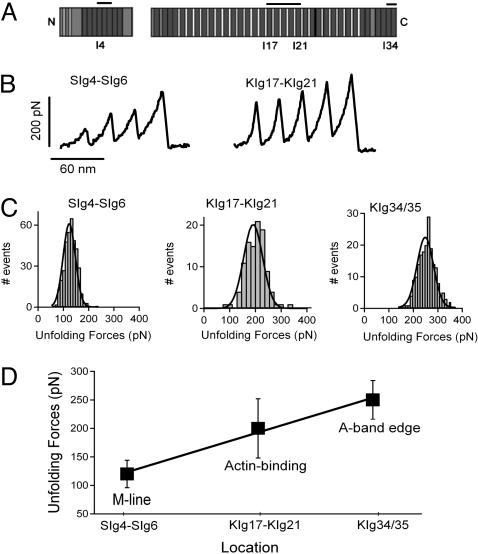
We analyzed the force–extension spectra of three different recombinant kettin proteins (Fig. 3A): (i) a three-Ig-domain fragment, SIg4–SIg6, from the eight-Ig segment in the N-terminal region of Sls upstream of kettin (these are part of a splice isoform that is in the M-line in IFM, rather than the I-band), (ii) a five-Ig-domain fragment from the actin binding region of kettin (KIg17–KIg21), and (iii) a two-Ig-domain fragment from the putatively elastic kettin region near the A-band edge (KIg34/35).

Fig. 3.

Force–extension relationships of recombinant kettin and N-terminal Sls fragments. (A) Location of the SIg4–SIg6, KIg17–KIg21, and KIg34/35 in the Sls/kettin sequence. The two blocks of sequence are spliced products of the Drosophila sls gene; the longer protein is kettin. (B) Examples of force–extension patterns obtained from the three-Ig (Left) and five-Ig (Right) fragment. (C) Histogram of unfolding forces for the proteins SIg4–SIg6, KIg17–KIg21, and KIg34/35 show that their mean unfolding forces are 123 ± 24 pN (n=371), 193 ± 52 pN (n=104), and 248 ± 34 pN (n=192), respectively. (D) Plot of the mean unfolding forces of SIg4–SIg6, KIg17–KIg21, and KIg34/35 proteins vs. their locations in the Sls and kettin sequence. Linear regression shows a slope of 4.4 pN per domain.

Fig. 3B shows examples of force–extension patterns obtained from the SIg4–SIg6 and KIg17–KIg21 fragments. There are clear differences in unfolding forces between these two proteins. The Ig domains in SIg4–SIg6 tend to unfold at lower forces (≈100 pN) than the Ig domains in KIg17–KIg21 (≈200 pN). In addition, in SIg4–SIg6, the first peak is of lower force than the last peak, suggesting that the three Ig domains have different mechanical stabilities. This rising force effect is less pronounced in KIg17–KIg21, for which all domains show similar unfolding forces.

Frequency histograms measured from SIg4–SIg6, KIg17–KIg21, and KIg34/35 show that the mean unfolding forces are 120 pN (123 ± 24 pN, n=371), 190 pN (193 ± 52 pN, n=104), and 250 pN (248 ± 34 pN, n=192), respectively (Fig. 3C). Fig. 3D shows an interesting mechanical hierarchy: Ig domains closer to the N terminus of Sls/kettin are mechanically less stable than those nearer the C terminus

Force-Clamp Unfolding of Kettin and Projectin.

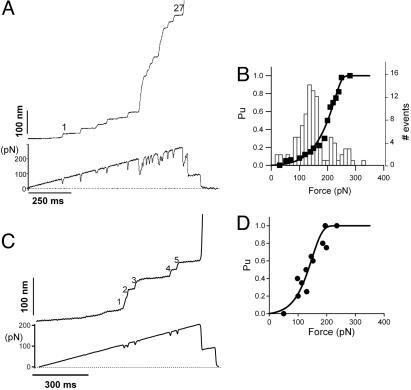
We also used the force-clamp mode of the AFM for stretching single kettin and projectin molecules (Fig. 4). The advantage of this mode is that it is possible to measure the force dependence of the unfolding probability of single protein domains (17, 30). In these experiments, we applied a force that increases linearly with time (Fig. 4 A, lower trace, and C, lower trace) and observe the unfolding of single domains as a stepwise elongation of the proteins (Fig. 4 A, upper trace, and C, upper trace).

Fig. 4.

Measurements of the force dependence of the unfolding probability of projectin and kettin molecules. (A and C) Stepwise unfolding of single native projectin and a five-Ig kettin (KIg17–KIg21) fragment using the force-ramp method. The lower trace shows the time course of the force. (B) Frequency histogram of unfolding forces (bars) and the unfolding probability, P_u (filled squares) as a function of the applied force measured for six projectin molecules with similar number of unfolding events (86 total steps). The pulling speed was 200 pN/s. The lines correspond to the prediction of Eq. 5 using α₀₁=7 × 10⁻² s⁻¹ and Δx_u1=0.1 nm and α₀₂=0.3 × 10⁻³ s⁻¹ and Δx_u2=0.2 nm (continuous line). (D) Plot of the unfolding probability, P_u, as a function of the applied force for the KIg17–KIg21 kettin fragment (filled circles, 19 steps from 4 experiments). The pulling speed was 150 pN/s. The line corresponds to the prediction of Eq. 4 using α₀=9 × 10⁻³ s⁻¹ and Δx=0.17 nm.

Fig. 4A shows the stepwise elongation (upper trace) of a single projectin molecule observed after increasing the force at a rate of 200 pN/s (lower trace; the downward transients are caused by the feedback lag and can be used as markers for the unfolding events). In this example, the protein first elongates slowly (we count five steps within the first 200 pN), and then there is rapid elongation of the protein during the next 70 pN (the large steps are due to the simultaneous unfolding of several domains). At ≈300 pN, the protein detached from the surface, which is seen as a sudden drop of the force due to the loss of the force-clamp. From these data, we can calculate the distribution function for the probability of unfolding, P_u, as a function of the applied force. Fig. 4B shows the frequency of unfolding events (bars) and the unfolding probability distribution, P_u (squares), as a function of the force. The probability of unfolding changes from P_u=0.1–0.9 over a wide range of forces (≈150 pN; from 90 to 240 pN). In contrast, stretching a five-Ig kettin fragment (KIg17–KIg21) with a force ramp (Fig. 4C) shows an unfolding probability that changes from P_u=0.1–0.9 over a smaller force range of ≈80 pN (90–170 pN; Fig. 4D, filled circles).

To analyze the data of Fig. 4 B and D quantitatively, we used a simple two-state kinetic model for mechanical unfolding (see Supporting Text and Figs. 7–10, which are published as supporting information on the PNAS web site) (17, 30). In this model, a protein is exposed to a force that increases linearly with time, simulating the conditions of our force-ramp experiment; the variables in the model are the rate constant at zero force (α₀) and the distance the transition state (Δx_u). For the kettin fragment, KIg17–KIg21, values of α₀=9 × 10⁻³ s⁻¹ and Δx_u=0.17 nm readily describe the data (Fig. 4D, solid line; see also Supporting Text, Eq. 4). For projectin, the P_u vs. force data were best described by using two sets of parameters: α₀₁=7 × 10⁻² s⁻¹ and Δx_u1=0.1 nm and α₀₂=0.3 × 10⁻³ s⁻¹ and Δx_u2=0.2 nm (Fig. 4B, solid line; see also Supporting Text, Eq. 5). The simplest interpretation is that, in the case of projectin, FnIII domains have a higher unfolding rate constant at zero force (α₀=7 × 10⁻² s⁻¹) than the Ig domains (α₀=0.3 × 10⁻³ s⁻¹), which would result in higher unfolding probability for FnIII domains at a given force than for the Ig domains. The kettin construct has only Ig domains, which are more stable.

Refolding of FnIII/Ig Projectin Domains.

To test whether projectin domains refold after mechanical unfolding, we repeatedly stretched and relaxed single proteins. We found that single projectin molecules could be subjected to hundreds of stretching/relaxation cycles for which the force–extension curves displayed similar patterns (Fig. 10), demonstrating that domain unfolding is fully reversible and that, unlike mammalian titin domains (31), projectin domains can undergo multiple cycles of extension/relaxation with no signs of molecular fatigue or rundown.

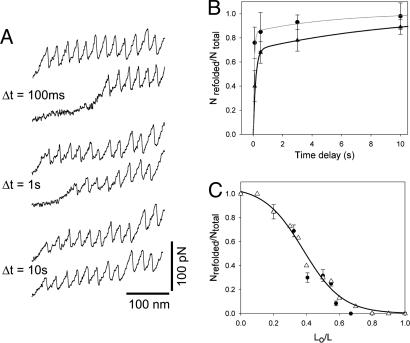
To measure the refolding kinetics, we used a double pulse protocol in which the pulse interval was varied (Fig. 5A). In addition, the temperature was varied between 25°C (room temperature) and 13°C in these experiments. We found that, at 25°C, the number of force peaks in the first and second stretching pulse was very similar, even at the shortest time interval between stretching pulses (≈100 ms), indicating that projectin domains refold in the millisecond time scale. To better resolve the refolding kinetics, we repeated these experiments at the lower temperature of 13°C (Fig. 5A). The top two traces of Fig. 5A correspond to the first and second stretching pulse, using a time delay of 100 ms. Only ≈50% of the domains were seen to refold. Increasing the time interval between stretching pulses allows a larger fraction of domains to refold, ≈70% (delay of 1 s) and 100% (delay of 10 s), respectively. We observed that the number of projectin domains refolded recovered with a double exponential time course (Fig. 5B, open triangles). Approximately 68% of the recovery (at 13°C) occurred at a fast rate (6 s⁻¹), whereas 32% occurred at a much slower rate (0.1 s⁻¹), indicative of two populations of domains refolding with very different rate constants. At 25°C, the fast rate increased by 2.5-fold to ≈15 s⁻¹ (Fig. 5B, filled circles).

Fig. 5.

Refolding kinetics of projectin domains. (A) The time interval between extensions affects the fraction of refolded domains (recorded at 13°C). (B) Fraction of refolded domains as a function of the time delay between stretching pulses, measured at 13°C (filled triangles) and 25°C (filled circles). The solid lines are a two-exponential fit of the data to the function N_refolded/N_total=A₁(1 − e^{−t·β 1}) + A₂(1 − e^{−Δt·β 2}), where A₁=0.7, A₂=0.3, β₁=6 s⁻¹, and β₂=0.1 s⁻¹ at 13°C, and A₁=0.85, A₂=0.15, β₁=15 s⁻¹, and β₂=0.18 s⁻¹ at 25°C. (C) Plot of the fraction of refolded domains, N_refolded/N_total, vs. the degree of relaxation, L₀/L_c, for two projectin molecules. The open triangles correspond to a Monte-Carlo simulation using an β₀=15 s⁻¹ and Δx_f=1.1 nm. The line is a polynomial fit to the Monte-Carlo simulation data.

The Refolding of Projectin Domains Depends on the Degree of Relaxation.

If a projectin segment was relaxed to only about one-half its length, the characteristic sawtooth pattern of the force–extension curve (on restretch) disappeared. Fig. 5C shows a plot of the fraction of refolded domains, N_refolded/N_total, vs. the degree of relaxation, L₀/L_c. We used a three-pulse protocol (32) to first completely unfold and extend the protein and obtain the contour length of the unfolded protein, L_c. Then the protein was rapidly relaxed to a length L₀ for a fixed period (10 s). A second extension measures the number of domains that refolded during the relaxation period at that particular length, L₀. The open triangles correspond to a Monte-Carlo simulation of a two-state kinetic model with a folding distance, Δx_f=1.1 nm. From this plot, we can estimate how the applied force affects the refolding rate (see Supporting Text). The plot shows that ≈20% of the domains can refold at L₀/Lc of 0.5, which corresponds to a force of ≈20 pN. Hence, from this analysis, we can conclude that projectin domains can refold under large stretching forces.

Collapse of Unfolded Projectin Domains Under Force.

To examine the effect of a mechanical force on domain refolding in more detail, we used force-clamp AFM techniques (17, 30, 33). In these experiments, we first unfolded and extended the protein at a high force and then relaxed the protein at lower forces. Figs. 6and 8 show several examples of native projectin molecules held at different force values.

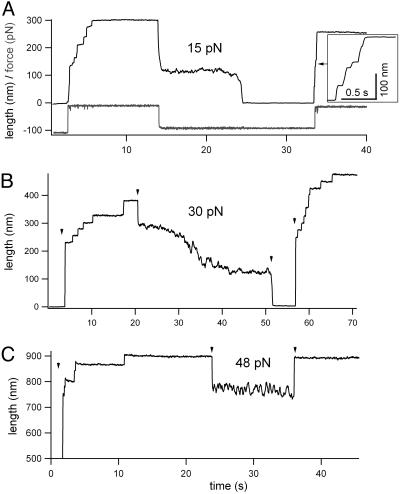
Fig. 6.

Collapse of unfolded projectin domains under force. (A) Example of a projectin molecule that was first unfolded and extended at a high force (97 pN; the applied force is shown in the lower trace), then relaxed to a force of 15 pN and extended again at a force of 97 pN. (B) Example of a projectin molecule that was first unfolded and extended at 124 pN then relaxed to 30 pN and then to ≈5 pN (marked by arrowheads). After ≈5 s, the force was increased to 150 pN. (C) A projectin molecule was extended at a force of 115 pN then relaxed to 48 pN and, after 12 s, extended again at a force of 100 pN.

In Fig. 6A, a projectin molecule was first unfolded and extended at a high force (97 pN). We observed 10 unfolding events. There was an initial large step elongation of ≈100 nm upon application of force. (This initial phase most likely corresponds to the length of the folded polypeptide chain plus a few already unfolded domains.) Then after ≈12 sec, the protein was relaxed to a force of 15 pN; before the protein reached its fully collapsed state, there was a dramatic increase in the noise level with length fluctuations of up to 10 nm peak-to-peak. The source of this noise is not clear, but the phenomenon may reflect the transient formation of secondary structures or intermediate folded conformations, as suggested for ubiquitin domains (33). Similar to ubiquitin refolding trajectories, we also find three main phases: (i) a fast phase (<200 ms) corresponding to the elastic recoil of the unfolded polypeptide chain and accounting for ≈60% of the unfolded length of the protein, (ii) a slow phase (≈1–8 nm/s) characterized by large fluctuations in end-to-end length (up to 10 nm in this example), and (iii) again a fast phase (>100 nm/s) that corresponds to the final collapse of the polypeptide chain to its folded length. To test whether the domains are folded, we unfolded the protein by applying a second stretching pulse to 97 pN after 30 s (we count nine steps). Hence, this experiment clearly shows that projectin domains refolded at a force of 15 pN.

Fig. 6B shows another example. In this experiment, the protein was first unfolded and extended at 124 pN. There was an initial large-step elongation of ≈200 nm upon application of force, which was followed by eight unfolding steps. Then the force was dropped to 30 pN; the polypeptide chain is seen to quickly (≈200 nm/s) recoil and then slowly contract. To minimize the effect of drift, after ≈30 s we dropped the force to ≈5 pN (marked by the arrow). We then increased the force to 150 pN and counted a total of 12 steps, indicating that domains refolded at the low force of 5 pN.

Fig. 6C shows that during the initial stages of the slow phase, the domains do not fold. We first unfolded and extended the molecule at a high force of 115 pN (many steps are detected), then the protein was relaxed to a force of 48 pN and, after 12 s, the polypeptide was extended again at a force of 100 pN. There are no detectable steps during this transition from low to high force, indicating the absence of folded domains.

Discussion

Here, we examined the mechanical properties of kettin and projectin and their individual domains by using single-molecule AFM. We found that kettin and projectin have different mechanical architectures, which are likely to be related to their different functions in the sarcomere.

Force–extension and force-clamp curves obtained from single projectin molecules revealed a complex elongation pattern, with some domains unfolding in a low force range (≈50–150 pN) and a second population unfolding at higher forces (≈150–250 pN). Similar experiments done on recombinant fragments revealed that the FnIII domains are mechanically weaker than the Ig domains. These differences seem to be well conserved, because studies on human titin also showed that FnIII domains unfold at lower forces than Ig domains (29). These differences in mechanical strengths may result from different mechanical topologies. Both types of domain consist of two antiparallel β-sheets packed against one another, and they have a similar Greek key strand topology (34). However, the domain types differ in the number of strands and the pattern of hydrogen bonds exposed to a mechanical force (35–37).

Two fragments of kettin and a fragment derived from a spliced isoform of Sls upstream of kettin displayed a strong mechanical unfolding hierarchy requiring 100 pN of force to unfold the weakest Ig domain and 250 pN for the most stable Ig domain. Interestingly, this mechanical hierarchy is correlated with the location of the Ig domains along the Sls and kettin sequence: Ig domains closer to the N terminus of Sls/kettin are mechanically less stable than those nearer the C terminus. Apparently, different regions of Sls/kettin in the sarcomere require different mechanical stabilities. The low unfolding force for SIg4–SIg6 is consistent with its position bound to myosin in the M-line in the center of the sarcomere. In contrast, the property of KIg17–KIg21 to bind to actin may require high stability. The KIg34/35 domains at the end of kettin may experience stretching forces because they are linked to the end of the thick filament (3) and therefore may require a very high stability.

Another interesting finding is that projectin domains refold very fast at room temperature: ≈85% of the domains refolded at a rate of 15 s⁻¹. This refolding rate is much faster than that of human cardiac titin Ig domains (≈1 s⁻¹) (15, 24, 32) or of native Lethocerus kettin Ig domains (≈0.1 s⁻¹) (14), but it is comparable with that recorded from tenascin FnIII domains (≈40 s⁻¹) (16). In addition, our data show that the refolding of projectin domains follows a double exponential time course (Fig. 5B). This time course may result from different refolding kinetics of FnIII and Ig domains. To test this idea, we included in our refolding analysis only the low force peaks (<100 pN) and found that they mainly contribute to the double exponential time course (see also Fig. 10). These data suggest at least two independent pathways for the refolding of FnIII domains with different rate constants.

The speed at which projectin domains recover from the unfolded state was found to depend on the temperature. Fig. 5 showed that the fast refolding rate is 2.5-fold slower at 13°C than at 25°C. These data, which to our knowledge represent the first measurement of the temperature dependence of the mechanical refolding rate of a single protein, indicates a Q₁₀ for the refolding rate of ≈2.5. In contrast, domain unfolding is affected much less by temperature.

The mean unfolding forces are 97.4 ± 36.7 pN at 14°C and 74.7 ± 38.9 pN at 26°C (see Supporting Text), which translates into a Q₁₀ for unfolding of 1.3. The low Q₁₀ for unfolding in this temperature range is slightly higher than the temperature dependence of the mechanical unfolding of spectrin repeats (Q₁₀ ≈ 1) (38) and bacteriorhodopsin helical regions (Q₁₀ ≈ 1.2) (39). These findings show that the temperature dependence of the forces driving mechanical refolding are higher than that for unfolding and probably reflect the cooperative nature of the folding mechanism.

Some insects have relatively high temperatures during flight (35–40°C) (1, 40); e.g., the temperature of the IFM in Lethocerus during flight is ≈40°C. At this temperature, projectin domains would refold at a rate of ≈40 s⁻¹ (estimated from our data considering a Q₁₀ of ≈2.5), a value that is almost 2-fold higher than the natural wing-beat frequency of Lethocerus indicus (≈25 Hz). In this estimate, we assumed that the domains are refolding at zero force. However, we found that the domains still refold at higher forces and that the refolding rate slows down with the force level (Figs. 5–6). At high forces, the refolding rate would be slower, following an exponential relationship with the force according to:

where β₀ is the rate at zero force, Δx_F is the folding distance, and kT=4.1 pN/nm. Using Δx_F=1.1 nm (Fig. 5C), we calculate that, at a physiological force of 5 pN (24), the refolding rate would be ≈11 s⁻¹ (at 40°C). Although we do not know the exact number of domains in the extensible part of projectin, it has been estimated to be ≈15 domains (18). If we assume that only a fraction of these domains unfold during a stretching event (e.g., five), we then calculate that during a single wing-beat, ≈50% of the domains would refold (probability of folding=number of unfolded domains·β(5 pN)·Δt). Hence, at low forces, projectin could function as a folding-based spring.

The observation that domains can refold under force is not a unique feature to projectin and kettin molecules but is a property found in titin (31), kettin (can refold at forces of up to 30 pN) (14), I27 polyproteins (can refold at forces of ≈15 pN; estimated from figure 5 in ref. 32), and ubiquitin (can refold at forces of up to 40 pN) (33). In addition, recent molecular dynamics simulations (41, 42) demonstrate that refolding can occur at high forces (≈40 pN).

In conclusion, our data show that projectin domains can refold sufficiently fast under relatively high forces at physiological temperatures, suggesting a robust refolding mechanism that may operate over a large range of sarcomere lengths. Given the structural and functional similarity of projectin and other proteins of the titin family, it is possible that this property may also be found in other titin-like proteins. This mechanism might be subjected to biochemical modulation through signaling pathways or molecular chaperones (43), providing a way of modulating muscle-passive elasticity. Whether this mechanism operates in vivo is an important question for future experiments.

Materials and Methods

Proteins.

Native projectin (800–1,000 kDa) was isolated from L. indicus leg muscle as described in ref. 12. Cloning and expression of Drosophila projectin and kettin fragments: Projectin sequences coding for PIg24–PIg26 (GenBank accession no. AF047475) and the kettin sequences coding for KIg17–KIg21 (GenBank accession no. AJ245406) were obtained by PCR with Drosophila genomic DNA. Plasmid construction, protein expression, and protein purification are described in detail in Supporting Text.

Rotary-Shadowed EM and AFM.

Projectin and kettin in 50% glycerol were sprayed onto freshly cleaved mica and rotary-shadowed at 7° with platinum and palladium and at 90° with carbon. Replicas were floated on distilled water and picked up on uncoated copper grids. Micrographs were taken at 100 kV and at ×40,000 magnification in a Philips EM 400. To study the mechanical properties of kettin and projectin, we used a home-built, single-molecule AFM as previously described (16–18; see Supporting Text).

Abbreviations

AFM

atomic force microscopy

FnIII

fibronectin type III

IFM

indirect flight muscle.