Modeling the role of bacteriophage in the control of cholera outbreaks

Abstract

Cholera is a waterborne diarrheal disease that continues to plague the developing world. Individuals become infected by consuming water from reservoirs contaminated by virulent strains of the bacterium Vibrio cholerae. Epidemiological and environmental observations of a cholera outbreak in Dhaka, Bangladesh, suggest that lytic bacteriophage specific for V. cholerae may limit the severity of cholera outbreaks by killing bacteria present in the reservoir and in infected individuals. To quantify this idea and generate testable hypotheses, we analyzed a mathematical model that combines the epidemiology of cholera with the population dynamics of the bacteria and phage. Under biologically reasonable conditions, we found that vibriophage can ameliorate cholera outbreaks. If phage predation limits bacterial density before an outbreak, a transient reduction in phage density can disrupt that limitation, and subsequent bacterial growth can initiate a cholera outbreak. The severity of the outbreak depends on the density of phage remaining in the reservoir. If the outbreak is initiated instead by a rise in bacterial density, the introduction of phage can reduce the severity of the outbreak and promote its decline. In both situations, the magnitude of the phage effect depends mainly on vibrio growth and phage mortality rates; the lower the rates, the greater the effect. Our analysis also suggests that either bacteria in the environmental reservoir are hyperinfectious or most victims ingest bacteria amplified in food or drinking water contaminated by environmental water carrying few viable V. cholerae. Our theoretical results make a number of empirically testable predictions.

Cholera, a waterborne gastroenteric infection, remains a significant threat to public health in the developing world. The disease in its severest form causes copious diarrhea lasting from 3 to 7 days. Death from dehydration is typical in the absence of treatment. Pathogenic serotypes of the bacterium Vibrio cholerae, expressing cholera toxin encoded by a lysogenic bacteriophage (1), are responsible for the majority of cases. V. cholerae and other members of this bacterial genus naturally colonize lakes, rivers, and estuaries (2, 3); local outbreaks are precipitated and prolonged by contamination of local water supplies in areas of poor sanitation. Disease transmission usually occurs through ingestion of contaminated water or feces rather than through casual human–human contact.

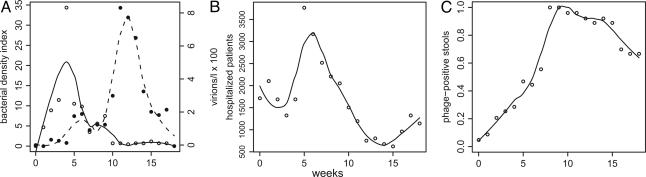
Outbreaks of cholera occur cyclically, usually twice per year in endemic areas, and the intensity of these outbreaks varies over longer periods. Extrinsic factors, such as large-scale weather cycles (e.g., the El Niño–Southern Oscillation), and intrinsic factors such as postinfection immune periods have been shown to correlate in time with components of the epidemic cycle (4–6). Recently, Faruque et al. (7) proposed that lytic bacteriophage predation on pathogenic vibrio may be an important extrinsic factor influencing the epidemic cycle on short time scales and may act to modify the duration and severity of cholera outbreaks. In support of this interpretation, they reported longitudinal observations of cholera cases and environmental vibrio and phage densities during a local cholera outbreak in Dhaka, Bangladesh (Fig. 1). These data included cholera incidence, concentrations of the responsible V. cholerae strain (streptomycin-resistant O1 serotype), and a strain-specific lytic phage (JSF4) in the stool of hospitalized patients and in nearby water bodies. Their study was unique, in that the outbreak could be attributed to a single V. cholerae clone, the density of which could be readily monitored in the environment by its resistance to streptomycin. Disease incidence (inferred from hospitalizations) and reservoir bacterial concentrations rose and fell together. The density of JSF4 phage in the reservoir and the patient also waxed and waned with the outbreak.

Fig. 1.

Epidemic and microorganism data from ref. 7. (A) Environmental bacterial density index and phage densities. (B) Numbers of hospitalized cholera patients. (C) Estimated proportion of phage-positive infected patients. Lines are less-smoothed fits (24) to the data, provided for visual convenience.

On the basis of these population dynamic observations, Faruque et al. (7) suggested that infections are caused by ingestion of vibrio deriving from a common reservoir, in which bacteria and phage also reproduce and interact independently of the human population. First, transient environmental conditions set the stage for both a reduction of phage and a bloom of vibrio in the reservoir. As a consequence of the increase in the density of virulent V. cholerae in the reservoir, humans become infected and begin to shed increasing numbers of bacteria into the reservoir, further elevating bacterial density and exacerbating the outbreak. Next, phage production is renewed in the reservoir. Phage replicate on the increasing numbers of bacteria in both the reservoir and infected individuals. Decline in bacterial density ultimately results from increasing phage predation, returning reservoir bacterial populations to pre-outbreak levels and ending the outbreak. The rate of reduction of bacterial density presumably is faster than it would be if the reduction were solely the consequence of the decline in the numbers of susceptible individuals. Faruque et al. (7) stress the assumption that large numbers of phage might be generated within infected individuals and shed into the reservoir, and that this “amplification” may be critical component of phage-modulated cholera epidemics.

Although the observed changes in bacterial and phage densities are qualitatively consistent with this hypothesis, these dynamics may also be incidental to the epidemic process. For example, the decline in bacterial concentration could be entirely due to immune-mediated recovery or death of infected individuals. The consequent reduction of bacteria numbers in the effluent might fully account for the decline in disease incidence and density of phage preying on these bacteria. In this interpretation, the outbreak drives the changes in phage populations, rather than the reverse.

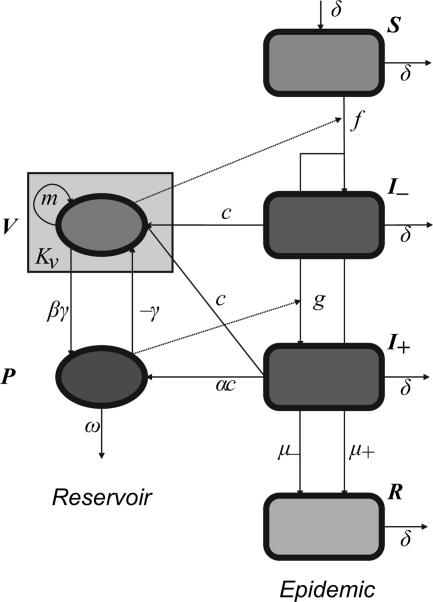
In an effort to evaluate the potential importance of phage predation to the epidemic course of cholera, we have developed a mathematical model incorporating both the population dynamics of the bacteria and phage and the epidemiology of cholera (Fig. 2). Our model is based on the conceptual model presented in ref. 7 and extends and modifies existing models of the epidemiology of cholera (8, 9) to allow interaction between populations of bacteria and phage. We explore the conditions under which phage can impact the epidemic course. In our numerical analysis of the properties of this model, we give particular consideration to the parameter conditions under which the data obtained in the studies of Faruque et al. (7) can be recovered and are consistent with those estimated for the interactions between bacteria and phage. We discuss the implications of our theoretical analysis for empirical tests of hypotheses about the role of lytic phage in the cyclic behavior of cholera outbreaks.

Fig. 2.

Flow diagram for cholera and phage model. Compartments: S, susceptible individuals; I₋, infected with V. cholerae; I₊, infected with V. cholerae and phage; R, recovered/dead; V, reservoir bacterial density; P, reservoir phage density. See text for detailed description and Table 1 for parameter definitions.

Results

Bacteria-Phage Dynamics: Resource vs. Phage Control.

If the bacteria have a positive net growth rate (m > 0) in the reservoir, there are three equilibrium states for the bacteria and phage populations (see Supporting Text, which is published as supporting information on the PNAS web site, for details). The first, where bacteria and phage densities are both zero, is always unstable. That is, the system will drive small increases in both bacteria and phage densities to one of the other equilibria, for which either (i) only bacteria persist, or (ii) bacteria and phage coexist. Stability of these equilibria depends on the composite parameter φ = K_vβγ/ω.

One interpretation of φ is as the basic reproductive number of the phage “epidemic” in the bacterial population; a single infected cell introduced to a naive equilibrium population will be responsible for φ new “infections.” If φ < 1, bacterial densities tend to the carrying capacity K_v, and phage densities decay to zero. We will refer to this situation as “resource control.” If φ > 1, bacterial density tends to K_v/φ < K_v, and phage density tends to a nonzero equilibrium, coexisting with the bacteria. We refer to this as “phage control.”

The conceptual model (7) supposes a preexisting balance between bacteria and phage, upset by a transient loss of phage at the start of an epidemic. In our treatment, this is equivalent to an outbreak induced by phage instability, in the context of phage control (φ > 1). We also considered resource control (φ < 1) and asked to what extent introduced phage would ameliorate an epidemic induced by a bacterial bloom. Below, we show that the two situations result in different outbreak dynamics.

Resource Control: Bloom-Induced Outbreaks.

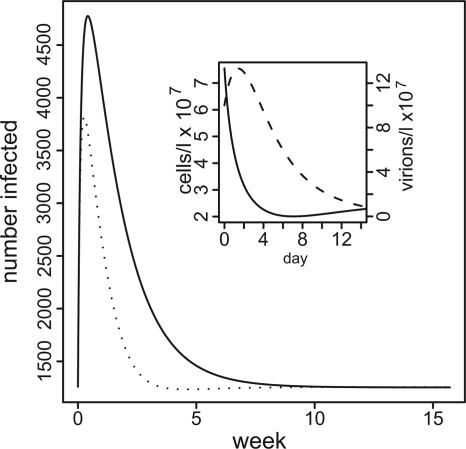
We consider an example of bloom-induced outbreak dynamics in Fig. 3, with phage present and absent. Bacterial density quickly drops to carrying capacity in both cases, but the presence of phage speeds this process, reducing the peak and duration of the outbreak. Phage densities peak within a couple of days, and microbial densities return to equilibrium by ≈2 weeks. These dynamics are much faster than those reported for reservoir densities in the Dhaka outbreak (7). For this example, we chose φ = 2/3, which implies a carrying capacity K_v = 2.5 × 10⁶ − 3.8 × 10⁷ cells per liter over the experimental range of the phage decay rate ω.

Fig. 3.

Epidemic curves, with and without phage, for bloom-induced epidemics. y axis, number of disease cases; x axis, time in weeks; solid line, no phage present; dotted line, phage-moderated epidemic, initial phage density 10⁶ virions per liter. (Inset) Bacteria and phage density over time. Other parameters: initial bacterial density, 5 × K_v (K_v = 2.5 × 10⁶ cells per liter), m = 0.3, ω = 0.525, k = 4 × 10⁷, l = 2.1 × 10⁷, α = 1, π = 0.1, μ₋ = μ₊ = 0.1, φ = 0.67, δ ∼ 10⁻⁴, a = 7.

The magnitude of the epidemic, as measured by the number of cases above the expected endemic number (the “excess cases”), is inversely related to the bacterial growth rate and directly related to the magnitude of the bloom. For example, in the phage-free situation for the low growth rate of 0.3 per d, 8,000 excess cases would develop if the bloom is 10 times the carrying capacity, or 2.5 × 10⁷ cells per liter. However, if the growth rate is 0.8 per d, 2,500 excess cases would occur and only ≈200 cases for a bacterial growth rate of 5 per d. These results are for parameters as given in the legend to Fig. 3. For a more complete sensitivity analysis, see Figs. 6–8, which are published as supporting information on the PNAS web site. The main results here are (i) low bacterial growth rates are required to achieve epidemics similar in magnitude to those observed, and (ii) the severity is sensitive to changes in growth rate at the low end of the range.

Adding relatively large numbers of phage to the reservoir at the time of the bacterial bloom decreases the size of the epidemic. If there are too few phage, 10⁵ virions per liter or less, there is virtually no effect on the epidemic. On the other hand, if the initial density of phage is 10⁸ and the decay rate of the phage is low (0.525 per d), phage predation on vibrio would prevent ≈3,000 cases of cholera compared with the phage-free outbreak. At any initial phage density, the efficacy of the phage in reducing the number of cases declines as the phage decay rate increases. For more detail, see Supporting Text.

Phage Control: Instability-Induced Outbreaks.

In this scenario, phage and bacteria coexist in the reservoir at equilibrium. Phage control of disease is demonstrated simply by the fact that outbreaks ensue when phage density is reduced below its equilibrium value. This allows bacterial density to increase and infection to proceed.

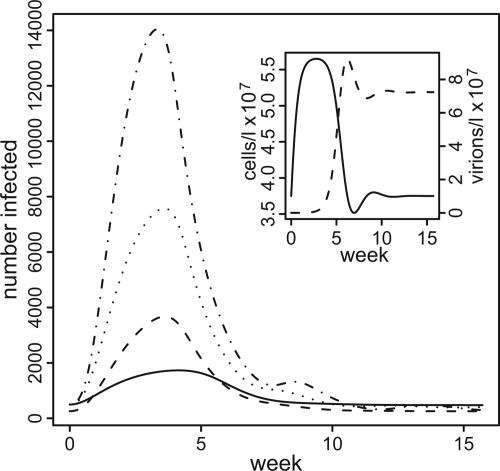
Example outbreaks for varying ω (which forces φ to vary) are given in Fig. 4. Initial phage densities were set to zero to give the most severe epidemic. These examples can be construed as quantitative support for the conceptual model of ref. 7, because the parameters are within biologically relevant ranges, to the extent they are known. In Fig. 4 Inset, we show the microbial dynamics for the case φ = 1.5, with phage decay ω = 0.525 per d. Note that the interval between the bacterial and phage density peaks is 3–5 weeks, longer than in the resource control scenario. Outbreak severity increases with increasing φ, as expected, because the larger φ is, the greater is the potential increase of reservoir bacterial density (from K_v/φ to K_v) when phage are removed. Oscillatory dynamics occur with higher values of φ.

Fig. 4.

Epidemic curves, epidemics induced by phage instability. Initial phage density was set to zero; phage are provided by a small input from phage-infected individuals. y axis, number of disease cases; x axis, time in weeks; φ (ω, a), solid line, 1.5 (0.525, 7); dashed line, 2.0 (0.394, 7); dotted line, 3.0 (0.263, 5); dot-dashed line, 5.0 (0.158, 3). (Inset) Bacteria and phage densities over time, φ = 1.5, δ ∼ 5 × 10⁻⁵. Other parameters as in Fig. 3.

If the phage are not eliminated completely, the extent to which the epidemic will rise varies inversely with the drop in the phage density. For example, assuming a decay rate of 0.525 per day (φ = 1.5), we obtain 4,000 excess cholera cases by eliminating phage at the outset, but only 1,000 cases if we reduce initial phage density to 10% of equilibrium. For more detail, see Supporting Text.

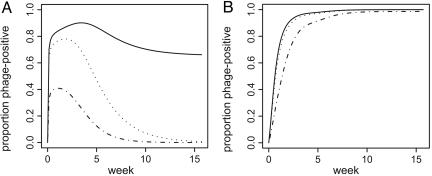
Proportion of Phage-Positive Infecteds.

In Fig. 5, the change in the fraction of phage-positive infected individuals, for different values of the phage, median infection dose l, is shown for resource- and phage-controlled scenarios. The larger l is, the more phage must be consumed to become phage-positive. Note that in the resource-controlled scenario, there is a threshold phage susceptibility, above which a steady-state number of phage-positive infecteds persists. In this situation, the endemicity of phage infection leads to a nonzero equilibrium level of phage in the reservoir and a consequent reduction in equilibrium bacterial density. In the phage-control scenario, all values lead to high equilibrium levels of phage infection of patients. Although the dynamics of phage-positive infecteds were sensitive to changes in the rate of phage infection, this rate did not strongly influence epidemic severity, for α = 1 (data not shown).

Fig. 5.

Increase in phage-infected cholera patients. y axis, proportion of infected individuals harboring phage; x axis, time in weeks. Phage median infectious dose (l): solid line, 10⁶; dotted line, 10⁵; dot-dashed line, 10⁴. (A) Bloom-induced epidemic, initial bacterial density 3 × K_v, initial phage density 7.2 × 10⁵ virions per liter, φ = 0.67. (B) Instability-induced epidemic, initial phage density 7.2 × 10⁵ = 0.01 × equilibrium density, zero initial phage-positive individuals, φ = 1.5. Other parameters as in Fig. 3.

Discussion

We interpret the results of our analysis as support for the following propositions: (i) that bacteriophage are not necessary for either the induction or the termination of cholera outbreaks; but (ii) if bacteriophage are present, persistently or transiently, predation on V. cholerae in the reservoir can influence the course of cholera outbreaks. When conditions are such that, before an outbreak, V. cholerae and their lytic phage coexist stably in the reservoir, externally caused reductions in steady-state phage density could lead to bacterial outgrowth and consequent outbreaks of disease. The extent and duration of these epidemics can be similar to those of the natural outbreak studied in ref. 7. In the model, the delay between the rise in cholera cases and in reservoir phage density can be a matter of weeks in the parameter regions we examined. When phage cannot maintain their densities, and the fluctuations in V. cholerae densities are due to other ecological processes such as resource limitation, externally introduced phage may still lead to reductions in outbreak severity. Although the phage will eventually be lost under these conditions, there will still be a peak in reservoir phage density that follows the peak in cholera cases. In this case, the delay between these two peaks is on the order of days.

Our model predicts that the magnitude of the effect of bacteriophage on outbreaks of cholera will be sensitive to the rates of phage mortality and bacterial replication. Phage decay (mortality) rates must be low (phage half-life on the order of days) to observe outbreaks of similar size to that in ref. 7. Bacterial growth rates must also be low (doubling time of days) to obtain similar outbreaks when bacterial populations are limited by resources rather than phage. In a situation where bacteria are limited by resources, the introduction of lytic phage at sufficiently high densities can profoundly reduce the number of cases relative to that expected in the absence of phage.

Our simple model provides a reasonably accurate description of the time course of the Dhaka cholera outbreak. The most significant inconsistency between the model and the observations is that, in the model, high final proportions of phage-infected individuals also imply that those high proportions persist after the epidemic. However, no individuals were observed harboring phage before the outbreak in Dhaka. We discuss possible resolutions of this discrepancy below.

Model Limitations.

We see this mathematical model of cholera outbreaks as the simplest possible, given the constraints imposed by the conceptual model and the observations in ref. 7. Among these constraints were the requirement that disease transmission occur via consumption of bacteria, rather than by human–human contact, and that the responsible bacterial strain always be present at some concentration in the reservoir. The observations also required that phage ultimately reach reservoir densities large enough to coinfect all individuals receiving cholera-causing doses of bacteria from the same reservoir.

To us, the major limitation of our model lies in our definition of the reservoir. Individuals are unlikely to consume the quantities of contaminated water required to obtain an infectious dose of bacteria, given the observed densities of viable etiologic V. cholerae in the environmental samples taken by ref. 7. There are time points before the peak of the outbreak when environmental V. cholerae are not detected, but cholera is present (see ref. 7). If the densities in the sampled areas are not zero, but below the limit of detection [≈10³ cells/ml (10)], and water consumption is 2–5 liters per day, this would give a daily dose of <2–5 × 10⁶ bacteria. This may account for the level of endemicity, but it is at the low end of estimates based on vibrio challenge experiments [10⁶–10⁸ median infectious dose (11)]. Furthermore, to obtain outbreaks of a similar magnitude to that observed in Dhaka, phage densities of ≈10⁷ virions per liter were required to appropriately control bacterial densities (Figs. 3 and 4). Observed phage densities were ≈1,000-fold lower (Fig. 1). Two reasonable explanations for this discrepancy are (i) bacteria in the environmental reservoir are hyperinfectious, because they have been recently shed from cholera victims (12), and fewer such bacteria (and fewer phage to control them) are necessary to cause an outbreak of a given size, or (ii) that the infectious reservoir for both bacteria and phage is not the environmental water per se, but rather household food and water that support amplification of the infectious dose before ingestion. In the second case, the density of bacteria and phage is directly proportional to that at the sample sites but substantially higher in the actual “infectious reservoir.” The conversion factor C (see Materials and Methods) is a crude acknowledgment of this “preamplification.” This scenario introduces the possibility of variability in rates of spread within and among households that we do not explicitly consider. The dynamics of the present preliminary model can be interpreted as an average among all household reservoirs. Our future models will take this variability into account.

In our analysis, outbreaks were triggered in a simple way, by manipulating the initial densities of bacteria or phage. The ecological reasons for these changes were not specified and were external to this model. We can make some conjectures. For example, if the rate of bacterial growth depended on the concentration of a limiting resource (13), an increase in the density of bacteria could be induced by an influx of resource. Cyclical influx of bacteria or phage from other sources (as considered in ref. 9) could produce arbitrary epidemic patterns on any desired time scale. Our results imply that, whatever the reason, modest increases in the density of bacteria in the reservoir can result in cholera outbreaks of the size and extent observed in Dhaka.

Next Steps.

The process of constructing and deconstructing our mathematical model and the analysis of the model’s properties led us to ask questions about V. cholerae and vibriophage that can be addressed empirically. Perhaps the most important of these is: Could physiological and/or genetic changes in bacteria lead to changes in the bacteria/phage interaction during the epidemic?

Our model assumes that rates of growth, death, and interaction for bacteria and phage are constant. The predictions of the models do not match the observed rates of increase and decline of phage-positive infected individuals. (Fig. 1C vs. Fig. 5). Furthermore, parameter values that lead to high intraepidemic rates of phage coinfection (as observed) also lead to high equilibrium (i.e., interepidemic) rates of coinfection, which are not observed before the epidemic.

Several hypotheses that might account for this discrepancy relax our assumption of constant rates. First, bacteriophage are known to grow poorly on slowly growing bacteria (14). If interepidemic environmental V. cholerae are in a resting state or are mainly associated in aggregates or biofilms (5), they may be unable to support large populations of phage. As an epidemic matures, however, increasing numbers of actively growing planktonic bacteria are being introduced to the environmental reservoir. Alternatively, it has been suggested that V. cholerae from the stool of symptomatic patients achieve an altered physiologic state that increases their infectivity or virulence (12). If this state also increases intrinsic growth rate (m) or susceptibility to phage (γ), this could lead to dynamic changes in the environmental growth of phage that depend directly on the input of virulent bacteria from infected individuals during the epidemic. It is also possible that changes in bacterial habit (e.g., aggregation) or physiology that accompany increases in vibrio infectiveness will also affect the ability of phage to colonize or persist within the gut of human hosts. As the epidemic burns out, the bacteria may return to a state of reduced phage susceptibility, and the number of coinfections may decline, contrary to our present model.

An alternative hypothesis would suppose that the bacteria develop phage resistance during the epidemic (15, 16). Epidemics may provide increased opportunity for the required mutations to arise during exponential growth occurring within infected individuals. Phage would be unable to persist, and coinfections would have to decline. However, it is unlikely that resistance plays a significant role in the Dhaka epidemics, because laboratory O1 mutants resistant to lytic phages are usually highly attenuated in intestinal colonization due to O antigen alterations (S.M.F. and J.J.M., unpublished data). Thus, rare shifts in O antigen (e.g., O1 to O139) may be the only effective way to escape phage predation during periods of high phage prevalence in the environment (17). Host phage resistance may be important in other circumstances, for lytic phage with different adsorption targets or for temperate phage. For example, although JSF4 is lytic, we have observed that viable V. cholerae cells can apparently harbor naked JSF4 DNA, which confers reduced susceptibility to JSF4 infection (S.M.F. and J.J.M., unpublished data). The ecological genetic implications of such phenomena on cholera remain to be explored. Either of the above hypotheses is amenable to in vitro and/or model animal testing.

Because the model predicts different dynamics, depending on whether the bacteria are resource- or phage-controlled, it would be valuable to estimate the bacterial carrying capacity in the infectious reservoir and compare it to the phage growth parameters. That is, one may want to estimate the parameter φ more precisely. This also requires the positive identification of the infectious reservoir, which may be difficult in Dhaka but perhaps easier in other locales. To move the model from the qualitative to the predictive would require accurate viable counts of bacteria and measurements of phage decay and bacterial growth rates in the infectious reservoirs.

We model bacteria and phage as well mixed and homogenous. But the state of vibrio and vibriophage in the environment probably bears little resemblance to this. V. cholerae in the environment is often found aggregated and adhering to plants and plankton (5). It is possible that aggregation, by increasing local concentrations of bacteria, could enhance the effective rate of phage adsorption, which may counter reductions in phage replication due to reduced bacteria growth in the aggregates. Little is known about the growth of phage in bacterial aggregates, but the experiments would be straightforward.

Although it is satisfying to see a model support the observations, we realize that a good fit does not make a model correct. It may fit for reasons that have nothing to do with the model. On the other hand, both the assumptions made in the construction of the model and the predictions generated from the analysis of its properties can be tested experimentally and the validity of the model thereby evaluated. We believe the suggestions above provide a good starting point for such investigations. A better general understanding of the interaction among bacteria, phage, and water-borne disease may help clarify the driving forces behind the cyclical nature of these diseases, and also provide a rationale for phage-based environmental interventions aimed at mitigating their effects on human communities.

Materials and Methods

Conceptual and Mathematical Models.

The key assumptions in the conceptual model of ref. 7 that inform our mathematical treatment are (i) relatively low pre-outbreak bacterial densities are maintained by a coexisting population of phage; (ii) the chance that a susceptible individual is infected depends directly on the numbers of V. cholerae ingested; (iii) high levels of bacterial growth and shedding among infected humans significantly increase the bacterial density of the reservoir, leading to increases in numbers of infections; and (iv) reintroduction of phage, from an external source or a latent nonreplicating state, leads to phage replication rapid enough to reduce the density of bacteria to preoutbreak levels. In mathematical terms, assumption i implies a nondegenerate bacteria–phage equilibrium, and ii implies that the probability of infection is a monotonically increasing function of bacterial dose. We will be less concerned here with the specific environmental mechanisms that upset bacteria–phage balance or introduce phage.

Fig. 2 is a schematic of the dynamical model. The human population is divided into four compartments: susceptibles (S), phage-negative infecteds (I₋), phage-positive infecteds (I₊), and recovereds/deceased (R). The microbial populations are described by the bacterial (V) and phage (P) densities.

Following refs. 8 and 9, we assume that humans acquire the vibrio by ingestion of bacteria derived from a common contaminated reservoir, and that the probability of a symptomatic infection increases with the number of bacteria consumed. The probability increases with number of bacteria for relatively low numbers and levels off at probability 1 for higher numbers.

The median infectious (daily) dose, i.e., the number of bacteria ingested per day that will infect 50% of susceptibles challenged, is given by K. The parameter k in the model must formally be in units of concentration. We suppose Ck = K, where C is a consumption factor, such that consuming K bacteria is equivalent to ingestion of C liters of reservoir water with bacterial density k. For convenience, we take C = 1 and refer to k as the median infectious dose.

We have also elaborated the model of ref. 9 by introducing a parameter, a, that controls the steepness of the infection probability curve at the median infectious dose. When a = 1, the infection probability curve reduces to the case considered in ref. 9. When a > 1, the threshold behavior allows for low endemic prevalence when liter-equivalents of environmental bacterial densities are relatively close to the median infectious dose, as the data suggest.

Infected individuals are assumed to shed bacteria into the reservoir at a constant average rate of c cells per liter of reservoir volume. The chance per day that infection results in severe symptoms leading to bacteria shedding is π. The variables I₋ and I₊ track only these severely infecteds.

Human acquisition of phage also depends on the density of phage virions in the common reservoir, with median “infectious dose” l. We assume that phage cannot replicate in the gut without coinfection with bacteria. Phage-positive infecteds contribute on average α virions per bacterial cell they shed back to the reservoir. We allow for the possibility that ingestion of phage could affect the course of disease by including separate phage-positive and -negative death/recovery rates (μ₊ and μ₋), but we do not analyze the impact of differing rates in this work. We also ignore the possibility of phage-negatives becoming phage-positive, on the basis of the rapid course of the disease.

The total number of individuals N remains constant over time. Birth or emigration of new susceptibles occurs at a rate δ per day.

Phage and bacteria in the reservoir are modeled as predator and prey, similar to the treatment in ref. 16. We assume that bacteria and phage interact according to mass action, with the rate of successful phage attacks (phage adsorption rate) denoted by γ. The number of phage produced per infected bacterium (burst size) is denoted by β. The death rate of phage in the reservoir is ω per day.

In the cholera model of ref. 9, which did not include phage or other limitation on bacterial growth in the reservoir, the net growth rate of the bacteria (m) was required to be negative, to prevent explosive growth of bacteria. Faruque et al. (7) assume that bacteria start out at a positive steady-state density in the environment, which is more consistent with environmental surveys of vibrio (5). To ensure this behavior, we suppose that bacterial growth is limited by available resources in a logistic manner (18), so that (in the absence of phage) bacterial densities attain a “carrying capacity” of K_v cells per liter (see, e.g., chapter 3 in ref. 19).

In Table 1, we give model parameter definitions, dimensions, empirical estimates, and references.

Table 1.

Model parameters

Parameter	Description	Dimensions	Estimate	Reference
m	Bacterial growth rate	Day−1	0.3 − 14.3	25
Kv	Bacterial carrying capacity	Cells per liter	≈106	10, 20
β	Phage burst size	Virions per cell	80 − 100	26, 27
γ	Phage adsorption rate	Liters per virion per day	1.4 × 10−9	27
ω	Phage decay rate	Virions per day	0.5 − 7.9	28
k	Bacterial 50% infectious dose	Cells per day	106 −108	11
l	Phage 50% infectious dose	Virions per day	N/A
π	Severe disease rate	Day−1	0.1	WHO
μ	Phage-negative recovery rate	Day−1	0.1	WHO
μ+	Phage-positive recovery rate	Day−1	N/A
c	Mean bacterial shed rate	Cells per liter per day	10 − 100
α	Mean phage shed rate	Virions per cell	10−6 − 1	17, 21
a	Threshold parameter	N/A	7
δ	Death/immigration rate	Day−1	5 × 10−5 − 10−4

WHO, World Health Organization rates. N/A, not applicable.

Model Equations.

The system of differential equations corresponding to the model of Fig. 2 is

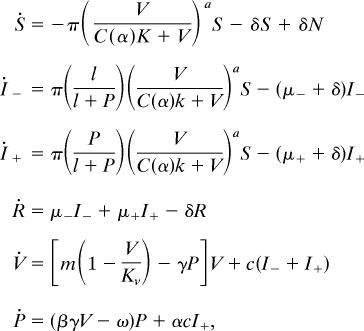where N = S + I₋ + I₊ + R, C(a) = 2^1/a –1, the dot represents the derivative with respect to time t in days, and parameters are as in Table 1. Nondimensionalized equations, calculation of equilibria, stability analysis, and determination of basic reproductive number can be found in Supporting Text.

Data.

Data are described in detail in ref. 7 and reproduced in Fig. 1. Here we are concerned with numbers of infected individuals, proportion of infecteds also harboring phage (phase-positive infecteds), relative environmental bacterial densities, and environmental phage densities. Data were gathered during an outbreak in Dhaka, Bangladesh over the period mid-August to mid-December 2004.

Parameter Estimates.

Our interest lies mainly in determining the conditions under which phage predation can influence the severity of outbreaks for parameter values in known biological ranges, and whether the observed dynamical pattern can be reproduced for a subset of these values. We therefore constrain our analysis by using parameter values in ranges that are consistent with empirical estimates (Table 1). In Supporting Text, we provide detailed rationales for the values chosen for the parameters (c, μ₊, α, and a) lacking direct estimates in the literature.

Initial Conditions and Endemic Prevalence.

Besides choosing parameters, we must also choose initial values of the variables: the densities of bacteria and phage and the numbers of susceptible, infected, and recovered individuals before the onset of the outbreak. For our analysis, we used the stable equilibrium values of these “state variables” that obtain in the absence of the perturbation, e.g., a bacterial bloom in the reservoir that initiates the outbreak. These equilibrium values were calculated by using expressions given in the Supporting Text.

The numerical analyses of the model equations were performed with a total human population of 10⁶ and a birth/immigration rate δ of susceptibles tuned to give an equilibrium cholera prevalence of 0.5 per 1,000. This is in line with recent observations of endemic cholera in Southeast Asia (22) and is approximately the level of detection at the International Centre for Diarrhoeal Disease Research, Bangladesh hospital in Dhaka, assuming all severe cases in the city are treated there (S.M.F., unpublished work). Using these values, the model outbreaks are of similar magnitude to the numbers of cases observed in ref. 7.

Model Outbreaks.

We simulated outbreaks in our model system in two ways, by either increasing the initial bacterial density above the equilibrium level (imitating a bacterial bloom) or decreasing initial phage density below equilibrium (imitating sudden phage decay or “instability”). These are referred to as bloom- or instability-induced epidemics. The initial values of the other state variables were left at their equilibrium values. For some parameter values, phage do not persist stably in the reservoir. In these cases, the effect of phage on the (bloom-induced) epidemic was modeled by specifying different initial concentrations of phage (see Results).

Numerical Analysis.

Numerical solution of the dynamical system was carried out by using the interactive solver xpp (23), or the package odesolve in the R statistical programming environment (24). Scripts may be obtained from the authors.