Abstract
The study of base composition evolution in Drosophila has been achieved mostly through the analysis of coding sequences. Third codon position GC content, however, is influenced by both neutral forces (e.g., mutation bias) and natural selection for codon usage optimization. In this article, large data sets of noncoding DNA sequence polymorphism in D. melanogaster and D. simulans were gathered from public databases to try to disentangle these two factors—noncoding sequences are not affected by selection for codon usage. Allele frequency analyses revealed an asymmetric pattern of AT vs. GC noncoding polymorphisms: AT → GC mutations are less numerous, and tend to segregate at a higher frequency, than GC → AT ones, especially at GC-rich loci. This is indicative of nonstationary evolution of base composition and/or of GC-biased allele transmission. Fitting population genetics models to the allele frequency spectra confirmed this result and favored the hypothesis of a biased transmission. These results, together with previous reports, suggest that GC-biased gene conversion has influenced base composition evolution in Drosophila and explain the correlation between intron and exon GC content.
THE evolution of base composition, the percentage of A, C, G, and T of genomic sequences, has been a topic of interest in a number of taxonomic groups (e.g., Jermiin et al. 1994; Galtier and Lobry 1997; Bernardi 2000; Eyre-Walker and Hurst 2001), possibly because it is a typical instance of the neutralist/selectionist debate of molecular evolution: we want to identify the evolutionary forces (e.g., mutation, natural selection, and recombination) shaping base composition variation within and between genomes and their relative importance.
In Drosophila, this question is closely linked to the issue of synonymous codon usage bias. The various codons encoding a given amino acid are not used randomly: some codons are “preferred” over synonymous alternatives, probably because they allow more efficient/accurate translation (Akashi et al. 1998). For an unknown reason, 19 preferred codons of 20 end in G or C in Drosophila (Marais et al. 2001). Understanding the evolutionary dynamics of codon usage bias, therefore, requires disentangling selection on codon choice from forces acting on the GC content of genomic sequences irrespective of their coding/noncoding status (Marais et al. 2001; Hey and Kliman 2002; Marais et al. 2003).
The GC content of noncoding DNA varies between regions of the Drosophila genome, and the GC content of introns (GCi) is correlated with the GC content at third codon position of exons (GC3; Kliman and Eyre-Walker 1998) of a gene. This correlation was correctly taken into account by Kliman and Hey (1993) when analyzing codon usage data and interpreted as the consequence of a variable mutation bias: the ratio of AT → GC over GC → AT mutation rates would vary along the genome. An alternative hypothesis was recently proposed, however: the GC3/GCi correlation could be due to GC-biased gene conversion (BGC) (Marais 2003). Allelic gene conversion is a molecular process associated with recombination in which a fragment of one of the two recombining chromosomes is “copied/pasted” onto the other one—a unidirectional genetic exchange. It is a fundamental process of DNA metabolism occurring during the repair of double-strand breaks. Although little empirical molecular evidence has been reported to date, numerous arguments indicate that gene conversion is biased toward GC in yeast (Birdsell 2002) and mammals (Galtier et al. 2001; Galtier 2003; Kudla et al. 2004; Meunier and Duret 2004): G or C alleles tend to convert A or T more frequently than the reverse, resulting in a higher fixation probability for G and C alleles. GC content is positively, but very weakly (R2 < 1%), correlated to local recombination rate in Drosophila melanogaster (Marais et al. 2001), suggesting that BGC might also impact GC content in this species.
Demonstrating the existence of BGC in Drosophila would be of interest for several reasons. First, this would be an additional species in which this up-to-now neglected evolutionary force applies, adding some credit to the “universality” of BGC advocated by Birdsell (2002). Second, this would provide a plausible explanation for the GC3/GCi correlation in the Drosophila genome. Third, this would ask for a reappraisal of coding-sequence polymorphism patterns in Drosophila and of hypotheses about the relationship between selection on codon usage, GC content, and recombination.
BGC is a neutral process that mimics natural selection by conferring a higher fixation probability to G and C alleles—heterozygotes produce a larger amount of G and C than of A and T gametes. This effect is not distinguishable from a selective advantage of GC over AT alleles (Nagylaky 1983). Such a selective pressure in favor of GC actually occurs at synonymous sites for codon usage optimization. Our strategy, therefore, was to analyze polymorphism patterns in noncoding sequences of D. melanogaster and D. simulans, where selection for codon usage does not apply. In the absence of BGC and of selection for genomic GC content—our null hypothesis—AT and GC polymorphisms should have similar allele frequency spectra.
DATA
Two noncoding sequence polymorphism data sets from D. melanogaster were obtained from the EMBL database (version 73, March 2004). The first data set, hereafter called “Dme_exhaustive,” was built as a part of the Polymorphix database (Bazin et al. 2005). Nuclear sequences from D. melanogaster were extracted from EMBL and grouped into 283 families, first according to sequence similarity (at least 80% similarity required) and then using a bibliographic criterion (a sequence S was kept in its family F only if at least 3 other sequences in F were published in the same article as S). Sequence families were inspected by eye. Those not corresponding to polymorphism studies (e.g., transposons) were manually deleted. Four families including paralogous loci were cleaned or split to ensure orthology. Families including <10 sequences were removed. Sequences were aligned using the MABIOS algorithm (Abdeddaim 1997), which is especially efficient for a quick alignment of highly similar sequences. Alignments were slightly modified manually. Ambiguously aligned regions (e.g., microsatellites) were manually discarded, as well as sequences containing too many gaps or missing nucleotides. Coding regions were removed from the alignments. The Dme_exhaustive data set finally included 221 families (i.e., loci), including 10–100 sequences.
The Dme_exhaustive data set is highly heterogeneous with respect to population sampling—worldwide for some loci, local for others. Allele frequencies are mostly unknown: what we have are haplotypes (EMBL entries), some of which are being shared possibly by several individuals in a sample. This data set is therefore not suitable for standard population genetics analyses. It should be noted, however, that sampling peculiarities should affect AT → GC mutations and GC → AT mutations in a similar way. Under the null, no-BGC hypothesis, an AT/GC symmetric pattern is expected whatever the sampling and whatever the population history.
The second D. melanogaster data set, hereafter called “Dme_Glinka,” is a subset of the Dme_exhaustive one corresponding to data from Glinka et al. (2003). In this study, 105 X-linked DNA fragments were sequenced in 19–24 D. melanogaster lines from Europe and Africa. We decided to make use of African data only since natural selection significantly affects polymorphism patterns in the European data set (Glinka et al. 2003). The Dme_Glinka data set is restricted to X-linked loci and to a single African population, but its homogeneous sampling allows more elaborate analyses using population genetics models. Model fitting was performed on a subset of 94 loci for which exactly 12 African lines have been sampled and sequenced.
A similar strategy was conducted in D. simulans. A “Dsi_exhaustive” data set of 58 loci was built by gathering sequences from Polymorphix. A minimal number of eight sequences per family were required. Again, the Dsi_exhaustive data set is too heterogeneous to allow proper population genetics model fitting. A data subset called “Dsi_Begun” was built by using data obtained by D. Begun's group only (41 loci). These studies used samples from a single Californian population of D. simulans. All these data sets are available from http://kimura.univ-montp2.fr/data.
ANALYSIS
D. melanogaster:
The Dme_exhaustive data set included 4672 polymorphic sites, among which were 3364 A or T vs. G or C biallelic sites. Figure 1 shows the distribution of the observed frequency of the G or C state in these sites. Under the hypothesis of unbiased transmission (i.e., no BGC, no selection) and stationary GC content, this distribution should be symmetric (Eyre-Walker 1999; Lercher et al. 2002). This was not the case here. The number of sites for which the G or C state occurs at a frequency strictly >0.5—call them GC sites—was 1875, whereas 1408 sites showed a frequency of G or C strictly <0.5. The difference is highly significant (P < 10−8, binomial test).
Figure 1.
Frequency distribution of the G or C allele in 3508 (respectively, 648) AT vs. GC polymorphisms from an exhaustive D. melanogaster (respectively, D. simulans) data set. The leftmost bar of the D. melanogaster histogram is for polymorphic sites with GC frequency <0.1, the next bar is for sites with GC frequency between 0.1 and 0.2, etc….
Then loci from the Dme_exhaustive data set were split into an arbitrary three categories of equal size according to their GC content, and the above binomial test was reconducted. A significant excess of GC sites was detected in the high-GC (expected, 501; observed, 626; P < 10−10) and medium-GC (expected, 672; observed, 765; P < 10−6) data subsets, but not in the low-GC data subset (expected, 468; observed, 484), indicating that the evolutionary force causing this asymmetric pattern is stronger in GC-rich regions. This trend was confirmed when we plotted the difference between the numbers of AT and GC sites of a locus (normalized by the total amount of polymorphism) vs. locus GC content (Figure 2, r2 = 0.167, P < 10−4). GC-rich loci showed an excess of AT mutations, while AT-rich loci appeared to be at equilibrium.
Figure 2.
Asymmetry of GC → AT and AT → GC polymorphisms among loci in the “Dme_Glinka” data set. Each dot is for one locus. x-axis, locus GC content; y-axis, (nAT − nGC)/nXY, where nAT is the number of AT ↔ GC polymorphic sites showing a frequency of the A or the T <50%, nGC the number of AT ↔ GC polymorphic sites showing a frequency of the A or the T >50%, and nXY is the total number of polymorphic sites for the considered locus.
The detected GC-biased segregation of polymorphisms must be caused by a departure from at least one of the two assumptions of the null model, namely unbiased transmission and stationary GC content. Transmission distortion in favor of GC would lead to an increased number of GC sites (Eyre-Walker 1999), consistent with the asymmetric Figure 1. Alternatively, the observed pattern could be explained in a neutral context by an excess of GC → AT over AT → GC mutations, i.e., a decrease of the genomic GC content in the GC-richest regions. Both hypotheses predict a higher than expected number of GC sites, but make distinct predictions about the shape of the allele frequency distribution, as illustrated by Figure 3. We made use of the Dme_Glinka data set to try to distinguish between the two scenarios.
Figure 3.
Expected allele frequency distribution under three biallelic population genetics models. Shaded boxes: polymorphic sites having arisen through an AT → CG mutation. Open boxes: polymorphic sites having arisen through a CG → AT mutation. Models M1 (nonstationary) and M2 (nonneutral) differ from M0 largely in that the expected distributions are asymmetric. Expectations under M1 and M2 are similar but distinct. For instance, with the parameter values chosen here for illustration, the less probable allele frequency is 5 under M1, but 6 under M2.
Loci in the Dme_Glinka data set were split into three GC-content categories, as explained above. The total numbers of AT vs. GC segregating sites were 524, 505, and 372 for the low-GC (average GC content: 33.5%), medium-GC (39.4%) and high-GC (47.8%) categories, respectively. The distributions of G or C allele frequency in the three data subsets are shown (Figure 4). Just like for the Dme_exhaustive data set, the AT/GC asymmetry appears stronger for GC-rich than for GC-poor loci.
Figure 4.
Observed allele frequency distribution for three subsets of the “Dme_Glinka” data set.
Four population genetics models were fit to each of these data subsets. The most general model is M3, in which we assume simply that sites are independent from each other and that the individuals were sampled from a panmictic population at mutation/transmission distortion/drift equilibrium, possibly with nonstationary GC content (where transmission distortion refers either to natural selection or to BGC). This model is described by two parameters, namely W = 3Ne.w, the population transmission distortion coefficient in favor of C and G alleles in the X chromosome, and α = μGC/(μAT + μGC), the probability that a GC ↔ AT mutation is an AT → GC one (μGC is the mutation rate from AT to GC, and μAT is the mutation rate from GC to AT).
For a given W and α, the proportion of polymorphic sites consisting of i C or G and 12 − i A or T (0 < i < 12) expected under M3, f*(i), was calculated by adapting the theory in Lercher et al. (2002). Equations are given in the appendix. The log-likelihood of the model was computed using the multinomial formula
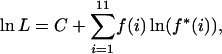 |
(1) |
where C is a constant, and where f(i) is the observed number of sites consisting of i C or G and 12 − i A or T. This method is very similar to the approach of Lercher et al. (2002) and Duret et al. (2002).
The other models investigated are special instances of model M3. Model M2 (one parameter) assumes stationarity, which is obtained by forcing α to be such that the equilibrium GC content, given W, equals the observed GC content. Model M1 (one parameter) allows for nonstationary evolution, but assumes neutrality (no transmission distortion). This is obtained by leaving α free but setting S = 0. Model M0 (zero parameter), finally, assumes both stationarity and neutrality. The likelihood under models M0, M1, and M2 was calculated just like that under M3.
Parameters were estimated by the maximum-likelihood method. The likelihood curve (or surface) was traced using a grid on the parameter space. To maintain parameter values within a reasonable range, the maximization was performed under the constraint that the equilibrium GC content had to be within 27 and 60%, the lowest and highest GC content of the analyzed loci. This was necessary for model M3, for which the likelihood was maximal for a very high W and a very low α, implying an irrelevant equilibrium GC content close to 100%. For each model, the log-likelihood for the whole data set was obtained by summing the log-likelihoods of the three data subsets. Models were compared using likelihood-ratio tests: if M (n parameters) is the null model, and M′ (n′ parameters, n′ > n) is an alternative model such that M is a special case of (nested in) M′, then twice the difference of log-likelihood between the two models is asymptotically distributed as a χ2 with n′ − n d.f. The 1% significance level was retained.
The results are given in Table 1. When the three data subsets were considered jointly, models M1 (nonstationary) and M2 (transmission distortion) vastly improved the fit over the null model M0 (M2 vs. M0: 2.Δ ln L = 71.2, 3 d.f., P < 10−6), confirming the asymmetric nature of the distributions in Figure 4. Model M2 fit the data better than model M1, but the significance of this difference could not be assessed directly by a likelihood-ratio test since the two models are not nested. Model M3 (nonstationary plus transmission distortion) did improve the fit over M1 (2.Δ ln L = 20.3, 3 d.f., P = 1.5 × 10−4), but only marginally over M2 (Δ ln L = 9.9, 3 d.f., P = 1.9 × 10−2). M2 was the model favored by Akaike's criterion of model choice (not shown). These results indicate that the AT/GC asymmetry of SNP segregation cannot be explained by a departure from the stationarity hypothesis only. Transmission distortion, when invoked, significantly improved the fit as compared to the neutral model, either under stationarity (M2 vs. M0) or under nonstationarity (M3 vs. M1).
TABLE 1.
Maximum-likelihood analysis of the allele frequency spectrum in D. melanogaster
| Low GC | Medium GC | High GC | ||
|---|---|---|---|---|
| Sites | 443 | 444 | 362 | |
| % GC | 33.5 | 39.4 | 47.8 | |
| M0 ln L | −47.67 | −59.69 | −63.03 | → −170.39 |
| S | 0 | 0 | 0 | |
| α | 0.335 | 0.394 | 0.478 | |
| % eqGC | 33.5 | 39.4 | 47.8 | |
| M1 ln L | −45.67 | −50.03 | −44.30 | → −140.00 |
| S | 0 | 0 | 0 | |
| α* | 0.275 | 0.259 | 0.243 | |
| % eqGC | 27.5 | 25.9 | 24.3 | |
| M2 ln L | −45.41 | −48.40 | −40.99 | → −134.80 |
| S* | 0.3 [0.1-0.6] | 0.7 [0.5-1] | 1.2 [0.9,1.5] | |
| α | 0.272 | 0.244 | 0.216 | |
| % eqGC | 33.5 | 39.4 | 47.8 | |
| M3 ln L | −44.00 | −46.29 | −39.56 | → −129.85 |
| S* | 1.5 | 1.6 | 1.7 | |
| α* | 0.250 | 0.226 | 0.213 | |
| % eqGC | 59.9 | 59.1 | 59.7 |
eqGC, equilibrium GC content.
Similar results were found when the three GC categories were considered separately. The medium-GC and high-GC categories revealed a strong asymmetry, best explained by transmission distortion. No strong departure from the neutral, stationary M0 model was detected from the low-GC data set, however, in agreement with results from the Dme_exhaustive data set. The population transmission-distortion coefficient estimated under M2 increased from 0.3 (low-GC data subset) to 1.2 (high-GC data subset).
A goodness-of-fit test was conducted by fitting a degenerate model in which every allele frequency class has its own free-to-vary frequency (11 parameters). This model significantly improved the fit over any of the M0 to M3 models (not shown). This is indicative of a poor fit of the population genetics models to the Dme_Glinka data set.
D. simulans:
The Dsi_exhaustive data set yielded results comparable to the Dme_exhaustive one (Figure 1): the number of GC sites (354) was significantly higher (P = 5.1 × 10−4) than the number of AT sites (271). The proportion of GC sites (66.6%) was nearly identical to that obtained from the Dme_exhaustive data set (67.0%). When the 58 loci were split into 29 GC-poor and 29 GC-rich ones, only the GC-rich subset yielded a significant excess of GC sites (observed, 209; expected, 174; P = 1.3 × 10−4), while GC-poor loci appeared to be at equilibrium (observed, 145; expected, 138).
We then attempted to fit models M0 to M3 to the Dsi_Begun data set. Neither when all 41 loci were analyzed jointly nor when they were split in a GC-poor and a GC-rich subset did we detect any significant departure from the null hypothesis of neutrally evolving, equilibrium GCcontent (M0), in contrast with the Dme_Glinka analysis. There are, however, two important differences between the two data sets: the Dme_Glinka data set is larger (1249 polymorphic sites vs. 380 in Dsi_Begun) and includes a higher proportion of GC-rich loci (33% of loci have a GC content >42%, while this proportion is 19% in Dsi_Begun). When the 8 loci from Dsi_Begun having a GC content >42% were analyzed, a (marginally) significant departure from the null hypothesis was detected, and alternative models were favored (M1 vs. M0 and M2 vs. M0: P = 5.0 × 10−2), despite the very low amount of data (51 polymorphic sites). Population genetics models appeared appropriate for the Dsi_Begun data set since they were not rejected by tests for goodness-of-fit.
DISCUSSION
The analysis of the Dme_exhaustive and Dsi_exhaustive data sets revealed a significant AT vs. GC asymmetry of noncoding polymorphism segregation in D. melanogaster and D. simulans, reflecting a biased-transmission process and/or nonstationary base composition: GC → AT mutations are more frequent or less likely to increase in frequency, or both, than AT → GC mutations, leading to an excess of low-AT-frequency polymorphisms. This effect is strong in GC-rich loci, but undetected in GC-poor loci. Normalized data sets were built to try to discriminate between the two (nonmutually exclusive) hypotheses. The biased-transmission hypothesis explained allele frequency distribution in the Dme_Glinka data set significantly better than neutral models, either stationary or nonstationary. The fit of population genetics models to this data set was not good, however. This poor fit suggests that some of the assumptions underlying these models (e.g., panmixy, constant population size) are not met by the data, perhaps questioning the relevance of the likelihood-ratio tests. The Dsi_Begun data set revealed the same trends, but was smaller and less informative. These analyses, therefore, do not allow unambiguous distinction between the “biased-transmission” and “nonstationarity” hypotheses, although the former is best supported. We now discuss these two hypotheses in the light of our and other results.
Given that both D. melanogaster and D. simulans show an asymmetric segregation of AT vs. GC polymorphism, it is tempting to propose that this pattern resulted from a change of mutation bias prior to the split between these two lineages, in a neutral (i.e., unbiased transmission) context. This hypothesis, however, is not easy to reconcile with the correlation observed between AT vs. GC polymorphism asymmetry and GC content—only GC-rich loci show a departure from the null hypothesis. It is difficult to imagine why a change in the mutational pattern should affect some, but not all regions of the genome. In addition, the mutation bias hypothesis would predict an accumulation of GC → AT substitutions. Kern and Begun (2005), however, recently reported that noncoding fixations were consistent with equilibrium base composition evolution in both D. melanogaster and D. simulans.
The hypothesis of a biased transmission of GC vs. AT alleles appears to accommodate the observed features more easily. The biased-transmission hypothesis predicts the strong correlation between asymmetric polymorphism and GC-content—loci undergoing a GC-biased segregation of polymorphisms tend to be GC richer. Consistently, Singh et al. (2005) reported a significant correlation between recombination rate and GC-substitution bias of a genomewide repeated element in D. melanogaster. The GC-biased-transmission model is also consistent with the stationary evolution of GC content of noncoding sequences in D. melanogaster and D. simulans reported by Kern and Begun (2005).
We are concerned by the fact that the M2 hypothesis involves a constant population size in time. Analysis of sequence variation at synonymous sites of coding sequences, however, has revealed a reduction of selection efficacy for codon usage in the melanogaster lineage (Akashi 1996), leading to an accumulation of preferred → unpreferred substitutions, and has been interpreted as the consequence of a recent drop of effective population size in D. melanogaster (Akashi 1996). This probable bottleneck should have affected the efficiency of GC-biased transmission in noncoding DNA as well, so that one would expect to observe an accumulation of GC → AT substitutions in D. melanogaster noncoding sequences. Why Kern and Begun (2005) did not report a significant asymmetry in the divergence pattern can be explained by a combination of several factors. First, the drop of population size might be too recent for a detectable accumulation of biased substitutions in noncoding sequences. Second, the strength of the transmission bias might be too weak, and the departure from equilibrium too small. Third, the segregation bias reported here was detected from the GC-richest fraction of noncoding loci only, while Kern and Begun (2005) pooled all loci in their analysis.
It should be recalled that base composition shifts have been quite common in the Drosophila genus (Rodriguez-Trelles et al. 2000; Takano-Shimizu 2001; Tarrio et al. 2001). The mutation bias hypothesis, therefore, would require several changes of the mutation process in a relatively short period of time. Under the transmission bias model, however, such compositional shifts are expected when the effective population size changes, an event arguably more frequent than changes in the mutation process. For these various reasons, the most plausible model explaining recent GC-content evolution in noncoding sequences of D. simulans and D. melanogaster appears to be one in which (i) a GC-biased transmission process generally applies to some regions of the genome, leading to local increases in GC content, and (ii) this process is interrupted, or its efficacy substantially reduced, when the effective population size declines, as is suspected in D. melanogaster. Note that the base composition of noncoding DNA might also be affected by events of insertion and deletions. To account for the observed pattern, one may then assume that incoming insertions should be GC rich in general and deletions preferentially GC poor. However, we have up to now no evidence for a bias in the base composition of insertions vs. deletions.
One may be surprised that we could have detected a transmission bias from noncoding allele frequency patterns while comparable analyses applied to synonymous polymorphisms in D. melanogaster yielded equivocal results (Akashi 1997; Kliman 1999). If BGC was effective, one should expect a stronger signal from synonymous than from noncoding sites since synonymous sites undergo both BGC and selection for the GC-ending preferred codons. The number of sites examined in the above studies of synonymous polymorphism was much lower, however, than the 3508 + 648 used in the current analysis, reducing the power to detect biased segregation. Using a comprehensive D. yakuba/D. simulans/D. melanogaster data set, Kern and Begun (2005) obtained results essentially in agreement with ours. These authors, however, reported an intriguing difference between intron and intergenic sequence variation: introns, not intergenic sequences, showed a GC-biased segregation of polymorphisms in D. melanogaster. When we analyzed introns and intergenic loci from the Dme_Glinka data set separately, we did not detect any difference between the two subsets of loci—both supported a GC-biased segregation.
Another difference between these studies and ours is that the former oriented polymorphisms using D. simulans as an outgroup. We refrained from doing so in the current study. Orienting sites potentially increases the power to detect a segregation bias, but could strongly bias the analysis in the case of a nonnegligible amount of misorientation. A misoriented site will be seen, say, as a high-frequency AT → GC mutation when it is actually a low-frequency GC → AT one. To check this, we used the D. simulans outgroup available for the Dme_Glinka data set to orient A ↔ T and G ↔ C polymorphisms, thus avoiding biases related to the AT vs. GC mutation and fixation processes. We found a bimodal distribution of allele frequency, in which mutations with a frequency >90% were 1.6 times as numerous as mutations with a frequency between 75 and 90%. One would expect a ratio of 0.58 under neutral evolution at demographic equilibrium and an even lower proportion of high-frequency mutations in the case of a bottleneck. We estimated that the proportion of misoriented mutations was >5%, and probably ∼10%, which makes a big difference when fitting population genetics models (e.g., see Baudry and Depaulis 2003), as we did, although this should not greatly affect the results of previous analyses (e.g., Kern and Begun 2005).
The transmission bias we detected, if confirmed, could be natural selection for G and C or GC-biased gene conversion. Although our data do not allow us to discriminate between these two models, we tend to favor the BGC hypothesis over the selective one. This is because a large body of evidence demonstrates the effectiveness of BGC in yeast and mammals (Birdsell 2002; Galtier 2003; Kudla et al. 2004), whereas not a single example of selection on base composition in noncoding regions has been reported until now. Even hyperthermophilic prokaryotes, for which a putative advantage of C:G pairs at the DNA or RNA level could make sense, and in which population sizes are much higher than in Drosophila, show no evidence of selection on genomic GC content (Galtier and Lobry 1997). The BGC model also accounts for the correlation between recombination rate and GC content. BGC was recently invoked by Bartolome et al. (2005) to explain patterns of coding sequence variation in D. miranda. Whatever its origin, this transmission bias might explain the correlation between intron and exon GC content. It also implies that the strength of selection for codon usage was previously overestimated, since a part of the AT ↔ GC asymmetry observed at synonymous sites must be a consequence of this bias.
Acknowledgments
We thank Adam Eyre-Walker and two anonymous referees for thoughtful comments on the manuscript. This work was supported by the Centre National de la Recherche Scientifique Equipe Projet Multi Laboratoires “Méthodes Informatiques pour la Phylogénie Moléculaire.”
APPENDIX: DERIVATION OF F*(i)
The expected proportion of polymorphic sites consisting of i C or G and n − iA or T (0 < i < n) in a sample of size n under model M3 is given by
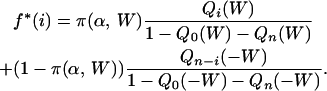 |
(A1) |
The first part of Equation A1 considers polymorphic sites having arisen through AT → GC mutations: π(α, W) is the expected proportion of such sites given distortion bias W and mutation bias α, and Qi(W) is the probability that a mutant allele with distortion bias W shows frequency i in the sample. Symmetrically, the second part of Equation A1 is for polymorphic sites having arisen through a GC → AT mutation. π(W) in Equation A1 was calculated according to Equation 3 in Smith and Eyre-Walker (2001), and Qi(W) is given by
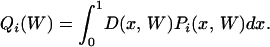 |
(A2) |
Here, D(x, W) is the probability density of allele frequency x in the population given W, and Pi(x, W) is the probability that a site be at frequency i in the sample given frequency x in the population. D(x, W) is obtained from standard population genetics (e.g., Sawyer and Hartl 1992):
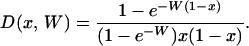 |
(A3) |
Pi(x, W) corresponds simply to a binomial sampling:
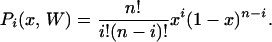 |
(A4) |
The integration was performed numerically.
References
- Abdeddaim, S., 1997. Fast and sound two-step algorithms for multiple alignment of nucleic sequences. Int. J. Artif. Intell. Tools 6: 179–192. [Google Scholar]
- Akashi, H., 1996. Molecular evolution between Drosophila melanogaster and D. simulans: reduced codon bias, faster rates of amino acid substitutions and larger proteins in D. melanogaster. Genetics 144: 1297–1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akashi, H., 1997. Codon bias evolution in Drosophila. Population genetics of mutation-selection-drift. Gene 205: 269–278. [DOI] [PubMed] [Google Scholar]
- Akashi, H., R. M. Kliman and A. Eyre-Walker, 1998. Mutation pressure, natural selection, and the evolution of base composition in Drosophila. Genetica 102/103: 49–60. [PubMed] [Google Scholar]
- Bartolome, C., X. Maside, S. Yi, A. L. Grant and B. Charlesworth, 2005. Patterns of selection on synonymous and nonsynonymous variants in Drosophila miranda. Genetics 169: 1495–1507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baudry, E., and F. Depaulis, 2003. Effects of misoriented sites on neutrality tests with outgroup. Genetics 165: 1619–1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazin, E., L. Duret, S. Penel and N. Galtier, 2005. Polymorphix, a polymorphism sequence database. Nucleic Acids Res. 33: 481–484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardi, G., 2000. Isochores and the evolutionary genomics of vertebrates. Gene 241: 3–17. [DOI] [PubMed] [Google Scholar]
- Birdsell, J. A., 2002. Integrating genomics, bioinformatics, and classical genetics to study the effects of recombination on genome evolution. Mol. Biol. Evol. 19: 1181–1197. [DOI] [PubMed] [Google Scholar]
- Duret, L., M. Semon, G. Piganeau, D. Mouchiroud and N. Galtier, 2002. Vanishing GC-rich isochores in mammalian genomes. Genetics 162: 1837–1847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker, A., 1999. Evidence of selection on silent site base composition in mammals: potential implications for the evolution of isochores and junk DNA. Genetics 152: 675–683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker, A., and L. D. Hurst, 2001. The evolution of isochores. Nat. Rev. Genet. 2: 549–555. [DOI] [PubMed] [Google Scholar]
- Galtier, N., 2003. Gene conversion drives GC content evolution in mammalian histones. Trends Genet. 19: 65–68. [DOI] [PubMed] [Google Scholar]
- Galtier, N., and J. R. Lobry, 1997. Relationships between genomic G + C content, RNA secondary structures and optimal growth temperature in prokaryotes. J. Mol. Evol. 44: 632–636. [DOI] [PubMed] [Google Scholar]
- Galtier, N., G. Piganeau, D. Mouchiroud and L. Duret, 2001. GC-content evolution in mammalian genomes: the biased gene conversion hypothesis. Genetics 159: 907–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glinka, S., L. Ometto, S. Mousset, W. Stephan and D. De Lorenzo, 2003. Demography and natural selection have shaped genetic variation in Drosophila melanogaster: a multilocus approach. Genetics 165: 1269–1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey, J., and R. M. Kliman, 2002. Interactions between natural selection, recombination and gene density in the genes of Drosophila. Genetics 160: 595–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jermiin, L. S., D. Graur, R. M. Lowe and R. H. Crozier, 1994. Analysis of directional mutation pressure and nucleotide content in mitochondrial cytochrome b genes. J. Mol. Evol. 39: 160–173. [DOI] [PubMed] [Google Scholar]
- Kern, A. D., and D. J. Begun, 2005. Patterns of polymorphism and divergence from non-coding sequences of D. melanogaster and D. simulans: evidence for non-equilibrium processes. Mol. Biol. Evol. 22: 51–62. [DOI] [PubMed] [Google Scholar]
- Kliman, R. M., 1999. Recent selection on synonymous codon usage in Drosophila. J. Mol. Evol. 49: 343–351. [DOI] [PubMed] [Google Scholar]
- Kliman, R. M., and A. Eyre-Walker, 1998. Patterns of base composition within the genes of Drosophila melanogaster. J. Mol. Evol. 46: 534–541. [DOI] [PubMed] [Google Scholar]
- Kliman, R. M., and J. Hey, 1993. Reduced natural selection associated with low recombination in Drosophila melanogaster. Mol. Biol. Evol. 10: 1239–1258. [DOI] [PubMed] [Google Scholar]
- Kudla, G., A. Helwak and L. Lipinski, 2004. Gene conversion and GC-content evolution in mammalian Hsp70. Mol. Biol. Evol. 21: 1438–1444. [DOI] [PubMed] [Google Scholar]
- Lercher, M. J., N. G. C. Smith, A. Eyre-Walker and L. D. Hurst, 2002. The evolution of isochores: evidence from SNP frequency distributions. Genetics 162: 1805–1810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marais, G., 2003. Biased gene conversion: implications for genome and sex evolution. Trends Genet. 19: 330–338. [DOI] [PubMed] [Google Scholar]
- Marais, G., D. Mouchiroud and L. Duret, 2001. Does recombination improve selection on codon usage? Lessons from nematode and fly complete genomes. Proc. Natl. Acad. Sci. USA 98: 5688–5692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marais, G., D. Mouchiroud and L. Duret, 2003. Neutral effect of recombination on base composition in Drosophila. Genet. Res. 81: 79–87. [DOI] [PubMed] [Google Scholar]
- Meunier, J., and L. Duret, 2004. Recombination drives the evolution of GC-content in the human genome. Mol. Biol. Evol. 21: 984–990. [DOI] [PubMed] [Google Scholar]
- Nagylaky, T., 1983. Evolution of a finite population under gene conversion. Proc. Natl. Acad. Sci. USA 80: 6278–6281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez-Trelles, F., R. Tarrio and F. J. Ayala, 2000. Fluctuation mutation bias and the evolution of base composition in Drosophila. J. Mol. Evol. 50: 1–10. [DOI] [PubMed] [Google Scholar]
- Sawyer, S. A., and D. L. Hartl, 1992. Population genetics of polymorphism and divergence. Genetics 132: 1161–1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh, N. D., P. F. Arndt and D. A. Petrov, 2005. Genomic heterogeneity of background substitutional patterns in Drosophila melanogaster. Genetics 169: 709–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, N. G. C., and A. Eyre-Walker, 2001. Synonymous codon bias is not caused by mutation bias in human. Mol. Biol. Evol. 18: 982–986. [DOI] [PubMed] [Google Scholar]
- Takano-Shimizu, T., 2001. Local changes in GC/AT substitution biases and in cross-over frequencies on Drosophila chromosomes. Mol. Biol. Evol. 18: 606–619. [DOI] [PubMed] [Google Scholar]
- Tarrio, R., F. Rodriguez-Trelles and F. J. Ayala, 2001. Shared nucleotide composition biases among species and their impact on phylogenetic reconstructions of the Drosophilidae. Mol. Biol. Evol. 18: 1464–1473. [DOI] [PubMed] [Google Scholar]






