Functional Mapping of Quantitative Trait Loci That Interact With the hg Mutation to Regulate Growth Trajectories in Mice

Abstract

The high growth (hg) mutation increases body size in mice by 30–50%. Given the complexity of the genetic regulation of animal growth, it is likely that the effect of this major locus is mediated by other quantitative trait loci (QTL) with smaller effects within a web of gene interactions. In this article, we extend our functional mapping model to characterize modifier QTL that interact with the hg locus during ontogenetic growth. Our model is derived within the maximum-likelihood context, incorporated by mathematical aspects of growth laws and implemented with the EM algorithm. In an F₂ population founded by a congenic high growth (HG) line and non-HG line, a highly additive effect due to the hg gene was detected on growth trajectories. Three QTL located on chromosomes 2 and X were identified to trigger significant additive and/or dominant effects on the process of growth. The most significant finding made from our model is that these QTL interact with the hg locus to affect the shapes of the growth process. Our model provides a powerful means for understanding the genetic architecture and regulation of growth rate and body size in mammals.

THE high growth (hg) gene is a spontaneous mutation that results in a 30–50% increase in postnatal body growth in mice (Bradford and Famula 1984). Earlier physiological studies suggest that the increase of growth efficiency by the hg locus stems from increased energy metabolism without altering overall body composition (Calvert et al. 1985, 1986). Using an interval-mapping approach (Lander and Botstein 1989), Horvat and Medrano (1995) have localized the hg locus near Dl0Mit41 on the distal half of mouse chromosome 10 in both female and male F₂ populations. These authors further found that the hg phenotype is the result of a 500-kb deletion in chromosome 10 that includes three genes, suppressor of cytokine signaling-2 (Socs2), CASP2 and RIPH1 domain containing adaptor with death domain (Raidd/cradd), and viral encoded semaphorin receptor (Vespr or Plexin C1) (Wong et al. 2002). The HG phenotype results from the lack of expression of Socs2 (Horvat and Medrano 2001), which regulates growth hormone signal transduction.

Given the genetic complexity of growth, it is unlikely that the hg gene triggers a marked effect on growth rate and body size with no mediation by environment and other loci. As observed by Corva and Medrano (2000), for example, the nutritional environment confounds the expression of the hg effect on the high growth phenotype in mice. To identify modifiers of the hg locus, Corva et al. (2001) developed an F₂ population segregating for hg to examine interactions between hg and other growth genes. They identified a significant quantitative trait locus (QTL), Q2Ucd2, located on chromosome 2, affecting weight gain from 2–9 weeks. This QTL accounts for 10.4% of the phenotypic variance in the homozygous hg/hg mice and also exerts effects on carcass ash and protein and femur length.

Comparing two F₂ subpopulations, one homozygous for the mutant allele (hg/hg) and the other homozygous for the wild-type allele (+/+), Corva et al. (2001) detected a growth QTL that was expressed differently between the two subpopulations and, therefore, thought to interact with the hg locus. Such an hg background-dependent QTL identified from single-trait mapping makes it worthwhile to perform more thorough QTL analyses for ontogenetic growth using functional mapping (Ma et al. 2002; Wu et al. 2004a,b,c; Zhao et al. 2004). Functional mapping that integrates mathematical aspects of growth laws into a mapping framework can localize dynamic QTL responsible for the biological process of a trait measured at a finite number of time points and provide biologically meaningful results about QTL detection. By estimating the parameters that determine shape and function of a particular biological process, rather than directly estimating gene effects at all possible points during the entire time course, functional mapping strikingly reduces the number of parameters to be estimated and, hence, displays increased statistical power to detect hidden QTL for growth processes.

The motivation of this article is to develop a statistical model for detecting QTL that interact with the hg locus to influence the growth process within the context of functional mapping. Unlike single time point analyses by Corva et al. (2001), this model provides a quantitative and testable framework for studying the interplay between epistasis and growth pattern. Also, unlike our earlier interaction model for a pair of unknown QTL (Wu et al. 2004a), this model attempts to detect epistasis between modifier QTL and a known gene on the genome, which is supposed to provide better estimates of the QTL locations. Although motivated to solve a practical problem in mouse QTL mapping (Corva et al. 2001), we have developed a general epistasis-detecting model that can be used to unveil the genetic secrets of growth trajectories for other species.

MODEL

Background and problem:

The hg mutation has been introgressed into the C57BL/6J (C57) background through nine backcrosses to create congenic line C57BL/6J-hg/hg (HG). A mapping population was founded by mating smaller CAST/EiJ (CAST) males to HG females, which produced a total of 75 F₁ and 1132 F₂ mice (Corva et al. 2001). To test the segregation of hg in the mapping population, these F₂ mice were genotyped by using D10Mit41 on chromosome 10, detected to be linked with hg and D10Mit69, a marker that maps within the hg deletion (Horvat and Medrano 1995). Mice homozygous for HG alleles at D10Mit41 and without a PCR amplification product for D10Mit69 (indicating homozygosity for the hg deletion) were thought to be homozygous for the mutant allele (expressed as hg/hg). On the other hand, mice homozygous for CAST alleles at D10Mit41 and amplifying for D10Mit69 were regarded as being homozygous for the wide-type allele (expressed as +/+). It was found that there were 274 +/+ mice, 596 +/hg mice, and 262 hg/hg mice in the F₂ cross, which conforms to Mendelian segregation ratios.

Our hypothesis is that there exist particular QTL for body growth that are expressed differently among the three hg-typical genotypes. Such QTL are thought to be modifiers that epistatically modulate the effects of hg. Below, we modify our functional mapping model (Ma et al. 2002; Wu et al. 2004a,c) to detect QTL modifiers that display epistatic effects with the hg locus on growth trajectories.

The likelihood function:

Suppose there are n mice for the F₂, which is composed of three subpopulations for the hg gene with size n_j (j = 2 for genotype hg/hg, 1 for genotype hg/+, and 0 for genotype +/+). Assume that a QTL for growth curves or trajectories is segregating to form three genotypes, expressed by k (k = 2 for QQ, 1 for Qq, and 0 for qq), with alleles Q from the HG parent and q from the CAST parent. Consider a genetic linkage map constructed for the F₂ using molecular markers. The foundation of interval QTL mapping is laid on the mixture model in which each F₂ individual is assumed to arise from one and only one of the possible QTL genotypes within known genotypes of two markers that bracket the QTL (Lander and Botstein 1989). The frequencies of each QTL genotype within marker interval genotypes, i.e., the conditional QTL genotype probabilities given markers (see Table 1), are embedded within the mixture model to reflect the genomic position of the QTL within the marker interval.

TABLE 1.

Conditional probabilities (ϖ_k|i) of QTL genotypes given marker genotypes for M_ℓ and M_ℓ+1 in the F₂ population

	QTL genotype
Marker genotype	QQ	Qq	qq
MℓMℓMℓ+1Mℓ+1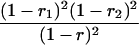
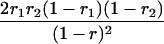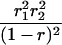MℓMℓMℓ+1mℓ+1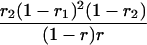
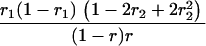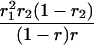MℓMℓmℓ+1mℓ+1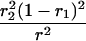
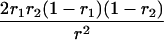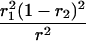MℓmMℓMℓ+1Mℓ+1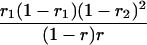
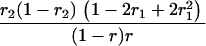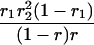MℓmℓMℓ+1mℓ+1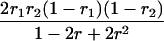
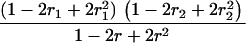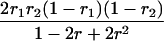Mℓmℓmℓ+1mℓ+1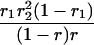
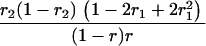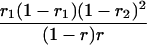mℓmℓMℓ+1Mℓ+1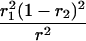
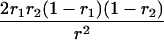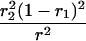mℓmℓMℓ+1mℓ+1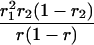
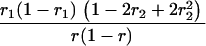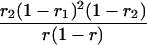mℓmℓmℓ+1mℓ+1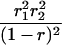

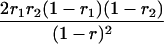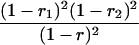r₁, r₂, and r are the recombination fractions between marker M_ℓ and the QTL, between the QTL and marker M_ℓ+1, and between the two flanking markers. Marker alleles M_ℓ and M_ℓ+1 are assumed to be from the HG parent and m_ℓ and m_ℓ+1 from the CAST parent, respectively.

Let ϖ_k(j)|i be the conditional probability of a joint hg-QTL genotype for individual i given a marker genotype. The likelihood function of growth data, y, measured at T different time points for the hg gene and putative QTL is written as

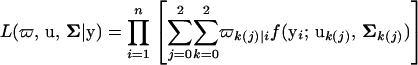(1)

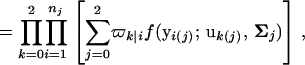(2)

where ϖ is the parameter for QTL position contained in the matrix of the QTL conditional probability, u contains the genotypic mean vector for different hg-QTL genotypes, and Σ is the residual covariance matrix within hg-QTL genotypes. Equation 1 can be converted to Equation 2 because for each individual the hg genotype is known and, thus, the product of the likelihood over different individuals is made among three different hg genotypes. In Equation 2, nine joint hg-QTL genotypes in the mixture model for a given individual i can be simply expressed by three QTL genotypes separately for three hg genotypes. For this reason, ϖ_k(j)|i can be expressed by ϖ_k|i. We assume that the residual covariance matrix is different among the hg genotypes but the same within different QTL genotypes (see Equation 2).

The conditional probability ϖ_k|i can be differently calculated when the QTL and hg are located at different marker intervals and when they are located next to each other. In the former case, ϖ_k|i's have the same form for each of the three hg genotypes (see Table 1). In the latter case, ϖ_k|i's have different forms for different hg genotypes, but they still can be obtained from Table 1 by treating the hg gene as a marker. The choice of one of the two flanking markers M_ℓ and M_ℓ+1 in Table 1 as the hg gene depends on the left or right side of the hg gene at which the QTL is located.

In the mixture model of Equation 2, the multivariate normal distribution of hg-QTL genotype jk for growth traits measured for individual i in each subpopulation k is expressed as

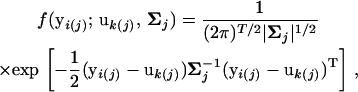where y_i(j) = [y_i(j)(1),…, y_i(j)(T)] is a vector of subpopulation-specific observation measured at T time points, and u_k(j) = [u_k(j)(1),…, u_k(j)(T)] is a vector of expected values for genotype jk at different points. At a particular time t, the relationship between the observation and expected genotypic value can be described by a linear regression model,

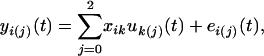where x_ij is the indicator variable denoted as 1 if a QTL genotype k is considered for subject i and 0 otherwise; and e_i(j)(t) is the residual error that is i.i.d. normal with the mean of zero and the variance of 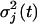. The errors at two different time points, t₁ and t₂, are correlated with the covariance of cov_j(t₁, t₂). These (co)variances compose a (T × T) matrix Σ_j.

Modeling the mean vector and (co)variance matrix:

The estimation of the mean vector u_k(j) and the (co)variance matrix Σ_j is statistically difficult because they involve too many unknown parameters given a possible sample size. Also, such direct estimation does not take into account the biological principles of growth and development. We incorporate the universal growth law, as described by a logistic equation, into the estimation process of the likelihood function (Equation 2). Thus, the mean value of hg-QTL genotype jk at time t is expressed by

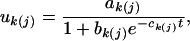(3)

where the growth parameter set 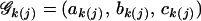describes the asymptotic growth, initial growth, and relative growth rate, respectively. With this growth equation, we need only estimate the growth parameters, rather than estimate genotypic values at every point, to detect genotypic differences in growth. This can significantly reduce the number of unknown parameters to be estimated, especially when the number of time points is large. Moreover, the statistical significance of a QTL and its interaction with the hg gene can be tested by comparing these growth parameters among the three different QTL genotypes across different subpopulations.

Similarly, the covariance matrix can be structured with an appropriate model. Statistical analysis of longitudinal data has established a number of structural models that capture most of the information contained in the matrix (Diggle et al. 2002). Here, we use a first-order autoregressive [AR(1)] model to model the structure of the matrix, which is based on two assumptions, first, the variance σ² is constant over time, and, second, the correlation decays in a proportion of ρ purely with time interval. With the AR(1) model, we need only estimate 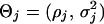instead of all elements in the matrix. The advantage of such a matrix-structuring model is to reduce the number of unknown parameters, without losing the information of the matrix. Many other structural models may be more advantageous over the stationary AR(1) model, but the choice of an optimal model in a particular situation should be based on statistical tests, as described in Kirkpatrick and Heckman (1989), Pletcher and Geyer (1999), Zimmerman and Nunez-Anton (2001), and Pletcher and Jaffrezic (2002).

Computational algorithms:

As classified above, the unknown parameters that build up the likelihood function (Equation 2) include the curve parameters, matrix-structuring parameters, and the QTL genotype frequencies specified by QTL position measured in terms of the recombination fractions (r₁ or r₂) between the QTL and its flanking markers (see Table 1). Arrayed by 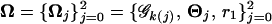, these unknowns can be estimated through differentiating the log-likelihood function of Equation 2 with respect to each unknown, setting the derivative equal to zero, and solving the log-likelihood equations. This estimation process can be implemented with the expectation-maximization (EM) algorithm (Dempster et al. 1977) as described below.

The log-likelihood function of growth and marker data (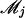) for subpopulation k based on Equation 1 is given by

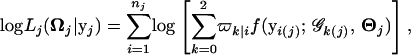with the derivative with respect to any element Ω_l

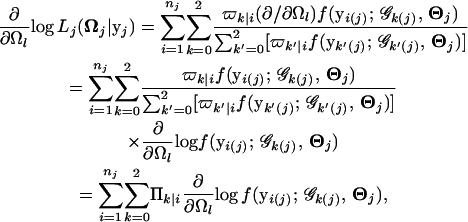where we define

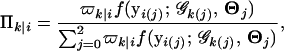(4)

which could be thought of as a posterior probability that progeny i with a particular marker genotype has QTL genotype j. We then implement the EM algorithm with the expanded parameter set {Ω, Π}, where Π = {Π_k|i}. Conditional on Π (the E step; Equation 4), we solve for

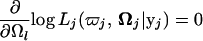(5)

to get the estimates of Ω (the M step; Equation 5). The estimates are then used to update Π, and the process is repeated between Equations 4 and 5 until convergence. The values at convergence are the maximum-likelihood estimates (MLEs) of Ω. The iterative expressions of estimating Ω from the previous step were given in Ma et al. (2002) and Wu et al. (2002, 2004b). In Wu et al. (2002), approximate estimates of the samplings errors from Fisher's information matrices were given.

As usual, the QTL position parameter can be viewed as a known parameter because a putative QTL can be searched at every 1 or 2 cM on a map interval bracketed by two markers throughout the entire linkage map. The amount of support for a QTL at a particular map position is often displayed graphically through the use of likelihood maps or profiles, which plot the likelihood-ratio test statistic as a function of map position of the putative QTL.

Hypothesis tests:

Different from traditional mapping approaches, our functional mapping for longitudinal traits allows for the tests of a number of biologically meaningful hypotheses (Wu et al. 2004a). These hypothesis tests can be a global test for the existence of significant QTL, a local test for the genetic effect on growth at a particular time point, a regional test for the overall effect of QTL on a particular period of growth process, or an interaction test for the change of QTL expression across times. These tests at different levels can be formulated to test the effects of QTL × hg interaction on the shape of growth.

Testing whether specific QTL exist to affect growth trajectories is a first step toward the understanding of the genetic architecture of growth and development. The genetic control over entire growth processes can be tested by formulating the following hypotheses:

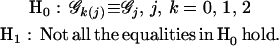(6)

The H₀ states that there are no QTL affecting growth trajectories and the three genotypic curves in each subpopulation overlap (the reduced model), whereas the H₁ proposes that such QTL do exist (the full model). The test statistic for testing the hypotheses in Equation 6 is calculated as the log-likelihood ratio of the reduced to the full model,

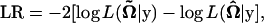(7)

where 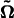and 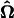denote the MLEs of the unknown parameters under H₀ and H₁, respectively. The LR is asymptotically χ²-distributed with 18 d.f. An empirical approach for determining the critical threshold is based on permutation tests, as advocated by Churchill and Doerge (1994). By repeatedly shuffling the relationships between marker genotypes and phenotypes, a series of the maximum log-likelihood ratios are calculated, from the distribution of which the critical threshold is determined.

After a significant QTL is detected, the next test is about the interaction effect between this QTL and hg on growth. We use the area under curve (A_k(j)) as a criterion for this QTL × hg interaction test, expressed as

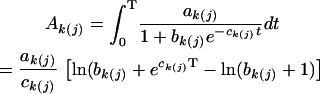In this case, the null hypothesis for testing QTL × hg interaction can be formulated as

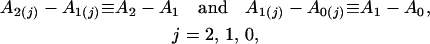i.e., the difference between the areas under curves of different QTL genotypes is set equal for the three hg genotypes.

In addition to testing overall genetic effects on growth trajectories, our model allows for the tests of the additive and dominant effects as well as the interaction effects between the QTL and hg locus. Let a₁ and a₂ be the additive effects of the hg and QTL; d₁ and d₂ be the dominant effect of the hg and QTL; and I, J, K, and L be the additive × additive, additive × dominant, dominant × additive, and dominant × dominant epistatic effects between the loci (Lynch and Walsh 1998). We tabulate A_k(j) in terms of their genetic compositions as

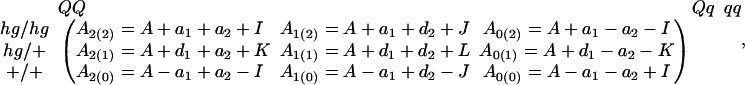where A is the overall mean. Hypothesis tests for these genetic effects are formulated with constraints

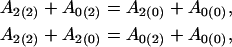for the additive genetic effects of the hg and QTL, respectively,

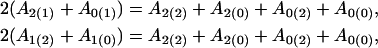for the dominant genetic effects of the hg and QTL, respectively, and

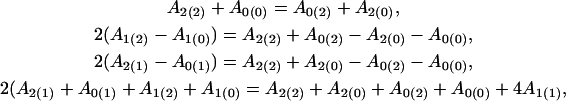for the additive × additive, additive × dominant, dominant × additive, and dominant × dominant genetic effect interactions between the hg and QTL, respectively.

RESULTS

To detect QTL modifiers, we need to genotype and phenotype F₂ mice from each of the three hg genotypes hg/hg, hg/+, and +/+. However, the animal material available to our QTL analysis contains only two subpopulations hg/hg and +/+ developed by Corva et al. (2001) with a two-step approach as follows: In the first step, a linkage map covering the 19 autosomes and one sex chromosome (X) was constructed with 83 molecular markers for 262 hg/hg mice from the F₂ cross. A simple analysis of variance approach was used to detect significant markers associated with growth rate and body weight. In the second step, the most significant markers genotyped in the hg/hg subpopulation were also typed for the 274 +/+ mice from the same F₂ population. These genotyped markers were found to be located at chromosomes 1, 2, 4, 9, and X (Corva et al. 2001), with which a common linkage map that integrates the two subpopulations was constructed.

Both the hg/hg and +/+ subpopulations were phenotyped for body weight on a weekly basis from 2 to 9 weeks of age. However, about one-third of the mice from each subpopulation were measured only at weeks 3, 6, and 9. Although our original model was designed for the same measurement schedule for all subjects (Ma et al. 2002), a recent model has been derived to handle subject-dependent measurement schedules with a reasonable convergence rate (Hou et al. 2005). Data for body weights at different ages were corrected for the effects of dam, litter, sex, and parity.

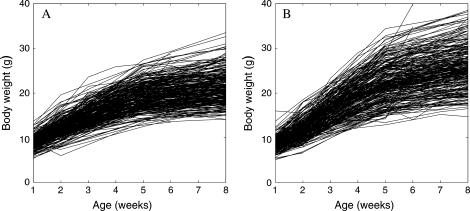
The logistic curve described by Equation 3 was used to fit the growth trajectory for each mouse, using nonlinear least-squares approaches. Statistical tests indicate a good fitness at the significance level P < 0.001. There is a substantial difference in growth pattern between the two F₂ subpopulations, hg/hg and +/+ (Figure 1). On average, these two subpopulations are similar from birth to age 3 weeks, but after 3 weeks the hg/hg mice display much greater growth (Figure 1B) than do the +/+ mice (Figure 1A). Substantial variation in growth curve among different animals in each subpopulation suggests that specific QTL may be involved in shaping developmental trajectories.

Figure 1.

Plots of body mass vs. ages for (A) 2xx +/+ mice and (B) 2xx hg/hg mice in an F₂ progeny derived from HG and CAST lines (Corva et al. 2001).

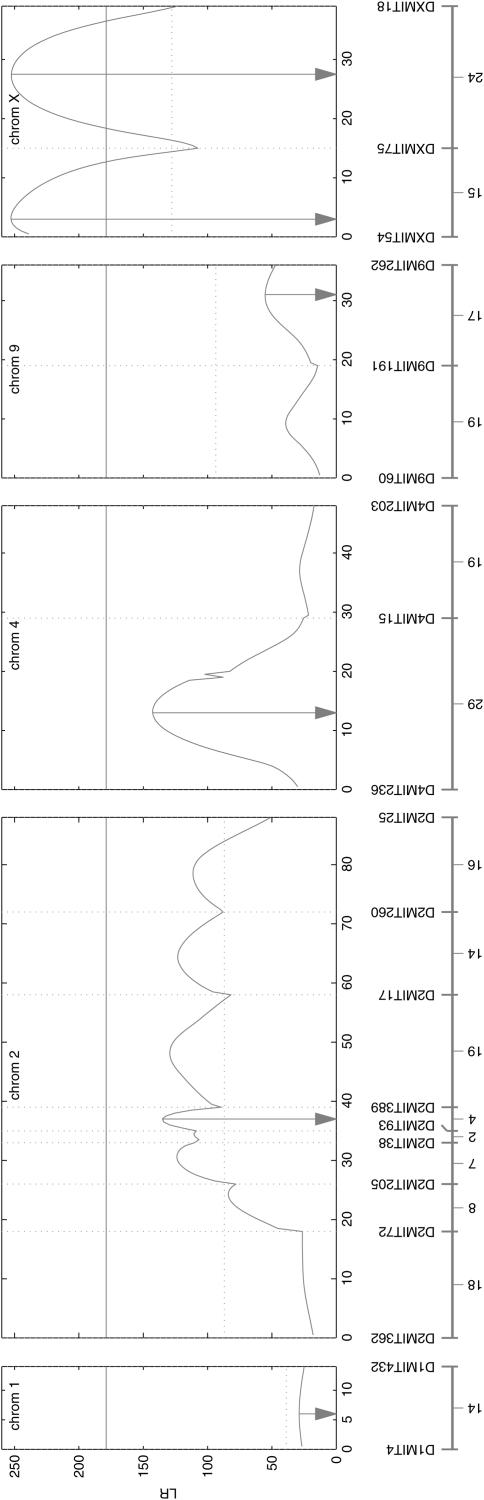
Our mapping model is employed to search for growth QTL through a genome-wide scanning approach. Figure 2 illustrates the profile of the log-likelihood ratio (LR) test statistics throughout the common linkage map for the two subpopulations. The “genome-wide” critical threshold value throughout the common linkage map at the α = 0.01 significance level was estimated as 155.2 on the basis of 1000 permutation tests. According to this criterion, two separate QTL each corresponding to a peak of the LR profile were detected on chromosome X. We also computed the chromosome-wide critical thresholds with the LR peaks of individual chromosomes. A few distinct peaks on chromosome 2 may carry multiple QTL according to this criterion. On the basis of earlier studies with the same mapping material, the locations of these suggestive QTL (Figure 2) contain important QTL for many growth-related traits (Corva et al. 2001). For this reason, we perform an in-depth hypothesis test for the QTL located at the highest peak (Figure 2), as for the two QTL on chromosome X.

Figure 2.

The profile of the log-likelihood ratios (LR) between the full and reduced (no QTL) model for body mass growth trajectories across the linkage map constructed from molecular markers. The genomic positions corresponding to the peak of the curve, as indicated by vertical dotted lines, are the MLEs of the QTL positions. The genome- and chromosome-wide threshold values for claiming the existence of QTL are given as the horizonal solid and dotted lines, respectively. The positions of markers on chromosomes are given beneath the x-axis.

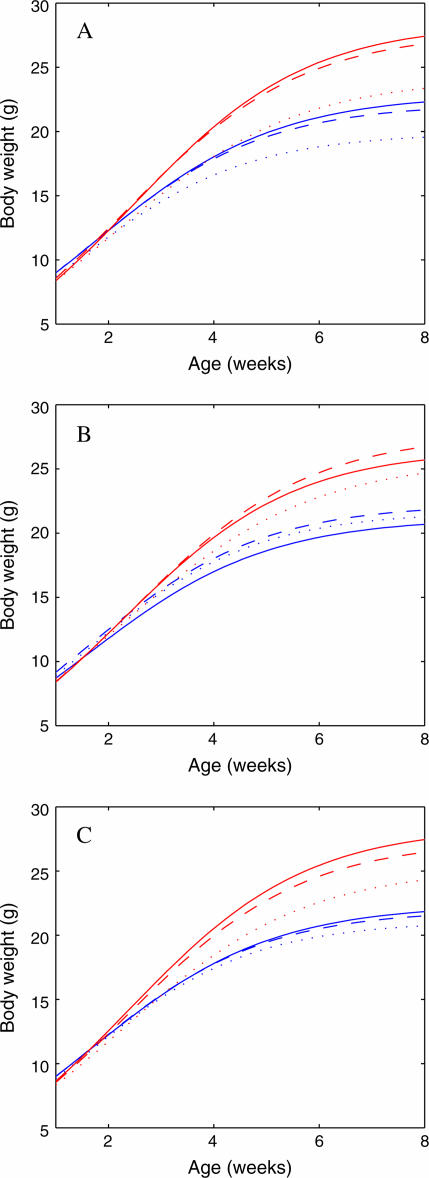
The three growth curves each determined by a genotype at each of these significant QTL are drawn separately for the hg/hg and +/+ mice (Figure 3), using the MLEs of curve parameters (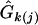; Table 2) from our model. As expected, the hg locus displays a striking (additive) effect on growth trajectories (Table 3). The growth trajectories of the same QTL genotype are different between the two subpopulations, suggesting that the genetic expression of QTL is affected by genetic background. In general, the three detected QTL start to exert their effects on growth in both subpopulations when the mice are 3 weeks of age (Figure 4). After this age, the QTL effects tend to increase with age.

Figure 3.

Three growth curves, each presenting a group of genotype QQ (solid curves), Qq (dashed curves), and qq (dotted curves), in the hg/hg (red) and +/+ (blue) mice at the QTL, detected by our joint model, on chromosomes 2 (A) and X (B and C).

TABLE 2.

The MLEs of the QTL position, QTL effects described by growth parameters 𝒢_k(j)=(a_k(j), b_k(j), c_k(j)), residual variance (σ_j), and correlation (ρ_j) in two different subpopulations of the F₂ mouse population

		QQ			Qq			qq			Residual
Subpopulation	Position (cM)	a2(k)	b2(k)	c2(k)	a1(k)	b1(k)	c1(k)	a0(k)	b0(k)	c0(k)	ρj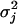
Chromosome 2
+/+	37	22.88	2.77	0.58	22.15	2.68	0.60	19.86	2.41	0.63	0.88	6.75
hg/hg	28.40	4.36	0.60	27.73	4.06	0.60	24.16	3.35	0.57	0.87	12.05
Chromosome X
+/+	3	21.16	2.58	0.59	22.25	2.61	0.60	21.65	2.68	0.63	0.89	7.06
hg/hg	26.47	3.96	0.61	27.72	4.12	0.59	25.74	3.41	0.55	0.87	13.08
Chromosome X
+/+	29	22.38	2.66	0.58	21.95	2.64	0.60	21.08	2.61	0.63	0.90	7.34
hg/hg		28.43	4.15	0.59	27.36	4.00	0.59	25.21	3.59	0.57	0.87	12.77

Position indicates the map distance in centimorgans from the first marker on a chromosome. Uppercase Q and lowercase q stand for the alleles from the HG and CAST parents, respectively.

TABLE 3.

The LR values and the corresponding P-values (in parentheses, estimated from simulation studies) for testing the additive effect of the hg locus (a₁), the additive (a₂) and dominant (d₂) effects of QTL, and the additive × additive (I) and additive × dominant (J) epistatic effects between hg and QTL on overall growth curves

Mutation/QTL	a1	a2	d2	I	J
Hg	83.5 (0.000)
Chromosome 2	13.6 (0.001)	8.7 (0.004)	6.6 (0.023)	5.3 (0.030)
Chromosome X	2.7 (0.082)	7.7 (0.021)	13.6 (0.003)	1.6 (0.120)
Chromosome X		3.1 (0.087)	4.8 (0.041)	12.7 (0.004)	15.1 (0.002)

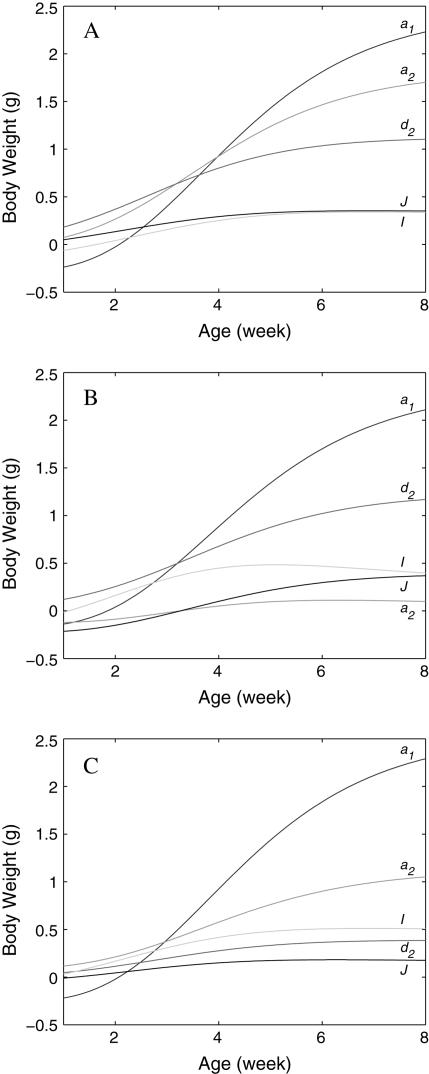
Figure 4.

Dynamic changes of the genetic effects of the hg gene (a₁) and QTL (a₂ and d₂) as well as their epistatic interactions (I and J) for the QTL, detected by our joint model, on chromosomes 2 (A) and X (B and C).

We further tested the QTL effects and how they interact with the hg locus to affect growth trajectories. On the basis of the hypothesis test given in Equation 7 and others, we calculated the LR values for the additive and dominant effects of the QTL and its interaction effects with hg for all three QTL (Table 3). The QTL detected on chromosome 2 has highly significant additive and dominant effects on growth trajectories, operating in a dominant gene action manner as shown by small differences between genotypes Qq and QQ in both subpopulations (see Figure 3). This QTL also displays significant additive × additive and additive × dominant epistatic effects with the hg locus.

Located on the same chromosome, the two QTL detected on chromosome X exhibit different modes of gene action for growth. The first QTL at 3 cM from the first marker has a nonsignificant additive effect but highly significant dominant effect (Table 3; Figure 3B). When interacting with the hg gene, however, this dominant QTL displays an inverse pattern, i.e., with a significant additive × additive but nonsignificant additive × dominant epistatic effects (Table 3). The second QTL at 37 cM from the first marker seems to act in a partial dominant manner (Figure 3C), with both types of epistatic effects being significant (Table 3). Except for the first QTL on chromosome X with a nonsignificant additive effect, the favorable allele at the other QTL that contribute to greater growth originates from the HG parent.

Because only two hg genotypes are included, we cannot estimate all the QTL-hg epistatic effects. The dynamic changes of different types of genetic effects for the hg and QTL across ages that can be estimated are

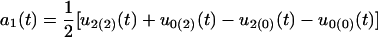for the additive genetic effect of the hg locus,

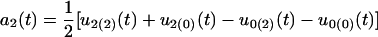for the additive genetic effect of the QTL,

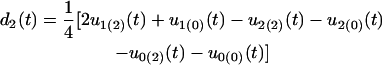for the dominant genetic effect of the QTL,

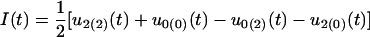for the additive × additive genetic effect, and

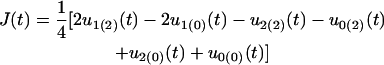for the additive × dominant genetic effect between hg and QTL. All these age-dependent changes of genetic effects are illustrated in Figure 4. The additive effect (a₁) of the hg locus increases rapidly with age, and so do the additive (a₂) and/or dominant effects (d₂) of the QTL, but with a lesser extent. The interaction effects (I and J) between the QTL and hg are quite stable over age, contributing to a significant part of the genetic variation throughout growth ontogeny.

DISCUSSION

Traditional quantitative genetic theory proposes that genetic variation in a quantitative trait is due to polygenes each with a small effect on the phenotype and being sensitive to the environment (Lynch and Walsh 1998). Although this theory has led to substantial successes in the explanation of quantitative variation, it has been challenged by recent discoveries of QTL based on polymorphic markers. According to these QTL mapping results, a quantitative trait may be governed by unequally sized loci with a few having larger effects than many others (Mackay 2001). A 30–50% increase of body size in mice caused by the hg mutation (Bradford and Famula 1984) provides excellent evidence for the inclusion of a major gene in the genetic control of a quantitative trait.

As part of the complex network of genetic control, the expression of the hg locus should not be independent of the genetic background (Corva et al. 2001). It thus is of great interest to identify individual QTL that interact with the hg locus using mapping approaches. The identification of such QTL can improve our understanding of the interactions between pathways of signal transduction involved in the regulation of growth. This information can then be transferred to the development of techniques targeted to manipulate these growth-regulating pathways in mammals.

In this article, we have presented a statistical model for detecting interacting QTL involved in the regulation of growth through the hg locus. This model is the extension of our functional mapping approach (Ma et al. 2002; Wu et al. 2004a; Zhao et al. 2004) proposed to shed light on the genetic architecture of growth by incorporating its underlying developmental principles (von Bertalanffy 1957; Rice 1997; West et al. 2001) and the statistical methods for growth analysis (Diggle et al. 2002). A QTL is thought to be epistatic with the hg gene if its expression depends on the genetic background containing segregating hg. The extended model has power to estimate the differences in the gene action of a QTL expressed in different hg genotypes. Corva et al. (2001) constructed a segregating F₂ population using a congenic hg/hg line and a wild-type inbred line. Molecular markers at genomic regions that may contain QTL for growth rate and body size were genotyped to construct a common linkage map for two F₂ subpopulations, hg/hg and +/+. Thus, by estimating and testing the genetic effects of a QTL in these two different subpopulations, we can determine how the QTL, as a modifier, influences the expression of the hg/hg gene.

Our model has successfully detected three QTL that interact with the hg gene to govern the shape of growth trajectories. These detected QTL on chromosomes 2 and X affect growth curves with different modes of gene action. The estimation for the location of the QTL on chromosome 2 is broadly in agreement with that by previous QTL mapping based on a single-trait analysis (Corva et al. 2001), although our analysis is more informative in terms of age-dependent changes of QTL effects and the detection of epistasis in the genetic control of growth traits. The epistasis between the detected QTL and the hg locus is relatively small, relative to their main effects, but is thought to play a significant role in shaping growth processes. As illustrated by Figure 4, there are different patterns for the change of different genetic effects across ages. The additive effect of the hg locus increases rapidly with age, and so do the additive and/or dominant effects of the QTL, but to a lesser extent. The interaction effects between the QTL and hg are quite stable over age, contributing a significant part of the genetic variation throughout growth ontogeny.

The genetic control of body size across age has been observed in mice by both quantitative genetic (Cheverud 1984; Atchley and Zhu 1997) and QTL mapping approaches (Cheverud et al. 1996; Vaughn et al. 1999). It is suggested that the formation of such age-specific patterns is regulated by different genetic mechanisms. Falconer et al. (1978) speculated two general physiological mechanisms that determine the increase in body size in mice, but these mechanisms appear to act at different life stages (Atchley and Zhu 1997). This has been confirmed by QTL mapping of mouse growth traits in that early and late growth in mice were affected by distinct QTL, mapping to separate chromosome locations (Cheverud et al. 1996; Vaughn et al. 1999). In other animals, Carlborg et al. (2003) found that epistasis is important for early growth when the foundation for rapid growth is set by the development of internal organs, but less important for later growth involving the main deposition of body tissues. Our model has the capacity to quantify the patterns of the age-dependent change of genetic effects and, thus, to gain more insights into the interplay between gene action and development in developmental biological research.

In this study, we have reported only on the additive effect of the hg gene as well as its additive-related epistatic effects with other QTL detected by molecular markers. An F₂ subpopulation heterozygous for the mutant and wild-type alleles that would allow estimation of effects due to dominance was not available. Using the available material, we have found three QTL on chromosomes 2 and X that interact with the hg locus to affect the shapes of the growth process. These genetic interactions are thought to play an important role in mediating the expression of the hg gene. Our model is fit by one modifier QTL, but it can be readily extended to include more modifiers that interact with each other and with the hg gene. The involvement of more QTL in the model can better reflect a practical situation in which there is a web of interacting genes in trait control (Segre et al. 2005). Although the available genetic data from Corva et al. (2001) were not subject to a multi-QTL analysis because of their low coverage of the mouse genome (including only chromosomes 1, 2, 4, 9, and X), our model derived in this article provides a powerful tool to shed light on the genetic architecture and regulation of growth rate and body size in mammals.