Abstract
The role of protein flexibility in molecular motor function has previously been studied by considering a Brownian ratchet motor that is connected to its cargo by an elastic spring, with the result that the average velocity of the motor/cargo system is increased by reducing the stiffness of the linkage. Here, we extend this investigation to the case of chromosome transport during anaphase A, in which the relevant flexibility is not primarily in the motor/cargo linkage but rather in the cargo itself, i.e., in the chromosome. We model the motor mechanism as an imperfect Brownian ratchet with a built-in opposing load and the chromosome as a collection of discrete segments linked by an elastic energy function that discretizes the potential energy of an elastic rod. Thermal fluctuations are produced in the model by random forces, as in Brownian dynamics. All of the parameters that characterize the chromosome are known or can be estimated from experimental data, as can all but one of the motor parameters, which is adjusted to give the correct transport velocity of normal-length chromosomes. With the parameters so determined, we then reproduce the experimental finding of Nicklas [Nicklas, R. B. (1965) J. Cell Biol. 25, 119–135] that chromosome speed is essentially independent of chromosome length, even though our model contains no “velocity governor.” We find instead that this effect is a consequence of chromosome flexibility, as it disappears when stiffer than normal chromosomes are considered.
Keywords: Brownian ratchet, molecular motors, protein elasticity, velocity governor, thermal fluctuations
The dramatic segregation of chromosomes during the anaphase A stage of mitosis has fascinated scientists for decades. During that time, researchers have discovered that the sister chromatids are attached via their kinetochores to bundles of microtubules known as kinetochore microtubules (kMTs). The kMTs connect the chromosomes to the centrosomes, which form the poles of the mitotic spindle. The mechanism that actually moves the chromosomes poleward, however, has remained elusive until relatively recently, and some aspects of that mechanism are still unexplained.
Whatever the force-generating mechanism, it is clear that the forces involved are large enough to deform the chromosomes substantially, as they bend significantly when dragged through the viscous intracellular millieu. This bending raises the question of whether chromosome flexibility plays an important role in chromosome transport. That question is the subject of this article. Our aim is to answer it by mathematical modeling and computer simulation. The answer will, of course, be provisional, in the sense that it will be only as good as the assumptions used in formulating the model. These assumptions necessarily involve the motor mechanism and the flexible nature of the chromosomes, and the reader should keep in mind that different hypothetical motor mechanisms might interact with chromosome flexibility in different ways. Other motor mechanisms can be investigated on a case-by-case basis by using methods similar to those introduced here.
Many basic properties of anaphase chromosome motion were discovered in a series of elegant experiments by Nicklas (1–3). By severing the microtubules connecting the kinetochore to the pole, Nicklas was able to show that the force was being produced at or near the kinetochore (3). Interestingly, he also found that the mean anaphase A velocities of the various chromosomes in a single cell were roughly the same, despite many-fold variations in chromosome size (1). These experimental results led him to suggest the existence of “velocity governors” at the kinetochore to explain the disparity in forces required to pull large and small chromosomes.
Current evidence seems to show that chromosome motion may be produced by either or both of two mechanisms: (i) force produced at the kinetochore as shown by Nicklas, and (ii) force produced at the centrosome by the pulling of kMTs [“poleward flux” (4)]. Note that both mechanisms are accompanied by depolymerization of kMTs but from opposite ends. In the first case the microtubule is depolymerizing at its “plus” end, which is near the kinetochore, and in the second it is depolymerizing at its “minus” end near the centrosome. The relative contribution of these two mechanisms to total force production varies depending on the organism. In Xenopus egg extracts, poleward flux appears to dominate the motion (5), whereas kinetochore-based force production is dominant in vertebrates (reviewed in ref. 6), and both mechanisms contribute roughly equally in Drosophila early embryos (7). In this article, we consider only the first mechanism, in which force is produced by depolymerization of kMTs at the end of the microtubule that makes contact with the kinetochore itself.
Despite the progress made in understanding the mechanics of chromosome motion, the nature of the molecular mechanisms by which the force is produced have remained controversial. The natural candidate for force production would be one of the various microtubule motor proteins. The plus-to-minus directionality of the chromosome movement along kMTs would appear to suggest a role for dynein, but efforts to find such a role have had only limited success (8, 9) and are complicated by the task of disentangling the multiple roles that dynein plays in various mitotic mechanisms (nicely discussed in ref. 8). The directionality of the movement would also seem to preclude the involvement of a conventional kinesin, although the plus-end-directed motor CENP-E has been implicated, seemingly paradoxically, in chromosome movements (10–12). For a theoretical explanation of the role that a plus-end-directed motor can play in minus-end-directed transport see ref. 13.
Lately, a consensus has formed around a “Pac-Man” model whereby depolymerization at the plus end of the associated kMT provides a net poleward motion of the kinetochore, and hence of the chromosome of which it is a part (14, 15). A clear candidate for a type of molecule involved in this process is the kinesin-13 family of kinesin-related proteins, which have been shown to be ATP-dependent microtubule depolymerizers (16–20). Several recent studies have indicated a role for microtubule-depolymerizing kinesin-13 kinesins and their relatives in anaphase A chromosome motion (7, 21–23), providing a biochemical basis for the Pac-Man model.
A natural physical interpretation of the Pac-Man mechanism is the Brownian ratchet, as applied to depolymerization-driven transport by Peskin and Oster (13). One can fit the problem of chromosome motion into the Brownian ratchet framework by considering the kinetochore as an object diffusing along the length of the microtubule but linked to it in such a manner that it cannot diffuse off the end of the microtubule. As the kinetochore diffuses poleward, away from the terminal tubulin dimer, that dimer may be depolymerized, i.e., detached from its protofilament of the microtubule, thereby “ratcheting” the kinetichore poleward. As this process repeats itself, a net poleward motion is created, thus providing the “force” necessary to move chromosomes. The Brownian ratchet has many properties that distinguish it from a simple force generator, however. For example, in the case of a load attached to a Brownian ratchet motor by means of a spring, the mean speed of the motor (and hence the load) depends on the elasticity of the spring joining the motor to the load (24), and not just on the friction coefficient of the load as it would if the motor were a pure force generator. This result suggests (but certainly does not prove) that if a Brownian ratchet motor were assigned the task of pulling an extended elastic body like a chromosome, then the flexibility of the chromosome would influence the mean speed at which the chromosome would be transported.
In this article, we postulate an especially simple form of a Brownian ratchet motor for chromosome transport. It is an imperfect Brownian ratchet, which means that it receives a finite amount of free energy as it passes each ratchet site in the “forward” (poleward) direction. This free energy may come from the energy that was stored during microtubule assembly and is released upon depolymerization, or perhaps it comes more directly from ATP hydrolysis by the motor protein itself. Between ratchet sites, the motor works against a built-in internal load that gives it an activation barrier that must be climbed to reach the next ratchet site. This load may represent the force caused by a conventional kinesin located elsewhere in the kinetochore such as CENP-E or the internal activation energy of the depolymerizing enzyme itself. Such a bias may serve the purpose of keeping the kinesin close to the plus end of the microtubule, where it can best catalyze depolymerization (see ref. 13). Because of the wealth of biophysial data available for Drosophila early embryos and the simple nature of the motor mechanism chosen, we were able to fix or reasonably estimate all of the chromosome's physical parameters and all but one of the motor parameters, allowing for both quantitative and qualitative comparison to experiment. Interestingly, when the one free parameter was adjusted to reproduce the experimentally measured chromosome velocities, the model also produced nearly equal velocities for both long and short chromosomes. This independence of velocity on chromosome length strongly depended on the flexibility of the chromosome and was only apparent within the experimentally measured range of chromosome flexibility. Thus, we are able to explain the puzzling load indepedence that a kinetochore seems to possess without invoking any hypothetical velocity governor of the sort that Nicklas (1) had originally postulated, or, to put it another way, chromosome flexibility is the velocity governor.
We conclude that the Brownian ratchet/Pac-Man model is a physically plausible mechanism for chromosome transport during anaphase A and that chromosome flexibility plays an important role in determining the speed of chromosome transport as produced by such a motor. In particular, one role of chromosome flexibility is to make the speed of chromosome transport insensitive to the length of the chromosome that is being transported.
Model
We modeled the chromosome as a series of small segments subject to viscous and random forces and elastic forces coupling the segments to each other. The kinetochore, considered to be rigidly attached to the central segment of the chromosome, was then allowed to diffuse in a 1D potential along a track representing the depolymerizing microtubule. The potential that the kinetochore feels has two parts, one coming from its interaction with the microtubule, and the other from its elastic interactions with the nearby segments of the chromosome.
Model for Chromosomal Dynamics.
For simplicity, and in particular to avoid issues related to stochastic partial differential equations, we modeled the chromosome as a collection of discrete segments linked by elastic forces and buffeted by thermal fluctuations. We were careful, however, to construct the model in such a way that it has a definite continuum limit as the number of computational segments of the chromosome approaches infinity, and we checked that our computational results were insensitive to the number of segments chosen once that number was sufficiently large.
In this spirit, the chromosome of rest length 2s0 is discretized by placing 2N + 1 nodes on the chromosome at locations sj = jΔs, where Δs = s0/N and j = −N. . . N. Each of these nodes can be thought of as representing a segment of the chromosome. Each interior node is centered on the segment that it represents, and that segment has rest length Δs. The nodes at the ends of the chromosome are at the outer ends of their respective segments, which have rest length Δs/2. Note in particular that the node j = 0 lies at the center of the chromosome and represents the segment of the chromosome corresponding to −Δs/2 < s < Δs/2. It is to this segment that the kinetochore is rigidly attached in our model.
The spatial configuration of the model chromosome at any particular time is described by giving the coordinates of the 2N + 1 nodes x̄ = (x−N, …, xN), where xj ∈ ℝ3 is the position of the jth node of the chromosome. The energies caused by bending and stretching then take the form
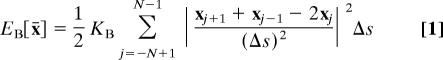 |
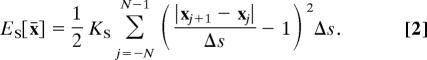 |
Here, KB is the bending modulus and KS is the stretching modulus of the chromosome. Both are proportional to the Young's modulus, Y, which is a size- and shape-independent measure of the elasticity of the chromosomal material. The formulae for the bending and stretching moduli in terms of the Young's modulus are as follows:
where r is the cross-sectional radius of the chromosome (25).
Two ways in which the above model might be inaccurate are: first, the Young's modulus and/or the radius of the chromosome might vary along the length of the chromosome, with the result that the bending and stretching moduli would be functions of position instead of constants; or second, the elastic properties of the chromosome may vary over its cross section, thus altering the relationship between KB, KS, and Y.
With regard to the first issue, experimental studies have shown that for chromosomes of both newt lung epithelial cells and Xenopus A6 cells the bending and stretching moduli are roughly uniform along the length of the chromosome and are, in particular, no different in the vicinity of the centromere than elsewhere on the chromosome (26). Of course, the situation in Drosophila early embryos may be different, and studies of chromosome flexibility in Drosophila were unable to rule out this possibility (27). Given the evidence from other cell types, however, we are fairly confident that the bending and stretching moduli do not vary significantly along the length of the chromosome. Experimental data bearing on the second issue are somewhat contradictory. Simple in vitro bending and stretching experiments seem to indicate a thin, stiff core at the center of the chromosome (28), but later in vivo experiments are in good agreement with the predictions of a homogenous chromosome (26), like that considered here.
The total elastic energy E is the sum of the bending energy and the stretching energy introduced above:
and the elastic force density (i.e., the force per unit unstressed length arising from the elastic deformation of the chromosome) evaluated at node j of the chromosome is given by the principle of virtual work, which here takes the form
for |j| < N, i.e., for all interior nodes, and
for the nodes at the ends of the chromosome, for which |j| = N. Here, (Fjelastic)i is the ith spatial component of Fjelastic and xji is the ith spatial component of xj.
An important aspect of chromosomal dynamics is the drag force exerted by the viscous fluid through which the chromosome moves. One possibility would be to use a fluid mechanical model implemented by a stochastic version of the immersed boundary method (29). Such a model would automatically take into account the fluid-mediated interaction between different parts of the chromosome, and also the orientation-dependent aspect of the fluid drag, i.e., that the viscous resistance to transverse motion of a slender cylindrical segment is greater than the corresponding resistance to axial motion (by about a factor of 2). Here, however, we include neither of these effects and adopt the simpler approach of treating each segment of the chromosome as though it experiences simply a drag force proportional to its own local velocity and pointing in the opposite direction to the velocity vector. We further assume that the constant of proportionality, which we call the friction coefficient, is completely isotropic, i.e., having the same value for all orientations of the segment with respect to the direction of motion.
We remark that in simplifying the problem by ignoring the orientation-dependent aspect of the fluid drag we are being conservative with regard to assessing the effects of chromosome flexibility on chromosome transport. That is, we are leaving out one obvious source of such an effect: the bending of the flexible chromosome reduces its drag by partially aligning the distal parts of the chromosome with the direction of motion through the fluid. This drag-reduction effect is explicitly excluded from our present model, because such alignment in our model does not alter the isotropic friction coefficient. Thus, if chromosome flexibility has an effect in our model, it must be caused by a more subtle effect related to the influence of that flexibility on the thermal fluctuations of the Brownian ratchet motor.
To assign a friction coefficient to each segment of the model chromosome, we first estimate the friction coefficient f of the whole chromosome by using the formula for total transverse friction of a long, needle-like ellipsoid (30):
where η is the dynamic viscosity of the intracellular medium. Dividing f by the length of the chromosome (2s0), we obtain an expression for ζ, the friction coefficient per unit length.
Now we assign to each interior node the friction coefficient ζΔs, and to each of the nodes at the ends of the model chromosome we assign the friction coefficient ζΔs/2, because each interior node represents a segment of length Δs and each terminal node represents a segment of length Δs/2, as described above.
The above procedure for the assignment of friction coefficients to nodes has the property that the total friction coefficient is correct (for transverse motion) under the assumption that the chromosome can be modeled as a slender ellipsoid with circular cross section of radius r and total length 2s0. Note, however, that the friction per unit length ζ depends on the length of the chromosome through the logarithmic term in the denominator. This weak, but still somewhat paradoxical, effect reflects the long-range character of viscous interaction in Stokes flow and points to the need for a true hydrodynamic model, which, as mentioned above, is under development.
To include the kinetochore in the above scheme, we simply calculate the friction of the central chromosome segment (f0) as follows:
where fkinetochore = 6 πηrkinetochore, assuming a spherical shape for the kinetochore. Here, we assume that the kinetochore is rigidly attached to the central segment of the chromosome. That the friction coefficients of two connected bodies should be added can be derived by considering them as independent bodies connected by a stiff spring.
Model for the Brownian Ratchet Force-Generating Mechanism.
The motion of the kinetochore must, of course, depend on the Brownian ratchet-like potential describing the depolymerization behavior and the elastic forces described above. Here, we postulate a simple model for this ratchet potential, which will then be coupled to the chromosome dynamics to obtain equations of motion for the whole system.
The kMT is modeled as a segmented track, each segment representing a tubulin heterodimer of length L. We then assume that the kinetochore is tethered to the kMT in some manner. Physically, this tether is most likely one of the kinesin-13 kinesins, because inhibition of these molecules results in defects in chromosome attachment and anaphase A movement (7, 22, 23). These kinesins have been shown to display both a non-ATP-dependent diffusive mode of attachment to microtubules (in which the kinesin is able to move passively along the length of the microtubule) (19) and an ATP-dependent depolymerizing mode of attachment to microtubule ends (17–19, 21). This depolymerization occurs in a processive manner (19). Given the role that the plus-end-directed motor CENP-E may play in keeping the kinetochore located toward the end of the microtubule (10–12), it seems likely that the depolymerizing enzyme is most often associated with the terminal subunit of the kMT. Accordingly, we assume that the kinetochore moves in a tilted periodic potential landscape with a large, sudden drop representing the energy released upon depolymerization, i.e., a ratcheting potential. The natural period for such a potential would be L, the length of a tubulin dimer.
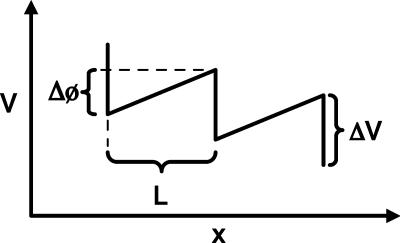
Of course, one could construct many such potentials, and the exact shape of the potential for kinesin-13 kinesins has not yet been experimentally determined. Thus, for simplicity, we chose a tilted sawtooth potential characterized by only two parameters (in addition to the period L): ΔV, representing the free energy released upon depolymerization, and Δφ, representing the work done in moving through a distance L against a constant opposing force. The resulting potential U(x), where x measures distance along the microtubule with x increasing toward the minus end, which is the direction in which the chromosome ultimately moves, is given by
as depicted in Fig. 1. Here, Δφ = 0 corresponds to the case of a simple (but imperfect, because ΔV is finite) Brownian ratchet. The interpretation of Δφ/L as a constant opposing force may perhaps represent the action of a plus-end-directed micotubule motor such as CENP-E. Alternatively, Δφ may represent the activation energy for the depolymerization of the terminal tubulin dimer.
Fig. 1.
Schematic of the potential in which the kinetochore travels. x refers to the position of the kinetochore along the microtubule track. ΔV is the potential drop upon depolymerization, and Δφ is the total linear increase in the potential in period L.
Equations of Motion.
Combining the above models for kinetochore motion and chromosome dynamics leads to the following system of stochastic ODEs describing the motion of the system:
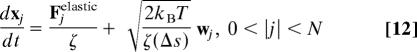 |
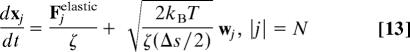 |
 |
Here, wj ∈ ℝ3 is a 3D temporal white noise with the following statistical properties: 〈wj(t)〉 = 0 and 〈wji(t)wkm(t′)〉 = δ(t − t′)δjkδim, where 〈 〉 denotes the expected value of the enclosed quantity. The motion of the kinetochore is represented by the equation corresponding to j = 0; because the kinetochore is only allowed to move along the microtubule, all spatial components, except those along the unit vector e1 (corresponding to the x axis), are ignored. Fkinetochore is a term that represents the force produced by the potential in which the kinetochore moves, corresponding to −dU/dx.
Numerical Method
Our numerical scheme combines a lattice method for the motor with a standard Euler-Maruyama method (31) for the chromosome. The lattice method is needed for the motor because of the discontinuities in the potential U(x) in which it moves. The particular lattice method that we use has been described by Wang et al. (32). It introduces a computational lattice along the microtubule with a uniform spacing that is considerably smaller than the period L. The motor does a random walk on this computational lattice, jumping forward or backward with rate constants determined by the potential energy difference between lattice sites. The energy that is used to determine the rate constants involves not only the potential U(x) of the motor itself, but also the elastic energy determined by the configuration of the central part of the chromosome. Once these rates are computed, a time increment is randomly chosen for a jump to another lattice point by using the Gillespie method (33). This time increment is then used as a time step to update the position of the rest of the chromosome by using the forward Euler method. If the time increment chosen is above the empirically determined stiffness threshold of the underlying partial differential equation, then the time increment is divided equally into p smaller time steps each below the stiffness threshold, and the chromosome is then updated p times by using the smaller time step before the next lattice event is sampled. This method prevents occasional large time increments from causing numerical instability.
Effectively, the time step is controlled by the distance between computational lattice sites along the microtubule. The overall numerical scheme may thus be checked for convergence of mean computed chromosome velocity as this computational lattice is refined (Fig. 3, which is published as supporting information on the PNAS web site). Similarly, we need to check that the computed results are insensitive to the number of segments into which the model chromosome has been subdivided, once that number of segments is sufficiently large (shown in Fig. 4, which is published as supporting information on the PNAS web site.
The numerical method is more completely described in Appendix, which is published as supporting information on the PNAS web site.
Parameters
The parameters used in this study are given in Table 1.
Table 1.
Parameters used in this study
| Parameter | Value | Source/notes |
|---|---|---|
| Young's modulus | 38 ± 20 Pa | Ref. 27 |
| Dynamic viscosity | 0.2 ± 0.1 Pa/s (200 cP) | Ref. 27 |
| Chromosome length | 3.0 ± 1.0 μm (long autosomes) | David Sharp, personal communication |
| 1.0 μm (hypothetical) | ||
| 0.5 ± 0.25 μm (fourth chromosome) | ||
| Chromosome radius | 0.19 ± 0.10 μm | Ref. 27 |
| kBT | 4.116 × 10−21 J | At 25°C |
| Ratchet potential, ΔV | 12.5 kBT | Amount from ATP hydrolysis |
| Activation energy barrier, Δϕ | 8.0 kBT | Chosen to make autosomal velocity physiological |
| Period of motor potential, L | 8.3 nm | Length of tubulin dimmer |
| Radius of kinetochore | 30 nm | Chosen within physically reasonable limits |
Although drawn from a variety of sources, the parameters in Table 1 are those of Drosophila melanogaster early embryos. The dynamic viscosity was computed by estimating the force generated during anaphase A by the shape of the moving chromosome (27) with a formula from a previous study (34). This formula is not strictly correct in that it neglects the drag on a chromosome segment moving parallel to its axis, but an independent determination of the viscosity involving microbeads has obtained a similar result: 0.282 Pa/s (35).
There are no data available for the radius of the kinetochore in this particular system, but there certainly are reasonable physical limits one can place on the size of the kinetochore. We chose a value considerably smaller than the radius of the chromosome itself, but still large enough to allow the attachment of multiple microtubules, each of which have a diameter of ≈25 nm.
The motor potential itself, as modeled, requires the specification of three parameters. We set the period L equal to the known length of a tubulin heterodimer, which is the natural repeat distance (or “unit cell”) along any one protofilament of a microtubule. The driving ratchet potential ΔV is set equal to the amount of free energy released by the hydrolysis of one ATP molecule. This value is intended merely as an order of magnitude estimate, because the details of the motor mechanism are not known. As long as ΔV >> kBT, the precise value of ΔV will not matter much, because the ratchet will be essentially irreversible.
The potential of the opposing load Δφ (which can also be thought of as an activation energy that must be overcome for the motor to move from one ratchet site to the next) is the one freely adjustable parameter of the model. We chose it so that the computed velocity of an autosomal chromosome of normal dimensions and normal Young's modulus moves at the experimentally measured velocity. It is encouraging that the value of Δφ chosen in this way turns out to be reasonable: it is 8.0 kBT, or ≈2/3 the amount of energy liberated by the hydrolysis of one ATP molecule. It is important for the qualitative behavior of the model that this activation energy turns out to be substantially greater than kBT. Although we do not report those results here, we found that the presence of such a significant activation barrier strengthens the influence of chromosome flexibility on the velocity of chromosome transport.
Results and Discussion
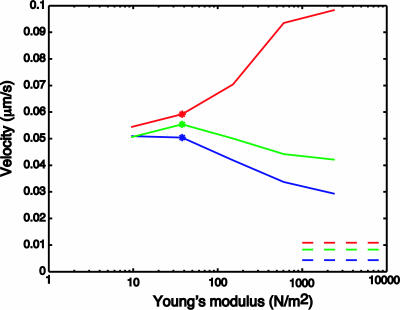
The results of our study are summarized in Fig. 2, which shows computed chromosome velocity as a function of Young's modulus (a measure of stiffness that affects both the stretching and bending rigidity of the chromosome) for three different length chromosomes. The lengths chosen are 0.5 μm (Fig. 2, red line), 1.0 μm (Fig. 2, green line), and 3.0 μm (Fig. 2, blue line). These values were chosen so that the longest length is that of the longest Drosophila chromosome, the shortest length is that of the (shortest) fourth chromosome, and the intermediate length is included in our study for comparison with the other two. Movies 1–4, which are published as supporting information on the PNAS web site, show simulations corresponding to several of the individual data points in Fig. 2.
Fig. 2.
Computed steady chromosome velocities for long (3 μm, blue), medium (1 μm, green), and short (0.5 μm, red) chromosomes as a function of Young's modulus for Δφ = 8 kBT. The starred data point corresponds to the physiological Young's modulus of 38 N/m2. See Movies 1–4 for animations of simulated chromosome motions comparing a variety of data points.
The physiological value of the Young's modulus is 38 Pa; it is indicated by the symbols in Fig. 2 that have been plotted on each of the lines to highlight that case. Despite the 6-fold ratio of their lengths, the velocities of the longest and shortest chromosomes in our study differ by only ≈20% at physiological stiffness.
This approximate load independence is qualitatively consistent with the fundamental discovery of Nicklas (1) that chromosome velocity during anaphase A is essentially independent of chromosome length, and it is in quantitative agreement with the observation of D. Sharp (personal communication) made in Drosophila early embryos that the fourth chromosome moves ≈20% faster than the largest chromosome.
A glance at Fig. 2 shows, moreover, that this result is a consequence of chromosome flexibility. For stiffer chromosomes, the velocity is by no means independent of length. Indeed, the velocity of the shortest chromosome in our study increases substantially as its stiffness increases from the physiological value, whereas the velocity of the longest chromosome decreases as the stiffness is increased. By the time the stiffness has increased by two orders of magnitude, the velocity of the shortest chromosome is about three times greater than the velocity of the longest one (compare Movies 1 and 2).
The increase in velocity with increasing stiffness that is seen in the case of the shortest chromosome is a surprise for which we have no intuitive explanation (see Movie 4). A hint that this trend may not continue indefinitely comes from the chromosome of intermediate length, which shows a slight rise in velocity as stiffness increases to the physiological value, but then a more pronounced decrease in velocity as the stiffness increases further. To see what happens at very large stiffness, we computed the chromosome transport velocity in the limiting case of infinite stiffness by evaluating a formula derived in ref. 24 (see equation 13 of that reference). The infinite-stiffness results are plotted in Fig. 2 as dashed horizontal lines. Note, first, how much smaller these infinite-stiffness velocities are than the corresponding velocities computed at physiological chromosome stiffness. Moreover, the velocities of these rigid chromosomes do not show anything like the length independence of their physiologically flexible counterparts. In particular, at infinite stiffness the shortest rigid chromosome is transported ≈2.5 times faster than the longest rigid chromosome.
Summary and Conclusions
To study the possible role of chromosome flexibility in chromosome transport, we have introduced a mathematical model of a flexible chromosome being pulled by an imperfect Brownian ratchet biomolecular motor with a built-in opposing load. The postulated motor mechanism is admittedly idealized, but the focus of this article is not on the motor mechanism but rather on the flexible nature of its chromosomal cargo. Moreover, the methods introduced here are applicable to chromosome transport by any of a wide class of motor mechanisms, and so may be used in the future to reassess the role of chromosome flexibility as our knowledge of the motor mechanism becomes more definite.
An important feature of the model studied in this article is that all of its parameters but one are either known or can reasonably be estimated a priori, without any comparison of model predictions to experimental measurements. The one parameter that cannot be determined a priori is the activation energy barrier, here called Δφ, that must be overcome for the motor to move from one ratchet site to the next. We chose this activation energy by matching the predicted and observed transport velocities of autosomal chromosomes. With all parameters fixed, we then proceeded to use the model to predict the transport velocities of three different length chromosomes over a wide range of stiffnesses (Young's moduli), including the limiting case of infinitely stiff (i.e., rigid) chromosomes.
At normal chromosome stiffness (Young's modulus = 38 Pa) we have reproduced the classical observation of Nicklas (1) that chromosomes or chromosome fragments of drastically different lengths are transported at approximately the same speed during anaphase A. Specifically, in our model study, a chromosome that is six times shorter moves only 20% faster than its longer counterpart. By varying the stiffness, moreover, we have been able to show that this effect is a consequence of chromosome flexibility, because it disappears (i.e., the transport velocity becomes much more length-dependent) as the chromosomes become more rigid.
Experimentally, one might be able to test the theory put forth here by finding some method of stiffening chromosomes without affecting the motor mechanism at the kinetochore. One possibility for such a method might be inhibiting or overexpressing some chromatin remodeling factor, like topoisomerase II or a condensin; changes in stiffness could be measured by persistence length methods similar to those developed in ref. 27. We predict that stiffened chromosomes will move at different rates than normal chromosomes, as computed by using the methods here. Moreover, we predict that stiffened chromosomes of different lengths (for instance, the four chromosomes in Drosophila) will move at much different rates as compared with the relatively constant rate at which different chromosomes move in the unperturbed setting. Such an experiment would determine whether chromosome flexibility is indeed the velocity governor postulated by Nicklas (1).
An important limitation of this study is that the stochastic model of chromosome movement that we have used does not take into account hydrodynamic effects, i.e., the influence of one part of a moving chromosome on another through the viscous incompressible fluid in which the chromosome is immersed. Instead, we have used a simple isotropic fluid drag model. This limitation could be remedied in work based on an immersed boundary method with thermal fluctuations (29).
Another interesting extension of this work would be to include the effects of poleward flux, which is the dominant mode of chromosome transport in some organisms (5) and plays a significant role in Drosophila. Given the fact that kinesin-13 kinesins also play a role in depolymerization at the poles (7), a Brownian ratchet model might apply for that situation as well, although in that case the relevant diffusion would be that of the microtubule rather than the enzyme/kinetochore. Moreover, such a mechanism could produce an additional tension on the microtubule at the kinetochore, potentially altering the kinetochore dynamics as well.
Supplementary Material
Acknowledgments
We thank David Sharp for enlightening discussions and providing many of the parameters used in this work; Lev Iserovich for his preliminary work on this problem; and Paul Atzberger, Thomas Bringley, and Samuel Isaacson for helpful discussions and comments. This work was supported by National Institutes of Health Research Grant R01 GM-59875-01A1 (to C.S.P.), a New York University Graduate School of Arts and Science MacCracken Fellowship (to A.R.), and National Institutes of Health Research Grant GM-070357 (to A.R.).
Abbreviation
- kMT
kinetochore microtubule.
Footnotes
Conflict of interest statement: No conflicts declared.
References
- 1.Nicklas R. B. J. Cell Biol. 1965;25:119–135. doi: 10.1083/jcb.25.1.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nicklas R. B. J. Cell Biol. 1983;97:542–548. doi: 10.1083/jcb.97.2.542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nicklas R. B. J. Cell Biol. 1989;109:2245–2255. doi: 10.1083/jcb.109.5.2245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mitchison T. J. J. Cell Biol. 1989;109:637–652. doi: 10.1083/jcb.109.2.637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Desai A., Maddox P. S., Mitchison T. J., Salmon E. D. J. Cell Biol. 1998;141:703–713. doi: 10.1083/jcb.141.3.703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rieder C. L., Salmon E. D. Trends Cell Biol. 1998;8:310–318. doi: 10.1016/s0962-8924(98)01299-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rogers G. C., Rogers S. L., Schwimmer T. A., Ems-McClung S. C., Walczak C. E., Vale R. D., Scholey J. M., Sharp D. J. Nature. 2004;427:364–370. doi: 10.1038/nature02256. [DOI] [PubMed] [Google Scholar]
- 8.Sharp D. J., Rogers G. C., Scholey J. M. Nat. Cell Biol. 2000;2:922–930. doi: 10.1038/35046574. [DOI] [PubMed] [Google Scholar]
- 9.Savoian M. S., Goldberg M. L., Rieder C. L. Nat. Cell Biol. 2000;2:948–952. doi: 10.1038/35046605. [DOI] [PubMed] [Google Scholar]
- 10.Lombillo V. A., Nislow C., Yen T. J., Gelfand V. I., McIntosh J. R. J. Cell Biol. 1995;128:107–115. doi: 10.1083/jcb.128.1.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Brown K. D., Wood K. W., Cleveland D. W. J. Cell Sci. 1996;109:961–969. doi: 10.1242/jcs.109.5.961. [DOI] [PubMed] [Google Scholar]
- 12.Yen T. J., Li G., Schaar B. T., Szilak I., Cleveland D. W. Nature. 1992;359:536–539. doi: 10.1038/359536a0. [DOI] [PubMed] [Google Scholar]
- 13.Peskin C. S., Oster G. F. Biophys. J. 1995;69:2268–2276. doi: 10.1016/S0006-3495(95)80097-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Inoue S., Salmon E. D. Mol. Biol. Cell. 1995;6:1619–1640. doi: 10.1091/mbc.6.12.1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gorbsky G. J., Sammak P. J., Borisy G. G. J. Cell Biol. 1987;104:9–18. doi: 10.1083/jcb.104.1.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maney T., Wagenbach M., Wordeman L. J. Biol. Chem. 2001;276:34753–34758. doi: 10.1074/jbc.M106626200. [DOI] [PubMed] [Google Scholar]
- 17.Desai A., Verma S., Mitchison T. J., Walczak C. E. Cell. 1999;96:69–78. doi: 10.1016/s0092-8674(00)80960-5. [DOI] [PubMed] [Google Scholar]
- 18.Moores C. A., Yu M., Guo J., Beraud C., Sakowicz R., Milligan R. A. Mol. Cell. 2002;9:903–909. doi: 10.1016/s1097-2765(02)00503-8. [DOI] [PubMed] [Google Scholar]
- 19.Hunter A. W., Caplow M., Coy D. L., Hancock W. O., Diez S., Wordeman L., Howard J. Mol. Cell. 2003;11:445–457. doi: 10.1016/s1097-2765(03)00049-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shipley K., Hekmat-Nejad M., Turner J., Moores C., Anderson R., Milligan R., Sakowicz R., Fletterick R. EMBO J. 2004;23:1422–1432. doi: 10.1038/sj.emboj.7600165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kline-Smith S. L., Walczak C. E. Mol. Biol. Cell. 2002;13:2718–2731. doi: 10.1091/mbc.E01-12-0143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kline-Smith S. L., Khodjakov A., Hergert P., Walczak C. E. Mol. Biol. Cell. 2004;15:1146–1159. doi: 10.1091/mbc.E03-08-0581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Maney T., Hunter A. W., Wagenbach M., Wordeman L. J. Cell Biol. 1998;142:787–801. doi: 10.1083/jcb.142.3.787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Elston T. C., Peskin C. S. SIAM J. Appl. Math. 2000;60:842–867. [Google Scholar]
- 25.Landau L., Lifshitz E. Theory of Elasticity. Tarrytown, NY: Pergammon; 1986. [Google Scholar]
- 26.Poirier M. G., Eroglu S., Marko J. F. Mol. Biol. Cell. 2002;13:2170–2179. doi: 10.1091/mbc.01-08-0401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Marshall W. F., Marko J. F., Agard D. A., Sedat J. W. Curr. Biol. 2001;11:569–578. doi: 10.1016/s0960-9822(01)00180-4. [DOI] [PubMed] [Google Scholar]
- 28.Houchmandzadeh B., Dimitrov S. J. Cell Biol. 1999;145:215–223. doi: 10.1083/jcb.145.2.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kramer P., Peskin C. In: Incorporating Thermal Fluctuations into the Immersed Boundary Method. Bathe K., editor. Amsterdam: Elsevier; 2003. pp. 1755–1758. [Google Scholar]
- 30.Berg H. Random Walks in Biology. Princeton: Princeton Univ. Press; 1993. [Google Scholar]
- 31.Kloeden P., Platen E. Numerical Solution of Stochastic Differential Equations. New York: Springer; 1993. [Google Scholar]
- 32.Wang H. Y., Peskin C. S., Elston T. C. J. Theor. Biol. 2003;221:491–511. doi: 10.1006/jtbi.2003.3200. [DOI] [PubMed] [Google Scholar]
- 33.Gillespie D. T. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- 34.Houchmandzadeh B., Marko J. F., Chatenay D., Libchaber A. J. Cell Biol. 1997;139:1–12. doi: 10.1083/jcb.139.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Alexander S. P., Rieder C. L. J. Cell Biol. 1991;113:805–815. doi: 10.1083/jcb.113.4.805. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.