Function of Redox-Active Tyrosine in Photosystem II

Abstract

Water oxidation at photosystem II Mn-cluster is mediated by the redox-active tyrosine Y_Z. We calculated the redox potential (E_m) of Y_Z and its symmetrical counterpart Y_D, by solving the linearized Poisson-Boltzmann equation. The calculated E_m(Y^˙/Y⁻) were +926 mV/+694 mV for Y_Z/Y_D with the Mn-cluster in S2 state. Together with the asymmetric position of the Mn-cluster relative to Y_Z/D, differences in H-bond network between Y_Z (Y_Z/D1-His¹⁹⁰/D1-Asn²⁹⁸) and Y_D (Y_D/D2-His¹⁸⁹/D2-Arg²⁹⁴/CP47-Glu³⁶⁴) are crucial for E_m(Y_Z/D). When D1-His¹⁹⁰ is protonated, corresponding to a thermally activated state, the calculated E_m(Y_Z) was +1216 mV, which is as high as the E_m for P_D1/D2. We observed deprotonation at CP43-Arg³⁵⁷ upon S-state transition, which may suggest its involvement in the proton exit pathway. E_m(Y_D) was affected by formation of 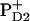(but not 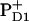) and sensitive to the protonation state of D2-Arg¹⁸⁰. This points to an electrostatic link between Y_D and P_D2.

INTRODUCTION

O₂ on earth is generated by water oxidation at the Mn-cluster of the photosynthetic protein-pigment complex, photosystem II (PSII). The photosynthetic reaction in PSII is initialized by light absorption, resulting in electronic excitation that is ultimately converted to chemical potential by a charge separation process at the P680 chlorophyll a (Chla) of the PSII reaction center (RC). Charge separation leads to formation of an oxidized positively charged radical P680^+˙ while the released electron travels along the electron transfer (ET) chain. The ET chain is located in the D1/D2-chain harboring a quasi-dimer Chla (P_D1/D2), and pairs of accessory Chla (Chl_D1/D2), of pheophytina (Pheo_D1/D2) and of plastoquinone (Q_A/B). In intact PSII, P680^+˙ is reduced by the redox-active tyrosine D1-Tyr¹⁶¹ (Y_Z), which is subsequently reduced by an electron from the Mn-cluster. An overview of the location of these cofactors in the complete PSII protein complex is shown in Fig. 1.

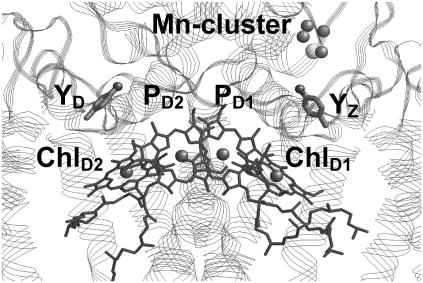
FIGURE 1.

Location of the Mn-cluster (manganese, dark-shaded spheres; calcium, light-shaded sphere), Y_Z, Y_D (side chains only, light-shaded spheres for oxygen), and four Chla P_D1/D2 and Chl_D1/D2 in the reaction center (dark-shaded) of PSII. Polypeptide chains are shown by ribbon bands.

Sequential excitations of P680 drive the redox state of the Mn-cluster from the lowest S0 to the highest oxidized state S4. Release of O₂ as a product of water oxidation is associated with transition from S4 to S0 that completes the redox cycle. Y_Z possesses D1-His¹⁹⁰ while the symmetrical counterpart D2-Tyr¹⁶⁰ (Y_D) possesses D2-His¹⁸⁹ as H-bond partner (Fig. 2). The apparent proximity of Y_Z to the Mn-cluster (edge-to-edge distance between Mn-cluster and Y_Z is 5 Å (1)) and its redox-activity supports its significant role in water oxidation at the Mn-cluster. It is a matter of debate whether the role of Y_Z in water oxidation is to function as hydrogen abstractor (2) or electrostatic promoter (3). The exit pathway of protons released upon water oxidation (4) as supported by the recent crystal structure of PSII (1,5,6) is a new aspect to be considered. The other tyrosine Y_D is 28 Å from the Mn-cluster (1) and can therefore not directly be involved in water oxidation occurring at the Mn-cluster. Nevertheless, it plays an important role in tuning the energy of the charge state of P680 and of the S-states of the Mn-cluster before ET from Y_Z to P680, as has been discussed (7–9).

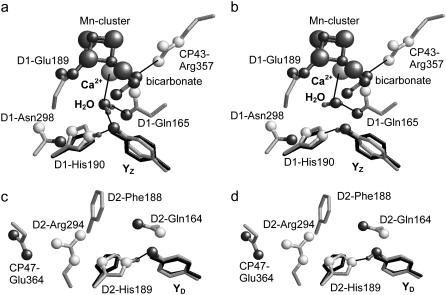
FIGURE 2.

H-bond network around Y_Z/D. Energetically optimized atomic coordinates for (a) deprotonated Y_Z, (b) protonated Y_Z, (c) deprotonated Y_D, and (d) protonated Y_D. Only for D1-His¹⁹⁰/D2His¹⁸⁹ and H₂O, polar hydrogen atoms involved in H-bonds are displayed explicitly by small-sized dark-shaded spheres. Nitrogen atoms are displayed by medium-sized light-shaded spheres, oxygen atoms by medium-sized dark-shaded spheres, and Mn and Ca ions are shown by large spheres (manganese, dark-shaded; calcium, light-shaded). Original positions of Y_Z/D and D1-His¹⁹⁰/D2-His¹⁸⁹ from the PSII crystal structure are shown by dark-shaded sticks; energetically optimized positions are shown in light shading. Orientations of H-atoms and some H-bonds are indicated by thin lines.

There are, in principle, three possible mechanistic patterns for the involvement of tyrosine in the redox reaction between P680 and Mn-cluster. These are the following redox reactions with corresponding redox pairs (notation: YH, protonated neutral species; Y⁻, deprotonated anion; YH^˙+, protonated cationic radical; Y^˙, deprotonated neutral radical):

1. Y⁻ → Y^˙ + e⁻ involving Y^˙/Y⁻ (E_m(Y^˙/Y⁻) = +680 mV, measured for N-acetyl-_L-tyrosinamide).

2. YH → Y^˙ + H⁺ + e⁻ involving Y^˙/YH with pKa_red of 9.6 referring to YH (E_m(Y^˙/YH) = +970 mV, measured for N-acetyl-_L-tyrosinamide in aqueous solution at pH 5.0).

3. YH → YH^˙+ + e⁻ involving YH^˙+/YH with pKa_ox of –2 referring to YH^˙+ (E_m(YH^˙+/YH) = +1380 mV, measured for N-acetyl-_L-tyrosinamide; reviewed in (10)).

In the following, the pKa for tyrosine is generally used as pKa_red, if not otherwise specified. In aqueous solution, the availability of these three possible redox reactions depends predominantly on pH. In a protein, these reactions can also be controlled by its environment as, for instance, H-bond network, presence of charged residues, and cofactors.

For efficient function of PSII, E_m(Y_Z) should lie between the E_m values of P680 (+1110–1300 mV) (11,12) and water (+820 mV). Based on the equilibrium constants of the redox reactions involving Y_Z and Y_D and the pH-dependence of these redox reactions, the E_m(Y_Z) and E_m(Y_D) were estimated to be ∼+970 mV (13) and +720 to +760 mV (13,14), respectively. On the other hand, equilibrium constants measured for the redox reaction between P680 and Y_Z suggest that E_m(Y_Z) operating in the ET process between P680 and Y_Z should be relatively high, yielding a value of +1200 mV, which is ∼100 mV below E_m(P680) (3,15) (reviewed in (10)). However, the mechanism of how the Y_Z/D environment of PSII shifts E_m(Y_Z/D) needs further investigations to be clarified (see discussion in (9)). To obtain a stable Y_Z radical, many investigations on its function were, for technical reasons, performed on Mn-depleted PSII, since under these circumstances spectroscopic signals originating from Y_Z/D could be detected under stationary conditions. However, it was suggested that Mn-depleted PSII samples could be subject to critical changes in conformation or H-bond network (see for instance (16,17)). Hence, an interpretation of these experiments involves uncertainties.

Recently, higher resolution crystal structures of PSII isolated from the thermophilic cyanobacterium Thermosynechococcus elongatus were obtained, revealing side-chain arrangements and their interactions with redox-active cofactors (1,18). Here, we report on E_m(Y_Z/D) calculated by solving the linearized Poisson-Boltzmann (LPB) equation for the whole PSII complex based on the PSII crystal structure (1), taking into account the atomic coordinates of all amino-acid residues and bound cofactors. All computations presented here were performed under the same conditions and parameterization as in previous computations on PSII (for instance, (19,20)).

METHODS

Coordinates

In our computations, all atomic coordinates were taken from the crystal structure of PSII from thermophilic cyanobacterium T. elongatus at a 3.5 Å resolution (PDB: 1S5L) (1). Hydrogen atom positions were energetically optimized with CHARMM (21), while positions of all nonhydrogen atoms were fixed and all titratable groups were kept in their standard protonation states, i.e., acidic groups ionized and basic groups (including titratable histidines) protonated. Simultaneously, Chla, Pheoa, and Q_A/B were kept in the neutral charge redox states. Histidines that are ligands of Chla were treated as nontitratable with neutral total charge.

Atomic partial charges

Atomic partial charges of amino acids were adopted from the all-atom CHARMM22 (22) parameter set. To account implicitly for the presence of a proton, the charges of acidic oxygens were both increased symmetrically by +0.5 unit charges. Similarly, instead of removing a proton in the deprotonated state, all hydrogen charges of the basic groups of arginine and lysine were diminished symmetrically by a unit charge in total. The atomic charges for the redox-active tyrosine were adopted from Popovic et al. (23); deprotonated with negative charge (Y⁻); deprotonated radical with neutral charge (Y^˙) in the redox pair Y^˙/Y⁻; protonated with neutral charge (YH); and protonated radical with positive charge (YH^˙+) in the redox pair YH^·+/YH.

Molecular systems and dielectric media

Although a formidable and still unsolvable task, a complete description of a molecular system (as for instance, a protein immersed in solvent) can in principle be achieved by solving the Schrödinger equation for all atoms comprising electrons and nuclei for a statistical average of conformations. In such a complete description there is no space to introduce a continuum dielectric medium. The other extreme is to ignore the atomic structure and conformations of the molecular system completely. In this case the dielectric medium is necessary to describe polarization effects emerging from of the dipoles in the molecular system, which create a reaction field in response to explicit charges or dipoles. Polarization effects have contributions not only from distortions of electronic wave functions (electron polarization) and conformational changes of the nuclei (nuclear polarization), but also from nonhomogeneous distributions of charged groups and their variations (for instance, titratable groups in a protein).

In theoretical computations, often mixed models are used where part of the molecular structure is treated explicitly, while the nonexplicit parts are considered by an effective dielectric medium. Here as in a number of preceding studies (19,20,24–26), we consider the atomic partial charges and variations of charge pattern due to titratable groups explicitly, while we ignore electronic polarization and nuclear polarization. The latter is true, since we consider only a single conformation, which is directly related to the atomic coordinates of the protein crystal structure. Based on a number of studies (19,20,24–26) we obtained best results for redox-active and titratable groups with a dielectric constant of ɛ_P = 4 inside the protein and ɛ_W = 80 outside to model the polarization of bulk water. The same values were used in computational studies of other groups (27,28). If we ignore the influence of charged groups and their variations in a protein, the value of the dielectric constant would vary depending on the molecular system considered and exhibit spatial dependencies related to the distribution of titratable residues. It should be noted here that a dielectric constant used for such mixed models is a model parameter like atomic partial charges but not a quantity directly amenable to experimental measurement.

In other computational work, also larger values than ɛ_P = 4 were used for the protein dielectric constant, for instance ɛ_P = 20 (29). Since the dielectric constant accounts for the molecular components that are not explicitly modeled, a description with lower dielectric constant is superior as long as the agreement with experimental data is of the same level. In this respect it is interesting to note that considering conformational flexibility (i.e., including nuclear polarization) by energy minimization yields best results by lowering the dielectric constant from 4 to 2 to account for only electron polarization (30).

Experimental determinations of the static dielectric constant in a molecular system are generally based on the assumption to describe polarization effects solely by a dielectric continuum. In bacterial RC the dielectric constant was determined by measuring the Stark effect (31). In these measurements the influence of electrostatic interactions of a chromophore with the protein environment is probed in terms of a double difference in energies, namely ground and electronic excited state energies in presence and absence of a strong external electrostatic field. For such double differences the direct influence of charged groups cancels, if they do not change their charge state with the external electrostatic field. However, such changes are likely to occur for titratable residues. Interpreting such contributions in terms of an inhomogeneous dielectric medium would result in a spatially varying dielectric constant. The measured values of ɛ_P in the bacterial RC vary between 2.1 and 9.5 (31), presumably due to variations in the protonation pattern of titratable residues. However, the average of the measured dielectric constants is close to the value used in our electrostatic energy computations.

Protonation pattern and redox potential

Our computation is based on the electrostatic continuum model treated by solving the LPB equation with the program MEAD (32). To facilitate a direct comparison with previous computational results, we used uniformly the same computational conditions and parameters such as atomic partial charges and dielectric constants (for instance, (19,20)). To obtain absolute values of the E_m(Y) in the protein, we calculated the electrostatic energy difference between the two redox states of tyrosine in a reference model system with known experimental E_m. The shift of E_m in the protein relative to the reference system was added to the known E_m. As reference model system, the following solution E_ms versus normal hydrogen electrode were used: E_m(Y^˙/Y⁻) = +680 mV for one-electron reduction; and E_m(YH^˙+/YH) = +1380 mV for one-electron oxidation in aqueous solution (10). Although the radical pair of YH^˙+/YH could be also relevant for the radical state of Y_Z/D in PSII, in this study we did not focus on this radical pair (see Discussion). The redox states of all other cofactors (i.e., Car, Chla, Pheoa, quinone) were kept in their neutral charge state. Cytochrome b559 and cytochrome c550 were kept in the reduced state. Specifically, unless titrated, Y_Z and Y_D were kept in the neutral charge state. The ensemble of protonation patterns was sampled by a Monte Carlo method with our own program Karlsberg (B. Rabenstein, Karlsberg Online Manual, http://agknapp.chemie.fu-berlin.de/karlsberg/(1999)). All computations were performed at 300 K with pH 7.0 and an ionic strength of 100 mM. The LPB equation was solved using a three-step grid-focusing procedure with 2.5 Å, 1.0 Å, and 0.3 Å resolution. The Monte Carlo sampling yielded the probabilities [A_ox] and [A_red] of the two redox states of molecule A. The E_m was evaluated from the Nernst equation. A bias potential was applied to obtain an equal amount of both redox states ([A_ox] = [A_red]), yielding the redox midpoint potential E_m as the resulting bias potential. For convenience, the computed E_m was given with mV accuracy, without implying that the last digit is significant. In general, a few 10 mV in E_m is in a sufficiently reproducible range of our computational method (see, for instance, (33)). With the Henderson-Hasselbalch equation, the pKa can be calculated as the pH where the concentration of [⁻A_deprotonatel] and [A_protonated] are equal. For further information about computational procedure and error estimate, see our previous work for E_m (for instance, (19,20)) and pKa (for instance, (34,35)).

Modeling water between the Mn-cluster Ca²⁺ and Y_Z

The existence of a water molecule located in H-bond distance to Y_Z and D1-His¹⁹⁰ has been proposed to play a significant role in the redox reaction of Y_Z for years. Although crystal structures of PSII could not reveal water molecules due to their limited resolutions, the crystal structure of PSII (1,6) indicates a possible water binding site X21 at Ca²⁺ of the Mn-cluster and Y_Z, which is in agreement with ¹⁸O isotope exchange measurements that pointed to a Ca-bound water (36). The exact mechanism of PSII water oxidation as mediated by Y_Z and the Mn-cluster remains a matter of debate, but the majority of the proposed mechanisms seem to place at least one water molecule in the neighborhood of Y_Z and the Mn-cluster (37,38).

We modeled this water molecule in the vicinity of Y_Z and optimized its geometry energetically with CHARMM (21) while all other atomic coordinates except Y_Z/D and D1-His¹⁹⁰/D2-His¹⁸⁹ were fixed. Both Y_Z/D were treated as 1), negatively charged deprotonated tyrosine (Y⁻ model, Fig. 2, a and c) (17,39,40); or 2), neutral protonated tyrosine (YH model, Fig. 2, b and d)) (10,41,42). Alternatively, in a geometry optimization with positively charged tyrosine YH^˙+, the side chains of Y_Z and D1-His¹⁹⁰ moved apart, disrupting the common H-bond (data not shown), rendering this H-bond unstable. Hence YH^˙+ might be relevant only as a transient state.

The exact PSII conformations for Y_Z/D radical states are so far unknown. One of the most relevant studies to refer to this issue is a structural refinement of Högbom et al. (43) for a tyrosine radical position in a single crystal of ribonucleotide reductase R2 protein by combined x-ray and high-field EPR crystallography (43). Although the protein environment of the tyrosine radical in the two proteins are different, in the R2 protein a displacement of the side chain was observed predominantly at this tyrosine upon generation of its radical state. Therefore, in our study we released the atomic coordinates only for the minimum set of relevant residues, i.e., Y_Z/D1-His¹⁹⁰ (Y_D/D2-His¹⁸⁹) pair. As a consequence of the geometry optimization, atom pair distances of tyrosines and histidines were changed by 0.1–0.8 Å with an RMS deviation of 0.63 Å for the Y⁻ model and 0.51 Å for the YH model with respect to the side-chain atoms (excluding hydrogen and backbone atoms; see Table 1). These displacements of side chains are in the same range as those observed in the generation of tyrosine radicals in the R2 protein (PDB 1MXR; see also Fig. 5 in (43)). The energy-optimization procedure did not alter the O_Y–Nɛ_His distance for Y_Z-D1-His¹⁹⁰. In contrast, the corresponding Y_D-His¹⁸⁹ atom pair distance decreased by 0.4 Å to 2.6 Å, which is nearly identical to the distance of 2.7 Å for the Y_Z/D1-His¹⁹⁰ pair. In the geometry-optimized PSII structure, the water molecule is 3.0 Å from the Ca²⁺ ion at the Mn-cluster, 2.6 Å from the hydroxyl oxygen atom of Y_Z, and 3.0 Å from the side-chain oxygen atom of D1-Gln¹⁶⁵ (Fig. 2). This completely agrees with the suggestion of a Ca-bound water that is H-bonded to Y_Z (5,37,38). We obtained the H-bond formation between the modeled water and D1-Gln¹⁶⁵, which agrees with a suggestion in McEvoy and Brudvig (37). The optimized atomic coordinates of Y_Z, D1-His¹⁹⁰, and the X21 water as well as Y_D and D2-His¹⁸⁹ used in this study are available online as Supplementary Material (files YZ_deprot.pdb and YD_deprot.pdb for Y⁻ model, and YZ_prot.pdb and YD_prot.pdb for YH model, respectively).

TABLE 1.

Geometry of the H-bond network at Y_Z/D after energy optimization of Y_Z/D and D1-His¹⁹⁰/D2-His¹⁸⁹ side chains in the presence of negatively charged tyrosine

	Distance [Å]
Atom pair	Original*	Optimized†
YZ
NɛHis‡-OηYZ§	2.7	2.7
NδHis‡-OδAsn¶	3.3	4.1
Obicarbonate-OηYZ§	3.4	2.9
OH2O-OηYZ§	(2.7)‖	(2.6)‖
OH2O-NɛHis‡	(3.4)‖	(3.0)‖
YD
NɛHis‡-OηYD§	3.0	2.6
NδHis‡-NɛArg**	2.4	3.2
NδHis‡-NηArg**	3.2	3.5

^*Based on the atomic coordinates of the PSII crystal structure (1).

^†Based on energy optimized atomic coordinates of PSII with CHARMM (see text).

^‡D1-His¹⁹⁰ for Y_Z and D2-His¹⁸⁹ for Y_D.

^§Hydroxyl oxygen atom of Y_Z/D.

^¶Side-chain oxygen atom of D1-Asn²⁹⁸.

^‖The H₂O molecule was placed in the PSII crystal structure between the Mn-cluster Ca²⁺ and Y_Z. It was first energetically optimized alone and subsequently together with Y_Z and the D1-His¹⁹⁰ side chains.

^**Side-chain nitrogen atom of D2-Arg²⁹⁴.

The dielectric constant for the explicit modeled water X21 was set to ɛ_P = 4, i.e., to the same value as in the protein volume, in contrast to ɛ_W = 80 used for bulk water. With higher dielectric constant, electrostatic interactions are shielded more efficiently, as it is for instance the case in bulk water. The screening ability of electrostatic interactions caused by a single, explicitly modeled water molecule buried in the protein can be understood by reorientation of its dipole to stabilize atomic charges in the protein. One focus in this study is to investigate explicit H-bond pattern of water X21 to protein cofactors. Atomic coordinates of this modeled water near Y_Z/D were energetically optimized to form explicit H-bonds with the protein environment, which can establish sufficient electrostatic screening of protein charges in the neighborhood. However, the electrostatic screening is effective only if the water volume possesses a low dielectric constant as, for instance, ɛ = 4.

Evaluation of E_m(Y_Z/D) with/without energy minimization

When we used the original atomic coordinates from the crystal structure, we calculated 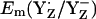and 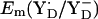to be +944 mV and +586 mV at pH 6 for the S2 state, respectively. After energy minimization of the side chains of Y_Z/D and D1-His¹⁹⁰/D2-His¹⁸⁹, we obtained at pH 6 for the S2 state 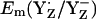= +985 mV and 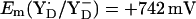(see main text). The E_m difference between Y_Z and Y_D was formerly estimated to be +240 meV from the equilibrium constant for Y_Z/Y_D (14) or +210 meV from the equilibrium constants for Y_Z/S_2/1 and Y_D/S_2/1 (13). From this E_m difference, Vass and Styring (13) estimated 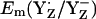and 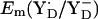to be ∼+970 mV and +760 mV, respectively (13). The E_m difference E_m(Y_Z) − E_m(Y_D) of +243 mV as well as the absolute values of E_m(Y_Z/D) obtained in our computations using the energy-minimized coordinates are in good agreement with the estimated values of Vass and Styring (13). On the other hand, using the original atomic coordinates from the PSII crystal structure, the calculated 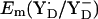is lower by ∼150 mV than by using the energy-minimized coordinates. In contrast, the calculated 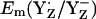is nearly the same in the two atomic coordinate sets. The resulting E_m difference of +358 mV between Y_Z and Y_D in the original atomic coordinates is by ∼100 mV larger than the corresponding values from the estimate of Vass and Styring (13) and our computations using the atomic coordinates from the energy-minimized model. Analyzing the two structures in atomic detail, it becomes evident that the low value of 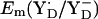in the original PSII structure originates mainly from the relatively large Nɛ_His-Oη_YD distance of 3.0 Å in the PSII crystal relative to the smaller distance of 2.6 Å in the geometry-optimized SPII structure (Table 1). The same distance of 2.6 Å was also obtained by DFT computations of Faller et al. (44) considering the same H-bond pattern between Y_D and D2-His¹⁸⁹. Indeed, the distance of 2.6 Å is nearly identical to the corresponding distance of 2.7 Å in the Y_Z side of the PSII crystal structure (Table 1). Although the Nɛ_His-Oη_Tyr in the Y_D side was thus affected, it is quite remarkable that the same energy-minimization process did not alter the corresponding distance in the Y_Z side. Despite the alteration in E_m(Y_D) by the energy minimization, the other features (e.g., protonation pattern in PSII) remained unchanged in our computation. Therefore, in the following part, we focused on the computation based on the atomic coordinates with these side chains being energetically optimized.

RESULTS AND DISCUSSION

E_m(Y_Z^˙/Y_Z⁻)

At pH 6 in the S₂ state, the calculated 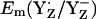is +985 mV, which agrees with the measured E_m(Y_Z) of ∼+970 mV, as reported by Vass and Styring (13). This value is also close to E_m(Y^˙/Y) = +970 mV measured for the neutral tyrosine radical in aqueous solution at pH 5.0 (10,45). At pH 7, the calculated 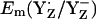are +926 mV (+959 mV) in the S₂ (S₃) state (Table 2). EPR signals from a tyrosine radical in PSII were assigned to Y_Z interacting with the Mn-cluster in the S2 state and its pH-dependence observed in these experiments was attributed to a pH-dependent E_m(Y_Z) (46). In our computations, we observed pH-dependence of E_m(Y^˙/Y⁻) for Y_Z and Y_D with a slope of ∼–60 mV/pH in the S₂ state.

TABLE 2.

Computed E_m(Y_Z/D) in [mV] at pH 7.0

Redox couple	Mn-cluster S-state	Em(YZ)	Em(YD)
Y˙/Y−*	S0	+932	+686
	S1	+931	+689
	S2	+926	+694
	S3	+959	+702
	Mn-depleted†	+780	+685
Y˙+/Y*	S2	+1669	+1907

^*For the E_m values used as reference model system, see Tommos and Babcock (10).

^†All the titratable groups in PSII were titrated, as was done in computations with intact Mn-cluster.

When we calculated 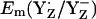in the S₂ state at pH 7.0 (i.e., at [Y^˙] = [Y⁻] = 0.5), D1-His¹⁹⁰ was to 50% protonated, implying a neutral charge state of the residue pair Y_Z/D1-His¹⁹⁰. On the other hand, a number of experimental studies proposed that D1-His¹⁹⁰ is protonated (i.e., positively charged) before relaxing to the S2 state (reviewed in (47)). In our computation, at pH 7 D1-His¹⁹⁰ was fully protonated if Y_Z was fully reduced as tyrosinate (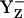) for all S-states investigated.

Considering protonated D1-His¹⁹⁰, which presumably prevails in a thermally activated state of PSII, we obtained 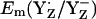= +1216 mV. Quite interestingly, the E_m(Y_Z) value obtained in presence of a fully protonated D1-His¹⁹⁰ is nearly as high as E_m(P680) of ∼+1200 to +1300 mV (11,12). The proximity between E_m(Y_Z) and E_m(P_D1/D2) is consistent with a small E_m difference between P680 and Y_Z, governing the ET between these cofactors in the nanosecond time domain before possible structural relaxation (3,15). This E_m difference is time-dependent and increases in the microsecond time regime, yielding finally under equilibrium conditions in the S2 state E_m(Y_Z) = +970 mV (13) (E_m(Y_Z) = +985 mV computed in this study). Thus, in our computational model, a change in protonation at D1-His¹⁹⁰ (using the same atomic coordinates from the PSII crystal structure (1)) has a predominant impact on E_m(Y_Z), yielding an upshift of 260–290 mV. This mechanism may be necessary to reduce P680⁺ by Y_Z quickly in the nanosecond time regime (48).

E_m(Y_D^˙/Y_D⁻)

At pH 6 in the S2 state, the calculated 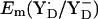is +742 mV. At pH 7 we calculated 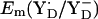to be +694 mV in the S2 state and +702 mV in the S3 state (Table 2). The experimentally estimated 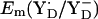lies between +720 and +760 mV according to redox titration with strong oxidants (14) or from determination of the E_m difference, E_m(Y_Z) – E_m(Y_D) (13). Interestingly, these estimated 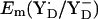in PSII (13,14) are very similar to the E_m(Y^˙/Y⁻) value in aqueous solution where it was measured to be +680 mV for pH >9.9 independent of pH (10) although the very polar solvent environment differs considerably from the PSII environment. The different redox behavior of the two symmetry-equivalent tyrosines seems to be mainly due to the asymmetric location of the Mn-cluster being close to Y_Z and distant to Y_D with edge-to-edge distances of 5 Å and 28 Å, respectively. As observed in 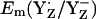, we found also 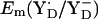to be pH-dependent with ∼–60 mV/pH in our electrostatic energy computations.

Model of ET from Y_Z to P680⁺ in intact PSII

The calculated E_m(YH^˙+/YH) were +1576 mV for Y_Z and +1804 mV for Y_D at pH 7 in the S2 state, which indicates less stability of YH^˙+/YH relative to the deprotonated redox pair Y^˙/Y⁻. In agreement with our computed results on E_m(YH^˙+/YH), Tommos and Babcock (10) also estimated E_m(YH^˙+/YH) for the PSII protein environment to be +1680 mV to +1830 mV (10). These large values for Y_Z/D are not only far from +970 mV (+985 mV) obtained by Vass and Styring (13) (computed in this study for 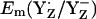), but also far from 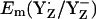= +1216 mV, computed for protonated D1-His¹⁹⁰.

Although we obtained for E_m(Y_Z) values as low as +985 and +1216 mV only by considering the redox pair 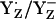, it does not exclude the possibility that Y_Z is protonated (Y_ZH) before its radical reaction, as found in Fourier-transform infrared (FTIR) studies (41,42). Hence, our computations suggest that 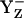relative to 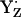is energetically more stabilized than YH^·+ relative to Y_ZH, such that the redox pair 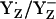is likely more relevant than Y_ZH^˙+/Y_ZH.

Tommos and Babcock (10) argued that 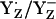is not the functional redox pair in PSII unless positive charges near Y_Z lower the pKa of Y_ZH to values <5, concluding that 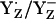is unlikely to be the relevant redox pair (10). However, we remark that not only positive charges but also appropriate H-bonds with the titratable redox-active Y_Z are able to lower the pKa and stabilize its anionic form. A number of studies suggest that, in the Y_Z side, a Ca-bound water exists (1,6,37,38). Indeed, the fixation of a water at the Ca²⁺ of the Mn-cluster results in a strong H-bond between this water and the hydroxyl oxygen of Y_Z (Fig. 2 a and Table 3). Due to the H-bond with this Ca-bound water, we obtained a pKa of 7.4 for Y_ZH (Fig. 3, panels 1 and 4), which is relatively low with respect to the pKa of 9.6 for tyrosine in aqueous solution. However, this pKa value for Y_Z is in agreement with the pKa values of 7.0–8.3 derived by Ahlbrinck et al. (3) and Diner et al. (40) from the ET rate involving Y_Z and P680⁺. A further support for this pKa is the FTIR result of Berthomieu et al. (42), which observed the disappearance of a band at 1238–1255 cm⁻¹ with an apparent pKa of ∼8–9, corresponding to a δ(COH) tyrosine-bending mode (cited as personal communication in (49)). When Y_Z is equilibrated in the 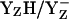states then we calculated pKa of D1-His¹⁹⁰ to be 6.6 (Fig. 3, panel 1). Hence, the Ca-bound water plays a role in stabilizing transient Y_Z states such as Y_Z^δ− (where Y_Z and D1-His¹⁹⁰ share a proton, thus being in the neutral charge state) or , which otherwise would be very unstable.

TABLE 3.

Influence of P_D1P_D2 and D2-Arg¹⁸⁰ charge states on E_m(Y_Z/D) at pH 7.0 in the S2 state

Charge state	Em(YZ) [mV]	Em(YD) [mV]
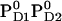	+926	+694
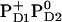	+918	+732
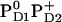	+924	+802
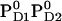with D2-Arg180 deprot.	+926	+564

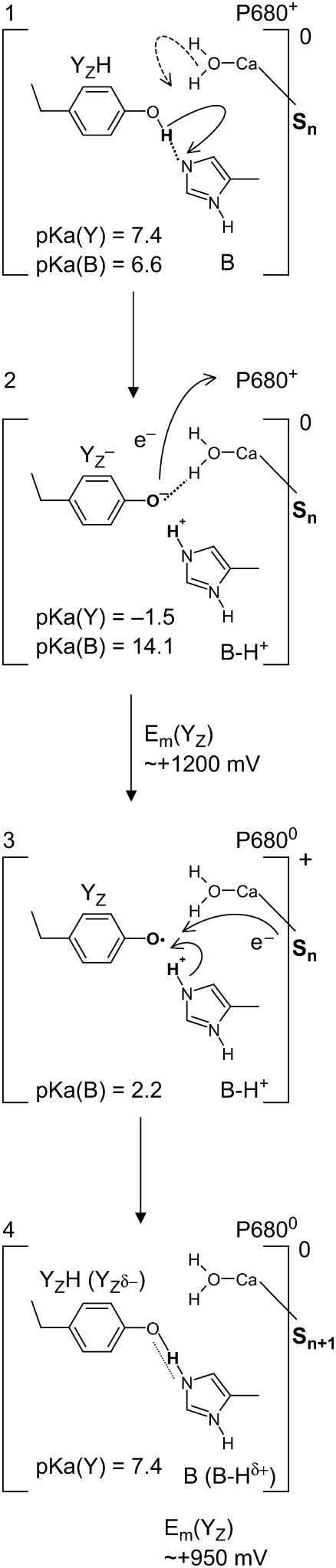
FIGURE 3.

Scheme for ET from Y_Z to P680. Y and B stand for Y_Z and D1-His¹⁹⁰, respectively, and the calculated pKa values of Y and B for these residues at each step are listed in the scheme.

We interpreted our results for 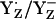by the following redox reaction scheme of Y_Z/D visualized in Fig. 3:

1. In the initial state, Y_ZH dissociates the phenolic proton (Fig. 3, panel 1).

2. The presence of the Ca-bound water stabilizes the 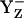state transiently with fully protonated D1-His¹⁹⁰ (BH⁺) (E_m(Y_Z) = +1216 mV) (Fig. 3, panel 2). This step is particularly unstable and should therefore exist only transiently, since according to our calculated pKa Y_Z and B are an extremely strong acid and base, respectively. Since in the initial state proton release of Y_ZH, producing 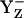(Fig. 3, panel 2), is immediately quenched by an oxidation process where 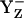decays to the neutral radical state 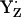, the intermediate reaction state 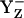displayed in Fig. 3, panel 2, is often not considered explicitly. Thus, the resulting net redox reaction of these two steps involves 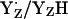(Fig. 3, panels 1–3).

3. For the neutral radical state 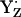, the pKa of B is 2.2, still considerably low (Fig. 3, panel 3). As a consequence, the protonated BH⁺ becomes unstable, donating its proton to the neutral radical 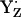. In this proton transfer step, the residue pair Y_Z and B remains positively charged.

4. This energetically unfavorable charge state relaxes by charge compensation receiving an electron from the Mn-cluster, which in turn changes from state Sn to Sn+1 (Fig. 3, panel 4).

It is a matter of debate whether the H-bond between the Ca-bound water and Y_Z remains unchanged even in this state (Fig. 3, panel 4), but if it does, then it leads to a protonated Y_Z and a deprotonated B, which are H-bonded [B···HY_Z] or alternatively to a partially polarized (but also uncharged) species [B-H^δ+···Y_Z^δ−] where the proton is delocalized in the H-bond, yielding E_m(Y_Z) = +926 for the S2 state (+959 mV for the S3 state) (Fig. 3, panel 4). Hereby, our computations yielded a partially protonated Y_Z (∼0.7 H⁺), which as a consequence carries a fractional negative charge. This fractional negative charge is practically completely neutralized by a complementary fractional protonation of D1-His¹⁹⁰ (∼0.3 H⁺). This polarized H-bond resembles the tyrosinate intermediate model (17,39,40). Hence, in FTIR measurements the predominantly protonated Y_Z species may still be detected as protonated Y_ZH (41,42).

E_m(Y_ZH^˙+/Y_ZH) in the Mn-depleted PSII model

Although it has been suggested that Mn-depleted PSII may possess considerably different H-bond pattern around Y_Z compared to those in intact PSII (16,17), we tentatively modeled an Mn-depleted PSII by simply removing the Mn-cluster, the attached bicarbonate, Ca²⁺, and water, without considering any conformational change of the protein environment nearby. To distinguish this model from the actual Mn-depleted PSII in vitro, we denote this model as Mn-depleted PSII model. This model possesses different H-bond pattern from those in intact PSII mainly due to the removal of the Ca-bound water, which was H-bonded to the Y_Z hydroxyl oxygen (O_H2O–O_Tyr distance of 2.6 Å) in the intact PSII. In contrast to the enormously high potential of +1576 mV for E_m(Y_ZH^˙+/Y_ZH) in intact PSII, the Y_ZH^˙+/Y_ZH calculated in the Mn-depleted PSII model was lower, yielding +1264 mV. This value is also lower than +1380 mV for YH^˙+/YH measured in the aqueous solution (10), indicating that YH^˙+ is dramatically stabilized in the Mn-depleted PSII model with respect to intact PSII or aqueous solution. Furthermore, the calculated E_m(Y_ZH^˙+/Y_ZH) = +1264 mV in the Mn-depleted PSII model is approximately as high as E_m(P680) of ∼+1200 to +1300 mV (11,12), implying that Y_ZH^˙+/Y_ZH may serve as functional electron donor to P680⁺ in the Mn-depleted PSII. The lack of electron donor for Y_Z (i.e., the Mn-cluster) in the Mn-depleted PSII might energetically, thus, be able to accumulate Y_ZH^˙+. Indeed, an interpretation that Y_ZH^˙+ may be the functional species in PSII was made based on EPR spectroscopy on Mn-depleted PSII (50,51). To investigate the stability of Y_ZH^˙+, we calculated the pKa_ox for Y_ZH^˙+. Indeed, in the Mn-depleted PSII model the calculated pKa_ox was 0.0, being increased by two units from the aqueous solution value of –2.0. Nevertheless, this value is still too low to maintain a stable Y_ZH^˙+ in the Mn-depleted PSII under physiological conditions, implying that this species is likely to occur only transiently also in the Mn-depleted PSII model. An alternative interpretation for these EPR signals would be that another titratable residue, whose position is ∼5 Å from Y_Z, is responsible for the positively charged intermediate (50). According to this interpretation of EPR studies, the involvement of this unidentified residue occurs specifically after the S2 state (50). Since the distance estimate of 5 Å is ambiguous, the involved titratable residue may be different from D1-His¹⁹⁰, as discussed in the next section. In the following, we will focus our discussion on the redox couple Y^˙/Y⁻ for Y_Z/D in intact PSII. Accordingly, the notation E_m(Y_Z/D) refers to “E_m(Y^˙/Y⁻) for Y_Z/D” unless otherwise stated.

Influence of CP43-Arg³⁵⁷ on E_m(Y_Z^˙/Y_Z⁻)

Surprisingly, our computations yielded very similar values for 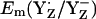in the S0 state (+932 mV) and the S2 state (+926 mV), while for the S3 state we calculated 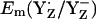= 959 mV, which is ∼30 mV higher than for the S2 state (Table 2). In general, the presence of two additional positive unit charges in the S2 state of the Mn-cluster relative to the S0 state should upshift 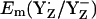considerably. Considering the calculated difference of 30 mV for 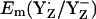between the S2 and S3 states, we estimate 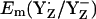to be as low as +860 mV in S0 state but the actual calculated 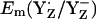for the S0 state is +932 mV. The apparent insensitivity of 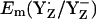to changes of Mn-cluster charges is due to charge compensation by a protonation change of titratable residues nearby. In this connection, we found that CP43-Arg³⁵⁷ deprotonates as the S-state shifts from S0 to S2. This residue was observed to be fully protonated in the S0 state, partially deprotonated in the S1 state, and fully deprotonated in the S2 state. Indeed, when we forced CP43-Arg³⁵⁷ to be fully deprotonated also in the S0 state, the calculated 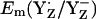decreased by 108 mV to +824 mV. Similarly, when we forced CP43-Arg³⁵⁷ to be fully protonated in the S2 state, the calculated 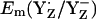increased by 63 mV to +989 mV in the S2 state. Thus, mainly CP43-Arg³⁵⁷ is responsible for the S-state independence of 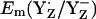observed in our computations. Hence, the variable protonation of CP47-Arg³⁵⁷ seems to function as buffer for 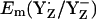during S0–S2 state transitions.

CP43-Arg³⁵⁷ is at an edge-to-edge distance of 4 Å from the Mn-cluster, close to one of the three possible substrate water binding sites, X22, which differs from the suggested Ca-bound water X21 proximal to Y_Z (1,5,6). In this location, an intermediate oxygen product before O=O bond formation of the final product O₂ might be stabilized by H-bonds with CP43-Arg³⁵⁷ as proposed in Ferreira et al. (1). These suggestions are in line with the mutation study from CP43-Arg³⁵⁷ to Ser that resulted in severely inhibited O₂-evolution (52). Based on these arguments, McEvoy and Brudvig (37) suggested that CP43-Arg³⁵⁷ is protonated in the S-states below S2 and becomes deprotonated in the higher oxidized S-states due to its proximity to the positively charged Mn-cluster (37). This is in perfect agreement with our results on CP43-Arg³⁵⁷ protonation. Thus, as they suggested, CP43-Arg³⁵⁷ may play a central role in organizing the S-state-dependent flow of protons from the Mn-cluster, which may transfer protons to D1-Asp⁶¹ belonging to the proton exit pathway (37). Instead of the proton pathway consisting mainly in Y_Z and D1-His¹⁹⁰ as proposed by Hoganson and Babcock (2), an alternative pathway not directly via Y_Z and D1-His¹⁹⁰ was proposed by Haumann and Junge (4). The deprotonation of CP43-Arg³⁵⁷ observed here favors these alternative proton exit pathways.

Factors determining the E_m difference between Y_Z and Y_D

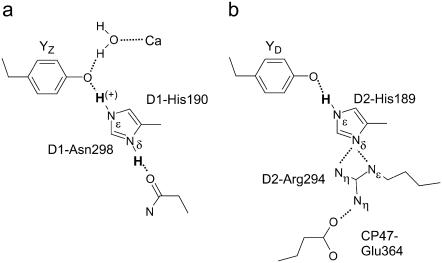
The E_m difference, E_m(Y_Z) – E_m(Y_D), was estimated to be +240 meV from the equilibrium constant for Y_Z/Y_D (14) or +210 meV from the equilibrium constants for Y_Z/S_2/1 and Y_D/S_2/1 (13). The E_m(Y_Z) – E_m(Y_D) of +232 meV in the S2 state (+257 meV in the S3 state) obtained in our computations are in good agreement with these experimental estimates. The main factors contributing to the difference between E_m(Y_Z) and E_m(Y_D) are differences in 1), the distance between the Mn-cluster and Y_Z/D; and 2), the H-bond pattern involving the histidines D1-His¹⁹⁰ and D2-His¹⁸⁹, respectively (see Fig. 4).

FIGURE 4.

H-bond network around (a) Y_Z and( b) Y_D. Only residue side chains are shown. Dotted lines indicate H-bonds or salt-bridges. Only protons belonging to Y_Z/D are shown in the figure. H⁽⁺⁾ denotes the proton whose presence depends on the redox state of Y_Z.

According to the PSII crystal structure (1) the edge-to-edge distances of the Mn-cluster to Y_Z and to Y_D are 5 Å and 28 Å, respectively, which is quite different. The removal of the Mn-cluster from PSII in vitro could result in drastic changes of protein environment, especially around Y_Z (16,17). However, solely for the purpose of distinguishing the direct influence of Mn-cluster on E_m(Y_Z/D) from other influences, we performed electrostatic energy computations in the absence of the Mn-cluster (removing also Ca²⁺ and bicarbonate) without considering any conformational change of the remaining protein. To elucidate the actual electrostatic influence in the computation, this treatment is more appropriate. Hereby, E_m(Y_Z) was downshifted by 150 mV, relative to the S2 state, to be now +780 mV (Table 2). The corresponding decrease in E_m(Y_D) was only 10 mV due to the much larger distance between the Mn-cluster and Y_D. Thus, the main contribution to the E_m difference is due to the asymmetric location of the Mn-cluster relative to the D1/D2 proteins. But, there still remains an E_m difference of ∼100 mV between Y_Z and Y_D.

For the computation of E_m(Y_Z/D), the total net charge of Y_Z-D1-His¹⁹⁰/Y_D-D2-His¹⁸⁹ was found to be +0.5/0.0. Thus, the radical pair Y^˙/Y⁻ is stabilized more for Y_Z than for Y_D. In the PSII crystal structure (1), both Y_Z and Y_D form H-bonds with Nɛ of D1-His¹⁹⁰ and D2-His¹⁸⁹, respectively. Nδ of D1-His¹⁹⁰ is close to the side-chain oxygen of D1-Asn²⁹⁸ (Fig. 4). The Nδ_His–O_Asn distance is 3.3:4.1 Å before/after constrained optimization of the atomic coordinates of the Y_Z-D1-His¹⁹⁰ pair in the reduced state. This contrasts with D2-His¹⁸⁹, whose Nδ forms a strong H-bond of salt-bridge character with the guanidinium nitrogens of the positively charged D2-Arg²⁹⁴ (Nδ_His–Nɛ_Arg distance of 2.4 Å/3.2 Å and Nδ_His–Nη_Arg distance of 3.2 Å/ 3.5 Å before/after geometry optimization). The more distant Nη of this arginine is also involved in a strong salt-bridge with the acidic oxygen of CP47-Glu³⁶⁴ (Nη_Arg–O_Glu distance of 2.9 Å) from the neighboring antenna complex CP47. Although the total net charge of the salt-bridged pair, D2-Arg²⁹⁴ and CP47-Glu³⁶⁴ at Y_D vanishes, the two H-bonds from D2-Arg²⁹⁴ to Nδ at D2-His¹⁸⁹ do not allow this Nδ to be protonated.

Only for deprotonated D2-Arg²⁹⁴, Nδ of D2-His¹⁸⁹ could have a chance to protonate. But, due to the salt-bridge with CP47-Glu³⁶⁴, D2-Arg²⁹⁴ remains positively charged. Indeed, the calculated pKa are ∼15–17 for D2-Arg²⁹⁴ and ∼0–2 for CP47-Glu³⁶⁴, independent of the Y_D redox state. Thus, protonation of D2-His¹⁸⁹ at Nδ is very unlikely. In fact, D2-Arg²⁹⁴ was fully protonated even when we removed the CP47 subunit. Contrary to D2-His¹⁸⁹, we observed Nδ of D1-His¹⁹⁰ to be permanently protonated, forming an H-bond with D1-Asn²⁹⁸. To estimate the influence of the positively charged D2-Arg²⁹⁴ on E_m(Y_D), we also considered D2-Arg²⁹⁴ in its deprotonated neutral charged state and obtained E_m(Y_D) = +823 mV in the S2 state. The resulting upshift of 129 mV in E_m(Y_D) demonstrates the significant role of the positively charged D2-Arg²⁹⁴ in lowering E_m(Y_D), which may explain the remaining E_m difference of 100 mV between Y_Z and Y_D.

Although there was no report about an explicit role of D2-Arg²⁹⁴ in Y_D redox function, the importance of D2-Arg²⁹⁴ for stability and function of PSII was suggested from random mutagenesis studies of PSII from Synechocystis PCC 6803 (53). PSII mutated from D2-Arg²⁹⁴ to Trp was still capable of O₂ evolution but with a four-times-smaller initial rate, very sensitive to light, and rapid inhibition (53). An enhanced light-sensitivity, photoinhibition, and a limited ability to evolve O₂ were also observed in the CP47-Glu³⁶⁴ mutant for PsbV-depleted PSII, where D2-Arg²⁹⁴ is unable to form the salt-bridge with the residue Glu³⁶⁴ in CP47 (54). Among cyanobacteria and higher plants, the three residues D1-Asn²⁹⁸, D2-Arg²⁹⁴, and CP47-Glu³⁶⁴ are highly conserved. Thus, the asymmetry in protein sequence and structure of D1/D2 and CP43/CP47 proteins differentiates the function of Y_Z and Y_D by the H-bond and salt-bridge pattern.

Electrostatic interactions between Y_Z/D and P_D1/D2

So far all computations were performed for the neutral charged state of P_D1/D2 i.e., 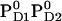. Here we report the influence of the other charge states at P_D1/D2 on E_m(Y_Z/D). In general, an increase of the net charge in the proximity of a redox-active group upshifts its E_m. Thus, formation of 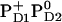or 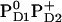is expected to upshift E_m(Y_Z/D). Nevertheless, the calculated E_m(Y_Z) remains almost unchanged among these P_D1/D2 redox states, yielding values of +918 mV and +924 mV in the states 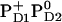and 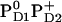, respectively (Table 3). In contrast, E_m(Y_D) showed a remarkable upshift of 38 mV for 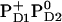and 108 mV for 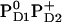. Thus, Y_D is much more sensitive to the redox state of P_D1/D2 than Y_Z with a strong electrostatic link to P_D2.

The stronger interaction between Y_D and P_D2 is likely due to the hydrophobic environment at Y_D as opposed to Y_Z, the latter having the polar Mn-cluster in its proximity (1). Furthermore, a cluster of titratable residues extends from the Mn-cluster to the luminal surface (involving D1-Asp⁶¹, D1-Glu⁶⁵, D2-Lys³¹⁷, and D2-Glu³¹², and six residues of the PsbO protein, which are Asp^O158, Asp^O222, Asp^O223, Asp^O224, His-^O228, and Glu^O229), forming a hydrophilic channel with D1-Asp⁶¹ at its mouth (5). On the other hand, the space near Y_D, which is equivalent to the position of the Mn-cluster at Y_Z, is filled with bulky hydrophobic residues (D2-Phe¹⁶⁸, D2-Phe¹⁸⁴, D2-Phe¹⁸⁵, D2-Phe¹⁸⁸, CP47-Phe³⁶², and CP47-Phe³⁶³) (5). These nontitratable residues cannot compensate for charges induced at Y_D or P_D2. Furthermore, the region between Y_D and P_D2 seems to be relatively rigid. Thus, the low dielectric medium at Y_D/P_D2 does not screen electrostatic interactions between Y_D and P_D2.

Faller et al. (7) measured the ET rate from Y_D to P680⁺ with a half-time of 180 ns (7). Their observed ET was much faster than that from earlier estimates (reviewed in (55)). To explain the kinetics of this ET process, they suggested that the cationic state of P680 should be localized on P_D2 (7), where it can be pushed onto P_D1 electrostatically if Y_D is in the oxidized state, thereby accelerating ET from Y_Z to P680⁺ (7,9). The specifically strong electrostatic interaction between Y_D and 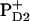observed in our computations may corroborate these suggestions. Hence, presence of nontitratable residues in the neighborhood of Y_D/P_D2 and their absence near to Y_Z/P_D1 may be necessary to favor ET from Y_Z to P680⁺.

Influence of D2-Arg¹⁸⁰ on E_m(Y_D)

D2-Arg¹⁸⁰ is suggested to have an impact not only on P680 (12,56) but also on Y_D, because mutation of this residue led to a loss of EPR signal originated from the oxidized state of Y_D (57). To investigate the influence of this residue, we calculated E_m(Y_Z/D) in the S2 state in forcing D2-Arg¹⁸⁰ to be deprotonated. The resulting E_m(Y_D) is +564 mV, significantly downshifted by 130 mV (Table 3). Surprisingly, E_m(Y_Z) did not shift upon deprotonation of D2-Arg¹⁸⁰, confirming the EPR studies of D2-Arg¹⁸⁰ mutants (57) and thereby suggesting that this arginine has a predominant impact on Y_D but not Y_Z. To explain this large effect, it was previously proposed that D2-Arg¹⁸⁰ was capable of accepting a proton released from Y_D or stabilizing the proton on D2-His¹⁸⁹ (57). However, our computation yielded a pKa of 11.3 for D2-Arg¹⁸⁰, which is standard for arginine. Hence, this arginine residue is generally protonated regardless of the redox states for P_D1/D2 and Y_Z/D.

Indeed, the persistence of the D2-Arg¹⁸⁰ protonation is also one of the reasons that in our computation deprotonation/protonation by redox change at P_D1/D2 and Y_D occurs predominantly at D2-His⁶¹. Interestingly, the symmetrical counterpart of D2-His⁶¹ is the acidic D1-Asp⁶¹, which is very close to the Mn-cluster, belonging to the hydrophilic channel leading to the luminal bulk surface (1,5,6). Both D1-Asp⁶¹ and D2-His⁶¹ are highly conserved among cyanobacteria and higher plants.

In the absence of light, the majority of PSII is adapted to the S1 state, not the lowest oxidized state S0 (58). This is probably due to the oxidative ability of Y_D (9,59). The corresponding E_m(S1/S0) is estimated to be ∼+700 mV (10,13). Since with deprotonated D2-Arg¹⁸⁰ the computed E_m(Y_D) is only +564 mV, in a PSII mutant with depleted D2-Arg¹⁸⁰, Y_D might not be able to oxidize the S0 state to S1 efficiently. Hence, we suggest that the loss of EPR signal from Y_D in mutant PSII with depleted D1-Arg¹⁸⁰ can be associated with the inability of Y_D to oxidize the S0 to the S1 state. Therefore, Y_D in the wild-type PSII could play a redox-active role in photoassembly of the Mn-cluster as suggested in Rutherford et al. (9), and the ability to oxidize S0 to S1 by Y_D could depend on the value of E_m(Y_D) with respect to E_m(S1/S0).

CONCLUDING REMARKS

The calculated E_m(Y^˙/Y⁻) were +926 mV/+694 mV for Y_Z/Y_D in S2 state of the Mn-cluster in agreement with former estimates (13,14). The differences in the distances of Y_Z and Y_D from the Mn-cluster as well as those in the H-bond network of Y_Z (Y_Z/D1-His¹⁹⁰/D1-Asn²⁹⁸) and Y_D (Y_D/D2-His¹⁸⁹/D2-Arg²⁹⁴/CP47-Glu³⁶⁴) are responsible for the differences in E_m. If D1-His¹⁹⁰ is protonated, 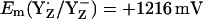is nearly as high as E_m(P680). E_m(Y_ZH^˙+/Y_ZH) calculated in the Mn-depleted PSII model was +1264 mV, lower than that of +1576 mV calculated in intact PSII, implying that Y_ZH^˙+/Y_ZH may serve as functional electron donor to P680⁺ in the Mn-depleted PSII as suggested by EPR spectroscopy on Mn-depleted PSII (50,51). CP43-Arg³⁵⁷ deprotonates as the S-state shifts from S0 to S2, suggesting its participation in water oxidation and proton translocation. A strong electrostatic link was found specifically between Y_D and P_D2. This is probably because of the presence of bulky hydrophobic residues (D2-Phe¹⁶⁸, D2-Phe¹⁸⁴, D2-Phe¹⁸⁵, D2-Phe¹⁸⁸, CP47-Phe³⁶², and CP47-Phe³⁶³) in the Y_D side. These residues cannot compensate for charges induced at Y_D or P_D2, in contrast to the hydrophilic residues likely serving as proton channel in the Y_Z side (D1-Asp⁶¹, D1-Glu⁶⁵, D2-Lys³¹⁷, D2-Glu³¹², and several residues of the PsbO protein). This difference in protein environment may explain the former suggestion that the cationic state of P680 should be localized on P_D2 and can be pushed onto P_D1 electrostatically, thereby accelerating ET from Y_Z to P680⁺ (7,9). The positively charged D2-Arg¹⁸⁰ upshifts E_m(Y_D) significantly. Upshifting of E_m(Y_D) by D2-Arg¹⁸⁰ might play a significant role in maintaining the redox ability of Y_D in intact PSII, as demonstrated by mutational studies (57).

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.