Structural Instability of the Prion Protein upon M205S/R Mutations Revealed by Molecular Dynamics Simulations

Abstract

The point mutations M205S and M205R have been demonstrated to severely disturb the folding and maturation process of the cellular prion protein (PrP^C). These disturbances have been interpreted as consequences of mutation-induced structural changes in PrP, which are suggested to involve helix 1 and its attachment to helix 3, because the mutated residue M205 of helix 3 is located at the interface of these two helices. Furthermore, current models of the prion protein scrapie (PrP^Sc), which is the pathogenic isoform of PrP^C in prion diseases, imply that helix 1 disappears during refolding of PrP^C into PrP^Sc. Based on molecular-dynamics simulations of wild-type and mutant PrP^C in aqueous solution, we show here that the native PrP^C structure becomes strongly distorted within a few nanoseconds, once the point mutations M205S and M205R have been applied. In the case of M205R, this distortion is characterized by a motion of helix 1 away from the hydrophobic core into the aqueous environment and a subsequent structural decay. Together with experimental evidence on model peptides, this decay suggests that the hydrophobic attachment of helix 1 to helix 3 at M205 is required for its correct folding into its stable native structure.

INTRODUCTION

In prion diseases, like the Creutzfeldt-Jakob disease, scrapie, or the bovine spongiform encephalopathy, the central pathogenic process is the refolding of cellular prion proteins (PrP^C) into the pathological and β-sheet-rich isoform PrP^Sc, which aggregates into amyloid fibers (1). The occurrence of such a template-guided refolding process indicates that the native solution structure of PrP^C cannot be very stable. According to nuclear magnetic resonance (NMR) spectroscopy (2,3), in this solution structure only the C-terminal domain (residues 125–28) exhibits a well-defined tertiary folding pattern, whereas the remaining N-terminal part is randomly coiled. Moreover, the major result of a refined NMR analysis was the precise structural definition of a large fraction of side chains, showing that the globular domain of PrP^C contains a tightly packed hydrophobic core (4). Due to the marginal stability of the PrP^C structure, small perturbations such as point mutations of single residues in the globular C-terminal domain are likely to cause large-scale structural changes.

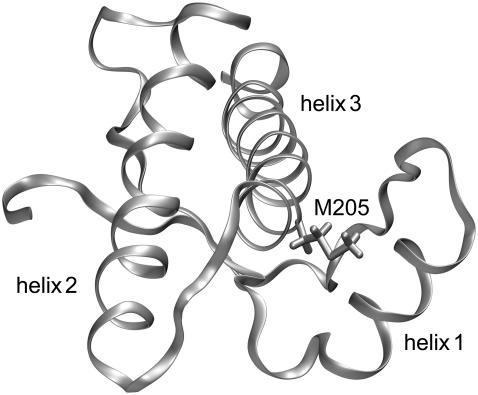
A candidate for such a perturbing mutation is methionine 205. The position of M205 within the C-terminal domain of human PrP^C (3) is shown in Fig. 1. M205 is part of helix 3 and its hydrophobic side chain is buried in the region of contact with helix 1. Therefore, a replacement of M205 by a hydrophilic residue could weaken this hydrophobic contact and thereby destabilize the hydrophobic core. Indeed, a previous study in cell culture (5) revealed that the two mutations M205S and M205R significantly interfere with folding and maturation of PrP^C in the secretory pathway of neuronal cells. In contrast to wild-type PrP^C, both mutants adopt a misfolded and partially protease-resistant conformation, lack the glycosylphosphatidylinositol anchor, and are not complex glycosylated. Interestingly, PrP-ΔH1, a different PrP mutant in which helix 1 was completely deleted, shows the same phenotype (5).

FIGURE 1.

Backbone folding pattern of the human prion protein in the C-terminal domain (residues 125–228) according to the NMR structure in Zahn et al. (3). Besides a two-stranded antiparallel β-sheet, the structure comprises three α-helices, helix 1 (144–154), helix 2 (173–194), and helix 3 (200–228). Also drawn is the hydrophobic side chain of methionine 205, which is part of helix 3. According to the figure, this side chain is buried in the contact region between helix 3 and helix 1. This structural arrangement suggests that the replacement of M205 by a hydrophilic residue like serine or arginine could induce an intrusion of water molecules into the contact region and, thus, loosen the attachment of the two helices.

The question as to whether helix 1 is stable or not has been a central topic in a series of further studies, which applied circular dichroism (CD) (6) and NMR spectroscopy (7–10), bioinformatics tools of secondary-structure prediction (7,11), molecular modeling (12,13), or molecular-dynamics (MD) simulations (11) to peptides covering the helix 1 sequence. Some of these studies came to the conclusion that helix 1 is stable (9), or even remarkably stable (7), whereas others came to the opposite conclusion (8,10). Its sequence is characterized by an unusual abundance of charged residues (13), which are all exposed to the solvent. The region of contact with helix 3, however, exhibits mildly polar (Y149, Y150, N153) or nonpolar (M154) residues, such that helix 1 acquires an amphiphilic character.

The interest in the stability of helix 1 has been driven by the little available knowledge on the structure of the pathogenic PrP^Sc isoform of PrP^C, according to which PrP^Sc is largely formed by β-sheets and has a reduced α-helical content (14,15). Therefore, certain parts of the PrP sequence, which in PrP^C form α-helices, must refold into β-sheets during the conformational transition from PrP^C to PrP^Sc. The question, then, is which parts do refold, and, in particular, do they cover helix 1?

Unfortunately, PrP^Sc is currently inaccessible to high-resolution techniques of structural analysis: conventional solution NMR fails, because the PrP^Sc amyloid fibers are too large, and x-ray diffraction cannot be applied, because nobody has succeeded in arranging these fibers into three-dimensional crystals. Therefore, one has to resort to necessarily somewhat speculative modeling considerations when addressing the structure of PrP^Sc.

According to recent modeling suggestions, helices 2 and 3 are preserved in the PrP^C-to-PrP^Sc transition, whereas the role of helix 1 is controversial (16–19). According to one of these PrP^Sc models (16), which was designed to match electron microscopy data on two-dimensional crystals of PrP^Sc building blocks, helix 1 refolds and becomes a part of a large, left-handed, and triangular β-helix. Because such a structure cannot tolerate charged residues within its hydrophobic core, other alignments of parts of the PrP sequence onto such a β-helix were recently developed (17,18). In contrast, helix 1 remains stable according to a simulation-based model for a PrP^Sc protofibril (19).

Motivated by these discussions and by the specific results on the putative significance of M205 for the stabilization of helix 1 (5), we decided to carry out computer experiments aimed at checking whether the point mutations M205S and M205R can actually induce a destabilization of helix 1. As our testing scenario, we have chosen MD simulations of the C-terminal domain of human PrP^C as well as of two suitably modeled mutants in pure water at room temperature and ambient pressure. Arguments explaining the thermodynamic and statistical background of the applied testing scenario can be found in Stork et al. (18).

METHODS

Simulation system

As the starting structure for our simulation of the C-terminal domain (residues 125–228) of human PrP^C, which we call wtPrP, we chose the NMR structure (entry 1QM2 of the Protein Data Bank (20)) determined by Zahn et al. (3). In addition, we created simulation models for the two variants PrP-M205S and PrP-M205R by introducing the respective point mutations M205S and M205R into the structure of wtPrP using Swiss-PdbViewer (21). Charged N- and C-terminal groups were chosen for all three models. A rhombic dodecahedron just covering an enclosed sphere with a radius of 52 Å has been chosen to define the geometry of a periodic simulation system. Because the maximum extension of the PrP is ∼51 Å along helix 3, the simulation cell is larger than twice the maximum extension of PrP in any direction. Initially this unit cell was filled with molecular mechanics (MM) models of water molecules. The transferable three-point interaction potential originally suggested in Jorgensen et al. (22) and modified in MacKerell et al. (23) was chosen as the MM force field for these water models. The force-field parameters of the proteins were adopted from CHARMM22 (23).

All simulations were carried out using the NPT ensemble with the MD program EGO-MMII (24). The temperature T and the pressure p were controlled by a thermostat (τ = 0.1 ps) and a barostat (τ = 1.0 ps, β = 5.0 Pa) (25), respectively. Covalent bonds involving hydrogen atoms were kept fixed by the M-SHAKE procedure (26). A basic time step of 2 fs was chosen for the multiple time-step integration (27) of Newton's equations of motion employed by EGO-MMII. The long-range Coulomb interactions were treated by the combination of structure-adapted multipole expansions (28,29) with a moving-boundary reaction-field approach explained and tested by Mathias and co-workers (24,30). Here, the dielectric and ionic continuum surrounding each atom in the system at a distance of ∼52 Å were described by a dielectric constant ɛ = 79.0 and a Debye-Hückel parameter κ = 0.13 Å⁻¹, respectively. That value of κ corresponds to a 165-mM NaCl concentration. Van der Waals interactions were calculated explicitly up to distances of 10.5 Å; at larger distances, a mean-field approach (31) was applied.

The water system was initially equilibrated for 1 ns at T = 300 K and p = 1.013 × 10⁵ Pa. For solvation the proteins were positioned at the center of the equilibrated water box and all water molecules closer than 2.0 Å to a protein atom were removed, resulting in a total amount of ∼25,800 water molecules surrounding a given protein. This corresponds to a 2.15-mM protein concentration. In addition, ∼150 of the water molecules were randomly selected and replaced by Na⁺ and Cl⁻ ions, yielding a neutral simulation system and the 165-mM NaCl concentration used above for the characterization of the Debye-Hückel continuum. Thus, the simulation system covered ∼79,200 atoms. For equilibration, the proteins were initially kept fixed, whereas the surrounding solvent molecules were thermally moving for several hundred picoseconds at T = 500 K and T = 300 K. Next, the rigid constraints were removed and solely the positions of the protein C_α atoms were constrained by harmonic potentials (force constant 2.1 × 10² kJ/(mol Ų)). These systems were cooled by energy minimization within 1 ps to T < 0.1 K and subsequently heated within 120 ps to T = 300 K. Within another 300 ps, the constraining force constants were slowly reduced to zero until the proteins were free to move within the solvent. This procedure served to adjust the modeled protein structures to the MM force field, or, equivalently, to partially remove the prejudices imposed onto the structures by the modeling. The simulation systems thus obtained were the starting points for the following unconstrained 10-ns simulations at T = 300 K and p = 1.013 × 10⁵ Pa. Coordinates were saved every picosecond. Note, here, that 10-ns simulations of systems with ∼80,000 atoms are computationally quite expensive. Using six processors (1.6 GHz), the total computation time for all three simulations was ∼20 weeks.

Measures of overall stability

To obtain an overall measure for the structural stability of the three PrP variants during MD simulation, the three trajectories were separately analyzed by computing root mean-square deviations from average initial structures. Restricting the analysis to the backbone as given by the coordinates of the C_α atoms, the average initial structures were calculated from the first 100 ps of the free simulations. Each backbone structure sampled by the unconstrained simulation was subsequently fitted onto the respective initial structure by minimization of the root mean-square deviation, and the resulting time series of minimal values d_rms(t) was saved for plotting.

Classification of backbone trajectories and determination of protein conformations by hierarchical cluster analysis

For a detailed analysis of the backbone conformations sampled by the MD trajectories of the three PrP variants, the φ/ψ dihedral angles along the protein backbones were collected resulting in time series of 206-dimensional feature vectors α ≡ (ψ₁₂₅, φ₁₂₆, ψ₁₂₆, …, φ₂₂₇, ψ₂₂₇, φ₂₂₈) ∈ [−π, π]²⁰⁶. The corresponding data sets {α(t) | t = 1, …, 10,000} represent point densities in the angular configuration space [−π, π]²⁰⁶, for which we derived smooth, parametric, and analytical maximum-likelihood (ML) density models p(α |σ_ML) in the form of mixtures of R = 100 univariate normal distributions with identical statistical weights 1/R and widths σ_ML. The parameters of these mixture models, that is the centers w_r ∈ [−π, π]²⁰⁶, r = 1, …, 100 and the common width σ_ML of the Gaussians, were optimized by a safely converging algorithm maximizing the likelihood of the density estimates provided by the mixture models p(α |σ_ML) (32–34).

As is well known (see, e.g., Carstens et al. (34) for further references and a discussion), each conformation of a peptide whose dynamics is sampled by a MD trajectory corresponds to a local maximum of the point density in the reduced configuration space [−π, π]²⁰⁶, because such a maximum marks a local minimum of a corresponding free energy landscape. However, the distinction of a local density maximum from a statistical density fluctuation requires a smoothening of the density at multiple scales. Therefore, to identify the hierarchies of conformations and subconformations, we constructed scale-space representations p(α | σ) = p(α | σ_ML) × g(α | σ_conv) of the ML models by convolution with a Gaussian kernel g(α | σ_conv) of varying width σ_conv. The resulting models p(α | σ) are mixtures of normal distributions at fixed centers w_r and of variable width σ. For these smoothened models p(α | σ), we employed gradient ascents to detect all of their local maxima and, thus, the number N(σ) and prototypical geometries α_k(σ) of all conformations k = 1, …, N(σ) at the given spatial resolution σ.

By considering plots of N(σ) vs. σ obtained for the three protein models we selected a common resolution σ_c = 1.85 rendering N(σ_c) = 4, 3, and 7 conformational states for wtPrP, PrP-M205S, and PrP-M205R, respectively (cf. the figure in the Supplementary Material). The resulting prototypical states k of the three PrP variants are denoted by wt1-wt4, S1-S3, and R1-R7, respectively. For graphical illustration of these prototypical structures, we picked those snapshots from the MD trajectories whose feature vectors α(t) are closest to the density maxima at α_k(σ_c) in dihedral space [−π, π]²⁰⁶. Finally, at the selected resolution σ_c every protein geometry α(t) contained in the time series was classified by gradient ascent as belonging to one of the conformations k.

We checked by comparison with other possible choices that the selected resolution σ_c = 1.85 represents a reasonable compromise between a sufficiently simplified but still detailed representation of the backbone fluctuations and relaxations sampled by the trajectories. For instance, an increase of the resolution by reducing σ from 1.85 to 1.7 slightly increases the number N(σ) of conformations from four to five for wtPrP, leaves that number invariant at the value of three for PrP-M205S, and strongly increases it from 4 to 11 for PrP-M205R. The latter increase indicates that many major conformational transitions must have been sampled by the corresponding trajectory. This conjecture will be substantiated further below.

Classification of trajectories in terms of secondary-structure elements

For an analysis of local secondary-structure motifs we applied the software tool DSSP (Database of Secondary Structure in Proteins) by Kabsch and Sander (35), which employs H-bonding patterns and various other geometrical features to assign secondary-structure labels to the residues of a protein. DSSP classifies each residue in every snapshot as belonging to one of the eight classes “α-helix”, “isolated β-bridge”, “extended strand”, “3-10-helix”, “π-helix”, “H-bonded turn”, “bend”, or “other”. Snapshots taken every 50 ps from the trajectories served as input for DSSP. As a result, one obtains trajectories of secondary-structure labels. Using suitable color coding, one can represent the local secondary-structure dynamics sampled by a trajectory as a graph covering as many lines as there are residues in the simulated protein model.

RESULTS

To allow a most vivid insight into the processes described by our three 10-ns simulations of the wild-type and the two mutant PrP models, we have provided three mpg-movies in the online supplement to this article (http://www.biophys.org). The movies show the backbone fluctuations of the three proteins in a ribbon representation. The M205 residue and its mutated variants are highlighted by an all-atom representation. Snapshots taken every 20 ps were collected to generate these movies.

Movies cannot be printed, nor does their format permit a quantitative comparison between the three simulations. For this reason, the observation and classification tools described above have to be used.

PrP-M205S and PrP-M205R are less stable than wtPrP

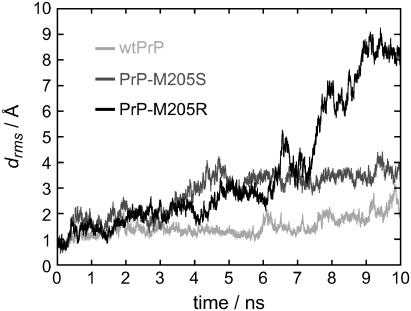
Fig. 2 shows the time series d_rms(t) of the root mean-square deviations from the initial backbone structures (cf. Methods) for the three PrP variants. For wtPrP (light shaded), the values of d_rms(t) are smaller than those for the two mutants throughout the whole simulation time of 10 ns, indicating that the MD simulation preserves the starting structure of wtPrP much better than those of the mutants. Among the mutants, PrP-M205R (solid) is seen to deviate much more strongly from the starting structure than PrP-M205S (dark shaded).

FIGURE 2.

Time series of the minimal root mean-square deviations d_rms(t) of the PrP structures from their respective initial structures.

According to Fig. 2, for wtPrP the values of d_rms(t) fluctuate around 1.5 Å for the first 6 ns. In the remaining time span the deviation d_rms(t) increases to values of ∼2.5 Å, indicating that a conformational change occurred at ∼6 ns.

For PrP-M205S, the values of d_rms(t) initially exhibit a rapid increase. Within the following first 3 ns, they fluctuate around 2 Å before they subsequently rise to a second plateau characterized by values near 3.5 Å. These data indicate that the starting conformation of PrP-M205S, which had been chosen close to the native structure of PrP^C, is changed by two major conformational transitions. Correspondingly, the data suggest that each of the two plateaus represents a meta-stable conformation, in which PrP-M205S happens to be temporarily caught during the 10-ns computer experiment.

In the case of PrP-M205R, the values of d_rms(t) moderately increase in two consecutive stages during the first 6 ns until they cross the d_rms(t)-trajectory of PrP-M205S. After 6 ns, the d_rms(t) trajectory of PrP-M205R steeply increases to reach a peak of 5 Å at ∼6.5 ns. After a short decline at ∼7 ns, this trajectory exhibits further jumps toward larger values until it seems to reach a plateau at ∼8.5 Å within the last nanosecond of the simulation. This behavior suggests that the R-mutant undergoes substantial conformational changes by passing through several short-lived intermediate states.

For the two mutants, the above analysis of the d_rms(t) time series has shown that the assumed PrP^C-like starting structures do not represent stable conformations. In contrast, for wtPrP, significantly smaller deviations were observed. For all three PrP variants time points of conformational transitions were identified. However, the inspection of the d_rms(t) trajectory did not provide any insights into the structural changes described by the 10-ns computer simulations. Clearly, viewing the movies of the trajectories gives detailed impressions of the conformational changes sampled by the simulations. A coarse-grained and printable version of these movies, which catches in a sketchy manner their essential contents, is obtained by applying our hierarchical classification scheme to the three trajectories. Here the backbone configurations sampled by the trajectories are represented in terms of coarse-grained prototypical conformations as described in Methods. The results of that conformational analysis will now be individually presented for each of the three simulation trajectories, starting with wtPrP.

Conformational equilibrium fluctuations of wtPrP

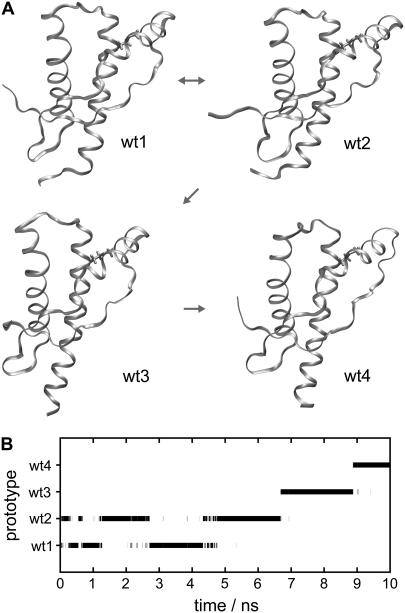
Fig. 3 A shows the prototypical structures wt1–wt4, representing the coarse-grained states identified by our classification scheme in the MD trajectory of wtPrP, and Fig. 3 B shows the corresponding classification of the trajectory (cf. Methods). Within the first 6.7 ns, the wtPrP model repeatedly fluctuates between the backbone conformations wt1 and wt2, before it subsequently changes to conformation wt3 and finally to wt4. By comparing the drawings in Fig. 3 A we can now identify the structural contents of these transitions.

FIGURE 3.

(A and B) Conformations of wtPrP and time series of classifications. The structures of wt1, wt2, wt3, and wt4 are related to local density maxima in dihedral space. Thus, they represent classes of structurally similar configurations within the simulation time series of wtPrP. (A) The small arrows between the conformations indicate the chronological order in which they were occupied during the simulation. (B) The protein configurations sampled by the simulation of wtPrP are assigned to the classes defined by the prototypical configurations wt1–wt4.

For instance, one of the features of the conformational transition at ∼6–7 ns, whose occurrence was already indicated by the d_rms(t) trajectory (cf. the discussion of Fig. 2), and which now has been identified as the wt2 → wt3 transition, appears to be a spontaneous refolding of the C-terminal part of helix 3. This part of helix 3 loses its original NMR shape during the first few picoseconds of the simulation and thus is disordered in wt1 and wt2. It regains its α-helical structure in wt3 and wt4. Inspection of the movie of the wtPrP trajectory (see Supplementary Material) clearly shows these processes. The marginal stability of the C-terminal part of helix 3 thus described by our MD simulation agrees with the NMR data presented by Zahn et al. (3), who found an enhanced accessibility to amide proton exchange at the corresponding residues. A second feature of the wt2 → wt3 transition seems to be a slight loosening of the extended polypeptide chain between the disordered N-terminal tail and helix 1. According to NMR (3), this sequence portion partially contributes to a rather rigid, small β-sheet found in the PrP structure. The wt3 → wt4 transition observed at 9 ns is characterized by a bending of the C-terminal part of helix 2, a straightening of helix 3, and a change of the connecting loop.

The trajectory in Fig. 3 B indicates an equilibrium between the conformations wt1 and wt2, which mainly differ in the orientations of the flexible N- and C-termini. Unfortunately, our 10-ns trajectory is too short to provide corresponding evidence also for the transitions to conformations wt3 and wt4: a return to the wt1 or wt2 conformation has not (yet) been observed.

In PrP-M205S, helix 2 is decaying

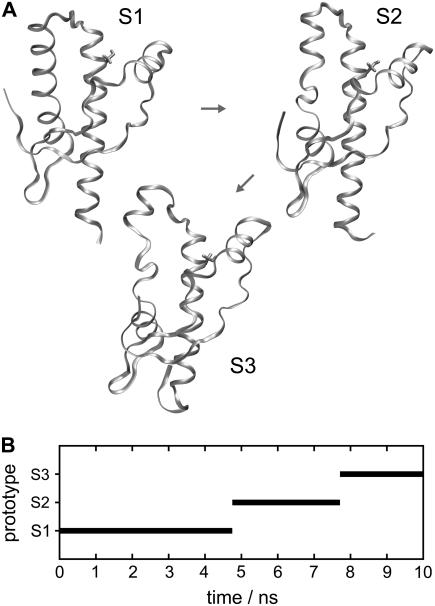
Fig. 4 A shows the three conformations S1, S2, and S3 identified by our classifier for PrP-M205S. Conformation S1 closely resembles the PrP^C-like initial structure. The main difference is a slight increase of the gap between helix 1 and helix 3 near position 205 (as compared to the native structure in Fig. 1 or to the nearly native conformations wt1–wt4 in Fig. 3 A) and indicates a partial solvation of the Ser-205 by water molecules (not shown) entering the interfacial region between the two helices. As is apparent from the classification of the trajectory in Fig. 4 B, conformation S1 persists for the first 4.7 ns of our computer experiment. According to Fig. 2, at about this time the d_rms(t) trajectory reaches a second plateau, indicating a major conformational transition.

FIGURE 4.

Conformations of PrP-M205S (A) and time series of occupancies (B).

Fig. 4 B identifies the new conformation of PrP-M205S as S2, and the drawing in Fig. 4 A reveals the structural nature of the S1 → S2 transition. Apart from small fluctuations at the C- and N-termini it mainly consists in an unfolding of ∼1.5 coils of helix 2 covering the region between residues 181 and 186. As revealed by Fig. 4 B, conformation S2 lives for ∼3 ns, until it further decays to conformation S3, which is the conformation persisting until the end of our simulation. Fig. 4 A demonstrates that the S2 → S3 transition is characterized by a continued unfolding of helix 2 such that the unfolded region now covers residues 181–188. This continued unfolding of helix 2 is accompanied by an unfolding of the C-terminal part of helix 3 by 1.5 coils.

According to the NMR data on amide hydrogen exchange in native PrP^C (3), helix 2 is quite rigid in the region between 181 and 186, whereas the part from residues 187–194 is supposed to exhibit a considerable conformational flexibility. Earlier MD studies on PrP fragments spanning a part (residues 180–193) of helix 2 (36) or helices 2 and 3 (11) essentially agreed with these NMR data, although the latter study indicated a decreased helical order already for residues 182–186. The latter finding thus agrees with our result that the mutation-induced unfolding of helix 2 starts in the supposedly rigid sequence range 181–186. These data suggest that the 181–186 part of helix 2 is stabilized into its natively rigid structure by the unperturbed structural ensemble characteristic for the native PrP sequence.

Note here that the large-scale processes of conformational decay exhibited by Fig. 4 are hardly reflected by the d_rms(t) time series in Fig. 2, underlining the limited value of this simple observable. To monitor the further fate of the observed decay, which most probably will go on after 10 ns, more extended simulations will be required.

However, independent of that fate, already the observed processes appear to mark a fast and unidirectional decay of the PrP^C-like initial structure for PrP-M205S. Because our wtPrP model of a natively stable structure did not show any comparable signs of instability, particularly concerning the 181–186 sequence of helix 2, we conclude that this rigid part of the native PrP structure is destabilized by the M205S mutation. Furthermore we conclude from the observed instability of the PrP-M205S model that this protein, if it happened to assume a PrP^C-like structure, would leave this conformation rapidly. Conversely, the M205S mutant will most likely never acquire the native PrP^C structure, because it apparently represents an unstable state of very high free energy.

One would now expect that helix 2 decays also in our mutant model PrP-M205R, because in this mutation, too, the hydrophobic M205 is replaced by a polar residue. In fact, it is likely that such a decay will be observed in corresponding computer experiments. However, our single computer experiment on PrP-M205R happened to reveal a further and different property of the native PrP^C structure.

In PrP-M205R, helix 1 is decaying

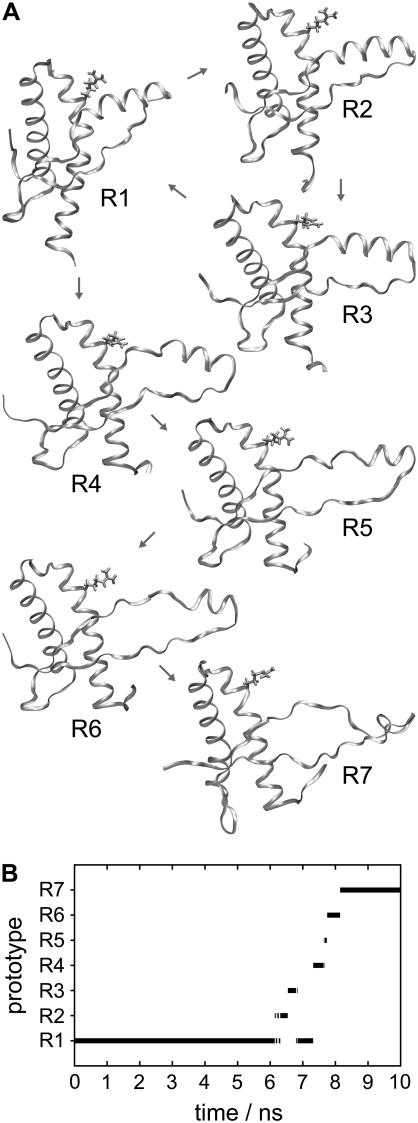
In the case of the experiment on PrP-M205R, our statistical tool for classification of backbone conformations identifies a set of seven prototypical structures, R1–R7 (see Fig. 5 A). Fig. 5 B shows that the PrP-M205R model remained in conformation R1 during the first 6.2 ns. According to Fig. 5 A, the main feature of conformation R1 is an opening of a gap between helices 1 and 3 (cf. conformations wt1–wt4 in Fig. 3 A), which, as in the S1 conformation discussed above, serves to allow a solvation of the polar residue replacing M205 by water molecules entering the interfacial region (further data concerning the water are not shown). Because the charged arginine residue is larger and more polar than the small serine, the gap between the two helices is larger in R1 than in S1. Thus the M205R mutation induces a stronger perturbation into the native PrP^C structure than M205S.

FIGURE 5.

Conformations of PrP-M205R (A) and time series of occupancies (B).

Fig. 5 B shows that shortly after 6.2 ns, the PrP-M205R conformation switches to states R2 and R3, returns to R1, and through the very short-lived intermediates R4–R6 jumps to R7, where it happens to remain for the last 2 ns of our simulation. According to Fig. 5 A, the initial fluctuations within the set of states R1–R3 mainly consist of reversible and strong fluctuations of helix 1 into the aqueous phase, strongly increasing the gap and corresponding angle between helices 1 and 3. However, at ∼7.5 ns the water-exposed helix 1 starts to unfold in several stages. In the R1 → R4 transition, a first coil of helix 1 unfolds. The R4 → R5/R6 transition is characterized by the partial unfolding of a second coil resulting in a complete unfolding of the amphiphilic part of helix 1. Finally, in the transition to R7, residues D144 and Y145 also leave the original α-helical structure. In R7 only the four residues 146–149 remain in an α-helical structure. Note here that the above decay process is accompanied by an unfolding of 1.5 coils in the C-terminal part of helix 3, whereas the remaining parts of the PrP^C structure remain essentially unchanged. Also in this case the fate of the ongoing decay process is unclear.

As in the case of M205S, the instability observed for the M205R model indicates that the M205R protein will most likely never acquire the native PrP^C structure. Furthermore, our finding supports the suggestions by Winklhofer et al. (5) that the point mutation M205R destabilizes helix 1 and that M205R differs structurally from wtPrP.

Trajectories of secondary-structure features

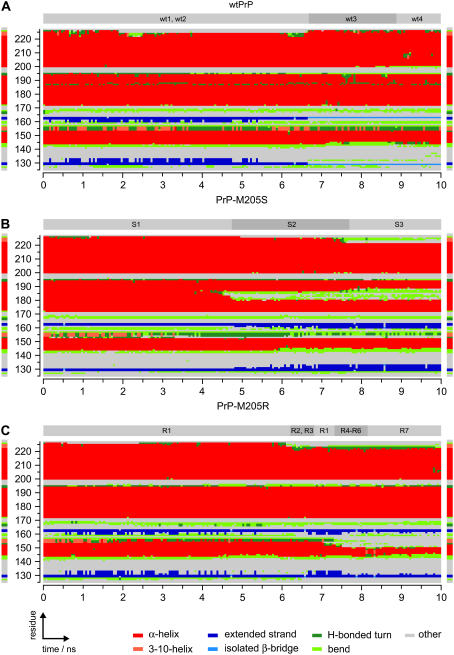
Fig. 6 shows the classification of the three trajectories in terms of secondary-structure elements obtained by the software tool DSSP (cf. Methods). The DSSP plots enable a local structural analysis complementing the above characterization of the backbone conformational dynamics.

FIGURE 6.

Classification of trajectories in terms of secondary-structure elements by DSSP (35). The residue-wise DSSP classifications are shown for the trajectories for wtPrP (A), PrP-M205S (B), and PrP-M205R (C). As a reference, the DSSP classification of the NMR structure (3) is displayed at the left and right margins. For comparison, the classification in terms of prototypical backbone structures from Figs. 3 B, 4 B, and 5 B is indicated at the top of the DSSP plots.

Before examining the time series, consider the DSSP classification of the NMR structure of PrP^C by Zahn et al. (3), which is depicted in Fig. 6 at the left and right margins of the DSSP time series. Generally, the DSSP classification agrees quite well with the secondary-structure assignments given by Zahn et al. (3) (cf. legend to Fig. 1). DSSP, however, classifies the C-terminal residues 223–226 of helix 3 as forming 3-10-helical (light red) or bend (light green) structures and classifies residues 227 and 228 as “other” (gray). Furthermore, DSSP marks only residues 129 and 130, as well as 162 and 163, as “extended strands” (blue), whereas according to Zahn et al. (3) the small β-sheet covers residues 128–131 and 161–164.

When one examines the DSSP time series for wtPrP shown in Fig. 6 A, one gains complementary insights into the conformational dynamics. During the first 6.7 ns covering the wt1 ↔ wt2 equilibrium, the C-terminal residues of helix 3 unfold and show an enhanced flexibility (green or gray instead of red at the top lines of the graph). Correspondingly, in the conformations wt1 and wt2 (cf. Fig. 3 A), the terminal part of helix 3 is unfolded. Likewise, DSSP confirms its subsequent refolding during the lifetime of states wt3 and wt4. As we have pointed out above, in the discussion of the wtPrP conformations, this C-terminal flexibility agrees with NMR (3).

A detail that cannot be detected by visual inspection of wt1–wt4 in Fig. 3 A but is revealed by Fig. 6 A is the growth of the two short β-strands (blue) toward helix 1 during the first half of the simulation time, as well as their subsequent shortening toward a single pair of isolated β-bridges present during the lifetimes of wt3 and wt4 (light blue). This shortening can only be partially guessed from the loosening of the polypeptide chain between the flexible N-terminal tail and helix 1 displayed by the backbone conformations in Fig. 3 A. However, this loosening also covers the loop region between β-strand 1 and helix 1 (132–143) and this feature is not reflected in the DSSP plot. The corresponding residues are simply classified as “other” or “bend”.

The shortening of the β-strands is accompanied by an enhanced flexibility at the two N-terminal residues 144 and 145 of helix 1, which temporarily switch to bend (light green) or turn (green) structures in the period between 7.2 ns and 9.7 ns. The fact that these two residues rejoin helix 1 at 9.7 ns indicates the equilibrium character of these fluctuations. Such a conformational equilibrium has been suggested earlier by Zahn et al., who found an increased amide proton exchange at these residues (3). These authors additionally reported enhanced proton exchange for residue 155 (3) at the C-terminus, which is consistent with the fluctuations of residues 154–156 between 3-10-helical (light red) and turn (green) structures observed in the DSSP time series for wtPrP.

Further details revealed by the DSSP time series for wtPrP and overlooked by our previous coarse-grained conformational analysis are certain fluctuations in helix 2. Here, residues 187 and 188 persistently switch and residues 189–194 occasionally fluctuate between α-helical (red) and turn structures (green). Also this flexibility agrees with an enhanced proton exchange (3), as noted above in our discussion of PrP-M205S.

In part, the DSSP time series for PrP-M205S and PrP-M205R in Fig. 6, B and C, show features similar to the one just discussed for wtPrP. For instance, they also show large-scale fluctuations from α-helical to bend or turn structures at the C-terminal residues 221–228 of helix 3. Because these particular fluctuations were reversible in the case of wtPrP and were shown to be in agreement with NMR data on amide proton exchange (3), they are equilibrium fluctuations. However, in the DSSP trajectories for PrP-M205S and PrP-M205R these fluctuations happen to occur at much larger timescales. They are observed only in the second parts of the two simulations, and a return to the integral helical structure does not occur until the end of the simulations. However, this does not mean that helix 3 cannot be restored later. It simply shows that certain fluctuations can cover vastly different time spans and that the simulation time of 10 ns is too short to cover all equilibrium processes although it is near the limits of computational feasibility for such a large system.

According to the DSSP analysis, the small β-sheet (blue) is stable for the first 5 ns and subsequently grows in the case of PrP-M205S, whereas it persistently fluctuates between a larger and normal size in PrP-M205R. A shortening, which happened to occur in the wtPrP simulation, is missing. For the stated reason of limited sampling, these findings do not imply that such a shortening will never occur in the mutants nor that a restoration to the original size cannot occur in the wtPrP model. Instead, the tendency of β-sheet growth found in parts of all three simulations when taken together with the stability of the β-sheet revealed by NMR appears to indicate that the employed CHARMM22 force field can satisfactorily describe this type of structural element.

Besides the discussed fluctuations, which seem to be equilibrium processes, the DSSP plots of the mutant models show two remarkable features, which do not even remotely find any correspondence in the DSSP plot of wtPrP. Starting at 4 ns, the DSSP time series for PrP-M205S in Fig. 6 B exhibits a large green and gray zone in the red band that serves to mark helix 2. Its onset approximately coincides with the S1 → S2 transition, which we have assigned to a beginning unfolding of helix 2 starting at residues 181–186 and continuing toward residues 187 and 188 during S3. Similarly, the DSSP time series for PrP-M205R in Fig. 6 C clearly indicates the partial decay of helix 1 noted further above: after 7 ns, the red band marking helix 1 becomes sizably smaller, covering solely residues 146–150 at 10 ns (instead of 144–154, as in the NMR structure of native PrP^C). However, the reason for and structural nature of this helix 1 decay are not revealed by the DSSP analysis. In this respect, our backbone conformational classification has proven its strengths. It has clearly revealed that helix 1, before it starts to decay, bends away from the hydrophobic core of the protein and concomitantly intrudes into the aqueous phase. Thus, only this classification suggests that helix 1 is mainly stabilized by the attachment to the hydrophobic core found in the native structure.

DISCUSSION AND CONCLUSIONS

Despite the progress of computer technology, the MD simulations presented here, each covering the motion of 80,000 atoms over a time span of 10 ns, are still quite costly. For very stable proteins the corresponding limitation to the 10-ns timescale does not represent a severe restriction, because this timescale still enables at least a partial sampling of the equilibrium conformations. However, for simulations of marginally stable proteins like PrP^C and even worse for nonequilibrium simulations, which start at an unstable initial structure (like our M205S- and M205R-PrP models), this limitation becomes severe.

In the case of a marginally stable protein, one may happen to sample a rare fluctuation for a few nanoseconds, which nevertheless has a very small statistical weight in the equilibrium ensemble. The shortening of the small β-sheet observed during the last 3 ns of our wtPrP simulation may be an example of such bad luck. This conjecture is motivated by the fact that a different MD study (37) starting at the same NMR structure of wild-type human PrP and covering the same 10-ns time span did not show any such shortening of the small β-sheet. It revealed only elongating fluctuations like those observed during the first 7 ns of our wtPrP simulation. Furthermore, the hydrogen exchange data of Zahn et al. (3) argue for a quite stable β-sheet structure. Nevertheless, our computer experiment on wtPrP has illustrated once again that this protein exhibits large regions of conformational flexibility, which not only cover the various loops connecting the secondary structural elements, but also comprise helical regions. In agreement with NMR (3), these are the two termini of helix 1 and the C-termini of helices 2 and 3. The large-scale fluctuations revealed by our 10-ns simulation fit with the notion that native PrP is only a marginally stable protein.

In the case of nonequilibrium decay processes induced by point mutations, computational limitations restrict our simulation approach to single attempts and preclude frequent repetitions, which would allow us to gain at least some limited statistics on possible decay paths. Each of these single attempts has, then, the character of a random experiment sampling only one of many possible decay paths. It would be another instance of bad luck, of course, if the particular random experiment happened to choose a highly unlikely instead of a highly probable decay path. But independent of the likeliness of the chosen path, the outcome of such a random experiment clearly indicates the existence of a particular decay path and, therefore, the existence of a structural weak point. Such an experiment on an unstable mutant model additionally shows how the native protein is stabilized and which of its elements are susceptible to weak perturbations.

Our simulations of mutant PrP models have thus identified two elements of the native PrP^C structure, which are susceptible to weak perturbations. A first weak point is helix 2 in the sequence range 181–188, and a second weak point is the amphiphilic helix 1, which is destabilized as soon as it becomes completely exposed to the aqueous phase. As will be discussed now, the former result agrees with previous findings, whereas the latter is at variance with certain claims found in the literature, but agrees with many others and with the available data.

In the presentation of our results, we had already mentioned that the instability of helix 2 identified by us agrees with conclusions derived from earlier but more restricted MD studies (11,36). It is interesting to note that it also agrees with previous suggestions derived by application of secondary-structure prediction tools. For instance, according to Kallberg et al. the sequence 179–191 of PrP should adopt a β-strand structure (38), because this sequence portion mainly consists of the three bulky branched amino acids threonine (T), valine (V), and isoleucine (I), which are known to have a high β-strand propensity (39). In fact, corresponding peptides have been shown to form amyloid fibers and to exhibit a β-sheet structure (40,41). Similarly, a peptide covering the residues 173–195 from helix 2 was found to prefer α-helical over extended β-type conformations only by the small free energy difference of 5–8 kJ mol⁻¹ (42).

In contrast, our identification of the amphiphilic helix 1 as a second weak point of the PrP^C structure disagrees with the interpretations by Ziegler et al. (7) of NMR and CD data on various short peptides spanning helix 1. According to these authors, helix 1 allegedly is remarkably stable, with its stability creating a barrier for the conversion of PrP^C to PrP^Sc. Other authors (8,9), however, who also studied helix 1 peptides by NMR and CD, came to less stringent conclusions concerning the stability of helix 1, ranging from the cautious statement that “it would be no surprise if … helix 1 were preserved during the conformational transition from PrP^C to PrP^Sc” (9) to the conclusion that “despite the propensity of the individual residues to preferentially populate helical space there is no well-formed helical conformation” (8). Even more remarkably, Kozin et al. (10) determined by NMR for yet another helix 1 peptide in aqueous solution a well-defined β-hairpin structure and no α-helix content at all.

If one looks more closely at the experimental data gained for those peptides, which actually showed a certain helical propensity for the residues belonging to helix 1 (7–9), one notices close similarities despite the strongly different interpretations. At room temperature in aqueous solution, several of these peptides showed no medium-range NOEs whose presence would be indicative of a helical structure that is stable at the NMR timescale (7,8), whereas yet another peptide gave rise only to a few very weak signals of this type (9). Even Ziegler et al. (7), who strongly advocated the “remarkable stability” of helix 1 in their conclusion, had to admit in their results section that the absence of tertiary NOE peaks “suggests high conformational flexibility” of the helix 1 peptides.

The CD data presented in Ziegler et al. (7), Sharman et al. (8), and Liu et al. (9) for these peptides (dilute aqueous solution, room temperature) consistently indicate α-helical content in the range of 10–25% (cf., e.g., Fig. 4 in Liu et al. (9) or Fig. 2 b in Sharman et al. (8)). Together with the conformational flexibility following from NMR, these data indicate that the helix 1 residues are in rapid equilibrium of helical and random coil conformations. At the stated conditions, these conformations are thus essentially isoenergetic and are connected by small barriers. In the case of the particular peptide studied by Kozin et al. (10), a β-hairpin structure even marks a pronounced free energy minimum in conformational space.

For the other peptides, the NMR data on chemical shifts of the H^α-protons or the ¹³C^α-atoms of the helix 1 residues indicate a somewhat larger helix propensity than the percentage given by the CD helix content. Concerning the NMR chemical shifts, the peptide data presented by Liu et al. (9) allow a direct comparison with corresponding data for native PrP^C (3). Taking the conformation-dependent chemical shift differences Δδ(¹³C^α) as a measure (compare Figs. 2 a in Liu et al. (9) and 3 b in Zahn et al. (3)), one finds that the helical propensity of the helix 1 residues is less pronounced in the isolated peptide than in PrP^C by a factor of 2.

The thus emerging high conformational flexibility of the helix 1 sequence at room temperature in aqueous solution fully agrees with an extended MD study on a correspondingly solvated helix 1 peptide, in which only the initial coil (residues 144–148) remained in the initial α-helical conformation (11). Note that this remaining structure roughly agrees with the conformation of helix 1 observed by us after 10 ns in our PrPM205R simulation. On the other hand, the apparent stability of helix 1 in the native PrP^C structure, which follows from the NMR data of Zahn et al. (3), also agrees with our MD simulations, according to which helix 1 remained stable as long as it remained in the vicinity of the hydrophobic core of the protein made up of helices 2 and 3 (wtPrP, PrP-M205S and initial phase of PrP-M205R). Thus, it seems that in PrP^C helix 1 is stabilized by the nearby hydrophobic core, and the question arises, by which physical mechanism is this stabilization effected?

Concerning the answer to this question the quoted peptide studies, and a recent investigation by Megy et al. (43) provide important clues. It has been shown that the addition of large amounts of organic solvents can strongly stabilize α-helical structures (7–9) even in the case of the peptide (43), which folds into a β-hairpin in aqueous solution (10). Notably the effect of trifluoroethanol as cosolvent, which is well-known for its helix-stabilizing effect, was comparable to that of methanol. Therefore, the stabilization is largely nonspecific and, thus, should be due to the corresponding reduction of the dielectric constant ɛ_s (cf. Megy et al. (43) and Munishkina et al. (44)). If this conjecture holds, our simulation data concerning the behavior of helix 1 find a neat explanation.

According to our simulations, the amphiphilic helix 1 is stable as long as it is attached with its nonpolar face to the nonpolar surface (e.g., M205 of helix 3) of the hydrophobic core of the protein. At the surface of such a hydrophobic core, ɛ_s is smaller than within the bulk aqueous solvent, arguing that in wild-type PrP^C the amphiphilic helix 1 is stabilized by this low-dielectric environment. As observed in our M205R simulation, helix 1 becomes destabilized upon exposure to an aqueous environment, i.e., to an environment of larger ɛ_s. Thus, the increasing α-helical content of the helix 1 peptides at increasing concentrations of organic cosolvents determined by NMR and CD (7–9,43) agrees with and explains our M205R result.

Conversely, the suggested ɛ_s-dependence of the helix 1 stability sheds light on the functional role of residue M205. When this residue is present, it provides a hydrophobic attachment site to the few nonpolar residues contained in helix 1, which, during folding, can pull this highly charged part of the PrP sequence from the aqueous phase into the low-dielectric environment near the protein surface. By providing an environment of low ɛ_s, the hydrophobic core of PrP can thus act as an intramolecular chaperone supporting the folding of helix 1 into a stable structure. If that attachment site is eliminated by mutation into a polar or charged residue, as in M205S or M205R, this chaperone function is eliminated. The highly charged residues of helix 1 will stay solvated in a high ɛ_s environment, away from the hydrophobic core, and their folding into the rigid α-helical structure characteristic for native PrP^C will be prevented. This hampered folding explains why the two mutations have an effect identical to that of the deletion of helix 1 on the maturation of PrP^C (5). Thus, the functional role of M205 appears to be mainly to ensure the correct folding of helix 1.

Our study has thus provided evidence that the formation of the tightly packed hydrophobic core plays a major role in the folding of native PrP^C. It is interesting that this core can also be impaired by mutations linked to inherited prion diseases in humans. In a recent study, it was shown that two pathogenic PrP mutations within the hydrophobic core, T183A and F198S, show the same biochemical behavior as M205S/R (45), which, according to our results, is explained by a destabilization of the tertiary structure.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophys.org.