Gated Binding of Ligands to HIV-1 Protease: Brownian Dynamics Simulations in a Coarse-Grained Model

Abstract

The internal motions of proteins may serve as a “gate” in some systems, which controls ligand-protein association. This study applies Brownian dynamics simulations in a coarse-grained model to study the gated association rate constants of HIV-1 proteases and drugs. The computed gated association rate constants of three protease mutants, G48V/V82A/I84V/L90M, G48V, and L90M with three drugs, amprenavir, indinavir, and saquinavir, yield good agreements with experiments. The work shows that the flap dynamics leads to “slow gating”. The simulations suggest that the flap flexibility and the opening frequency of the wild-type, the G48V and L90M mutants are similar, but the flaps of the variant G48V/V82A/I84V/L90M open less frequently, resulting in a lower gated rate constant. The developed methodology is fast and provides an efficient way to predict the gated association rate constants for various protease mutants and ligands.

INTRODUCTION

The important first step in many biological processes is the encounter of protein-protein or protein-ligand molecules. For example, in the system of human immunodeficiency virus type 1 (HIV-1), the viral polyprotein has to bind to the active site of the HIV-1 protease to produce active structural and replicative proteins (1). HIV-1 protease drugs also have to associate with the protease and typically compete with the polyprotein binding. The binding begins with the encounter of the two molecules by random walks, and the association presumably occurs at a rate that approaches the diffusion-controlled limit (2–4). However, in the HIV-1 protease system mentioned above, the experimentally measured association rate constant is a few orders of magnitude smaller than that expected if the molecules were uniformly reactive spheres (5,6). Deviation of this limiting rate may result from geometric constraints of the binding sites, interaction potentials, hydrodynamic interactions, and the binding site accessibility due to protein internal motions (7–11). Strong electrostatic steering may enhance the rate of association, and the requirement of high steric specificity of both molecules may reduce the association rate (3,12). In some cases, the association rate constants may be further lowered by the dynamic nature of a protein, which modulates the binding site accessibility and can be viewed as a “gated” binding site (13,14).

A number of experimental works show that some enzymes have loops over their active sites whose conformational changes can “gate” ligand binding (15–17). For example, the active site loop of triosephosphate isomerase (TIM) exhibits a hinged-lid motion, which alternates between the two well-defined open and closed conformations (18). The fluctuations of the protein chain of myoglobin serve as a gate that opens and closes the reaction binding site, and permit small ligands (O₂ and CO) to enter the heme “pocket” (19,20). The concept of gating has been applied to study association rate constants coupled to conformational changes in the active sites of enzymes, both in equilibrium and out of equilibrium (21–26). Earlier theoretical works use the kinetics schemes of gate opening and closing, together with the characteristic diffusional relaxation time of the ligand-protein system, to estimate gated association rate constants (14). Computer simulations have also been applied directly to estimate the gating effects on protein-ligand association, i.e., with explicit modeling of the gate motion (27,28), though such studies are challenging due to the limited configurational sampling that is possible with typical simulation techniques.

This study focuses on the fluctuations of HIV-1 protease flaps, which modulate the binding site accessibility. We studied wild-type protease and three mutants, G48V/V82A/I84V/L90M, L90M, and G48V with three clinically used drugs, amprenavir, indinavir, and saquinavir, where experimental data are available (29). The work uses a coarse-grained model to simulate substantial protein conformational changes (30), and Brownian dynamics to perform microsecond (μs) timescale simulations (31,32). The use of a flexible force field allows study of the opening/closing of the flaps of the active site. Applying such a flexible force field is necessary, as simpler Go-like models cannot describe the complicated flap dynamics (30). The computed association rate constants of HIV-1 variants yield good agreements with experimental values.

Theoretical background

To estimate the effects on the association due to the flap motions, we assume that the protein has two conformational states: open and closed. The opening and closing of a gate modulates the accessibility of a binding site of the protein, and may be described as

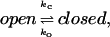(1)

where k_o and k_c are rate constants of gate opening and closing, respectively. For systems which have such a gating effect on ligand binding, the gated association rate constant k_G is given by (14)

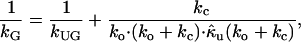(2)

where 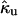(k) is the Laplace transform of the time-dependent rate constant of the ungated protein, a quantity defined for the ungated situation (the binding site is completely open and accessible by a ligand), and k_UG is the steady-state rate constant for the ungated protein. Based on the characteristic diffusional relaxation time τ_d of the ligand-protein system, it may be a slow or fast gating system. In these cases, Eq. 2 may be further rewritten as (13,14,26,33):

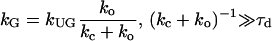(3)

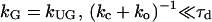(4)

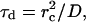(5)

where r_c is the collision distance between the molecules and D is their relative translational diffusion constant. We call it “slow gating” if the opening and closing of the gate is slow compared to the characteristic time for diffusion τ_d (see Eq. 3). The association rate constant is then simply the steady-state association rate constant for the ungated reaction k_UG multiplied the probability that the gate is open. If the gate fluctuation is fast compared to τ_d as shown in Eq. 4, it appears to the ligand that the binding site is always open.

For a diffusion controlled reaction between uniformly reactive spheres with the absorbing boundary condition, k_UG = k_D = 4π r_c D. If ligand-protein interactions U(r) are centrosymmetric when r > r_c, an analytical expression for k_UG can be written as

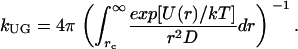(6)

However, if the ligand-protein interactions include realistic descriptions of the irregular surface topography and the molecular interactions, the above equation is not accurate, and one must rely on computer simulations, as described in previous publications (7,34–36).

Simulation methods

Coarse-grained model of HIV-1 protease

A coarse-grained model is used here to represent HIV-1 protease, and has been implemented into the University of Houston Brownian Dynamics (UHBD) simulation package (37). Each amino acid is represented by a single interaction center (bead), and an effective residue radius (r_i) is assigned to each bead (38–42). The center of each bead is placed on the alpha carbon, and ± 1e charge is assigned to a charged residue. These centers are linked by virtual bonds, bond angles, and dihedral angles for consecutive residues. A coarse-grained force field for HIV-1 protease, previously developed by Tozzini and McCammon (30), was extended to include the solvent effects, via screened electrostatics and Brownian dynamics. The effective residue radius of each bead was taken from a previous publication of Reva et al. (43). The potential energy function is a sum of five kinds of interactions:

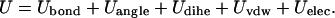(7)

The bond and dihedral interactions are harmonic, and the angle term is in the quartic form:

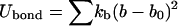(8)

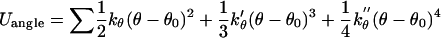(9)

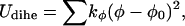(10)

where k_b = 70 kcal/mol/Ų, k_θ = 38 kcal/mol/rad², k_φ = 5 kcal/mol/rad², b₀ = 3.8 Å, and θ₀ = 90° (30). The other parameters, k′_θ, k_θ″, and φ₀ are computed based on a reference structure, Protein Data Bank code 1hhp in this study (44), and are amino-acid specific.

For nonbonded interactions (two beads not connected by a virtual bond, bond angle, or dihedral angle), a cutoff is set to be 15 Å for intramolecular interaction. The Coulombic interaction between each pair of beads i and j is U_elec = q_iq_j/ɛr_ij and U_vdw is

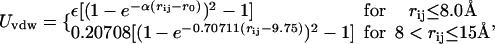(11)

where U_vdw is the intramolecular van der Waals interaction, and ε and α are parameters defined from the force field. Also, r_ij is the distance between beads i and j, and r₀ is the equilibrium distance taken from a reference conformation. No detailed solvent model was used, but a distance dependent dielectric constant (ɛ_ij = 4r_ij) was used to avoid unrealistic in vacuo Coulombic interactions.

Brownian dynamics approach

The detailed derivation of the Brownian dynamics simulation algorithm used here was reported in a previous publication (31). Please note that the use of Brownian dynamics is crucial since it provides appropriate timescales to compute Eqs. 3–5 for determining the gating effects. In this algorithm, we solve the Langevin equation of internal motion in the overdamped limit, and the resulting equation gives a Brownian trajectory:

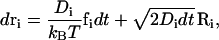(12)

where D_i is the diffusion coefficient of bead i, k_B is the Boltzmann constant, and T is the absolute temperature. The systematic force on each bead f_i is the negative gradient of the potential energy given above, f_i = −∇U(r_i), and R_i is a random displacement due to the collision with the solvent. During the simulation, the time step dt is set to 0.1 ps.

The diffusion coefficient D_i of bead i was computed by

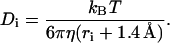This is essentially the Stokes-Einstein equation, and the hydrodynamic radius is approximated by the effective radius of each bead, r_i, plus the water radius, 1.4 Å, used in this study (31,32). The viscosity of water η is 1 cp (T = 293 K).

RESULTS AND DISCUSSION

HIV-1 protease internal motion

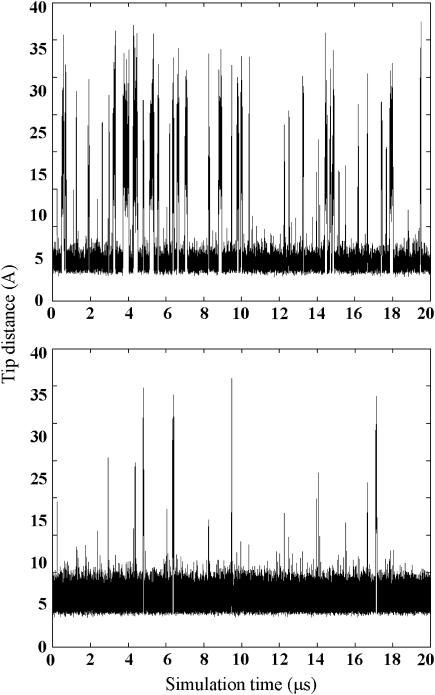
The motions of the wild-type enzyme and three variants of HIV-1 protease (G48V, L90M, and G48V/V82A/I84V/L90M) were studied (Fig. 1). The flaps of the wild-type protease and mutants sample completely open and closed conformations in the Brownian dynamics simulations, as detailed in a previous publication (30); such conformations are shown in Fig. 2. The open/closed conformations of the mutants are similar to those found in the wild-type protease, but the average time of the open fractions are not all the same. The opening events have no significant difference between the wild-type and both L90M and G48V mutants, and all have ∼14% open conformations in a 20-μs simulation. Note that no experimental data reported the fraction of time that the flaps are open/closed. However, in the wild-type protease, the fraction of open conformations is consistent with the value reported recently by all-atom molecular dynamics simulations (45). In contrast, it is harder for the G48V/V82A/I84V/L90M mutant to open, and only ∼2% conformations are in an open form. Although such a coarse-grained model cannot accurately represent the detailed atomic interactions, it still can provide the overall structure and flexibility of the protein with less specific side-chain interactions, e.g., hydrophobic interactions and steric clashes. The substitution of Leu-90 by Met has little effect on the protein internal motion, presumably because residue 90 does not directly interact with the flaps. Interestingly, although the G48V substitution is in the flap region, the change does not cause significant difference in the protein dynamics. Simultaneous substitution of G48V, V82A, I84V, and L90M causes more significant changes of the intramolecular interactions, resulting in more rigid flaps. The flap-tip distance versus simulation time of the wild-type protease and the G48V/V82A/I84V/L90M mutant is illustrated in Fig. 3. The flaps of the mutant open less frequently and the opening time is also shorter. In the wild-type protease, G48V and L90M mutants, the average flap open and closed times are ∼70 and 430 ns, respectively, but the average open time drops by half to ∼35 ns in G48V/V82A/I84V/L90M mutant. We can calculate the opening and closing rate constants from these simulations. For example, the rate constants k_o and k_c of the wild type protease may be estimated by 1/430 and 1/70 ns⁻¹, respectively.

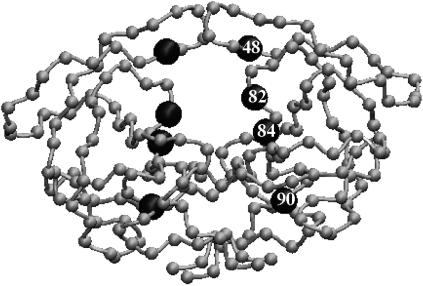
FIGURE 1.

Representation of the HIV-1 protease in the coarse-grained model. Each bead represents a residue and the mutated residues are marked by enlarged spheres.

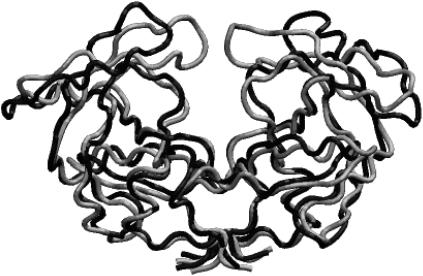
FIGURE 2.

Open (black) and closed (gray) conformation of the wild-type HIV-1 protease from the coarse-grained model.

FIGURE 3.

Flap tip distance (GLY51–GLY51) as a function of time in (top) the wild-type HIV-1 protease and (bottom) variant G48V/V82A/I84V/L90M.

Gated rate constant

Based on the computed rate constants, the flap motions may be viewed as “slow gating”, as described by Eq. 3. Our simulations yield (k_c + k_o)⁻¹ ≈ 60 ns. This is much larger than the diffusional relaxation time if we assume that binding will occur when r_c = 20 Å and the protein and ligand have approximate radii of 30 Å and 8 Å, respectively. As a result, the gated association rate constant may be estimated by the ungated rate constant multiplied by the opening probability, k_o/(k_o + k_c). For HIV protease + substrate, the experimentally measured k_G ranges from 10⁴ to 10⁶ M⁻¹s⁻¹ (5,46), so if the flaps are always open, the association rate may be approximated roughly as 10⁵ to 10⁷ M⁻¹s⁻¹. The association rate still is smaller than the diffusion limit for uniformly reactive spheres, ∼10¹⁰ M⁻¹s⁻¹, estimated from the size of both molecules. As described earlier, this difference is of the expected size, given that successful complex formation hinges on a proper orientation and conformation of both the substrate and the protein (7). Since the charges of mutated residues do not change, the change of the association rate caused by electrostatic effect is less significant. As a result, it is the flap dynamics that may determine most of the changes of the association rate constant due to the mutations considered here. The flap motion in mutants G48V and L90M is very similar to that in the wild-type, so the gated association rate measured from a substrate binding to the mutant may remain nearly the same. Unlike the G48V and L90M variants, G48V/V82A/I84V/L90M mutant shows less flexible flap motions, so a decrease of a few fold in k_G may be estimated, as the opening probability is only 2%.

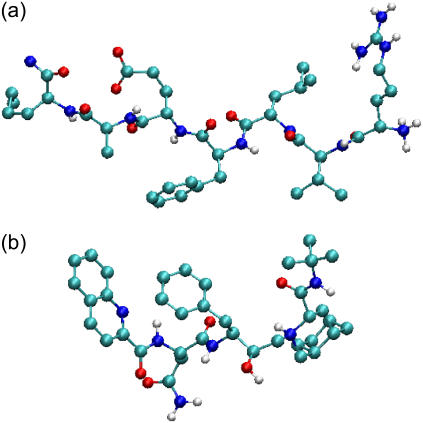
Because experimentally measured association rates of the binding between a substrate and HIV-1 protease variants are not available, the kinetics data of clinically used drugs and protease mutants are considered here. Table 1 lists experimental association rate constants of the proteases and three clinically used protease drugs, amprenavir, indinavir, and saquinavir. Note that different experimental methods may result slightly different kinetics constants. For an easier comparison, we used a data set obtained from the same assay method for all of the HIV drugs (29). It has been suggested that these peptidomimetic drugs have similar binding modes to the substrate, but the drugs are smaller as shown in Fig. 4 (47). Based on the assumption that the flaps of the protease have to be in an open conformation to allow ligand access, we estimate that k_G for the binding of drugs to the wild-type and variants G48V and L90M proteases will be similar. In contrast, the association rate for drugs binding to the G48V/V82A/I84V/L90M mutant may decrease up to sevenfold, since the flaps are only open ∼2% of the time, compared to ∼14% open fraction in the wild-type protease.

TABLE 1.

Association rate constants of interactions between the HIV-1 proteases and ligands

Enzyme	Inhibitor	No.of atoms	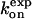M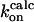−1s−1	M−1s−1
Wild-type	Amprenavir	70	>5.00 × 106
	Indinavir	94	2.4 × 106 ± 0.3 × 106
	Saquinavir	100	1.1 × 106 ± 0.2 × 106
	Substrate	∼150	104–10 6
Mutant	Amprenavir	70	>5.00 × 106	>5.00 × 106
L90M	Indinavir	94	>5.00 × 106	∼2.4 × 106
	Saquinavir	100	1.7 × 106 ± 0.7 × 106	∼1.1 × 106
	Substrate	∼150	n.a.	∼104–106
Mutant	Amprenavir	70	3.3 × 106 ± 0.8 × 106	>5.00 × 106
G48V	Indinavir	94	2.3 × 106 ± 0.6 × 106	∼2.4 × 106
	Saquinavir	100	2.1 × 106 ± 0.7 × 106	∼1.1 × 106
	Substrate	∼150	n.a.	∼104–106
Mutant	Amprenavir	70	1.0 × 106 ± 0.1 × 106	∼106
G48V/V82A/I84V/L90M	Indinavir	94	7.2 × 105 ± 0.5 × 105	∼3.4 × 105
	Saquinavir	100	3.3 × 105 ± 1.1 × 105	∼1.5 × 105
	Substrate	∼150	n.a.	∼103–105

The experimental values of HIV drugs are taken from an article by Shuman et al. (29) and the data of the substrates are from references of Katoh et al. (5) and Szeltner et al. (46) (n.a., not available).

FIGURE 4.

HIV-1 protease substrate H-ARG-VAL-LEU-PHE-GLU-ALA-NLE-NH2 (a) and a saquinavir bound state conformation taken from crystal structures (Protein Data Bank code 1A8K and 1FB7).

The computed association rates are listed in Table 1. For example, the estimated value of k_G of saquinavir to enzyme with substitutions at G48V/V82A/I84V/L90M is ∼1.5 × 10⁵ M⁻¹s⁻¹. The k_G of saquinavir to enzyme with substitution at G48V and L90M are both ∼1 × 10⁶ M⁻¹s⁻¹. Our estimation successfully predicts the trend of the change of association rate constants, but the approximated k_G is up to twofold lower than those determined in experiments for drugs binding to the G48V/V82A/I84V/L90M mutant. Given the approximations in our coarse-grained model, the level of agreement seems surprisingly good. Some errors may result from the absence of complicated drug-protein interactions and/or from our definition of an open form. For example, we define open conformations when the flap tip distances are >15 Å, but the flaps also fluctuate when the tip distances are ∼15 Å. Thus a drug may be able to access the binding site for some conformations which are counted as “closed form” in our simulations, and a real population of the open form may be larger than what we obtained here. Moreover, unlike substrates that have an extended structure, the drugs shown here are smaller and they may not need a fully open conformation to bind to the enzyme, yielding a larger k_G.

CONCLUSIONS

This article uses Brownian dynamics simulations of a coarse-grained model to study the gated association rate constants in HIV-1 proteases. The simulations showed that in the wild-type and variants G48V and L90M proteases, the flaps open ∼14% of the time, and the opening fraction drops to 2% in mutant G48V/V82A/I84V/L90M. The computed k_c and k_o suggest the flaps show a “slow gating” effect, so the gated association rate constant is simply the ungated rate constant times the probability of the gate opening (see Eq. 3 and reference (14)). As a result, we can predict the gated association rate constants for mutant proteases, which are in reasonable agreements with the experimental data, as shown in Table 1. The use of a flexible force field provides large-scale internal motions of HIV-1 protease. The calculation is fast and a 1-μs simulation takes <2 h CPU time for the systems studied here. With very modest computational resources, the method may be applied to estimate the changes of the association rate constants of different protease mutants when experimental data are not available, thus provides a greater understanding of drug-resistance due to protease mutation.