Cytochrome c Interaction with Cardiolipin/Phosphatidylcholine Model Membranes: Effect of Cardiolipin Protonation

Abstract

Resonance energy transfer between anthrylvinyl-labeled phosphatidylcholine as a donor and heme moiety of cytochrome c (cyt c) as an acceptor has been employed to explore the protein binding to model membranes, composed of phosphatidylcholine and cardiolipin (CL). The existence of two types of protein-lipid complexes has been hypothesized where either deprotonated or partially protonated CL molecules are responsible for cyt c attachment to bilayer surface. To quantitatively describe cyt c membrane binding, the adsorption model based on scaled particle and double layer theories has been employed, with potential-dependent association constants being treated as a function of acidic phospholipid mole fraction, degree of CL protonation, ionic strength, and surface coverage. Multiple arrays of resonance energy transfer data obtained under conditions of varying pH, ionic strength, CL content, and protein/lipid molar ratio have been analyzed in terms of the model of energy transfer in two-dimensional systems combined with the adsorption model allowing for area exclusion and electrostatic effects. The set of recovered model parameters included effective protein charge, intrinsic association constants, and heme distance from the bilayer midplane for both types of protein-lipid complexes. Upon increasing CL mole fraction from 10 to 20 mol % (the value close to that characteristic of the inner mitochondrial membrane), the binding equilibrium dramatically shifted toward cyt c association with partially protonated CL species. The estimates of heme distance from bilayer center suggest shallow bilayer location of cyt c at physiological pH, whereas at pH below 6.0, the protein tends to insert into membrane core.

INTRODUCTION

Lipid-protein interactions are currently regarded as a key factor determining the structural and functional characteristics of membrane proteins. One thoroughly investigated membrane protein is cytochrome c (cyt c), a component of the electron transport chain in the inner mitochondrial membrane. Numerous studies have revealed the distinct high affinity of cyt c for lipids (1–6). Yet, the molecular level interactions are complex and involve several important issues:

1. The interplay between different binding modes responsible for the location and orientation of cyt c relative to the lipid-water interface (1–3).

2. Conformational changes of the protein upon its association with lipids (4–6).

3. Protein-induced structural rearrangement of lipid bilayer (7,8).

4. Functional implications of the binding of cyt c to membranes (9,10).

Among the different phospholipids capable of forming complexes with cyt c, particular attention has been given to cardiolipin, which is the most likely candidate for the anionic phospholipid attaching cyt c to the inner mitochondrial membrane (11). Cardiolipin (CL) is a structurally unique phospholipid containing two phosphate groups and four acyl chains (12). To date, the mechanisms underlying cyt c-CL binding are rather well characterized in all of the above aspects.

Several lines of evidence from NMR (13), SPR (14), IR (15), and fluorescence spectroscopy (16,17) studies strongly suggest that not only electrostatic, but also hydrogen bonding and hydrophobic interactions, may be involved in the complex formation. CL was found to cause loosening and reversible unfolding of cyt c (5). On the other hand, it was demonstrated that cyt c can exert influence on the molecular organization of CL-containing bilayers giving rise to phase separation and formation of nonbilayer structures (7). Physiological consequences of the association of cyt c with CL are not restricted to its functioning as a component of the mitochondrial respiratory chain, but are also connected with the recently discovered ability of this protein to trigger programmed cell death (apoptosis), presumably involving cyt c release from its complexes with CL (9,10). Despite the wealth of knowledge about the nature of cyt c-CL interaction, important details of this process still remain unclear.

Although most studies emphasize the importance of electrostatic effects in the complex formation of cyt c and lipids, only a few attempts have been made to interpret these effects quantitatively (18–20). Adequate description of the electrostatically driven protein adsorption onto lipid bilayer requires allowing for dependence of association constant on membrane electrostatic potential or surface charge density. The latter, in turn, is a function of the mole fraction of anionic phospholipids, pH, ionic strength, and the extent of protein binding (surface coverage). All these interrelated factors, except pH, have been taken into account in the models developed by Heimburg and Marsh while analyzing the association of cyt c with 1,2-dioleoyl-sn-glycero-3-phosphoglycerol (DOPG) and phosphatidylcholine (PC)/DOPG bilayers (18,19). However, a factor such as pH, accounting for the protonation state of anionic phospholipids, may not only contribute to surface potential by modulating the strength of electrostatic protein-lipid interactions, but may also change the electrostatic binding to hydrogen bonding. This concept was put forward by Rytömaa and Kinnunen in interpreting the effects of pH and ionic strength on the binding of cyt c to PC/phosphatidylglycerol (PG) and PC/CL bilayers (16). The existence of two distinct acidic phospholipid binding sites in cyt c, denoted as A- and C-sites, was hypothesized (17). It was assumed that the A-site accounts for electrostatic interactions between cyt c and deprotonated phospholipids, whereas the C-site is responsible for the protein binding to protonated phospholipids via hydrogen bonding. The degree of acidic phospholipid protonation was suggested to be a critical factor governing cyt c association with membrane via either A- or C-sites. Due to the presence of two phosphate groups, CL exhibits complex ionization behavior, which so far has not been thoroughly analyzed in the context of cyt c-CL interaction.

In view of this, our study was undertaken to extend the model of Rytömaa and Kinnunen with special attention to the effects of CL protonation. Accordingly, our goal was severalfold. Firstly, we examined cyt c binding to PC/CL membranes as a function of experimental variables influencing the degree of CL protonation, notably pH, ionic strength, CL content, and protein surface coverage. Resonance energy transfer was employed with anthrylvinyl-labeled PC as a donor, and heme group of cyt c serving as the acceptor. Secondly, we analyzed the protonation behavior of CL in PC/CL membranes, and formulated a binding model allowing for changes in the degree of CL protonation with varying pH, ionic strength, and lipid/protein molar ratio (L/P). Thirdly, based on global analysis of the resonance energy transfer (RET) data, we estimated the binding parameters and characterized the structure of cyt c-CL complexes in terms of the location of the heme moiety relative to lipid-water interface.

MATERIALS AND METHODS

Materials

Chemicals

Egg yolk PC and beef heart CL were purchased from Biolek (Kharkiv, Ukraine). Both phospholipids gave single spots upon thin layer chromatography in the solvent system (chloroform/methanol/acetic acid/water, 25:15:4:2, v/v). 1-acyl-2-[12-(9-anthryl)-11-trans-dodecenoyl]-sn-glycerophosphocholine, 1-acyl (AV-PC), 16:0/18:0 = 3/1, was synthesized as described in detail elsewhere (21). Bovine heart cyt c (oxidized form) was from Sigma-Aldrich (St. Louis, MO). All other chemicals were of highest purity grade.

Preparation of lipid vesicles

Large unilamellar vesicles composed of PC and CL (10, 20, and 40 mol %) were prepared by the extrusion technique. Lipids were dissolved in ethanol and mixed in this solvent. Lipid films were then made by evaporation of this solvent and subsequently hydrated with either 5 mM Na-phosphate or Na-acetate buffer to cover the pH intervals of 7.6–5.9 and 5.6–3.4, respectively. The pH of the buffer solutions was adjusted to the desired values with hydrochloric acid. The resulting lipid dispersions were subsequently extruded through a 100-nm pore-size polycarbonate filter (Nucleopore, Pleasanton, CA). Phospholipid concentrations were determined according to the procedure of Bartlett (22). AV-PC (∼0.3 mol % of total lipid) was added to the mixed PC/CL ethanol solutions before the removal of the solvent. The concentration of the fluorescent lipid was determined spectrophotometrically using anthrylvinyl extinction coefficient ɛ (367 nm) = 7.9 10³ M⁻¹ cm⁻¹ (in ethanol) (23).

Fluorescence measurements

Fluorescence measurements were performed at 20°C with a CM 2203 spectrometer (SOLAR TII, Minsk, Belarus) using 10-mm pathlength cuvettes. Emission spectra for AV-PC were recorded with excitation at 375 nm. Excitation and emission bandpasses were set at 5 nm. Fluorescence intensities measured in the presence of cyt c at the maximum of AV-PC emission (434 nm) were corrected for reabsorption and inner filter effects using the coefficients (24) of

(1)

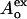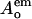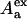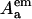where and are the donor optical densities at the excitation and emission wavelengths in the absence of acceptor, and and are the acceptor optical densities at the excitation and emission wavelengths, respectively.

Methods

Binding model

Binding of cyt c to the phospholipid membranes was described in terms of the scaled particle adsorption model developed by Chatelier and Minton (25) and further extended by Minton (26) to allow for the possibility of multiple adsorbate conformations. This model is currently regarded as providing the most adequate description of excluded area interactions between the adsorbing protein molecules (20). Importantly, scaled particle theory (SPT) expressions derived for the case of multiple conformations of bound protein appear to be applicable to treating protein association with heterogeneous surfaces where binding sites differ in their size and free energy of adsorption. The partitioning of a protein between solution and the sites of i^th type can be described by

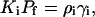(2)

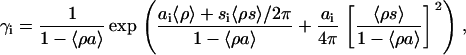(3)

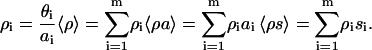(4)

The value θ_i is the fraction of surface area occupied by the protein molecules bound to the sites of i^th type; a_i and s_i are the area and circumference of the site of i^th type; K_i is the equilibrium constant for the protein partitioning between solution and the sites of i^th type; and P_f is the protein concentration in solution. The equilibrium binding constant is generally represented as a product of electrostatic (K_el) and nonelectrostatic (K_o) terms, (K = K_elK_o). The former depends on ionic strength and surface coverage, whereas the latter accumulates contributions from hydrophobic effect, hydrogen bonding, lipid redistribution, protein conformational changes, etc. Electrostatic component of the binding constant is given by (18)

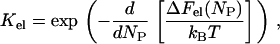(5)

where T is the temperature, k_B is Boltzmann's constant, and ΔF_el is the total gain in electrostatic free energy, which is a function of the number of adsorbed protein molecules, N_P,

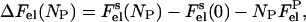(6)

with 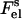and 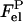denoting electrostatic free energies of a membrane surface and a protein, respectively. In the approximation of uniform charge distribution on a surface of spherical protein molecule with a net charge +ze and radius r_o, the electrostatic free energy of a protein in solution can be written as (27)

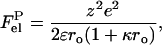(7)

where κ is the reciprocal Debye length

(8)

with e being the elementary charge, N_A is Avogadro's number, ɛ is the dielectric constant, and c is the concentration of monovalent ions (mol/l). The electrostatic free energy of a membrane of area S_m = S_LL is given by the Gouy-Chapman double-layer theory (28) as

(9)

Here, S_L is the mean area per lipid molecule (S_L = f_PCS_PC + f_CLS_CL); f_PC and f_CL are the mole fractions of PC and CL; S_PC and S_CL are mean areas per PC and CL headgroups, respectively (S_PC = 0.65 nm², S_CL = 1.2 nm² (29)); L is total lipid concentration; and σ is the charge density determined by the mole fraction of acidic phospholipid (f_A), the degree of its ionization (α), and the extent of neutralization of membrane charge by adsorbed counterions (here Na⁺ ions) and bound protein

(10)

where B_Na and B_P = N_P/N_A are the molar concentration of Na⁺ and bound protein, respectively. In the simplest case of one-step deprotonation of an acidic phospholipid, α can be expressed via the ionization constant (K₁) and the surface proton concentration as

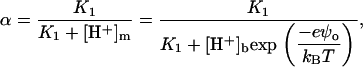(11)

where [H⁺]_b is the bulk proton concentration, and ψ_o is the electrostatic surface potential of a membrane. Taking into account Na⁺ accumulation in the interfacial layer according to the Boltzmann law, the concentration of membrane-bound Na⁺ can be calculated from

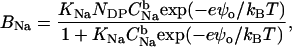(12)

where 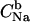is the bulk Na⁺ concentration, K_Na is the sodium-phosphate binding constant, taken here as 1 M⁻¹ (30), and N_DP is the concentration of ionized phosphate groups (which serve as binding sites for cations).

Given the Gouy-Chapman relationship between σ and ψ_o,

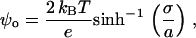(13)

the exponential in Eqs. 11 and 12 can be substituted for 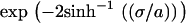so that Eq. 10 takes the form appropriate for numerical solution.

Resonance energy transfer model

The results of RET measurements were quantitatively interpreted in terms of the model of energy transfer in two-dimensional systems developed by Fung and Stryer (31). In this study, the model was extended to allow for orientational effects and the possibility of acceptor distribution over two planes residing at different distances from the bilayer center. For donors and acceptors randomly distributed over different planes separated by a distance d_a, the donor fluorescence decay is given by

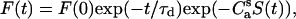(14)

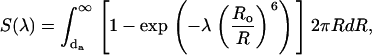(15)

where F(0) is the initial fluorescence intensity, τ_d is the lifetime of excited donor in the absence of acceptors, λ = t/τ_d, R_o is the Förster radius, and 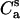is the concentration of acceptors per unit area related to the molar concentrations of lipids accessible to acceptor (0.5L) and bound acceptor (B_a) as

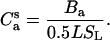(16)

Relative quantum yield of a donor is given by

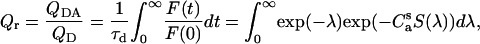(17)

where Q_D and Q_DA are the donor quantum yields in the absence and presence of acceptor, respectively. The Förster radius depends on the donor quantum yield, the overlap between the donor emission (F_D(λ)) and acceptor absorption (ɛ_A(λ)) spectra (J), refractive index of the medium (n_r = 1.37), and orientation factor (κ²) (32), as

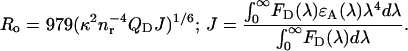(18)

Since the donor emission and acceptor absorption transition moments experience reorientation during the transfer time, they are usually considered as being distributed within the cones with half-angles ψ_D,A. If the axes of these cones (D_x and A_x) make the angles α_D,A with bilayer normal N, the dynamically averaged value of orientation factor is given by (33)

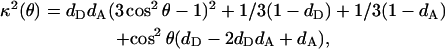(19)

where 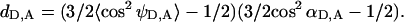Depolarization factors d_D and d_A are related to the steady-state r and fundamental r₀ anisotropies of donor and acceptor, as

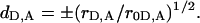(20)

Given that cos² θ = (d_a/R)², the orientation factor can be represented as a function of donor-acceptor separation (R), as

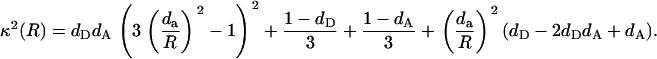(21)

Then, making the substitution 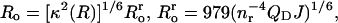Eq. 15 may be rewritten in the form

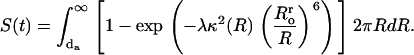(22)

Analogously, one can describe energy transfer in the system containing one donor plane and two acceptor planes located at the distances d₁ and d₂ from the donor plane. In this case, the following relationships hold:

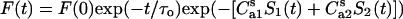(23)

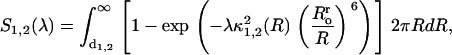(24)

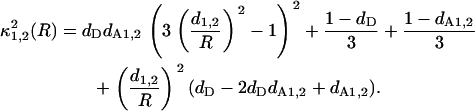(25)

Here, S₁ and S₂ are the quenching contributions characterizing energy transfer to different acceptor planes. Notably, anthrylvinyl fluorophore employed as a donor in this study is attached to the terminal methyl group of the acyl chain. Due to the high mobility of these groups, AV moieties located at the outer and inner bilayer leaflets seem to be indistinguishable, so that the donor plane can be regarded as coinciding with the bilayer midplane. Therefore, the above model parameters d₁ and d₂ virtually characterize the distances of two different populations of acceptors (in our case, heme groups of cyt c) from the membrane center.

Ultimately, denoting molar concentration of acceptors distributed over two planes by B₁ and B₂, respectively, and substituting Eq. 23 into Eq. 17, one obtains

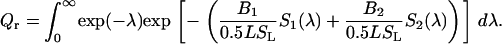(26)

The donor depolarization factor d_D was calculated from Eq. 20 using the results of AV-PC anisotropy measurements (λ_ex = 375 nm, λ_em = 434 nm). The r_D values appeared to be similar (∼0.05) for PC/CL model membranes differing in CL content. The fundamental anisotropy of anthrylvinyl fluorophore was taken to be ∼0.08 (23). According to the linear dichroism data, the transition moment of cyt c lies within the porphyrin plane (34), i.e., ψ_A = π/2. If cyt c adopts a certain specific orientation relative to the lipid-water interface, the porphyrin plane makes an angle α with the bilayer surface. Since preferable orientation of membrane-bound cyt c is still a matter of controversy, we found it reasonable to treat experimental data with two limiting assumptions:

1. α_A = 0 (porphyrin plane is parallel to the bilayer surface).

2. α_A = π/2 (porphyrin plane is perpendicular to the bilayer surface).

RESULTS AND DISCUSSION

The RET experiments were designed to obtain multiple data sets suitable for global analysis. The relative quantum yield of donor (AV-PC) was measured as a function of the following variables:

1. Cyt c concentration (P), six values in the range 0.2–2.7 μM.

2. Lipid concentration (L), three values in the range 30–190 μM.

3. Mole fraction of cardiolipin (0.1, 0.2, and 0.4).

4. pH, eight values from 7.55 to 3.45.

5. Ionic strength, 5, 20, and 60 mM.

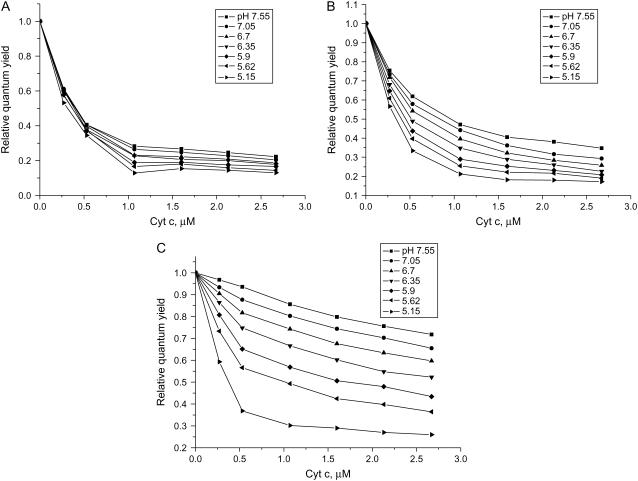
Typical dependencies of the relative quantum yield of AV-PC on the total concentration of cyt c are depicted in Fig. 1. Decrease of pH was accompanied by the rise of sample turbidity, being indicative of the protein-induced changes in liposome structure finally leading to vesicle aggregation. This process was initiated at different pH values depending on the protein and lipid concentrations, cardiolipin content, and ionic strength of the medium. To avoid errors in the quantitative interpretation of RET data, the sets of experimental variables giving rise to turbidity increase were excluded from the global analysis. For this reason, the total number of experimental points being analyzed was reduced to 540, with only four pH values 7.55, 7.05, 6.7, and 6.35 being chosen for the parameter-estimation procedure.

FIGURE 1.

Relative quantum yield of AV-PC in liposomes containing 20 mol % CL as a function of cyt c concentration, pH, and ionic strength. Lipid concentration is 35 μM. Ionic strength was 5 mM (A), 20 mM (B), and 60 mM (C).

The Q_r changes observed at varying pH, ionic strength, and CL content may reflect variation in the concentration of membrane-bound cyt c and the AV-PC–heme distance. As seen in Fig. 1, decreasing pH was followed by an increase of RET efficiency, suggesting the enhancement of cyt c association with liposomes and/or deeper bilayer penetration of the protein. However, the latter possibility could not be reconciled with the finding that impact of pH became more pronounced with increasing ionic strength and CL content (Figs. 1 and 2). This led us to assume that pH-induced Q_r decrease arises mainly from increasing the amount of bound protein (B_P = B_a). Although the relation between Q_r and B_P is not straightforward, the behavior of ΔB_p dependencies on experimental variables in the main features should be similar to that of ΔQ_r. There are at least two possible explanations for the enhancement of cyt c binding to liposomes at lowering pH:

1. Increase of the effective protein charge resulting in higher K_el (Eq. 5).

2. Increase in the number of protein-binding sites on the bilayer surface.

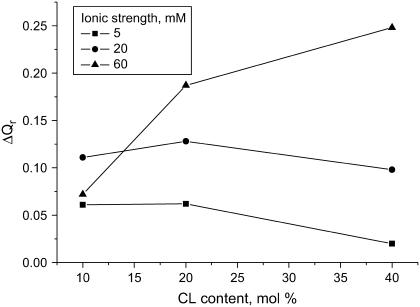
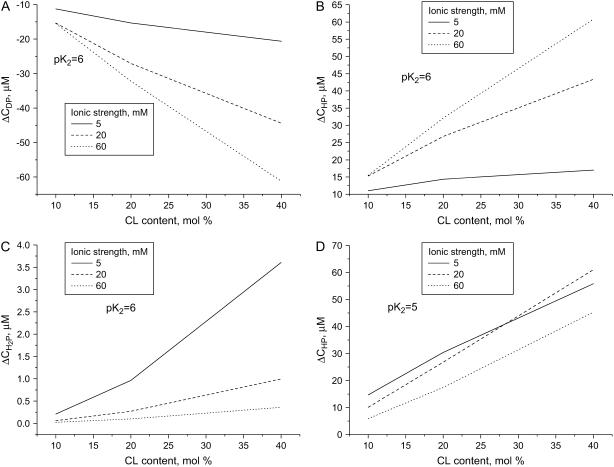
Since the former explanation is inconsistent with the observation that pH effect enhances upon increasing ionic strength and CL content (Fig. 2), we have assumed that pH-induced modification of the bilayer surface plays primary role in the observed enhancement of cyt c membrane association. In turn, such a modification is most likely to involve the changes in the extent of CL protonation. Since CL is known to exhibit peculiar protonation behavior, it seemed of importance to analyze this point in more detail (Appendix). By solving the set of Eqs. A2–A4 we evaluated the degree of CL ionization as a function of pH, ionic strength, and CL content. Fig. 3 illustrates how the concentration of the various CL species varies as pH decreases from 7.55 to 6.35 (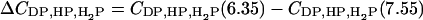). Comparison of the theoretical dependencies of ΔC_DP, ΔC_HP, and 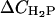on f_CL with the experimental ΔQ_r (f_CL) plots obtained at different ionic strengths (Fig. 2) shows that increase in the amount of partially protonated CL species (Fig. 3 B) is most likely to account for the increased extent of cyt c binding to liposomes at lower pH. As seen in Fig. 3 C, fully protonated CL species display ionic-strength dependence opposite to that of ΔQ_r, while the number of deprotonated species decreases with pH lowering (Fig. 3 A). Notably, satisfactory agreement between ΔC_HP and ΔQ_r behavior was observed only for pK_i2 at ∼6, while at pK_i2 ≤ 5 ionic-strength dependence of ΔC_HP was different from that of ΔQ_r (Fig. 3 D). One should also bear in mind that apparent flattening or downward drift of ΔQ_r (f_CL) dependencies, observed at ionic strengths 5 and 20 mM, could originate from the decreased slope of the Q_r (C_A) curves at the lower Q_r values (Fig. 1) (i.e., coefficient of proportionality between ΔQ_r and ΔB_P decreases with increasing B_p). Based on the above rationales and taking into account that upward drift of pK_a2 recovered by Kates et al. (36) was observed mainly at basic pH, we found it reasonable to put pK₂ equal to 6.0 in the further data treatment.

FIGURE 2.

Difference between relative quantum yields measured at pH 7.55 and 6.35 as a function of CL content and ionic strength. Lipid concentration was 84 μM and was calculated by taking one CL to be equivalent to two double-chain lipids.

FIGURE 3.

Change in the concentration of deprotonated (A), partially protonated (B, pK₂ = 6; D, pK₂ = 5), and fully protonated (C) CL species calculated from Eqs. A1–A4 for pH decreasing from 7.55 to 6.35 (ΔC(pH) = C(6.35) − C(7.55)). Lipid concentration was 30 μM.

As the next step of data analysis, we formulated for the membrane binding of cyt c a model, which, in combination with the RET model, would give a consistent interpretation of all data sets obtained at different pH, ionic strengths, and CL content. This model is based on the following assumptions:

1. While adsorbing on the surface of PC/CL membranes, cyt c may associate with two different types of binding sites (denominated here as DPS and HPS), where either deprotonated or partially protonated CL molecules mediate the attachment of cyt c to the membrane.

2. Electrostatic interactions are involved in the formation of both cyt c-DPS and cyt c-HPS complexes, but the latter is additionally stabilized by hydrogen-bonding to CL.

3. The size of DPS and HPS is determined by the cross-sectional area of cyt c in the plane of membrane (DPS and HPS are supposed to be formed by n_DPS and n_HPS lipid molecules, respectively).

4. Two main orientational and conformational states of membrane-bound cyt c exist, corresponding to DPS- and HPS-anchored protein, i.e., B_P = B_DPS + B_HPS.

The concentrations of DPS- and HPS-bound protein (B_DPS and B_HPS) depend on the number of deprotonated and partially protonated CL species that, in turn, is controlled by interfacial pH. To allow for pH-dependent variation in B_DPS and B_HPS, we have introduced effective binding constants K_DPS and K_HPS. In terms of the scaled particle theory, the probability that a randomly selected site at the bilayer surface with the dimensions of the footprint of DPS-bound protein is vacant and contains a deprotonated CL molecule, can be written as 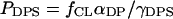(26). Analogously, the probability for HPS is 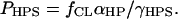The rate constants for protein adsorption to DPS or HPS are proportional to the above probabilities (26): 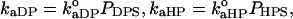where 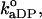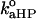are intrinsic rate constants. On the contrary, the rate constants for the protein desorption from the membrane were assumed to be independent of α_DP and α_HP (this may be the case, for instance, when cyt c is capable of forming ionic or hydrogen-bonding contacts with only one CL molecule of those occurring at the binding site): 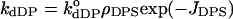and Here, Boltzmann factors reflect additional energy required for bound protein to escape the adsorption potential well. Thus, effective equilibrium constants can be represented as product of intrinsic ( 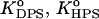), electrostatic ( 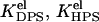), and pH-dependent (P_DPS, P_HPS) terms, as

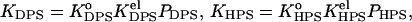(27)

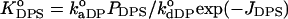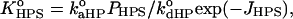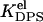where and and and 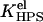are determined by Eqs. 2–13. Defined as above, the effective binding constants depend on CL content, ionic strength, pH, and degree of the surface coverage. Taking m = 2 and making the substitutions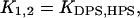 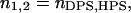and 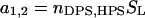in Eqs. 2–4 we obtained the set of equations for the adsorption isotherm. Numerical solution of these equations yielded the values of B₁ = B_DPS and B₂ = B_HPS, which were subsequently used in calculating the relative quantum yield for a given set of parameters {K_DPS, n_DPS, d_DPS, K_HPS, n_HPS, d_HPS, z}. The data-fitting procedure involved minimization of the function

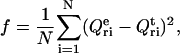(28)

where N is the total number of experimental points involved in global analysis, 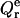is the experimental Q_r value, 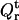is the relative quantum yield calculated by numerical integration of Eqs. 23–26, with B₁ and B₂ being calculated numerically from Eqs. 2–4, while using effective binding constants derived from Eqs. 5–10 and Eqs. A2–A4. Since simultaneous estimation of multiple parameters (which are commonly cross-correlated) seems to be unfeasible, we made some simplifications, as follows.

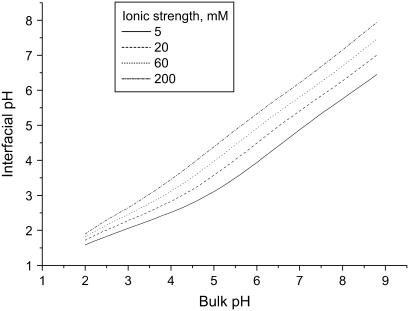
Firstly, it was assumed that DPS and HPS do not significantly differ in their size, i.e., n_DPS ≈ n_HPS. While associating with the membrane, cyt c undergoes conformational changes, which may involve loosening and reversible unfolding of the overall protein structure (4,5), decrease of α-helical content (37), and alterations in the geometry, spin, and the ligation state of porphyrin (38). The interplay among these effects essentially depends on the chemical nature of the membrane lipids, electrostatic surface potential, lipid/protein molar ratio, etc. (38,39). The lowered interfacial pH of negatively charged bilayers is believed to promote cyt c transition to a molten globule state, being an intermediate in the protein denaturation process (40). Despite the increased intramolecular mobility and partial unfolding of the tertiary structure, hydrodynamic radius of a protein on its transition to a molten globule state was found to increase by no more than 20% (41). Using Eqs. A1–A4 we estimated the interfacial pH for the systems under study. As seen in Fig. 4, at the lowest pH included in the data fitting procedure (6.35) pH in the membrane vicinity decreases at most to ∼4.3 (f_CL = 0.4, I = 5 mM). Such pH decrease is unlikely to promote complete unfolding of cyt c, but transition of the protein to a molten globule state is highly probable. Approximating cyt c molecule by a spheroid 3 × 3.4 × 3.4 nm (42) and allowing for the possibility of partial unfolding of the protein structure, the limits for varying n_DPS and n_HPS while data fitting were estimated to be 10–14, 9–13, and 8–11 for liposomes with CL mole fractions of 0.1, 0.2, and 0.4, respectively.

FIGURE 4.

Relationship between interfacial and bulk pH derived from Eqs. 10–13 with CL mole fraction f_CL being 0.4, pK₁ = 2.8, and pK₂ = 6.0.

Secondly, to make the parameter estimation unambiguous, the values of K_DPS and d_DPS were derived for a given protein effective charge, z, from the two-parameter fitting of the data obtained for the case where equilibrium between occupied DPS and HPS is strongly shifted to DPS (f_CL = 0.1, I = 60 mM, pH = 7.55). It appeared that in this case RET profile is best described by the model of one type of binding center (Fig. 5). Next, the values of z, K_DPS, and d_DPS were held constant, while K_HPS and d_HPS were optimized. This process was repeated until self-consistency was reached for all kinds of liposomes, three ionic strengths, four values of pH (7.55, 7.05, 6.7, 6.35), and three lipid concentrations. Global analysis revealed that all RET profiles can be consistently described with the following basic set of model parameters: z = 4.1, 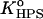= 10⁻⁴, 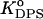= 1.2 × 10⁻⁵, (α_A = 0), or 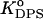= 7.6 × 10⁻⁶ (α_A = π/2). These parameters provide satisfactory fit with f-values falling in the range 4 × 10⁻⁴–2 × 10⁻³. Notably, the value recovered for the effective protein charge is close to that obtained by Heimburg and Marsh, ∼3.8, while examining the association of cyt c with DOPG membranes (18). This value is less than the net charge of cyt c (+9), most probably because of the finite size of the protein relative to Debye length (43).

FIGURE 5.

FRET profiles obtained for liposomes containing 10 mol % CL at ionic strength 60 mM and lipid concentration 38 μM. The solid lines represent theoretical curves calculated in terms of the combined RET-binding model assuming that cyt c associates with the centers of one type at pH = 7.55 (DPS, d_DPS = 4 nm) or two types at pH = 6.35 (DPS and HPS, d_DPS = 4 nm, d_HPS = 3.8 nm); α_A = 0, n_DPS = n_HPS = 10.

The above basic set of model parameters was used in calculating B_DPS, B_HPS, and the effective binding constants as a function of pH, ionic strength, and CL content. The principal trends in the redistribution of bound protein between DPS and HPS are demonstrated in Fig. 6. Notably, K_DPS and K_HPS may decrease by more than an order-of-magnitude because of lowering the membrane surface potential upon binding of cyt c (Fig. 7).

FIGURE 6.

Distribution of bound protein between DPS and HPS as a function of pH, ionic strength (A), and CL content (B). Fraction of bound protein was defined as B_DPS,HPS/(B_DPS + B_HPS). Calculations were made with f_CL = 0.2, protein concentration 4 μM, and lipid concentration 100 μM.

FIGURE 7.

Dependence of effective binding constants on protein concentration calculated with f_CL = 0.4, lipid concentration 60 μM, and ionic strength 5 mM.

The model proposed in this study can predict some principal features of the RET profiles obtained at varying pH, ionic strength, L/P ratio, and CL content. All these experimental variables determine the distribution of bound protein between DPS and HPS. At 10 mol % CL and neutral pH, cyt c associates with membranes predominantly via DPS, but lowering pH or increasing the CL mole fraction strongly shifts the equilibrium toward HPS-bound protein. Specifically, cyt c association with liposomes containing 10 mol % CL leads to the redistribution of bound protein between DPS and HPS: at pH = 7.55, B_DPS = 0.6 μM, and B_HPS = 0.003 μM, whereas at pH = 6.35, B_HPS exceeds B_DPS (B_DPS = 0.02 μM and B_HPS = 0.66 μM). Similarly, upon increasing CL content to 40 mol %, B_HPS increases to 1.3 μM, while B_DPS decreases to 0.07 μM (all the above estimates were obtained with I = 5 mM, P = 2.67 μM, and L = 76 μM). Based on the model parameters recovered here, it was of interest to assess the extent of cyt c binding to PC/CL membranes under physiological conditions and CL content close to that reported for the inner mitochondrial membrane (20 mol %). At pH = 7.4, f_CL = 0.2, and I = 0.15 M, the dissociation of cyt c from the membrane at physiological ionic strength is incomplete. For instance, at L = 174 μM and P = 2.67 μM, the model yields B_DPS = 0.09 μM and B_HPS = 0.11 μM, suggesting that ∼8% of the protein is not released from the membrane by increasing the ionic strength to 0.15 M. Our model thus agrees with the findings of Cortese et al. (38), indicating that one-tenth of cyt c remains bound to the inner mitochondrial membrane at physiological ionic strength. These findings were interpreted in terms of a cyclic model suggesting the existence of equilibrium between soluble cyt c and three membrane-associated protein species differing in their location and conformational state. Of these, electrostatically bound cyt c resides at the membrane surface, while formation of the two other conformers involves protein unfolding and partial bilayer penetration. Several lines of evidence indicate that the mode of binding and the number of structurally different cyt c species depend on the lipid/protein molar ratio. Specifically, a recent study by Oellerich et al. (44) revealed three modes of association of cyt c with DOPG membrane at low ionic strength:

1. Electrostatic binding at L/P ratios exceeding 18 (surface coverage < 56%).

2. Augmented partial bilayer penetration upon L/P ratios approaching saturation level (∼11).

3. Cyt c association with the protein monolayer covering the vesicle surface at L/P < 11.

By analogy with the so-called carpet-mechanism, it was assumed that protein insertion into the membrane becomes possible at certain critical surface coverage at which lateral pressure of two-dimensional adsorbate gas reaches its threshold value. Decrease of L/P ratio after achieving full surface coverage was followed by vesicle aggregation, flocculation, and sedimentation (44). As judged from the turbidity measurements, in the lipid systems examined here vesicle aggregation was observed at pH < 6.7 and protein concentrations exceeding 1 μM. At near-neutral pH, no liposome aggregation occurred over the entire range of protein concentrations, suggesting that full surface coverage was not achieved. Accordingly, based on the above considerations, it might be expected that at neutral pH peripheral electrostatic binding prevails over the insertion process. This viewpoint was supported by the estimates of heme location relative to the bilayer midplane. It was found that RET profiles obtained at pH 7.55, 7.05, and 6.7 for ionic strengths 5, 20, and 60 mM can be described by the basic set of model parameters with d_DPS from the range 3.6–4 nm and d_HPS from the range 3.0–4.1 nm. It is worth noticing that these ranges include all d_DPS and d_HPS values recovered upon varying n_DPS and n_HPS in the aforementioned limits and with α_A equal to 0 or π/2. Taking bilayer half-width as 2.3 nm, and using cyt c radius of ∼1.5 nm for the native and ∼1.8 nm for the molten globule state, it follows that the above d_HPS values are consistent with the location of bound protein in the interfacial region with partial bilayer penetration up to the level of upper acyl-chain carbons, next to the glycerol backbone. However, d_HPS estimates obtained for reduced pH (6.35) suggest cyt c to insert into the nonpolar membrane region. In this case, only the initial part of RET curves (P < 1 μM) can be approximated by the Eqs. 23–26 and 31, with d_HPS falling in the range 3.6–4 nm. At higher protein concentrations, experimental curves lie lower than those predicted by the model, indicating that the distance of the heme from the bilayer center decreases with increasing surface coverage. This observation supports the above concept of a threshold lateral pressure needed to overcome the energy barrier for protein insertion. In the model proposed here, the possibility of protein penetration into the membrane interior was implicitly allowed for via intrinsic association constants. However, more strict description of the binding process requires consideration of at least two additional factors:

1. Increase of the surface area upon protein insertion resulting in the reduced charge density.

2. The total edge tension depending on the bilayer elastic properties and spatial characteristics of the inserted protein species.

These factors have been taken into account in the SPT-based sophisticated model of Zuckermann and Heimburg (20), describing the equilibrium between interfacially adsorbed and inserted protein species. In our case, most experimental points included in the parameter-estimation procedure are expected to be insignificantly influenced by the insertion phenomena. It is also noteworthy that our model ignores the possibilities of nonrandom distribution of donors or acceptors that may originate from

1. Cyt c-induced lipid clustering (19,45).

2. Aggregation of lipid-bound proteins (46).

3. Formation of nonbilayer structures by CL (8).

These possibilities were analyzed in our previous work (47) and addressed in our recent experimental study using anthrylvinyl-labeled PG (48). We concluded that the above phenomena did not manifest themselves under the experimental conditions employed in our RET measurements.

In analyzing the data presented here, the best quality of fit was achieved for the near-neutral pH values. In view of this, there are some grounds for believing that the proposed model and recovered parameters can adequately describe the principal features of cyt c-lipid interactions occurring under physiological conditions. Our model predicts that at CL content higher than 10 mol %, cyt c binds preferentially to partially protonated CL species with initial association constant being approximately two orders-of-magnitude higher than that for deprotonated CL (Fig. 7). Such a pronounced difference in K_DPS and K_HPS values strongly suggests that cyt c binding to HPS is governed not only by electrostatic interactions but by specific hydrogen bonding as well. Importantly, consistent quantitative interpretation of the multiple data sets proved to be possible only when assuming that both K_DPS and K_HPS depend on ionic strength. When K_HPS was considered as being constant or dependent only on pH, we failed to describe ionic strength effects. This fact supports the viewpoint that hydrogen-bonding of cyt c to protonated phosphate can be coupled with the formation of electrostatic contacts with deprotonated phosphate (17). Structural features of cyt c do not exclude this possibility. Cyt c has two hydrophobic channels connecting the heme crevice with the protein surface. The opening of one of these channels is surrounded by oppositely located Asn-52, Lys-72, and Lys-73. It has been hypothesized that cyt c association with CL involves hydrogen bonding of one protonated phosphate moiety to Asn-52 with simultaneous electrostatic binding of deprotonated phosphate to the lysine residues and accommodation of one acyl chain within the hydrophobic channel (17,49).

To summarize, this study provides additional arguments in favor of the idea that cyt c can form two types of complexes with PC/CL membranes where either deprotonated or partially protonated CL molecules are responsible for the surface adsorption of the protein, with electrostatic interactions being essential for the formation of both types of complexes. To describe the adsorption process, the binding model was employed in which area exclusion was treated in terms of the scaled particle theory, while electrostatic effects were quantitatively interpreted on the basis of double-layer theory. This model allows for the dependence of the association constant on electrostatic membrane potential being considered as a function of surface charge density, degree of CL protonation, ionic strength, and the fraction of membrane area covered by the protein. Membrane association of cyt c was monitored by examining resonance energy transfer between anthrylvinyl-labeled phosphatidylcholine as a donor and heme group of cyt c as an acceptor. The data sets obtained at varying CL content, pH, ionic strength, and lipid concentration were simultaneously analyzed in terms of the RET model combined with the model of electrostatically controlled adsorption. Global analysis revealed that at low CL content (10 mol %) and neutral pH electrostatic binding of cyt c to deprotonated CL strongly prevails over the protein association with protonated CL. However, increasing the CL mole fraction to 20 mol % (the value close to that characteristic of the inner mitochondrial membrane) dramatically shifts the equilibrium toward complex formation by cyt c and partially protonated CL. Estimation of the heme distance from the bilayer center suggests that at physiological pH, cyt c is located in the lipid-water interface in both types of complexes, while at pH below 6.0, the surface coverage is becoming high enough to overcome the energy barrier for the protein insertion into membrane core.

APPENDIX

Protonation behavior of cardiolipin

In most studies, CL is regarded as being fully deprotonated, bearing a charge of −2e at neutral pH. This view rests on the early finding that CL has a single pK below 4.0 (35). However, further studies revealed CL to exhibit two widely separated pK values, one at 2.8 and the second varying between 7.5 and 9.5 (36). Such a dramatic pK shift could not be explained exclusively by electrostatic effects arising from the high affinity of the negatively charged membrane for protons. Comparing the protonation behavior of beef heart CL with that of 2′-deoxyCL, Kates et al. (36) concluded that the anomalously high pK₂ of CL originates from the formation of an intramolecular hydrogen bond between the free hydroxyl of the central glycerol and a protonated phosphate. The above pK₂ estimates were derived from the titration of beef heart CL in methanol/0.05 M KCl (1:1, vol/vol), because in water this phospholipid tends to form a hexagonal H_II phase instead of a lamellar one. This measured apparent pK (pK_a) is related to the intrinsic interfacial pK (pK_i), independent of electrostatics, as

(A1)

Considering CL as a dibasic acid, the fractions of deprotonated (P²⁻), partially (HP⁻), and fully protonated (H₂P) species can be written as

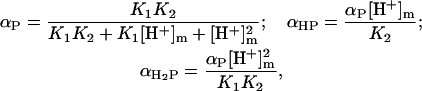(A2)

where K₁, K₂ are intrinsic ionization constants, and 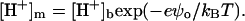Surface charge density of PC/CL membranes is given by Eq. 10 in which α should be replaced by (2α_P +α_HP),

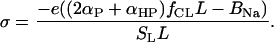(A3)

Allowing for Gouy-Chapman relationship (Eq. 13), one obtains

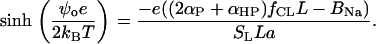(A4)

To roughly estimate the possible limits for pK_a2 the set of Eqs. A1–A4 was solved numerically, taking pK_a2 = 7.5 (or 9.5), pK_a1 = 2.8, and f_CL = 1, ionic strength I = 0.05 M (conditions of the titration experiments performed by (36)). It was found that the measured pK_a2 values lying between 7.5 and 9.5 correspond to an intrinsic pK₂ ranging from 4.0 to 6.0.