IPRO: An Iterative Computational Protein Library Redesign and Optimization Procedure

Abstract

A number of computational approaches have been developed to reengineer promising chimeric proteins one at a time through targeted point mutations. In this article, we introduce the computational procedure IPRO (iterative protein redesign and optimization procedure) for the redesign of an entire combinatorial protein library in one step using energy-based scoring functions. IPRO relies on identifying mutations in the parental sequences, which when propagated downstream in the combinatorial library, improve the average quality of the library (e.g., stability, binding affinity, specific activity, etc.). Residue and rotamer design choices are driven by a globally convergent mixed-integer linear programming formulation. Unlike many of the available computational approaches, the procedure allows for backbone movement as well as redocking of the associated ligands after a prespecified number of design iterations. IPRO can also be used, as a limiting case, for the redesign of a single or handful of individual sequences. The application of IPRO is highlighted through the redesign of a 16-member library of Escherichia coli/Bacillus subtilis dihydrofolate reductase hybrids, both individually and through upstream parental sequence redesign, for improving the average binding energy. Computational results demonstrate that it is indeed feasible to improve the overall library quality as exemplified by binding energy scores through targeted mutations in the parental sequences.

BACKGROUND AND INTRODUCTION

The ability to proactively modify protein structure and function through a series of targeted mutations is an open challenge that is central in many different applications. These include, among others, enhanced catalytic activity (1–3) and stability (4,5), creation of gene switches for the control of gene expression for use in gene therapy and metabolic engineering (6,7), signal transduction (8,9), genetic recombination (10), motor protein function, and regulation of cellular processes (see Bishop et al. (11) for a review). This task is complicated by the fact that proteins rely on complex networks of subtle interactions to enable function (12–14). Therefore, the effect of a mutation is difficult to assess a priori requiring the capture of its direct or indirect effects on many neighboring amino acids. As a result, most protein engineering paradigms involve the synthesis and screening of multiple protein candidates (protein library) as a way to enhance the odds of identifying proteins with the desired functionality level. These directed evolution design paradigms (15–20) typically involve juxtaposition of repeated library generation and screening (Fig. 1). On the other hand, most computational approaches for guiding protein design are focused on the downstream redesign of single parental sequences or promising hybrids (Fig. 1). Notable exceptions include the work of Bogarad and Deem (21) and efforts by Saven (22) that describe computational methods for protein library design.

FIGURE 1.

(a) Promising hybrid sequences from the library are selected for downstream redesign that involves either random or site-directed mutagenesis. (b) Illustration of the upstream parental sequence redesign. Note that the mutations in the parental sequences propagate downstream into the combinatorial library effectively designing the combinatorial library at once, thereby improving the overall quality of the library.

A number of computational models and techniques have been developed (see Moore and Maranas (23) for review) to aid in the in silico evaluation of protein redesign candidates. Typically these techniques attempt to find single or multiple amino acid sequences that are compatible with a given three-dimensional structure specific to a targeted function (e.g., enzymatic activity). The protein fold is usually represented by the Cartesian coordinates of its backbone atoms, which are fixed in space so that the degrees of freedom associated with backbone movement are neglected. More recent approaches (24–29) allow for some backbone movement. Candidate protein designs are generated by selecting amino acid side chains (using atomistic detail) along the backbone design scaffold. For simplicity, side chains are usually only permitted to assume a discrete set of statistically preferred conformations referred to as rotamers (see Dunbrack (30) for a review of current rotamer libraries). Thus, a protein design consists of both a residue and a rotamer assignment for each amino acid position. To evaluate how well a possible design fits a given fold, rotamer/backbone and rotamer/rotamer interaction energies for all the rotamers in the rotamer library are tabulated. These energies are approximated using standard force fields (e.g., CHARMM (31), DREIDING (32), AMBER (33), and GROMOS (34)). Scoring functions customized for protein design (35–37) (see Gordon et al. (38) for a review) typically include van der Waals interactions, hydrogen bonding, and electrostatics, solvation, along with entropy-based penalty terms for flexible side chains (e.g., arginine) (39–42). Because activity level or other performance objectives are very difficult to compute directly, alternative surrogates of hybrid fitness, such as stability or binding affinity, are employed in most studies. The use of these indirect objectives further necessitates the need for designing a combinatorial library rather than a single hybrid to improve the chances of success.

Even for a small 50-residue protein, an enormous number (i.e., 153⁵⁰ ≈ 10¹⁰⁹ assuming a 153-rotamer library (43)) of designs is possible. Both stochastic and deterministic search strategies have been used to tackle the computational challenge of finding the globally optimum design within this vast search space. Despite these challenges, a number of success stories of combinatorial design for many different applications has been reported (42,44–50) in the last few years demonstrating the feasibility of using computations to guide protein redesign. Briefly, successes include manyfold improvements in enzyme activity and thermostability (50–52), improved enantioselectivity (53–55), enhanced bioremediation (56–58), and even the design of genetic circuits (6,7,10) and vaccines (59–61). It is increasingly becoming apparent, however, that instead of computationally generating a set of distinct protein redesigns, it is more promising to use computations to shape the statistics of an entire combinatorial library. This allows one to assess and then “steer” diversity toward the most promising regions of sequence space (62). This paradigm is more likely to succeed compared to constructing, one at a time, protein designs. On the other end, construction of combinatorial libraries based on mutation and/or recombination without any guidance from models/computations is a daunting task because only an infinitesimally small fraction of the diversity afforded by DNA and protein sequences can be examined regardless of the efficiency of the screening procedure.

In response to these challenges, in this article we introduce a new computational procedure IPRO (iterative protein redesign and optimization) that allows for the upstream redesign of parental sequences (Fig. 1). The key idea here is that the residue changes within the parental sequences will propagate in the combinatorial library; effectively introducing mutations within the hybrid sequences in the library (see Fig. 1). Judicious selection of these mutations in the parental sequences can simultaneously relieve unfavorable interactions or clashes (63–65) within the hybrid sequences and therefore enhance the overall quality of the library in one step mirroring the experimental protocol design. Note that even though IPRO is geared toward parental sequence redesign, it can be used, as a limiting case, for the redesign of a single or handful of individual sequences.

The key feature of the IPRO protocol is the cycling between sequence design, ligand redocking, and backbone movement of a set of sequences representative of the combinatorial library. The goal of the sequence design here is to choose mutations within the parental sequences, and therefore in the hybrid sequences, that optimize the average binding energy/score (or alternative surrogates of design objectives) of the hybrid sequences in the library. The genetic algorithm of Desjarlais and Handel (66) and the Monte Carlo minimization protocol of Kuhlman and co-workers (41) involve similar sequence design and backbone perturbation moves. However, they only allow for the design of a single sequence at a time and involve full-scale optimization over rotamers for only a local backbone perturbation. On the other hand, IPRO allows for the design of the entire combinatorial library and involves optimization over the local perturbation region using a globally convergent mixed-integer linear programming (MILP) formulation. In addition, IPRO allows for the redocking of the associated ligands (e.g., substrates, cofactors, solvent, etc.) after a prespecified number of design iterations.

In the next section, we describe in detail the IPRO procedure and introduce the globally convergent mixed-integer linear program that drives residue redesign. We also discuss the methods used for generating and identifying hybrid Escherichia coli/Baccilus subtilis dihydrofolate reductase (DHFR) and B. subtilis/Lactobacillus casei DHFR enzymes containing single crossover positions and assays for DHFR activity. Next, we provide an example application of IPRO to highlight the features and type of output obtained with IPRO. The study involves the computational identification of parental redesigns that are likely to improve a single crossover E. coli/B. subtilis DHFR combinatorial library composed of 16 hybrids (64). We conclude by discussing the implications of our results and some of the modeling and algorithmic enhancements that we are currently incorporating to further improve the IPRO framework.

MATERIALS AND METHODS

The IPRO procedure

The IPRO procedure is composed of four parts (see Fig. 2):

1. A set of hybrid sequences matching the members of the combinatorial library, if <∼100, is generated. For larger libraries, only a representative sample of the diversity of the combinatorial library is considered.

2. For each hybrid sequence, an initial structure is computationally generated. This is a critical step as the efficacy of the identified redesigns depends heavily on the accuracy of the modeled structures.

3. A set of positions, ranging from a single residue position to the entire sequence length, to be targeted for redesign is compiled. Note that the larger the number of design positions is, the more expansive the search space becomes leading to higher computational requirements. Typically we only consider between 3 and 20 design positions that include residue positions within or in the neighborhood of the active site. In addition, restrictions on the type of allowable residue redesigns (e.g., hydrophobic, charged, etc.) can be imposed for each redesign position.

4. Next, a set of residue changes is identified in the parental sequences, which upon propagation among the combinatorial library members, lead to the optimization of the average library score (e.g., binding energy or stability (35–37)). This optimization step is carried out globally using a MILP model within a local perturbation window, whereas simulated annealing is used to accept or reject the residue redesigns associated with each backbone perturbation step.

FIGURE 2.

Four key steps involved in the IPRO procedure. Details of each of these steps are described separately in the text.

Generating a set of sequences representative of the combinatorial library

A set of hybrid sequences is selected to exhaustively or statistically represent the combinatorial library. This step begins with the sequence/structural alignment (67) of the parental sequences. A statistical description of the combinatorial library is obtained by considering the specifics of the combinatorialization protocol. For example, in case of DNA shuffling, models such as eShuffle (68) or those developed by Maheshri and Schaffer (69) can be used to estimate the library diversity. Alternatively, for an oligonucleotide ligation-based protocol such as GeneReassembly (70), SISDC (71), and degenerate homoduplex recombination (72), a statistically unbiased sample of fragment concatenations is constructed that broadly captures the diversity of the resulting combinatorial library. In the limiting case when there is only a single starting sequence to be redesigned, IPRO reverts back to the traditional single protein sequence design procedure. Note, however, that the concept of designing for the optimum of the average of a library of sequences can also find utility in this case when not a unique but rather an ensemble of putative structures is available for the protein to be redesigned. The ensemble of modeled structures then plays the role of the combinatorial library when fed to IPRO. By optimizing with respect to the ensemble average of the putative structures, a more robust redesign strategy is likely to be obtained.

Generation of starting hybrid protein structures

The initial putative structures of the hybrid proteins forming the library are obtained by splicing fragments of the parental structures consistent with its sequence (see Fig. 3). The coordinates of the fragment structures are taken from the structural alignment of the parental sequences. The fold at the junction point(s) typically involves a “kink” as a result of the “ad hoc” concatenation of the parental structures, which becomes even more prominent in case of insertions. This is “smoothened” by allowing the backbone around the junction point to move. The backbone φ and ψ angles of seven residues on either side of the crossover position(s) are allowed to vary and their new positions are determined through energy minimization. In the current implementation of IPRO, we use the CHARMM (73) energy function and molecular modeling environment. Note that during the energy minimization, the bond lengths (b), bond angles (χ₁, χ₂, etc.), and internal coordinates of the side chains are restrained to their original values (b_o, χ_o) by penalizing any deviations (see Eqs. 1 and 2). The bond stretching is penalized using Hooke's law formula (Eq. 1) and the distortions in the bond angles are penalized using the harmonic function (Eq. 2). In addition, distances between certain key atoms can also be restrained using Eq. 1. Note that because less energy is required to distort an angle than to stretch a bond, the force constant associated with bond angle distortion is accordingly smaller:

(1)

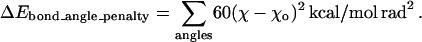(2)

FIGURE 3.

This figure highlights the key steps for constructing the initial structure of a hybrid protein from a set of parental structures with known crossover position(s). These involve i), backbone splicing, ii), backbone relaxation at the crossover positions, and iii), ligand redocking. These steps are repeated for different crossover positions to generate the combinatorial library.

Alternative methods to parental fragment splicing and relaxation for modeling the hybrid structures include techniques such as homology modeling (74,75) and ab initio structure prediction methods (75,76). After the structure of the hybrid protein is modeled, the missing hydrogen atoms are added to the hybrid protein in accordance with the standard procedure used in CHARMM (31). Finally, the positions of the associated ligands are identified using crystallographic data (whenever available) in conjunction with the ZDOCK docking software (77,78). Notably the ZDOCK software allows for the user-specified rough placement of the docked molecules, thus significantly reducing the computational expense of the docking calculations.

Selecting design positions

The selection of the set of positions that will be allowed to mutate (i.e., candidate redesign positions) for each of the parental sequences is largely dependent on the design objective and associated surrogate criterion. Typically, design objectives involve one or more of the following: i), protein stability, ii), binding affinity, iii), specific activity, and iv), substrate specificity. Protein stability is associated with the ability of the protein to fold correctly under a set of conditions. Generally, unfavorable interactions present within the proteins such as the electrostatic repulsion, hydrogen bond disruptions, steric clashes, or a combination of these tend to prevent these proteins from folding correctly (63). A number of structure or sequence data based (SCHEMA (79), SIRCH (65), and clashMaps (63)) and functionality based (FamClash (64)) scoring strategies can be used to quantify the extent of such unfavorable interactions in each hybrid. Residue positions that participate in a disproportionate number of such clashing interactions serve as design positions. On the other hand, when binding affinity, specificity, or specific activity is the design objective, residues within or in the neighborhood of the binding site are chosen as candidates for design. In general, the design positions are either the clashing residues, binding pocket residues, or a combination of both. In most cases, the set of candidate design positions is subsequently revised (either upward or downward) by using information, found in some cases in the literature, about the direct or indirect impact of different residues on the presence, absence, or extent of functionality.

Iterative protein optimization step

The optimization procedure of IPRO involves iterating between sequence design, backbone optimization, and ligand redocking (see Fig. 4). This iterative procedure involves six main steps as follows:

• i. Backbone perturbation. Different backbone conformations are sampled by iteratively perturbing small regions of the backbone that are randomly chosen during each cycle along the length of the sequence (N). For this purpose, a segment (from one to five contiguous residues (k to k′) excluding prolines) of the protein sequence is randomly chosen for perturbation. Because the special structure of proline makes the polypeptide backbone more rigid, prolines, whenever present, are considered part of the backbone. The φ and ψ angles of the positions within the perturbation window are perturbed by up to ±5° from their current values. The probability distribution of the perturbation (between −5° and +5°) follows a Gaussian distribution with a mean of zero and a standard deviation of 1.65°. This ensures that smaller perturbations are chosen more often (64% chance that the perturbations are between −1.65° and +1.65°) compared to larger ones that in most cases are found to result in steric clashes. Note that the backbone conformations of both parental and hybrid sequences are perturbed during each cycle. Although the perturbation positions are the same for every hybrid and parental sequences, the perturbation magnitude in the backbone angles may vary. This allows different parental and hybrid sequences to assume diverse backbone conformations to better accommodate the differing side chains.

• ii. Rotamer-rotamer/rotamer-backbone energy tabulations. Given the backbone conformations determined in Step i and the rotamers and rotamer combinations permitted at each position, this step involves the calculation of the interaction energies of all rotamer-backbone and rotamer-rotamer combinations within an interaction-dependent cutoff distance (cutoff distance for van der Waals = 12 Å, hydrogen bond = 3 Å, and solvation = 9 Å). This energy tabulation must be performed separately for each hybrid and parental structure. The computational expense is reduced by only updating the part of the tables that are affected by the current perturbation. These values are then fed as parameters to the side-chain/sequence optimization model.

• iii. Side-chain/sequence optimization. This step optimizes the amino acid choices and conformations (rotamers) for the given backbone structure over a 10–15 residue window that includes the perturbation positions and five residue positions flanking it on either side (see Fig. 5). Specifically, the design positions within the perturbation region are permitted to change amino acid type, whereas the flanking residue positions (five residues on either side) can only change rotamers but not the residue type. This entails two discrete decisions: 1), identifying the choice of amino acid at any given position; and 2), selecting the rotamer of the chosen amino acid that minimizes the selected surrogate objective function. To model these discrete decisions, IPRO draws upon the MILP optimization model formulations that use binary variables to mathematically represent these discrete decisions.

FIGURE 4.

IPRO is an iterative protein redesign software that includes the following steps: i), A local region of the protein (1–5 consecutive residues as shown in black circle) is randomly selected for perturbation. The backbone torsion angles of these residues are perturbed by up to ±5°. ii), All amino acid rotamers consistent with these torsion angles are selected at each position from the Dunbrack and Cohen rotamer library (86). Rotamer-backbone and rotamer-rotamer energies are calculated for all the selected rotamers using a suitable energy function (87). iii), A mixed-integer linear programming formulation is used to select the optimal rotamer at each of these positions such that the binding energy is minimized. iv), The backbone of the protein is relaxed through energy minimization to allow it to adjust to these new side-chains. v), The ligand position is readjusted with respect to the modified backbone and side chains using the ZDOCK (78) docking software. vi), The binding energy of the protein-ligand complex is evaluated and the move is accepted or rejected using the Metropolis criterion.

FIGURE 5.

Design positions within the perturbation region (shown in orange) are permitted to change amino acid type, whereas the flanking residue positions (five residues on either side shown in green) can only change rotamers but not the residue type. Positions outside this 10–15 residue window (gray) are fixed and cannot change either rotamer or residue type.

For clarity of presentation, we will first describe the MILP formulation for the special case, i.e., redesign of a single parental sequence. This description will then serve as the starting point for the more general combinatorial library design optimization formulation. In both cases, the set of allowed side-chain conformations and amino acid choices at any position is encoded within sets (R_i and R_ih, respectively), where i denotes the residue position and h denotes a hybrid sequence in the combinatorial library in case of parental sequence redesign. Positions within the perturbation window but outside the set of redesign candidates are restricted to the original amino acid type but can change their rotamer state. All other residue positions outside the perturbation window are fixed and cannot change either residue type or rotamer. As expected, the parental sequence redesign problem is much more complex than the single hybrid design. This is because a substituted residue need not assume the same rotamer conformation in each library member. In other words, the hybrids are “tied together” at the sequence level, but not necessarily at the rotamer level. Starting with the simpler MILP formulation for the design of a single hybrid sequence, we first outline the sets, parameters, and variables used in the model as described below:

Sets

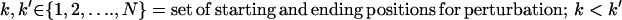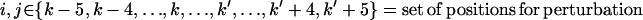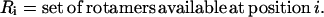Binary variables

Continuous variables

Parameters

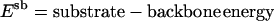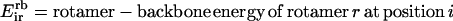Based on the above defined sets, variables, and parameters, the single sequence design problem (SSDP) is implemented as the following MILP formulation, which is a special case of the quadratic assignment problem (80):

(3)

(4)

(5)

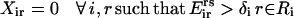(6)

(7)

The objective function (Eq. 3) here entails the minimization of the binding score between the substrate and the protein as an example. The objective function can be changed depending on the design requirements. In many cases, (e.g., binding score) the objective function does not encode information about the interactions in the entire protein. Therefore, the minimization step may lead to mutations or rotamer changes that adversely affect the overall stability of the protein. Constraint Eq. 4 is included to safeguard against this by requiring that the total energy of the protein be below a prespecified cutoff value, E_cutoff. The versatility of the adopted MILP modeling description enables the incorporation of this explicit stability requirement that is absent in most other frameworks proposed for protein design/redesign. In the same spirit, additional energy-based requirements can be imposed to ensure, for instance, retention of important hydrogen bonds between a donor and an acceptor. Constraint Eq. 5 ensures that only one rotamer is selected at any given position i along the sequence. Note that the rotamers may be that of the original residue or of other residues, depending on whether or not position i is a design position. Constraint Eq. 6 prevents any rotamers from being selected at position i that have sufficiently high energy values 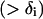that preclude them from the optimal solution. This rotamer elimination procedure formalizes the “background optimization” concept proposed by Looger and Hellinga (81) and allows for eliminating rotamers that are guaranteed not to be part of the optimal solution (see Looger and Hellinga (81) for details) . This concept allows us to a priori trim down the search space and therefore reduces the computational time. Constraint Eq. 7 determines which rotamers r and s are simultaneously selected at positions i and j, respectively. This is encoded with variable 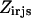, which is equal to one only if both variables and 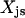are equal to one. This implies that is equal to the product of the two binary variables. These nonlinear terms are then recast into an equivalent linear form by summing 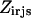over s and r, respectively, as shown below:

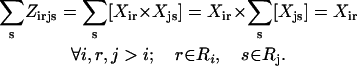(8)

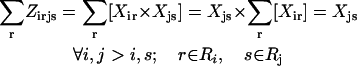(9)

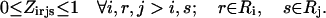(10)

By replacing constraint Eq. 7 with constraints Eqs. 8–10, the linearity of the SSDF formulation is preserved. The complete MILP formulation for SSDP includes constraints Eqs. 3–10 excluding constraint Eq. 7.

Unlike the single sequence protein design formulation SSDP, the hybrid library design problem (HLDP) involves the simultaneous optimization of the hybrids (h) comprising the combinatorial library. Because the hybrid sequences in the combinatorial library are derived from the parental sequences, their amino acid composition must be restricted to the amino acid type present in the corresponding parental sequences after the targeted mutations. To this end, we introduce parameters 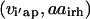that link the amino acid type a selected at a given position i′ in parental sequence p to those present in the hybrid sequences at the corresponding position i. In case of insertions and deletions, the positions i and i′ in the hybrid and parental sequences, respectively, may not be the same. Therefore, one needs to keep track of both the parental sequence p and what position i′ in that sequence corresponds to a given position i in a hybrid sequence h. Specifically, parameter 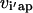is equal to one if amino acid a occurs at position i′ in parental sequence p, whereas parameter 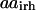stores the amino acid type of rotamer r at position i in hybrid h. In addition, binary variable 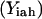is introduced and set to be equal to one if amino acid a is selected at position i in hybrid sequence h. Unlike amino acid type changes, which are propagated throughout the entire library, rotamer choices can differ between hybrid and/or parental sequences. These new complexities give rise to the following additional sets, parameters, and variables definitions.

Sets

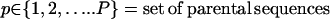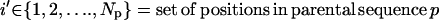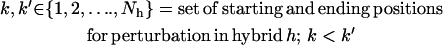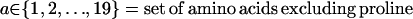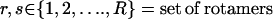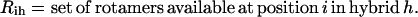Binary variables

Continuous variables

Parameters

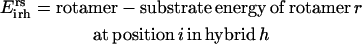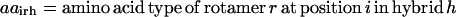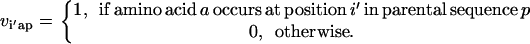By building on the SSDP formulation using the new additional sets, variables, and parameters, the problem of parental sequence redesign and associated HLDP is modeled as the following MILP formulation:

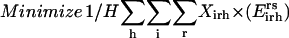(11)

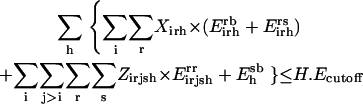(12)

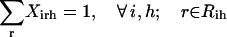(13)

(14)

(15)

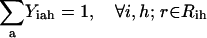(16)

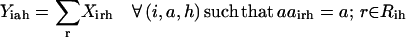(17)

(18)

Slightly modified versions of constraints Eqs. 11–15 were also present in the SSDP formulation. Briefly, constraint Eq. 11 is the objective function of HLDP involving the minimization of the average surrogate score (e.g., binding energy) of the hybrids in the library. Constraint Eq. 12 ensures the stability of the hybrid sequences in the library by imposing an energy cutoff. Constraints Eqs. 13 and 14 ensure selection of only one rotamer r at any given position i in any hybrid sequence h while eliminating any rotamers with a high enough energy to preclude them from the optimal solution. Equation 15 is identical to Eq. 7 in SSDP. Constraint Eq. 16 ensures that only one amino acid type a is permitted at any given position i in a hybrid h. Constraint Eq. 17 determines the amino acid type 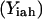of the rotamer selected at position i in a hybrid h. Finally, Eq. 18 ensures that amino acid type a at position i in the hybrid sequence h is the same as the amino acid type at position i′ in parental sequence p. This is in accordance with position i of hybrid h being retained from position i′ of parental sequence p. Equation 15, as in the case of Eq. 7, involves the product of two binary variables. It is exactly recast into a linear form in the same manner as shown below.

(19)

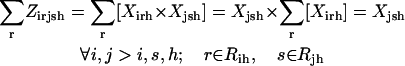(20)

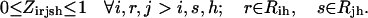(21)

Formulation HLDP is composed of constraints Eqs. 11–21 excluding constraint Eq. 15. We use the CPLEX MILP solver accessed through the GAMS modeling environment to solve both SSPD and HLPD. This optimization step is integrated with CHARMM using a FORTRAN 90 interface.

• iv. Backbone relaxation. The optimization step described above may lead to a number of new residues and/or rotamers for the hybrid structures. These new side chains and/or conformations may no longer be optimally interacting with the previous backbone. To remedy this, a backbone relaxation step is included here allowing for dihedral angles to vary, whereas the bond lengths and angles are constrained to their original values using Eqs. 1 and 2. Note that each hybrid structure undergoes a separate backbone relaxation procedure to optimize the backbone conformation with respect to its associated rotamers. Here the side-chain conformations are fixed while the backbone torsion angles are optimized over the same 10–15 residue window using the adopted basis-set Newton-Raphson algorithm within CHARMM and the same energy function used for sequence design (41). A maximum of 4000 steps are allotted for backbone relaxation though energy minimization.

• v. Ligand redocking. Because of the alterations in the backbone and the change of rotamers/residue type, the location of the ligands may need to be adjusted with respect to the new structure. Therefore, the ligands are redocked separately for each of the hybrid and parental sequences using the ZDOCK docking software (77,78). This redocking step is performed only after a number of prespecified design cycles to cut down on computational requirements. Tight bounds are introduced into ZDOCK to constrain ligand placement in only the relevant pocket or active site. The ligand redocking step using the ZDOCK software is integrated with the backbone relaxation and side-chain optimization steps using a FORTRAN interface.

• vi. Accepting/rejecting moves. After the redocking step, the average score of the hybrid library is calculated and the perturbation imparted in Step i is accepted or rejected on the basis of the difference between the final and starting average scores according to the Metropolis criterion. We have also experimented with a temperature-lowering schedule as it pertains to simulated annealing without finding significant differences in the results. The procedure is repeated for 200–10,000 iterations depending on the complexity and size of the design study.

Upon completion, IPRO provides a set of low energy solutions and associated mutations to be performed within the parental sequences whose propagation to the hybrid library improves the average score of the library. Due to the decomposable structure of the parental sequence redesign problem, most of the computation can be done in parallel with little information cross-flow. Specifically, hybrid structure refinement, backbone relaxation, backbone perturbation, calculation of rotamer-backbone and rotamer-rotamer energies, and ligand docking for each hybrid are performed on separate processors. After the rotamer-backbone and rotamer-rotamer energy calculations for each hybrid, the information is fed as parameters to the “master” processor, which subsequently solves the MILP model (i.e., SSPD or HLDP) to determine the optimal residues at each of the design positions in the parental sequence(s). The choice of the residues/rotamers determined using the MILP for each of the hybrids is then passed to the “slave” processors for further backbone relaxation and ligand docking. All computational studies listed in this article were performed on a Linux PC cluster using a 3.06GHz Xeon CPU/4GB RAM.

Hybrid construction and functional screening

Construction of DHFR hybrid libraries

Previously constructed plasmids pAZE-BE and pAZE-EB (64) were used in this work to construct plasmids for the generation of the L. casei-B. subtilis DHFR libraries in both orientations (pAZE-LB and pAZE-BL). First, the E. coli DHFR fragments containing residues 1–120 and 31–159 were removed from pAZE-EB and pAZE-BE plasmids by NdeI/BamHI and PstI/SpeI restriction digests, respectively. The L. casei DHFR fragments 1–124 and 30–162 were obtained by NdeI/BamHI and PstI/SpeI restriction digests of pAZE-EL and pAZE-LE plasmids (gift from Alex R. Horswill, University of Iowa). The L. casei DHFR fragment 1–124 was then inserted into the cut pAZE-EB by ligation, taking advantage of the complementary NdeI and BamHI sites. Analogously, the L. casei DHFR fragment containing residues 30–162 was inserted into the cut pAZE-BE by ligation. Plasmids pAZE-LB (L. casei residues 1–124-B. subtilis residues 31–159) and pAZE-BL (B. subtilis residues 1–121-L. casei residues 30–162) were confirmed by sequencing at the Nucleic Acids Facility of The Pennsylvania State University.

To construct the hybrid libraries, plasmids pAZE-LB and pAZE-BL were linearized at a unique SalI site between the L. casei and B. subtilis DHFR fragments. Incremental truncation for the creation of hybrid enzymes (ITCHY) method was used to construct libraries of hybrid L. casei-B. subtilis DHFRs in both orientations (82). Libraries were transformed and stored in E. coli strain DH5α.

Selection and determination of specific activities of active DHFR hybrids

The plasmids containing the hybrid DHFR genes were purified and electroporated into modified E. coli stain MH829, which has a deletion of DHFR (folA) gene. Transformed cells were washed twice in minimal media A and plated on minimal media A agar plates supplemented with 0.5% glycerol, 0.6 mM arginine, 50 μg/mL thymidine, 25 μg/mL kanamycin, 100 μg/mL ampicillin, 1 mM MgSO_4, and 100 μM isopropyl β-D-thiogalactose. The plates were allowed to grow for 5 days at room temperature and colonies were picked and restreaked onto the same media and grown at 30°C for 24 h. The selectants were sequenced at the Nucleic Acids Facility of The Pennsylvania State University to identify crossover positions and confirm the absence of insertions, deletions, or mutations.

The specific activities of hybrid DHFRs were determined in cell-free lysates as previously described (64). Briefly, the plasmid pAZE was used to express all DHFR hybrids. To increase expression levels, lacI gene was destroyed on all plasmids by EcoRV and SfoI restriction digests. Plasmids were transformed into the strain MH829, and 50 mL cultures were grown at 30°C in Luria Broth with 100 μg/mL ampicillin, 50 μg/mL thymidine, and 0.5 mM isopropyl β-D-thiogalactoside. Cultures were grown to OD₆₀₀ of 1.0, centrifuged, washed with 25 ml of buffer (20 mM Tris, pH 7.7, 2 mM DTT), and resuspended in 1 mL of buffer. The cells were broken by sonication and insoluble material was removed by centrifugation. The lysates were assayed at 25°C in MTAN buffer at pH 7.0 using the Cary 100 Bio UV-Vis spectrophotometer by Varian (Palo Alto, CA). Cell-free lysate was preincubated with 100 μM cofactor NADPH and the reaction was initiated by adding substrate dihydrofolate to 100 μM. Reaction progress was monitored by following absorbance at 340 nm (NADPH absorbance maximum) (Δɛ= 13,200 μM⁻¹cm⁻¹).

APPLICATION EXAMPLE

DHFR library characterization and analysis

The construction, identification, and characterization of the above discussed sixteen E. coli/B. subtilis DHFR hybrids were described previously (64). E. coli and B. subtilis DHFRs share a 28% sequence identity at the protein level. Below is discussed the isolation and characterization of 10 B. subtilis/L. casei DHFR hybrids used here to validate the computationally derived overall binding scores. The B. subtilis/L. casei DHFR hybrid library was constructed from the B. subtilis/L. casei DHFR pair sharing a 36% sequence identity at the protein level. A previously developed (64) genetic selection utilizing an E. coli strain containing a complete deletion of chromosomal DHFR (folA) was used to select hybrid enzymes with DHFR activity from the library. For this reason, it was necessary to use inactive DHFR fragments to make the ITCHY libraries, which limited the crossover window to residues 31–121. The combined library put through the selection included ∼2.1 × 10⁶ members. There are (90 × 3)² or 72,900 possible hybrid proteins. To determine the number of library members that must be examined for complete library coverage, the number of hypothetical members is typically multiplied by 10. Since we examined >729,000 members, complete library coverage can be assumed. From the DHFR enzymes that passed the selection, 40 hybrids were randomly chosen and sequenced. Only two contained insertions; the remaining 38 were free of insertions, deletions, and mutations. Ten out of 38 hybrids were chosen for this study based on their even distribution of crossover positions over the 90 amino acid crossover position window (see Table 1). The crossover position in the B. subtilis/L. casei hybrids is defined as the last residue (by alignment position) of B. subtilis DHFR. It is clear from the number of active DHFR hybrids identified that 36% sequence identity on the amino acid level between two DHFR proteins can be sufficient for the generation of active hybrids.

TABLE 1.

Crossover positions for the E. coli/B. subtilis and B. subtilis/L. casei DHFR hybrids and their specific activities (μmol/min/mg)

E. coli/B. subtilis		B. subtilis/L. casei
Crossover position	Specific activity	Crossover position	Specific activity
0	20.22	0	0.197 ± 0.114
32	2.17	32	0.915 ± 0.086
35	0.39	40	0.067 ± 0.008
46	0.17	53	0.001 ± 0.000
49	0.12	62	0.025 ± 0.004
53	0.12	85	0.001 ± 0.000
55	0.12	103	0.003 ± 0.001
62	0.09	114	0.035 ± 0.16
73	0.01	123	0.063 ± 0.005
79	0.15	160	6.622 ± 0.157
81	0.06
96	0.10
100	0.36
108	0.70
122	0.84
159	1.43

The errors in the specific activity for the B. subtilis/L. casei hybrids are given at 95% confidence interval.

The crossover positions for the E. coli/B. subtilis and B. subtilis/L. casei hybrids are defined as the last reside position (in alignment) of the E. coli and B. subtilis DHFR sequences, respectively.

Specific activities (μmol/min/mg) of the B. subtilis/L. casei hybrid enzymes were measured to compare these values to the overall binding scores obtained using the SSDP formulation. Note that the listed specific activities are crude lysate activities. This means that total lysates of cells expressing the hybrid of interest, not the purified hybrids, are used in the assays. Specific activity is the amount of product formed by an enzyme in a given amount of time per milligram of enzyme. Experimentally, specific activity here is the amount of cofactor NADPH converted to NADP⁺ by a DHFR hybrid in 1 min per milligrams of total protein in the crude lysate. The specific activities (μmol/min/mg) are quantified by measuring the decrease in absorbance at 340 nm (NADPH absorbance maximum) during the enzymatic reaction to determine how many μmoles of NADPH are converted to NADP⁺ per minute using the extinction coefficient of NADPH (13,200 μM⁻¹ cm⁻¹). The resulting value is then divided by the milligrams of total protein in the crude lysate, which is determined by the colorimetric Bradford assay.

The B. subtilis/L. casei hybrids with the highest activities were found to have crossover positions close to the N- or C-terminus. These hybrid proteins consist mostly of one DHFR (i.e., B. subtilis or L. casei) and have only a short amino acid sequence replaced by the sequence of the other DHFR at either the N- or the C-terminus. Consequently, these hybrids have a relatively small number of new interactions since a large percentage of the sequence is retained from one species. The hybrids with the lowest activities have their crossover positions in the central region of the crossover position window, between amino acids 53 and 103. This region belongs to the adenosine binding subdomain of DHFR, which is involved in binding of the cofactor NADPH (83). These hybrids contain long sequence fragments from both B. subtilis and L. casei DHFRs and are thus expected to have many new interactions not present in the wild-type proteins. Similar results were seen for the E. coli/B. subtilis DHFR hybrids; the lowest specific activities were found for the hybrids with crossover positions in the central region consisting of amino acids 55–96.

IPRO analysis of DHFR libraries

In this section, we provide a step-by-step application of the IPRO procedure, starting with the SSDP formulation, to test whether it is feasible to improve the computationally derived overall binding scores of two separate DHFR hybrid systems: i), 16 E. coli/B. subtilis, and ii), 10 B. subtilis/L. casei hybrid DHFR sequences. These results are contrasted against the experimentally determined specific activity values to check whether the trends observed for the specific activity can be explained using the computed binding scores. First we apply the SSDP formulation to individually design each one of the 16 E. coli/B. subtilis DHFR hybrids considering two different sets of design positions followed by the HLDP formulation, which is used to optimize the average binding energy of the 16 E. coli/B. subtilis DHFR hybrids.

Starting with Step a, IPRO first generates the sequences for the 16 E. coli/B. subtilis and 10 B. subtilis/L. casei DHFR hybrids corresponding to the crossover positions shown in Table 1. This simply involves splicing of the parental sequence fragments consistent with the given crossover positions. Putative structures for two different sets of DHFR hybrids are generated as described in Step b. The alignment of the parental structures required for this step is performed using the combinatorial extension method (84). An approximate structure of each of the hybrid sequences is constructed by concatenating the corresponding parental structure fragments obtained from the aligned structures. The structures of the E. coli (PDB code: 1RX2) and L. casei (PDB code: 1AO8) parental sequences were obtained from the Protein Data Bank (85), while the structure of the B. subtilis DHFR was provided to us by Dr. Gregory A. Petsko at Brandeis University (personal communication). Each one of these putative structures was refined by allowing the backbone around the junction point (14-residue window) to relax through energy minimization, and subsequently the hydrogen atoms were added as described in Step b. Although no residue changes are made, SSDP is used to drive side-chain movements (rotamer changes and/or backbone relaxation) for best binding. The optimized binding scores (kcal/mol) for these hybrid sequences were then contrasted against the experimentally measured specific activities (μmol/min/mg). The specific activity values of the B. subtilis/L. casei and E. coli/B. subtilis hybrids (64) are shown in Table 1. The calculated binding scores in each case is found to be linearly correlated to the natural log of the specific activities suggesting that binding energy is a good predictor of specific activity (see Fig. 6, a and b, corresponding to E. coli/B. subtilis and B. subtilis/L. casei DHFR hybrid sequences respectively). Specifically, 72.7% of the variance in the specific activity trend for the E. coli/B. subtilis DHFR hybrids and 75.4% for the B. subtilis/L. casei DHFR hybrids is explained by the log-linear relation with the binding scores.

FIGURE 6.

Plot of the natural log of the specific activities against the binding scores for two different types of DHFR hybrids (a) E. coli/B. subtilis and (b) B. subtilis/L. casei. Along each point is shown the corresponding hybrid sequence with its crossover position.

The next step involves the redesign of each one of the sixteen E. coli/B. subtilis DHFR hybrid sequences individually using SSDP formulation to enhance their computationally derived binding energies. Two separate sets of design positions were considered, as required in Step c, for mutation: i), positions that were identified to be involved in clashes (63,64), and ii), all residues within the binding pocket (i.e., within 4 Å distance from the substrate) that are likely to contribute directly to the binding score. Clashing positions for each one of the hybrid structures was determined using the clashMap (63) and FamClash (64) procedures. Positions that were frequently involved in clashes were identified and considered for redesign. The same design positions were considered for all the hybrid sequences to identify any significant patterns in the residue substitutions. On average, 20 design positions were considered in either case, and each run was submitted to an individual processor for a total of 1000 iterations for binding score minimization using SSDP. Interestingly, out of 20 positions considered for redesign, we found that only 7 positions (results shown in Table 2) are mutated away from the wild-type. The maximum number of mutations introduced in any one hybrid sequence did not exceed four mutations (see Table 2). Notably, a number of mutations are prevalent in all designs. Also many residues that are within or close to the binding pocket persist at the wild-type even though they are treated as design candidates.

TABLE 2.

Individual redesigns of the (a) clashing positions and (b) binding site residues for the E. coli/B. subtilis hybrid DHFR sequences

(a)	30	62	63	96	97	98	103
B. sub	Y	V	T	G	A	Q	L
E. coli	W	L	S	G	G	R	F
0	F
33	F				K
36	F				Q
47	F
50	F				K
54	F
56	F
62	F/A
73	F		T			K	M
79	F
81	F
96	F
101	H					K
109	H/F					K
123	F				Q		L
160	F		A			K	L
(b)	57	61	63	64	65	67	68
B. subt	R	V	S	S	A	D	S
E. coli	R	I	T	S	Q	G	T
0		T		R	R/Q	R/D	R/F
33		T		R	Q	R	E
36				R	R/Q	R/D	R/Y
47		T		R	Q	E	Q
50		I		K	Q	K	R
54				R	Q
56	N			R	K	T	Q
62				R	H	K	D
73	K		A	R	R		Q
79			A	R	H		F
81			A	R	R		F
96	T			R	R/Q		F
101				R	R		F
109	N			R	R		F
123				R	T		Y
160			A	R	R		F

The original B. subtilis and E. coli residues are shown in bold, and underlined, respectively. Positions with consistent mutations are 30, 64, and 68 (for crossovers after position 63). Note that position 0 corresponds to the B. subtilis parental sequence, whereas 160 corresponds to E. coli sequence.

Redesigning the clashing positions (a total of 17 positions) provides approximately the same improvement (−6.9 kcal/mol) in the average binding score as compared to designing only the binding pocket residues (−6.2 kcal/mol) including 22 residues. This means that at least in this study, relieving clashes can indirectly improve binding at the same extent as active site residue redesign. The binding scores of the hybrid sequences before and after design for the two set of design positions are compared in Fig. 7, a and b, respectively. Notably, when only clashing residue positions are considered for redesign, most of the improvement in the binding scores of the hybrid sequences (average score, −149.0 kcal/mol) is found to be the result of a single mutation in the B. subtilis DHFR sequence fragment (S64R) and two mutations in the E. coli sequence fragment (S64R and T68F). On the other hand, when only binding pocket residues are considered for redesign, a single mutation in the E. coli (W30F) and a single mutation in the B. subtilis (Y30F) DHFR sequence fragments appear to contribute most to the improvement in the binding score (average score, −148.3 kcal/mol). Not surprisingly, these mutations are found to be consistently occurring in the design of most of the hybrid sequences (see Table 2). Many alternate mutations leading to the same binding score improvement are found particularly for design positions 65, 67, and 68 (see part b in Table 2).

FIGURE 7.

Binding score profile before and after redesign of the E. coli/B. subtilis DHFR hybrids using the SSDP framework when (a) only clashing residue positions are considered and (b) only binding pocket residues are considered for redesign.

The results highlighted above describe the application of the SSDP optimization formulation, which enables the one-by-one optimization of each one of the 14 hybrids. Note that mutations predicted for the same position can vary for different hybrids. Next, we describe the application of HLDP, which unlike the SSDP formulation enforces the same set of mutations for all hybrids. The objective here is to contrast the overall results obtained from the two optimization formulations. Both the clashing positions and residues within the binding pocket are considered simultaneously. The HLDP formulation was run on a 16-node Linux PC cluster with 3.06 GHz Xeon CPU/4 GB RAM, with one node assigned to each sequence (14 hybrid sequences and 2 parental sequences). One of these nodes served as the “master” node that solved the HLDP framework every iteration. This procedure was run for a total of 48 h that permitted on average 315 design iterations. The energy profile of the library before and after the redesign of the parental sequences is shown in Fig. 8. Note that even though we obtained an improvement in the binding scores (see Table 3) for all hybrid sequences, this may not always be the case as the improvement in the average binding score of the library may be in some cases due to a handful of hybrid sequences. We find that the most prevalent mutations based on the SSDP results are again present. HLDP identified mutations at only three positions in the parental sequences (positions 30, 64, and 68) that yielded an average binding score of −149.0 kcal/mol. Notably, this is very close to the average binding score of the library where each sequence is individually redesigned. Whereas the upstream parental redesign using HLDP requires in total only five mutations in the parental sequences, the downstream hybrid sequence design involves up to four different mutations for each hybrid sequence. This example, therefore, demonstrates that upstream parental sequence redesign can indeed optimize all resulting hybrids in one step in contrast to one-by-one redesign of the hybrid sequences.

FIGURE 8.

Binding score profile before and after redesign of parental E. coli and B. subtilis DHFR sequences using the HLDP framework. Both clashing residue positions and the binding pocket residues are considered for design.

TABLE 3.

Redesign of parental E. coli and B. subtilis DHFR

	30	64	68
B. sub	Y	S	S
E. coli	W	S	T
0	F	R
33	F	R
36	F	R
47	F	R
50	F	R
54	F	R
56	F	R
62	F	R
73	F	R	F
79	F	R	F
81	F	R	F
96	F	R	F
101	F	R	F
109	F	R	F
123	F	R	F
160	F	R	F

Examination of the resulting structures of the redesigned sequences reveals that most of the improvement in the average binding score of the library results from a new salt bridge between the substituted arginine at position 64 and the cofactor NADPH (Fig. 9 a). Moreover, substitution of tyrosine and tryptophan at position 30 with a smaller aromatic residue phenylalanine perhaps reduces steric hindrance with the substrate DHF (Fig. 9 b). We also find that the designs identified using the IPRO procedure are consistent with the residue types observed in the DHFR protein family sequences (at position 30, F = 15.73%; and at position 64, R = 57.98%). It is important to note that no information of the protein family sequences was a priori provided to the IPRO model.

FIGURE 9.

(a) Substitution of serine with an arginine at position 64 stabilizes the binding with the cofactor NADPH due to formation of a new salt bridge. (b) Substitution of tyrosine and tryptophan at position 30 with a smaller aromatic residue phenylalanine perhaps reduces steric hindrance with the substrate DHF.

SUMMARY AND DISCUSSION

In this article, we introduced the computational framework IPRO for the computational design of protein combinatorial libraries. IPRO identifies targeted mutations in the parental sequences that when propagated in the combinatorial library systematically optimizes a computationally accessible quantitative metric of library quality (e.g., stability, binding affinity, specific activity, etc.). A new design paradigm is thus proposed that improves the entire library in one step instead of “rescuing” individual hybrids one at a time. IPRO allows for ligand redocking and backbone movement, whereas a globally convergent MILP formulation drives side-chain selection. Two separate MILP formulations (SSDP and HLDP) are included in the IPRO procedure that allow for both the downstream redesign of promising hybrids and the upstream redesign of parental sequences, respectively. Sixteen different E. coli/B. subtilis DHFR hybrids were computationally redesigned individually, (i.e., one-by-one using the SSDP formulation) and as well as in a single step through parental sequence redesign (i.e., HLDP formulation). We found similar improvements in the binding energy for both cases, demonstrating the feasibility of redesigning combinatorial libraries in a single step.

IPRO can thus be used to guide the design of a combinatorial library in two ways: i), through formulation HDLP that pinpoints a handful of mutations among the parental sequences before recombination, or ii), using formulation SSDP that redesigns a single sequence at a time. By aggregating all the mutations predicted by IPRO to improve your design criterion, a combinatorial library can be constructed. The current implementation of IPRO can only handle design objectives exemplified by a single energy-based surrogate function, (e.g., binding score as a measure of specific activity). However, in many cases, library quality depends on multiple, and sometimes competing, requirements. For example, altering ligand (or substrate) specificity requires redesigning the binding pocket to recognize the new ligand but also eliminate any affinity for the old one(s). We are working toward extending IPRO using a two-stage optimization procedure where the outer problem drives residue mutations by minimizing the binging energy with respect to the new ligand while the inner problem ensures that the new design does not bind the old ligand(s) for any rotamer combination. Although modifying an existing active site to accommodate new interacting partners can be achieved by targeted point mutations as described before, introducing a completely new functionality in an existing protein scaffold requires a new computational design paradigm. We are also working toward extending IPRO procedure to allow for the “grafting” of binding sites from one protein to another. Again, this leads to a nested optimization structure where the outer problem performs active site geometry optimization while the inner problem tests/prevents distortion of the grafted binding site upon energy minimization.