Water properties from first principles: Simulations by a general-purpose quantum mechanical polarizable force field

Abstract

We have recently introduced a quantum mechanical polarizable force field (QMPFF) fitted solely to high-level quantum mechanical data for simulations of biomolecular systems. Here, we present an improved form of the force field, QMPFF2, and apply it to simulations of liquid water. The results of the simulations show excellent agreement with a variety of experimental thermodynamic and structural data, as good or better than that provided by specialized water potentials. In particular, QMPFF2 is the only ab initio force field to accurately reproduce the anomalous temperature dependence of water density to our knowledge. The ability of the same force field to successfully simulate the properties of both organic molecules and water suggests it will be useful for simulations of proteins and protein–ligand interactions in the aqueous environment.

General-purpose force fields, from Levitt’s early protein potential (1) to modern models such as charmm, opls-aa, mmff, and amber (2–5), which approximate molecular potentials by simple analytical formulas, are in wide use for computational studies of biological systems ranging from the simplest molecular clusters to large complexes involving proteins. In the latter case, the investigations encounter serious computational problems, primarily related to proper conformational sampling and adequate treatment of the long-range intermolecular interactions; however, with advancements in simulation methodologies and the increase in computer speed these difficulties are alleviated so the accuracy of the underlying models becomes the dominant factor.

Protein and protein–ligand interactions usually take place in an aqueous environment, which contributes critically to their energetics, e.g., by hydrogen bonding and the hydrophobic effect. Hence, a force field should accurately reproduce the properties of both organic compounds and water if it is to be used for precise calculations of protein–ligand binding, as required for example in drug-design applications. Moreover, the quality of the applications of a force field to water can be considered as a criterion for the accuracy of the approach as a whole. Hence, it is disconcerting that no general-purpose force field has previously succeeded in accurately describing key properties of liquid water.

On the other hand, impressive progress has been made in theoretical studies using specialized water potentials. Many of these potentials are empirical, i.e., they have been fitted to experimental data on the thermodynamics and kinetics of liquid water and in some cases ice. The most advanced of these models, such as the pairwise additive tip5p (6) and polarizable (7–9) potentials, generally provide an accurate description of the most important properties of water and/or ice. However, no one model is yet able to reproduce in detail the diversity of thermodynamic and kinetic experimental data on both gas and condensed phases under a range of conditions. Moreover, these empirical water potentials cannot be transferred to more general molecular systems such as proteins because of the assumptions incorporated and the lack of data on which to calibrate them.

Given these limitations, it would seem preferable to perform simulations by using potentials fitted to high-quality ab initio quantum mechanical (QM) data. Such calculations are now possible because of major advances in methods and vast increases in computer speed. However, because of the complicated functional form of advanced ab initio potentials, their direct use for many-particle systems is very computationally intensive, impeding their applicability to liquid-phase simulations (10–13). Moreover, such studies have generally been performed by using classical molecular dynamics (MD) applied to the QM potentials; application of quantum statistics via the path integral MD (PIMD) technique is even more time-consuming and rare (14). Yet quantum effects in water are non-negligible because of the strong hydrogen-bond interactions that depend sensitively on the positions of H atoms. These positions, in turn, are sensitive to quantum zero-point vibrations caused by the relatively small H atom mass. Thus, quantum effects must be taken into account to obtain a proper assessment of the accuracy of the ab initio approach. By contrast, the empirical potentials, which use classical MD, implicitly include the quantum effects in their parameterization.

We had previously presented a general-purpose ab initio QM polarizable force field (QMPFF) (referred to here as QMPFF1), which is based on physically well grounded considerations of intermolecular interactions and is fitted to an extensive set of high-quality vacuum QM data on properties of simple molecules and their dimers. QMPFF1 accurately simulates the interactions in many organic complexes (15). In this article we present the results of classical and PIMD simulations of liquid water by using a second, more refined version of the force field, QMPFF2. The parameterization process used in QMPFF2 for the atom types and bonds that appear in a water molecule is exactly the same as that used for the types appearing in other molecules. Moreover, in QMPFF there is no separate water model as such because the parameters of the atom and bond types for water are fitted to QM data on interactions in both homodimers of water molecules and their heterodimers with other molecules.

Hence, the high accuracy of the water simulations described below represents crucial validation of the overall QMPFF concept and suggests that the same force field can be applied to both the simulation of biomolecular interactions occurring in water and the study of water itself.

Results

QMPFF2 Performance in Gas Phase.

QMPFF2 parameters were fitted to QM data on properties of 144 molecules and 79 molecular dimers, the total number of dimer conformations being 2,916. The relative rms deviations (RMSD) for absolute values of dipole moments and quadrupole and polarizability tensors were 6.2%, 23% and 3.7%, respectively. QMPFF2 fits the QM energies of all of the dimers in the training set well with a RMSD of 0.38 kcal/mol. For the 165 training dimers that have been optimized to have minimum energy, the RMSD of the energy and geometry calculated by QMPFF2 relative to ab initio QM were 0.50 kcal/mol and 0.09 Å.

Table 1 compares QMPFF2 and QM values for basic properties of the water molecule: absolute value of dipole moment, eigenvalues of quadrupole, and polarizability tensors. As seen, QMPFF2 simulates dipole moment exactly, whereas relative errors are 5.0% and 3.2% for quadrupole and polarizability, respectively.

Table 1.

Absolute value of dipole moment (D), eigenvalues of quadrupole (Q₁, Q₂, Q₃), and polarizability (P₁, P₂, P₃) tensors for water molecule

Approach	D, Debye	Q1	Q2	Q3	P1, Å3	P2, Å3	P3, Å3
		(Buckingham)
QMPFF2	1.87	−5.22	0.16	5.04	1.42	1.42	1.42
QM	1.87	−5.02	−0.12	5.14	1.37	1.41	1.48

As for interactions of water molecules, Fig. 6, which is published as supporting information on the PNAS web site, illustrates the typical accuracy of QMPFF2 fit for different conformation sets of water dimer, whereas Table 2 compares QMPFF2 and QM energies for optimized water multimers. As seen from Table 2, for the optimized dimer conformations (presented in the QMPFF2 training set) the overall accuracy is 0.4 kcal/mol, which is comparable with the accuracy for dimers of other molecules. On the other hand, QMPFF2 performance outside the training set is validated by comparison of calculated and QM energies of water multimers, which is a challenging test because of the role of many-body effects. As seen the agreement (including even correct ranking of the hexamer energies) is excellent considering that no systems larger than dimer were used in the parameterization of QMPFF2.

Table 2.

Water multimer energies (kcal/mol) in different optimized conformations

Approach	Dimer			Trimer cyclic	Tetramer cyclic	Pentamer cyclic	Hexamer
	Linear	Cyclic	Bifurcate				Prism	Book	Ring
QMPFF2	−5.08	−3.39	−2.56	−15.2	−25.9	−32.9	−43.2	−42.2	−39.9
QM	−4.68	−3.68	−2.92	−14.6	−25.4	−33.4	−42.7	−42.1	−41.4

QMPFF2 also reasonably predicts dimerization Gibbs energies: rms deviations between calculated and experimental values was found to be 0.35 kcal/mol for 27 different homodimers and heterodimers, consistent with the overall QMPFF2 accuracy. These values, which are closely related to the second virial coefficients, were calculated by using standard methodology neglecting the molecule flexibility with the quantum effects being taken into account in the framework of semiclassical approach. However, we have found from careful path integral calculations that the molecular flexibility may contribute rather essentially to the virial coefficient values (up to several dozen percent in the relevant temperature range), especially in the case of water vapor for which the quantum effects are not negligible.

Bulk Properties.

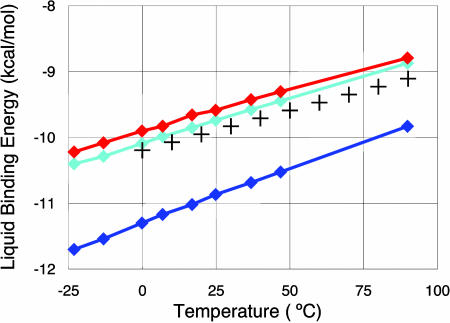
Classical and PIMD simulations have been performed to calculate water characteristics in liquid phase (see Materials and Methods for details of MD protocols). The bulk water properties calculated from the MD trajectories are compared in Table 3 with experimental data taken from ref. 14, except for the diffusion constant taken from ref. 15. As seen, the QMPFF2 classical MD results are close to the experimental values. With quantum MD the agreement is even better. Quantum MD decreases the liquid binding energy by 1.3 kcal/mol to give a value within 3% of experimental. A similar improvement is seen for the heat capacity. The temperature dependence of the liquid binding energy is also reasonably described by QMPFF2 as seen in Fig. 1.

Table 3.

Liquid water properties obtained from MD simulations with QMPFF2 compared with experimental values

Approach	E = Eliq − Egas, kcal·mol−1	Cp, cal·mol−1·K−1	105D, cm2·s−1	ρ, g·cm−3	105 α, K−1	ρmax, g·cm−3	Tmax, °C
QMPFF2 (classical MD)	−10.9	19.6	1.2	1.003	26	1.005	8
QMPFF2 (quantum MD)	−9.6	18.6	1.9	0.992	30	—	—
Experimental	−9.9	18.0	2.3	0.998	26	1.000	4

E, liquid binding energy; C_p, specific heat capacity; D, diffusion constant; ρ, density; α, coefficient of thermal expansion, all under ambient conditions; ρ_max, maximum density; T_max, temperature of occurrence of ρ_max.

Fig. 1.

Temperature dependence of liquid binding energy at normal pressure. Red and blue curves correspond to quantum and classical MD simulations, respectively; the cyan curve represents classical simulations with the rigid molecules. For all of the curves the statistical errors are comparable with the marker sizes except of the leftmost points for classical curves. The crosses represent the experimental data (16).

Fig. 1 indicates that the classical simulations resulted in essential underestimation of the liquid binding energy, whereas the quantum effects taken into account by PIMD calculations contribute up to 1–1.5 kcal/mol within the considered temperature range, bringing the curve much closer to the experimental one. This contribution is caused mainly by intermolecular motions, which are adequately treated by calculations with a comparatively low PIMD discretization index, P = 4. As for intramolecular vibrations, the change of QM zero point energy transferring from gas to liquid is small for harmonic intramolecular potentials used in QMPFF2 so the corresponding corrections can be neglected. On the other hand, for essentially anharmonic potentials the correction could lower the liquid binding energy by about a half of kcal/mol (14). Note also that the classical simulations with rigid molecules result in less-bonded liquid phase, which mimics the quantum effects so the liquid binding energy is incidentally very close to the PIMD result (see Fig. 1).

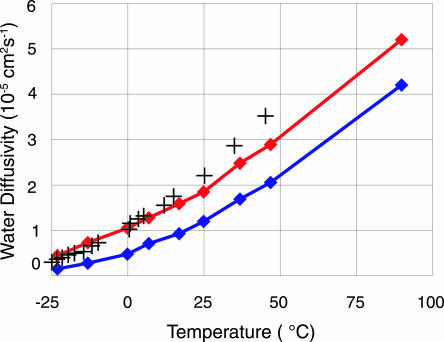
It follows from Table 3 that the greatest improvement provided by quantum MD is a >50% increase in the diffusion constant [which is in agreement with other results (18 and 19)] to fit experiment much better. This finding is also illustrated by Fig. 2 where the temperature dependence of water diffusivity is plotted as found from both classical and PIMD calculations. Note that this QM correction can only be considered an approximation, as the traditional path integral technique does not simulate kinetic properties with sufficient accuracy.

Fig. 2.

Temperature dependence of water diffusivity. Red and blue curves correspond to quantum and classical MD results, respectively. The crosses represent the experimental data (17).

Water Has a Density Maximum.

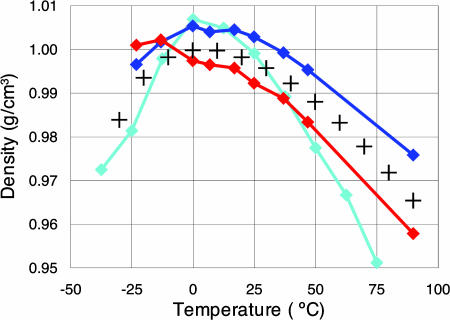
At room temperature, the QMPFF2 density calculated with either classical or quantum MD fits experiment to 0.5%. The QMPFF2 results for other temperatures are plotted in Fig. 3. As seen, the classical MD curve reproduces the density maximum, which is certainly the best-known anomalous property of water. The calculated value ρ_max = 1.005 g·cm⁻³ is in very good agreement with the experimental value 1.000 g·cm⁻³. The temperature T_max of the maximum density turns out to be near 8°C, which is between the experimental result 4°C and the value of ≈14°C recommended in ref. 20 for comparison with the results of classical MD. More generally, QMPFF2 with classical MD reproduces the density of water over the entire range −25°C to 100°C to within 0.6% (Fig. 3). With quantum MD, the results are even slightly better for temperatures >0°C, but the density for lower temperatures is incorrectly high. The reason for this discrepancy probably results from problems with the MD algorithm in the supercooled region but more investigation is needed.

Fig. 3.

Temperature dependence of water density at normal pressure. Red and blue curves correspond to quantum and classical MD with QMPFF2, respectively; the cyan curve represents results (6) for the TIP5P empirical water potential. For all of the curves the statistical errors are comparable with or less than the marker sizes. The crosses represent the experimental data (16).

Radial Distribution Functions.

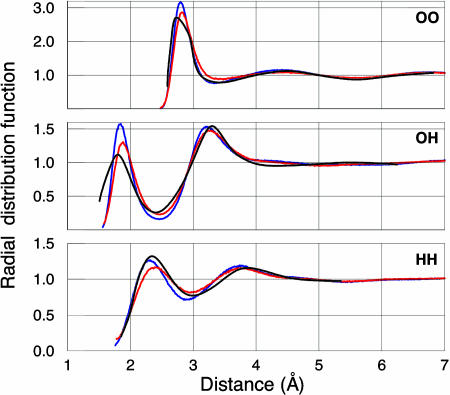
The radial distribution functions that characterize the structure of liquid water are presented in Fig. 4 for both classical and quantum MD. The QMPFF2 positions of all of the extremes agree very well with the experimental values to within 0.1 Å. The amplitudes are fairly good for OO and HH, but the first OH peak height is overestimated, which is also typical for other models. The quantum MD simulations result in less structured water, giving better overall description of the experiment than classical MD, in agreement with other results (14, 18, 19). Thus, the amplitude of the first OO peak is decreased from the classical MD value of 3.17 to the quantum MD estimate of 2.87, which approaches the experimental value (21, 22) of 2.8. Also, the height of the first OH peak is decreased from 1.58 to 1.30, which should be compared with the experimental value (21) of 1.10. As for the first HH peak, quantum result is worse than the classical, which is likely because of too soft flap angle bending in potential energy surface for water dimer.

Fig. 4.

Radial distribution functions for HH (Bottom), OH (Middle), and OO (Top) pairs in liquid water at room temperature and pressure. Blue and red curves correspond to classical and quantum MD simulations with QMPFF2, respectively. Black curves represent experiment (21).

Comparison to Specialized Water Models.

The quality of QMPFF2 predictions of water properties is overall at least as good as the best specially designed water models. For example, the classical and QM estimates of the liquid binding energy are respectively −11.34 and −9.8 kcal/mol for the MCDHO potential (14); for other ab initio models the classical energy is −10.65, −9.49, and −11.2 kcal/mol for NCC (10), NEMO (11), and TTM2-R (13), respectively. The diffusion coefficient at ambient conditions is found to be 2.6·10⁻⁵, 1.3·10⁻⁵, and 2.2·10⁻⁵ cm²·s⁻¹ for the NCC, NEMO, and TTM2-R potentials. As these values have been determined from classical MD simulations, the diffusion constants should probably be increased by a factor ≈1.5 or greater to account for the increased mobility with quantum MD. Hence, the values for TTM2-R and NCC are less accurate than appears at first glance and the value for NEMO is more accurate.

Most significant is the success of QMPFF2 in reproducing the density/temperature relationship. Water density at room temperature was found to be 1.02 ± 0.01, 0.983, and 1.046 g·cm⁻³ for MCDHO, NEMO, and TTM2-R, respectively (11–13), which differ from the experimental value by 2–4%, compared with 0.5% for QMPFF2. Moreover, for these models, there are no data on the temperature dependence of the density except for NEMO, where no density maximum was found. On the other hand, a number of empirical water models do find a density maximum, with the T_max value varying from −40°C to +30°C; nevertheless, most of these models give too sharp a dependence of density on temperature (20) (e.g., see the curve for one of the best models, TIP5P, plotted in Fig. 3).

Conclusions and Outlook

The results of MD simulations of liquid water with QMPFF2 demonstrate very good agreement with experimental results on the structure of liquid water and a wide set of basic thermodynamic properties, with the use of accurate quantum path integral techniques generally needed to best realize this agreement. This conclusion indicates that careful, physically grounded simulation of intermolecular interaction in vacuum, taking into account its main features and avoiding oversimplification, does allow accurate simulation of the properties of the condensed phase. The approach is further supported by successful results of MD simulations with QMPFF2 of the solvation energies of small organic molecules in water (unpublished data). The results are especially promising because further progress is possible and its direction is clear: extremely accurate ab initio calculations can be performed with advanced methods, e.g., ref. 23, followed by further refinement of the functional forms and parameterization of the QMPFF interaction potentials to track the ab initio data.

In this connection, the alternative fully QM parameter free approach based on Car-Parinello molecular dynamics (24) should be mentioned. However, these calculations are too computationally expensive so presently they are applicable only to short-time simulations of simplest molecular systems (25–27) that essentially restricts the performance capabilities of the method in comparison with the force field approach, in particular, preventing an adequate treatment of boundary effects and therefore of the bulk properties. The relation between the two approaches will change in the future with the growth of computer speed and the sizes of simulated systems providing a basis for joint QM/molecular mechanical methodologies. Probably the most exciting feature of our results is that the model is based strictly on ab initio-calculated QM data, unlike empirical water potentials, which are fitted to experimental data and therefore cannot be said to be predicting the properties of water. Our results show that the state of the art has now advanced to where even subtle properties of water such as the anomalous density/temperature dependence can be predicted solely from the basic principles of quantum physics. Following this approach, a complete, accurate theoretical treatment of water may now be in sight, including solution of the water structure problem recently highlighted as one of the 125 outstanding problems of science (28).

Materials and Methods

Description of QMPFF2.

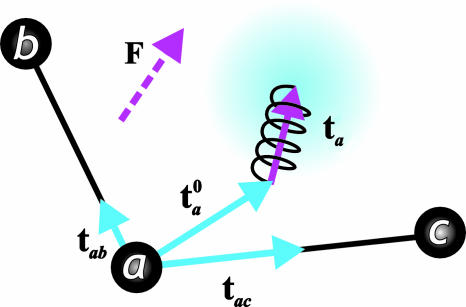
Because QMPFF1 has already been described (15), here we present QMPFF2 by reference to QMPFF1. In both versions of QMPFF, a molecule is represented as a set of interacting atoms, with each atom consisting of a positive point charge (the core) and a diffuse negatively charged electron density (the cloud). This electron density is represented by an isotropic, exponential distribution, which is centered on the core for an isolated atom, but which shifts in an external field, e.g., in the presence of other atoms (see Fig. 5). It is this movement of the electron clouds that provides a natural way to simulate electronic molecular polarizability.

Fig. 5.

The QMPFF2 model of a representative molecule. Atomic cores are shown for three atoms labeled as a, b, and c; the electron cloud is shown only for atom a (proportions are distorted). The cloud is attached by a nonharmonic spring to a reference point shifted with respect to the atomic core by vector t_a⁰, which is the sum of the partial shifts t_ab and t_ac. Each partial shift vector is directed along a bond to atom a, with a length that depends on the types of the bonded atoms. In the presence of an external field (the force vector, F), the cloud shifts by t_a relative to its reference position so as to minimize the total energy of the molecular system (generally t_a is not parallel with F because of anisotropic polarizability).

In both versions of QMPFF, nonbonded interactions between atoms consist of four components: electrostatic, exchange, induction, and dispersion. The functional form of the components imitates that of their QM counterparts. Specifically, electrostatics represent the classical Coulomb interaction of point charges and exponential charge densities. Exchange repulsion is a result of cloud–cloud interactions that decay almost exponentially with distance; the precise form was modified from QMPFF1 to QMPFF2, cf. ref. 15 and Eqs. 6 and 7 in Supporting Text, which is published as supporting information on the PNAS web site. Induction is simulated by a “spring” attaching each mobile electron cloud to a reference position (Fig. 5). The restraint potential provided by the spring is close to harmonic at small distances, but the stiffness becomes infinite as the distance approaches a limiting value, thus preventing the “polarization catastrophe” (15). For QMPFF1 the induction term is isotropic, whereas for QMPFF2 it is anisotropic (see Eq. 10 in Supporting Text) to provide a better description of the molecular polarizability tensor. Dispersion is represented by a term decaying as r⁻⁶ at large distances in QMPFF1, but as a sum of terms decaying as r⁻⁶ and r⁻⁸ in QMPFF2 for greater accuracy, cf. ref. 15 and Eqs. 8 and 9 in Supporting Text.

In QMPFF1, only nonbonded interactions were taken into account, i.e., molecules were assumed rigid. In QMPFF2, the bonded interactions are conventionally subdivided into stretching, bending, and torsion terms. The first two terms use a quadratic function, whereas the torsion term uses a threefold cosine function. Also, more atom types are used in QMPFF2 to allow better resolution of related, but electronically distinct, atom types, and to cover other biologically important elements not treated by QMPFF1, cf. ref. 15 and Tables 4 and 5, which are published as supporting information on the PNAS web site. To accommodate the more refined functional forms of the QMPFF2 nonbonded interactions, each atom type requires eight parameters, and each general bond type requires five parameters (two parameters for symmetric bonds). For the bonded interactions, each bond length, bond angle, and torsion angle function uses two, two, and three parameters, respectively, which is comparable with most advanced empirical force fields (2–5). The atom and bond types in a water molecule use a total of 18 nonbonded and 4 bond parameters.

QMPFF parameterization of nonbonded interactions is based on two fundamental principles. (i) The parameters of the model are fitted only to data from high-level ab initio QM calculations without use of any experimental data [for QMPFF1, the ab initio data were calculated at the MP2/aTZ(-hp) level, whereas for QMPFF2 more accurate QM techniques are used, see Supporting Text]. (ii) Each component of the interaction energy (electrostatic, exchange, induction, and dispersion) is separately fitted to the corresponding component in a decomposition of the QM-derived interaction energies of representative conformations of simple dimers. Such separate fitting prevents errors in various components from compensating for each other and is a crucial requirement for reliable transferability of the force field. In addition, we fit the QM components of dipole vectors and quadrupole and polarizability tensors of single molecules. Notably, no systems with more than two molecules are used in the parameterization. Parameters of bonded interactions, including those in water, are fitted to ab initio calculations at the MP2/TZ(-hp) level of the variation of bond lengths, bond angles, and torsion angles about their equilibrium values.

MD Protocol.

The QMPFF2 model was incorporated into our in-house MD package, which allows both classical and quantum (path integral) simulations. We performed simulations with an isothermal–isobaric NPT ensemble consisting of 256 flexible water molecules in a cubic box under periodic boundary conditions. Equations of motion were generally integrated for 2 ns with a 1-fs time step by using the velocity Verlet scheme (29) combined with the Nose–Hoover chain thermostat (30) and Berendsen barostat (31). The electron cloud positions were optimized at every time step.

In our PIMD package the staging transform (32) of coordinates is used as well as application of independent thermal bath to every degree of freedom. To evaluate energy and pressure the virial estimators are used. The path integral discretization index P for quantum MD was generally chosen to be equal to 4. Certainly simulations with P = 4 do not provide the convergence with respect to internal molecular motions (e.g., bond stretching). However, this level is adequate to describe quantum effects in intermolecular motions, as has been verified by a few calculations that were performed with simulation time up to 5 ns and a P value of up to 20; for further details see Supporting Text.

Abbreviations

QM

quantum mechanical

QMPFF

QM polarizable force field

MD

molecular dynamics

PIMD

path integral MD.