Abstract
Multivalent interactions play a critical role in a variety of biological processes on both molecular and cellular levels. We have used molecular force spectroscopy to investigate the strength of multiple parallel peptide-antibody bonds using a system that allowed us to determine the rupture forces and the number of ruptured bonds independently. In our experiments the interacting molecules were attached to the surfaces of the probe and sample of the atomic force microscope with flexible polymer tethers, and the unique mechanical signatures of the tethers determined the number of ruptured bonds. We show that the rupture forces increase with the number of interacting molecules and that the measured forces obey the predictions of a Markovian model for the strength of multiple parallel bonds. We also discuss the implications of our results to the interpretation of force spectroscopy measurements in multiple bond systems.
INTRODUCTION
Organisms perform many biological functions using multivalent interactions where multiple weak individual bonds between receptor-ligand pairs combine to produce a much stronger interaction. Multivalent bonds feature prominently in a variety of biological processes, such as activation of T cells (1) and intercellular adhesion (2). Biomedical researchers also use multivalent binding to increase the binding time of pharmaceuticals to their targets (3,4). In one particular example, researchers link multiple antibody fragments to produce therapeutic agents with strong recognition and affinity to specific markers on cancer cell surfaces (5). These recognition constructs can then deliver therapeutics or imaging agents to the tumors.
Although it is clear that multivalent interactions increase the overall bond strength, quantifying this increase is surprisingly difficult. Experimentalists typically use a variety of ensemble techniques such as fluorescence (6), radiolabeling (7), and surface plasmon resonance (8) to determine the overall strength of the multivalent interactions. However, the primary problem for these measurements is determining the actual valency of the binding. The creation of a multivalent construct does not guarantee that all ligands are bound to a receptor during the observation time interval. Rather, the number of interacting ligands will typically vary from molecule to molecule, especially for higher valency constructs. Bulk ensemble measurements will almost always include contributions from interactions of different valency and thus reflect only the average bound number of ligands per construct. Force spectroscopy (9,10), which uses mechanical force to rupture the bond, provides a direct method for measuring binding strength with a resolution at the single molecule level. In a typical force spectroscopy experiment, the bond strength is defined by the force that produces the most frequent bond failure in repeated tests of bond breakage on a given timescale (11). Methods capable of resolving single molecule binding, such as antibody-antigen pairs, have an advantage over techniques that measure ensembles of molecules because they avoid spatial and temporal averaging that can obscure the details of the interaction (10,12–14). Despite the conceptual simplicity of these experiments, there have been very few measurements of the strength of multiple bonds (15,16), especially in the parallel binding arrangement where the force is distributed among several binding units. The main difficulty in interpreting multiple bond measurements remains is the absence of a reliable way to determine the number of interacting molecules independent of the binding force values. Of three main force spectroscopy techniques—atomic force microscopy (AFM), surface forces apparatus (SFA), and optical tweezers—only SFA provides independent contact area assessment; yet the contact area in the SFA measurements tends to be large and thus makes it difficult to probe a limited number of bonds. Determination of the number of the interacting bonds solely by measuring rupture force with AFM or optical tweezers is equally problematic since stochastic rupture (17) and variation in the bond load rate (11) typically produce overlapping binding force distributions.
We have recently demonstrated that we can discriminate between single and multiple binding events in AFM measurements by attaching the interacting molecules to the ends of flexible polyethyleneglycol tethers. We have used this system to determine the kinetic parameters for single and multiple bonds. In this work we focus on how the measured binding strength varies as a function of the peptide-antibody bond number. We demonstrate that elastic properties of the PEG tethers provide an independent and accurate measure of the number of bonds. With this system we demonstrate that the measured dynamic bond strength follows the predictions of a Markovian dissociation model of multiple bonds. Finally, we discuss the specific applicability of this model to the binding strength measurements using AFM.
MATERIALS AND METHODS
A detailed description of the preparation of MUC1 peptide and anti-MUC1 single chain Fv fragment (scFv) was presented in a previous publication (18).
Functionalization of the AFM tips and substrates
Silicon nitride cantilevers (Veeco, Santa Barbara, CA) were coated on the tip side with a thin layer of gold (750 Å with a 50-Å chromium adhesion underlayer), cleaned with a piranha etch, rinsed, and then incubated in 1-mM cystamine solution to form an amine-terminated self-assembled monolayer (SAM).
Bifunctional PEG linkers (3400 Da, Nektar Therapeutics, Huntsville, AL) linked the scFv to the probe tip. N-hydroxysuccinimyl (NHS) on one end of the PEG linked to the amine derivatized tip surface. Maleimide (Mal) groups linked to terminal cysteine residues on the scFvs. The MUC1 peptide was linked to a flat gold surface similarly but through the terminal amine group in the peptide. We controlled the density of functional molecules by varying the molar ratio of scFv/MUC1 functionalized PEG to short (2000 Da), passivating methoxy (OMe) terminated PEG molecules. The dilution ratio is critical for controlling the final density of the functional tethered molecules on the AFM tip, and we typically used a 1:50 dilution ratio, which resulted in ∼10% probability of detecting a tethered molecule interaction. To increase the frequency of multivalent interactions, some measurements were made at a dilution ratio of 1:30.
Force spectroscopy
Force measurements were made using a Nanoscope IIIa AFM (DI-Veeco) in force calibration mode. Measurements were performed at 0.5–3-Hz frequencies with an actuator retraction of 50–400 nm. All measurements were carried out in 20 mM phosphate-buffered saline and 100 mM NaCl.
Data analysis
Rupture traces were analyzed using Igor Pro 5.0 (WaveMetrics, Lake Oswego, OR) and a custom-written set of procedures. We collected the cantilever deflection data at a 14-kHz acquisition rate, which helped to visualize multiple rupture events occurring in close succession. If necessary, the force versus distance traces were corrected for laser optical interference. Traces were low-pass filtered before and after the rupture event to reduce noise and improve the curve-fitting routine accuracy. We fit the region of PEG stretching to an extensible freely jointed chain (EFJC) model (see Eq. 5 in the Results and Discussion section) by solving the force-extension relationship numerically. The model contained two fitting parameters: the number of tethers, Nt, and the number of PEG monomers in a tether, nm (i.e., tether contour length). The values of all other parameters were taken from Oesterhelt et al. (19): the Kuhn length, Lk of 7 Å, the monomer stiffness, Ks of 150 N/m per monomer, the monomer lengths in planar and helical configurations, Lplanar and Lhelical of 3.58 and 2.8 Å respectively, and the difference between the planar and helical conformation free energies in absence of applied load, ΔG of 3kBT.
Stepwise rupture events were fit by a two-step process. First, we determined the length of the first (longer) tether by fitting the tether extension preceding the final rupture. Second, we used this value to remove the contribution from the first tether to the multiple tether extension region preceding the first rupture. Finally, we fit the remaining force versus extension curve to determine the length of the second (shorter) tether. The slope of the individual force versus extension curves at rupture determined the instantaneous loading rate. For the first rupture, we assumed that the loading rate was distributed in proportion to the individual tether forces at the point of rupture. The loading rate for the second rupture was determined directly from the stretching trace.
For kinetic analysis of the rupture events we have plotted the rupture force, F, as a function of instantaneous loading rate, r. Evans and Ritchie showed that the rupture force increases linearly as a function of the logarithm of the loading rate (20):
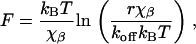 |
(1) |
where the χβ is the distance to the transition state, r is the loading rate, and koff is the bond dissociation constant in absence of applied force. We determined the value of χβ and koff by fitting our data to Eq. 1.
RESULTS AND DISCUSSION
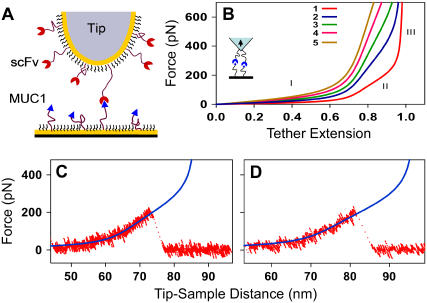
We have recently demonstrated that we can detect specific interactions between single and multiple pairs of a MUC1 peptide and an scFv-recognizing MUC1 (18,21). MUC1 is a cell-surface marker for prostate, breast, and lung cancer, and clinical researchers use antibodies against MUC1 to deliver therapeutic agents to the tumor cells (4). To measure the interactions of the antibody with its target, we have attached MUC1 and the antibody to the surfaces of the sample and tip of the AFM using long flexible PEG linkers (Fig. 1 A). These linkers provide several critical advantages to the detection of the specific forces. First, they separate the specific interaction that occurs at the tip-sample separation equal to the combined tether length for MUC1 and the antibody from the nonspecific interactions that occur at smaller tip-sample separations. A second advantage, which we want to emphasize in this work, is that the rupture event in this system is always preceded by the tether stretching (Fig. 1, C and D). Significantly, this stretching region provides a mechanical signature that we can use to obtain an independent estimate of the number of the interacting molecules (Fig. 1 B). Rief et al. have also used a similar concept to distinguish the unfolding of green fluorescent protein domains to identify intermediate states (22).
FIGURE 1.
(A) Schematics of the experimental setup showing MUC1 peptide and scFv antibody fragment attached to the surfaces of the probe and sample of the atomic force microscope with flexible tethers. (B) Calculated force versus extension (relative to tether contour length) traces for different numbers (as indicated in the legend) of identical PEG tethers connected in parallel. (C,D) Representative force versus extension traces recorded in the experiment showing stretching of the PEG tethers before the rupture of the MUC1-scFv bond. The solid blue lines indicate fits to the EFJC model (Eq. 1).
Oesterhelt and co-workers (19) analyzed the configuration of PEG polymers in solution and showed that in apolar solvents the length of a PEG polymer, L, under stretching force, F, follows closely the prediction of an extended Langevin function. However, stretching of PEG chains in water leads to a structural transition in the polymer. Molecular dynamics simulations and the experimental measurements suggest that this transition represents breakage of supramolecular helical formations stabilized by water bridges (19). Applied forces larger than 100 pN break these water bridges, lengthening the polymer. The model accounts for this transition by allowing each PEG segment to exist in two states, a compact (helical) state and extended (planar) state. The equilibrium population of these two states is thermally distributed and tilted toward the compact state at zero force and toward the extended state at high force. The force-extension relationship for a single PEG tether containing nm monomers is described by (19)
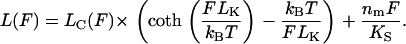 |
(2) |
Here, Lk is the Kuhn length, Ks is the chain stiffness, and Lc(F) is a force-dependent contour length, which is simply a sum of the lengths of the compact and extended monomers in the chain at a given force F. Lc(F) is described by
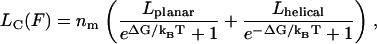 |
(3) |
where Lplanar and Lhelical are the monomer length in planar and helical configuration, and ΔG is the energy difference between the planar and the helical conformation state. Under applied load this energy difference becomes
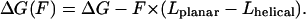 |
(4) |
If we consider Nt identical parallel PEG tethers (each containing nm monomers), then the force as a function of extension will simply be a linear combination of each individual tether force. Therefore, the force-extension relationship for Nt PEG tethers will be identical to Eq. 2 but with F replaced by F/Nt:
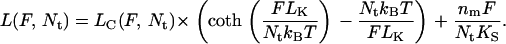 |
(5) |
As we extend the single tether model to the case of multiple tethers connecting the tip and sample, we can neglect the variation in the position and length of the individual PEG tethers on the AFM tip. This is a valid assumption because our tethers are much longer than any offset introduced by such position variations. In this case the distribution of the loading force among the multiple tethers will be defined by the stiffness of the individual PEG tethers at a given common extension, and the total force acting on the AFM cantilever will be equal to the sum of the forces from individual tethers.
The model shows that PEG linker stiffness follows three distinct regions (Fig. 1 B). In the “soft” regime below 100 pN, only the entropic forces contribute to the molecule stiffness (region I). The stiffness at moderate forces between 100 and 300 pN represents breaking of water bridge-mediated helical structures and results in a relatively constant stiffness value (region II). High stiffness region III represents enthalpic stretching of the covalent bonds within each monomer. Fig. 1, C and D, shows that the measured single PEG tether extension traces fit this model very well, even if the model uses only a single parameter—the number of PEG monomers.
Stepwise rupture of MUC1-antibody bonds
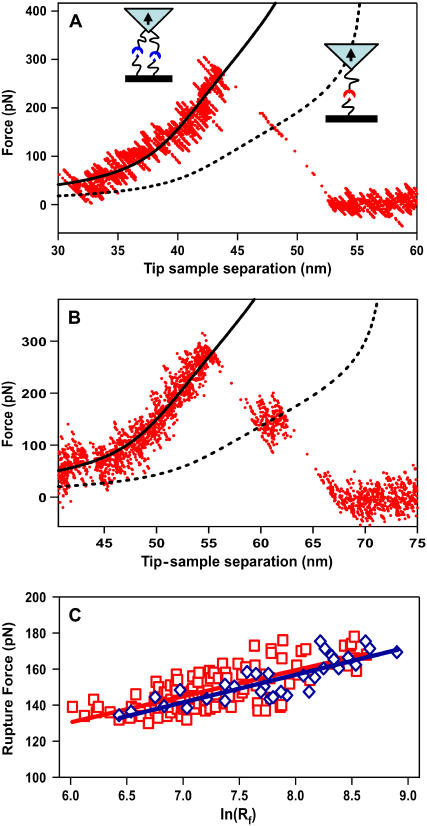
The majority of the rupture traces for the specific MUC1-scFv interactions fit the signature of a single trace (as shown in Fig. 1, C and D), and the subsequent analysis showed that these ruptures corresponded to the rupture of a single MUC1-Ab bond (18). However, a fraction of the specific rupture traces corresponded to the rupture of two MUC1-scFv units connected to the AFM tip and sample through the tethers of slightly unequal length. In this situation the force versus extension traces showed the characteristic stepwise rupture profile (Fig. 2, A and B) where the AFM tip was initially stretching both tethers until one of the bonds broke. Then the remaining slack in the second, longer tether allowed the applied force to drop. The instrument trace showed a brief region corresponding to the loading of the remaining tether followed by rupture of the remaining bond. In the case of the unequal length tethers, we can no longer apply Eq. 5. In this case, we used a two-step procedure that first determined the length of the longer tether and then used this value to remove the contribution of the longer tether to the two-tether stretching region. Finally, a second fitting step determined the length of the shorter tether (for a detailed description of the procedure, see the Materials and Methods section).
FIGURE 2.
(A) A rupture trace showing stepwise rupture of two MUC1-scFv bonds. The dashed line corresponds to the fit of the brief one-tether stretching region to the EFJC model, and the solid line represents the fit of the two-tether stretching region to a linear combination of two tethers of unequal length. The fit to the one-bond loading region determined the length of one of the tethers (54.3 nm), which was then used in the fit of the two-bond stretching region to determine the length of the remaining tether (49.9 nm). (B) A similar trace showing another stepwise rupture of two MUC1-scFv bonds with the tether length of 61.6 nm and 70.3 nm. (C) Plot of the rupture force for the MUC1-scFv interactions as a function of the logarithm of the instantaneous loading rate (Rf) for stepwise rupture events (blue diamonds,◊) and individual rupture events (red squares, □). Solid red and blue lines indicate the best fits of the data to the linear functions.
This procedure also allowed us to determine instantaneous loading rates corresponding to the rupture of both bonds. The plot of the rupture forces for both rupture events as a function of loading rate (the dynamic force spectrum) that we obtained for these stepwise rupture events shows the characteristic linear dependence of the force on the logarithm of the loading rate. Significantly, the dynamic force spectrum for the stepwise rupture of MUC1-scFv bonds matches the dynamic force spectra for the individual bond ruptures (Fig. 2 C). The kinetic parameters obtained from both dynamic force spectra are identical to within the fit margin of error (Table 1). This comparison indicates that the EFJC model fit provides a robust instrument for analyzing complex rupture events in our system.
TABLE 1.
The distances to the transitions state, xβ, kinetic off-rates koff, and the average bond lifetime τoff = 1/koff values determined from the fits of the data in Fig. 2 to Eq. 1
| Parameter | Stepwise bond rupture | Single bond rupture |
|---|---|---|
| χβ (Å ) | 2.7 ± .3 | 2.8 ± .2 |
| koff (s−1) | 6.9 × 10−3 ± 7.0 × 10−3 | 3.3 × 10−3 ± 2.8 × 10−3 |
| toff (s) | 145 | 303 |
Rupture of multiple MUC1-scFv bonds
If the connecting tethers have equal length, the stepwise rupture becomes impossible to observe. In this case, there is no slack in the remaining tethers to absorb the loading, and the force simply redistributes among the remaining bonds. We can use kinetic parameters for the single bond (Table 1) to estimate that abrupt increase in the applied load will drop the bond lifetime to nanosecond levels. Therefore it is reasonable to expect that the remaining bonds would rupture very shortly after the rupture of the first bond, and the finite bandwidth of the force microscope would cause these successive bond failures to register as a single rupture event. Fortunately, we can use the mechanical signature of tethers to discriminate multiple bond ruptures.
Stretching of multiple identical PEG tethers
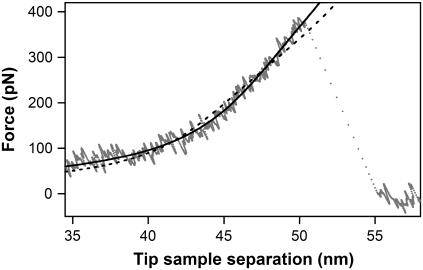
It is straightforward to generate an expression describing stretching of multiple PEG tethers of identical length. Since the load force is shared equally among all tethers, the total force will simply be a multiple for the force generated by an individual tether. A comparison of the stretching profiles for multiple identical PEG tethers (Fig. 1 B) shows that an increase in the number of tethers produces a stiffness increase in the intermediate regime II. This difference in the force-extension profiles accounts for a unique signature that identifies the number of tethers that produce a particular rupture trace. Fig. 3 shows an example of such a determination. Even if we allow the tether contour length change to obtain the best possible fit, the stretching profile for three tethers still produces a quantifiably better fit to the experimental data than the stretching profile for the two tethers in the critical conformational transition regime (region II in Fig. 1 B).
FIGURE 3.
Use of the mechanical signatures of the PEG tethers for discriminating the number of bonds ruptured in a particular measurement. A comparison of a multibond rupture trace (gray dots) with the calculated force versus extension profiles for three (solid line) and two (dashed line) tethers. The calculated profile for the three-tether case provides a noticeably better fit with a 40% reduction in the χ2 value.
Rupture of multiple MUC1-scFv bonds
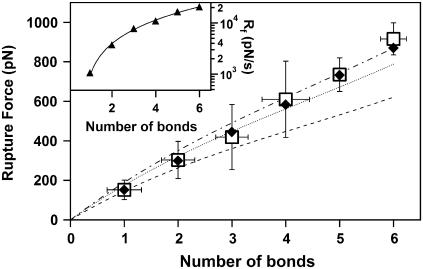
We have used this procedure to determine the number of bonds corresponding to each of the large number of the specific rupture events that we measured in our experiments. These data (Fig. 4) showed that an increase in the number of bonds lead to the increase in the measured rupture force. It is interesting to note that the measured force appears to increase nearly linearly with the number of bonds. Williams (23) and subsequently Williams and Evans (24) have analyzed rupture of multiple identical bonds and showed that the measured rupture force, f*, will scale with the number of bonds, NB, and the measured loading rate, rf, as
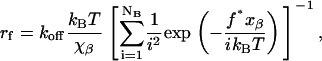 |
(6) |
where xβ is the characteristic bond width, koff is the thermodynamic off rate for a single bond, and kBT is the thermal energy scale. The rupture forces that we calculated using Eq. 6 and the kinetic parameters that we obtained from the dynamic force spectrum in Fig. 2 C show reasonable agreement with the experimental data for the full range of loading rates used in our experiments (Fig. 4). However, all calculated curves show a more pronounced curvature than the experimental data for both high and low loading rates.
FIGURE 4.
Plot of the measured rupture forces (open squares, □) as a function of the number of MUC1-scFv bonds between the AFM tip and sample. Solid diamond symbols (♦) correspond to the rupture forces calculated using the Markovian model for the strength of multiple bonds using the average loading rate determined for each particular number of bonds. Lines correspond to the predictions of the same model using a single value of the average measured loading rate for one (dashed), three (dotted), and six (dash-dotted) bonds over the whole range of bond numbers. The inset shows the average measured instantaneous loading rates (solid triangles, ▴) for the full range of bond numbers used in our experiments. The solid line is provided as a guide to the eye.
This deviation disappears, however, when we take into account the details of the bond loading in the AFM experiment. Nonlinear stiffness of PEG tethers and fluctuations in the binding force cause every rupture event to occur at a different instantaneous loading rate. The increase in the number of bonds produces stronger connections that need to be loaded by higher forces, which then produce increased loading rates even if the AFM transducer retracts at a constant velocity. The net result is that the rupture events recorded in our experiments show a bias toward higher loading rates at a higher bond number (Fig. 4, inset). Indeed if we use the average loading rates for each number of bonds to calculate the expected rupture force, the calculated forces match the experimental data over the entire range of the number of bonds observed in our experiments (Fig. 4).
Interestingly, the apparent-linear dependence of the measured rupture forces on the number of bonds seen in Fig. 4 can hint at the reasons some AFM-based force measurements at first seem to match the predictions of the Poisson statistics model (25). This method is based on the assumption that the rupture force for multiple parallel bonds scales linearly with the number of bonds; this assumption has since been proved to be incorrect (23). We note that in our experiments the “linear” scaling reflects the bias in loading rates specific to the AFM measurement with tethered ligands and not the fundamental scaling relationship for the strength of multiple bonds. Therefore, we stress that the Poisson statistical analysis will not produce a meaningful value for the single bond strength even in this case. Researchers need to use a full Markovian model for the strength of multiple bonds (23) to analyze force spectroscopy measurements.
CONCLUSIONS
We have demonstrated that it is possible to design force spectroscopy measurements that will determine the bond rupture strength and the number of interacting molecules independently. Our results show that connecting the interacting molecules to the surfaces of the AFM tip and sample provides a means to determine the number of the interacting molecules using a unique mechanical signature of a flexible polymer tether. This system allowed us to measure the rupture strength for several peptide-antibody bonds connected in parallel for various numbers of bonds. We found that the measured rupture forces obey the predictions of a Markovian model for the strength of parallel bonds if we account for differences in loading rates used in our experiment. Interestingly, this loading rate bias tends to produce an almost linear dependence of the rupture force on the bond number, which may create a false indication of a “quantized” adhesion. We stress that the rupture force measurements alone do not provide sufficient information about the multivalent interactions, and researchers always need to explore the full parameter space that includes the loading rate and the number of bonds. Our measurements specifically underscore the need for an independent means of determining the bond number in the multivalent interactions measurements.
These measurements open up several avenues for fundamental and applied research. Biophysicists could use our measurement system to investigate how different configurations of multivalent ligands influence the binding strength and kinetic parameters of the interactions. This research could then directly translate into the next generation of multivalent drugs and labels that show tighter binding and improved specificity.
Acknowledgments
The authors thank Dr. Huguette Albrecht and Prof. Sally J. DeNardo (UC Davis Medical Center) for providing the peptides and antibodies used for this study, and Dr. Kevin Langry for help with AFM probe functionalization.
This work was performed under the auspices of the U.S. Department of Energy by the University of California, Lawrence Livermore National Laboratory under Contract W-7405-Eng-48 and was supported in part by an LLNL Laboratory Directed Research and Development grant and NCI CA47829 grants. R.W.F. is supported by a LLNL Student Employee Graduate Research Fellowship program.
Todd Sulchek and Raymond W. Friddle contributed equally to this work.
References
- 1.Casares, S., C. S. Zong, D. L. Radu, A. Miller, C. A. Bona, and T.-D. Brumeanu. 1999. Antigen-specific signaling by a soluble, dimeric peptide/major histocompatibility complex class II/Fc chimera leading to T helper cell type 2 differentiation. J. Exp. Med. 190:543–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yipp, B. G., S. Anand, T. Schollaardt, K. D. Patel, S. Looareesuwan, and M. Ho. 2000. Synergism of multiple adhesion molecules in mediating cytoadherence of plasmodium falciparum-infected erythrocytes to microvascular endothelial cells under flow. Blood. 96:2292–2298. [PubMed] [Google Scholar]
- 3.Holliger, P., T. Prospero, and G. Winter. 1993. Diabodies: small bivalent and bispecific antibody fragments. Proc. Natl. Acad. Sci. USA. 90:6444–6448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Richman, C. M., and S. J. DeNardo. 2001. Systemic radiotherapy in metastatic breast cancer using 90Y-linked monoclonal MUC-1 antibodies. Crit. Rev. Oncol. Hematol. 38:25–35. [DOI] [PubMed] [Google Scholar]
- 5.Kortt, A. A., M. Lah, G. W. Oddie, C. L. Gruen, J. E. Burns, L. A. Pearce, J. L. Atwell, A. J. McCoy, G. J. Howlett, D. W. Metzger, R. G. Webster, and P. J. Hudson. 1997. Single-chain Fv fragments of anti-neuraminidase antibody NC10 containing five- and ten-residue linkers form dimers and with zero-residue linker a trimer. Protein Eng. 10:423–433. [DOI] [PubMed] [Google Scholar]
- 6.Underwood, P. A. 1993. Problems and pitfalls with measurement of antibody affinity using solid phase binding in the ELISA. J. Immunol. Methods. 164:119–130. [DOI] [PubMed] [Google Scholar]
- 7.Ong, G. L., and M. J. Mattes. 1993. Re-evaluation of the concept of functional affinity as applied to bivalent antibody binding to cell surface antigens. Mol. Immunol. 30:1455–1462. [DOI] [PubMed] [Google Scholar]
- 8.MacKenzie, C. R., T. Hirama, S.-j. Deng, D. R. Bundle, S. A. Narang, and N. M. Young. 1996. Analysis by surface plasmon resonance of the influence of valence on the ligand binding affinity and kinetics of an anti-carbohydrate antibody. J. Biol. Chem. 271:1527–1533. [DOI] [PubMed] [Google Scholar]
- 9.Rief, M., M. Gautel, F. Oesterhelt, J. M. Fernandez, and H. E. Gaub. 1997. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 276:1109–1112. [DOI] [PubMed] [Google Scholar]
- 10.Merkel, R., P. Nassoy, A. Leung, K. Ritchie, and E. Evans. 1999. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 397:50–52. [DOI] [PubMed] [Google Scholar]
- 11.Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alon, R., D. A. Hammer, and T. A. Springer. 1995. Lifetime of the P-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 374:539–542. [DOI] [PubMed] [Google Scholar]
- 13.Thoumine, O., P. Kocian, A. Kottelat, and J.-J. Meister. 2000. Short-term binding of fibroblasts to fibronectin: optical tweezers experiments and probabilistic analysis. Eur. Biophys. J. 29:398–408. [DOI] [PubMed] [Google Scholar]
- 14.Florin, E. L., V. T. Moy, and H. E. Gaub. 1994. Adhesion forces between individual ligand-receptor pairs. Science. 264:415–417. [DOI] [PubMed] [Google Scholar]
- 15.Patel, A. B., S. Allen, M. C. Davies, C. J. Roberts, S. J. B. Tendler, and P. M. Williams. 2004. Influence of architecture on the kinetic stability of molecular assemblies. J. Am. Chem. Soc. 126:1318–1319. [DOI] [PubMed] [Google Scholar]
- 16.Strunz, T., K. Oroszlan, R. Schäfer, and H.-J. Güntherodt. 1999. Dynamic force spectroscopy of single DNA molecules. Proc. Natl. Acad. Sci. USA. 96:11277–11282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- 18.Sulchek, T. A., R. W. Friddle, K. Langry, E. Y. Lau, H. Albrecht, T. V. Ratto, S. J. DeNardo, M. E. Colvin, and A. Noy. 2005. Dynamic force spectroscopy of parallel individual Mucin1-antibody bonds. Proc. Natl. Acad. Sci. USA. 102:16638–16643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Oesterhelt, F., M. Rief, and H. E. Gaub. 1999. Single molecule force spectroscopy by AFM indicates helical structure of poly(ethylene-glycol) in water. N. J. Phys. 1:1–11. [Google Scholar]
- 20.Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Albrecht, H., P. A. Burke, A. Natarajan, C.-Y. Xiong, M. Kalicinsky, G. L. DeNardo, and S. J. DeNardo. 2004. Production of soluble ScFvs with C-terminal-free thiol for site-specific conjugation or stable dimeric ScFvs on demand. Bioconjug. Chem. 15:16–26. [DOI] [PubMed] [Google Scholar]
- 22.Dietz, H., and M. Rief. 2004. Exploring the energy landscape of GFP by single-molecule mechanical experiments. Proc. Natl. Acad. Sci. USA. 101:16192–16197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Williams, P. M. 2003. Analytical descriptions of dynamic force spectroscopy: behaviour of multiple connections. Anal. Chim. Acta. 479:107–115. [Google Scholar]
- 24.Evans, E., and P. Williams. 2002. Dynamic force spectroscopy: II. Multiple bonds. In Physics of Bio-Molecules and Cells. H. Flyvbjerg, F. Jülicher, P. Ormos, and F. David, editors. Springer and EDP Sciences, Heidelberg. pp. 187–203.
- 25.Williams, J. M., T. J. Han, and T. P. Beebe. 1996. Determination of single-bond forces from contact force variances in atomic force microscopy. Langmuir. 12:1291–1295. [Google Scholar]