How reliable are empirical genomic scans for selective sweeps?

Abstract

The beneficial substitution of an allele shapes patterns of genetic variation at linked sites. Thus, in principle, adaptations can be mapped by looking for the signature of directional selection in polymorphism data. In practice, such efforts are hampered by the need for an accurate characterization of the demographic history of the species and of the effects of positive selection. In an attempt to circumvent these difficulties, researchers are increasingly taking a purely empirical approach, in which a large number of genomic regions are ordered by summaries of the polymorphism data, and loci with extreme values are considered to be likely targets of positive selection. We evaluated the reliability of the “empirical” approach, focusing on applications to human data and to maize. To do so, we considered a coalescent model of directional selection in a sensible demographic setting, allowing for selection on standing variation as well as on a new mutation. Our simulations suggest that while empirical approaches will identify several interesting candidates, they will also miss many—in some cases, most—loci of interest. The extent of the trade-off depends on the mode of positive selection and the demographic history of the population. Specifically, the false-discovery rate is higher when directional selection involves a recessive rather than a co-dominant allele, when it acts on a previously neutral rather than a new allele, and when the population has experienced a population bottleneck rather than maintained a constant size. One implication of these results is that, insofar as attributes of the beneficial mutation (e.g., the dominance coefficient) affect the power to detect targets of selection, genomic scans will yield an unrepresentative subset of loci that contribute to adaptations.

A central focus of evolutionary biology is to map the genetic basis of adaptations, thereby increasing our understanding of selective processes (e.g., Abzhanov et al. 2004; Aminetzach et al. 2005; Colosimo et al. 2005) and helping to identify functionally important regions of the genome (e.g., Bustamante et al. 2005; Voight et al. 2006). The classical approach would be to start with phenotypic variation and map it onto genotypes. However, when the phenotype is fixed in a species, there may not be substantial variation among extant individuals (Yamasaki et al. 2005); even if there were, the genetic loci that underlie existing variation may not be those on which natural selection acted in the past. Evolutionary geneticists have therefore suggested taking the opposite approach: Start with patterns of variation along the genome, identify loci that appear to have been the targets of positive selection, then examine what phenotype they might influence (e.g., Clark et al. 2003).

This approach is feasible because adaptation shapes patterns of genetic variation within and between loci (e.g., Maynard-Smith and Haigh 1974; Sawyer and Hartl 1992). In particular, polymorphism data from extant individuals carry information about adaptations that have occurred in recent evolutionary history. Indeed, under simplifying assumptions, the advantageous substitution of an allele at one site is expected to distort patterns of polymorphism at linked neutral sites for approximately N_e generations, where N_e is the diploid effective population size of the species (Przeworski 2002). As an illustration, in humans, the signature of a single beneficial substitution with a selection coefficient of 1% could extend up to a megabase (Kaplan et al. 1989). Thus, assuming that the effects of natural selection are well characterized, it should be possible to search for their footprint in genomic data.

With the increasing availability of polymorphism data, the approach has been applied to a wide range of species (e.g., Huttley et al. 1999; Harr et al. 2002; Glinka et al. 2003; Kayser et al. 2003; Schlötterer 2003; Hammer et al. 2004; Schofl and Schlötterer 2004; Storz et al. 2004; DuMont and Aquadro 2005; Stajich and Hahn 2005; Wright et al. 2005). In domesticated plants, where selection has been strong and recent, these scans offer a relatively efficient way to screen for genetic loci that were selected by early farmers or in subsequent crop improvement (Yamasaki et al. 2005). The approach also holds great promise in humans, both because alternative methods are often impractical, and because anatomically modern humans are thought to have emerged only in the past 150–200 thousand years. Since this time frame represents less than N_e generations, the adaptations that accompanied the emergence of our species may still be detectable in extant polymorphism data. Moreover, humans, as well as Drosophila melanogaster and Drosophila simulans, are thought to have an African origin and to have only recently become cosmopolitan (Aquadro et al. 2001). Several adaptations are likely to have occurred in response to the new environments, many of which should be detectable in polymorphism data from non-sub-Saharan African populations. Interestingly, some of the adaptations to novel habitats appear to be linked to differential susceptibility to disease in humans (e.g., Thompson et al. 2004; Young et al. 2005), suggesting that these efforts may also be of more practical relevance.

The general approach to selection scans has been to consider polymorphism data from a large number of loci and identify outliers, either by use of a statistical model or by a more informal comparison. Success therefore depends on the ability to recognize the signature of selection and to distinguish it reliably from purely neutral effects (e.g., those of geographic structure). To date, however, most scans focus on finding a signature of selection characterized for a model of constant population size and random mating (Maynard-Smith and Haigh 1974). The effects of positive selection on nucleotide variability have been characterized for a limited set of models (e.g., Maynard-Smith and Haigh 1974; Braverman et al. 1995), but appear to be fairly sensitive to model assumptions (Slatkin and Wiehe 1998; Teshima and Przeworski 2006). In particular, the signature of selection on standing variation can differ markedly from that expected when selection acts on a new mutation (Orr and Betancourt 2001; Innan and Kim 2004; Przeworski et al. 2005), and we know little about which mode of adaptation is more frequent (Dykhuizen and Hartl 1980; Orr and Betancourt 2001; Hermisson and Pennings 2005). Thus, many genetic changes contributing to adaptations may be missed because their footprint in polymorphism data is not recognized.

A second difficulty is that departures from the demographic assumptions can mimic the effects of natural selection (Robertson 1975; Tajima 1989a; Fu 1996; Andolfatto and Przeworski 2000; Nielsen 2001; Przeworski 2002; Wall et al. 2002; Haddrill et al. 2005; Jensen et al. 2005). In particular, the effects of recent directional selection at a site may be hard to distinguish from those of a population bottleneck (Barton 1998; Wall et al. 2002). This possibility is particularly troubling given that many species or populations of interest, including non-sub-Saharan African humans, as well as domesticated plants and D. melanogaster, are thought to have experienced a recent population size reduction (e.g., Haddrill et al. 2005; Ramachandran et al. 2005; Voight et al. 2005; Wright et al. 2005).

Although the difficulty in distinguishing selective from demographic effects was originally pointed out for studies of candidate loci, it is especially acute for genome scans, for which there is no or little prior information about the loci considered. The past couple of years have therefore seen a concerted effort to address the problem. The specific implementations take many forms, but they can be loosely classified into two categories. In the first approach, summaries of the polymorphism data are used to estimate the parameters of a sensible demographic model. The fit of the model is then tested against specific loci, and a poor fit is interpreted as evidence for natural selection (Glinka et al. 2003; Akey et al. 2004; Tenaillon et al. 2004; Ometto et al. 2005; Stajich and Hahn 2005; Thornton and Andolfatto 2006; Walsh et al. 2006). One problem with the goodness-of-fit tests is that rejecting a neutral model does not guarantee that selection is a more likely explanation. Moreover, by necessity, the estimation of a demographic model is based on a highly summarized version of the data and the search of the space of possible models is far from exhaustive.

The second approach is to compare the probability of the data under a model with selection at a linked site versus without, and reject the null model of no selection if the difference in probabilities is large (e.g., Nielsen et al. 2005; Wright et al. 2005). This requires specifying a demographic and selective model; until recently, the null model was the standard neutral model of a random-mating population of constant size, and the alternative was the standard selective sweep model, in which selection acts on a new, co-dominant mutation (Kim and Stephan 2002; Przeworski 2003). These methods are not robust to departures from demographic assumptions (Jensen et al. 2005). An important improvement was proposed by Nielsen et al. (2005). They suggested that, rather than assuming a particular null model history, one use the observed allele frequencies at putatively neutral sites across the genome. An explicit model of population history is nonetheless required when assessing how unusual any particular region is relative to the background. Moreover, because the approach relies on an explicit model of selection, its reliability still depends in part on how sensitive the signature of selection is to the demographic setting.

Faced with these problems, and given the large amount of polymorphism data now available, researchers have avoided specifying a model and instead taken a purely empirical route (cf. Akey et al. 2002). The idea of the “empirical approach” is to order large multilocus data sets by several summary statistics (most commonly, a summary of diversity levels and a summary of allele frequencies) and consider loci in the tails of the distributions as likely targets of positive selection (e.g., Akey et al. 2002; Kayser et al. 2003; Carlson et al. 2005; International HapMap Consortium 2005; Yamasaki et al. 2005). Thus, the approach is very similar to goodness-of-fit tests; only the cutoffs for significance are determined by comparison to many other data sets, rather than derived from a model.

The implicit assumptions of the empirical approach are that most loci in the tails of the distributions are targets of recent selection and conversely, that most targets of selection will be outliers. Whether this is true is unknown. In humans, some loci known to be involved in adaptations from independent evidence show unusual patterns of variation, but others do not (Hamblin and Di Rienzo 2000; McVean et al. 2005). The same mixed picture emerges when considering loci known to have played an important role in plant domestication (Gallavotti et al. 2004; Wang et al. 2005). These isolated examples raise the possibility that many adaptations may be missed. If so, it may be difficult to reach general conclusions about the genetic basis of adaptations. Perhaps more importantly, a substantial fraction of loci identified as targets of selection may in fact be neutrally evolving, in which case considerable time and money may be spent pursuing spurious candidates. Thus, the reliability of empirical approaches needs to be assessed.

We did so by generating simulated data sets under a coalescent model of demography and directional selection, focusing on applications to human populations and to maize, as an exemplar of a domesticated grass species. The demographic model is loosely based on what is known of the history of the species. It is undoubtedly much too simple, yet it seems to capture important features of their history, as it provides a reasonable fit to many aspects of polymorphism data, including allele frequencies, diversity, and linkage disequilibrium levels (Voight et al. 2005; Wright et al. 2005). To avoid potentially unrealistic assumptions about modes of adaptation, we implemented a more general model of directional selection than has been considered previously, allowing for an arbitrary dominance coefficient of the beneficial allele and for selection to act either on a new mutation or on standing variation.

Results

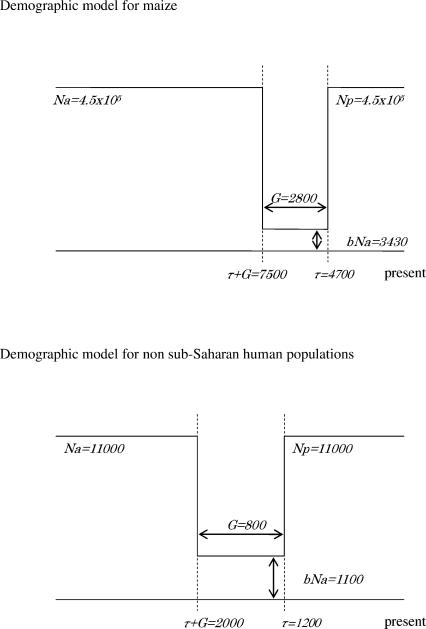
To model the demographic history of the species or population, we considered the bottleneck model depicted in Figure 1. In this scenario, the diploid effective population size N_a decreases to bN_a, G + τ generations ago (b ≤ 1). The population size recovers to its original size τ generations ago, such that the present effective population size, N_p, is equal to N_a.

Figure 1.

The population bottleneck models considered in this study. The effective population sizes of the present and ancestral population are denoted N_p and N_a, respectively. From τ + G to τ generations ago, the population size was reduced to bN_a. Note that the picture is not drawn to scale.

To mimic empirical approaches applied to polymorphism data from human populations currently outside sub-Saharan Africa, we relied on the parameter values estimated by Voight et al. (2005) from multiple aspects of polymorphism data at 50 non-coding loci sequenced in samples of Chinese and Italians. For sake of comparison, we also considered a constant population size model (so b = 1). This model is often used as the null hypothesis in tests of selection. While it is a poor fit to the data from non-sub-Saharan African populations (Przeworski et al. 2000; Frisse et al. 2001; Schaffner et al. 2005; Voight et al. 2005), it provides a reasonable fit to polymorphism data from the Hausa from Cameroon (Adams and Hudson 2004; Voight et al. 2005).

For maize, the parameter estimates were obtained from Wright et al. (2005), based on diversity, allele frequencies, and linkage disequilibrium levels at several hundred short fragments. Since our goal is to illustrate qualitative behaviors rather than to make quantitative predictions, we ignored the relatively small error associated with these point estimates. We further assumed that the population mutation rate is the same for all loci, but allowed the recombination rate to vary (see Methods).

Selection in maize

To model the domestication of maize, we followed Innan and Kim (2004) in assuming that strong directional selection started at the beginning of domestication (at time G + τ). Thus, we ignored subsequent selection for crop improvement (cf. Yamasaki et al. 2005). We set the selection coefficient s = 5% to reflect the strong artificial selection imposed by early farmers (see Methods for details) and considered two cases: (1) selection acted on a new allele (the standard selective sweep assumption) that arose at time G + τ; or (2) selection acted on a previously neutral, derived allele, present at frequency f at time G + τ. For our choice of parameters, the beneficial allele always reached fixation in the population by the end of the bottleneck (τ generations ago). Given these assumptions, we used coalescent simulations (cf. Hudson 1990) to generate polymorphism data for a neutrally evolving region of 5 kb linked to a selected site (see Methods).

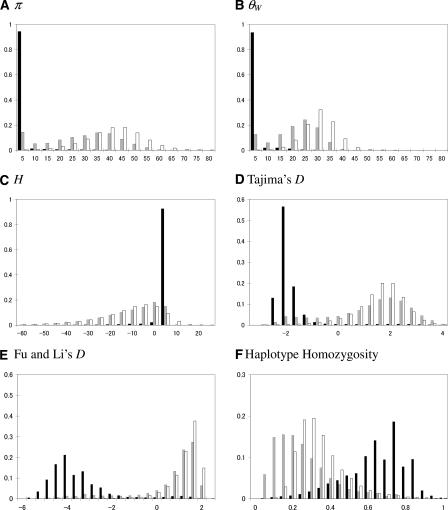
Figure 2 shows the distributions of six summary statistics for the neutral locus under a model with no selection (white), for the case in which the allele was favored upon introduction into the population (black) and for the case in which selection acted on a previously neutral allele (f = 0.05; gray). As expected from previous studies, a recent population bottleneck leads to a loss of rare alleles at neutral sites compared to a constant population size model, resulting in decreased diversity and a shift toward positive values of Tajima’s D and Fu and Li’s D (Tajima 1989b; Fay and Wu 1999).

Figure 2.

The distribution of summary statistics under the model for maize. The value of the summary is on the x-axis, and the proportion of simulated data sets with a given value is on the y-axis. The statistics presented are (A) π, (B) θ_W, (C) H, (D) Tajima’s D, (E) Fu and Li’s D, and (F) haplotype homozygosity (see Methods for details). The length of the simulated region is 5 kb; for the other parameter values, see Methods. In calculating D and E, we excluded cases with no segregating sites (0.03% of cases where selection acted on new mutations). The black histogram is for a model of directional selection on a new mutation (where h = 0.5), the gray for a model of directional selection where f = 0.05, and the white for the neutral model. Note that under a neutral, constant size population model, E(π) = E(θ_W) = 58.5, E(H) = 0, and E(D) ≈ 0.

If directional selection acted on a new mutation at a closely linked site, diversity levels tend to be even lower. Moreover, allele frequencies tend to be skewed toward rare variants, as shown by the left shift of the distribution of Tajima’s D and Fu and Li’s D, and haplotype homozygosity tends to be increased. These findings are consistent with characterizations of a selective sweep in a constant-size population (Maynard-Smith and Haigh 1974; Simonsen et al. 1995; Fu 1997; Kim and Stephan 2002; Przeworski 2002). They support the notion that directional selection on a new mutation can be thought of as creating a more severe bottleneck at linked loci (Wright et al. 2005).

When selection acted on previously neutral standing variation rather than a new mutation, the distributions of diversity levels and allele frequency summaries overlap substantially with the neutral case (Fig. 2). As noted previously (Innan and Kim 2004; Przeworski et al. 2005), selection on standing variation also leads to a much larger variance in allele frequencies than do the standard selective sweep and the neutral models (see Fig. 2D,E). In particular, some loci linked to a target of selection show an excess of intermediate rather than rare alleles. A more detailed analysis of the effect of f on patterns of genetic variation can be found in Innan and Kim (2004) and Przeworski et al. (2005).

Estimated error rates of the empirical approach in maize

These results suggest that, when data sets contain a small fraction of loci involved in domestication, considering the tails of the distributions will be a reliable approach to detect targets of selection on new mutations but not targets of selection on standing variation. To test this prediction, we constructed a hypothetical data set of 1000 loci, y% of which are closely linked to a selected site and (1 − y)% of which are not. We then estimated the empirical distribution of π and Tajima’s D, two commonly used statistics in empirical approaches (e.g., Stajich and Hahn 2005; Yamasaki et al. 2005), and considered the x% lower tail of the distribution as significant. To estimate the “false-discovery” and “false-negative” rates, respectively, we tabulated the number of loci in the lower tail of the distribution that are neutrally evolving and the number of targets of selection not in the tail. We note that in practice the power and false-discovery rates cannot be determined in the empirical approach, as no model is specified.

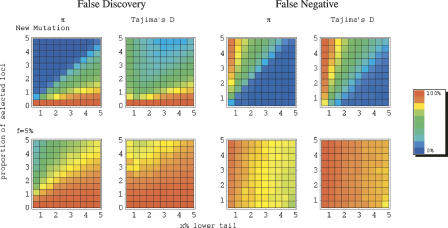
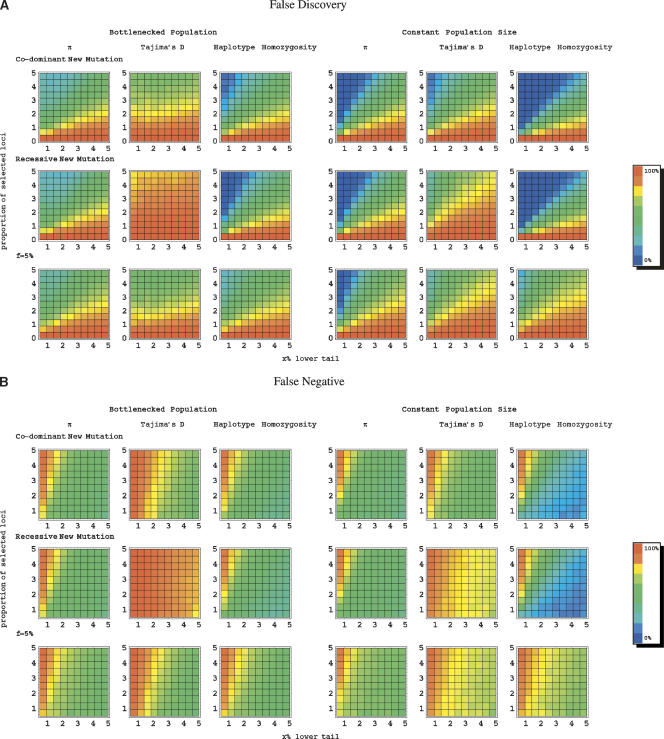
The results for our maize model are presented in Figure 3. As can be seen, when selection acted on a new mutation, the majority of loci in the lower tails of the distributions are closely linked to a target of selection. Thus, a purely empirical approach should yield several interesting candidate loci in maize. However, our simulations suggest that even in this case, many loci linked to a selected site will be missed (Fig. 3). Moreover, resequencing larger regions has little effect (Supplemental Fig. S1). Thus, the observation that a particular candidate region is not unusual in an empirical comparison provides only limited support against it being the target of selection.

Figure 3.

An estimate of error rates using π and Tajima’s D under the model for maize. Our aim was to mimic the approach of considering the lower tail of the empirical distribution of a summary statistic as significant. To do so, we generated 100 simulated data sets of 1000 loci, some fraction of which were linked to a selected site (see Methods for details). Shown are estimates of the proportion of loci in the tail that are neutrally evolving (i.e., the false-discovery rate) and the proportion of targets of selection not in the tail (i.e., the false-negative rate). Two selection models are considered (from top to bottom): (1) selection acted on a new mutation; (2) selection acted on a previously neutral allele and f = 5%. On the x-axis is the cutoff for significance, that is, the percentile of the distribution considered. On the y-axis is the proportion of loci linked to a target of selection in our simulated data set of 1000 loci.

As expected from Figure 2, when f = 0.05, the empirical approach leads to much higher error rates than when directional selection acted on a new mutation. For example, if the cutoff for significance and the true fraction of loci under selection are set to 5%, then the false-discovery and -negative rates under a model on selection on a new mutation are 8.3% using π and 20.3% using Tajima’s D; when f = 0.05, they are 73.8% for π and 82.2% for Tajima’s D. Using a more stringent cutoff of 1%, and assuming 5% of the loci are targets of selection, the estimated false-discovery rates for the standard sweep model are roughly 1.9% (for π) and 30.5% (for Tajima’s D), and the false-negative rates are ∼80.4% and 86.1%, respectively. For f = 0.05, in contrast, the estimated false-discovery rates are as high as 33.4% (for π) and 70.4% (for Tajima’s D), while the estimated false-negative rates are estimated to be 86.7% and 94.1%, respectively. When f = 0.05, examining variation in larger genomic regions does not help. For example, when we considered polymorphism data for 10-kb regions instead of 5 kb, the false-discovery rate is actually increased, presumably because regions farther from the selected site are included in the analyses (cf. Fig. 3 and Supplemental Fig. S1). These results confirm that if selection commonly acts on previously neutral mutations at appreciable frequency in the population, targets of selection will be hard to distinguish from neutrally evolving loci (Innan and Kim 2004).

Selection in human populations outside sub-Saharan Africa

To model selection in response to the novel environments encountered by anatomically modern humans, we assumed that selection occurred after the bottleneck, starting 1200 generations ago (see Fig. 1). The selection coefficient is set to s = 1% and the neutral region considered is 10 kb in length (see Methods for details). Given our choice of parameters, the favored allele has usually reached fixation by the present time (the expected frequency is 98.8%). We also considered selection pressures that arose since the advent of agriculture. In this case, selective pressures began 400 generations ago and the expected frequency in the population is only 10.4% by the present time; thus, the favored allele is almost always still segregating in the population.

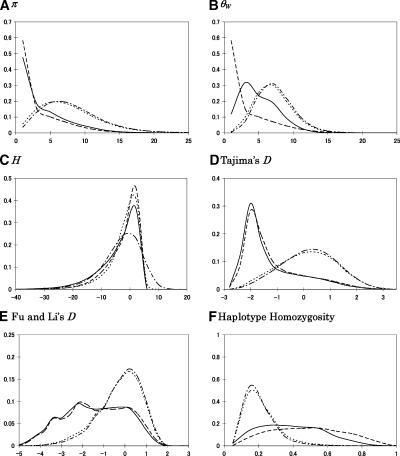
The distributions of summary statistics for these different models of selection are shown in Figure 4 for a bottleneck model (Fig. 4) and a model of constant population size (Supplemental Fig. S2). As can be seen by comparing the (dashed lines in Fig. 4 and red lines in Supplemental Fig. S2) distributions in Figure 4 and Supplemental Figure S2, the population bottleneck leads to decreased diversity and a skew toward positive D values at neutrally evolving loci relative to a model of constant population size. The effects are not quite as strong as in maize, however, as the bottleneck is thought to have been milder (Voight et al. 2005).

Figure 4.

The distribution of summary statistics under the model for a human population. The value of the summary is on the x-axis and the proportion of simulated data sets with a given value on the y-axis. The statistics presented are (A) π, (B) θ_W, (C) H, (D) Tajima’s D, (E) Fu and Li’s D, and (F) haplotype homozyogosity (see Methods for details). The length of the simulated region is 10 kb; for the other parameter values, see Methods. The broken line is for a model of directional selection on a new mutation, the solid line for a model of directional selection where f = 0.05, the dotted line for a model of an incomplete selective sweep in which the favored allele arose 400 generations ago, and the dashed line for the neutral model. In calculating D and E, we excluded cases with no segregating sites (0.047% for the model of selection on a new mutation, 0.002% for the case where f = 0.05, and 0.004% for selection starting 400 generations ago). Note that under a neutral, constant size population model, E(π) = E(θ_W) = 11, E(H) = 0, and E(D) ≈ 0.

Directional selection on a new mutation starting immediately after the bottleneck (1200 generations ago) leads to a marked shift toward lower diversity levels, more rare alleles, and increased haplotype homozygosity. In contrast, the model in which the favorable allele arose only 400 generations ago has almost no effect on these summary statistics. These results suggest that, unless it is very strong, directional selection starting 400 generations ago will be hard to distinguish from neutrality using summaries of diversity and allele frequencies (Fig. 4). When selection is stronger, such that the favorable allele reaches higher frequency in 400 generations, there is a greater shift toward rare alleles and increased haplotype homozygosity, and its effects are more easily detectable (data not shown). For frequencies of the favored allele >40%, there also appears to be substantial power to detect selection using the decay of haplotype homozygosity over larger genetic distances than considered here (Voight et al. 2006).

Interestingly, in our model for non-sub-Saharan African human populations, the distributions of summary statistics are very similar whether selection acted on a new mutation or a previously neutral allele (Fig. 4). This is likely because of our assumption that selection occurs after a population size reduction: Since bottlenecks lead to a loss of diversity, the favored allele tends to be associated with only one genetic background whether selection acted on a new mutation or on standing variation. Viewed another way, even if the allele was previously neutral, the genealogy at the site is shallow because of the small population size during the bottleneck. To explore this explanation at more length, we ran simulations in which selection occurred during the bottleneck and compared the results to the case in which selection occurred afterward, for the same demographic parameters and strength of selection (see Supplemental Fig. S3). As expected, assumptions about the frequency f were much more important when selection occurred during the bottleneck, as it does in our maize model. Thus, the importance of the mode of selection depends on the demographic history of the population.

Estimated error rates for the empirical approach in humans

These findings suggest that the mode of selection should not have much effect on the reliability of the empirical approach when applied to data from non-sub-Saharan human populations. We explored this further by estimating false-discovery and -negative rates for different models of adaptations (Fig. 5A,B). As expected, under a bottleneck model, error rates were comparable in almost all cases. The only exception is a higher error rate when Tajima’s D is used to detect directional selection on a recessive mutation. Tajima’s D has greater power to detect completed selective sweeps (Voight et al. 2006; data not shown); given an origin 1200 generations ago, recessive beneficial alleles are less likely to reach high frequencies by the present than co-dominant mutations (cf. Teshima and Przeworski 2006). When selection is stronger, such that both co-dominant and recessive alleles have usually reached fixation, the error rates become very similar (Supplemental Fig. S4).

Figure 5.

An estimate of error rates using π, Tajima’s D, and haplotype homozygosity under the models for a human population. (A) The false-discovery rate and (B) the false-negative rate (see legend to Fig. 3 and Methods for details). The results for the following three scenarios are presented (from top to bottom rows): (1) Selection acted on a new, co-dominant allele (h = 0.5) at time τ. (2) Selection acted on a new, recessive allele (h = 0.1) at time τ. (3) Selection acted on a previously neutral mutation at frequency f = 0.05 at time τ.

In general, error rates for Tajima’s D are higher than for π or the haplotype homozygosity, suggesting that the latter two may be more reliable statistics. However, we have assumed that mutation rates do not vary among loci. Since this is unlikely to be true, comparing π and haplotype homozygosity among loci will require an accurate estimate of the mutation rate (e.g., obtained from divergence from closely related species).

Figure 5 also reveals interesting differences between demographic models. When selection acted on a new mutation, error rates are higher under the bottleneck model than under the model of constant population size. As an illustration, if the cutoff for significance is set to 1% and a large fraction (5%) of loci are linked to a selected site, then the estimated false-discovery rate is 21% and the false-negative rate close to 84% using π, 58% and 92% for D and 8% and 82% for the haplotype homozygosity (for h = 0.5). In contrast, under a constant population size model, there would be 0% false discoveries for a false-negative rate of ∼80% using π, 14% versus 83% using D, and 0% versus 80% using haplotype homozygosity. Thus, in this scenario, there seems to be a higher rate of false discoveries in populations that have experienced a population bottleneck than those that have not (for the same significance level). The difference in error rates between the two demographic models is less pronounced when selection acted on a previously neutral mutation. Taken together, these finding suggest that it may not be straightforward to compare the evidence for directional selection in populations with distinct evolutionary histories.

Discussion

Error rates for selection on a new mutation

Our simulations suggest that empirical approaches to detecting recent adaptations from polymorphism data will lead to the discovery of a number of interesting candidate genes. For example, in the maize model, if selection acted on a new mutation in 2% of the regions considered (as estimated by Wright et al. 2005), 47.8% of selected loci would lie in the 1% tail of the distribution of π (Fig. 3). Application of the approach to other domesticated plants, such as sorghum, should be equally fruitful, so long as ancestral diversity is sufficiently high and the bottleneck is not extremely strong (K. Teshima and M. Przeworski, unpubl.).

This said, the empirical approach also appears likely to miss a large number of selected loci (Figs. 3 and 5). For example, when selection acted on a new mutation, the false-negative rate in maize is only below 10% when the false-discovery rate is above 40% (using either π or Tajima’s D). The same trade-off between false-discovery and false-negative rates is found under the human model. Given the overlap in the distributions of the summary statistics under a model of directional selection on a new mutation and under neutrality (Figs. 2 and 4), this trade-off is expected. It exists under both constant and bottleneck models (Fig. 5), but is more pronounced under the latter, reflecting the added difficulty of the task. The goal is to distinguish loci that have experienced a population size reduction from those that experienced a population size reduction and selection at a closely linked site. However, the effects of a bottleneck are extremely variable and mimic those of directional selection (Barton 1998).

In interpreting these findings, it is worth noting that they depend heavily on the strength of selection, about which little is known. For some human adaptations, such as resistance to malaria or lactose tolerance, the selective advantage (s) associated with the phenotype appears to have been large (Schliekelman et al. 2001; Saunders et al. 2005; Voight et al. 2006). If these cases were the norm, the error rate might be lower than we estimate using s = 1% (Supplemental Fig. S4). Instead, it is thought that these represent cases of unusually strong selection; consistent with this notion, the gene underlying lactose tolerance in northern Europeans stands out as an outlier in genome scans, as do some malaria-related genes (International HapMap Consortium 2005). More generally, little is known about the fitness advantage of advantageous mutations. However, the selection coefficients of most deleterious mutations are thought to be smaller than 1% (e.g., Yampolsky et al. 2005), and theoretical considerations suggest that most advantageous changes will also have small fitness effects and selection coefficients (Orr 2003). Thus, the error rates may actually be quite a bit higher.

Given these limitations, how can the error rates be decreased? As discussed in the Results, considering larger regions of the genome has only a small effect (cf. Fig. 3 and Supplemental Fig. S1). A more promising strategy may be to consider only loci with similar recombination rates in the empirical comparison (McVean et al. 2005). Although the power to detect selection is limited when the recombination rate at selected loci is high, a substantial gain can be obtained by matching the recombination rates for the selected and neutral loci (Supplemental Fig. S5). In practice, matching recombination rates is not straightforward, as independent measurements of fine-scale recombination rates are rarely available. One possibility is to use rates estimated from linkage disequilibrium levels (McVean et al. 2005). In this regard, it will be important to evaluate how robust linkage disequilibrium-based estimators of recombination are to the effects of natural selection at linked sites.

While we have considered one statistic at a time, as has been done in practice, error rates can be further decreased by using combinations of summaries. In doing so, it is not obvious how to weight the contribution of each summary, especially since the optimal choice will depend on how much importance one accords to false negatives versus false discoveries. As an illustration, we simply estimated the joint distribution of π and Tajima’s D for the human model of selection on a new mutation (weighting them equally). This revealed that even when both statistics are considered simultaneously, an appreciable number of selected loci are not among outliers (Supplemental Fig. S6). Thus, while using combinations of statistics is clearly advisable, it may not decrease the error rates dramatically.

Selection on a new mutation versus standing variation

In addition to considering the standard model of directional selection, we also considered a model in which the favored allele was previously neutral and only became beneficial when at appreciable frequency in the population. In this model, we have assumed that the allele drifts neutrally to 5% frequency and only then becomes beneficial; thus, it will tend to be associated with multiple haplotypes when first selected. If more than one of the haplotypes increased in frequency along with it, diversity may not be as sharply reduced, and there may be a high proportion of intermediates (rather than rare alleles) in the sample. In this case, selection on standing variation may be hard to pick up. Consistent with this, we find that both false-discovery and -negative rates can be substantially higher than when selection acted on a new mutation (Figs. 3 and 5).

Of course, our model is but one of many possible models of selection on standing variation, since we assumed that the favored allele had a single mutational origin, and that it was previously neutral, rather than deleterious. Under simplifying assumptions, directional selection on a previously deleterious allele will leave a similar signature to the standard selective sweep (Hermisson and Pennings 2005); thus, it should be easier to detect than selection on a previously neutral allele.

The difference between the signatures of selection on a new mutation and on standing variation is much smaller for the human than the maize model. This reflects our modeling assumption that selection acts during the bottleneck in maize, but after the bottleneck in humans (see Results). This assumption will not always hold: Selection for crop improvement clearly took place after the domestication bottleneck in maize (Yamasaki et al. 2005), while selection in humans is also likely to have taken place in the bottlenecked population. The results presented here help predict what outcomes we would expect in these cases; for example, that selection on standing variation should be easier to detect if it took place during crop improvement than during the early domestication process.

More generally, our simulations reveal an interesting interplay between the population history and the mode of selection: In some demographic histories, the effects of directional selection depend heavily on the model of adaptation while in others less so (Fig. 5; Supplemental Fig. S3). This interplay makes sense when considered from a genealogical perspective. Indeed, the signature of selection depends to a large extent on the genealogy at the selected site, which is shaped by both the demographic and selective history of the region. If the genealogy is shallow and star-shaped, as expected under a model of standing variation after a bottleneck, then the adaptive substitution will leave the classical signature of a selective sweep and should be easier to detect. If, instead, the genealogy at the selected site is deeper and has longer internal branches, as expected under a model of standing variation during a bottleneck, then the footprint of selection may not be so easily recognizable.

Caveats

This study only considered resequencing data, in which every base pair is called in every individual. Thus, our results are not directly applicable to genotyping studies, which type a pre-ascertained set of SNPs. Given the huge genotyping data sets now available for humans (Hinds et al. 2005; International HapMap Consortium 2005), as well as increasingly for other organisms, it will be of interest to assess the reliability of genomic scans using this type of data.

In addition, while we have tried to base ourselves on a realistic demographic model for both species, the model is still quite restrictive and, in particular, does not include population structure. This choice was motivated largely by technical considerations, rather than because these features are unimportant. Thus, much more work needs to be done to characterize the signature of directional selection in realistic demographic settings. What is clear from this initial set of simulations is that the power and reliability of selection scans depend on the evolutionary history of the species as well as the genetic architecture of the adaptation. Thus, these results highlight the relevance of demography, even to purely empirical approaches.

Implications

The ability to detect recent directional selection from polymorphism data depends on the recombination environment of the selected site (Supplemental Fig. S5), the dominance coefficient of the favorable allele (Fig. 5), the selection coefficient of the favorable allele (Supplemental Fig. S4), and whether the allele was favored from introduction or not (Figs. 3 and 5). Thus, if a candidate region does not stand out in empirical comparisons, it may be that there is little power to detect the mode of selection acting on it. This possibility has important implications for the interpretation of genomic scans of polymorphism data. Ultimately, we would like to use the results of genome scans to make inferences about which phenotypes were recently selected, and how selective pressures differ between populations. But we know that phenotypes differ in their genetic architectures, and thus the power to detect selection on different phenotypes may vary considerably. This raises the possibility that biological processes (e.g., GO categories) picked up in genomic scans are not those on which there was the most selection but those on which selection tended to act on new, co-dominant mutations in regions of low recombination.

Methods

The model

Our demographic model is presented in Figure 1. For maize, we used the parameters estimated for this model by Wright et al. (2005); specifically, N_a was taken to be 4.5 × 10⁵ and b = 0.0076. The domestication event starts 7500 generations ago (G + τ), and the bottleneck phase lasts 2800 generations (Wright et al. 2005). The average diversity levels (as measured by the heterozygosity π) are reduced by 33% relative to constant size population. Similarly, for human populations, we relied on the estimates of Voight et al. (2005) for Italian and Chinese populations. We chose a set of parameter values consistent with results from both Italian and Chinese populations, namely, N_a = 1.1 × 10⁴, G + τ = 2000 generations, b = 0.1, and G = 800 generations. In this case, diversity levels are 26% lower than in the constant size population.

We considered two selection scenarios, one that seems plausible for the domestication of members of the grass family, maize in particular, and one that may be applicable to non-sub-Saharan African populations of humans. The model for maize domestication is meant to capture important features of the artificial selection imposed by early farmers. Following Innan and Kim (2004), strong selection occurred during the bottleneck phase, starting G + τ generations ago. In humans, it seems more plausible that selection occurred after the bottleneck, as populations adapted to selective pressures brought on by new environments or by the advent of agriculture and sedentarism (e.g., Akey et al. 2004; Bersaglieri et al. 2004; Thompson et al. 2004). We therefore considered selection starting either τ = 1200 generations ago (∼30 thousand years ago [Kya]), immediately after the bottleneck, or 400 generations ago (∼10 Kya).

Selection in maize

We used coalescent simulations (cf. Hudson 1990) to generate polymorphism data from a neutral locus linked to a site under selection. We assumed that the favored allele has a single origin and considered two cases: (1) Selection acted on a new mutation, such that its frequency when first favored, f, is equal to 1/(2bN_a) (i.e., the mutation arises at the beginning of the bottleneck, 7500 generations ago); and (2) selection acted on a previously neutral allele, present at 5% frequency in the population when first favored (at the beginning of the bottleneck, 7500 generations ago).

The specific parameters are as follows: We set the length of the neutral locus to 5 kb. The sample size was 50 chromosomes. Within the neutral locus, mutations occur according to the infinite sites mutation model, at rate μ = 6.5 × 10⁻⁹ per site per generation (Gaut et al. 1996). Given an effective population size N_p = 4.5 × 10⁵, this yields θ = 4N_aμ = 4N_pμ = 0.0117 (where μ is the mutation rate per site per generation). Recombination rate is constant per base pair, and there is no gene conversion. Motivated by the evidence for rate heterogeneity in maize, we chose the value for each locus from an exponential distribution with mean 2 cM/Mb (Civardi et al.1994; Remington et al. 2001). The relative fitnesses of the three genotypes aa, Aa, and AA are 1, 1 + 2hs, and 1 + 2s, respectively, where s is the selection coefficient and h the dominance coefficient. We set h = 0.5, and set s equal to 5%, to reflect the strong artificial selection imposed, so that 4bN_ps is ∼700. The distance between the selected site and the edge of the neutrally evolving region is uniformly distributed from 0 to 2000 bp, which corresponds to a genetic distance of 0–0.004 cM if the recombination rate is 2 cM/Mb.

Selection model for humans

To model selection in human populations, we considered the following three cases: (1) Selection acted on a new allele that arose 1200 generations ago and is either still segregating in the population, or has reached fixation. (2) Selection acted on a previously neutral allele at frequency f = 5% when first favored 1200 generations ago, and the allele is either still segregating in the population, or has reached fixation. (3) The favorable mutation arose 400 generations ago and is (almost always) still segregating in the population. If the favorable mutation was still polymorphic in the present-day population, the frequency of the favored allele in the sample was chosen from a binomial distribution with mean given by the current population frequency.

We considered a sample size of 25 individuals (50 chromosomes). Mutation and recombination parameter values were chosen based on Voight et al. (2005). They reported that the average diversity at 50 non-coding loci is π = 0.0011 for the Hausa. This sub-Saharan population appears to have had a relatively stable demographic history (Adams and Hudson 2004); thus we used it as a proxy for the ancestral population (as did Voight et al. 2005), and set the population mutation rate θ = 4N_aμ = 4N_pμ = 0.0011 per site. Using the same data, Voight et al. (2005) estimated that the average population crossover parameter is 0.0006 per base pair (ρ = 4Nc). Given recent evidence that recombination rates in the human genome are highly heterogeneous on the scale of kilobases and approximately exponentially distributed (McVean et al. 2004; Myers et al. 2005), the ρ value is chosen from an exponential distribution with mean 0.0006 per base pair. Within a locus, the recombination rate is constant and there is no gene conversion. We considered loci of 10 kb, the sequence length spanned by a locus pair in Voight et al. (2005). The selection coefficient s is fixed at 1%, so that the population scaled selection coefficient in the present-day population is 4N_ps = 440. The distance between the target of selection and the edge of the neutrally evolving region is chosen from a uniform distribution from 0 to 100 kb, which corresponds to a genetic distance of 0–0.14 cM if the recombination rate is 1.4 cM/Mb (the latter figure is obtained by dividing by the estimate of N_a from Voight et al. 2005).

The simulation method

To simulate a genealogical history for the neutral region, the first step is to generate the frequency trajectory of the favored allele. To do so, we used a variable size jump random walk approximation of the diffusion process (Przeworski et al. 2005). For most of the scenarios that we considered, the frequency trajectory was constructed by (1) generating a trajectory for the selected allele from f to fixation, or if the allele did not reach fixation by the present time, from f to its present frequency, conditional on it not being lost; (2) for f > 1/(2N), generating a neutral trajectory from frequency f to loss, conditional on absorption at 0. The two trajectories were then concatenated to obtain a single one from introduction to fixation or to its present frequency. This process is described in detail in Przeworski et al. (2005).

The human model for selection on a previously neutral allele required a different implementation, as the allele that becomes beneficial can have arisen either in the bottlenecked population or in the ancestral population. If the allele arose in the ancestral population, then the trajectory of the allele from f to loss took place in a population of changing size. For this case, we used an importance sampling method proposed by Slatkin (2001); see the Supplemental material for details of the implementation.

This approach allowed us to generate trajectories of an allele from introduction to fixation, accounting for changes in population size and selection on standing variation. We then simulated an ancestral recombination graph for the neutrally evolving region conditional on this trajectory (for details, see Przeworski et al. 2005). The source code for the simulation program, written in C, is available upon request to K. Teshima.

Calculation of summary statistics

We compared the distributions of statistics obtained from 10⁵ replicates for the human model and 10⁴ replicates for the maize model. Specifically, we summarized the simulated data by π (Tajima 1983), θ_W (Watterson 1975), H (Fay and Wu 2000), Tajima’s D (Tajima 1989a), Fu and Li’s D (Fu and Li 1993), and the haplotype homozygosity. π and θ_W are estimators of the population mutation parameter θ, based on the average number of pairwise nucleotide differences per site and the observed number of segregating sites, respectively. Under the equilibrium neutral model, they provide unbiased estimates of θ. Tajima’s D and Fu and Li’s D are widely used summaries of the allele frequencies. Tajima’s D is obtained from the (approximately) normalized difference (π − θ_W). Fu and Li’s D considers the normalized difference (θ_W − θ_η), where θ_η is an estimator of θ based on the number of singletons in the sample. H is calculated as (π − θ_H), where θ_H is another estimator of θ that gives more weight to high frequency derived alleles. To calculate θ_H, we assumed the ancestral state is known. The expectations of Tajima’s D, Fu and Li’s D, and Fay and Wu’s H are ∼0 under the equilibrium neutral model. Haplotype homozygosity was calculated as the sum of the square of haplotype frequencies, assuming haplotypes are known. To generate the distribution of statistics under the human model of selection on a previously neutral allele, we constructed a histogram of the importance weights (see the Supplemental material).

Estimating error rates

To mimic genomic scans for selection, we considered simulated data sets of 1000 regions, some fraction of which were taken from the constructed distribution under a selection model and the rest of which were generated from the constructed distribution under the neutral model. The polymorphism data were summarized by three statistics that have been widely used in this type of approach, π, Tajima’s D, and haplotype homozygosity. We considered two types of error, estimated based on 100 simulated data sets of 1000 loci: (1) the proportion of loci in the tail of the distribution that are not targets of selection (i.e., the false-discovery rate) and (2) the proportion of selected loci not in the tail of the simulated distribution (i.e., the false-negative rate).