Flexible Histone Tails in a New Mesoscopic Oligonucleosome Model

Abstract

We describe a new mesoscopic model of oligonucleosomes that incorporates flexible histone tails. The nucleosome cores are modeled using the discrete surface-charge optimization model, which treats the nucleosome as an electrostatic surface represented by hundreds of point charges; the linker DNAs are treated using a discrete elastic chain model; and the histone tails are modeled using a bead/chain hydrodynamic approach as chains of connected beads where each bead represents five protein residues. Appropriate charges and force fields are assigned to each histone chain so as to reproduce the electrostatic potential, structure, and dynamics of the corresponding atomistic histone tails at different salt conditions. The dynamics of resulting oligonucleosomes at different sizes and varying salt concentrations are simulated by Brownian dynamics with complete hydrodynamic interactions. The analyses demonstrate that the new mesoscopic model reproduces experimental results better than its predecessors, which modeled histone tails as rigid entities. In particular, our model with flexible histone tails: correctly accounts for salt-dependent conformational changes in the histone tails; yields the experimentally obtained values of histone-tail mediated core/core attraction energies; and considers the partial shielding of electrostatic repulsion between DNA linkers as a result of the spatial distribution of histone tails. These effects are crucial for regulating chromatin structure but are absent or improperly treated in models with rigid histone tails. The development of this model of oligonucleosomes thus opens new avenues for studying the role of histone tails and their variants in mediating gene expression through modulation of chromatin structure.

INTRODUCTION

The hierarchical process through which nuclear double-stranded DNA packs itself into micrometer-sized nuclei of cells while maintaining its template-directed gene expression activities is remarkable (1). At the first level of compaction, the DNA wraps itself around approximately cylindrical-shaped protein aggregates known as nucleosomes. This DNA/nucleosome array then folds itself into the chromatin fiber, which has a nominal diameter of ∼30 nm. The chromatin fiber undergoes several higher levels of folding thereafter, culminating in the highly compact chromosomes.

The crystal structure of the nucleosome and the DNA wrapped around it was first solved in 1997 (2), and more recently determined at high resolution (3,4). The nucleosome comprises two copies each of the H2A, H2B, H3, and H4 histones, a single copy of either an H1 or H5 linker histone, and the DNA double-helix which makes ∼1.75 turns around the curved face of the nucleosome core (see Fig. 1). The central domains of the H2A, H2B, H3, and H4 histones are fairly rigid and define the nucleosome core, while their terminal domains, the histone tails, are much more dynamic and extend outward. The linker histone resides in the triangular space formed between the nucleosome core and the entering and exiting linker DNAs.

FIGURE 1.

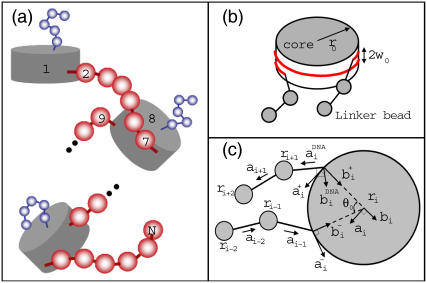
Nucleosome core modeling using DiSCO. The top figure shows the crystal structure of the nucleosome without the histone tail residues (nucleosome core). The bottom figure shows our model nucleosome core with discretized charges. The charges on the nucleosome core are deliberately shown smaller than their excluded volume for clarity, and they are color-coded according to their magnitude relative to the electronic charge (e), as shown in the color chart. The surface of the nucleosome core has been displaced inwards by 2 Å to allow visibility of the charges.

The internal structure of chromatin has been a topic of intense study over the past two decades. It is likely that chromatin is compact during the transcription silent states but flexible and ordered to allow proper unfolding during the template-directed transcription process. Several models consistent with the above argument have been proposed for the internal structure of chromatin. These include the solenoid (5,6), the helical ribbon (7), the cross-linker (8), and the global irregular zigzag (9) models. At present, most consistent with available data is the irregular zigzag model where the linker DNA zigzags back and forth across the chromatin axis; this permits the chromatin fiber to fold and unfold in an accordionlike fashion. However, structural and energetic details of this folding/unfolding process and how the chromatin fiber further folds into the higher-level condensed structures are not yet known.

Although the core histone domains clearly maintain the tightly wound DNA supercoil around the nucleosome, the positively charged linker histones are crucial for compacting chromatin by reducing the separation angle between the incoming and outgoing linker DNAs (10,11). Moreover, the histone tails critically regulate chromatin structure and function by charge modification. Namely, the tails' positive charge and highly flexible nature allows them to extend and electrostatically interact with the negatively charged regions of neighboring nucleosomes and proteins. This shielding can bring neighboring nucleosomes into closer spatial proximity. Altering the positive charge on the histone tails can thus substantially modify this attraction between nucleosomes. Indeed, acetylation of certain residues on the histone tails (which partially neutralizes the histone tails' charge) is believed to be the primary cause for the partial unfolding of the chromatin fiber resulting in an enhanced transcription of genes (12,13). Other covalent modifications of histone tails involve methylation, phosphorylation, and ubiquitination (14,15). Collectively, various residue-specific modifications play important roles in selectively modulating the structure of chromatin either through direct modification of the physical histone tail interactions or via the recruitment of chromatin modifying proteins; this is known as the histone-code hypothesis.

Undoubtedly, understanding the physical mechanism through which histone tail modifications lead to modulation of chromatin structure is important from the point of view of transcriptional activation and repression of genes. Due to the natural variability in the length, position, and constitution of the histone tails, as well as the anisotropy in the position and orientation of nucleosomes within the chromatin fiber, we anticipate tail-specific roles. Thus, elucidating the positional distribution of individual histone tails and the role of each unit within chromatin is crucial. Indeed, innovative experimental studies attempting to systematically dissect the role of each histone tail are only beginning to appear (16–19). Still, due to the highly dynamic nature of histone tails, only time and configuration-averaged properties of the histone tails are generally obtained, rather than transient dynamics of each histone tail. Thus, theoretical and computational techniques subject to the usual limitations and approximations have great potential to contribute to an understanding of the function and properties of histone tails.

Several models of chromatin structure and dynamics have been developed and examined. The existing theoretical models can be broadly classified into two categories:

1. Simple but insightful wire-frame, mechanical models (9,20,21), which relate the structure of chromatin only to a few geometrical parameters such as the linker DNA length, linker DNA entry/exit angle, and the nucleosome/nucleosome twisting angle; and

2. Coarse-grained dynamic models of oligonucleosomes (22–30), which include stretching, bending, and twisting of linker DNA and also account for distance- and orientation-dependent interactions among linker DNA and nucleosomes using effective energetic potentials.

These representations are typically coupled to computational sampling techniques such as Monte Carlo and Brownian dynamics to determine the structural and dynamical properties of the oligonucleosomes. The models range in complexity from nucleosomes treated as spherical particles (22) to models that treat both the excluded volume surface as well as the electrostatic potential of nucleosomes to high accuracy (24–30).

Our group has recently begun to incorporate the effect of histone tails into a macroscopic chromatin model (30) developed several years ago (24), where the nucleosome cores were treated as rigid bodies and the linker DNAs as elastic chains. Even though the histone tails were approximated as rigid charged entities that protrude outwards from the rigid nucleosome core, the study nonetheless demonstrated theoretically the role of tails in mediating the salt-dependent folding of oligonucleosomes via electrostatic interactions with neighboring nucleosome cores.

Here, we extend the recent coarse-grained model of oligonucleosomes (30) to incorporate flexibility into each histone tail. This is accomplished by representing the histone tails as a set of connected charged beads with optimized salt-dependent charges at the bead centers that reproduce the electric field surrounding the charged tails. The nucleosome cores and linker DNA are modeled as in earlier studies (27,30), where the nucleosome core is represented as a set of discrete optimized charges on its surface with appropriate excluded volumes, while the linker DNA is modeled using a discrete elastic chain model with physically derived parameters (31). The effect of linker histone H1 or H5 is not yet considered. Brownian dynamics simulations with complete hydrodynamic interactions among the DNA, nucleosome cores, and histone tails are employed for capturing the dynamics and structure of oligonucleosomes of different sizes under different salt conditions.

We demonstrate that the new model of oligonucleosomes reproduces well a range of available experimental data, including salt-dependent variation of maximal extension of mononucleosomes, self-diffusion coefficients of dinucleosome and trinucleosome, and sedimentation coefficients of 12-unit nucleosomal arrays, and better than that of the previous model with fixed histone tails (30). Predictions concerning the positional distribution of each histone tail at low and high salt are also presented, illustrating the highly dynamic and salt-dependent nature of histone tails, which allows them to mediate internucleosomal interactions to a moderate degree and, in the case of H3 tails, partially shield the electrostatic repulsion between the linker DNA emerging from a nucleosome core. We conclude by suggesting how the new model may be used to study the role of histone tails and their modifications and variants in modulating chromatin structure and dynamics.

FLEXIBLE-TAIL MODEL

Our coarse-grained model of chromatin (oligonucleosomes) consists of three components: nucleosome core, DNA linker, and histone tails. Each component requires a different modeling strategy. Building on our earlier model of chromatin (30), we regard the histone tails as flexible entities rather than rigid protrusions from the nucleosome core. Details of the linker DNA and nucleosome core modeling are given elsewhere (24,25,27,30), so their modeling is only briefly described. The histone tail modeling is provided in greater detail.

Nucleosome core and DNA linker

Model

Fig. 1 illustrates the basic nucleosome core comprising the eight core histones H2A, H2B, H3, and H4 (excluding their terminal regions) accompanied by 1.75 turns of DNA wrapped around it. Our model is based on the recent crystal structure of the nucleosome by Davey et al. (3) with PDB code 1KX5. Table 1 lists the protein residues that constitute our definition of the histone tails. Briefly, these include N-terminal portions of all the core histones and short C-terminal portions of H2A. Since the nucleosome core is fairly rigid, the motion of the nucleosome core is effectively modeled using rigid-body dynamics. For hydrodynamic purposes, the nucleosome cores are considered as spheres with a hydrodynamic radii R_c (see full parameter values in Table 2).

TABLE 1.

Flexible histone tail residues selected for the protein bead modeling

			All residues		Fixed residues
Histone	Chains*	Terminal	PDB†	Model‡	PDB¶	Model§	Charges on bead model (e)
H3	A, E	N	1–40	1–8	36–40	8	+3,+2,+1,+2,+1,+2,0,+3
H4	B, F	N	1–25	1–5	21–25	5	+3,+1,+1,+4,0
H2A	C, G	N	1–20	1–4	16–20	4	+3,+1,+3,+2
H2A	C, G	C	114–128	1–3	114–118	1	+1,0,+2
H2B	D, H	N	1–25	1–5	21–25	5	+2,+2,+2,+2,+2

^*Chain labels of histone proteins in the crystal structure 1KX5.pdb.

^†Amino acids in 1KX5.pdb belonging to the histone tail.

^‡Protein beads used to model the histone tail.

^¶Amino acids represented by the protein bead attached to nucleosome core.

^§Identity of the protein bead attached to the nucleosome core.

TABLE 2.

Parameter values employed in Brownian dynamics simulations of nucleosomal arrays

Parameter	Description	Value
l0	Equilibrium DNA segment length	3.0 nm
h	Stretching constant of DNA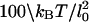
g	Bending constant of DNA	LpkBT/l0
s	Torsional rigidity constant of DNA	3.0 × 10−12 erg.nm
Lp	Persistence length of DNA	50 nm
θ0	Angular separation between linker segments at core	90°
2w0	Width of wound DNA supercoil	3.6 nm
r0	Radius of wound DNA supercoil	4.8 nm
htc	Stretching constant for tail bead attached to core	h
Rc	Hydrodynamic radius of nucleosome core	5.46 nm
Rl	Hydrodynamic radius of linker bead	1.5 nm
Rt	Hydrodynamic radius of histone tail bead	0.6 nm
σtt	Excluded volume distance for tail/tail interactions	1.8 nm
σtc	Excluded volume distance for tail/core interactions	1.8 nm
σcc	Excluded volume distance for core/core interactions	1.2 nm
σtl	Excluded volume distance for tail/linker interactions	2.7 nm
σcl	Excluded volume distance for core/linker interactions	2.4 nm
ɛ	Dielectric constant of solvent	80
kev	Excluded volume interaction energy parameter	0.001 kBT
kevt	Tail/tail excluded volume interaction energy parameter	0.1 kBT
Δt	Brownian dynamics simulation timestep	5 ps

Using the irregular discrete surface charge optimization (DiSCO) algorithm (27), N_c = 300 discrete charges are uniformly distributed across a finely-discretized representation of the nucleosome core surface to mimic the surrounding electrostatic potential (and electric field). The discrete charges are assigned optimized values, such their electric field obtained via a Debye-Hückel approximation matches the electric field of the atomistically described nucleosome core at distances >5 Å away from the surface of the core. This is achieved with the truncated-Newton TNPACK optimization routine (32–34), which is integrated within the DiSCO software, as described in Beard and Schlick (25) and Zhang et al. (27). The electric field landscape of the atomistic nucleosome is computed by using the nonlinear Poisson-Boltzmann equation solver QNIFFT 1.2 (35–37) where the atomic radii are assigned using the default extended atomic radii based loosely on Mike Connolly's Molecular Surface program (38), and the charges are assigned using the AMBER 1995 force field (39). In addition, to mimic the excluded volume of the entire nucleosome core, each charge is also assigned an effective excluded volume, modeled using a Lennard-Jones potential.

The linker DNA connecting two adjacent nucleosome cores is modeled using the discrete elastic chain model of Allison et al. (31,40), as sketched in Fig. 2. Thus, double-stranded DNA is modeled as a chain of charged beads where each bead represents a 3-nm-long strand of relaxed DNA. The hydrodynamic radius associated with each linker bead is represented by R_l, and each linker bead is assigned a salt concentration-dependent negative charge according to the procedure of Stigter (41). The linker DNA is governed by stretching, bending, and twisting potential energy terms.

FIGURE 2.

Discrete elastic bead model for linker DNA. The top figure shows the atomistic linker DNA while the bottom figure shows our model.

Geometry

The geometry of an oligonucleosome constituting a total of N linker DNA and nucleosome core components is shown schematically in Fig. 3; I_l and I_c denote, respectively, the subset of linker beads and nucleosome cores. Each nucleosome core other than the first nucleosome core of the nucleosomal array is attached to two DNA strands, which are termed the “entering” and “exiting” linker DNA. The two points on the nucleosome at which the entering and exiting linker beads are attached enclose an angle θ₀ about the center of the nucleosome core, and are separated by a distance of 2w₀ normal to the plane of the nucleosome core (see figure). The first nucleosome core is attached to a single linker DNA.

FIGURE 3.

(a) Schematic representation of our model nucleosomal arrays with a total of N nucleosome cores and linker DNA beads. Each linker DNA is represented by six beads in red for this illustration. For clarity, nucleosome cores are drawn as gray cylinders while only one out of 10 histone tails with five beads is shown in blue. Missing portions between the second nucleosome and the last are shown as thick dots. (b) Schematic representation of the nucleosome core without histone tails showing the wound DNA supercoil and the relative positions of the entering and leaving linker DNA. (c) Model geometry showing the coordinate systems adopted for modeling linker DNA-nucleosome mechanics.

The center-of-mass positions of the nucleosomal array components are given by r_j, where j = 1, ···, N. For discussion, we will consider the i^th component of the array to be a nucleosome core, as in the figure. The orientation of the nucleosome core is represented by the mutually orthonormal set of unit vectors {a_i, b_i, c_i}, where a_i and b_i lie in the plane of the nucleosome core. The vector a_i points along the tangent at the attachment site of the exiting linker DNA, b_i points in the direction normal to this tangent and inwards toward the nucleosome center, and c_i = a_i × b_i. The coordinate system of other nucleosome cores is similarly represented. A similar coordinate system is adopted when j is a linker bead. The vector a_j points from r_j toward r_j+1 when j + 1 is also a linker DNA bead. When j + 1 is a nucleosome core, the vector a_j points from r_j in the direction of the linker bead's attachment point. For the case when j is a nucleosome core and j + 1 is a linker DNA bead, we have to define another coordinate system 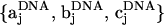. Here 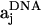points along the exiting linker DNA, i.e., toward r_j+1 from its point of attachment at the nucleosome core j. Two additional coordinate systems are required to describe the trajectory of the wrapped DNA on the nucleosome cores at the point where it diverges from the core to form the two linker DNA, as given by 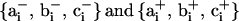. The former represents the local tangent on the nucleosome core at the point of attachment of the entering linker DNA, while the latter represents the tangent corresponding to the exiting linker DNA. Note that with this formalism, 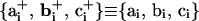. These additional coordinate systems are required for determining the forces and torques on the rigid nucleosome core due to DNA bending and twisting at their points of attachments to the nucleosome cores.

The bending and twisting potential energies of the nucleosome-linker DNA complex are expressed in terms of Euler angles {α_i, β_i, γ_i} and 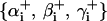, which transform one coordinate system to the next. The two Euler angles and their transformations are given below.

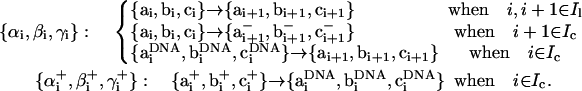(1)

To ensure that no torsion is introduced in the Euler transformation 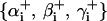, we set 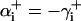. The mathematical details of computing the coordinate system vectors the associated Euler angles is provided elsewhere (25).

Energetics

The potential energies associated with linker DNA stretching, bending, and twisting are respectively given by

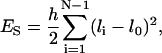(2)

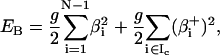(3)

(4)

where h, g, and s are the stretching, bending, and torsional force constants; l_i and l₀ are the linker DNA segment lengths and the corresponding equilibrium lengths, respectively; α_i, β_i, γ_i, and 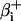are Euler angles.

The linker DNA beads and the discrete charges of the nucleosome cores interact via a combination of electrostatic and excluded volume interactions, which are respectively modeled using the Debye-Hückel (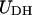) and Lennard-Jones (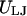) potentials given by

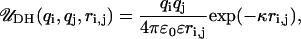(5)

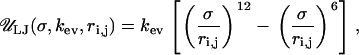(6)

where q_i and q_j are the charges on two interacting beads separated by a distance r_i,j in a medium with a dielectric constant of ɛ and an inverse Debye length of κ; ɛ₀ is the electric permittivity of vacuum; σ is the effective diameter of the two interacting beads; and k_ev is an energy parameter that controls the steepness of the excluded volume potential. The electrostatic energy of the nucleosome core and linker DNA system is given by the superposition of three electrostatic interactions: linker/linker, linker/core, and core/core interactions, as given by

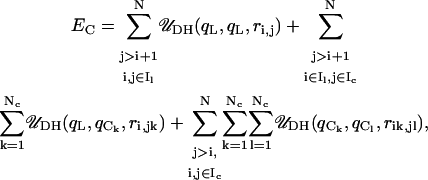(7)

where q_L represents the effective charges on the linker DNA beads, and q_Ck represents the k^th discrete charge on the nucleosome core. The excluded volume energy of the nucleosome-linker DNA system is given by

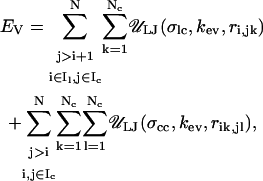(8)

where the two terms represent excluded volume energies for linker/nucleosome and nucleosome nucleosome interactions, respectively. The parameters σ_lc and σ_cc represent the excluded volume parameters for the two types of interactions, respectively. No excluded volume interactions are considered for linker/linker interactions since they remain separated due to strong electrostatic repulsions. The values for all parameters mentioned in this section are given in Table 2.

Histone tails

Our model for the histone tails, which we term the protein-bead model, began with the thesis work of Qing Zhang (42). It is obtained in two steps (see Fig. 4). First, the fully atomistic histone tails are simplified using the subunit model of Levitt and Warshel (43–45). Second, we build the protein bead model from the subunit model via a matching procedure where the force field parameters of the protein bead model are adjusted to mimic the Brownian dynamics of the subunit model corresponding to that histone tail. This additional level of coarse-graining avoids severe size inconsistency between the tail subunits and the other units, and also expedites computations substantially.

FIGURE 4.

Two-step modeling of histone tails. The top figure shows the atomistic description of the H3 histone tail. The middle figure portrays the subunit model corresponding to that tail. The bottom figure shows the protein-bead model developed in this study derived from the subunit model.

Model development

The specific residues constituting the histone tails were identified based on the experimental study of Tse and Hansen (16) and are listed in Table 1. A total of 10 histone tails are modeled: eight N-terminal regions of the H3, H4, H2A, and H2B histones and two C-terminal regions of the histone H2A. Next, a subunit model of each histone tail is constructed where each protein residue is replaced by a spherical bead located at each amino acid C^β atom (43–45). This procedure as applied to the H3 histone tail is sketched in Fig. 4. We use hydrodynamic radii of 3.5 Å for all the subunits and employ harmonic bonds and angles between the subunits based on the work of Weber et al. (46). Briefly, the energy of the subunit model consists of electrostatic, bond-stretching and bond-angle, nearest-neighbor nonbonded, solvation, and excluded volume terms. Since the histone tails are simulated in the absence of salt, the electrostatics of the subunit model are represented via a Coulombic potential. The force-field details of the subunit model are provided in the Appendix. We employ the University of Houston Brownian Dynamics program (47) to perform Brownian dynamics on the subunit models corresponding to each of the 10 individual histone tails for 100 ns. The temperature and timestep of the simulations are set at 300 K and 0.01 ps, respectively.

For the protein bead model, five adjacent beads of the subunit model are represented by a single macro bead with an effective hydrodynamic radius of R_t. Thus, 50 tail beads per nucleosome are employed to model the 250 or so histone tail residues that comprise each nucleosome. The center of each macro bead is placed at the C^β atom of the third amino acid. For the matching procedure, each bead is assigned a charge equal to the sum of the charges on the five amino acids it represents, as tabulated in Table 1. Later, we will show how these charges are further adjusted for our final oligonucleosome simulations. The total intramolecular energy of the protein-bead histone tail is given by four components: electrostatics, excluded volume, bond-stretching, and bond-angle bending, which are described in detail next.

The excluded volume interactions are given by the Lennard-Jones potential with fixed parameters of k_evt and σ_tt. The electrostatic interactions between protein beads are modeled via Coulombic terms for the matching procedure only. In all our subsequent simulations of oligonucleosomes, we employ the Debye-Hückel potential to model the histone tail electrostatics. The bond-stretching and bond-bending potentials are given by quadratic functions of the deviations in the bond-length and bond-angle from their equilibrium values, respectively. For a histone tail consisting of N_b protein beads, the adjustable parameters in our model are: the equilibrium bond distance between beads, l_i0, and the associated force constants k_bi, where i = 1, ···, N_b − 1; and the equilibrium bond angle, θ_i0, and the associated force constants, k_θi, where i = 1, ···, N_b − 2.

For our protein bead model to realistically represent the fully atomistic histone tails, we require it to closely reproduce the dynamical and configurational properties of the subunit model (assuming that the subunit model reasonably represents polypeptide flexibility in solution). To this end, we seek the most suitable values of l_i0, 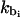, θ_i0, and 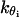for the protein bead model to yield the same bond-length and bond-angle distributions as those observed between every fifth bead in the Brownian dynamics simulations of the subunit model. Accordingly, l_i0 is taken as the average distance between the subunit beads (5i − 2) and (5i + 3) observed in the simulations, and θ_0i is taken as the average angle between the (5i − 2), (5i + 3), and (5i + 8) subunit beads observed in the simulations. The chosen values of l_i0 and θ_i0 are shown in bold in the third column of Tables 3 and 4, respectively.

TABLE 3.

Bond-stretching comparisons of our protein bead model with the subunit model for the five different pairs of tails; values in bold denote parameters chosen for the protein bead model

		Subunit model		Protein bead model
Tail	Bondi-j	Average [Å]	SD [Å]	kb (kcal/mol/Å)	Average [Å]*	SD [Å]*
N-ter H3	1-2	14.8	2.4	0.09	15.6	2.3
	2-3	13.4	3.1	0.06	15.0	3.0
	3-4	14.5	2.9	0.07	15.6	2.9
	4-5	15.0	2.5	0.07	16.1	2.6
	5-6	14.8	2.7	0.07	16.2	2.6
	6-7	13.9	2.8	0.07	15.1	2.9
	7-8	13.7	2.3	0.11	14.9	2.4
N-ter H4	1-2	13.2	2.6	0.10	14.1	2.6
	2-3	13.9	2.4	0.10	15.2	2.4
	3-4	13.7	2.7	0.06	14.8	2.8
	4-5	14.4	1.8	0.20	14.7	1.8
N-ter H2A	1-2	13.4	2.7	0.08	14.1	2.6
	2-3	14.5	2.5	0.09	15.3	2.5
	3-4	11.0	3.4	0.03	14.5	3.4
C-ter H2A	1-2	14.1	2.7	0.07	15.7	2.6
	2-3	12.6	3.1	0.07	13.7	3.0
N-ter H2B	1-2	13.5	2.8	0.08	14.7	3.1
	2-3	12.7	2.6	0.10	14.1	2.3
	3-4	15.2	2.4	0.08	16.2	2.4
	4-5	14.2	2.6	0.08	15.1	2.7

^*Average bond length and their standard deviation obtained from protein bead model simulations using the parameters in bold match those obtained from subunit simulations.

TABLE 4.

Bond-angle comparisons of our protein bead model with the subunit model for the five different pairs of tails; values in bold denote parameters chosen for the protein bead model

		Subunit model		Protein bead model
Tail	Anglei-j-k	Average [°]	SD [°]	kθ (kcal/mol/rad2)	Average [°]*	SD [°]*
N-ter H3	1-2-3	115.8	29.5	1.1	108.6	28.8
	2-3-4	116.7	30.2	1.0	108.1	28.6
	3-4-5	117.3	24.3	1.7	111.3	25.4
	4-5-6	123.0	29.2	1.2	117.6	27.8
	5-6-7	111.8	30.7	1.2	110.4	29.3
	6-7-8	114.9	26.5	1.5	110.5	27.2
N-ter H4	1-2-3	112.5	31.8	1.0	103.2	31.8
	2-3-4	116.3	27.5	1.1	106.0	25.8
	3-4-5	111.6	36.5	0.5	103.6	35.5
N-ter H2A	1-2-3	121.2	28.4	1.1	108.5	29.0
	2-3-4	100.1	29.5	0.6	100.1	29.3
C-ter H2A	1-2-3	113.8	32.1	1.0	100.7	31.8
N-ter H2B	1-2-3	118.4	32.7	0.9	104.9	35.1
	2-3-4	118.9	31.5	0.6	103.9	28.4
	3-4-5	124.5	24.2	1.6	113.8	26.7

^*Average bond angle and their standard deviation obtained from protein bead model simulations using the parameters in bold match those obtained from subunit simulations.

To obtain the ideal force constants k_bi and k_θi, we perform Brownian dynamics simulations of the protein bead model at the same conditions as the subunit model simulations with varying values of force constants. The standard deviations in the bond-length and bond-angle distributions of the protein bead model are collected, and the values of 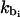and 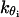that produce the best match between these standard deviations and those accumulated from the subunit model simulations between the aforementioned subunits, are chosen. The selected values of the force constants for each histone tail are provided in bold in the fifth column of Tables 3 and 4.

We next compute the electric field surrounding a histone tail from the superposition of Debye-Hückel potentials arising from the bead charges in the protein bead model of a histone tail at different salt conditions. Recall that each protein bead carries a charge equal to the sum of the charges of its constituents. We found that the electric field of the protein bead model consistently underestimated the electric field computed for the fully atomistic histone tail (by solving the Poisson-Boltzmann equation with QNIFFT 1.2 (37)) at high salt conditions. On the other hand, the protein bead model overestimated the electric field of the histone tails at low salt conditions. This trend can be explained by the variation in the magnitude of the effective charges on the nucleosome core and linker DNA beads with salt concentration; effective charges higher in magnitude than the actual charges are required to accurately reproduce the surrounding electrostatic potential at high salt, and vice versa. It was therefore deemed necessary to rescale the charges on the histone tail beads. We found that rescaling the bead charges by factors of 0.75, 0.80, 0.90, 1.05, and 1.2 corresponding to salt concentrations of 0.01, 0.02, 0.05, 0.1, and 0.2 M yielded the best possible matches between the electric fields of each histone tail and its corresponding protein bead model.

Energetics

Once the protein bead model for each histone tail has been built and parameterized, the histone tails must be properly attached to the nucleosome core. We use a simple harmonic spring that attaches the first bead of each histone tail (as given in Table 1) to its idealized position in the nucleosome crystal structure (see Fig. 3). The stretching energy of histone tail beads is therefore composed of two terms: stretching of tail beads with respect to its immediate neighbors within the same tail, and an additional contribution due to the displacement of the histone tail bead from its assigned attachment site, as given by

(9)

In the first term, N_t represents the number of histone tails per nucleosome core, N_bj is the number of beads in tail j, 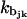is the stretching constant of the bond between the k and k + 1 beads of the j^th histone tail, and l_ijk and l_jk0 represent the distance between consecutive tail beads k and k + 1, and their equilibrium separation distance, respectively.

In the second term, h_tc is the stretching bond constant of the spring attaching the histone tail to the nucleosome core, r_ij is the position vector of the first tail bead in the coordinate system of its parent nucleosome, and r_ij0 is its ideal position vector in the crystal configuration. The intramolecular bending contribution to the histone tail energies, E_tB, is given by

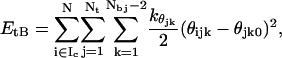(10)

where θ_ijk and θ_jk0 represent the angle between three consecutive tail beads k, k + 1, and k + 2, and their equilibrium angle, and 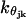is the corresponding bending force constant.

The total electrostatic energy of oligonucleosomes due to the histone tails is given by the superposition of various Debye-Hückel potentials energy terms arising from the interaction of histone tail charges among themselves and with nucleosome and linker bead charges, as given by

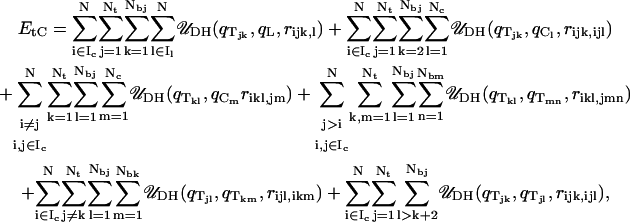(11)

where q_Tij represents the magnitude of the charge (in terms of the electronic charge e) on the j^th protein bead in the i^th histone tail.

The first term in Eq. 11 represents electrostatic energy arising from histone tail/linker DNA bead interactions. The second term in the equation arises from interactions between histone tail charges and the charges on its parent-nucleosome. Note that the first bead of each histone tail, which is attached to the nucleosome core, does not interact with that nucleosome core's charges. The third term represents interactions between charges on the histone tails and non-parent nucleosomes' charges. The fourth term represents intermolecular electrostatic interactions across different histone tails belonging to different nucleosome cores, and the fifth term represents intermolecular interactions between histone tails belonging to the same nucleosome cores. The last term represents intramolecular interactions between charges within the same histone tails; three consecutive charges within the histone tails do not interact electrostatically with each other.

The excluded volume interaction energy between the histone tail beads and the rest of the oligonucleosome components is given similarly by

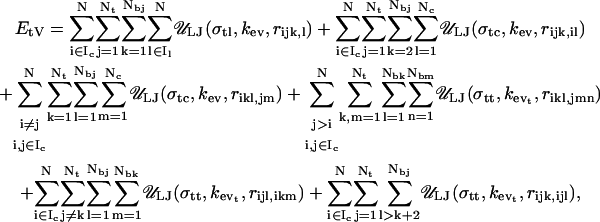(12)

where σ_tl, σ_tc, and σ_tt are excluded volume size parameters for tail/linker, tail/core, and tail/tail interactions, and k_evt is excluded volume energy parameter for tail/tail interactions. As in Eq. 11, the six terms in Eq. 12 respectively represent the van der Waals energies of histone tail beads interacting with: the linker DNA beads, parent nucleosomes charges, non-parent nucleosome charges, histone tail beads associated with non-parent nucleosome cores, beads of other histone tails belonging to the parent nucleosome core, and beads within the same histone tail. Again, three consecutive beads within a histone tail do not interact with each other, and the histone tail bead attached to the nucleosome cores does not interact with that core. Fig. 5 sketches our model integrating all the three components of the system.

FIGURE 5.

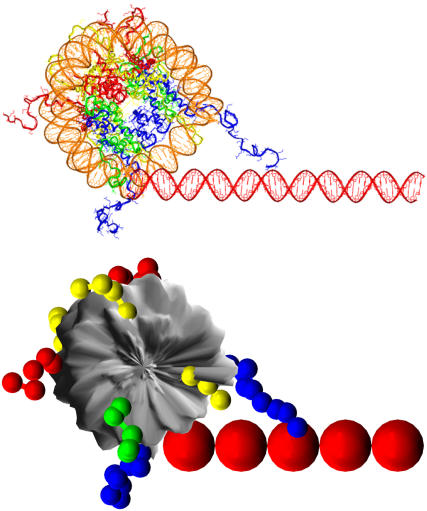
Repeating motif of an oligonucleosome containing 51-bp linker DNA. The top figure shows its atomistic representation, while the bottom figure shows its coarse-grained representation via flexible-tail model. The histone tails are color-coded as follows: H3 (blue), H4 (green), H2A (yellow), and H2B (red); the nucleosome cores and linker beads are colored gray and red, respectively.

To reduce computational costs, cutoff distances are employed for all the electrostatic (r_cut,c) and excluded volume interactions (r_cut,v) within a nucleosomal array. We employ a variable cutoff for both these interactions, which depends upon the temperature and salt concentration. The cutoff distances are taken as the distance at which the electrostatic potential energy and van der Walls energies of the linker beads becomes 0.5% of the thermal energy k_BT. Naturally, high salt conditions with enhanced screening effects results in smaller electrostatic interaction cutoffs than low salt conditions. For example, at 0.2 M salt, r_cut,c = 7 nm, while at 0.01 M salt, r_cut,c = 17 nm.

Forces and torques

The total energy of the oligonucleosome is given by the sum of all the different interaction energies above:

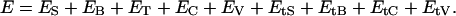(13)

The forces on the system components are defined by the relation

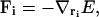(14)

where r_i and F_i are the position vector and deterministic force acting on component i, respectively. Expressions for forces on the DNA linker and the rigid nucleosome core due to stretching, bending, and twisting of DNA, and electrostatic and excluded volume interactions, are derived elsewhere (24). The internal forces arising within the oligonucleosome as a result of stretching, bending, electrostatic, and excluded volume interactions of the histone tails may also be derived in an identical fashion. The torque on the linker DNA beads, which arises due to the twisting potential (Eq. 4), acts only in the longitudinal direction a and is given by

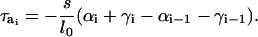(15)

The torque on each nucleosome core (τ_i), which acts along all three coordinate axes, is given as a sum of the three terms

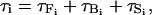(16)

where 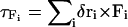is the torque acting on the nucleosome core due to forces applied at a positional vector δr_i away from the center of mass. The next two torque terms are associated with the bending and torsional potentials of DNA linkers entering or leaving the core. We again refer readers to Beard and Schlick (24) for more details on the two additional contributions. Note that no torque acts on the histone tail beads.

SIMULATION DETAILS

Brownian dynamics algorithm

We employ Brownian dynamics (BD) with complete hydrodynamics to simulate the dynamics of oligonucleosomes. A second-order, Runge-Kutta-based Brownian dynamics algorithm following the approach of Iniesta and de la Torre (48) is employed to update the rotational and position vectors of the various components of the oligonucleosomes. This approach is based on predicting the value of an arbitrary time-varying vector p at time t + Δt from its value at time t using the average of the time derivatives of p at times t and t + Δt, as given by

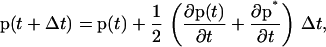(17)

where p* is the predicted p(t + Δt). The procedures for obtaining p* and p(t + Δt) (using Eq. 17) are referred to as first and second-order updates, respectively.

First-order rotational updates of the coordinate frames of reference a_i, b_i, and c_i are given by

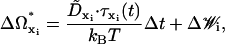(18)

where ΔΩ_xi(t) represents the change in the rotational state of the i^th bead about its original coordinate system x_i = {a_i, b_i, c_i}, τ_xi(t) is the instantaneous torque on bead i along vector x_i at time t, Δt is the BD timestep, and 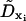is the rotational diffusion matrix. For hydrodynamic purposes, the nucleosome core is treated as a sphere with a rotational diffusion coefficient given by

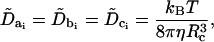(19)

where η is the solvent viscosity. For linker DNA beads, only rotation about the a_i axis is allowed and the rotational diffusion coefficient along that axis is

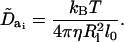(20)

The term 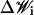in Eq. 17 represents random (Brownian) rotations applied to the core along all three reference axes, or along the a_i axis only for the linker DNA beads. The random rotations obey the fluctuation-dissipation relation given by

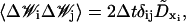(21)

where δ_ij is the Kronecker delta-function. First-order updates of the position vectors are now computed by using the Ermak-McCammon algorithm (49), as given by

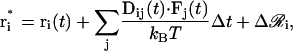(22)

where D_ij(t) is the configuration-dependent Rotne-Prager hydrodynamic diffusion tensor, Δt is the timestep, and 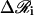represents the random fluctuations obeying the fluctuation-dissipation relation

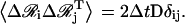(23)

Determination of 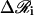requires factorization of the matrix D such that LL^T, where L is a lower triangular matrix. We employ the standard Cholesky decomposition method to achieve this (50). The vectors a_i, b_i, c_i, 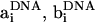, and 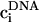are updated according the procedure described in Beard and Schlick (51).

The second-order rotational updates are computed as

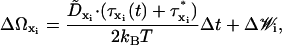(24)

where τ*_xi is the torque acting on the system components after the first-order translational and rotational updates. Second-order updates of the position vectors are computed as (52)

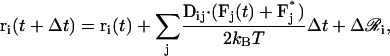(25)

where F_i* represents the force on bead i computed according to the temporary position vectors {r*} obtained after the first-order translational and rotational updates. To save computational time, the hydrodynamic tensor is computed only every 100 timesteps and is thus assumed to be fixed within that time frame. Our results remain unaffected with a change in this frequency as long as the frequency of recalculations is not decreased further, as found in simulations of supercoiled DNA (52).

Hydrodynamic interactions

The hydrodynamic diffusion tensor employed within our BD code is given by

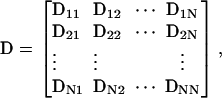(26)

where D_ij is a 3 × 3 matrix representing the interactions between beads i and j. Each D_ij can be calculated using modified forms of the Rotne-Prager tensor for unequal size beads (53–55). We consider two cases, nonoverlapping and overlapping beads. In the former,

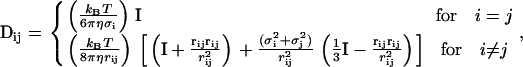(27)

where no overlap means 2r_ij > (σ_i + σ_j), and σ_i and σ_j are the sizes of the two beads; η is the solvent viscosity; r_ij = r_i − r_j is the vector joining the center of mass of the two beads i and j; r_ij is the distance between the two beads; and I is the 3 × 3 unit tensor. For overlapping beads (2r_ij < (σ_i + σ_j)), the hydrodynamic tensor is given by

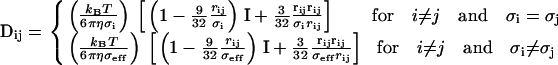(28)

Note that the top expression in Eq. 28 has been theoretically proven for equal-sized beads (53). No expression is available for the case of non-equal-sized beads, but we have found that with a choice of σ_eff = 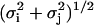, the tensor remains positive-definite as it should. Other researchers have likewise proposed similar expressions (55). In our simulations, σ_i equals R_c, R_l, or R_t, depending upon whether the component is a nucleosome core, linker DNA bead, or histone tail protein bead.

RESULTS

We show here how the flexible-tail model for oligonucleosomes reproduces existing experimental data, notably better than its predecessor, which considered the histone tails as rigid bodies (fixed-tail model). We also present predictive data on tail distribution as a function of salt. All simulations were performed at 20°C to be consistent with the experiments conducted at 20–23°C (56–60).

Histone tail configurations

Recently, Livolant and co-workers (17,56) undertook an exhaustive experimental study on the conformation of histone tails and their dependence on salt (NaCl) concentration of the surrounding buffer. They employed nucleosome core particles with intact histone tails carrying 146 ± 3 bp DNA and performed small-angle X-ray scattering experiments to determine their radius of gyration, R_g, and maximum extension of the particle, D_max. The radius of gyration of nucleosome particles, which was obtained from the scattering intensity according to the Guinier approximation, is defined as

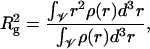(29)

where ρ(r) is the mass (electron) density of the nucleosome at a distance r from its center of mass and 𝒱 is the volume of the nucleosome. The other quantity of interest, D_max, is defined as the distance at which the function describing the distribution of the intramolecular distance r between scattering elements within the nucleosome becomes zero. In essence, D_max captures the maximum observable separation distance between histone tails and hence provides information on whether the histone tails are collapsed onto the nucleosome core or extended.

To compute D_max and R_g, Brownian dynamics simulations were performed on mononucleosomes without the linker DNA at varying monovalent salt concentrations in the range C_s = 0.01–0.3 M. The wound DNA length utilized in the experiments exactly matches the values in the crystal structure of the nucleosome on which our model is based (3). The simulations were performed over 50 μs at six different salt concentrations within the same concentration range investigated by the experimentalists, and D_max and R_g were computed every 100 timesteps and averaged over the second half of the simulation run. D_max was calculated as the maximum observable distance between two histone tail beads, and R_g was computed from the formula

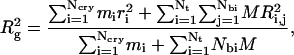(30)

where N_cry is the number of atoms constituting the nucleosome core crystal structure excluding those belonging to the histone tails, m_i is the molecular weight of the individual atoms, r_i is the distance of the atoms from the center of mass of the nucleosome, M is the mass assigned to each histone tail bead (equal to the total molecular weight of the 10 histone tails divided by the total number of protein beads representing them), and R_i,j is the distance of the histone tails protein beads from the center of mass of the nucleosome. The first and second terms in the numerator and denominator of Eq. 29 therefore compute the contribution to R_g from the tail-less nucleosome core and the histone tails, respectively.

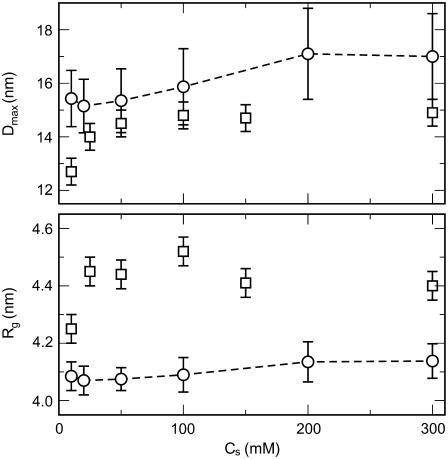
Fig. 6 compares our computed salt-dependence of D_max values to those obtained by Livolant and co-workers (56). Both studies predict a moderate increase in the magnitude of D_max with salt concentration. The magnitude of this increase in D_max from the lowest to the highest salt concentrations explored here (ΔD_max ∼ 2 nm) also agrees well with experiments. The data thus suggest that the histone tails maintain a fairly compact conformation at low salt conditions (relatively small values of D_max) and gradually extend outwards as the salt concentration increases.

FIGURE 6.

Variation of the maximum nucleosome extension (top) and the radius of gyration (bottom) versus the monovalent salt concentration. Simulation results are represented by circles and experimental data from Bertin et al. (56) as squares. The dashed line for the simulation results serves as a guide to the eye.

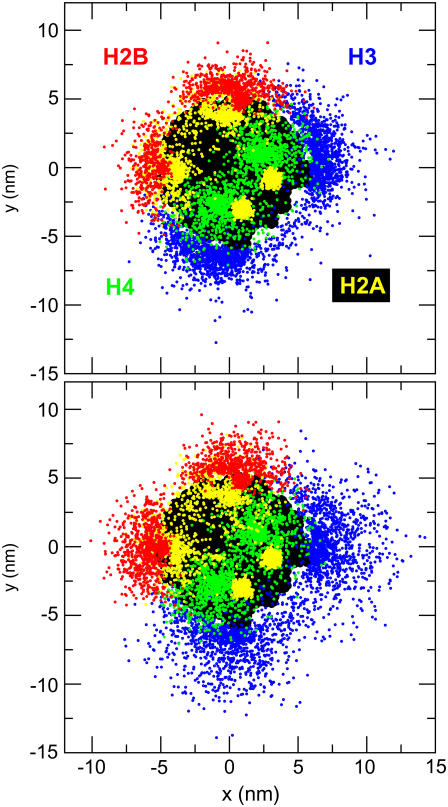
The extension of histone tails with salt concentrations is better visualized in Fig. 7, where we plot the positional distribution of histone tail beads at two different salt concentrations: 0.01 M and 0.2 M. To obtain the figure, we collect the position vectors of histone tail beads relative to the center of the nucleosome core, r′_i, within a 5-μs Brownian dynamics simulation of a mononucleosome at time intervals of 25 ns. We then project these position vectors onto the plane of the nucleosome core represented by the a-b axis (see Fig. 3), as given by x_i = r′_i · a and y_i = r′_i · b. The individual dots in the figure therefore represent the collection of points {x_i, y_i} sampled in our simulations. The larger spread of the histone tail bead distribution observed at 0.2 M salt concentration as compared to 0.01 M salt concentration clearly indicates the extension of histone tails with salt concentration. This behavior can be explained by the diminished electrostatic attraction (due to charge screening) between the histone tails and the nucleosomal DNA as the salt concentration increases—the overall electrostatic energy of interaction of histone tails with the nucleosome core becomes less favorable as the salt concentration is increased from 0.01 M (−63.9 kcal/mol) to 0.2 M (−18.5 kcal/mol). The generally broad spatial distributions of the histone tails in Fig. 7 highlights their highly flexible and dynamic nature, which is totally neglected in the fixed-tail models.

FIGURE 7.

Positional distribution of histone tail beads projected onto the a-b plane of the nucleosome. Top and bottom figures correspond to monovalent salt concentrations of 0.01 M and 0.2 M, respectively. Color-coding for the histone tails is as follows: H3 (blue), H4 (green), H2A (yellow), and H2B (red). The nucleosome core in the background is colored black.

Note that our values of D_max consistently overestimate the values from experiments by 1–2 nm. This likely results from the tendency of experiments to underestimate the value of D_max, as pointed out by the authors (17). Still, at low salt concentrations, particularly at 0.01 M, the discrepancy is larger, which can be explained by our Debye-Hückel approximation to the electrostatic interactions between the histone tails and the nucleosome core. Electrostatic interactions at distances smaller than the Debye length are more poorly predicted. Because the Debye length at 0.01 M salt concentration (κ⁻¹ ∼ 7 nm) is larger than the distances spanned by the histone tails, the electrostatic attraction between the histone tails and the nucleosome cores is possibly underrepresented, thus making the histone tails less prone to collapsing onto the nucleosome core.

The variation in the radii of gyration with salt as obtained via simulations and experiments is also compared in Fig. 6. Again, both the experiments and the simulations predict a moderate increase in R_g with salt; R_g increases by ∼0.1–0.2 nm as the salt concentration is increased from 0.01 M to 0.3 M. The consistently larger experimental values of R_g relative to simulations (by 0.3–0.4 nm) might be explained by the apparent swelling of the nucleosome cores in the experiments when compared to their structure in the crystal state (1KX5.pdb). Namely, we observed that the radius of gyration of the nucleosome core (without the tails) computed from the crystal structure (3.8 nm, using only the first summation terms of the denominator and numerator in Eq. 29) is smaller than that obtained experimentally (4.2–4.4 nm).

In summary, the flexible-tail model predicts correctly the trends and their respective magnitudes in the conformational changes that the histone tails undergo as the salt concentration is varied. The overall high degree of conformational freedom that each histone tail possesses, in addition to their dependence on salt conditions, plays a key role in mediating internucleosomal interactions within folded chromatin at physiological salt concentrations, and thus the current model improves upon the fixed tail representation, which completely neglects such conformational effects.

Diffusion coefficients

We now compare the flexible-tail model's self-diffusion coefficients (D_s) for mononucleosomes, dinucleosomes, and trinucleosomes at infinite dilution to values obtained experimentally. Mononucleosomes without linker DNA were employed in our simulations to model the experimental mononucleosomes of Yao et al. (57). Dinucleosomes containing two linkers and trinucleosomes containing three linkers were employed to mimic the experimental dinucleosomes (58) and trinucleosomes (59), respectively. The linker DNA length in both these models was fixed at seven linker beads to model the 22-nm-long linker DNA in the dinucleosome and trinucleosome experiments. All three experimental systems lack linker histones, as in our basic model. Multiple Brownian dynamics simulations on individual oligonucleosomes (to mimic infinite dilution), each starting from a different starting configuration, were performed. Each simulation run was 50-μs long. The self-diffusion coefficients of the oligonucleosomes were computed from the mean-square deviation of their center of mass as follows

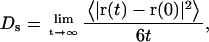(31)

where 〈⋯〉 denotes an ensemble average, and r(t) denotes the center of mass of the nucleosomal array at time t.

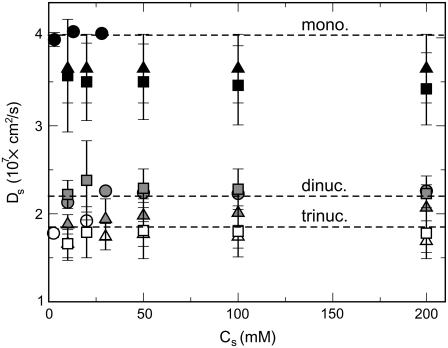
The diffusion coefficients of the mononucleosomes, dinucleosomes, and trinucleosomes computed in this study for the fixed-tail and flexible-tail models as well as those obtained experimentally are plotted in Fig. 8. The quantitative agreement between the simulation results and the experiments is excellent. The flexible-tail model matches the experimental diffusion coefficients better than the fixed-tail model in the case of dinucleosomes and trinucleosomes. Both models indicate that the diffusion coefficients of the dinucleosomes and trinucleosomes increases slightly with the salt concentration, especially between 0.01 M and 0.02 M salt concentration, as in the experiments. For mononucleosomes, the fixed-tail model performs marginally better than the flexible-tail model in terms of agreement with experiments. Again, both models predict the same trend as the experiments, i.e., insensitivity to salt. These results demonstrate that Brownian dynamics simulations of the flexible-tail model reproduce the Brownian motion and dynamics of oligonucleosomes reasonably well.

FIGURE 8.

Dependence of the diffusion constant of mononucleosome (solid symbols), dinucleosomes (gray symbols), and trinucleosomes (open symbols) on the salt concentration. Circular symbols represent experimental values from Yao et al. (57) (mononucleosomes), Yao et al. (58) (dinucleosomes), and Bednar et al. (59) (trinucleosomes). Square and triangular symbols represent results from Brownian dynamics simulations of flexible-tail and fixed-tail model of oligonucleosomes, respectively. The dashed lines, which represent the mean experimental diffusion values for the three array sizes, serve to guide the eye.

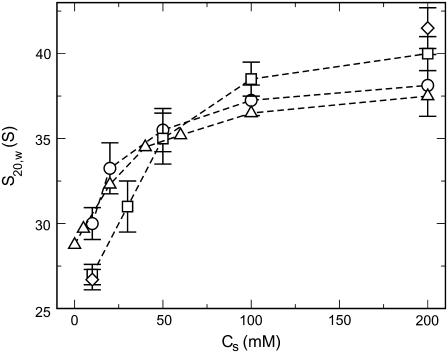
Sedimentation coefficients

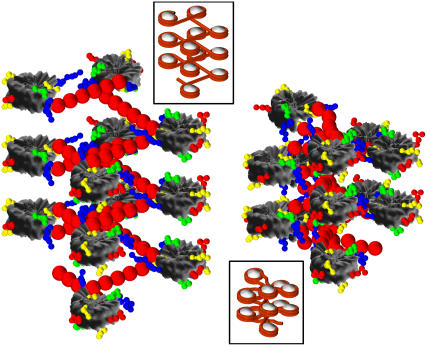
As a final validation of our flexible-tail model, we demonstrate that the structure of an oligonucleosome composed of 12 nucleosomes determined from Brownian dynamics simulations reproduces very well the structure obtained experimentally. Our comparison is against the reconstituted 12-unit nucleosomal arrays without linker histones employed by Hansen et al. (60) with linker DNAs of length 62 bps. To characterize the degree to which the arrays fold, the experiments have determined the sedimentation coefficient, S_20,w, of the arrays at varying monovalent salt concentrations. To model the above experimental system, we employ both the flexible-tail and fixed-tail models with 12 nucleosomes and linker DNAs where each linker is six beads long. Note that the six linker DNA beads represent a DNA length of 18 nm, close to the length of the experimental linker DNA (18.6 nm) obtained by assuming a rise/basepair of 3 Å. We start the simulations with two different initial configurations of the oligonucleosome to sample the feasible range of solenoid and zigzag conformations as done in Sun et al. (30) (see Fig. 9). Both sets of simulations yield a similar ensemble of oligonucleosome conformations. Multiple Brownian dynamics simulation runs with different random number seeds are performed for each type of starting configuration where each run is 5–10-μs long. The salt concentration is varied in the range 0.01–0.2 M, as in the experiments.

FIGURE 9.

Two starting configurations for the 12-unit nucleosomal array simulations corresponding to a solenoidlike (solenoid with straight linkers) configuration (left) and zigzag (right). Insets show corresponding stacking patterns without histone tails. In the main figures, the histone tails are color-coded according to: H3 (blue), H4 (green), H2A (yellow), and H2B (red); the nucleosome cores and linker beads are shaded gray and red, respectively. In the insets, the nucleosome core is white and the wrapped + linker DNA is red.

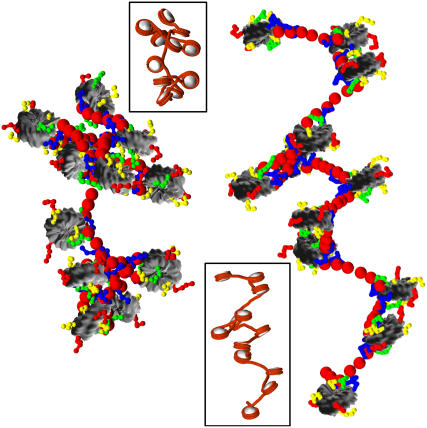
Fig. 10 shows two representative array configurations obtained at the end of the simulation run, one at 0.01 M salt concentration and the other at 0.2 M salt concentration, starting from solenoidlike configuration in Fig. 9. Clearly, the array at the higher salt concentration is more compact, and closely resembles the irregular zigzag configuration of oligonucleosomes obtained experimentally (9,20). The figure highlights the many features of histone tails: their inherently flexible and dynamic nature, their role in mediating internucleosomal interactions at high salt concentrations, and the tendency of the H3 tails, in particular, to attach to linker DNAs and screen out electrostatic repulsions. Such details are not easily obtained via experiments, and a detailed examination of the role of each histone tail in chromatin will be reported separately.

FIGURE 10.

Configuration of the 12-unit nucleosomal array at the end of 5-μs runs at 0.2 M (left) and 0.01 M (right) salt concentration. Insets show corresponding stacking patterns without histone tails. In the main figures, the histone tails are color-coded according to: H3 (blue), H4 (green), H2A (yellow), and H2B (red); the nucleosome cores and linker beads are shaded gray and red, respectively. In the insets, the nucleosome core is white and the wrapped + linker DNA is red.

Here we focus on model validation via comparisons to experimentally obtained S_20,w values. Neglecting the contribution of linker DNA, the sedimentation coefficient of our oligonucleosomes were computed using the relation (61,62)

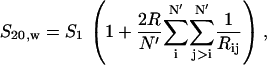(32)

where N′ = 12 represents number of nucleosome units in the oligonucleosome, R is the effective radius of the nucleosomes (taken as the hydrodynamic radius R_c here), S₁ is the S_20,w of a mononucleosome taken as equal to 11.1 Svedberg (S), and R_ij is the distance between two nucleosomes. The reported values sedimentation coefficients have been averaged over all the different starting configurations once the evolution of the sedimentation coefficient with time has stabilized, typically after 3–4 μs.

The sedimentation coefficients computed from our Brownian dynamics simulations using the fixed and flexible-tail models are plotted versus salt concentration in Fig. 11 along with corresponding values obtained from experiments (60) and Monte Carlo simulations of the fixed-tail model (30). Both the experimental and the simulation data show an increase in S_20,w as the salt concentration is increased, indicating an increased compaction of the nucleosomal arrays with the salt concentration. The widely accepted explanation for this trend is that the increased electrostatic screening at high salt concentration decreases linker/linker electrostatic repulsions and allows the linker DNA to come closer to each other, which naturally results in a compaction of the arrays. Our calculations suggest that reducing the salt concentration from 0.2 M to 0.01 M results in a 15-fold increase in the total electrostatic repulsion energy between the linker DNAs for moderately folded oligonucleosomes with S_20,w ≈ 38. The data also show that the flexible-tail model reproduces the experimental S_20,w much better than the fixed-tail model. The fixed-tail model underestimates experimental S_20,w by ∼3 S at low salt concentration (0.01 M) and overestimates S_20,w by ∼2.5 S at high salt concentrations (0.2 M).

FIGURE 11.

Sedimentation coefficients versus salt concentration obtained using Brownian dynamics of the oligonucleosome model developed in this study (open circles). Also shown are sedimentation coefficients obtained experimentally by Hansen et al. (60) (open triangles), and those obtained theoretically using the fixed-tail model (open squares and diamonds). The open squares represent results obtained by Sun et al. (30) via Monte Carlo simulations and the open diamonds represent results obtained via Brownian dynamics simulations in the current study.

We offer two possible explanations for the more dramatic unfolding of the fixed-tail nucleosomal arrays compared to flexible-tail arrays at 0.1 M salt. First, the fixed-tail model cannot account for the partial screening of the linker/linker electrostatic repulsions by the tails; note how the H3 tail of the flexible-tail model achieves this in Fig. 10. Second, the fixed-tail model leads to artificially large angles between the entering and exiting linker DNAs on each nucleosome due to electrostatic attraction between the linker beads and the two fixed H3 tail protrusions (see Fig. 1 of Sun et al. (30)) resulting in highly extended nucleosomal arrays. The angles between the entering/exiting linker DNAs are smaller in the flexible-tail nucleosomal arrays because the more mobile H3 tails (relative to the linker beads) are pulled toward the linker beads, and thus the linker beads do not separate as much as in the fixed-tail model.

At 0.2 M salt concentration, the fixed-tail arrays fold more strongly than the flexible-tail arrays. Our explanation here is that the fixed-tail model results in abnormally large internucleosomal attractive electrostatic energies as compared to the flexible-tail model. Compare the mean core/core attractive electrostatic interactions of −5.8 kcal/mol per nucleosome core (fixed tails) (30) versus −0.9 kcal/mol per core (flexible tails). The core/core energy in the latter scenario includes both direct core-core interactions as well as the internucleosomal core-core interactions mediated via the histone tails. Considering that the chromatin pulling experiments by Cui and Bustamante (63) estimate an internucleosomal attraction energy of −2 kcal/mol for linker-histone inclusive chromatin and that oligonucleosomes lacking the linker-histones (such as those explored in this study) are expected to yield smaller values of internucleosomal energies, our estimate of the internucleosomal electrostatic energy is reasonable. The significantly smaller core/core interactions in the flexible tail simulations are caused by the ability of the flexible histone tails to interact strongly with both the linker DNA (See Fig. 9) and the wound DNA around their parent cores, which discourages the histone tails from protruding out and interacting with other distant nucleosomes, as will be described separately (unpublished work). This feature of histone tails is missing in the fixed-tail model where the histone tails are long and highly charged rigid protrusions of the nucleosome core, which beg to interact with other nucleosome cores.

SUMMARY AND FUTURE APPLICATIONS

The developed coarse-grained model for oligonucleosomes (chromatin), compatible with Brownian dynamics simulations with complete hydrodynamics, is the first to our knowledge to include histone tails contribution directly, so that both the flexibility and charge distribution of the histone tails are properly incorporated. The nucleosome cores (without the histone tails) are modeled using the DiSCO approach developed previously (25,27), which essentially treats the electrostatic and excluded volume interactions of the nucleosome core as a set of discrete charges distributed uniformly on the surface of the core. The linker DNA is represented in a standard fashion using the discrete elastic bead model with physically established parameters. The histone tails are modeled as a chain of charged coarse-grained beads with optimized Debye-Hückel charges and force-field parameters that yield similar conformations as the subunit model of the atomistic histone tails. The comparison of results using Brownian dynamics simulations for the new model against existing experimental data on oligonucleosomes shows very good agreement. In particular, the model matches the histone tail conformations at different salt conditions, dynamics of short oligonucleotides (dimers and trimers of nucleosomes), and structure and energetics of 12-unit nucleosomal arrays. Of particular importance to the correct representation of chromatin is the histone tails' ability to dynamically interact with both linker and wound DNA; the flexible tails are required for correctly balancing tail-mediated internucleosomal interactions and electrostatic shielding of DNA linker repulsion. The cumulative geometric and energetic effect leads to conformations of nucleosomal arrays that agree with experiments.

The flexible-tail model of oligonucleosomes developed here can now be applied to many intriguing problems in chromatin structure and activity. Fundamentally, the model offers a systematic way to dissect the role of each histone tail in chromatin folding under physiological salt conditions. For example, the position distribution of each histone tail may be determined at varying salt concentrations to investigate the role of each tail in chromatin condensation (for example, whether tails prefer to remain free and unbound, bound to either the linker DNA or the nucleosomal DNA of parent or neighboring nucleosomes). The associated timescales of binding and unbinding events can also be estimated. Relevant experimental data on the positional preference of histone tails are emerging by Hansen group (18,19). Additionally, it will be interesting to investigate how the tail-mediated interactions change with the size of the nucleosomal arrays and what subunits of the chromatin fiber may define an appropriate building block for yet further coarse-grained models of chromatin. Brownian dynamics simulations should also allow us to investigate the dynamics of folding and unfolding at high and low salt concentrations, which may have profound applications in the repression and activation of genes.

The development of the flexible-tail model also opens opportunities to explore the impact of a range of histone tail modifications and variants on chromatin structure. Though it is well appreciated that acetylation of certain histone tail residues is associated with gene activation, it is not known whether this effect is mainly physical, i.e., due to reduction of electrostatic charge on the tails resulting in a concomitant reduction in tail-mediated internucleosomal interactions, or more biological, as a signal for recruitment of certain chromatin associated proteins. The effect of acetylation—and many other histone tail modifications such as ubiquitination, methylation, and phosphorylation—may easily be treated in our flexible-tail model through shifts in the charge carried by the protein beads of the histone tails, and concomitant adjustments in parameters related to the excluded volume of the histone tail protein beads, stretching and bending. A similar approach could also be followed to investigate the effect of the incorporation of histone tail variants such as H2A.X and H2A.Z.

Of course, further improvements in the flexible-tail model can be envisioned. The effect of linker histones (H1 or H5) may be incorporated, either through changes in the effective linker/linker interactions, or through incorporation of additional charged protein bead units to model the linker histones. Interchromatin fiber interactions, which likely play an important role in higher-order folding of chromatin, may also be pursued (64).

APPENDIX

The subunit model (43–45) in the University of Houston Brownian Dynamics program (47) represents each amino-acid residue as a sphere (subunit) with its center located at the C^β of the amino acid. Identical hydrodynamic radii of 3.5 Å are assigned for all the subunits, and harmonic bond stretching and bond angle bending potentials are employed according to Weber et al. (46). The temperature and time step of the Brownian dynamics simulations is set to 300 K and 0.01 ps, respectively. Simulations on each histone tail are performed for 100-ns time intervals. The energy of the subunit model is defined as

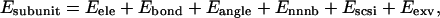(33)

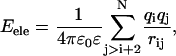(34)

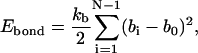(35)

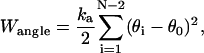(36)

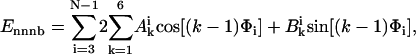(37)

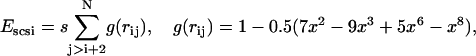(38)

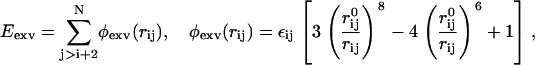(39)

where E_ele, E_bond, E_angle, E_nnnb, E_scsi, and E_exv are the Coulombic electrostatic energy, the bond energy, the bond-angle bending energy, the nearest-neighbor nonbonded energy, the side-chain solvation interaction energy, and the excluded volume energy; N is the number of subunits in the tail; and r_ij is the distance between subunits i and j. The value ɛ₀ is the electric permittivity of vacuum; ɛ is the solvent dielectric constant; q_i and q_j are the charges on subunits i and j, respectively (+ 1e for lysine and arginine, −1e for aspartic acid and glutamic acid, and 0 for the rest of the amino acids); b_i is the bond length between subunits i and i + 1; the equilibrium bond length b₀ = 5.14 Å and the bond constant k_b = 40 kcal/mol/Ų (44,46); θ_i is the angle between subunit i, i + 1, and i + 2; θ_i0 = 87.2° is the equilibrium bond angle and the bond angle constant is given by k_a = 40 kcal/mol/rad² (44,46); Φ_i is the dihedral angle defined for subunits i − 2, i − 1, i, and i + 1 with Φ_i = 0 corresponding to the eclipsed conformation; 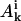and are the coefficients dependent on the identity of the subunit i (44); s is the side-chain solvent interaction force constant dependent on subunit i (44); x = r_ij/9, r_ij < 9 Å; and ε_ij and are the excluded volume force constant and distance dependent on subunits i and j (44).