Kinetic Definition of Protein Folding Transition State Ensembles and Reaction Coordinates

Abstract

Using distributed molecular dynamics simulations we located four distinct folding transitions for a 39-residue ββαβ protein fold. To characterize the nature of each room temperature transition, we calculated the probability of transmission for 500 points along each free energy barrier. We introduced a method for determining transition states by employing the transmission probability, P_trans, and determined which conformations were transition state ensemble members (P_trans ≈ 0.5). The transmission probability may be used to characterize the barrier in several ways. For example, we ran simulations at 82°C, determined the change in P_trans with temperature for all 2,000 conformations, and quantified Hammond behavior directly using P_trans correlation. Additionally, we propose that diffusion along P_trans may provide the configurational diffusion rate at the top of the barrier. Specifically, given a transition state conformation x₀ with estimated P_trans = 0.5, we selected a large set of subsequent conformations from independent trajectories, each exactly a small time δt after x₀ (250 ps). Calculating P_trans for the new trial conformations, we generated the P(P_trans|δt = 250 ps) distribution that reflected diffusion. This approach provides a novel perspective on the diffusive nature of a protein folding transition and provides a framework for a quantitative study of activated relaxation kinetics.

INTRODUCTION

Determining transition state structures is important for protein folding theory because the activated conformations are of pivotal importance for folding and unfolding kinetics. Given equilibrium sampling of a free energy barrier, the transition state ensemble (TSE) corresponds to the set of conformations of highest free energy along the path or paths of lowest free energy between the native folded (F) and unfolded (U) macrostates. Simple reactions such as bond breaking in a diatomic molecule have a clear pathway. In contrast, proteins have many degrees of freedom, and the conformational changes of proteins may be imperfectly captured in one- or two-dimensional reaction coordinates. Work from many groups has demonstrated the usefulness of root mean-square deviation (RMSD), the fraction of native contacts Q, principle components, or otherwise optimized structural reaction coordinates (1–5). Despite demonstrated utility, low dimensionality is an approximation and the search continues for more universal solutions to the “curse of dimensionality”.

Advances in computer power and new path sampling algorithms have allowed progress in this direction (6–9). It is now tractable to determine if a structure is a member of the TSE without constructing a reaction coordinate (10–12). For example, after defining folded and unfolded sink states, one can calculate the probability that a given conformation reaches the folded sink before it reaches the unfolded sink. If this commitment probability, P_fold, is ∼0.5, then the structure lies along the high dimensional hyperplane (separatrix) between the sink states. The TSE is a set of low free energy conformations on the separatrix.

Here, we introduce new methods related to P_fold and use them to probe the activated kinetics of the 39-residue N-terminal domain of L9 (L9–39). Although L9–39 is small, it is a challenging system to examine computationally, due to its complex topology and a relatively slow millisecond folding timescale. Although the system appears two state to experimental probes (13), we found an unfolding mechanism that included parallel unfolding pathways with intermediates. We will describe the detailed L9–39 folding mechanism elsewhere. Here, we focus on the methodology needed to characterize the observed free energy barriers with extensive kinetic simulations.

METHODS

P_fold determination

The division of the continuous free energy landscape into macrostates is arbitrary unless there is a dominant free energy barrier. One logical division scheme defines macrostates that mimic experimental observables. For example, Shakhnovich and co-workers tested folding cutoffs that calculate tryptophan burial (14). An alternate approach is to define kinetic macrostates. In the presence of a dominant barrier the system acquires a slow global relaxation time, τ_rxn, and it becomes possible to self-consistently divide the conformational space into stable macrostates (minima F and minima U).

The mean first passage time for trajectories released from a U microstate to capture at an F sink should yield the phenomenological rate constant. In comparison to the slow barrier-crossing timescale, relaxation of an activated conformation to a sink is rapid and rarely experimentally resolved (15). In this study, we are interested not only with the mean time to capture but with the identification of activated conformations. Activated conformations have a significant probability of absorption by sinks in both F and U. In the limit of an infinite number of trajectories of infinite length, the ratio of trajectories captured by the F sink is rigorously converted into a probability.

In practice, we have only a finite number of trajectories, and it is not trivial to precisely calculate mean first passage times or the relative probability of capture at sink F and U. Determining a P_fold value is a large computational expense. Instead, we take the following approach. For each tested conformation, x₀, N molecular dynamics (MD) trajectories are started from x₀ (with randomized initial velocities drawn from a Maxwell distribution). Since the trajectories are long enough to reach either the folded or unfolded state, every simulation has only two possible outcomes. Therefore, each simulation represents a Bernoulli trial. Given a conformation specific transmission probability, P_fold(x₀) = p, we expect a finite sequence of N independent Bernoulli trials to contain n folding events with probabilities determined by the binomial distribution .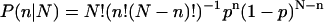

Unfortunately, statistical error is an obstacle to the application of this method. The uncertainty in each P_fold calculation may be estimated by the standard deviation of the binomial distribution mean, 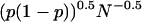, such that a P_fold value calculated using 80 simulations retains half the statistical error of a P_fold value calculated with 20 simulations. In this work, we employ an alternate treatment of the statistical error using Bayesian inference (Appendix) to estimate each specific transmission probability. Our error bounds are 95% credible intervals for each P_fold obtained by integrating the Bayesian posterior distribution.

The idea of conformation-specific transition probabilities has a long history, and the term P_fold has been used to describe several subtly different calculations. Onsager originally described a splitting probability for the case of ion-pair recombination (16). With increased computational power it became possible to apply this idea to complex reactions. Du et al. calculated the relative probability of reaching sink F before sink U for a lattice protein, where sink F corresponded to the native microstate and sink U corresponded to an unfolded macrostate with few native contacts (12). Thanks to the computational tractability of lattice protein models, they were able to run many trial Monte Carlo (MC) trajectories to completion (N = 400) from each initial conformation of interest. A similar approach was applied to all-atom MD simulations of a hairpin, terminating trial trajectories when they reached specified cutoffs (17). Whereas Du et al. originally termed their calculation a “transmission coefficient” it is now often termed the probability of folding, P_fold. Caflisch and co-workers have applied these methods to atomistic MD simulations of various systems including sizable proteins. For example, Gsponer and Caflisch calculated six approximate P_fold values (N = 10) for an SH3 domain (18). P_fold calculations are challenging because the relaxation times can be quite slow; 10% of the SH3 simulations had not reached either sink after 200 ns. Such uncommitted trajectories are common and are problematic because excluding uncommitted trajectories from the P_fold ratio decreases the precision and rigor of the calculated probabilities.

Timescale of commitment

Others have explicitly considered the timescale for commitment, adopting a methodology that eliminates uncommitted trajectories by construction. Rather than calculating the probability of reaching sink F before sink U, one calculates the probability of being within macrostate F after some elapsed time, τ_commit. To understand why a short relaxation time τ_commit is sufficient, we refer to nonequilibrium statistical mechanics. The Onsager regression hypothesis asserts that relaxation from a prepared nonequilibrium ensemble is related to the equilibrium relaxation of a spontaneous fluctuation (19,20). Chandler provides a derivation of this relationship using the fluctuation-dissipation theorem and linear response theory with the assumption that the initial perturbed ensemble is not far from equilibrium (21). Dellago, Bolhuis, and Geissler derive the Onsager regression hypothesis for arbitrarily large perturbations away from equilibrium (22).

Here, each initial nonequilibrium ensemble consists of a single activated protein conformation with randomly selected Maxwell-Boltzmann initial velocities. The activated conformation must relax to a nonequilibrium population of macrostates F and U within the transient τ_commit interval. From this initial nonequilibrium population of F and U, we may calculate the reactive flux across a dividing cutoff between F and U (21,23). After τ_commit, the reactive flux across the cutoff matches the phenomenological rate constant. The τ_commit time is much shorter than the barrier-crossing time τ_rxn. This separation of timescale between τ_commit and τ_rxn is a natural consequence of the free energy barrier. Long timescale behavior (δt > τ_rxn) is quite different: all correlation with x₀ is lost, the reactive flux goes to zero, and the ensemble fraction of F and U approaches the equilibrium constant. Roughly speaking, we may think of τ_commit as A), the timescale for relaxation from the transition state to the free energy minima, B), the timescale at which recrossing the dividing surface becomes negligible, or C), the timescale at which the ensemble fraction on either side of the cutoff reaches a plateau (24).

These properties allow us to calculate transmission probabilities after an elapsed time. For example, Hubner et al. calculated the fraction of MC trials that met various folding cutoffs after τ_commit = 10⁷ MC steps (14). In other words, Shakhnovich and co-workers estimated the time necessary for trial trajectories to commit to a stable macrostate and calculated the fraction within macrostate F at this time. They term this fraction P_fold. An alternate terminology was introduced by Bolhuis and co-workers, who define the “committor” P_A, the probability that short trajectories initiated from a particular configuration with randomly chosen initial moments will end inside cutoff F after a short interval τ_commit.

We employ a committor we call the probability of transmission, P_trans(δt,x₀). We define P_trans(δt,x₀) in the following manner: we choose a fixed dividing surface separating product from reactant, start N trajectories from a specific conformation x₀, and calculate the fraction of trajectories on the product side of the dividing surface after an elapsed time δt (Fig. 1). We call our committor P_trans because it is defined over four different transitions rather than a single folding transition. Also, we wish to avoid overloading the term P_fold. We defined P_trans values for each barrier in such a way that P_trans = 1 corresponds to commitment to the more folded state and P_trans = 0 corresponds to the less folded state. Where convenient, we include the arguments δt and x₀ to emphasize that each P_trans(δt,x₀) calculation is specific to an individual conformation and depends on the elapsed time. Qualitatively, P_trans(δt,x₀) and P_fold both aim to provide the same splitting probability. Excepting the placement and sensitivity analysis of the cutoff at the barrier top and the explicit consideration of the convergence with time, our P_trans(δt,x₀) calculations are quite similar to previous P_fold calculations (14).

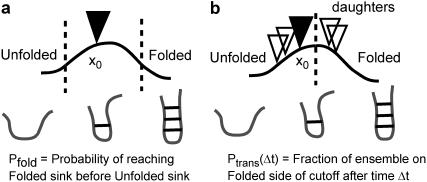
FIGURE 1.

Two kinetic parameters: P_fold and reactive flux. (a) The P_fold value is not defined until trajectories cross the cutoffs. Trajectories that do not commit within the simulation time are often ignored. In contrast, (b) the transmission probability P_trans(δt) is always defined but is a function of elapsed time. To compute a P_trans diffusion value at the barrier top, we start new ensembles of simulations from multiple daughter conformations.

L9–39 K12M, model system

Our model protein is L9–39 K12M, a truncated mutant of the ribosomal protein L9 (13). This system has a complex ββαβ topology and folds on the millisecond timescale. The parent molecule NTL9 has been thoroughly studied by the Raleigh laboratory (25–28). NTL9 consists of the first 56 residues of the L9 protein from Bacillus stearothermophilus. Crucially, Horng et al. reported that the first 39 residues (L9–39) are stable in isolation and that a point mutant (L9–39 K12M) folds more rapidly (13).

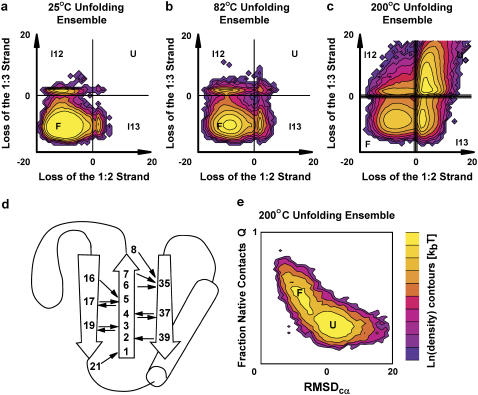
Native state simulations at moderate and high temperature have produced many unfolding events (complete loss of the β-sheet), and we describe new order parameters to track the loss of each strand pair (1:2 and 1:3). A set of native sheet hydrogen bonds was chosen from inspection of native state simulations (Fig. 2 D). A set of strand α-carbon positions was chosen from inspection of the native NMR model. The two strand pair order parameters (S1:2, S1:3) are the sum of the DSSP (http://swift.cmbi.ru.nl/gv/dssp/) hydrogen bond energy for the set of hydrogen bonds between each strand (E1:2, E1:3) and the RMSD of the inter-α-carbon distance matrix (dRMSD) to the equivalent native model strand pair (D1:2, D1:3). The electrostatic component provides dynamic range to distinguish strand pairs with strong native hydrogen bonds, and the dRMSD component tracks differences between conformations that lack native hydrogen bonds.

FIGURE 2.

Unfolding landscape and topology of L9–39 K12M. Large MD ensembles were started in the native state at (a) 25°C, (b) 82°C, and (c) 200°C. In each plot, the log probability of observing a conformation is calculated for all combinations of the strand quality parameters S1:2 and S1:3. Moving from left to right corresponds to breaking the 1:2 strand pair. Moving from bottom to top corresponds to breaking the 1:3 strand pair. The histograms are displayed as surfaces with k_BT contours. We study net ensemble population changes of each quadrant (folded F, unfolded U, intermediates I12 and I13). The 200°C ensemble illustrates cutoffs at ±0.5 in addition to the normal 0 cutoff. We also show (d) the topology of L9–39 and a set of native hydrogen bonds. (e) The 200°C ensemble was also projected along RMSD_cα and the fraction of native contacts Q. This projection obscures the strand pair intermediates.

We made precise kinetic calculations by collecting over 600,000 individual MD trajectories, representing over 11 ms of atomistic simulation (Table 1). MD trajectories were simulated in 10-ns segments by volunteer processors on the Folding@Home distributed computing platform (29). We used a 2-fs timestep and recorded protein conformations every 250 ps. Simulation details were similar to previous protein folding simulations (30) using the TINKER (31) implementation of Allen's stochastic integrator (32) with the OPLS unified atom force field (33) and the Still generalized Born/surface area implicit solvent model (34).

TABLE 1.

MD ensembles aggregate simulation time and lengths

L9–39 K12M Ensemble	Aggregate [μs]	No. to 10 ns	No. to 20 ns	…	No. to 100 ns
Unfolding at 200°C	203	4706	3636		491
F to I13 at 25°C	1694	75,000	74,999
F to I12 at 25°C	1365	69,928	47,438
I13 to U at 25°C	1359	69,993	47,286
I12 to U at 25°C	1359	69,911	47,360
F to I13 at 82°C	977	49,255	48,477
F to I12 at 82°C	976	49,188	48,430
I13 to U at 82°C	1438	72,928	70,906
I12 to U at 82°C	1435	72,829	70,678
Ptrans-diffusion at 25°C	1146	57,510	57,046

The transitions of interest are in the high friction or spatial diffusion limit. In this limit, inertia plays no role because the transitions of interest are much slower than the timescale at which velocities decorrelate. This is true by construction for our Langevin simulations because the polymer particles are impacted by a random force that mimics the thermal buffeting of solvent. This external buffeting is modeled via a friction coefficient (91 ps⁻¹) chosen to reproduce water viscosity (35). The protein experiences collisions that alter velocities unpredictably after several MD timesteps. In comparison, the collective transitions of interest occur over hundreds of thousands of MD timesteps.

RESULTS

Diffusive dynamics on the L9–39 projection

We bin all observed conformations from 25°C, 82°C, and 200°C unfolding ensembles in terms of the two strand pair order parameters and contour the log probability in Fig. 2, a–c. Two features stand out. First, unfolding trajectories are extremely rare at 25°C. Second, concerted loss of both β-strands is unusual compared to sequential loss through discrete hairpin intermediates. These plots do show comparable transitions at each temperature but do not quantitatively reveal the free energy surface because the underlying ensembles are not at equilibrium.

We show the same 200°C unfolding ensemble in terms of two other popular order parameters: α-carbon RMSD_cα to the native model and the fraction of native contacts retained, Q (Fig. 2 e). The set of native contacts was chosen from inspection of the 25°C native ensemble after 100 ns. The RMSD_cα and Q order parameters do not resolve the strand pair intermediates noted in Fig. 2 c. Similarly, we expect that additional distinct kinetic species are unresolved by the S1:2 and S1:3 strand quality order parameters. Unresolved kinetic species are troublesome when they persist for timescales exceeding the simulation length.

S1:2 and S1:3 successfully separate macrostates as shown in Fig. 2, a–c, but individual reactive trajectories cross the dividing cutoffs many times. Therefore, S1:2 and S1:3 are effective order parameters but are not optimal reaction coordinates. Interpreting single trajectory motion in terms of strand pair quality is difficult because the dynamics are diffusive, depend on orthogonal degrees of freedom, and are rough at the 250-ps frequency at which we record snapshots. These shortcomings make it difficult to directly extract barrier-crossing dynamics of single trajectories. Furthermore, it is inappropriate to interpret the strand pair order parameters physically because they combine geometric and energetic criteria and thus lack meaningful units.

Such difficulties can be bypassed with ensemble measurements. To characterize the rate of transition from the native basin to an intermediate, we may simply consider the net change in population. We divide the L9–39 conformational space into four quadrants (Fig. 2, a–c) corresponding to the folded state F, the intermediate state I13 that retains the 1:3 strand pair, the intermediate state I12 that retains the 1:2 strand pair, and the unfolded state U. The two dividing cutoffs are quite simple and correspond to S1:2 or S1:3 = 0. Shifting this cutoff ±0.5 along each barrier changed the P_trans values very little (0.048–0.063 RMSD). The transmission probability is robust with respect to the cutoff because the overlap between macrostates is minimized at the dividing surface.

Calculating P_trans for conformations along specific barriers is slightly complicated by the existence of four macrostates. It is an approximation to treat individual barriers as independent two-state transitions. For example, when measuring P_trans for an activated F-I13 conformation (loss of the 1:2 strand pair), a small fraction of the trajectories (<5%) appears to cross the other cutoff (loss of 1:3). These cutoff crossing events reflect both noise and true side reaction transitions. A meaningful P_trans(δt,x₀) value should exist as long as δt is short compared to subsequent processes that affect the ratio of product to reactant. When computing each P_trans value, including or excluding the small side reaction fraction produced similar results (data not shown). We included this fraction. For example, when measuring the P_trans for the F-I13 transition, the unfolded quadrant is treated as equivalent to the I13 quadrant and the I12 quadrant is treated as equivalent to the F quadrant (Fig. 2).

Kinetic memory, a transition state identification heuristic

We used a heuristic to select putative TSE members from a 200°C unfolding ensemble. The ensemble consisted of thousands of simulations of varying length (e.g., 4,700 simulations reach 10 ns, 1,500 continue to 50 ns) for an aggregate simulation time of more than 200 ms. This ensemble contains more than 500 independent unfolding events through each identified barrier (using S1:2 and S1:3). For each unfolding event, we selected the last conformation before barrier crossing. To filter out transitions that rapidly recross the cutoff, we provided each conformation with a 1-ns kinetic memory and considered only putative transition state conformations from trajectories that dwell in both the prior and posterior quadrant for 1 ns. We collected 500 putative conformations for each identified barrier and calculated the transmission probability for each conformation. Despite our efforts to pick conformations that correspond to pivotal barrier-crossing instances, only a subset (∼10%) of the putative TSE members had transmission probability values between 0.4 and 0.6 (Fig. 3 a). This reflects the difficulty of selecting TSE members using a heuristic and underscores the need to validate putative TSE conformations.

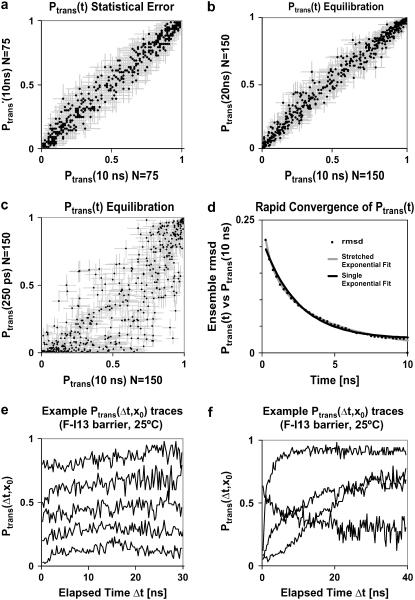
FIGURE 3.

We show P_trans values for 500 conformations along the F-I13 barrier (loss of the S1:2 strand pair) as calculated using a large ensemble of ∼70,000 simulations with ∼140 trajectories for each initial conformation. (a) To illustrate statistical P_trans error, we compare the P_trans estimate from each half of the data. (b) P_trans(20 ns) values were similar to P_trans(10 ns) values. Error bars represent the Bayesian posterior 95% interval. At short times many P_trans(δt,x₀) traces have not yet converged as seen in c, the correlation between P_trans(250 ps) and P_trans(10 ns). (d) As a function of time, the RMSD between the P_trans(δt,x₀) values and the P_trans(10 ns,x₀) values may be approximated as an exponential decay with k = (2.4 ns)⁻¹ or a stretched exponential with k = (1.8 ns)⁻¹ and β = 0.48. (e) Many P_trans(δt,x₀) traces plateau immediately or within 10 ns. Examples were chosen to minimize overlap. (f) Other P_trans(δt,x₀) traces equilibrate dramatically, or occasionally plateau slowly.

P_trans statistical error and convergence

It is difficult to precisely calculate P_trans because the statistical noise is proportional to N^−0.5. Increasing N to obtain higher precision has sharply diminishing returns. Despite the immense computational cost, we obtained thousands of precise P_trans values (N > 100) over the course of 9 months. Hundreds of thousands of simulations were provided by the Folding@Home distributed computing platform. For example, we determined P_trans (N = 150) for 500 different initial conformations across the F-I13 barrier (loss of the 1:2 strand pair). Fig. 3 a illustrates the statistical noise we must overcome; we plot the P_trans correlation between each half of the data set such that each axis is determined with N = 75 simulations (0.056 RMSD).

To most accurately estimate the probability of transmission, we must run simulations long enough that P_trans(δt,x₀) converges to a plateau. Unless otherwise noted, all P_trans values represent the ensemble fraction calculated at 10 ns, P_trans(10 ns,x₀). To demonstrate that 10 ns is a reasonable commitment time, we show the good correlation between P_trans(10 ns,x₀) values and P_trans(20 ns,x₀) values (Fig. 3 b) with RMSD values for each barrier (500 conformations) ranging from 0.043 to 0.058. Transmission probability values calculated after 5 ns, P_trans(5 ns,x₀), were also quite similar (RMSD = 0.061) to P_trans(10 ns,x₀). In contrast, P_trans values calculated in the first several nanoseconds had not yet converged. For example, the P_trans(250 ps,x₀) values were quite different (RMSD = 0.219) from the P_trans(10 ns,x₀) values (Fig. 3 c). The rate at which the P_trans(δt,x₀) values converged to a stable value could be observed by plotting the RMSD of all P_trans(δt,x₀) values versus all reference P_trans(10 ns,x₀) values (Fig. 3 d). Given the rapid decay in the RMSD of all P_trans values, we infer that most individual P_trans(δt,x₀) values quickly converge. This relaxation is imperfectly fit by a single exponential decay with rate constant k_decay = (2.4 ns)⁻¹ and is well fit by a stretched exponential 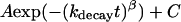with k_decay = (1.8 ns)⁻¹ and the stretching factor β = 0.51.

These rates provide a rough estimate for the molecular timescale τ_commit of this barrier. Stretched exponentials have been previously used to model downhill processes or processes with many relevant kinetic states (36). The rapid relaxation of an activated ensemble of varied initial states fits both criteria. It is difficult to extract additional information from this initial relaxation. At short times (Fig. 3 c), the P_trans is usually lower than the plateau value, reflecting a transient unfolded excess. This property might reflect the origin of the initial conformations from the high temperature 200°C ensemble or a tendency of the selection heuristic (which selects putative transition states immediately before unfolding events).

We show typical P_trans(δt,x₀) time courses in Fig. 3, e and f. A small fraction of the initial conformations do not reach stable P_trans(δt,x₀) values in the length of our simulations. This is a source of noise in the remaining analysis. We have not culled unconverged P_trans(δt,x₀) values to avoid introducing bias. One direction for future work is the careful time averaging and extraction of P_trans(δt,x₀) plateau values from each P_trans(δt,x₀) trace.

The challenges associated with precisely calculating P_trans values are significant: both the requirement for hundreds of MD simulations per trial conformation and the requirement that these simulations reach the characteristic timescale τ_commit. We have demonstrably satisfied these constraints here given four distinct strand pair transitions of a small protein that folds on the millisecond timescale. It is quite likely that longer proteins will exhibit transitions that require MD simulations of greater length. It may also be difficult to map larger protein motions to distinct two-state barrier-crossing events, a necessary precondition for studying the kinetics of activated conformations using these methods.

P_trans correlation and Hammond effects

Now we turn to the applications of detailed kinetic observations. One question we address is the effect of polymer temperature on the TSE. To consider the effect of temperature on both the protein and solvent, one would ideally employ an explicit solvent model parameterized to reproduce solvent properties and the hydrophobic effect over a large range of temperature values. In the absence of such models, we have employed an implicit solvent model that does not change with temperature. Accordingly, our high temperature simulations only reflect the effect of temperature on the polymer. This perturbation is useful to determine the nature of the folding reaction at room temperature through observable shifts in P_trans. Also, we probe the shape of the 25°C and 82°C free energy landscapes at points chosen from nonequilibrium high temperature unfolding ensembles. Ideally, such probe points would be selected from an equilibrium ensemble at room temperature to guarantee that the points sample a relevant portion of the landscape.

Caveats aside, we believe that we have sampled the relevant TSEs and can generalize the effect of polymer temperature. A drastic change in the L9–39 TSE due to polymer temperature seems unlikely given the similar saddle point positions observed in the strand quality projection (Fig. 2, a–c). Robust unfolding mechanisms with respect to temperature have been observed in previous simulations including explicit solvent unfolding simulations (37).

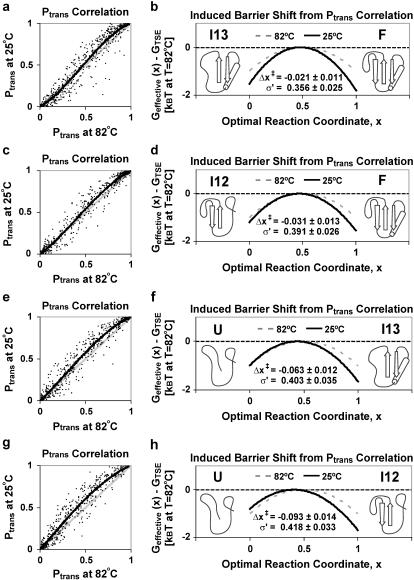
The expected effect of elevated temperature is Hammond behavior: the TSE should become more similar to the native state. For example, a conformation that is a transition state conformation with P_trans = 0.5 at room temperature would have P_trans < 0.5 at elevated temperature. Fig. 4 shows the P_trans correlation between 25°C and 82°C for each trial conformation. As expected, the room temperature P_trans values were higher than the P_trans values at the experimental T_m. Qualitatively, the 25°C and 82°C free energy barriers appear quite similar. We then calculated the transition state shifts (Δx^‡) and barrier width changes (σ′) most consistent with observed P_trans shifts, assuming a quadratic free energy barrier shape. For a more detailed explanation of the fitting routine and theory, we refer the reader to Rhee and Pande (38). In all cases, the small observed temperature shifts qualitatively matched expected Hammond effects, moving the TSE toward the more folded minima. Furthermore, the sigmoid shape of Fig. 4 a reveals that the F-I13 free energy barrier both shifts slightly and contracts as the temperature drops to 25°C. The barrier contraction may be rationalized by considering that low temperature is likely to stabilize I13 in addition to F. Since P_fold is exponentially dependent on the free energy barrier (38), we expect P_trans correlation to be a sensitive probe of perturbations to the free energy landscape.

FIGURE 4.

P_trans correlation along the (a) F-I13, (c) F-I12, (e) I13-U, and (g) I12-U barriers at room temperature (25°C) and the experimental T_m (82°C). Each room temperature (and T_m) P_trans value was calculated as the refolding fraction at 10 ns of ∼140 (∼100) trajectories. The correlation plots show the identity line (gray) and the fit obtained for a change in barrier mean and width (black). (b, d, f, and h) We show schematics for the best fit shift in the barrier width and position. With the T_m barrier as the quadratic reference (dashed), we show the best fit shift Δx^‡ and width σ′-values most consistent with the observed P_trans correlation upon reducing temperature to 25°C (solid) with 95% bootstrap confidence limits.

Due to finite sampling, there is noise in the P_trans(δt,x₀) values, but the deviations from the identity line are small. To gauge the certainty of the fitting process and construct confidence intervals for the calculated changes in barrier width and position, we use a bootstrap error analysis. Essentially, we repeated the P_trans correlation fitting process for 100 bootstrap samples. Each bootstrap sample contains 500 P_trans values drawn with replacement from the full P_trans distribution. Using 95% confidence bounds, we found that the most evident differences between each barrier were statistically justified (Fig. 4); namely, the TSE shift for the I12-U transition is larger than the TSE shift for I13-U, which is in turn larger than the TSE shift for the other two transitions. Also, the 25°C barrier width decreases more for the F-I13 transition than the other three transitions. These P_trans correlation calculations provide a first step toward quantitative Hammond effect analysis, with comparison of the magnitude of barrier shifts and width changes.

P_trans diffusion rate and transition rate theory

To the extent that the free energy profile along P_trans is the ideal one-dimensional coordinate for representing reaction kinetics, the intrinsic diffusion constant along this coordinate is the ideal configurational diffusion constant. In the limit of small perturbations around the TSE, we postulate that diffusion along the P_trans reaction coordinate should reflect flat one-dimensional diffusion (i.e., in the absence of a free energy gradient). If this hypothesis is correct, we would predict a Gaussian distribution of P_trans values to arise from a transition state after short times.

Calculating a configurational diffusion constant directly from simulation is an avenue for comparison with analytical folding theory. Theoretical work related to diffusion along structural reaction coordinates is quite extensive (39–45). For example, Wolynes and co-workers relate the configurational diffusion constant on a structural reaction coordinate Q to the autocorrelation time of Q within a neighboring basin of attraction (39). Baumketner and Hiwatari provide a recent example, calculating the configurational diffusion constant along a physical reaction coordinate for an off-lattice hairpin using an ensemble averaged time correlation (40). We believe that direct calculation of diffusion at the TSE using a kinetic reaction coordinate will complement theories that have been developed for the diffusion of proteins along structural reaction coordinates.

We calculated diffusion along the P_trans coordinate for the F-I13 transition. To do so, we constructed the distribution P(P_trans|δt = 250 ps) using 144 trial daughter conformations, each a snapshot 250 ps after an initial father conformation x₀ with P_trans ≈ 0.5. The father conformation is the validated transition state conformation shown in Fig. 5. We expected 250 ps to be a short interval relative to barrier crossing and thus anticipated that most of the 144 daughter conformations would also be transition state conformations. We calculated P_trans for each conformation. As expected, the daughter conformations were still activated (0.20 < P_trans < 0.70). The daughter distribution P(P_trans|δt = 250 ps) is shown in Fig. 6 a. For a finite number of shooting trajectories, N, the width of the daughter distribution is partially due to uncertainty in each P_trans calculation. To minimize the contribution of the statistical uncertainty, we simulated many (N » 400) trajectories for each daughter P_trans value.

FIGURE 5.

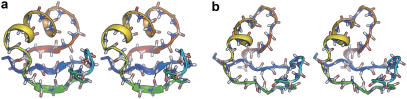
Stereodiagrams for L9–39 K12M, including (a) a native model derived from Protein Data Bank identification No. 1CQU and (b) a thoroughly characterized transition state (x₀) example for the loss of the strand 1:2 pair. This conformation has one clear hydrogen bond (black) between strands 1 and 2 (H-5–O-17). P_trans(10 ns) = 0.5 from 144 simulations after 10 ns, meaning that exactly half of the simulations refold the S1:2 strand pair.

FIGURE 6.

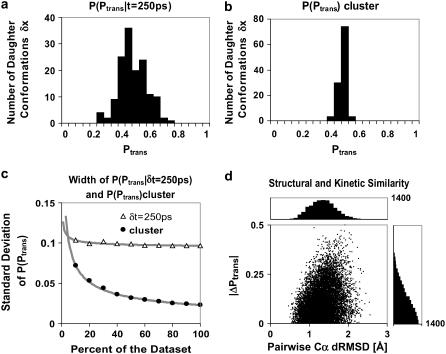
(a) Distribution of P_trans values P(P_trans|δt = 250 ps) for 144 daughter conformations of father conformation x₀ with P_trans(10 ns,x₀) ≈ 0.5. (b) We calculate the P_trans(10 ns) for the entire cluster of initial daughter conformations with 110 uniform samples (N ≈ 432). The P(P_trans)_cluster distribution width represents statistical noise. (c) Convergence of the standard deviation of P(P_trans|δt = 250 ps) and the cluster P(P_trans) as we include more trajectories for each P_trans value. (d) Because the 144 daughter conformations had only 250 ps to diverge from x₀, the C_α-C_α dRMSD between each pair of conformations ranges from 0.46 to 2.56 and the ΔP_trans between each pair ranges from 0.00 to 0.50. It is difficult to infer kinetic similarity from structural similarity, yet a cutoff under 1 Å C_α dRMSD might serve.

We present three arguments that N » 400 is sufficiently large. First, the standard deviation of each Bayesian P_trans estimate is small (∼0.024) relative to the observed standard deviation (0.097) of the P(P_trans|δt = 250 ps) distribution. Second, we extracted an estimate for the limiting standard deviation of the P(P_trans|δt = 250 ps) distribution by plotting the standard deviation for cumulative subsets of the data (Fig. 6 c). The standard deviation of the P(P_trans|δt = 250 ps) distribution decays with increasing N, converging to a limiting standard deviation. Specifically, the standard deviation trend was least squares fit by A × N^−0.5 + C with C = 0.093. Third, we directly illustrate the statistical noise (Fig. 6 b) by regrouping ∼50,000 simulation outcomes to construct 110 uniformly distributed samples (three trajectories per daughter conformation, N ≈ 432). In other words, we calculate P_trans for a cluster of similar conformations rather than one distinct conformation. Each of these 110 samples is an independent estimate of the P_trans value for the entire cluster of daughter conformations. Accordingly, the width of the resulting distribution, P(P_trans), reflects statistical noise, and the standard deviation trend was successfully least squares fit by A × N^−0.5. These three arguments demonstrate that the spread seen in Fig. 6 a is not merely the statistical noise associated with individual P_trans calculations but is instead related to the properties of the 250-ps daughter ensemble.

The calculation of P_trans for an entire cluster is not merely a control. One might wish to treat the entire set of daughter conformations as a homogeneous cluster because they are structurally and kinetically related. In fact, Rao et al. have provided a precedent, employing an algorithm that calculates P_fold for a cluster of structurally related conformations given a long equilibrium simulation (46). Given sufficient trajectories, the P_trans value of a cluster should converge to a single value corresponding to the ensemble average P_trans. Indeed, if we estimate P_trans using all data for the daughter cluster, n = 26,346 and N = 57,510, we obtain the most precise commitment fraction calculated to date (P_trans = 0.458 ± 0.002).

The P(P_trans|δt = 250 ps) distribution reflects diffusion along a kinetic reaction coordinate. The Gaussian shape of this distribution (0.01 skewness and 0.04 kurtosis) supports the hypothesis that kinetic diffusion near the TSE is flat. As a proof of concept, we use the P(P_trans|δt = 250 ps) distribution to obtain a configurational diffusion constant. As described above, the standard deviation of the P(P_trans|δt = 250 ps) distribution was estimated to be 0.093 in the limit of large N. Therefore, the most rapid motion along the P_trans coordinate, ΔP_trans/δt, was 0.093 per 250 ps, or 0.374 ns⁻¹. We take the inverse, δt/ΔP_trans = 2.7 ns per event, as an estimate of τ_commit, the molecular timescale for this transition. This corresponds well with 2.4 ns, the rough estimate of τ_commit obtained earlier as the timescale for P_trans(δt) plateau.

However, interpreting ΔP_trans/δt as a velocity is incorrect because the standard deviation of a diffusing distribution σ is proportional to the square root of the elapsed time δt and the diffusion constant D. For short δt, we extract a proper diffusion constant assuming diffusion along a flat one-dimensional coordinate, . We calculate D = 0.0175 ns⁻¹ at the barrier top. If ideal diffusion holds, a δ function at time zero (P_trans = 0.5) diffusing with D = 0.0175 ns⁻¹ will be completely absorbed by boundaries at 0 and 1 within 16 ns. This absorption process may be roughly approximated as an exponential decay (τ_commit = 5.3 ns). However, the observed ideal Gaussian diffusion will not hold after longer elapsed times. At longer δt the simulations will relax into product and reactant minima and the distribution P(P_trans|δt) should become bimodal. Also, an asymmetric P(P_trans|δt) distribution could arise from a free energy gradient or differential diffusion. Future simulations started from daughter conformations with longer δt should allow us to gauge these effects and to deduce the shape of the free energy barrier.

Classical transition state theory treats the folding process with a single constant prefactor, k₀, where 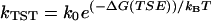. The P_trans diffusion rate provides a route to test this approximation by determining the configurational diffusion constant for different free energy barriers, altered temperature, mutation, or even for a different member of the same TSE. The transition state prefactor, which relates to the maximum speed of protein folding, depends on the nature of the conformational transition and polymer length. Eaton and co-workers have proposed a N_res/100-μs rule of thumb for the protein folding speed limit where N_res is the number of residues (47). This would predict a ∼400-ns speed limit for L9–39 which actually folds more than three orders of magnitude more slowly. This is unsurprising given the complexity of L9–39 topology relative to other small proteins. Also, in this work we are examining a single transition within the context of a larger folding process. Furthermore, barrier top diffusion may be rapid in comparison to diffusion along other portions of the free energy landscape. Our most rapid observed relaxation time was ∼3 ns, which is just faster than the most rapid events characterized by Kiefhaber and co-workers in studies of triplet-triplet energy transfer across various peptide sequences (48). The speed limit rule of thumb, our P_trans-diffusion calculations, and the presence of intermediates are all consistent with the premise that L9–39 could be optimized to fold more quickly. The K12M mutant itself is one such an example, as it folds more quickly (1209 ± 72 s⁻¹) than wild-type L9–39 (778 ± 72 s⁻¹) (13).

Kinetic similarity and structural similarity

Our data are well suited to address the connection between kinetic and structural similarity. As the structural deviation between two conformations goes to zero, ΔP_trans must also go to zero. How similar must two conformations become before we may assume that their kinetic properties are similar? With our P_trans-diffusion data set we can address this question (Fig. 6 D). For each pair of daughter conformations, we calculated the RMSD in the inter-α-carbon distance matrix (C_α dRMSD) and found a fairly normal distribution centered around 1.33 Å. In contrast, the absolute change in the transmission probability |ΔP_trans| between each pair of conformations was biased toward low changes because the possible values are restricted to the range from 0 to 1.

Plotting the correlation between these properties for each daughter pair, we found that larger structural deviations did not prevent similar P_trans values. However, conformations within 1 Å C_α dRMSD rarely had |ΔP_trans| > 0.25. Thus, we pose the hypothesis that a structural cutoff, C_α dRMSD < 1 Å may be sufficient to ensure kinetic similarity (|ΔP_trans| < 0.25) for sufficiently large protein conformation transitions. The ability to infer kinetic similarity from structural similarity is crucial when clustering conformations to build a Markovian state model, a master equation description of global kinetics (49–51). Specifically, a principal limitation of Markov state models is that one must only cluster protein conformations with similar kinetic properties. An ideal clustering metric would be sufficiently detailed to capture the precise structure-kinetics correlation yet would be general enough to detect every slow protein transition.

CONCLUSIONS

Imperfections in analysis of protein folding transitions due to high dimensionality can be avoided by studying the transition using a kinetic coordinate. Although this is a computationally expensive process (due to the statistical error of estimating the transmission probability for each conformation of interest), it is naturally parallelizable and well suited to distributed computing. We have applied this technique on a very large scale, calculating transmission probabilities for 2,000 putative transition state conformations spread over four distinct free energy barriers of the model system L9–39. We determined validated transition state conformations for a small protein of interest and demonstrated a new level of precision in such a kinetic ruler using hundreds of 10-ns atomistic simulations to determine each transmission probability value.

We demonstrated Hammond effects using kinetic measurements and found changes to both the free energy barrier position and width. Transition state shifts due to polymer temperature (25°C vs. 82°C) were small. Finally, we determined that it is possible to estimate a transmission probability diffusion rate. With precise P_trans values (∼400 simulations per conformation), we determined the molecular timescale and the rate of kinetic diffusion at the barrier top. These parameters should prove useful to decouple the kinetic and thermodynamic contributions to the rate theory of L9–39 folding.

APPENDIX

Here, we briefly review the use of Bayesian inference to estimate a specific commitment probability P_trans(x₀) = p from a finite number of trials. The probability density for p, given the observed data Ω, is 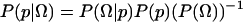. This expression has three important terms. The posterior distribution, 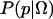, is proportional to the data likelihood, 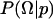, times the prior distribution, 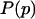. Because each simulation has two possible outcomes, the data likelihood is given by the binomial distribution .

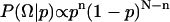The prior distribution contains any information about the distribution of p that is available before data collection. One may bias the result toward a predicted p value in exchange for more rapid convergence. Here, we used a so-called uninformative prior 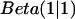that is simply a constant distribution and introduces no bias. The Beta distribution is also a conjugate prior, a convenient choice of prior distribution that simplifies the derivation of the posterior distribution. The form of the Beta distribution 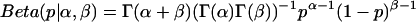reveals that the Beta distribution is similar to the binomial distribution, with the parameters α and β replacing n and N − n, respectively. The Γ-functions simply normalize the Beta distribution.

All factors that do not depend on p are constants and can be ignored, leaving a posterior distribution for p proportional to 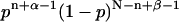. This posterior distribution is itself a Beta distribution and equals 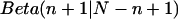for the uniform prior. As additional observations are collected, the posterior distribution depends only slightly on the prior. The peak of the posterior distribution may fall at any value between 0 and 1. 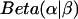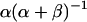The expectation value and variance of are and 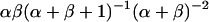, respectively. Upper and lower limits for 95% confidence intervals were determined to each exclude 2.5% of the probability distribution. All distribution statistics were calculated using Mathematica 5.0 (52).