Water transport by Na⁺-coupled cotransporters of glucose (SGLT1) and of iodide (NIS). The dependence of substrate size studied at high resolution

Abstract

The relation between substrate and water transport was studied in Na⁺-coupled cotransporters of glucose (SGLT1) and of iodide (NIS) expressed in Xenopus oocytes. The water transport was monitored from changes in oocyte volume at a resolution of 20 pl, more than one order of magnitude better than previous investigations. The rate of cotransport was monitored as the clamp current obtained from two-electrode voltage clamp. The high resolution data demonstrated a fixed ratio between the turn-over of the cotransporter and the rate of water transport. This applied to experiments in which the rate of cotransport was changed by isosmotic application of substrate, by rapid changes in clamp voltage, or by poisoning. Transport of larger substrates gave rise to less water transport. For the rabbit SGLT1, 378 ± 20 (n = 18 oocytes) water molecules were cotransported along with the 2 Na⁺ ions and the glucose-analogue α-MDG (MW 194); using the larger sugar arbutin (MW 272) this number was reduced by a factor of at least 0.86 ± 0.03 (15). For the human SGLT1 the respective numbers were 234 ± 12 (18) and 0.85 ± 0.8 (7). For NIS, 253 ± 16 (12) water molecules were cotransported for each 2 Na⁺ and 1 thiocyanate (SCN⁻, MW 58), with I⁻ as anion (MW 127) only 162 ± 11 (19) water molecules were cotransported. The effect of substrate size suggests a molecular mechanism for water cotransport and is opposite to what would be expected from unstirred layer effects. Data were analysed by a model which combined cotransport and osmosis at the membrane with diffusion in the cytoplasm. The combination of high resolution measurements and precise modelling showed that water transport across the membrane can be explained by cotransport of water in the membrane proteins and that intracellular unstirred layers effects are minute.

It is now generally accepted that cotransporters transport water (Agre et al. 2004; King et al. 2004) although the precise mechanism is debated. Some cotransporters function as passive water channels, but during cotransport another component of water transport emerges in parallel and independently of the passive component. By this mechanism water can move uphill, against the osmotic gradient; the energy contained in the substrate gradients is transferred to the transport of water (for reviews see Zeuthen & MacAulay (2002). We have demonstrated both active and passive water transport in a number of cotransporters in various preparations and by different techniques: KCC (K⁺–Cl⁻) (Zeuthen, 1991b), MCT (H⁺–lactate) (Zeuthen et al. 1996; Hamann et al. 2003), NDC1 (Na⁺–dicarboxylate) (Meinild et al. 2000); EAAT1 (Na⁺–glutamate) (MacAulay et al. 2001); GAT1 (Na⁺–GABA) (MacAulay et al. 2002b); SGLT1 (Na⁺–glucose) (Loo et al. 1996, 1999; Leung et al. 2000; Meinild et al. 1998; Zeuthen et al. 1997, 2001, 2002). Our data suggest that the capacity for water transport arises from a coupling within the cotransport protein itself; in other words, water is cotransported.

In the present paper, we took advantage of the fact that some cotransporters are able to transport several substrates and we investigated if the capacity for water cotransport depends on the size of the substrate. The Na⁺-coupled glucose transporters from rabbit (rSGLT1) and from human (hSGLT1) transport the glucose analogue α-MDG (MW 194) as well as the larger sugar arbutin (MW 272). Improved techniques also permitted a detailed study of the Na⁺-coupled iodide transporter (NIS), in which thiocyanate (SCN⁻, MW 52) can substitute for iodide (I⁻, MW 127) (Eskandari et al. 1987). We expressed the cotransporters in Xenopus oocytes and in order to evaluate the water transport we developed a high resolution volume recording system with a signal to noise ratio more than one order of magnitude higher than those used previously. To analyse the data we set up a complete model that combined the two used previously. The model of Zeuthen et al. (2002) used the fact that only about one third of the oocyte volume resembles free solution and is available for incoming substrate and water, while the model of Duquette et al. (2001) took account of intracellular diffusion and unstirred layer effects.

We found that less water was cotransported along with the larger substrates. This is opposite to what would be expected from unstirred layer effects (Duquette et al. 2001; Gagnon et al. 2004) and suggests that the coupling between water and substrate transport takes place within the protein. With the improved technique we re-examined our previous experiments and confirmed that water cotransport arises from a coupling between water and substrate within the protein. In particular, it was clear that rapid changes in rate of cotransport were mirrored by rapid changes in water transport. The combination of high resolution volume measurements and precise modelling demonstrated that this coupling could not be explained by unstirred layer effects. In that case the intracellular mobility of the substrates would have to be more than four orders of magnitude lower than in free solution, given the relatively low osmotic water permeability of the oocyte.

Methods

In terms of preparation of oocytes and two-electrode voltage clamp measurements, the methods were similar to those previously described (Zeuthen et al. 1997, 2001, 2002; Meinild et al. 1998). Human SGLT1 (hSGLT1), rabbit SGLT1 (rSGLT1), or rat thyroid Na⁺–I⁻ symporter (NIS) were expressed in Xenopus laevis oocytes (Hediger et al. 1987) and incubated in Kulori medium (mm: 90 NaCl, 1 KCl, 1 CaCl₂, 1 MgCl₂, 5 Hepes, pH 7.4, 182 mosmol l⁻¹) at 19°C for 3–7 days before experiments. In accordance with national guidelines, Xenopus oocytes were collected under anaesthesia (2 g l⁻¹ Tricain, 3-aminobenzoic acid ethyl ester, Sigma A5040). An ovarian lobe was removed from the abdominal cavity through a small (1 cm) incision. The anaesthetized frogs were finally killed by decapitation.

The experimental chamber was perfused by control solution which contained (mm): 90 NaCl, 20 mannitol, 2 KCl, 1 CaCl₂, 1 MgCl₂, 10 Hepes buffered to pH 7.4 by means of Tris, 213 mosmol l⁻¹). Isotonic sugar solutions were obtained by replacing mannitol by the non-metabolized sugar α-MDG (methyl-α-d-glucopyranoside, Sigma no. M-9376, MW 194), or with arbutin (hydroquinone β-d-glucopyranoside, Sigma no. A-4256, MW 272). To minimize differences in the optical properties of the bathing solutions, sugar concentrations were 5 mm or smaller; arbutin at higher concentrations induced significant optical artefacts (see Fig. 5). The inhibitor phlorizin (phloretin 2′-β-d-glucoside, Sigma no. P-3449) was dissolved directly in the test solution. In case of NIS the control solutions contained an extra 0.2 mm of NaCl which was replaced in the test solutions by 0.2 mm of NaI (MW of I⁻, 127) or NaSCN (MW of SCN⁻, 58). In order to measure the water permeability L_p, we added 20 mm of mannitol to the control solution. L_p values are given per true membrane surface area. This is about 9 times the apparent area due to membrane foldings (Zampighi et al. 1995). L_p is given in units of (cm s⁻¹ (osmol l⁻¹)⁻¹). To convert to units of (cm s⁻¹) this should be divided by the partial molal volume of water, 18 cm³ mol⁻¹.

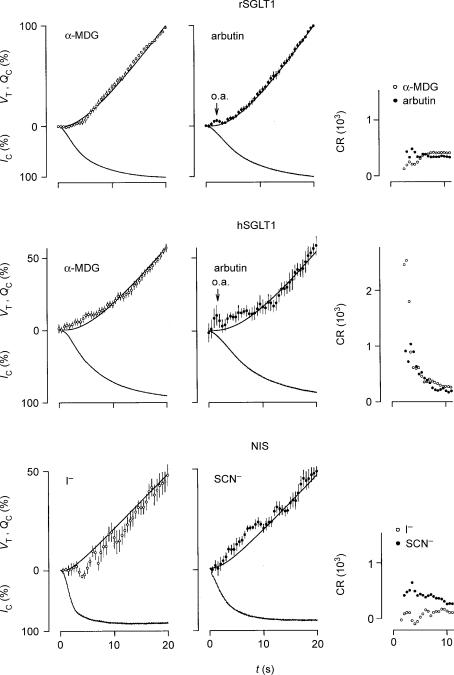
Figure 5. Initial changes in oocyte volume (V_T), clamp current (I_C), charge accumulation (Q_c), and coupling ratio (CR) induced by isosmotic application of substrate at t=0.

The average V_T values (open or filled circles) were calculated every 0.5 s and given with vertical s.e.m. bars. The values are compared with the accumulation of charge (Q_C, upper smooth line), which equal the integrated I_C (lower trace). The values for rSGLT1 were normalized relative to the values obtained after 20 s where I_C had reached more than 95% saturation. We employed clamp voltages of −50 mV and 2–5 mm of α-MDG (n= 13) or arbutin (n= 7); the s.e.m.s of the currents (not shown) were less than 1% in case of both α-MDG and arbutin. The values for hSGLT1 were normalized relative to the values obtained after 30 s where I_C had reached more than 95% saturation. We used 5 mm of α-MDG and clamp voltages of −50 and −90 mV (n= 18); the s.e.m.s of the currents (not shown) were less than 1%. Arbutin was tested at 5 mm and clamp potentials of −50 mV (n= 6); the s.e.m.s of the currents (not shown) were less than 3%. The application of arbutin induced an optical artefact seen as an apparent transient swelling (o.a.); this artefact was also present when wild type oocytes were tested and it was proportional to the concentration of arbutin. The values for the NIS were normalized relative to the values obtained after 40 s. Substrate concentrations were between 0.2 and 1 mm and the clamp potential was −70 mV. The s.e.m.s of the currents (not shown) were less than 4% for both I⁻ (n= 9) and SCN⁻ (n= 8). Running estimates of CR (proportional to V_T/Q_C, see text) are given in the right-hand panels. For rSGLT1, the CRs were relatively constant during the first 10 s; only at around t= 5 s was there a small reduction in CR in the case of α-MDG. After about 5 s the CRs were close to their steady-state values. For hSGLT1, however, with both α-MDG and arbutin, the CRs were initially up to 10 times higher than the CRs obtained when I_C saturated, which were 234 and 201, respectively. For NIS, the CR for I⁻ was lower, and that for SCN⁻ higher during the initial 10 s compared with the CRs obtained as I_C saturated, which were 162 and 257, respectively. Please note that it was not possible to evaluate CR during the initial 2 s where the signal-to-noise ratio for Q_C is small; nor was it possible when arbutin induced the optical artefact (o.a.).

The experimental chamber and oocyte volume recording system were improved versions of those used previously (Zeuthen et al. 1997). The oocyte was placed in a circular chamber 3 mm in diameter and 1 mm high. The bottom consisted of a 0.1 mm thick glass plate through which the oocyte could be viewed via a long distance objective (× 4) and a CCD camera. In order to achieve a stable image of the oocyte, the upper surface of the bathing solution was held by a Perspex rod of elliptical cross section 2 mm × 4 mm. The polished end of the rod provided the stable illuminated (green) background for the oocyte. The two-clamp microelectrodes were inserted in between the rod and the upper rim of the chamber. To obtain experiments lasting about 30 min, we used clamp voltages of not more than −120 mV; more negative values might cause instabilities in the clamp current and death of the oocyte. In order to ensure rapid shifts between control and test solution, a small mechanical valve (dead space of about 5 μl) was placed at the edge of the chamber. Accordingly, at flow rates of 12 μl s⁻¹ the time constant for changing the solution around the oocyte was about 0.5 s (Fig. 1). The solution was sucked from the chamber via a wick of filter paper 2 mm wide and 10 mm long. This continued into a 3 cm wide and 10 cm long layer of filter paper the end of which was drained by gravity. The image of the oocyte was particularly sensitive to changes in the level of the solution in the chamber and in the drainage system, i.e. to evaporation and drafts. Accordingly, the drainage system was protected by a glass lid. The whole set up was placed in a Faraday cage which also protected against drafts.

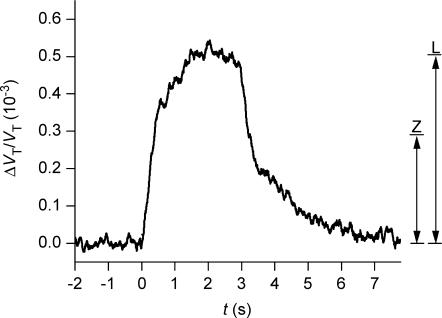
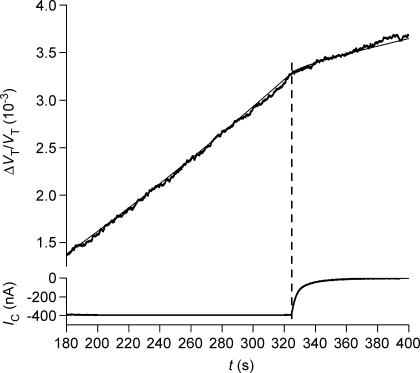
Figure 1. Sensitivity and time resolution of the volume recording.

The relative change in volume of a wild type oocyte (ΔV_T/V_T) was monitored at a noise level of 0.20 × 10⁻⁴ (0.02‰) calculated as two times the standard deviation of the data point obtained under baseline conditions. Previously published methods had noise levels 10–25 times higher: 0.3 × 10⁻³ (Zeuthen et al. 1997), and 0.5 × 10⁻³ (Gagnon et al. 2004) as indicated by the vertical lines Z and L. At time zero a volume increase of 0.5 × 10⁻³ was simulated by changing the bathing solution to one in which a low concentration of Lissamine green had been added (see text). The time constant of the solution change around the oocyte was about 0.5 s.

The video and computational techniques were improved versions of those used previously (Zeuthen et al. 1997). Images were captured directly to the random access memory (RAM) of a PC (Intel Pentium 4, 3.2 GHz) through a video signal digitizer expansion board (frame grabber, Data Translation DT 3155, High Precision A/D conversion board, monochrome) using a PCI–bus interface. The frame grabber allowed a 132 MB s⁻¹ data transfer, i.e. norma1 video frame rates (25 frames s⁻¹, 768 × 576 pixels, 8 bit per pixel grey scale) could be transferred without any loss of data or frames at standard PAL-video rate. The speed of the PC processor was sufficient for full frame rate live calculation of pixel data and on-screen presentation even when using advanced filtering algorithms. Two assumptions for volume calculation were used: the oocyte is spherical and in focus at the circumference. The oocyte viewed in bright-field microscopy was black, and there was a pronounced contrast in the image of the oocyte. This allowed assignment of dark pixels as oocyte material and bright pixels as non-oocyte material. To find the correct scoring level of pixel darkness, we applied a filter routine (threshold) that showed the pixels that would be scored as oocyte material at the given threshold level. From this area, the oocyte volume and other parameters such as surface area and diameter could be derived. Several types of (edge-defining) image analysis procedures could be applied at full video frame rate, e.g. sharpening filters, median filtering and rolling average. The oocyte volume was plotted in a live graph at 25 graph points per second. In the present investigation we used the rolling average method which calculates continuously the average of the 25 preceding images. This gave an effective time resolution of 1 s and a relative noise level of 0.2 10⁻⁴ (equivalent to 20 pl for an oocyte volume of 1 μl) taken as two times the standard deviation of the volume data obtained under baseline conditions (Fig. 1). This noise level is more than 10 times lower than that of our previous set-up and 25 times lower than that of Duquette et al. (2001) and Gagnon et al. (2004). Simple tools such as statistical line comparison (regression line comparison) were included for on-line analysis.

The time constant of changing the solution around the oocyte and signal-to-noise ratio were estimated with a wild type oocyte in the chamber (Fig. 1). The bathing solution was shifted between two control solutions, one of which contained 4 mg l⁻¹ of Lissamine green (Chroma-Gesellschaft, Stuttgart, Germany) in order to reduce its transparency slightly. In this solution pixels that were located at the edge of the oocyte and that were close to the cut-off level shifted from a light (non-oocyte) value to a dark (oocyte) value, a process which mimicked oocyte swelling.

Model simulations of volume changes were done by numerical integration in C⁺⁺ language using steps of 1 s (see Appendix).

Experiments were performed at room temperature (20–25°C). All numbers are given as means ±s.e.m., with n equal to the number of oocytes tested unless otherwise stated. Comparisons were done with Student's t test, and P≤ 0.05 was taken as criterion for statistical significant difference.

Results

The general aim of the experiments was to induce rapid changes in the rate of cotransport and to correlate these to the changes in rate of water transport. If the coupling between water and substrate transport takes place by a mechanism within the cotransporters, this would be revealed by a close temporal correlation between volume changes and clamp currents. Water transport induced by osmosis, however, would lag behind the changes in clamp currents and would correlate mainly to the much slower build-up or dissipation of concentration gradients.

A large fraction of the water influx was explained by a fixed stoichiometrical relationship between water transport and cotransport of the substrates, J_H2O,co. We define this by the coupling ratio (CR), i.e. the number of water molecules cotransported per turnover of the protein. rSGLT1 and hSGLT1 transport 2 Na⁺ and 1 sugar molecule. Accordingly, CR is the number of water molecules transported for each two unit charges or 2 F J_H2O,co (V_wI_C)⁻¹. NIS transports 2 Na⁺ and 1 I⁻ (or 1 SCN⁻), i.e. one unit charge per turnover, and CR equals F J_H2O,co (V_wI_C)⁻¹. F is Faraday's constant and V_w is the partial molal volume of water (18 × 10⁻³ l mol⁻¹). The rate of cotransport was monitored as the clamp current I_C. Experiments could be analysed by the model given in the Appendix, which divides the influx of water into a cotransport and an osmotic component. The osmotic water permeability L_p was derived from the shrinkage induced by applying 20 mosmol l⁻¹ of mannitol in independent experiments.

Isotonic addition of substrate

In order to test if the abrupt initiation of cotransport led to a coupled transport of water, substrate was added, isosmotically, under voltage-clamped conditions. This resulted in a rapid increase in clamp current (I_C) and a linear increase in oocyte volume (V_T), Figs 2, 3 and 4. These changes were coupled: the volume changes matched the integrated current (i.e. entry of charge, Q_C) closely for the first 40–50 s given a fixed coupling ratio CR (Fig. 2, curve B), and the time constants for the rise in V_T and for the integrated I_C were similar (Table 1). Consequently, CR was determined from the best fit between the changes in oocyte volume and the integrated clamp current over the initial 40 s. This method for determining CR is model-independent and analogous to that employed in previous papers (for references, see introduction). Effects specific to the early 10 s of substrate applications are treated below, in connection with Fig. 5.

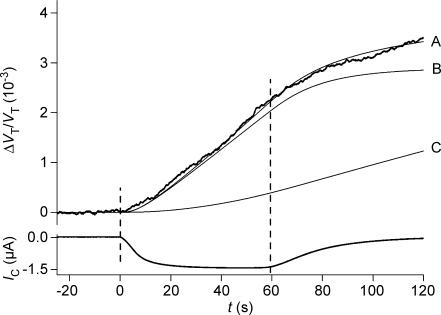
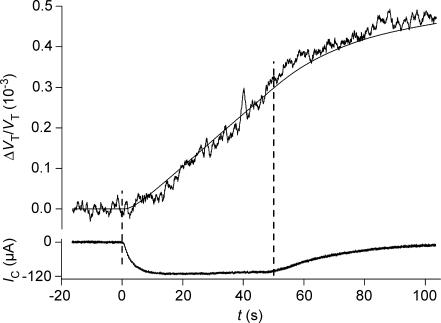
Figure 2. Volume changes of a hSGLT1-expressing oocyte during isosmotic exposure to α-MDG.

The oocyte was clamped to −50 mV and 5 mm of α-MDG was added to the bathing solution at time zero where it replaced mannitol. This initiated an increase in oocyte volume (given relative to the initial volume: ΔV_T/V_T) and an inward clamp current I_C, which rose with a time constant of about 10 s. A close approximation of the CR was derived from the initial 40 s of volume changes and the integrated I_C (curve B). The experiment was simulated by the model in the Appendix using a CR of 280, V_F/V_T= 0.6 and D_i= 0.75 × 10⁻⁵ cm² s⁻¹ (curve A). L_p= 0.7 × 10⁻⁵ cm s⁻¹ (osmol l⁻¹)⁻¹, r= 0.055 cm were obtained in separate experiments. In case of no cotransport (CR = 0) water transport is entirely osmotic and the model predicts curve C (D_i and V_F/V_T as above). The washout of the sugar began at about 60 s.

Figure 3. Volume changes of the hSGLT1-expressing oocyte during isosmotic exposure to arbutin.

The oocyte shown in Fig. 2 was clamped to −50 mV and 5 mm of arbutin replaced mannitol at time zero. This initiated an increase in relative oocyte volume ΔV_T/V_T and an inward clamp current I_C, which rose with a time constant of about 15 s. The experiment was simulated using a CR of 263 (curve B); simulations with CRs deviating 15% from 263 are shown in curves A and C (see Appendix). D_i was taken as 0.33 × 10⁻⁵ cm² s⁻¹ and V_F/V_T as 0.3. L_p= 0.7 × 10⁻⁵ cm s⁻¹ (osmol l⁻¹)⁻¹ and r= 0.055 cm were measured separately. Washout of arbutin began at 70 s.

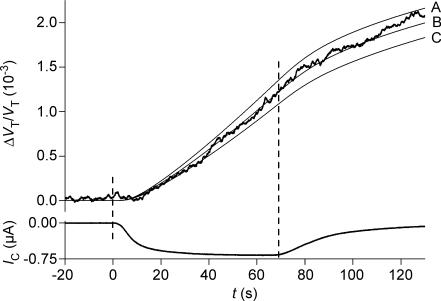
Figure 4. Volume changes of a NIS-expressing oocyte during isosmotic exposure to SCN⁻.

The oocyte was clamped to −70 mV and 0.2 mm of NaSCN replaced NaCl at time zero. This initiated an increase in relative oocyte volume (ΔV_T/V_T) and an inward clamp current I_C, which rose with a time constant of about 2 s. A close approximation of CR was derived from the initial 40 s of volume changes and the integrated I_C. The experiment was simulated with CR = 315, D_i= 0.3 × 10⁻⁵ cm² s⁻¹ and V_F/V_T= 0.28 (thin line). L_p= 0.33 × 10⁻⁵ cm s⁻¹ (osmol l⁻¹)⁻¹ and r= 0.062 cm were measured separately. Washout of SCN⁻ began at 50 s.

Table 1.

Time constants (τ, in seconds) for changes in clamp current (I_C), integrated I_C (Q_C), and volume (V_T) of oocytes expressing rSGLT1 and hSGLT1

	rSGLT1		hSGLT1
	α-MDG	Arbutin	α-MDG	Arbutin
τ (IC)	5.5 ± 0.3 (18)	9.1 ± 0.6 (15)	8.9 ± 0.5 (16)	11.1 ± 0.7 (7)
τ (QC)	4.4 ± 0.1 (18)	8.1 ± 0.6 (15)	8.8 ± 0.5 (16)	10.1 ± 0.4 (7)
τ (VT)	4.4 ± 0.3 (18)	6.3 ± 0.4 (15)*	8.0 ± 1.2 (16)	9.0 ± 1.5 (7)

The time constants of Q_C and V_T were taken as the intercept between the abscissa and the respective regression lines defining the first 40 s of linear change. Zero time was taken as the onset of I_C.

^*This value of τ (V_T) was significantly smaller than the corresponding values of τ (Q_C) and τ (I_C); P < 0.03.

In the present paper we extended the analysis in order to test how other cellular parameters affect the determination of CR. The cotransported components of water and substrates formed a solution, which was hyperosmolar by a factor of about two relative to the bathing solution. This resulted in a gradual build-up of an intracellular hyperosmolarity, which after about 40 s became noticeable as an osmotic influx of water in parallel with the cotransported one (Fig. 2, curve A). The value of CR, which takes this osmotic component into account, can be estimated from a model analysis over a 40-s period, to be about 5% lower than that determined from the integrated current alone (compare curve A and B in Fig. 2). This difference was not statistically significant. Neither did variations in the intracellular diffusion coefficient D_i within physiological limits affect the determination of CR significantly (Fig. 11A). Under the assumption of no cotransport of water, all influx of water is osmotic. In that case, however, the predicted swelling of the oocyte will be much smaller than the measured one, given physiological values of D_i (Fig. 2, curve C).

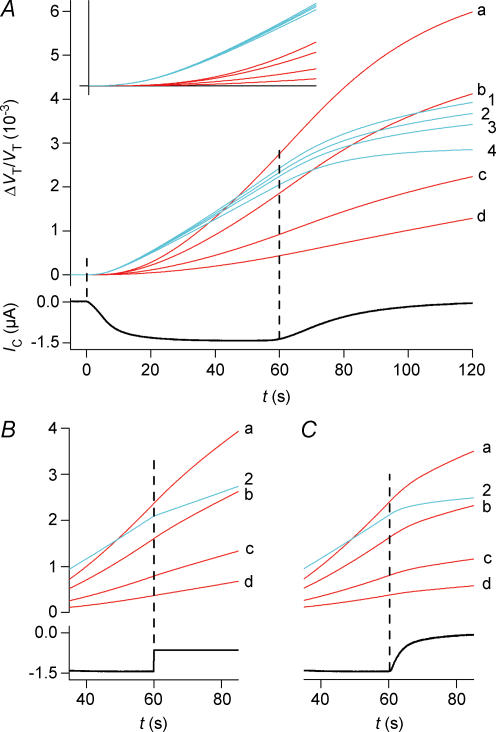
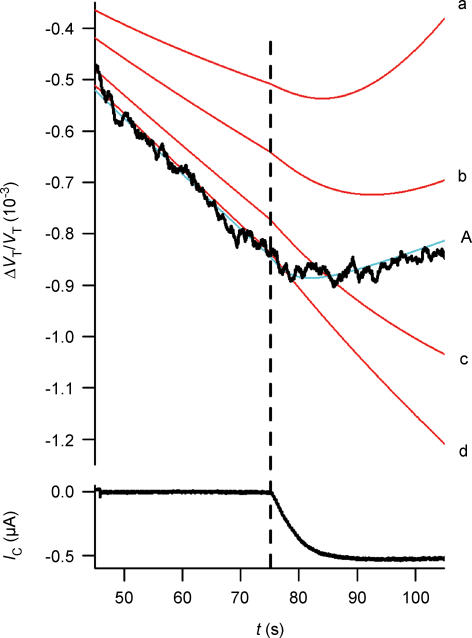
Figure 11. Simulation of volume changes.

Blue curves are simulations that involve cotransport of water; red curves involve only osmosis and unstirred layer effects. The simulations are based on the data from the hSGLT1-expressing oocyte shown in Fig. 2. A, isosmotic application of α-MDG. The activity of the cotransporter is given by I_C. The blue curves (1–4) are simulations with a CR of 280 and an L_p of 0.7 × 10⁻⁵ cm s⁻¹ osm l⁻¹)⁻¹. Three values of D_i (cm² s⁻¹) were tested: curve 1, 0.33 × 10⁻⁵; curve 2, 0.5 × 10⁻⁵; curve 3, 0.75 × 10⁻⁵. The corresponding values of V_F/V_T were 0.3, 0.4 and 0.6. Curve 4 represents the contribution from the cotransport of water alone, which equals the integrated current. For the red curves, the influx of water takes place by osmosis only (CR = 0, L_p= 0.7 × 10⁻⁵ cm s⁻¹ (osmol l⁻¹)⁻¹). Simulations with four values of D_i are shown: curve a, 0.5 × 10⁻⁸; curve b, 0.5 × 10⁻⁷; curve c, 0.5 × 10⁻⁶; and curve d, 0.5 × 10⁻⁵ cm² s⁻¹; V_F/V_T was constant at 0.4. The inset shows the initial 20 s of volume changes; vertical bar 0.55 × 10⁻³. B, the experiments were terminated by an abrupt change in I_C from 1400 nA to 650 nA elicited by a change in clamp voltage at 60 s (experiment as in Fig. 7). For the cotransport scenario only curve 2 is shown (blue). The red curves (a–d) have the same parameters as in A. C, the experiment was terminated by adding phlorizin at 60 s. This abolished the sugar-induced clamp current with a time constant of 5 s (see Fig. 9). Phlorizin was assumed to decrease the L_p from 0.71 to 0.42 × 10⁻⁵ cm s⁻¹ (osmol l⁻¹)⁻¹. For the cotransport scenario only curve 2 is shown (blue). The red curves (a–d) have the same parameters as in A.

For the rSGLT1 the coupling ratio CR for α-MDG was 378 ± 20 (18). The CR obtained for the larger sugar arbutin was smaller (compare Figs 2 and 3). In paired experiments in 15 oocytes, CR for arbutin was 0.86 ± 0.03 times the CR for α-MDG, i.e. on average 325 (Fig. 6). It should be noted that the increase in clamp current (I_C) at substrate addition was exponential. Accordingly, the coupled changes in the integrated clamp current and in the oocyte volume became noticeable only after a delay of several seconds (Fig. 5). At clamp potentials of −50 mV, oocytes had I_C values in the range 400–1360 nA for 2 mmα-MDG and 210–740 nA for 2 mm arbutin. In the absence of sugar, the phlorizin-dependent component of the Na⁺ leak current was 92 ± 6 (7) nA, given expression-levels of the rSGLT1 equivalent to saturating α-MDG-induced currents of 1000 nA. The L_p of the oocytes was 0.64 ± 0.04 × 10⁻⁵ cm s⁻¹ (osmol l⁻¹)⁻¹ (21) in the absence of sugar.

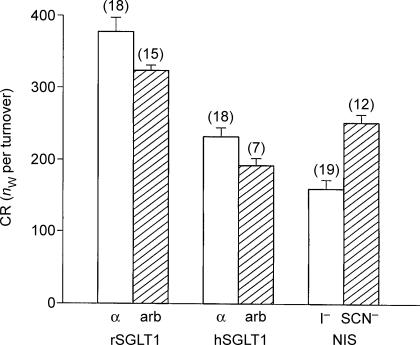
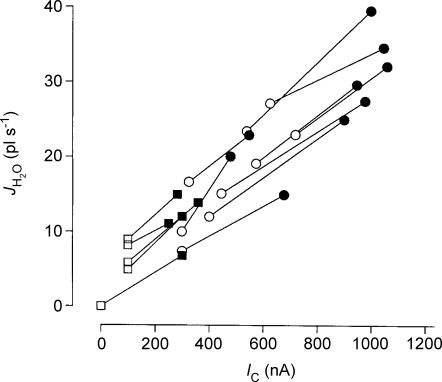
Figure 6. Coupling ratio (CR) as a function of substrate size.

The CR was compared for α-MDG (MW 194) and arbutin (MW 272) in rSGLT1- and hSGLT1-expressing oocytes, as in Figs 2 and 3. In 15 paired experiments on rSGLT1, CR for arbutin was 0.86 ± 0.04 times that for α-MDG (P < 0.002). In 7 paired experiments on hSGLT1, CR for arbutin was 0.85 ± 0.05 times that for α-MDG (P < 0.02). For NIS, the CR observed with SCN⁻ as anionic substrate (MW 58) was 1.73 ± 0.22 times that observed with I⁻ (MW 127), P < 0.0003. n_w, number of water molecules.

Similar data were obtained for the hSGLT1, although CR was lower than for the rSGLT1. CR for α-MDG was 234 ± 12 (18) while CR for arbutin was found in seven paired experiments to be 0.85 ± 0.05 times smaller, i.e. on average 201. The time constants for the increase in I_C and V_T were larger than those observed for the rSGLT1 (Table 1), which reflects the higher K_0.5 for the hSGLT1. We employed oocytes with I_C values in the range 380–1400 nA for 5 mmα-MDG and 170–680 nA for 5 mm arbutin at clamp potentials of −50 mV. In the absence of sugar, the phlorizin-dependent component of the Na⁺ leak current was 32 ± 2 (4) nA, given expression levels of the hSGLT1 equivalent to saturating α-MDG-induced currents of 1000 nA. The L_p of the hSGLT-expressing oocytes was 0.47 ± 0.05 × 10⁻⁵ cm s⁻¹ (osm l⁻¹)⁻¹ (21) in the absence of sugar.

The experiments described above were performed at clamp potentials of −50 mV. Accordingly, the SGLT1s were transporting under near-saturating conditions in the case of α-MDG, but further from saturation in the case of arbutin; K_0.5 for α-MDG is around 0.1 mm while that for arbutin is around 1 mm (see Discussion). In order to test the CRs at higher degrees of saturation, we employed clamp voltages of −90 to −120 mV using 5 mm of arbutin or α-MDG. These were the upper limits at which the experiments could be performed (see Methods). For arbutin, the conditions were close to saturation. The steady-state clamp currents (I_C) were about twice those obtained at −50 mV, and additional increases achieved by higher concentrations of arbutin and clamp voltages were small: when the concentration was increased from 5 to 10 mm, I_C increased by 6 ± 4% (5) for rSGLT1 and 9 ± 4% (7) for hSGLT1. A shift in clamp potential from −90 to −120 mV increased the clamp current for rSGLT1 by 11 ± 6% (5). For rSGLT1 the CR for arbutin was 0.69 ± 0.06 times that measured with α-MDG (5 paired experiments, at −90 mV and 5 mm of sugar). For hSGLT1 the ratio was 0.77 ± 0.08 (9 paired experiments, 7 at −90 mV and 2 at −120 mV, 5 mm of sugar). The CRs obtained with α-MDG were the same at −50 mV as at −90 mV. We therefore conclude that CRs for arbutin do not increase as the transporter approaches saturation.

It is interesting to compare the NIS with the SGLT1s, since the substrates of the NIS are small and inorganic. Apart from giving new information about the NIS transporter, this will also resolve questions of whether the effects seen with SGLT1 arise as a specific result of an unusually slow diffusion of sugar molecules in the oocyte cytoplasm (Gagnon et al. 2004). When 0.2 mm of I⁻ was added to the bathing solution (replacing Cl⁻) at clamp voltages of −70 mV (saturating conditions), the I_C increased with a τ of 2.0 ± 0.4 s (8) to maximal values of 166 ± 12 nA (15). Simultaneously, the oocyte volume initiated a linear increase equivalent to a CR of 162 ± 11 (19). When 0.2 mm of SCN⁻ was added under similar conditions, I_C rose with a τ of 4.1 ± 0.4 s (8) to maximal values of 112 ± 9 nA (12) (see Fig. 4). The associated increase in oocyte volume was equivalent to a CR of 253 ± 16 (12). A similar CR of 269 ± 34 (4) was obtained with saturating concentrations of SCN⁻ (1.0 mm). In nine paired experiments, the CR obtained with SCN⁻ as anion was 1.73 ± 0.22 times that seen with I⁻. Expression of NIS did not increase the L_p of the oocyte above that of native oocytes, which was about 0.3 × 10⁻⁵ cm s⁻¹ (osm l⁻¹)⁻¹.

When substrate is added the cotransporter proceeds from unsaturated towards saturated conditions. In order to examine the relation between the water transport and the clamp current under this transition, we compared the changes in oocyte volume (V_T), clamp current (I_C), charge accumulation (Q_C: integrated clamp current), and a running estimate of CR for the first 20 s after substrate application (Fig. 5). For the rSGLT1 there was good correspondence between volume and charge movements indicative of a constant CR throughout the period. In case of the hSGLT1, however, there was an initial influx of water lasting about 10 s which exceeded that predicted from the entry of charge. In other words, the CRs were much larger during the first seconds of substrate application than those obtained when the cotransporter had reached steady state. In order to test if this effect depended on the degree of saturation, we compared experiments performed at clamp voltages of −50 and −90 mV (5 mm of sugar). For α-MDG there was no difference between the effects seen at −50 mV (n= 13) and those seen at −90 mV (n= 5). For arbutin the effect was slightly larger at −50 mV (n= 6) than at −90 mV (n= 6). The NIS showed an extra component of water transport when transporting SCN⁻ as shown by a high initial value of CR. In contrast, there was a short-lasting decrease in the initial water transport in the case of I⁻ as shown by a low initial value of CR. After 10 s, the CR for all transporters were close to their steady-state values and there was good correspondence between water and charge movements. It should be noted that 5 mm of arbutin induced an optical artefact which appears as a small increase in volume (o.a. in Fig. 5). This artefact increased with concentration: at 10 or 20 mm it made an accurate evaluation of the cotransport-induced water transport difficult. The artefact was also present in wild type (non-injected) oocytes.

Effects of rapid changes of rate of cotransport

Abrupt changes in the rate of cotransport of the SGLT1s were achieved by (i) changing the clamp voltage abruptly or (ii) by adding phlorizin to the bathing solution. Such experiments will provide a clear distinction between the cotransport and the osmotic component of water transport. Cotransport will react rapidly to changes in driving forces or poisoning, while the osmotic component will mirror the relatively slow changes in the intracellular osmolarity.

Oocytes expressing rSGLT1 were clamped to a potential between −50 and −90 mV. Sugar (2 mm of α-MDG or arbutin) was added to the bathing solution and the CR determined as described above. After about 2 min the clamp voltage was jumped to a low value, typically between −10 and +20 mV. This induced immediate reductions in I_C and in the rate of volume change (Fig. 7). The corresponding changes in influx of water and I_C (Fig. 8) agreed with the cotransport component determined from the isotonic application of sugars: (ΔV_T/dt)_b− (ΔV_T/dt)_a divided by I_C,b−I_C,a gives a CR for α-MDG of 340 ± 46 (9) and a CR for arbutin of 326 ± 34 (5); the subscripts a and b refer to the values before and after the change in I_C. It should be noted that the method is not accurate enough to separate the CRs for α-MDG and arbutin. As a control, voltage jumps were performed with no sugar in the bathing solutions. The overall changes in oocyte volume could be simulated precisely by the model given in the Appendix (Fig. 7).

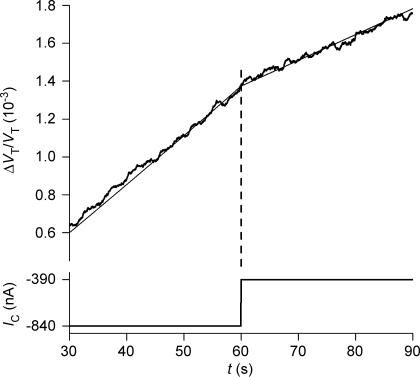
Figure 7. Effects on oocyte volume of abrupt changes in clamp voltage.

An rSGLT1-expressing oocyte was exposed, isosmotically, to 2 mm of α-MDG under voltage clamp conditions (−50 mV), as in Fig. 2. This resulted in an I_C of 840 nA. After about 60 s (at the vertical dashed line) the clamp voltage was jumped to +20 mV and I_C changed abruptly to 390 nA. The corresponding reduction in the rate of volume change corresponds to a change in influx of water (J_H2O=ΔV_T/dt) from 41 pl s⁻¹ to 28 pl s⁻¹. The thin line was obtained from simulation of the experiment by the model given in the Appendix. Radius of the oocyte was 0.064 cm. The difference in the two rates of swelling of 13 pl s⁻¹ (41–28) and the corresponding change in I_C of 450 nA (840–390) corresponds to a CR of 388.

Figure 8. The relation between influx of water (J_H2O) and clamp current (I_C) induced by abrupt shifts in clamp voltage.

Experiments as in Fig. 7 (rSGLT1). Filled symbols are data obtained at clamp voltages between −50 and −70 mV; open symbols between 0 to +20 mV. Data obtained from the same oocyte are connected by a line. Circles are from experiments using α-MDG; squares from experiments using arbutin.

In another type of experiment, phlorizin (100 μm) was added to the bathing solution after a period of α-MDG transport under voltage-clamp conditions (1–5 min). This reduced I_C and the rate of volume transport within 5–10 s (Fig. 9). When the rate of volume changes and I_C were compared before and after the application of phlorizin, we found a CR for rSGLT1 of 330 ± 23 (14 measurements in 4 oocytes) and for hSGLT1 of 208 ± 16 (4 measurements in 4 oocytes). These estimates were in agreement with those obtained from isotonic sugar application and from changes in clamp voltage. In addition, phlorizin reduced the L_p of the sugar-transporting, SGLT-expressing oocyte by about 20%, which, in itself, caused a minor reduction in the volume changes; this was corrected for in the simulation (Fig. 9).

Figure 9. Effects of phlorizin on sugar-induced oocyte swelling.

An hSGLT1-expressing oocyte was exposed to 5 mmα-MDG under voltage-clamped and isosmotic conditions (−90 mV). This gave an I_C of about 380 nA and, after about 320 s, a constant rate of volume increase of 14 pl s⁻¹. At 325 s 100 μm phlorizin was added. This reduced the rate of swelling to 5.6 pl s⁻¹ and abolished I_C with a constant of about 5 s. The experiment was simulated by the model of the Appendix (thin line) using the measured values for CR of 244, and of an L_p of 0.59 before phlorizin application and 0.42 after phlorizin application (units, cm s⁻¹(osmol l⁻¹)⁻¹). r was 0.063 cm, V_F/V_T 0.4, and D_i 0.5 × 10⁻⁵ cm² s⁻¹.

It should be emphasized that the determination of CR in the above experiments is model independent, since it is based upon a correlation between the rapid changes in the rate of volume change and in clamp currents.

Uphill transport of water

One feature that separates cotransport from osmosis is its ability to transport water from a low to a high water chemical potential. Voltage-clamped, rSGLT1-expressing oocytes were exposed to an osmotic gradient implemented by addition of 5 or 10 mm of mannitol to the external solution. After about 60 s of osmotic shrinkage, 5 mm of the mannitol was replaced by α-MDG. This induced a sugar-dependent I_C and an abrupt decrease in the rate of shrinkage (Fig. 10). The relative decrease represents a cotransport-induced influx of water with a CR of 392 ± 26 (4) similar to the coupling ratios determined in the other experiments.

Figure 10. Uphill transport of water.

An rSGLT1-expressing oocyte was exposed at time zero to an osmotic gradient of 5 mosmol obtained by adding mannitol to the bathing solution. This induced a constant rate of osmotic shrinkage as given by the relative volume changes, ΔV_T/V_T, jagged line. At t= 75 s the 5 mm mannitol was replaced by 5 mmα-MDG. This gave rise to an increase in I_C and oocyte swelling despite the adverse osmotic gradient. The change in oocyte volume could be simulated using the measured value for CR of 288 and an L_p of 0.5 before sugar application and 0.67 after sugar application, in units of cm s⁻¹ (osmol l⁻¹)⁻¹ (blue line, A). V_F/V_T was taken as 0.4 and D_i as 0.5 × 10⁻⁵ cm² s⁻¹. The volume changes were also simulated assuming only osmotic transport of water (red curves), D_i values of 0.5 × 10⁻⁵ (curve d), 0.5 × 10⁻⁶ (curve c), 0.5 × 10⁻⁷ (curve b), and 0.5 × 10⁻⁸ (curve a) were tested (units, cm² s⁻¹).

Discussion

This paper confirms and extends our previous observation that transport of water and non-aqueous substrates are closely coupled in cotransporters of the symport type. In the earlier investigations, performed at a lower resolution, the CR for rSGLT1 was found to lie between 320 and 420 and that for hSGLT1 between 210 and 265, both with α-MDG as substrate (see references in introduction), in good agreement with the present estimates of 378 and 234, respectively. Improved techniques allowed us to include the Na⁺–I⁻ cotransporter (NIS) in the present investigation, although this symporter has a relatively low expression in the Xenopus oocyte. We tested NIS under isotonic conditions: with I⁻ as substrate CR was 162, close to the value of 200 obtained from preliminary measurements under hypotonic conditions (Loo et al. 1996). All data were analysed by means of a model that combines cotransport and osmosis at the membrane with diffusion in the cytoplasm (see Appendix). The analysis shows that the data can be explained predominantly by cotransport of water.

Molecular significance

For each of the cotransporters rSGLT1, hSGLT1 and NIS, relatively less water was cotransported together with a large substrate than with a small substrate (Fig. 6). This indicates a molecular property, but is opposite to what would be expected from unstirred layer effects (see below). One type of molecular model for water cotransport is based upon the alternating access model. In this model, the symporter undergoes conformational changes that allow the substrate to bind inside a wide aqueous cavity open to the cis side, followed by occlusion of the substrate together with the water, and finally exit of substrate via a cavity that opens to the trans side. If the substrate-free conformation involves a closed state with a small or no aqueous cavity, water will be cotransported (Zeuthen, 1994). In addition, mechanisms analogous to those described for the three-compartment model (Curran & MacIntosh, 1962) might also be operative at the molecular level (Zeuthen & Stein, 1994). In molecular models, a larger substrate would leave less room for water, and thus to a smaller coupling ratio. Recently published high resolution structures of cotransporters are not incompatible with the models outlined above. The oxalate–formamate antiporter (OxlT) (Hirai et al. 2002), the bacterial H⁺–lactose symporter LacY (Abramson et al. 2003), the bacterial inorganic phosphate (P_i)–glycerol-3-phosphate antiporter (GlpT) (Huang et al. 2003), and the bacterial Na⁺–glutamate cotransporter Glt_Ph (Yernool et al. 2004) all have large hydrophilic cavities. The cavities contain substrate binding sites and may occlude the substrate or be open to one of the external solutions. The cavities have linear dimensions of up to 5 nm and could contain several hundred water molecules. These numbers are compatible with the range of coupling ratios we have observed, from 50 water molecules per turnover in a plant H⁺–amino acid cotransporter to 500 in an amphibian K⁺–Cl⁻ cotransporter (Zeuthen & MacAulay, 2002). To determine how cotransporters act as molecular water pumps it will require the crystallization of several conformational states for a given cotransporter. A final model will also have to consider that various conformational states have different water transport properties (MacAulay et al. 2002).

Determination of the coupling ratio, CR

The CR for water was the most important parameter for the description of the experiments. When substrates were added abruptly, the cotransport component gave a good approximation to the first 40 s of volume changes (Figs 2, 3 and 4). Cotransport of water also explained the rapid shifts in the rate of oocyte swelling induced by abruptly changing the clamp potential (Fig. 7). At the low relative noise level of 0.2 × 10⁻⁴ it can be seen that the rate of water transport changed within a couple of seconds of the shift in I_C. The changes in swelling rate correlates to the change in I_C given the same CR as determined in the other experiments (Fig. 8). Similar conclusions can be drawn from the rapid changes in swelling rates achieved by adding phlorizin (Fig. 9) (see also Fig. 11B and C).

The rSGLT1, the hSGLT1 and the NIS transported less water per turnover when transporting larger-sized substrates, i.e. the CR for water was smaller. To what degree is this finding obfuscated by the different transport modes, e.g. saturated versus unsaturated transport? The question is relevant, since the calculation of the CRs was based upon the assumption of a stoichiometry of two Na⁺ ions for each sugar molecule or anion, which has been found to apply primarily to saturating conditions (Eskandari et al. 1997; Mackenzie et al. 1998). In the case of α-MDG we worked close to saturation and observed no differences in the CRs under the various conditions. We used 2–5 mmα-MDG and K_0.5 is only 0.15 mm for rSGLT (Lostao et al. 1994) and 0.3 mm for hSGLT (Díes-Sampedro et al. 2000). Furthermore, we have previously found no differences between CRs obtained under a variety of saturated and unsaturated conditions (Meinild et al. 1998). In the case of arbutin, however, we worked at less than saturating conditions: we used 5 mm of arbutin and the K_0.5 is only 1.3 mm at −30 mV in rSGLT1 (Lostao et al. 1994). CR for arbutin did not increase, however, as transport became more saturated. The CRs were actually smaller at conditions close to saturation (5 mm and −90 mV) than those determined at half-saturating conditions (2–5 mm of arbutin at clamp potentials of −50 mV). Consequently, the CR for arbutin was smaller than that for α-MDG under all conditions tested. This suggests that the smaller CR for arbutin does not originate from the transport conditions, in which case the CR for arbutin would have increased as transport became more saturated. For NIS the CRs for I⁻ and SCN⁻ were both tested under saturating conditions. The transport of SCN⁻ had a higher CR than I⁻ despite the fact that SCN⁻ led to smaller clamp currents. This relation is opposite to that in the SGLT1s where lower currents (arbutin) were associated with lower CRs. This supports the notion that the CRs are specific for the interaction between the given substrate and its cotransporter and not linked to how often the cotransporter is allowed to turn over.

When several identical experiments were superimposed, it was possible to identify subtle changes in water transport rates during the early phases of substrate application (Fig. 5). For hSGLT1, the initial value of CR was larger by as much as one order of magnitude during the first few seconds of substrate application as compared with the values obtained when the cotransporter had reached steady state. The phenomenon could be important in the human intestine working at low luminal sugar concentrations. No such effects were observed with rSGLT1. For NIS, the CR was initially slightly larger for SCN⁻ but slightly smaller in the case of I⁻. The molecular mechanisms behind the variable CR are not clear. Following the application of the substrate the cotransporter proceeds from being unsaturated towards saturated states. For the SGLT1 it has been suggested that with addition of sugar, the increase of the sugar-coupled Na⁺ current is masked by a concomitant decrease in the phlorizin-dependent Na⁺ leak current (Mackenzie et al. 1998). Accordingly, an understanding of the early variations in CR would require detailed investigations into the kinetics of the transporters and of the water transport properties of both unsaturated and saturated transport modes. It should be noted that the initial variations in water transport are included in our overall determination of the CR which takes into account a 40-s period. The initial effects in water transport rates do not affect our conclusion that larger substrates give rise to smaller CRs in steady states.

The cotransport of water and substrates in steady state was hyperosmolar. For that reason, the intracellular osmolarity increased with continued transport, giving rise to an additional, osmotic influx of water. The magnitude of this component depends upon the osmotic water permeability of the oocyte membrane and on the osmotic driving force. The osmotic water permeability is small (about 3.5 × 10⁻⁴ cm s⁻¹ in the case of expression of SGLT1 (Meinild et al. 1998; Zeuthen et al. 2001, 2002) and it would require gradients of about 7 mosmol l⁻¹ to explain all transport by osmosis (Zeuthen et al. 2001). For physiological values of the intracellular diffusion coefficient D_i, however, the osmotic driving force that can build up with cotransport is small. From the model (see Appendix), it can be estimated to be less than 0.5 mosmol l⁻¹, which would result in an osmotic flux equivalent to about 5% of the cotransport component, an estimate that would vary by about 2% for D_i values between 0.3 and 0.75 × 10⁻⁵ cm² s⁻¹ (compare curves 1–3 in Fig. 11A). All available data show that the D_i for inorganic ions and smaller organic molecules in Xenopus oocyte resemble those of other cells, i.e. between one- and two-thirds of the free solution values (Zeuthen et al. 2002). In Xenopus oocytes, the D_i for ions has been derived from measurements of conductivity and found to agree with direct measurements of D_i both in Xenopus oocytes and other cells (Allbritton et al. 1992; Zeuthen et al. 2002). In the oocyte, D_i values for organic molecules such as inositol 1,4,5-triphosphate (InsP₃, MW 420) and immunoglobulin G were found to be between two-thirds and one-half of the free solution values (Allbritton et al. 1992). Given these values, D_i for glucose in the oocyte cytoplasm can be determined by extrapolation to 0.4 × 10⁻⁵ cm² s⁻¹, which is two-thirds of the free solution value (Longsworth, 1953). This agrees with estimates in oocytes in which human aquaporin (AQP1) and rSGLT1 were coexpressed (Zeuthen et al. 2001); here the D_i for glucose was found to be similar to that of Na⁺. The value for D_i of glucose in Xenopus oocyte was in close agreement with the value for sorbitol and sucrose in muscle cytoplasm (Kushmerick & Podolsky, 1969). For values for D_i around 0.5 × 10⁻⁵ cm² s⁻¹, the osmotic influx results from a uniform increase in oocyte osmolarity, and only to a minor extent from unstirred layer effects (Zeuthen et al. 2002) (see also curve C in Fig. 2 and curve d in Fig. 11A).

We conclude that CR can be determined from a number of experimental types and that CR is smaller for larger-sized substrates. The determination is model independent and does not arise as a result of the transporters being forced to transport at a slower (unsaturating) rate. Model-based calculations shows that the CRs are unaffected by diffusion inside the oocyte given physiological values of intracellular diffusion coefficients.

Evaluation of unstirred layer effects

It is now agreed that diffusion of small ions such as Na⁺, K⁺ and Cl⁻ in the cytoplasm of the oocyte does not lead to significant unstirred layer effects, i.e. the build-up of concentration of these ions at the inside of the membrane during transport is small. Oocytes in which the ionophore gramicidin or nystatin were inserted did not exhibit immediate volume changes at the onset of inward clamp currents carried by Na⁺ or Cl⁻ (Zeuthen et al. 1997, 2001, 2002; Meinild et al. 1998). Similar results were obtained with the channel protein connexin Cx50 (Wright et al. 1998) and the K⁺ channel ROMK2 (Duquette et al. 2001; Gagnon et al. 2004). Even high Li⁺ leakage currents through the GAT1 cotransporter did not elicit water transport, while Na⁺–GABA cotransport by the GAT1 was associated with large water fluxes (MacAulay et al. 2002b). Clamp currents up to 4000 nA were tested. Specific transport number effects (Barry & Hope, 1969) can be ruled out since it made no difference whether the current was maintained by K⁺ or Na⁺, two ions with markedly different concentration profiles across the membrane.

Could unstirred layers be generated by a slow migration of organic substrates such as glucose (Gagnon et al. 2004)? This suggestion ignores previous experimental evidence (references above), which showed that organic molecules behaved as inorganic ones in regard to diffusion. There was also no evidence in the present investigation that diffusion of the sugars (or anions) influenced the measurements. According to the square or cubic root relation between mole weight and diffusion coefficients (Stein, 1967), arbutin should diffuse 10–15% slower than α-MDG, and I⁻ 27–36% slower than SCN⁻. Consequently, if unstirred layers were significant, the coupling ratio should be larger by roughly the same amounts. Contrary to this prediction, however, CRs were found to be 15–40% smaller with larger substrates.

Model analysis supported this conclusion: given the rather low osmotic water permeability of the SGLT1-expressing oocytes, unstirred layer effects were either too small or too slow to explain the experimental findings. In Fig. 11A, the effects of isosmotic application of substrate were simulated in the case where water transport across the membrane was driven entirely by osmosis. The oocyte parameters were those of Fig. 2. For simplicity, it was assumed that three substrate molecules/ions were transported per turnover of the protein and that all had the same intracellular diffusion coefficient D_i. Four values of D_i were tested. It is noteworthy that even with a D_i of 0.5 × 10⁻⁸ cm² s⁻¹ (more than three orders of magnitude lower than free solution values) unstirred layer effects failed to explain the rapid onset of the volume changes. From a comparison with Fig. 2, it is clear that the predicted values lag behind the experimental volume changes by about 10 s. This is the time required to build up sufficient osmolarity in the unstirred layer, even at the lowest value of D_i. Unstirred layer effects were also unable to simulate the rapid shifts in volume changes obtained at changes in clamp current (Fig. 11B) and at the application of phlorizin (Fig. 11C). The curves simulating unstirred layer effects were based on three slowly diffusing substrate molecules. To obtain the same curves with only one diffusing substrate (i.e. the organic substrate in SGLT1) the parametric values of D_i should be about three times smaller, from around 0.2 × 10⁻⁵−0.2 × 10⁻⁸ cm² s⁻¹.

In summary, there are several reasons why unstirred layer effects can be ruled out: (i) Even low (unphysiological) intracellular diffusion constants (D_i) cannot explain the experimental findings. (ii) Published values for D_i of ions and small organic substrates are of the order of 0.5 × 10⁻⁵ cm² s⁻¹. This reflects basic physiological requirements; glucose, for example, has to move readily to sites of enzymatic treatment. D_i values of this magnitude do not give rise to unstirred layer effects. (iii) Transport of larger substrates gave relatively less water transport (Fig. 6), which is opposite to what would be expected from unstirred layer effects. (iv) Specific electrical effects and (v) effects originating from the organic nature of the substrates are unlikely to play a role: water cotransport has been observed with the electroneutral K⁺–Cl⁻ cotransporter (Zeuthen, 1991a, b) and with the 2 Na⁺–I⁻ cotransporter which transports inorganic ions only.

Technical requirements

The low relative noise level (0.2 × 10⁻⁴) employed in the present measurements allowed a precise recording of rapid changes in oocyte volume. The data confirmed previous recordings obtained at a higher noise level (0.3 × 10⁻³). In the latter measurements, however, rapid changes were quantified by regression analysis, which reduced the effective time resolution. The earlier findings have been challenged by Duquette et al. (2001) and Gagnon et al. (2004). The techniques employed by these authors, however, are inadequate to resolve fast changes in oocyte volumes. Their level of random (white) noise of the relative volume recording was high, 0.5 × 10⁻³, about 25 times that employed in the present paper (Fig. 1). In addition, this random noise was overlaid with spontaneous volume changes with a magnitude of 0.5 × 10⁻³ and a characteristic time course of about 10 s. The time constant for solution changes was slow (about 3 s compared with the 0.5 s employed in the present paper). With these noise levels it is difficult to estimate the exact time course of oocyte volume changes (see for example Figs 2, 6 and 8). In addition, the authors made three specific mistakes: (i) When correlating I_C and volume changes during the initial phases of the isotonic application of sugar they did not take into account the rather slow rise time of I_C of 5–10 s (Figs 2 and 3, and Table 1). If it is assumed that the I_C rises abruptly, given the high noise level, it might be concluded, erroneously, that the change in volume was delayed relative to I_C. (ii) When arresting transport in the SGLT1 by phlorizin, the inhibitor was taken from a stock solution of ethanol (Duquette et al. 2001). As a result, the test solution contained 0.5% of ethanol, which in itself induces significant increases in oocyte volume (Zeuthen et al. 2002). Consequently, abrupt decreases in swelling were masked. (iii) In agreement with the present data, Lapointe et al. (2002) did observe changes in oocyte volume when the clamp current was changed abruptly, but the underlying mechanism was not addressed.

Finally it should be noted that the clamp currents in the microelectrode do not affect the intracellular osmolarity significantly, as has been ascertained both theoretically and experimentally (Zeuthen et al. 2002). The electrode is filled with 1 m KCl, and K⁺ and the Cl⁻ ions have the same mobility. Consequently, inward clamp currents are primarily made up from an equal number of cations (K⁺) going into and anions (Cl⁻) going out of the electrode. Electrode effects can therefore be disregarded, in particular for short-term experiments.

Physiological relevance

Uphill water transport is well established in epithelial physiology (Ludwig, 1861; Reid, 1892). In the small intestine, for example, intraluminal osmolarity may increase more than 100 mosmol l⁻¹ above plasma osmolarity during digestion, yet water is absorbed (Parsons & Wingate, 1961; Kellett, 2001). It has been suggested that transepithelial water transport results from high passive water permeability and small osmotic gradients. Such models, however, would give rise to large back-fluxes of water in the face of adverse osmotic gradients. The existence of intraepithelial hyperosmolar compartments (in the lateral spaces, for example) would alleviate this problem, but despite considerable efforts, no such compartments have been demonstrated. We have suggested that coupling between salt and water fluxes could take place in cotransporters of the symport type and that this mechanism was an important building block in models of transport in epithelia and other tissues (Zeuthen et al. 2002; MacAulay et al. 2004). In the small intestine, for example, the luminal SGLT1 could collaborate with GLUT2 to ensure entry of Na⁺, sugars and water (Kellett, 2001); together with another molecular water pump, the basolateral K⁺–Cl⁻, it could energize transepithelial uphill water transport.

Appendix

The model of the oocyte was based upon two influx mechanisms for water – cotransport along with the non-aqueous substrates (J_H2O,co) and osmosis (J_H2O,os), Fig. 12. The trans-membrane osmotic gradient depended on how readily the substrates diffused in the cytoplasm; substrates with very low intracellular mobility may accumulate at the inside of the membrane and give rise to unstirred layer effects. The oocyte volume (V_T) consisted of a free fraction (V_F) and an inaccessible fraction (V_I). The oocyte was divided into concentric shells of identical thickness Δr. In each time interval the entry of substrate and water and the subsequent diffusion of substrate into the oocyte were calculated. After each calculation, the shells were adjusted to have the same thickness in order to maintain the geometry. The oocyte was divided into 100 shells and calculations were performed with a resolution of 1 s. Transport within the shells in the cytoplasm was described by Fick's equation: J_S=−D_i (c_i+1−c_i)/Δr where c is the concentration in the respective shells and r is the oocyte radius. To test the stability, thinner shells and shorter time intervals were tested with no difference in predictions.

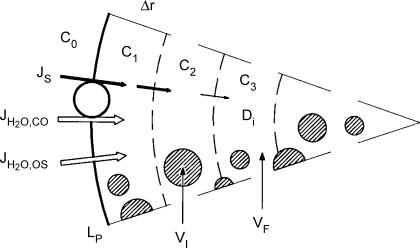
Figure 12. Model for water transport into oocyte.

Water enters the oocyte by two mechanisms. It is cotransported at a rate J_H2O,co together with the non-aqueous substrates which enter at a rate of J_S. Water also enters by osmosis at a rate J_H2O,os determined by the osmotic gradient across the membrane (c₁− c₀) and the osmotic water permeability L_p. Substrate transport in the cytoplasm is described by Fick's law and an effective diffusion coefficient D_i. The intracellular compartment is assumed to consist of a free fraction V_F which is about 0.4 times the total volume of the oocyte, V_T. The inactive fraction (V_I=V_T− V_F) is assumed to be inaccessible to ions and water.

Four parameters were determined prior to the simulations. The osmotic water permeability, L_p (with and without phloridzin), and the oocyte radius (r) were determined in separate experiments. The coupling ratio CR was determined to a first (and close) approximation from the proportionality between the initial volume changes and the integrated clamp current (I_C) in experiments where the substrate was added isosmotically (Figs 2, 3 and 4). A final estimation of CR could be obtained from iteration. The rate of substrate transport (J_S) was given by the clamp current (I_C) and the stoichiometry of the cotransporter. For the SGLT1s with three particles transported for two charges, J_S= 1.5 I_C F⁻¹. For NIS with three particles per charge J_S= 3 I_C F⁻¹. F is Faraday's constant. Any effects from the movements of ions in and out of the voltage clamp electrode can be neglected (see above and Zeuthen et al. 2002).

While CR was the most important parameter for the initial phases of simulation, the intracellular diffusion coefficient (D_i) was important for the slow rates of swelling observed after the removal of the substrate. Values of D_i in the physiological range of 0.2–0.8 × 10⁻⁵ cm² s⁻¹ were tested (Fig. 11A). D_i depends on the free fraction of the oocyte volume V_F, which constitutes around 0.4–0.6 of the total volume V_T (Zeuthen et al. 2002). V_F is accessible for rapid uptake of water and substrates from the outside and substrates have diffusion coefficients equal to that of free solutions, D_f. The other fraction (V_I) is inaccessible for rapid uptake of water and ions. If V_I is constituted by insulating spheres or ellipsoids, the effective D_i and D_f are related by 1/D_i= (3V_T/V_F− 1)/2D_f (Maxwell, 1881). For D_f= 1.5 × 10⁻⁵ cm² s⁻¹ and V_F/V_T= 0.4, D_i is calculated as 0.5 × 10⁻⁵ cm² s⁻¹, in close agreement with comparisons between published values of internal conductivities and concentrations in the oocytes (Zeuthen et al. 2002).