Evaluation of synthetic linear motor-molecule actuation energetics

Abstract

By applying atomic force microscope (AFM)-based force spectroscopy together with computational modeling in the form of molecular force-field simulations, we have determined quantitatively the actuation energetics of a synthetic motor-molecule. This multidisciplinary approach was performed on specifically designed, bistable, redox-controllable [2]rotaxanes to probe the steric and electrostatic interactions that dictate their mechanical switching at the single-molecule level. The fusion of experimental force spectroscopy and theoretical computational modeling has revealed that the repulsive electrostatic interaction, which is responsible for the molecular actuation, is as high as 65 kcal·mol⁻¹, a result that is supported by ab initio calculations.

Molecular motors have recently garnered considerable interest within the domains of microsciences and nanosciences (1, 2). Harnessing the ability to selectively, cooperatively, and repeatedly induce structural changes in molecules may hold the promise of engineered systems that operate with the same complexity, elegance, and efficiency as biological motors function in the human body. In natural systems, it has become apparent that both macro and micro processes are initiated and controlled by nanoscale molecular motors (3). For example, myosin and kinesin are associated with muscle contraction and intracellular trafficking, respectively, and have recently found their ways into engineered devices (4, 5). Moreover, initial work has been performed that demonstrates the ability of natural nanoscale molecular motors to power microfabricated systems (6).

Synthetic motor-molecules (7–11), which are designed to excel where their biological counterparts fall short, also have been investigated. Whereas devices powered by biological molecules require (4–6) chemical diffusion for actuation stimulus, synthetic molecules have been shown (2, 9) to operate with a variety of different stimuli, thereby lending much greater flexibility to a particular system’s design. Moreover, a synthetic nanoscale actuating molecule carries with it an inherent ability to be modified and optimized precisely for a specific task.

Switchable, bistable rotaxanes (2, 9), compounds comprised of a dumbbell-shaped component containing two different recognition sites for an encircling ring-shaped component, show particular promise as molecular actuators, given their ability to undergo controllable, reversible mechanical switching with the appropriate chemical, electrochemical, or photochemical stimulus in solution. Toward the goal of device applications, switching has been shown to operate in condensed phases such as in a polymer electrolyte gel (12), on a self-assembled monolayer (SAM) (13), on the solid supports of engineered systems (14), and in molecular switch tunnel junctions (15). Bistable rotaxanes benefit from their synthesis being highly modular, a virtue that allows for a considerable degree of flexibility in their design. Recently, the use of linearly actuating rotaxanes in microfabricated molecular devices has been demonstrated (16) where the redox-controlled switching of palindromic, doubly bistable [3]rotaxane molecules self-assembled on gold-coated microcantilevers was shown to generate enough surface stress to bend them reversibly and repeatedly. The successful operation of these fundamental devices demonstrates the potential for such rotaxanes to form the foundation on which a bottom-up fabricated actuator paradigm based at the nanoscale could be built.

In addition to the actuation characteristics of synthetic motor-molecules and their potential to be redesigned, the possibility of producing forces greater than their natural counterparts (16, 17) is a distinct benefit. Not only is this assertion critical to the pursuit of artificial motor-molecule engineering, but its verification is essential to any system’s design. Force spectroscopy using an atomic force microscope (AFM) has been demonstrated to be an effective probe (18) of the strengths of various covalent bonds (19) as well as the noncovalent bonding associated with the biotin–streptavidin complex (20) and hydrophobic cyclodextrin-based complexes in water (21). In addition, Gaub and coworkers (22) have used AFM force spectroscopy to investigate the force generated by polyazobenzenes operating as molecular motors.

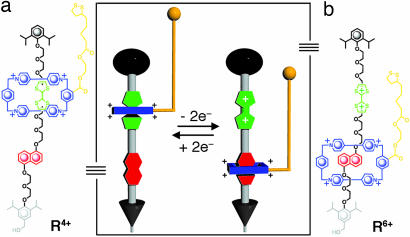
Along that same vein, we have expanded this field of research to include the probing of steric and electrostatic interactions within highly complex synthetic molecules. In so doing, we have been able to quantify the power stroke of the switchable, bistable [2]rotaxane R⁴⁺ (Fig. 1), which can function as a linear motor-molecule by harnessing the redox-controlled mechanical shuttling of its ring along its dumbbell. Although it features the same actuation mechanism as the doubly bistable [3]rotaxane recently used to drive a set of microcantilevers (16), R⁴⁺ was specifically designed (i) with a thioctic acid tethered to its ring component for attachment to a gold AFM tip and (ii) with a hydroxymethyl group on one of the stoppers of its dumbbell for attachment (Scheme 1b) to SiO₂ via covalently bound monolayers of isocyanatopropyl linkers (23). This dual functionality allows for AFM force spectroscopy studies to probe the steric and electrostatic interactions present in the ground (Fig. 1a) and oxidized (Fig. 1b) states of R⁴⁺. AFM probing of molecules in neat ethanol (EtOH) will measure the repulsive steric interactions (Fig. 2a) between the cyclobis(paraquat-p-phenylene) (CBPQT⁴⁺) ring and the diisopropylphenyl ether stopper and serves as a control. The probing of the R⁶⁺ molecules in an oxidizing solution will measure the repulsive force (Fig. 2b) between the CBPQT⁴⁺ ring and an oxidized tetrathiafulvalene (TTF²⁺), which is responsible for molecular actuation. In conjunction with computational chemistry, these experiments enable a thorough quantitative evaluation of the actuating energetics of a single-molecule motor. For further details, see Supporting Materials and Methods, Tables 1 and 2, Figs. 5–16, and Scheme 2, which are published as supporting information on the PNAS web site.

Fig. 1.

Structural formula and schematic representation of bistable [2]rotaxane R⁴⁺, in which an electron-poor cyclobis(paraquat-p-phenylene) (CBPQT⁴⁺) ring is confined to a dumbbell containing two electron-rich recognition sites, tetrathiafulvalene (TTF) and 1,5-dioxynaphthalene (DNP), by the presence of bulky 2,6-diisopropylphenyl ether stoppers at each end. One of these stoppers, the one closer to DNP, carries a hydroxymethyl group on its 4-position for subsequent attachment to silicon wafers. (a) The CBPQT⁴⁺ ring, which carries a tether terminated by a thioctic acid ester for attachment to a gold-coated AFM tip, displays a stronger interaction with TTF than with DNP and thus resides selectively (16) on the former. (b) Chemical oxidation of TTF to TTF²⁺ results in a strong charge–charge repulsion between the CBPQT⁴⁺ ring and TTF²⁺, a situation that causes the CBPQT⁴⁺ ring to shuttle to DNP (9, 12–16) in the oxidized [2]rotaxane R⁶⁺. The mechanical movement of the CBPQT⁴⁺ ring from TTF²⁺ to DNP resembles the power stroke of a linear motor. Reduction of the TTF²⁺ to its neutral state (TTF) prompts the ring to shuttle back thermally from a metastable state to its ground state where it encircles TTF in a manner reminiscent of the diffusive stroke of a linear motor. This externally controllable shuttling process and bistability allows [2]rotaxane R⁴⁺ to function as a nanoscale linear motor given its ability to contract and expand reversibly in the presence of a chemical oxidant or reductant, respectively.

Scheme 1.

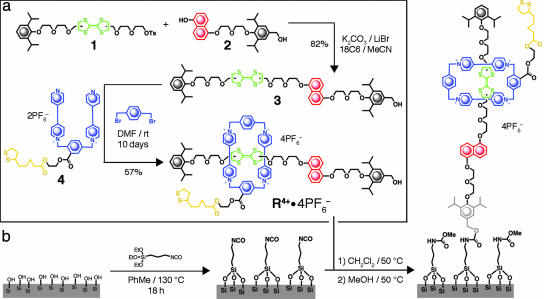
Reaction schemes illustrating the synthesis of dual recognition [2]rotaxane R⁴⁺ (a) and the attachment of R⁴⁺ to SiO₂ wafers via covalently bound isocyanatopropyl tethers (b).

Fig. 2.

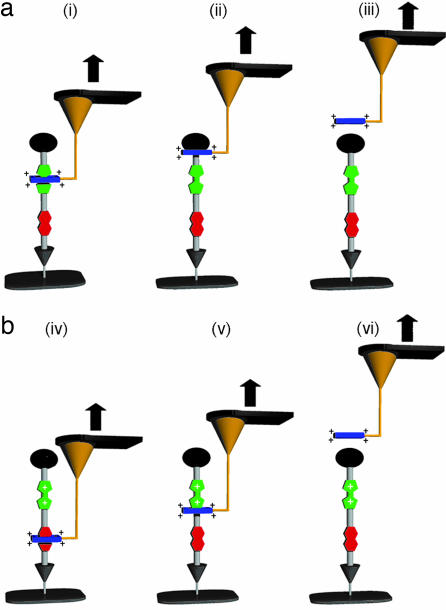
Schematics of AFM force spectroscopy of [2]rotaxane R⁴⁺. (a) Ground-state probing in the absence of oxidant. (i) [2]Rotaxane R⁴⁺ confined to a silicon surface and attached to a gold AFM tip via two gold–sulfur bonds. (ii) Retraction of the AFM tip from the surface pulls the CBPQT⁴⁺ ring away from the TTF unit and toward the bulky stopper. (iii) Continued retraction causes the CBPQT⁴⁺ ring to pass over the stopper (deslip) at which point the force required to overcome this physical barrier is measured. (b) Oxidized-state probing performed in the presence of 10⁻⁴ M Fe(ClO₄)₃ in EtOH. (iv) The attachment of a gold AFM tip to [2]rotaxane R⁶⁺ whose ring is now located on the lower DNP unit as a result of the chemically induced oxidation of the TTF unit to TTF²⁺ and subsequent electrostatic repulsion of CBPQT⁴⁺. (v) Retraction of the AFM tip forces the tetracationic CBPQT⁴⁺ ring toward the dicationic TTF²⁺ despite the electrostatic repulsion between the two moieties. The AFM will measure the repulsive force between the ring and the TTF²⁺ that was originally responsible for the molecule’s actuation. (vi) Continued retraction of the AFM tip enables the CBPQT⁴⁺ ring to overcome the electrostatic barrier imposed by TTF²⁺, resulting in rupture of the mechanical bond posed by the stopper. When measuring the higher-energy electrostatic repulsion of the oxidized molecule, the subsequent deslipping event will not be measured because of the dynamic instability of the AFM probe.

Results and Discussion

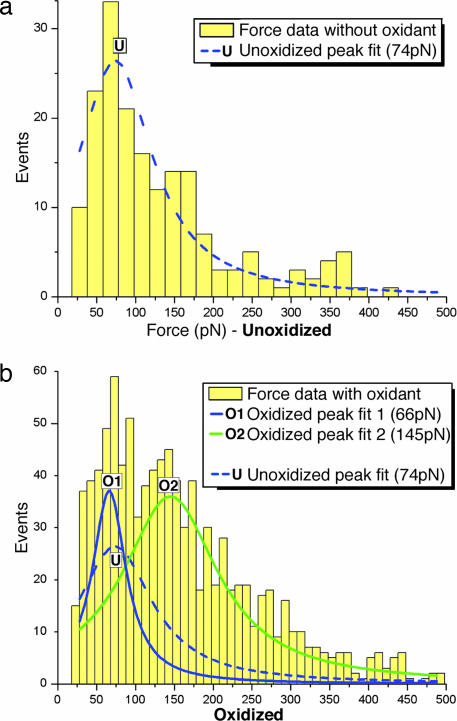
The routes used to synthesize the dumbbell-shaped compound 3 and the bifunctional [2]rotaxane R⁴⁺ are shown in Scheme 1a, and that used to covalently attach [2]rotaxane R⁴⁺ to SiO₂ wafers is shown in Scheme 1b. The concentration of R⁴⁺ was kept dilute, ≈1 per 100 nm², to promote the observation of single-molecule events. Compiled AFM force probe data are summarized (Fig. 3) in the form of histograms, which were analyzed by using commercial peak-finding and curve-fitting algorithms. The first histogram (Fig. 3a) summarizes the control experiments on unoxidized single molecules and reveals that the most probable molecular rupture force occurs at 74 pN. In these control experiments, any measured force peak stems from rupture either within the molecule or its linkages to the AFM tip or the substrate. As in any structural system, failure will occur at the weakest point. Published reports indicate that this ruptured 74-nN mechanical barrier is considerably weaker than any of the covalent bonds in the system, revealing that the failure occurs as the ring passes over the stopper, a process referred to as “deslipping” (24). To our knowledge, all experimental and theoretical data at comparable experimental conditions indicate that the rupture of any covalent bond requires >1 nN (see Table 2).

Fig. 3.

Force probe data obtained during single-molecule investigations of R⁴⁺ and R⁶⁺. (a) Histogram of compiled AFM force spectroscopy data of ground-state [2]rotaxane R⁴⁺ obtained in an EtOH solution with a loading rate of 6 pN·s⁻¹. The dashed blue curve (U) is obtained from commercial peak finding and curve-fitting algorithms and indicates a most probable rupture force of 74 pN. (b) Histogram of AFM force spectroscopy data obtained (for R⁶⁺) in an oxidizing solution of 10⁻⁴ M Fe(ClO₄)₃ in EtOH (loading rate of 6 pN·s⁻¹) displays two different force regimes, indicating two distinct force barriers having most probable rupture forces of 66 pN (O1, solid blue curve) and 145 pN (O2, solid green curve). The magnitude of the solid blue curve matches well with the dashed blue curve superimposed from a, indicating that not all molecules are oxidized. The solid green curve corresponds to the emergence of a new, larger barrier, which is a direct measure of the electrostatic repulsion between the TTF²⁺ dication and the CBPQT⁴⁺ tetracation responsible for molecular actuation.

The second histogram (Fig. 3b) summarizes the results of force probing in the presence of a 10⁻⁴ M Fe(ClO₄)₃ oxidizing enthanolic solution, which has been shown to induce ring translation to the 1,5-dioxynaphthalene (DNP) site as a result of electrostatic repulsion from the TTF²⁺ site (14). Whereas in the unoxidized situation the histogram reveals a singular force, this histogram indicates that there are two distinct force barriers, one at 66 pN (O1, solid blue curve) and the other at 145 pN (O2, solid green curve). We believe that the lower force regime is caused by the probing of single molecules that have not undergone redox-controlled switching despite the oxidizing environment. This belief is supported by comparing the peak value from the unoxidized histogram (U, dashed blue curve) with those from the oxidized histogram (Fig. 3b). The peak of the curve for the unoxidized molecules coincides well with the lower force peak curve from the oxidation experiments. This interpretation also is supported by earlier studies at a lower concentration of oxidant (10⁻⁶ M), which yielded results that were not easily distinguishable from those obtained for the unoxidized molecule with respect to peak-force magnitude and well defined peak distribution (see Fig. 16). An alternative explanation could be that electron transfer between the Fe(ClO₄)₃ oxidant and TTF occurs within the time frame of individual pulling experiments, resulting in an equilibrium of neutral and oxidized TTF, which would give rise to both unoxidized as well as oxidized force data. We believe, however, that results of probing an oxidant concentration of 10⁻⁶ M support the former explanation over the latter.

Although the second force regime at 145 pN has clearly emerged as a result of the presence of oxidant, it is more important to examine how these results enhance our understanding of the bistable rotaxane’s mechanical switching behavior. Previous experimental results have revealed that Fe(ClO₄)₃ oxidizes the TTF unit to TTF²⁺, resulting in concomitant shuttling of the CBPQT⁴⁺ ring to the DNP unit (9, 12–16) even when immobilized on a surface or between surfaces in a manner not dissimilar to that present in the AFM-based system. Therefore, the new higher-energy barrier can be ascribed to the electrostatic repulsion between TTF²⁺ and CBPQT⁴⁺ or covalent bond rupture. Given that the measured peak rupture force in the presence of the oxidant is still an order of magnitude lower than those associated with the rupture of relevant covalent bonds (see Table 2), it is clear that the second force regime present in the experiments on the oxidized molecules emerges as a result of the newly generated repulsive electrostatic barrier, which is ultimately responsible for the molecule’s actuation.

Although the results indicate that the 145-pN force peak is a measurement of the electrostatic repulsion between the bistable rotaxane’s CBPQT⁴⁺ ring at TTF²⁺ dication, and therefore a good indication of the maximum switching force producible under load by the oxidized molecule, force spectroscopy measurements require loading-rate analysis for a complete understanding of the energy barrier that was investigated. A direct corollary between force and energy through distance cannot be established because the work done by an AFM’s tip distorts the system’s energy landscape. According to Evans (25), forces measured by force spectroscopy will be altered by thermal fluctuations as a function of the probe’s loading rate such that the most probable measured force, f*, is defined as

where k_BT is the thermal energy, x_β is the bond length, t_off is the lifetime of the bond under no external force, and k_s and ν are the spring constant and retract velocity of the AFM probe, respectively. Previously, only with a detailed loading-rate analysis that spans several orders of magnitude can interactions be described (20, 25) by x_β and t_off. Although rotaxanes do operate reversibly (2, 9, 12–16), the irreversible rupture of molecules required by this experiment (see Loading Rate Analysis in Dynamic Force Spectroscopy in Supporting Materials and Methods) prohibits such a study. However, by augmenting the AFM data with molecular dynamics simulations (see Fig. 10), which describe (Fig. 4) the ground-state energy profile of R⁴⁺ as a function of the ring’s position on the dumbbell, an accurate description of the physical switching mechanism can be formulated.

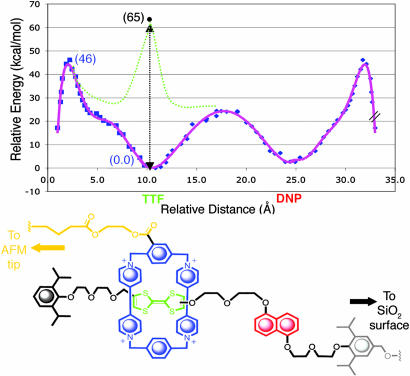
Fig. 4.

The ground-state energy profile obtained from molecular dynamics and mechanics simulations. The x axis indicates the position of the CBPQT⁴⁺ ring along the linear dumbbell (in Å), and the y axis displays relative energies of the different CBPQT⁴⁺ ring co-conformers (in units of kcal·mol⁻¹). The simulations correctly predict the co-conformation of the CBPQT⁴⁺ ring stationed on TTF to be the lowest-energy state and therefore the most favorable one. The energy barrier that exists when the CBPQT⁴⁺ ring passes over either of the bulky stoppering units (deslipping) is calculated to be 46 kcal·mol⁻¹. A combination of theoretical modeling and experimental AFM measurements predict oxidation of [2]rotaxane R⁴⁺ to result in a 65-kcal·mol⁻¹ repulsion between the CBPQT⁴⁺ tetracation and the TTF²⁺ dication. This result is supported by quantum mechanical calculations. The dashed green line is a schematic representation of what the full, oxidized energy profile may look like, but it is not quantitative.

t_off is the time at which a bond, described by an energy barrier with Arrhenius dependence, spontaneously ruptures (25, 26). Conversely, the Arrhenius equation relates the rate, k_r, of a first-order chemical process to the activation energy, E_a, associated with that process

where A is a constant preexponential factor and R is the molar gas constant. By substituting this relationship into Evans’ equation, a new relationship arises that describes the energy difference between two rupture events at a single loading rate

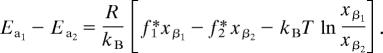By using the measured force spectroscopy values of 66 pN for the deslipping barrier under nonoxidative conditions and 145 pN for the oxidant-induced electrostatic repulsion barrier, along with x_β values, produced from molecular simulations, of 8.6 Å for the deslipping of the CBPQT⁴⁺ ring over the bulky stopper and 13.0 Å as the distance necessary for the CBPQT⁴⁺ ring to travel from the DNP recognition site to the TTF²⁺ dication, the difference in interaction energies can be calculated as 19 kcal·mol⁻¹. Although the value of 66 pN was generated in the presence of oxidant, this value was used instead of the 74-pN value produced in the nonoxidizing environment because of the availability of significantly more experimental data points. It should be noted that the use of the 74-pN value only changes the results of this study by 1 kcal·mol⁻¹. By combining the 19 kcal·mol⁻¹ difference in oxidative and nonoxidative interaction energies with the theoretically determined value of 46 kcal·mol⁻¹ for the energy associated with ground-state deslipping (Fig. 4), a final value of 65 kcal·mol⁻¹ was obtained, representing the amount of repulsive actuation energy between CBPQT⁴⁺ and TTF²⁺ produced by the oxidation of R⁴⁺ (Fig. 4). As measured by this approach, 65 kcal·mol⁻¹ represents the upper limit of the total actuation energy. In the experimental set-up, the retraction of the AFM tip forces the CBPQT⁴⁺ ring into the most energetically unfavorable conformation possible with respect to the TTF²⁺, thus maximizing the electrostatic repulsion between the tetracationic and dicationic moieties.

This value, although seemingly low for the repulsion of six positive charges confined within a radius of ≈5 Å, is strongly supported by ab initio calculations (see Model System and Calculations of Electrostatic Repulsion in Supporting Materials and Methods). Single-point quantum mechanical calculations were performed in EtOH by using atomic coordinates from the crystal structures of TTF, [TTF][ClO₄]₂, [CBPQT][PF₆]₄, and [CBPQT⊂TTF][PF₆]₄ as well as on five model systems for the hexacationic [CBPQT⊂TTF][Cl]₆ complex (see Fig. 11). The repulsive energy within this hexacationic complex was calculated to be 70.6–76.0 kcal·mol⁻¹. By using this value and that produced by the molecular force field simulations, computational analysis predicts that the electrostatic barrier resulting from the TTF²⁺ dication exceeds the steric barrier of the stopper by 25–30 kcal·mol⁻¹. This entirely theoretical value compares well with the value of 19 kcal·mol⁻¹ produced experimentally by means of AFM force spectroscopy. The similarity between the purely independent ab initio calculations, which only take into account the interaction between CBPQT⁴⁺ and TTF²⁺, and experimental AFM results lends support to the conclusion that single-molecule rupture events are being measured accurately as 65 kcal·mol⁻¹. Perhaps even more significant is the fact that this result lends validity to the methods developed in this work used to analyze force spectroscopy experiments at a single loading rate with the help of molecular force-field simulations.

Employing a combination of AFM force spectroscopy and molecular simulations, we have determined and verified that the energy output of a single synthetic motor-molecule operating within an engineered environment is 65 kcal·mol⁻¹. Assuming that the total energy available to biological systems from the hydrolysis of ATP (14.4 kcal·mol⁻¹ at physiological concentrations) (1) is 100% efficiently converted, rotaxanes still outperform nature by >4.5 times. Furthermore, the synthetic origin of switchable, bistable rotaxanes allows them to be designed and redesigned according to a particular application’s requirements as well as from the feedback obtained through characterization studies. Molecular-level characterization is a critical step in the iterative process that may eventually bring about viable engineered systems that extend far beyond mere scientific novelties. Meanwhile, the promise of up to 65 kcal·mol⁻¹ of energy production from bistable rotaxanes and its family of synthetic molecules will always headline systems that have the potential to exceed anything seen in nature.

Materials and Methods

General Methods.

Chemicals were purchased from Aldrich and used as received. Silicon wafers were purchased from Silicon Quest International (Santa Clara, CA). The TTF-containing tosylate 1 (27), the DNP-containing diol 2 (28), and the dication 4·2PF₆ (27) were all prepared according to procedures described in the literature. Solvents were dried following methods described in the literature (29). All reactions were carried out under an anhydrous argon/nitrogen atmosphere. Thin-layer chromatography (TLC) was performed on aluminum sheets coated with silica-gel 60F (Merck 5554). The plates were inspected by UV light and, if necessary, developed in I₂ vapor. Column chromatography was carried out by using silica-gel 60 (Merck 9385; 230–400 mesh). Melting points were determined on a melting point apparatus (Model 9100, Electrothermal, Dubuque, IA) and are uncorrected. All ¹H and ¹³C NMR spectra were recorded on either (i) an ARX500 (500 and 125 MHz, respectively) or (ii) an Avance500 (500 and 125 MHz, respectively) (both from Bruker, Billerica, MA) by using residual solvent as the internal standard. Samples were prepared by using CD₃COCD₃ or CD₃CN purchased from Cambridge Isotope Laboratories (Cambridge, MA). All chemical shifts are quoted by using the δ scale, and all coupling constants are expressed in hertz. Matrix-assisted laser desorption ionization spectra (MALDI) were recorded on a instrument from PerSeptive Biosystems (Framingham, MA). Electrospray mass spectra (ESI) were measured on a ProSpec triple focusing mass spectrometer (VG Analytical, Manchester, U.K.).

Synthesis of Dumbbell-Shaped Compound 3 and [2]Rotaxane R·4PF₆.

A MeCN solution of the tosylate 1 (27), the diol 2 (28), K₂CO₃, LiBr, and 18C6 was heated under reflux for 16 h. After work-up, the crude product was subjected to column chromatography (SiO₂:EtOAc/hexane, 1:1) to give 3 as a yellow solid in 82% yield.

The synthesis of R⁴⁺ was completed by stirring a solution of 3, 1,4-bis(bromomethyl)benzene, and the dication 4·2PF₆ (27) in anhydrous dimethylformamide (DMF) at room temperature for 10 d. The reaction mixture then was subjected directly to column chromatography (SiO₂), and unreacted 3 was recovered with Me₂CO, whereupon the eluent was changed to Me₂CO:NH₄PF₆ (1.0 g of NH₄PF₆ in 100 ml of Me₂CO), and the green band containing the [2]rotaxane R·4PF₆ was collected. After removal of solvent, H₂O was added, and the resulting precipitate was collected by filtration to afford 57% yield of [2]rotaxane R·4PF₆ as a green solid.

Attachment of R⁴⁺ to SiO₂.

A SAM of covalently bound isocyanatopropyl tethers (23) was formed by vapor deposition of 3-(triethoxysilyl)propyl isocyanate in PhMe onto BOE and piranha-treated 1 cm² SiO₂ wafers. R⁴⁺ then was covalently linked to the tethers upon reaction of its terminal alcohol with the isocyanate of the SAM. Unreacted isocyanates were capped with MeOH. Surface coverage and quality were evaluated through hydrophilicity and homogeneity studies. Freshly prepared SAMs were stored under Ar_(g) in glass vials until use.

Force Spectroscopy.

AFM-based dynamic force spectroscopy studies were performed at standard temperature and pressure with a Multimode scanning probe microscope with a Nanoscope 3A controller and Pico Force system (Digital Instruments/Veeco Probes, Santa Barbara, CA), both in degassed 200 proof EtOH and in the presence of an oxidizing solution of 10⁻⁴ M Fe(ClO₄)₃ in EtOH, which is consistent with previous work that demonstrated mechanical molecular switching within highly packed rotaxane-based thin films (14). Samples were exposed to the oxidant for no less than 10 min to ensure oxidation of the surface bound molecules but no more than 90 min to guarantee the integrity of the SAM. Control experiments for ground-state molecule investigation were conducted in the presence of pure EtOH. The nonaqueous solvent allowed the molecules to be exposed to a plasma-cleaned, Au-coated AFM tip for thiol bond formation. The bio-lever probe tip (Asylum Research, Santa Barbara, CA) was lowered to the surface and held at that position for 3 s at a force of 1.0–1.2 nN and then raised at a rate of 1.05 μm·s⁻¹. This procedure resulted in an ≈10% probability of specific bond formation, thereby minimizing the probability of multiple molecule binding events. Specific bond formation was assumed to have taken place when a measurable rupture force occurred while the tip was no longer in contact with the substrate. Each AFM probe had an average spring constant of 6 pN·nm⁻¹ leading to a loading rate of ≈6 nN·s⁻¹. Individual spring constants were measured by using the on-board thermal-tuning program, and data points were analyzed with their associated probes’ spring constant values. Experiments were conducted with new samples, fresh solution, and new probes and continued until the tip surface was saturated, as indicated by the lack of any binding events despite a change in probe position. Data were plotted in histograms prepared by using originpro software (OriginLab, Northampton, MA). Different bin sizes did not affect the analysis or conclusions drawn from the data. Peaks were identified and analyzed by using the Lorentzian function that best fit our data. In the case of the multiple peak data, the Levenberg–Marquardt algorithm was used in association with the Lorentzian function.

Molecular Force-Field Simulations of R⁴⁺.

A ground-state energy profile representing the relative energies of the different co-conformations of R⁴⁺ as the CBPQT⁴⁺ ring is moved along the dumbbell was generated by using the program maestro v3.0.038 (30) with the AMBER* force field (31) and GB/SA solvent model (32) for CHCl₃. Electrostatic point charges were calculated at the HF/6-31G* level by using the program gaussian 03 (33) and fit to each atom. To model the ring’s movement along the dumbbell, a “dummy” atom was placed at a fixed distance from the model system and constraints were used to “pull” the CBPQT⁴⁺ ring along the linear dumbbell in specified increments (see Fig. 10). A 50-ps molecular-dynamics simulation (1.5-fs time step) at a simulation temperature of 500 K, followed by energy minimization of 200 randomly selected co-conformations, was used for co-conformational searching at each fixed distance along the dumbbell reaction coordinate. The output of each step then was used as the input for the next. Energies were normalized relative to the overall lower-energy co-conformer of R⁴⁺, which corresponds to the CBPQT⁴⁺ ring encircling the TTF unit. The resulting energy differences (ΔE) plotted against CBPQT⁴⁺ ring position gave the ground-state energy profile of R⁴⁺. The same method also was applied to a series of single-station [2]rotaxanes containing stoppers of different sizes (see Fig. 8) as well as a degenerate [2]rotaxane containing two DNP recognition units and compared with experimental results to access the viability of the molecular modeling procedure. In the case of the degenerate [2]rotaxane, modeling predicted a shuttling barrier of 19 kcal·mol⁻¹, which is within 3 kcal·mol⁻¹ of experimental value of 16 kcal·mol⁻¹ (34).

Model System and Calculations of Electrostatic Repulsion Between CBPQT⁴⁺ and TTF²⁺.

Quantum mechanical calculations were used to theoretically examine the electrostatic repulsion between the CBPQT⁴⁺ tetracation and the TTF²⁺ dication that is responsible for redox-controlled mechanical actuation of R⁴⁺. Single-point quantum-mechanical calculations were performed at the HF/6-31+G* level by using the program gaussian 03 (33). Geometries of TTF (35), [TTF][ClO₄]₂ (36), [CBPQT][PF₆]₄ (37), and the [CBPQT⊂TTF][PF₆]₄ complex (38) were taken from x-ray crystal data (see Fig. 11). To minimize computational cost, all counterions present in crystal structures of charged species were replaced with Cl⁻ anions. As a result of its energetic instability, no crystal data exists for the hexacationic [CBPQT⊂TTF][PF₆]₆ complex. Therefore, five model systems for the hexacationic [CBPQT⊂TTF][Cl]₆ complex were constructed by using the crystal structure of [CBPQT⊂TTF][PF₆]₄ (38), with PF₆⁻ counterions replaced by Cl⁻ and two additional counterions to balance the charge of oxidized TTF. The two additional counterions were positioned within the most electropositive regions of the complex as determined by electrostatic potential calculations (see Fig. 12 and 13). The five model systems differed slightly in their positioning of the two new counterions to produce a range of values for the repulsion between [CBPQT][Cl]₄ and [TTF][Cl]₂. The CPCM solvent model for EtOH was included to account for solvent effects.

Abbreviations

AFM

atomic force microscope/microscopy

CBPQT⁴⁺

cyclobis(paraquat-p-phenylene)

TTF

tetrathiafulvalene

DNP

1,5-dioxynaphthalene

SAM

self-assembled monolayer.