Packing helices in proteins by global optimization of a potential energy function

Abstract

An efficient method has been developed for packing α-helices in proteins. It treats α-helices as rigid bodies and uses a simplified Lennard–Jones potential with Miyazawa–Jernigan contact-energy parameters to describe the interactions between the α-helical elements in this coarse-grained system. Global conformational searches to generate packing arrangements rapidly are carried out with a Monte Carlo-with-minimization type of approach. The results for 42 proteins show that the approach reproduces native-like folds of α-helical proteins as low-energy local minima of this highly simplified potential function.

The problem of determining the structure of a protein starting from its amino acid sequence has been approached from many different directions. Knowledge-based methods cannot predict entirely new folds, whereas ab initio methods have this capability but are generally less accurate and more computationally intensive. One class of ab initio methods is based on the minimization of a potential energy function. These methods immediately present the challenge of producing a potential function that identifies the native fold as the lowest-energy structure, yet remains simple enough to permit adequate sampling of the conformational space.

If the secondary structure is known, the space that needs to be searched becomes much smaller, but it still contains a very large number of incorrect packing arrangements. The secondary structure either can be predicted from the sequence [by using programs such as jpred/jnet (1, 2), psipred (3), etc.] or can be extracted from the preliminary output of another method. Here, we demonstrate the feasibility of using a highly simplified energy-based method to pack secondary structure elements in which the positions of residues within these elements are fixed. Each residue is represented by just one interaction center and the potential used is much simpler than in previous work (4). Because helical structures have a simple geometry, the procedure is applied to 42 mainly α-helical proteins. It is shown that, for most structures with six or fewer helices, a limited number of plausible conformations can be identified that contain native-like structures, whereas completely wrong folds are eliminated. The resulting ensemble of conformations can then be used as a starting point for a search with a more detailed model and potential, such as united residue (UNRES; ref. 5), to refine and rank the predicted conformations. Some of the proteins investigated are 100–200 residues long [which overcomes a limitation of some previous studies (6)], but this does not seem to present any problems.

Methods

Our procedure uses an energy-driven Monte Carlo-like search to generate an ensemble of plausible structures, and consists of three main parts. First, a simplified representation of a protein is constructed. Second, a potential function is developed to assign an energy to a given conformation. Third, a search is carried out to find the optimal (lowest-energy) arrangement of secondary structure elements.

Protein Representation.

Given a sequence of amino acids and the corresponding secondary structure assignment, we represent a protein by only its C^α atoms. Coordinates for loop residues are left unspecified (see Potential Energy Function), whereas coordinates for residues in α-helical regions are constructed by using ideal parameters (5, 7), namely, 3.6 residues per turn, 1.5 Å per residue along the helix axis, and 3.8 Å virtual C^α–C^α bond length. Helices are then treated as rigid objects, simply described by the positions of their centroids and their orientations, while the relative positions of the residues within a given α-helix are fixed.

Potential Energy Function.

The energy function is the pairwise interaction between two residues, m and n, of amino acid type i and j:

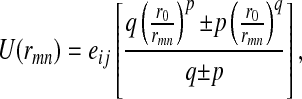1

where p, q (q < p) and r₀ are adjustable parameters, r_mn is the distance between the C^α atoms of residues m and n, and e_ij is the contact energy associated with residues of types i and j. The signs are chosen to obtain a repulsive interaction if e_ij > 0, or negative if e_ij < 0, and to ensure that U(r₀) = e_ij, as in a Lennard–Jones potential. The main purpose is to capture the tendency for nonpolar residues to be buried in the cores of proteins (7). The contact potential developed by Miyazawa and Jernigan (8) has been shown to represent the properties of nonpolar residues accurately (9), and it also provides interaction energies for the polar residues. The matrix of contact energies provided by Miyazawa and Jernigan (10) is used for the parameters e_ij. In their treatment, Miyazawa and Jernigan consider two residues to be in contact if the distance between their side-chain centroids is <6.5 Å. In Eq. 1, the interaction is smoothed and equals e_ij only at the special contact distance r₀ (even when the interaction is purely repulsive).

The energy for a multihelical structure is then calculated by summing over the interactions between all residue pairs belonging to distinct α-helices. There is no interaction between residues within an α-helix (since the relative coordinates are fixed), or with residues belonging to loops. For this reason, coordinates for residues in loops are not necessary. The only contribution that loops make to the energy is a penalty if the distance between the ends of two helices connected by a loop becomes greater than the maximum length allowed for that loop (the number of bonds times the virtual C^α–C^α bond length, 3.8 Å).

Global Optimization.

To search the conformational space of a particular structure, an efficient global optimization method, conformation-family Monte Carlo (CFMC; ref. 11), previously developed in our laboratory, was used with small modifications. This search is based on a conformational family database, which is an ensemble of conformations clustered into families.

The starting point for the search is the sequence and secondary structure information. Helices are then built, using values of ideal α-helices as mentioned above.

The procedure clusters structures into families, in which each structure is similar to at least one other conformation within its family. A structure is said to be similar to another structure or a family if a distance measure provides a value that is smaller than a chosen cutoff. The same is true for two structures being identical except that the cutoff values are stricter. The two distance measures used are explained in Distance Measures.

To control the computational expense, the number of families and the number of structures within one family have a limit of N_f and N_c, respectively. The ensemble is initialized with N_f nonredundant structures selected randomly and is then energy-minimized with the sumsl algorithm (12). This process defines the initial phase after which the actual search starts. In each iteration of the search, a conformation is selected with a probability according to its Boltzmann weight. This structure is subsequently perturbed, its energy is minimized, and similarity, energy, and metropolis tests are carried out to determine whether it will be kept in the ensemble and/or it forms a new family. The temperature was adjusted to maintain a reasonable fraction of new generating families. Thus, the conformations are improved iteratively, and the search is biased to investigate the regions of the lowest-energy families while trying to explore different areas of conformational space effectively. In every iteration, the perturbed structure is checked quickly to determine whether loops could be constructed without clashes. This check is done by treating the C^α atoms of the loops as spheres with diameter set to the bond length. By using a soft-sphere potential [cubic in the extent (distance) of overlap] and subject to bond-length constraints, the energies of these residues are then minimized and checked to determine whether any clashes within each loop or between loops and α-helices occurred.

Because CFMC was originally applied to the UNRES model, it had to be modified for a rigid-body treatment of secondary structure elements; i.e., a different method for producing new conformations, described in Methods for Producing New Conformations, was applied. Also, a new distance measure was devised to suit the objective of finding an ensemble of different folds.

Methods for Producing New Conformations.

Two major classes of moves were used for producing new conformations. The first class, called Global Move, produces radically different structures. This class involves moves, such as randomizing the positions and orientations of all helices, by translational and rotational motions of any number of helices. Helices are allowed to flip upside down or have the positions of any two swapped while keeping the relative orientation unchanged. Moves are chosen randomly and can be combined in any number of ways to perturb the generating structure.

The second class, called Local Move, is designed to produce very similar structures. Like global moves, it also involves translations and rotations of α-helices, but only by much smaller distances and angles. The values by which the helices are translated and rotated are chosen randomly, but they are bound by an upper limit that is different in global and local moves (global: translation up to 15 Å, rotation up to 360°; local: translation up to 4 Å, rotation up to 50°). Local moves can also rotate a helix (up to 180°) or shift it (up to 3 Å) along its axis. The idea behind these moves is that, if a conformation has correct packing but wrong relative orientation, a local move should try to improve it.

Distance Measures.

Two methods were used to describe the similarity of two structures.

1.

rms deviation (rmsd) between C^α atoms in helices. Unfortunately, the C^α rmsd does not provide an unambiguous measure to determine whether the correct (i.e., native-like) fold is obtained. For example, if the alignment is not very good, the rmsd will be high but the folded protein might have correct orientation of secondary structure elements. Also, this number grows with the size of the protein; therefore, comparison of performance of the method for two proteins of different size is not straightforward. This measure was used only to present the results.

2.

Center-of-mass rmsd and maximum angle (CMrmsd and MaxAngle). This distance measure was devised as a replacement for the C^α rmsd. The method works as follows: The centers of mass of each helix in the two conformations to be compared are superimposed. The angle between the axes of every pair of corresponding helices is calculated and the MaxAngle is taken. The CMrmsd and the MaxAngle are the two values used to determine similarity. This measure works better for differentiating the correct orientation of helices from the wrong ones, and was thus used in the search for the definition of the families.

Protein Targets.

Three main sources of target α-helical proteins were used in the simulations, namely, all 24 α-helical proteins from Zhang et al. (13), a set of α-helical proteins obtained from other simulations in our laboratory, and a set extracted from the scop database (Version 1.61; ref. 14), in which only proteins from the α-class and belonging to different families were considered. All three sources provided 42 proteins (36–188 residues long), which were a representative and diverse pool of target structures. The secondary structure information used in our simulations was determined by applying the dssp algorithm (15) to the native structure.

Results

To produce a set of consistent results, most of the adjustable parameters were kept uniform for all of the proteins tested. The potential parameters p, q, and r₀ were set to 15, 14, and 7.5 Å, respectively. Whereas a different set of parameters could perform slightly better for a particular protein, the values used were chosen for best performance over the entire set of 42 proteins, particularly the smaller ones (up to five helices).

The computations were carried out primarily on dual AMD Athlon MP 1800+ based machines (although only one processor was used). The searches for all 42 proteins consisted of 10,000 iterations each, which kept the time for a complete search between 1 and 10 h, depending on the protein size. Primarily, one such run was carried out for each protein, although several runs were carried out for a few models to check reproducibility. The similarity between structures was determined according to the CMrmsd and MaxAngle measure described above (to belong to the same family, the MaxAngle cutoff was 60° and the CMrmsd cutoff was between 2.5 and 4.5 Å, depending on the protein size and complexity, i.e., number of α-helices). To generate diverse packing arrangements, 75% of the moves were global, and only 25% were local. The size of the ensemble was increased with protein complexity (from 100 families, each containing four structures, to 250 families, each containing six structures). At the end of each search, the entire ensemble was reclustered according to a stricter criterion; each structure within a family had to be similar to the lowest-energy member, not just to any other structure in that family. This reclustering was done to strengthen the link between a given structure and its family number (which is determined by sorting families according to the energy of their lowest member). Naturally, this increases the number of families, but it also makes the family number a more relevant property of a structure.

Table 1 presents the results of the simulations. The protein 1dv5 had the structure closest to the native fold, with rmsd = 2.2 Å, which was also found as the global minimum (i.e., the lowest-energy structure in the lowest-energy family). Proteins 1i6z and 1a6s also had native-like global minimum structures, 1kdx and 1dlw had structures resembling the native-like fold within the lowest-energy family.

Table 1.

Simulation results

Protein	N	Nres		Best result rmsdmin, Å (family no.)
		Total	Helices	Low 20	Low 60	All
1cktA	3	61	47	3.6 (9)
1dv5	3	75	34	2.2 (1)
1fex	3	50	31	3.4 (6)
1g2h	3	36	28	3.4 (20)
1gab	3	42	35	2.9 (6)
1hdp	3	44	33	3.7 (11)
1i6z	3	114	102	2.5 (1)
1kdxA	3	66	50	2.6 (1)
1lbu*	3	60	32	3.9 (6)
1lea	3	48	39	3.1 (7)
1lre	3	66	55	3.4 (10)
2occH	3	53	42	4.0 (15)	3.0 (21)
1a04	4	56	45	4.9 (19)	4.7 (31)
1a6s	4	85	46	4.4 (1)
1bw6	4	43	29	4.1 (17)	3.6 (25)	2.7 (93)
1c5a	4	61	46	4.6 (7)	4.4 (23)
1eij	4	59	41	4.8 (5)	4.6 (21)	3.7 (159)
1ffh*	4	83	63	3.7 (11)	3.7 (11)	3.0 (75)
1hdj	4	61	40	5.2 (16)	3.9 (22)
1unkA	4	67	48	4.7 (18)	3.7 (28)	3.2 (146)
2abd	4	79	49	6.9 (16)	4.1 (28)
1aisB*	5	88	67	6.7 (4)
1b0nA*	5	60	42	5.4 (3)
1b0x	5	62	43	4.0 (7)	3.3 (29)
1beg	5	91	55	6.2 (11)	6.2 (11)	5.5 (83)
1bmtA*	5	79	61	6.6 (2)	6.6 (2)	3.7 (65)
1ctj	5	82	46	8.3 (20)	7.4 (35)	5.4 (230)
1f1f	5	85	48	5.9 (8)
1f68	5	100	66	8.8 (13)	8.2 (37)	6.2 (93)
1lpe	5	138	117	3.4 (6)
1nfo	5	136	110	3.0 (9)
1nkl	5	70	54	5.2 (14)	4.0 (25)
1qc7A	5	74	58	8.1 (14)	6.6 (34)	5.5 (145)
2ezyA	5	83	54	6.7 (17)	6.0 (46)	5.4 (129)
1bxm	6	92	50	7.0 (4)	7.0 (4)	6.4 (229)
1fio	6	188	162	10.3 (12)	6.1 (25)
1ngr	6	71	49	7.3 (18)	5.4 (59)
1rzl	6	71	49	7.1 (7)	5.7 (32)	4.8 (123)
1a0b	7	109	87	11.1 (4)	8.4 (24)	8.0 (140)
1dlw	7	112	72	6.1 (1)
1emy	7	145	107	11.4 (9)	8.4 (57)	8.1 (281)
1ezt	8	125	89	12.6 (13)	11.2 (59)	11.0 (175)

Protein name (PDB ID), followed by the number of helices, the total number of residues (excluding the non-helical residues at the N and C termini), and the number of residues only in helices. The last three columns show the best results obtained for the 20 and 60 lowest-energy, and all families, respectively. The rmsd value is measured on C^α atoms of helices from the native, followed by the corresponding family number (in parentheses). The empty fields indicate that the value to the left is not improved by including more families. 

^*The following are fragment proteins: 1lbu: 1lbu_1–83; 1ffh: 1ffh_2–88; 1aisB: 1aisB_1108–1205; 1b0nA: 1b0nA_1–68; 1bmtA: 1bmtA_651–740. 

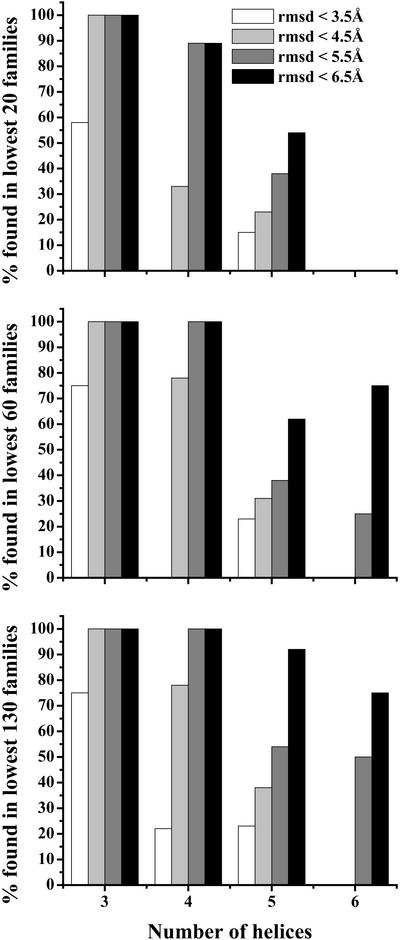
Fig. 1 shows the difficulty of obtaining structures with native-like folds for proteins with increasing numbers of helices. The three graphs are plots for the percentage of all proteins with the corresponding number of helices in the 20, 60, and 130 lowest-energy families, respectively, for which the method retrieves a fold within the rmsd indicated in the key. For example, the structures of all three-helix proteins were within 4.5 Å rmsd from their native, where the computed structures were ranked in the 20 lowest-energy families of the final ensemble. It is important to note that, as the number of helices increases, the percentage of successful computations within the same rmsd decreases.

Figure 1.

Percentage of all proteins with corresponding number of helices for which at least one structure was generated within the rmsd from the native indicated in the key. The graphs correspond to the 20, 60, and 130 lowest-energy families, respectively.

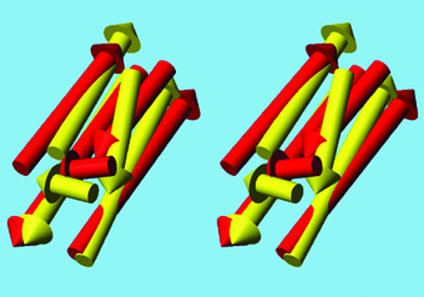
Fig. 2 shows a superposition of a computed structure for 1nfo with its native structure. The superimposed structures agree to within 4.8 Å rmsd and show that the overall orientation of all helices is qualitatively correct. This result is not the best conformation obtained; the rmsd of the best one is 3.0 Å (see Table 1).

Figure 2.

Stereoview of the superposition of a generated structure of the five-helix protein 1nfo (not the best) on the experimental structure. The C^α atoms agree to within an rmsd of 4.8 Å. The native structure is yellow and the generated structure is red. The figure was generated by using MOLMOL (20).

To determine the stability of the procedure with different positions of secondary structure elements in the sequence, several simulations were carried out on 6 of the 42 proteins (Protein Data Bank ID codes 1lre, 2abd, 1a6s, 1g2h, 1hdp, and 1ctj) with different assignments of secondary structure, according to dssp and jnet/jpred, respectively. The results are shown in Table 2 and are quite comparable with the ones from Table 1; thus, it seems that our procedure is stable with respect to secondary structure assignment.

Table 2.

Stability of procedure with respect to different secondary structure assignment

Protein	Hdssp	Hjnet	Q3	rmsdmin, Å (family no.)
				All	Low 10
1lre	3	3	76	3.6 (77)	5.5 (1)
2abd	4	4	86	3.9 (145)	4.9 (3)
1a6s	4	4	68	4.7 (9)	4.7 (9)
1g2h	3	4	53	5.1 (25)	5.2 (7)
1hdp	3	3	82	2.3 (3)	2.3 (3)
1ctj	5	4	83	5.2 (56)	8.3 (4)

Protein name, H_dssp, number of helices according to dssp. H_jnet, number of helices predicted by jnet/jpred. Q3, percentage of correctly predicted secondary structure. rmsd_min, lowest rmsd (corresponding family number in parentheses) from the native structure in the whole ensemble, and in the 10 lowest-energy families, respectively. 

From Fig. 1 it is clear that, as the number of helices grows, the performance of the method decreases. One source of difficulty is the imperfection of the potential function itself. Given all of the simplifications in this approach, it would be unreasonable to expect the global-energy minimum to identify the native structure in all cases. For example, loops can play a role in determining the structure (16), but are neglected here. Also, some of the proteins examined are only parts of larger structures, the effects of which are also neglected. However, native structures, ideally, should always be present among the low-energy conformations, as shown in Fig. 3. This result has been confirmed for 41 of the above proteins (the exception being 1ais) by performing searches restricted to the neighborhood of the native structure. Native-like structures with low energies are generally present, even when searches without such restrictions fail to find them (examples being 1a0b, 1emy, and 1ezt). The reason for this is the complexity of the fold and the large number of local energy minima in the search space. Even with a simplified potential, searches for proteins with six or more helices are not complete in 10,000 steps. In these cases, models within 6.0 Å from the native are found within the final ensemble only if two helices are omitted from the comparison (i.e., five- instead of seven-helix fragments for 1a0b and 1emy, and six- instead of eight-helix fragments for 1ezt). The protein 1ais is the only one for which native-like structures have significantly higher energies than the global minimum. Closer examination reveals that this structure is much more compact than the others, and in fact the results are improved by decreasing the parameter r₀ from 7.5 to 6.0 Å.

Figure 3.

Energy vs. rmsd for 1lpe. Black points are families in the final ensemble and gray points are families encountered during the search of 10,000 iterations.

Discussion

Packing of secondary structure elements is one of the important steps in achieving the ultimate goal of predicting a structure from sequence. We have developed an energy-based method to generate a variety of folds by treating α-helices as rigid bodies, applying a simple potential, and searching the conformational space with a Monte Carlo-type search. Despite the simplicity of our model, we were able to produce native-like folds ranked in low-energy families for many proteins.

Although the method provided good results for proteins with a small number of helices, there is considerable room for improvement in our procedure. It is important to note that it is the number of helices, rather than the size of the protein, that seems to cause difficulties. A more systematic approach to generate diverse topologies would increase the probability of locating native-like folds (17). Further improvements could come from modifications to the contact energies that take into account the environment of a residue (i.e., the kind of secondary structure element to which it belongs; ref. 18), or by carrying out a systematic optimization procedure for the potential parameters (19). Another possibility is the improvement of the functional form of the potential or the protein representation, which could be further simplified to reduce the large number of local minima in our conformational space.

Although generating folds is an important step, the main purpose of this exercise is to continue with the refinement of the generated models by using them as input for an algorithm with a more detailed representation of the polypeptide chain, such as the UNRES model (5). The procedure described here greatly reduces the number of helical conformations that have to be explored with the UNRES model.

Currently, only α-helices are treated by this simple procedure, but inclusion of β-strands and sheets in the model is a natural extension. For this to occur, it will be necessary to address the issue of hydrogen bonds, which is currently not treated.

Finally, the efficiency of the procedure can be improved by parallelizing the code instead of using only one processor.

Abbreviations

rmsd

rms deviation

CMrmsd

center-of-mass rmsd

MaxAngle

maximum angle

UNRES

united residue