Cluster dynamics transcending chemical dynamics toward nuclear fusion

Abstract

Ultrafast cluster dynamics encompasses femtosecond nuclear dynamics, attosecond electron dynamics, and electron-nuclear dynamics in ultraintense laser fields (peak intensities 10¹⁵–10²⁰ W·cm⁻²). Extreme cluster multielectron ionization produces highly charged cluster ions, e.g., (C⁴⁺(D⁺)₄)_n and (D⁺I²²⁺)_n at I_M = 10¹⁸ W·cm⁻², that undergo Coulomb explosion (CE) with the production of high-energy (5 keV to 1 MeV) ions, which can trigger nuclear reactions in an assembly of exploding clusters. The laser intensity and the cluster size dependence of the dynamics and energetics of CE of (D₂)_n, (HT)_n, (CD₄)_n, (DI)_n, (CD₃I)_n, and (CH₃I)_n clusters were explored by electrostatic models and molecular dynamics simulations, quantifying energetic driving effects, and kinematic run-over effects. The optimization of table-top dd nuclear fusion driven by CE of deuterium containing heteroclusters is realized for light-heavy heteroclusters of the largest size, which allows for the prevalence of cluster vertical ionization at the highest intensity of the laser field. We demonstrate a 7-orders-of-magnitude enhancement of the yield of dd nuclear fusion driven by CE of light-heavy heteroclusters as compared with (D₂)_n clusters of the same size. Prospective applications for the attainment of table-top nucleosynthesis reactions, e.g., ¹²C(P,γ)¹³N driven by CE of (CH₃I)_n clusters, were explored.

Eighty years of searching for table-top nuclear fusion driven by bulk or surface chemical reactions, which involved the production of deuterons by catalytic processes (1) or by electrochemical methods (2), reflect on a multitude of experimental and conceptual failures (3). This result is not surprising, because the typical reactivity parameter α = (range of interaction)/(de Broglie wavelength) for dd nuclear fusion, i.e., D⁺ + D⁺ → ³He + n + 3.3 MeV and T⁺ + H⁺ + 4.0 MeV, as estimated from the energy-dependent cross sections (4), falls in the range α = 4 × 10⁻³ to 0.1 for deuteron kinetic energies of 10–100 keV. This value characterizes the lower limit of the D⁺ energy domain for the accomplishment of nuclear fusion, which cannot be attained in ordinary chemical reactions in macroscopic bulk or surface systems.

Coulomb explosion (CE) of multicharged clusters (5–7) produces high-energy (1 keV to 1 MeV) ions (8–15) in the energy domain of nuclear physics. Nuclear fusion can be driven by energetic deuterons produced by CE of multicharged deuterium containing homonuclear (D₂)_n clusters (9, 10, 15) and heteronuclear [e.g., (D₂O)_n, (CD₄)_n, (DI)_n] clusters (11, 15–17). The stripping of all valence electrons, or of all electrons from first-row atoms [e.g., the production of (C^q_C+ (D⁺)_n) (q_C = 4–6) clusters (12, 15)], or of the production of highly charged heavy ions [e.g., (D⁺I^q_I⁺)_n (q_I = 7–35) clusters (17)], results in the formation of multicharged ions by extreme multielectron ionization of elemental and molecular clusters in ultraintense laser fields (peak intensities 10¹⁵ to 10²⁰ W·cm⁻²). Cluster multielectron ionization (12, 13) is induced by three sequential-parallel mechanisms: (i) inner ionization (because of the barrier suppression ionization of each constituent induced by the laser field and by the internal field, together with impact ionization), (ii) nanoplasma formation within the cluster, and (iii) outer ionization (because of barrier suppression of the entire cluster and quasiresonance effects). The concurrent-sequential process of CE in an assembly of deuterium-containing homonuclear or heteronuclear clusters (14, 15) produces a plasma filament within the laser focal region, where deuterons undergo nuclear fusion (9, 10). Compelling experimental (9, 10) and theoretical (15, 18) evidence was advanced for nuclear fusion driven by CE (NFDCE) in an assembly of (D₂)_n clusters. We proposed and demonstrated (15, 16, 19) a marked enhancement of yields for NFDCE of deuterium-containing heteroclusters because of energetic driving and kinematic effects, as experimentally confirmed by Grillon et al. (11) and Ditmire and coworkers (20).

Although the quest for table-top nuclear fusion was realized for cluster CE (9–11, 14–16, 18–20) as well as for neutron production driven by a piezoelectric crystal in a deuterium gas (21), these constitute low-yield processes. The neutron yield, Y, experimentally observed by Ditmire et al. (9) for NFDCE of (D₂)_n clusters (n = 10³ to 2 × 10⁴), is Y ≃ 10³ to 10⁴ per laser pulse (at I_M = 10¹⁷ W·cm⁻²). We demonstrate a 7-orders-of-magnitude enhancement of Y in the NFDCE of light-heavy heteroclusters (17), e.g., (DI)_n and (CD₃I)_n as compared with Y from (D₂)_n clusters of the same size. Prospective applications of nuclear reactions driven by CE of heteroclusters for exploring astrophysical nucleosynthesis also will be addressed.

Results

Nonuniform CE.

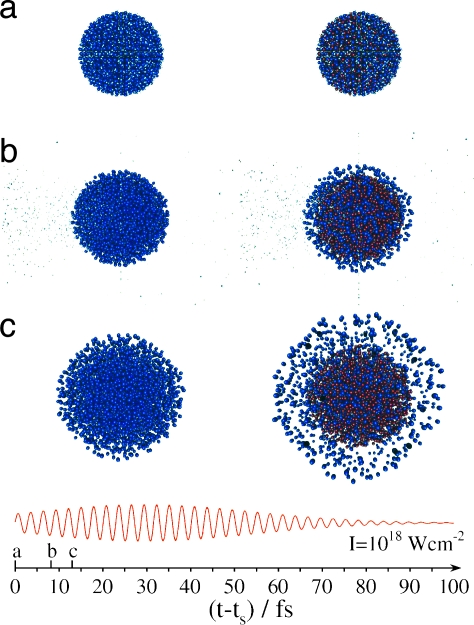
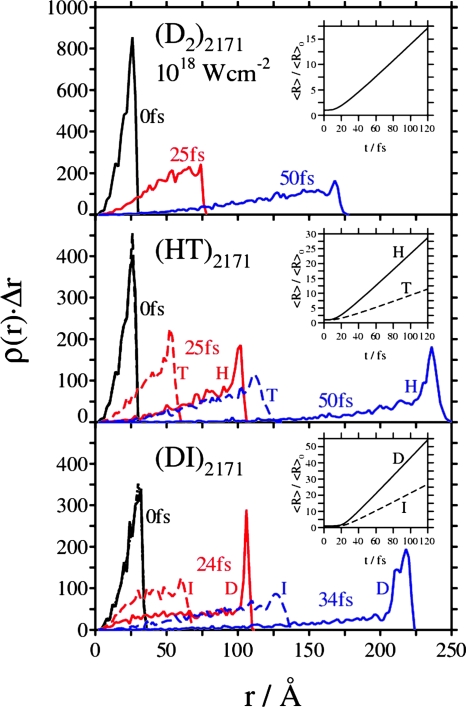
In the intensity domain I_M ≳ 10¹⁷ W·cm⁻² and for the cluster size domain (n = 55–4,213) used herein, the dynamics and energetics of CE were described by electrostatic models (EMLs) in the cluster vertical ionization (CVI) limit (14, 15, 17), which is applicable when inner and outer ionization are fast on the time scale of ion expansion, whereupon outer ionization is complete. The traditional view of CE under CVI conditions involves uniform ion expansion. This view prevails for homonuclear clusters with an initially uniform, constant charge and spherically symmetric ion distributions, which retain the succession of the ion distances from the cluster center throughout the expansion (14, 15). Time-dependent structures of the (D₂)₂₁₇₁ cluster at I_M = 10¹⁸ W·cm⁻² (Fig. 1) manifest uniform CE, which corresponds to complete stripping of all of the electrons from (D₂)₂₁₇₁. The CE exhibits a uninodal spatial expansion of the D⁺ ions, as evident from the time-resolved structures (Fig. 1) and from the single, broad time-dependent spatial distributions P(r) at each t (Fig. 2). For CE under CVI conditions of A_k^q_A⁺B_ℓ^q_B⁺ light-heavy heteroclusters, which consist of k light A^q_A⁺ ions of mass m_A and charge q_A, and ℓ heavy B^q_B⁺ ions of mass m_B and charge q_B (with m_A < m_B), the dynamics is governed by the kinematic parameter (15–17, 19) η_AB = q_Am_B/q_Bm_A. The nonuniform CE of (H⁺T⁺)₂₁₇₁ heteroclusters (Fig. 1), for which η_HT = 3, manifests kinematic run-over effects of the H⁺ ions relative to the T⁺ ions. These kinematic effects are characterized by a spatial segregation of the exterior distribution of H⁺ ions relative to an interior distribution of the T⁺ ions (Fig. 1). The distinct spatial distributions of the H⁺ and T⁺ ions (Fig. 2) overlap at short times and separate at longer times (Fig. 2). The case of CE of extremely charged light-heavy (A_k^q_A⁺B_k^q_B⁺)_n heteroclusters (ECLHH) (corresponding to m_A ≪ m_B and kq_A ≪ ℓq_B) exhibits the formation of exterior spherical nanoshells of the light ions, which manifest the attainment of transient self-organization driven by repulsive Coulomb interactions (17). The time-dependent structures (see Fig. 7, which is published as supporting information on the PNAS web site) of CE of (DI)₂₁₇₁ clusters at I_M = 10¹⁸ W·cm⁻² correspond to η_DI = 2.5 and q_I = 21–23, with q_D = 1 ≪ q_I (17), where q_I increases with increasing n because of ignition effects induced by the inner field (12). The femtosecond CE dynamics reveals an extreme case of spatial segregation between the light D⁺ ions and the heavy I^q_I+ ions, with the formation of a transient halo of the expanding light D⁺ ions, which surrounds the inner subcluster of the I^q_I+ions (Fig. 2).

Fig. 1.

Snapshots of the time-resolved structures of (D₂)₂₁₇₁ (Left) and (HT)₂₁₇₁ (Right) clusters in a Gaussian laser field (I_M = 10¹⁸ W·cm⁻² at τ = 25 fs marked on the images), at three different times t − t_s. The lowest part of the image portrays the time axis and the electric field of the laser. The instants of the snapshots are marked on the time axis by a, b, and c. H atoms are represented in blue, T atoms in red, and electrons in light gray. (a) The initial nanoplasma at t − t_s = 0. (b) At t − t_s = 8.2 fs, the beginning of spatial expansion of the clusters is manifested. In case of the (HT)_n cluster, a shell of H⁺ ions is displayed. At this time, a large number of electrons are stripped by outer ionization, which occurs repeatedly when the electric field of the laser is close to a maximum. (c) At (t − t_s) = 13.0 fs, the spatial expansion and shell formation of the HT cluster is pronounced. Also, all nanoplasma electrons have been removed at this time.

Fig. 2.

The radial distribution functions P(r) for the (D₂)₂₁₇₁, (HT)₂₁₇₁, and (DI)₂₁₇₁ clusters in a Gaussian laser field (I_M = 10¹⁸ W·cm⁻² and τ = 25 fs) at various times t − t_s. t_s is the starting time of the simulation with respect to the maximum of the Gaussian laser field envelope located at t = 0 (see Supporting Text). For the heteronuclear (HT)₂₁₇₁ and (DI)₂₁₇₁ clusters, P(r) = P(r)Δr is drawn separately for each ion (as marked on the images), exhibiting shell formations of the nonoverlapping distributions of different isotope/element ions at times t − t_s > 0. These shells expand with different velocities. (Insets) The time-dependent increase of the first moments 〈R〉 of P(r) relative to the first moment 〈R〉₀ at t − t_s = 0. Data are presented for different ions, as marked on Insets.

The dynamics of nonuniform CE (Fig. 2 Insets) will be characterized by the time dependence of 〈R〉/〈R〉₀, where 〈R〉 is the first moment of the spatial distribution of the I^q_A+light ions at time t, whereas 〈R〉₀ is the initial value of 〈R〉 (at t = t_s). The CE dynamics of the light ions is described by the near-linear time dependence 〈R〉/〈R〉₀ = a(t − t_onset) at t > t_onset (Fig. 2 Insets). The onset time t_onset in the linear dependence of 〈R〉 vs. t [e.g., t_onset = 22 fs for (DI)₂₁₇₁ at I_M = 10¹⁸ W·cm⁻²] is due to the completion of the outer ionization and the switching-off of acceleration effects. From the EML of CE under CVI conditions (a/fs⁻¹)1.074(ρ_molq_Aq_mol/m_A)^1/2 (14, 15), where ρ_mol(ρ_mol/Å⁻³) is the initial molecular ion density and m_A/atomic mass unit (amu). For uniform and nonuniform CE, q_mol = kq_A + ℓq_B, whereas for ECLHH q_mol = ℓq_B (with q/e). Note that a is independent of the cluster size at fixed I_M. The results of the EML (in parentheses) account well for the simulation data (Fig. 2 Insets), i.e., a = 0.16 fs⁻¹ (0.17 fs⁻¹) for H⁺ ions from (HT)₂₁₇₁, and a = 0.50 fs⁻¹ (0.45 fs⁻¹) for D⁺ ions from (DI)₂₁₇₁ at I_M = 10¹⁸ W·cm⁻². The agreement between theory and simulation provides benchmark reference data for CE in the CVI domain. The maximization of the energies of the light ions in the CE of ECLHHs requires the applicability of the CVI [I_M ≳ 10¹⁷ to 10¹⁸ W·cm⁻² (14, 15)] and use of the highest attainable laser intensities for the maximization of the heavy atom charge q_B for effective energetic driving.

Energetics of CE.

The maximum energy E_M and the average energy E_av of the light ions in the uniform CE of homonuclear clusters and in the nonuniform CE of heteronuclear clusters can be obtained from EMLs (14–18), which in the CVI limit result in the general expressions for the cluster size dependence E_M(n) = XR₀², where R₀ = (3n/4πρ_mol)^1/3 is the initial cluster radius, whereupon E_M(n) = Zn^2/3. The ratio between E_M and E_av is E_av(n) = κE_M(n) The parameters X, Z, and κ assume the following forms:

1. For homonuclear (A₂)_n clusters, X = (4π/3)B̄ρ_mol q_Aq_A2, with B̄ = 14.39 eV·Å, whereas Z = (4π/3)^1/3B̄_qA2ρ_mol^1/3 and κ = 3/5.

2. For (A_k^q_A⁺B_ℓ^q_B⁺)_n heteronuclear clusters with m_A < m_B and η_AB = 1, X(4π/3)B̄ρ_molq_Aq_mol, where q_mol = kq_A + ℓq_B, Z = (4π/3)^1/3B̄q_Aq_molρ_mol^1/3, and κ = 3/5.

3. For nonuniform CE of an ECLHH (A_k^q_A⁺B_ℓ^q_B⁺C_p^q_C⁺)_n with m_A < m_C ≪ m_B, kq_A ≪ ℓq_B and q_mol ≃ ℓq_B + pq_C (17), Z = 2πB̄ρ_molq_molq_A, X = (9π/2)^1/3B̄q_Aq_molρ_mol^1/3, and κ = 4/5.

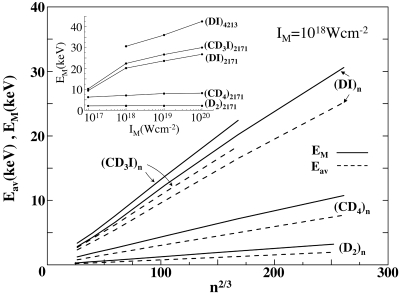
The simulation results for cluster CE at I_M = 10¹⁸ W·cm⁻² for (D₂)_n (case A), for (CD₄)_n (case B with q_C = 4) and for (DI)_n and (CD₃I)_n (case C with q_I = 21–23), obey the size dependence E_M,E_av ∝ n^2/3 (Fig. 3). The agreement between the Z parameters obtained from the simulations and the predictions of the EML (see Table 1, which is published as supporting information on the PNAS web site) is 10% for (D₂)_n and (CD₄)_n and 30% for the ECLHHs, whereas the κ parameters are accounted for within 10% by the EML. The laser intensity dependence of E_M at a fixed n (Fig. 3 Inset) is flat for (D₂)₂₁₇₁, reflecting a complete inner/outer ionization. It shows an increase for (CD₄)₂₁₇₁, which is due to the increase of q_C = 4 at I_M = 10¹⁷ to 10¹⁹ W·cm⁻² to q_C = 6 at I_M ≥ 10¹⁹ W·cm⁻², and exhibits a large increase of E_M with increasing I_M for (DI)_n (n = 2,171 and 4,213) and for (CD₃I)₂₁₇₁, manifesting the marked enhancement of the extreme ionization level of the I atom from q_I = 13–14 at I_M = 10¹⁷ W·cm⁻² to q = 21–23 at I_M = 10¹⁸ W·cm⁻² and to q_I = 35 at I_M = 10²⁰ W·cm⁻². The (DI)_n data (Fig. 3 Inset), which also demonstrate the cluster size dependence of E_M, reach the high value of E_M = 45 keV for n = 4,213 at I_M = 10²⁰ W·cm⁻². A dramatic energy enhancement of the D⁺ energy from CE of light-heavy heteroclusters and of the ECLHH, as compared with (D₂)_n clusters of the same size (Fig. 3), is exhibited. This marked increase of E_M and E_av of D⁺ in the series (D₂)_n ≪ (CD₄)_n ≪ (DI)_n < (CD₃I)_n (at fixed n) manifests energy driving by the multicharged heavy ions, which is determined by the ionic charge q_mol [e.g., at I = 10¹⁸ W·cm⁻², q_mol = 8 for (CD₄)₂₁₇₁, whereas q_mol = 22 for (DI)₂₁₇₁ and q_mol = 26 for (CD₃I)₂₁₇₁].

Fig. 3.

The cluster size dependence of the maximal energies E_M (solid lines) and average energies E_av (dashed lines) of D⁺ ions in the uniform CE of (D₂)_n clusters and in the nonuniform CE of (CD₄)_n, (DI)_n, and (CD₃I)_n clusters at I = 10¹⁸ W·cm⁻² and τ = 25 fs. The simulation data manifest the (divergent) power law E_M, E_av ∝ n^2/3. Slight deviations from this scaling dependence for small (DI)_n and (CD₃I)_n ECLHHs originate from ignition and screening effects for inner ionization (12). (Inset) The dependence of E_M and I_M for clusters marked on the curves.

Kinematic Effects and Energy Distribution.

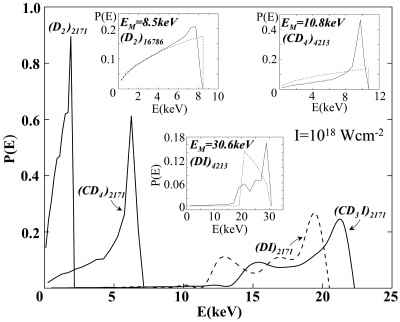
All of the kinetic energy distributions P(E) of the product D⁺ ions (Fig. 4) from CE of (D₂)_n and from several heteroclusters, exhibit a maximal cut-off energy E_M analyzed below. For (D₂)_n and (CD₄)_n clusters the onset of P(E) occurs at E = 0, whereas for the (DI)_n and (CD₃I)_n ECLHHs a narrow distribution of P(E) is exhibited with a relative energy spread ΔE/E_av ≃ 0.2. The EML for uniform CE results in (14, 15, 18) P(E) = (3/2E_M)(E/E_M)^1/2 (E ≤ E_M), in agreement with the simulated energy distribution for CE of (D₂)_n [Fig. 4 Inset for (D₂)₁₆₇₈₆]. For (CD₄)_n clusters, a marked deviation of P(E) from the E^1/2 relation is exhibited with ≈75% of the D⁺ ions lying in a narrow energy interval ΔE/E_av ≃ 0.4, below E_M, manifesting kinematic run-over effects [Fig. 4 Inset for (CD₄)₄₂₁₃]. The EML for CE of the ECLHHs for a frozen subcluster of the I^q_I⁺ ions predicts a low-energy onset of the energy distribution (17) at E_min = (4π/3)^1/3B̄q_Aq_Bρ_mol^1/2n^2/3 with P(E) = (3/E_min)[3 − (2E/E_min)]^1/2 for E_min ≤ E ≤ 3E_min/2, where E_M = 3E_min/2 and E_av = 6E_min/5. The narrow distribution of P(E) for CE of (DI)₂₁₇₁ and of (CD₃I)₂₁₇₁ (Fig. 4) is in accord with these predictions, while the narrow energy distribution is semiquantitatively accounted for by the EML [Fig. 4 Inset for (DI)₄₂₁₃]. This CE of ECLHHs constitutes an extreme manifestation of kinematic run-over effects, resulting in a narrow, high-energy distribution of the light ions.

Fig. 4.

The kinetic energy distributions of D⁺ ions from several clusters (marked on the curves) at I_M = 10¹⁸ W·cm⁻² and τ = 25 fs. Three Insets show the simulated data (solid curves) and the results of the ELM (dashed curves) for CE of (D₂)₁₆₇₈₆, (CD₄)₄₂₁₃, and (DI)₄₂₁₃ clusters.

Yields for NFDCE.

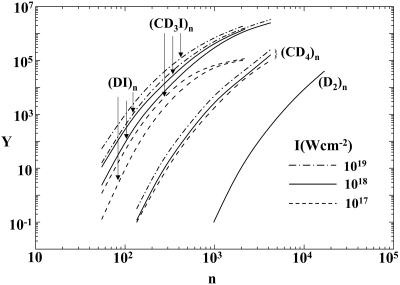
CE of multicharged deuterium-containing heteroclusters and, in particular, of ECLHHs manifests a marked increase of the average and maximal energies of the D⁺ ions. This increase is due to energetic driving effects by multicharged heavy ions and to the narrowing of the energy redistribution at high energies (just below E_M) due to kinematic run-over effects. These energetic and kinematic driving effects will result in a marked enhancement of the neutron yields Y from NFDCE of these heteroclusters, in comparison with NFDCE of (D₂)_n clusters of the same size. The fusion yield per laser pulse in a plasma filament is given by (15, 19) Y = 1/2)ρ_d²V_f(ℓ̄/v̄)〈σv〉, where ρ_d is the deuteron density within the (cylindrical) reaction volume V_f, v is the relative velocity of the colliding nuclei, v̄ is their average velocity, σ is the fusion cross section (4), ℓ̄ is the deuterons’ mean free path, and 〈〉 denotes an average over the energy distribution. By using the conditions of the Lawrence–Livermore experiment, ρ_d = 2 × 10¹⁹ cm⁻³ and V_f = 6 × 10⁻⁵ cm³, while ℓ̄ = 0.016 cm (9, 10). The size dependence of the calculated Y data for NFDCE of (D₂)_n (n = 55 to 2 × 10⁴), and for (CD₄)_n, (DI)_n, and (CD₃I)_n (n = 55–4,213) for I_M = 10¹⁷ to 10¹⁹ W·cm⁻² (Fig. 5), steeply increases for a fixed n value from (D₂)_n to (CD₄)_n, and to the (DI)_n and (CD₃I)_n ECLHHs. In the size domain n = 1,000–2,000 at I_M = 10¹⁸ to 10¹⁹ W·cm⁻², the very large ratios Y[(CD₃I)_n]/Y[(D₂)] ≃ 2 × 10⁵ to 7 × 10⁶ (Fig. 5) exhibit a dramatic increase of the neutron yields in the NFDCE of ECLHHs, manifestating energetic driving and kinematic effects.

Fig. 5.

Neutron yields per laser pulse (see text) for NFDCE of (D₂)_n, (CD₄)_n, (DI)_n, and (CD₃I)_n clusters in the intensity range 10¹⁷ to 10¹⁹ W·cm⁻².

Astrophysical Applications.

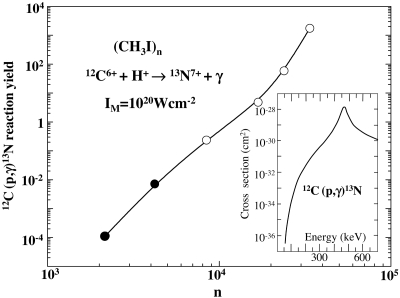
Some nuclear reactions involving protons and heavier nuclei, e.g., the ¹²C(p,γ)¹³N reaction ¹²C⁶⁺ + H⁺ → ¹³N⁷⁺ + γ, are of interest in the carbon–nitrogen–oxygen (CNO) cycle, which constitutes the energy supply in hot stars (22, 23). The cycle results in the fusion of four protons into ⁴He²⁺, with ¹²C⁶⁺ serving as a catalyst in this set of reactions, which is regenerated (22, 23). For the realization of an effective ¹²C(p,γ)¹³N table-top nucleosynthesis reaction, we propose to use CE of an assembly of (CH₃I)_n ECLHHs, with the I^q+ ion serving as an energetic driver for both H⁺ and ¹²C⁶⁺ nuclei. The production of ¹²C nuclei by CE of (CH₃I)_n is accomplished at I_M ≥ 10¹⁹ W·cm⁻². Molecular dynamics simulations performed for (CH₃I)_n (n = 2,171 and 4,213) clusters at I_M = 10²⁰ W·cm⁻² [taking relativistic and magnetic field effects into account (12)] revealed a narrow energy distribution for both the H⁺(p) and the ¹²C⁶⁺(C) nuclei, in the energy interval 0.8E_M^(J) ≤ E^(J) ≤ E_M^(J), where J = p,C. For (CH₃I)_n, E_av^(p) = 29.5 keV and E_av^(C) = 161 keV for n = 2,171, whereas E_av^(p) = 45.0 keV and E_av^(C) = 250 keV for n = 4,273. The CVI scaling laws for the energetics, E_av^(p) = Z_pn^2/3 (Z_p = 170 keV) and E_av^(C) = Z_Cn^2/3 (Z_C = 950 eV), allowed for the extrapolation to a larger cluster size, e.g., for n = 33,700 (R₀ = 94.1 Å) E_av^(p) = 181 keV and E_av^(C) = 1,000 keV. The yields Y (per laser pulse) for the ¹²C(p,γ)¹³N reaction were calculated by using the cross sections [Fig. 6Inset (23)] in an analogous way as for the dd nuclear fusion. The size dependence of Y(n) (Fig. 6) exhibits a sharp rise at n ≥ 2 × 10⁴, which corresponds to E_av^(p) ≥ 120 keV and E_av^(C) ≥ 700 keV with the collision energy (of the proton in the ¹²C nucleus frame) being E ≥ 350 keV, with E approaching the reaction resonance at 460 eV (Fig. 6 Inset). The Y data increase by 2 orders of magnitude from Y = 20 at n = 2 × 10⁴ (R₀ = 78 Å) to Y = 1,750 at n = 3.4 × 10⁴ (R₀ = 94 Å). This nucleosynthesis reaction is amenable to experimental interrogation.

Fig. 6.

Yields of the ¹²C(p,γ)¹³N nucleosynthesis reaction, with the energetic ¹²C and H⁺ nuclei being produced by CE of (CH₃I)_n clusters at I = 10²⁰ W·cm⁻². The yields were calculated from the E_av^(p) and E_av^(C) energetic data together with the reaction cross sections (Inset adapted from ref. 23). The energetic data for n = 2,171 (R₀ = 38 Å) and for n = 4,230 (R₀ = 47.1 Å) were obtained from simulations (filled circles), whereas for the size domain n = 8,426 (R₀ = 51.3 Å) to n = 33,700 (R₀ = 94.1 Å) the energetic data were evaluated from the n^2/3 scaling law.

Discussion

Nuclear reactions driven by CE of molecular clusters induced by extreme multielectron ionization involve “cold-hot” fusion, where the cluster beam constitutes a cold (or even ultracold) target, whereas the CE of an assembly of clusters provides the high-energy “hot” nuclei (with relative energy 10 keV to 1 MeV) required to induce nuclear reactions. The attainment of these table-top nuclear reactions is realized when (i) nuclei are formed by extreme ionization, which is accomplished at I ≳ 10¹⁵ W·cm⁻² for D⁺ and at I ≥10¹⁹ W·cm⁻² for C⁶⁺, and (ii) sufficiently high collision energies, E, for which σ ≳ 10⁻³⁴ cm², are realized, e.g., E ≥ 3 keV for dd fusion and E ≥ 100 keV for ¹²C(p,γ)¹³N. The maximization of the yields for nuclear reactions will be accomplished for (iii) the attainment of the largest cluster size for which the CVI energy scaling holds, (iv) the use of the highest practical I_M values for the formation of the highest charge of the heavy ion in a ECLHH, to enhance energetic driving of the light ions, and (v) the optimization of P(E) to assume a narrow distribution below E_M to facilitate kinematic run-over effects, as is the case for ECLHHs.

The size domain for CVI, where the CE energy can be optimized (according to the n^2/3 scaling law) by increasing the cluster size, is limited by the border radius R₀^(I) ∝ I_M^1/2/ρ_molq_mol (15). R₀^(I) constitutes the maximal R₀ for completion of cluster outer ionization (14, 15). The cluster size domain and the laser intensity range for the prevalence of the CVI are R₀ < R₀^(I), whereas in the non-CVI domain, when R₀ > R₀^(I), a saturation of E_av vs. n is exhibited, and the ion energies cannot be markedly enhanced by increasing R₀ beyond R₀^(I). At a fixed intensity (e.g., I_M = 10¹⁸ W·cm⁻²), R₀^(I) is maximal for (D₂)_n, (R₀^(I) = 200 Å, n = 8.4 × 10⁵), decreases for (CD₄)_n (R₀^(I) = 100 Å, n = 6.7 × 10⁴) (15), and is even smaller for (CD₃I)_n (R₀^(I) = 41 Å, n = 2,900), but all are larger than the n values used in the present simulations. For I_M = 10²⁰ W·cm⁻², R₀^(I) = 410 Å and n = 2.2 × 10⁶ for CE of (CH₃I)_n, establishing the upper cluster size limit for the exploration of the ¹²C(p,γ)¹³N astrophysical nucleosynthesis reaction. The limitations imposed by the size constraint R₀ ≲ R₀^(I) allow for the realization of dd NFDCE from ECLHHs. For (CD₃I)_n clusters at I_M = 10¹⁸ W·cm⁻², R₀ = R₀^(I) = 41 Å, with the highest attainable maximal energy of E_M = 22 keV (Fig. 3) resulting in Y ≃ 10⁷ (Fig. 5). At I_M = 10¹⁹ W·cm⁻², R₀ = R₀^(I) = −120 Å, with E_M = 220 keV, as extrapolated from the n^2/3 scaling law, and Y ≃ 10¹⁰. Concurrently, for large clusters, the effects of laser light absorption by the cluster assembly will limit the yields (9). Accordingly, the values of Y ≃ 10⁷ at I_M = 10¹⁸ W·cm⁻² and Y ≃ 10¹⁰ at I_M = 10¹⁹ W·cm⁻² characterize the range of upper limits for the yields (per laser pulse) for dd NFDCE of ECLHHs, such as iodine containing (DI)_n and (CD₃I)_n molecular clusters, and mixed deuterium-heavy atom Xe_n(D₂)_m or Pd_n(D₂)_m heteroclusters. The Pd_n(D₂)_m or Pt_n1Pd_n2(D₂)_m clusters can be deposited on surfaces (24) providing previously undescribed two-dimensional targets for NFDCE.

Methods

Molecular dynamics simulations of high-energy (0.5–2.0 keV) nanoplasma electrons and of ions (12, 13, 16, 17) were conducted to describe multielectron ionization, nanoplasma response, and CE in clusters subjected to Gaussian laser fields with peak intensities I_M = 10¹⁷ to 10²⁰ W·cm⁻², a pulse temporal width of 25 fs, and a frequency ν = 0.35 fs⁻¹ (see Supporting Text, which is published as supporting information on the PNAS web site). An initially truncated laser pulse, being switched on at t = t_s (12, 13) (see Supporting Text), was used. The simulation results and the theoretical energetic data were used for estimates of yields for NFDCE (18, 19).

Abbreviations

CE

Coulomb explosion

CVI

cluster vertical ionization

ECLHH

extremely charged light-heavy heteroclusters

EML

electrostatic model

NFDCE

nuclear fusion driven by CE.