DNA molecule provides a computing machine with both data and fuel

Abstract

The unique properties of DNA make it a fundamental building block in the fields of supramolecular chemistry, nanotechnology, nano-circuits, molecular switches, molecular devices, and molecular computing. In our recently introduced autonomous molecular automaton, DNA molecules serve as input, output, and software, and the hardware consists of DNA restriction and ligation enzymes using ATP as fuel. In addition to information, DNA stores energy, available on hybridization of complementary strands or hydrolysis of its phosphodiester backbone. Here we show that a single DNA molecule can provide both the input data and all of the necessary fuel for a molecular automaton. Each computational step of the automaton consists of a reversible software molecule/input molecule hybridization followed by an irreversible software-directed cleavage of the input molecule, which drives the computation forward by increasing entropy and releasing heat. The cleavage uses a hitherto unknown capability of the restriction enzyme FokI, which serves as the hardware, to operate on a noncovalent software/input hybrid. In the previous automaton, software/input ligation consumed one software molecule and two ATP molecules per step. As ligation is not performed in this automaton, a fixed amount of software and hardware molecules can, in principle, process any input molecule of any length without external energy supply. Our experiments demonstrate 3 × 10¹² automata per μl performing 6.6 × 10¹⁰ transitions per second per μl with transition fidelity of 99.9%, dissipating about 5 × 10⁻⁹ W/μl as heat at ambient temperature.

The function of DNA is to store hereditary information and regulate the expression of this information (1). The unique chemical properties of DNA encouraged its utilization in novel contexts. The highly selective base pairing renders DNA an excellent building block for supramolecular ensembles, one of the few that can assemble in an aqueous environment. DNA may serve either as a principal structural component or as a mediator that arranges tethered ligands or particles (2, 3). The former approach encompasses nanoscale DNA constructs (4) and extended spatial structures (5). The latter includes DNA-directed assembly of proteins (6), fullerenes (7), and golden particles (8) and DNA-templated nanowire formation (9). DNA also forms dynamic constructs, such as a molecular switch (10) and oscillating molecular machines (11, 12). DNA recognition properties are also exploited in antisense regulation of gene expression (13).

The combination of information-encoding and recognition capabilities of DNA, and the enzymatic machinery available for DNA manipulation, facilitated the emergence of the field of biomolecular computing. Experimental DNA computers (14–23) use single-stranded or double-stranded DNA to encode their data and possibly the software. These molecules interact in a programmed fashion, accompanied by enzymatic or manual manipulations, providing a DNA molecule encoding an output.

So far, little attention has been given to the energetic aspects of DNA computers. In practice, all of the protocols use ATP to allow ligation and/or heating to allow strand dissociation. However, the reverse operations, i.e., the hydrolysis of the DNA backbone and strand hybridization, are spontaneous because they are driven by the potential free energy stored in DNA itself. A molecular computer using these operations may, in principle, be fueled by its DNA input. In fact, the potential free energy of single-stranded DNA was used in noncomputational context to fuel oscillating devices (11, 12). Here we describe a DNA-based finite automaton that computes via repeated cycles of self-assembly and processing. The reversible self-assembly is driven by hybridization energy between input/software complementary sticky ends, whereas the irreversible processing step is driven exclusively by the energy released upon hydrolysis of the input DNA backbone and does not require ATP or heating. Our automaton can, in principle, use a fixed amount of software and hardware molecules to process any input molecule of any length without external energy supply, and as such provides experimental realization of the theoretical possibility to use the potential energy of a DNA input molecule to drive a molecular computation.

Materials and Methods

Materials.

FokI stock (54 μM, 60 units/μl), T4 DNA ligase (400 units/μl), and T4 polynucleotide kinase (PNK) (10 units/μl) were from New England Biolabs. Redivue [γ-³²P]ATP (≈3,000 mCi/mmol, 3.33 pmol/μl) and ATP (100 mM) were obtained from Amersham Pharmacia. Synthetic oligonucleotides (desalted and lyophilized, 1-μmol scale) were from Sigma-Genosys.

Assembly of the Machine Components.

Single-stranded components of the software and inputs were purified to homogeneity by using a 15% denaturing acrylamide gel (40 cm × 1.5 mm) containing 8 M urea (24). The oligonucleotides for the construction of the software were TN1368 (5′-AAGAGCTAGAGTCGGATGC), TN24 (5′-AAGAGCTAGAGTCGGATGCC), TN57 (5′-AAGAGCTAGAGTCGGATG), TN1-as (5′-AGCCGCATCCGACTCTAGCTCT), TN2-as (5′-AGCCGGCATCCGACTCTAGCTCT), TN3-as (5′-CCTGGCATCCGACTCTAGCTCT), TN4-as (5′-CCTGGGCATCCGACTCTAGCTCT), TN5-as (5′-GCCACATCCGACTCTAGCTCT), TN6-as (5′-GCCAGCATCCGACTCTAGCTCT), TN7-as (5′-CTGCCATCCGACTCTAGCTCT), and TN8-as (5′-CTGCGCATCCGACTCTAGCTCT).

The software molecules were prepared by annealing the following pairs of oligonucleotides: T1, TN1368 and TN1-as; T2, TN24 and TN2-as; T3, T1368 and TN3-as; T4, TN24 and TN4-as; T5, TN57 and TN5-as; T6, TN1368 and TN6-as; T7, TN57 and TN7-as; and T8, TN1368 and TN8-as.

The oligonucleotides for the construction of the inputs were: abb-s (5′-GGCTGCCGCAGGGCCGCAGGGCCGTCGGTACCGATTAAGTTGGA), abb-as (5′-CCAACTTAATCGGTACCGACGGCCCTGCGGCCCTGCGGC), abba-s (5′-GGCTGCCGCAGGGCCGCAGGGCCTGGCTGCCGTCGGTACCGATTAAGTTGGA), abba-as (5′-CCAACTTAATCGGTACCGACGGCAGCCAGGCCCTGCGGCCCTGCGGC), babb2-s (5′-CAGGGCCTGGCTGCCGCAGGGCCGCAGGGCCT), babb2-as (5′-AGCCAGGCCCTGCGGCCCTGCGGCAGCCAGGC), baaa2-s (5′-CAGGGCCTGGCTGCCTGGCTGCCTGGCTGCCT), baaa2-as (5′-AGCCAGGCAGCCAGGCAGCCAGGCAGCCAGGC), abbb3-s (5′-GGCTGCCGCAGGGCCGCAGGGCCGCAGGGCCG), and abbb3-as (5′-CCTGCGGCCCTGCGGCCCTGCGGCCCTGCGGC).

The input building blocks were prepared by annealing of the sense and antisense strands of each block, i.e., abb (abb-s and abb-as), etc. The inputs I3-I8 were prepared by stepwise ligation of the building blocks: I3 (babbabb), ligation of abb and babb2; I4 (babbabba), babb2 and abba; I5 (baaaabb), baaa2 and abb; I6 (baaaabba), baaa2 and abba; I7 (abbbbabbabb), abbb3, babb2, and abb; and I8 (abbbbaaaabba), abbb3, baaa2, and abba.

When radioactive inputs were required, 20 pmol of the abb-as and abba-as oligonucleotides were ³²P-labeled and added to a varying amount of unlabeled oligonucleotides (2,000–6,000 pmol each) before annealing. For radioactive labeling, 20 pmol of the substrate were mixed with 5 μl of [γ-³²P]ATP and 10 units of T4 PNK in 10 μl of T4 PNK reaction buffer and incubated at 37°C for 60 min. Labeled oligonucleotides were purified with a nucleotide removal kit (Qiagen, Valencia, CA), eluted into 50–100 μl of EB buffer (10 mM Tris⋅HCl, pH 8.5) (Qiagen), and dried in a SpeedVac. Termini bound to ligate were phosphorylated before annealing. Typically, 6,000 pmol of a substrate oligonucleotide was phosphorylated by 160 units of T4 PNK in 240 μl of PNK buffer supplied with 1 mM ATP, for 60 min at 37°C, ethanol-precipitated, and resuspended in TE buffer (10 mM Tris⋅HCl, 1 mM EDTA, pH 8.0). The annealing was performed by mixing equimolar (100–200 μM) amounts of the sense and antisense oligonucleotides in 50 mM NaCl, heating to 94°C, and slow-cooling to room temperature. Double-stranded blocks (1,500 pmol of each) were ligated by T4 DNA ligase (≈1,700 units) in 400 μl of T4 DNA ligase buffer at 16°C for 1 h. The ligation products were ethanol-precipitated, resuspended in TE buffer (pH 8.0), and purified from native PAGE (12%, 16 cm × 1.5 mm) (25). Purified duplexes were quantified by GeneQuant apparatus (Amersham Pharmacia). Single-nucleotide extrusions were introduced into all substrates to avoid blunt-end ligations in control experiments in the presence of ligase.

Computation Reaction.

In a typical reaction the FokI enzyme was added in a 1:1 ratio to the desired set of transition molecules, while each software molecule was maintained at least at 1 μM concentration and at the same time in excess of or equal to the input. The reactions were performed in 10 μl of NEB4 buffer at 8°C and assayed by 20% denaturing PAGE with input molecules labeled in the 5′ terminus of the antisense strands. In this assay, S0 and S1 outputs were represented by 15-nt and 16-nt bands, respectively.

Performance Optimization.

Performance was optimized with software A2 and input I3. To calculate the total number of operations, gel images were analyzed by using IMAGE GAUGE 3.41 software (Fuji). The relative amounts of unreacted input, intermediates, and output were measured by assuming linear dependence between signal intensity and the amount of radioactive label. The total number of steps S was calculated according to the formula S = N(χ₁ + 2 χ₂ + … L χ_L), where N is a total number of molecules, L is a number of symbols in an input molecule, and χ_i is a relative abundance of an ith intermediate.

Energy Dissipation Calculation.

A computation is a series of single-symbol cleavages, which occur sequentially for each input molecule but concurrently for the entire set of input molecules:

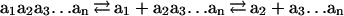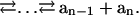Each elementary reaction is a hydrolysis of two phosphodiester bonds with ΔG^o = −44.31 kJ/mol at 25°C (26). A corrected value for 8°C assuming the same equilibrium constant is ΔG^o (281 K) = −41.78 kJ/mol. Actual ΔG values depend on the concentrations of the different species, thus energy dissipation rate depends on the reaction coordinate. For a particular reaction, we directly measure the number of moles of each intermediate a_i… a_n at a time t and denote it as α_i(t). We denote the number of moles of each cleaved symbol a_i as β_i(t),

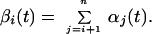To calculate average energy dissipation between time points t₁ and t₂, we measure the mole numbers of intermediates at these time points, then calculate the following for this time interval: (i) an average rate of each elementary reaction, which is equivalent to the transition rate of the molecular computer:

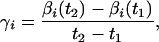and (ii) the average number of moles of each intermediate:

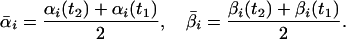The average value of ΔG for each elementary reaction in this interval is

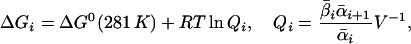where V is the reaction volume. The ΔG_i has the units of J/mole. To obtain energy dissipation rate, we multiply it by the average transition rate. For each elementary reaction, this dissipation rate is g = γ₁ΔG₁ and the total dissipation is g = γ₁ΔG₁ + γ₂ΔG₂ + … + γ_n-1ΔG_n-1, which has units of J/s or W. This includes both enthalpy and entropy contribution, whereas strictly speaking, heat dissipation refers to enthalpy change only. There is no accurate data on entropy change except that it is positive. The calculated value of g gives therefore an upper bound on heat dissipation.

Results

State Machines and Finite Automata.

Generally, a state machine consists of (i) a data tape divided into cells, each containing a symbol selected from the tape alphabet and (ii) a computing device driven by transition rules. The device is positioned over one of the cells and is in one of a finite number of internal states. Depending on the symbol detected and the internal state, a transition rule instructs the device to write a new symbol, change state, and move one cell to the left or to the right. The Turing machine (27) is the most general type of state machine, capable of writing on the tape as well as moving in both directions.

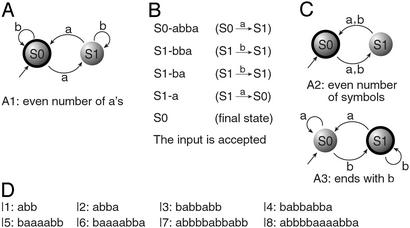
A more restricted, yet important, class of state machines is finite automata (28). A finite automaton is a unidirectional read-only Turing machine. Its input is a finite string of symbols. It is initially positioned on the leftmost input symbol in a default initial state, and in each transition moves one symbol to the right, possibly changing its internal state. Its software consists of transition rules, each specifying a next state based on the current state and current symbol. A computation terminates after the last input symbol is processed, the final state being its “output.” Alternatively, it may suspend without completion when no transition rule applies. Some states are deemed accepting. An automaton accepts an input if there is a computation with this input that ends in an accepting final state. A finite automaton with two states and an alphabet of two symbols is shown in Fig. 1A. It determines if an input over the alphabet {a, b} contains an even number of a symbols. Fig. 1B shows the intermediate configurations obtained during a computation of this automaton. A two-state, two-symbol automaton can have eight possible transition rules. Programming such an automaton amounts to selecting transition rules and deciding which states are accepting. A selection of such programs is shown in Fig. 1C.

Figure 1.

Finite automata and inputs for which we show molecular realizations. (A) Automaton A1. Incoming unlabeled arrow marks the initial state, and labeled arrows represent transition rules. A double circle represents an accepting state. (B) A computation of A1 scanning and digesting the input abba. Each row represents an intermediate configuration showing current state and remaining input. The transition rule applied is shown in brackets. (C) The two other automata for which we demonstrate molecular operation. (D) The set of inputs used as fuel.

Design and Mechanism of Operation of the Molecular Finite Automaton.

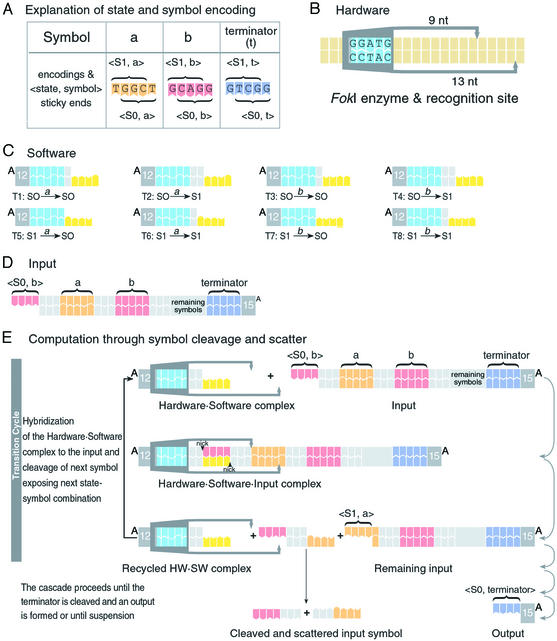
Double-stranded DNA molecules with sticky ends realize both the software (Fig. 2C) and the input (Fig. 2D) and the class IIS restriction enzyme FokI functions as the hardware (Fig. 2B). Unlike previous work (22), the core computational step (Fig. 2E) does not use energy-consuming ligase to bond the input and software molecules. Rather, it uses a hitherto unknown capability of FokI to cleave DNA in the presence of a noncovalent hybridization complex between its recognition and cleavage sites. As a beneficial side effect, the software molecule used in this step is not consumed, unlike previous work, because it dissociates spontaneously from the cleaved input symbol (Fig. 2E), rendering it reusable for subsequent transitions. The software molecules (Fig. 2C) effectively operate as a family of cofactors of variable specificity (29) to FokI, each determining a specific FokI cleavage site on the input molecule, and a fixed amount of software and hardware molecules can, in principle, process any input molecule of any length.

Figure 2.

A molecular finite automaton that uses input as fuel. (A) Encoding of a, b, and terminator (sense strands) and the <state, symbol> interpretation of exposed 4-nt sticky ends, the leftmost representing the current symbol and the state S1, similarly the rightmost for S0. (B) Hardware: The FokI restriction enzyme, which recognizes the sequence GGATG and cleaves 9 and 13 nt apart on the 5′ → 3′ and 3′ → 5′ strands, respectively. (C) Software: Each DNA molecule realizes a different transition rule by detecting a current state and symbol and determining a next state. It consists of a <state, symbol> detector (yellow), a FokI recognition site (blue), and a spacer (gray) of variable length that determines the FokI cleavage site inside the next symbol, which in turn defines the next state. Empty spacers effect S1 to S0 transition, 1-bp spacers maintain the current state, and 2-bp spacers transfer S0 to S1. (D) Input: The exposed sticky end at the 5′ terminus of the DNA molecule encodes the initial state and first symbol. Each symbol is encoded with 5 bp separated by 3-bp spacers. (E) Suggested mechanism of operation of the automaton. The computation proceeds via a cascade of transition cycles, each cleaving and scattering one input symbol, exemplified with the input molecule bab in the initial state S0 and the transition S0 →b S1. Both hardware and software molecules are recycled.

Each computational step cleaves and scatters one input symbol, a short molecule with an even shorter double-stranded region (3–5 bp), which probably dissociates in solution to single-stranded DNAs (Fig. 2E). For very long inputs the accumulation of input fragments may slow the computation down by reversibly binding to the sticky ends of the input and the software. It is conceivable that the residual energy of these fragments may be sufficient to dispose of them, for example, through selective hydrolytic digestion.

The computation proceeds until no software molecule matches the state-symbol pair encoded by the exposed sticky end or until the special terminator symbol is cleaved. This final state encoded by the output molecule can be identified according to either its length (Fig. 3) or its sticky end (22).

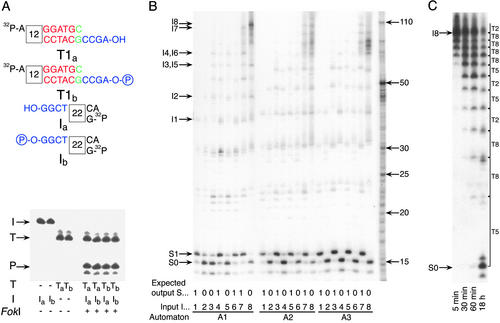
Figure 3.

Experimental results and mechanism analysis of the molecular automaton. (A) A demonstration that a computation does not require ligase. Different variants of the software molecule T1 (T1_a, nonphosphorylated, and T1_b, phosphorylated) and the input (I_a, nonphosphorylated and I_b, phosphorylated) were incubated with the hardware (FokI) at 8°C for 10 min. Input, software, and hardware concentrations were all 1 μM. Reaction components are shown below the lanes, and the locations of software molecule (T), input (I), and product (P) are indicated by arrows. (B) Executing automata A1–A3 (Fig. 1 A and C) on inputs I1–I8 (Fig. 1D). Input, software, and hardware concentrations were 1, 4, and 4 μM, respectively. Reactions were set in 10 μl and incubated at 8°C for 20 min. Each lane contains inputs, intermediate configurations, and output bands at the indicated locations. The programs, inputs, and expected outputs are indicated below each lane. Location of unprocessed input is shown on the left. Size markers are indicated by arrows on the right. (C) Software reusability with the four-transition automaton A1 applied to input I8 with each software molecule taken at 0.075 molar ratio to the input. Input, software, and hardware concentrations were 1, 0.3 (0.075 μM each kind), and 1 μM, respectively. After 18 h, molecules T2, T5, and T8 performed on the average 29, 21, and 54 transitions each. Input and output locations are indicated on the left, and intermediates and software molecules applied at each step are on the right.

Although a hint of ligase-free operation has been observed (22), its direct realization via removal of ligase and ATP proved impossible, requiring important design changes. We found that the ability of FokI to cleave DNA with its recognition and cleavage sites attached by sticky-end hybridization was limited to specific hybridization complexes. To identify them we varied the composition of the spacer between the FokI recognition site and the sticky end of the software molecule, the length of the spacer and the composition of the sticky end, with corresponding modifications to the input molecules. We observed that long spacers and low GC content often resulted in cleaving only one of the input strands, producing a computationally illegal configuration. Correct performance was achieved with short spacers and high GC content of the sticky ends. Our final design uses the shortest possible spacers of 0, 1, and 2 bp (Fig. 2C), which dictates a particular symbol encoding (Fig. 2A) and the introduction of spacers between the symbols (Fig. 2D).

To optimize reaction conditions, we calculated the relative abundance of the hardware/software/input complex for different initial concentrations of these molecules, assuming dissociation constants of 2 nM (30) for the hardware/software complex and 50 μM for software/input hybrid. The highest proportion of the complex was found at equimolar ratio of hardware and software molecules, the absolute concentrations of both being in the micromolar range and in excess of the input. This finding suggests that the reactive species is a tight (30) hardware/software complex (Fig. 2E), possessing both recognition and cleavage capabilities. Indeed, experiments showed that preincubation of hardware and software molecules before input addition resulted in almost a 2-fold rate increase, supporting this suggestion.

Proof of the Proposed Mechanism.

Conclusive evidence for the ability of FokI to perform a transition based on hybridization without ligation is shown in Fig. 3A. We incubated a one-symbol input, complementary software and FokI and compared phosphorylated and nonphosphorylated 5′ termini of the input and software molecules. The reaction proceeded independently of the 5′ phosphate availability and therefore it was ligase independent (1). In addition, the software molecule did not undergo any change as judged from the gel image and, as expected, served as a double-stranded DNA cofactor for the enzyme.

System Performance.

This ATP-free system retains the computational capabilities of the previous automaton and even outperforms it. Three programs (Fig. 1 A and C) were applied to a selection of eight inputs up to 12 symbols long (Fig. 1D). In each case the major output molecule was formed in agreement with the prediction (Fig. 3B). The byproducts visible at the locations of the incorrect outputs cannot be unambiguously assigned at this stage. The correctness of the computation, based on the worst-case assumption that the byproducts represent incorrect outputs, depends on the software. We obtained single-step fidelity of 99.9% with input I8 and software A3 whereas the average value for 12-symbol inputs was ≈99.5%. We also observed that the abundance of the putative erroneous bands was almost independent of input length, resulting in lower single-step fidelity values for shorter inputs. For example, program A1 applied to input I2 (four symbols long) rendered single-step correctness of only 95%. However, it is clear that the real fidelity is higher, otherwise the computations would randomize completely after 12 steps. Indeed, analysis of the correctness with detection molecules able to hybridize selectively to different outputs (22) indicates that at least some of the byproducts do not represent real errors, and the average single-step fidelity for long inputs determined by this method is ≈99.9% (data not shown). We have yet to explain this discrepancy.

The reusability of software molecules was demonstrated by using a small amount of software to process a large amount of input (Fig. 3C). During this computation one type of software molecule (T8) performed on the average 54 transitions per molecule, with some molecules necessarily performing many more transitions than the average.

Optimization of the Computation Reactions.

We optimized system performance in two respects. First, the duration of a single computational step was minimized. The fastest computation was achieved when 4 μM of program A2 (1 μM of each software molecule) and 4 μM of hardware were mixed with 10 nM of the I3 input at 8°C. This computation proceeded with an initial rate of 20 s per step per input molecule, about 50-fold improvement compared with the previous system (22) (1,000 s per step per molecule). We considered the initial rates obtained over the first 30 s of the reaction because at longer sampling times fully processed input molecules accumulated, introducing a bias toward lower numbers.

Second, the parallel performance of the system was improved by maximizing the total number of operations performed per s in a unit solution volume. Ten micromolar program A2 (2.5 μM of each molecule) and 10 μM FokI were preincubated at 8°C for 30 min and then mixed with 5 μM of the I3 input. A cumulative initial rate was 6.646 × 10¹⁰ operations per s per μl, an ≈8,000-fold improvement over the previous system (8.3 × 10⁶ operations per s per μl). The single-step duration at these conditions was ≈45 s, only about two times slower than in the fastest reaction.

Error rates in the optimized processes versus the slow computation with software recycling provided an insight into the speed/error rate tradeoff. In the fast reaction, the apparent single-step correctness rose slightly from 98.1% after the first 30 s to 98.9% after 4 min. In the reaction optimized for parallel performance, the correctness remained constant over time, equaling 99.5%. In the “slow” computation, the fidelity after 18 h was 98.7%. These results suggest that error rate is independent of computation speed and rather depends on the molecular structure of the reacting compounds.

Energy Dissipation.

Heat dissipation depends on reaction conditions, reaction coordinate, and the number of symbols in the input. We therefore selected a particular computation, namely the high-performance reaction, and estimated its average heat dissipation between 30 and 60 s from its onset (see Materials and Methods). The calculation provides an upper limit on the value of heat dissipation of ≈ 5.3 × 10⁻⁹ W/μl under these conditions and an average free energy change of ≈−33.9 kT per transition. Reaction rates were surprisingly insensitive to temperature and remained similar over the range of 2–20°C. This finding might represent a tradeoff between a decrease in stability of sticky end hybridization and an increase in enzyme activity as the temperature increases.

Discussion

We define the DNA energy balance of a molecular computation to be the difference between the free energy of the DNA output and byproducts and the free energy of the DNA input. Negative balance implies that, thermodynamically, the DNA input contains enough potential free energy to fuel the computation. The two types of compounds that contribute to the overall negative balance are self-assembled complexes of the input components or products of input hydrolysis. The former use hybridization energy between complementary strands whereas the latter use the energy-rich phosphodiester bonds of DNA backbone. Actual harvesting of the free-energy difference depends on the activation energies en route between intermediates and is a function of the molecular mechanism used.

Several theoretical and experimental molecular computing systems exhibit negative DNA energy balance. Ensembles of DNA tiles have lower energy than the individual tiles; assembled DNA representing paths in a graph have lower energy than the single strands representing vertices and edges. Because of its intrinsic instability, further processing of a self-assembled computational output may require covalent sealing using external energy. This is standard practice in the combinatorial approach and may also be required with tiling-based computations. Moreover, unlike our implementation, each logical operation in the tiling-based approach consumes a tile-representing software molecule. Even when the ligation is avoided, tile molecules cannot be reused during the same run and the amount consumed is linear in the length of the computation for simple automata and quadratic for universal automata.

Structural decomposition of DNA and other biopolymers is thermodynamically downhill because turning a spatially constrained sequence of bits into an unordered collection increases entropy and, furthermore, biopolymer cleavage dissipates heat. Hence input destruction can drive biomolecular computations. This principle is not readily realized by electronic computers, which destroy information via erasure. Erasure is thermodynamically uphill because resetting an unknown bit to zero decreases entropy (31–33), and past research on energy-efficient computing focused on reversible computers that avoid information destruction (31–40).

One hypothetical way to obtain energy from information proposed by Bennett (31) was based on scanning the input tape and replacing each input symbol by a random symbol. Information destruction by randomization can only extract energy from a nonrandom input, as randomizing an already random input does not increase entropy (31, 32). Furthermore, it is not clear how this method can be realized in practice. Another possibility is to destroy the input structure while preserving the input symbols, effectively turning the sequence of symbols (string) into an unordered collection (multiset). Indeed this increase in entropy is responsible in part for driving our computing machine.

The theoretical possibility of performing any computation with arbitrarily little energy was suggested three decades ago (31). Our automaton is very similar in its overall logical structure to a hypothetical biomolecular computing device envisioned by Bennett (ref. 35, p. 531) in 1973, as a possible design for such a low-energy computing device. The important difference is that unlike the reversible hypothetical device of Bennett, the use of input destruction by our automaton entails entropy increase and nontrivial heat dissipation, and therefore is irreversible. Our computing machine dissipates about 34 kT per transition, which is ≈50 times higher than kTln 2, the theoretical energy gain of randomizing a known bit (32). One can envision other computing machines that dissipate smaller amounts of heat at the expense of reduced speed and/or reduced precision (31, 32, 35, 37). Yet DNA cleavage together with its inverse operations of elongation and ligation seem to strike a very practical balance between energy, speed, and precision. Furthermore, we believe that the design choice made by living systems to package information in metastable polymers, namely DNA, RNA, and proteins, the decomposition of which dissipates heat and increases entropy, is of fundamental importance. This design inhibits the formation of unwanted random information and facilitates discarding dated, erroneous, or hostile information in the cell and recycling its constituent bits, rendering the cell an efficient information-processing device. These two observations regarding the packaging of information and fuel in DNA may help explain its selection as the basis of nature's information system.

Abbreviation

PNK

polynucleotide kinase