Abstract
Inferring positive selection at single amino acid sites is of particular importance for studying evolutionary mechanisms of a protein. For this purpose, Suzuki and Gojobori (1999) developed a method (SG method) for comparing the rates of synonymous and nonsynonymous substitutions at each codon site in a protein-coding nucleotide sequence, using ancestral codons at interior nodes of the phylogenetic tree as inferred by the maximum parsimony method. In the SG method, however, selective neutrality of nucleotide substitutions cannot be tested at codon sites, where only termination codons are inferred at any interior node or the number of equally parsimonious inferences of ancestral codons at all interior nodes exceeds 10,000. Here I present a modified SG method which is free from these problems. Specifically, I use the distance-based Bayesian method for inferring the single most likely ancestral codon from 61 sense codons at each interior node. In the computer simulation and real data analysis, the modified SG method showed a higher overall efficiency of detecting positive selection than the original SG method, particularly at highly polymorphic codon sites. These results indicate that the modified SG method is useful for inferring positive selection at codon sites where neutrality cannot be tested by the original SG method. I also discuss that the p-distance is preferable to the number of synonymous substitutions for inferring the phylogenetic tree in the SG method, and present a maximum likelihood method for detecting positive selection at single amino acid sites, which produced reasonable results in the real data analysis.
Keywords: Positive selection, Ancestral sequence, Parsimony, Bayesian, Likelihood
Introduction
In the study of evolutionary mechanisms of a protein, it is of particular importance to detect natural selection operating at the amino acid sequence level. In a protein molecule, however, different amino acid sites usually have different biochemical functions, indicating that the types and strengths of natural selection vary among amino acid sites. It is therefore interesting to detect natural selection at single amino acid sites.
The occurrence of natural selection may be inferred by comparing the rates of synonymous (rS) and nonsynonymous (rN) substitution in a protein-coding nucleotide sequence (Hughes and Nei 1988, 1989). The relationship rS > rN (or rN/rS < 1) indicates negative selection, whereas rS < rN (or rN/rS > 1) indicates positive selection. For inferring natural selection at single amino acid sites, Suzuki and Gojobori (1999) developed a method (SG method) in which rS and rN are compared at each codon site of the sequence.
In the SG method the following computation is done at each codon site for a given phylogenetic tree of nucleotide sequences. We first infer ancestral codons at all interior nodes of the tree using the maximum parsimony (MP) method (Fitch 1971; Hartigan 1973). We then compute the total numbers of synonymous (cS) and nonsynonymous (cN) substitutions per codon site as well as the average numbers of synonymous (sS) and nonsynonymous (sN) sites per codon site for the entire tree. Selective neutrality of nucleotide substitutions is tested under the assumption that cS and cN are binomially distributed and the probabilities of occurrence of synonymous and nonsynonymous substitutions are given by sS/(sS + sN) and sN/(sS+sN), respectively. When neutrality is rejected, negative selection is inferred if the relationship cS/sS > cN/sN is observed, whereas positive selection is inferred if cS/sS < cN/sN.
Computer simulation and real data analysis have shown that the SG method is generally reliable in inferring selected sites, and the method has been applied to various proteins including those involved in the host-parasite interactions (Suzuki and Gojobori 1999, 2001; Su et al. 2002). However, this method appears to have at least two problems. First, selective neutrality cannot be tested at a codon site, (1) if sS is 0 because the binomial distribution is not applicable for cS and cN, (2) if only termination codons are inferred at any interior node because it is biologically unlikely that the function of a protein once destroyed by a nonsense mutation is recovered by a reverse mutation, and (3) if the number of equally parsimonious inferences of ancestral codons at all interior nodes exceeds 10,000 because it requires an enormous amount of computer time. Second, it is not clear to what extent the errors in the phylogenetic tree inferred affect the detection of natural selection.
In this paper, I present the modified SG method which takes care of the first problem. The reliability of the modified SG method is examined by conducting computer simulation and real data analysis. I also discuss the second problem and present a maximum likelihood (ML) method for detecting positive selection at single amino acid sites.
Materials and Methods
Modified Suzuki–Gojobori Method
Here I assume that nucleotide sequences are translated into amino acid sequences according to the standard genetic code for explaining the method. However, the arguments can easily be extended to the case with any codon table. In the first problem mentioned above, condition (1) occurs at the invariable codon sites where all sequences have the same codon ATG (encoding methionine) or TGG (tryptophan), for which the probabilities of occurrence of synonymous and nonsynonymous substitutions are 0 and 1, respectively. For such a codon site, however, inference of natural selection is impossible because both cS and cN are effectively 0. Therefore, I do not consider these codon sites in this paper.
In contrast, conditions (2) and (3) may occur at highly polymorphic codon sites, where the number of nucleotide substitutions for each branch of the phylogenetic tree is so large that the inference of ancestral codons at interior nodes by the MP method becomes unreliable. To avoid the occurrence of condition (2), I consider only 61 sense codons as potential ancestral codons. In addition, to avoid condition (3), I infer the single most likely ancestral codon at each interior node. For these purposes, I use the distance-based Bayesian method (Zhang et al. 1998) for inferring ancestral codons. In this method, we first translate the nucleotide sequences into amino acid sequences and infer the single most likely ancestral amino acid at each interior node using the distance-based Bayesian method (Zhang and Nei 1997). We then infer the single most likely ancestral codon at each interior node using the same method but under the constraint that only the codons which encode the inferred ancestral amino acid were considered as potential ancestral codons. This method appears to be quite reliable according to the computer simulation and real data analysis so far conducted (Zhang and Nei 1997; Zhang et al. 1998).
Computer Simulation
A random nucleotide sequence with 300 codon sites was allowed to evolve following a symmetrical phylogenetic tree with 64 or 128 exterior nodes. All branch lengths (b) were assumed to be the same and set so that the expected number of synonymous substitutions per synonymous site was 0.01, 0.02, or 0.03. I also assumed that all codon sites in a sequence had the same rN/rS ratio of 0.2, 0.5, 1, 2, or 5, where the first two, middle, and last two values represent the cases of negative selection, no selection, and positive selection, respectively. The transition/transversion ratio (R) of nucleotide mutation was 0.5. This model is known as the Jukes–Cantor model (Jukes and Cantor 1969) and has been used frequently in simulation studies. The detailed simulation scheme has been described in Suzuki and Gojobori (1999).
The 64 or 128 sequences generated above were analyzed by the original and modified SG methods using the computer program ADAPTSITE (version 1.3) (Suzuki et al. 2001) with R = 0.5. Note that the same R value was used for both generating and analyzing sequences in the simulation. Under such a condition, the actual value of R did not appear to influence the results to a large extent. I used the true (model) and inferred phylogenetic trees and 5% significance level for detecting negative and positive selection. The entire procedure was repeated 50 times for each parameter set, so that the total number of codon sites analyzed was 15,000.
In order to examine the second problem for the original SG method as mentioned above, I also estimated the numbers of synonymous (dS) and nonsynonymous (dN) substitutions per synonymous and nonsynonymous sites for each codon site as cS/sS and cN/sN, respectively, in the simulation. I then computed the averages of dS and dN over all (15,000) codon sites for each parameter set under the assumption that the true phylogenetic tree is known, and they are denoted d̄S,True and d̄N,True, respectively. I also computed the averages of dS and dN under the assumption that the tree is inferred by the NJ method using the number of synonymous substitutions, and they are denoted by d̄S,Inferred and d̄N,Inferred, respectively. Note that the number of synonymous substitutions was proposed to be used for inferring the tree in the SG method (Suzuki and Gojobori 1999), because it appeared to be roughly proportional to the evolutionary time, which was used for computing iS and sN. I then computed the proportion of difference (eS) between d̄S,True and d̄S,Inferred as (d̄S,Inferred – d̄S,True)/d̄S,True and that (eN) betwen d̄N,True and d̄N,Inferred as (d̄N,Inferred – d̄N,True)/d̄N,True. I also computed the proportion of difference (eNeg) between the numbers of negatively selected sites detected by using the true tree (nNeg,True) and inferred tree (nNeg,Inferred)as(nNeg,Inferred – nNeg,True)/nNeg,True, and that (ePos) between the numbers of positively selected sites detected by using the true tree (nPos,True) and inferred tree (nPos,Inferred) as (nPos,Inferred – nPos,True)/nPos,True for each parameter set. Note that eS, eN, eNeg, and ePos could not be computed when d̄S,True, d̄N,True, nNeg,True, and nPos,True were 0, respectively. On the other hand, I computed the topological distance (dT) (Nei and Kumar 2000) between the true and the inferred trees for each replication in the simulation. Then the average proportion of different partitions for each parameter set was computed as d̄T/2(n−3), where d̄T is the average of dT for 50 replications and n the number of sequences (64 or 128). [Note that d̄T/2is the average number of topological differences between the true and the inferred trees and (n−3) the number of interior branches of the tree with n sequences.] eS, eN, eNeg, ePos, and d̄T/2(n−3) were also computed under the assumption that the tree was inferred by the NJ method using the p-distance. Here branch lengths were still estimated as the number of synonymous substitutions by using the ordinary least-squares method after inferring the topology.
Maximum Likelihood Method for Detecting Positive Selection at Single Amino Acid Sites
For detecting positive selection at single amino acid sites, Yang et al. (2000) also developed a method (Yang method) based on Bayesian approach. The SG and Yang methods, however, have their own pros and cons. In the SG method, we can test neutrality for each codon site independently. However, we may fail to infer positively selected sites when the branches of the phylogenetic tree are long, because the MP method does not correct for multiple substitutions. In contrast, in the Yang method, multiple substitutions may be corrected for by assuming the codon substitution model. However, we have to assume that the rN/rS value follows a particular statistical distribution among codon sites, and thus the result of the test of neutrality at a codon site depends on the rN/rS values at other codon sites.
These problems may be solved by developing an ML method as follows. In this method, I first assume that the phylogenetic tree of nucleotide sequences is known, in which the branch lengths are estimated as the number of synonymous substitutions. I also assume that the substitution rate from codon i to j is
(Goldman and Yang 1994; Muse and Gaut 1994). Here t is the scaling factor to set the average rate of codon substitution in the matrix at unity and πj the equilibrium frequency of codon j. For each codon site, I estimate the rN/rS value using the ML method under the constraint that the numbers of synonymous substitutions for branches of the tree are fixed. Note that I do not infer ancestral codons at interior nodes of the tree but all codons are taken into account. Once the rN/rS value is estimated, I compare its ML value with the ML value which was obtained by assuming that rN/rS = 1 (neutrality) using the likelihood ratio test (LRT). In the LRT, the null hypothesis is that rN/rS = 1 and the χ2 test is conducted with the degree of freedom of 1. When neutrality was rejected, I infer positive selection if the estimate of rN/rS was larger than unity, or negative selection if the estimate of rN/rS was smaller than unity. Note that it is also possible to estimate the R and πj values and branch lengths of the tree for each codon site, and detect positive selection at single or subset of branches using this model. However, the result should be subject to large stochastic errors.
Data Analysis
I analyzed the envelope glycoproteins 1 (E1) and 2(E2) of hepatitis C virus (HCV) for inferring positively selected amino acid sites by the original and modified SG methods and by the ML method. HCV is an etiological agent of chronic hepatitis, which may progress to cirrhosis and hepatocellular carcinoma (Choo et al. 1989). The genomic sequences from different HCV isolates are highly divergent (Kato et al. 1989) and divided into six clades which are further subdivided into various numbers of subtypes (Robertson et al. 1998). E1 and E2 consist of 192 and 426 amino acids, respectively (Kato et al. 1990). The protein region encompassing the amino-terminal 27–31 amino acids of E2 is the most variable throughout the amino acid sequences of all HCV proteins and called hypervariable region 1 (HVR1) (Hijikata et al. 1991; Weiner et al. 1991). HVR1 is known as the major neutralization epitope of HCV (Weiner et al. 1992).
I collected all subtype 1b HCV sequences coding for E1 and E2 from the international nucleotide sequence database (DDBJ release 48). After removing the sequences which included ambiguous nucleotides or minor gaps, I obtained 174 and 97 sequences for E1 and E2, respectively. For each coding region, I made a multiple alignment using the computer program CLUSTAL W (version 1.81) (Thompson et al. 1994) and inferred a phylogenetic tree using the NJ method (Saitou and Nei 1987) with the number of synonymous substitutions (Nei and Gojobori 1986). In both the original and the modified SG methods, I computed sS and sN taking into account the R value (Suzuki 1999), which was estimated as the ratio of the transitional nucleotide diversity to the transversional nucleotide diversity at the fourfold degenerate sites (Kimura 1980). The R values estimated were 7.3 and 6.1 for E1 and E2, respectively. In the ML method, I also assumed that the R values for E1 and E2 were 7.3 and 6.1, respectively, the equilibrium frequencies of 61 codons were 1/61, and the significance level for detecting negative and positive selection was 5%, to make the results from the ML and SG methods compatible. Note that it is also possible to estimate the R value and equilibrium codon frequencies in the ML method.
Results
Efficiencies of the Original and Modified SG Methods
In the computer simulation, I used the true and inferred phylogenetic trees in both the original and the modified SG methods as mentioned above. However, similar results were obtained regardless of the trees used in both methods, as described below. I therefore discuss only the results obtained by using the true tree in this section.
Table 1 presents the conditional efficiencies of the original and modified SG methods in detecting selected sites, which are defined as the proportions of negatively and positively selected sites inferred among all the codon sites where neutrality could be tested. In other words, if we let x be the number of negatively or positively selected sites inferred and y be the number of codon sites where neutrality could not be tested, the conditional efficiency is given by x/(15,000−y). In both the original and the modified SG methods, the conditional efficiency increased as the strength of selection and the number of nucleotide substitutions in the phylogenetic tree increased. The modified method appeared to have a slightly higher conditional efficiency of inferring negatively selected sites but a slightly lower conditional efficiency of inferring positively selected sites than the original method.
Table 1.
Proportions of negatively and positively selected codon sites inferred among all the codon sites where neutrality could be tested (conditional efficiencies) by the original and modified (in parentheses) SG methods in the computer simulation
|
rN/rS |
|||||||
|---|---|---|---|---|---|---|---|
| Sequences | b | Selection | 0.2 | 0.5 | 1 | 2 | 5 |
| 64 | 0.01 | Negative | 0.08 (0.09) | 0.05 (0.06) | 0.02 (0.03) | 0.00 (0.01) | 0.00 (0.00) |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.01 (0.01) | 0.21 (0.17) | ||
| 0.02 | Negative | 0.22 (0.22) | 0.09 (0.09) | 0.02 (0.02) | 0.00 (0.00) | 0.00 (0.00) | |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.05 (0.05) | 0.48 (0.42) | ||
| 0.03 | Negative | 0.33 (0.34) | 0.12 (0.12) | 0.02 (0.02) | 0.00 (0.00) | 0.00 (0.00) | |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.01 (0.01) | 0.08 (0.08) | 0.60 (0.54) | ||
| 128 | 0.01 | Negative | 0.22 (0.24) | 0.10 (0.12) | 0.02 (0.04) | 0.00 (0.01) | 0.00 (0.00) |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.06 (0.05) | 0.58 (0.42) | ||
| 0.02 | Negative | 0.43 (0.43) | 0.15 (0.15) | 0.02 (0.02) | 0.00 (0.00) | 0.00 (0.00) | |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.01 (0.01) | 0.15 (0.14) | 0.84 (0.74) | ||
| 0.03 | Negative | 0.57 (0.57) | 0.21 (0.21) | 0.03 (0.03) | 0.00 (0.00) | 0.00 (0.00) | |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.01 (0.02) | 0.21 (0.21) | 0.92 (0.86) | ||
The numbers of codon sites which were excluded from the test of neutrality by the original and modified SG methods (in the above notation, y) are presented in Table 2. In the original SG method, condition (1) occurred when the number of nucleotide substitutions in the phylogenetic tree was relatively small, whereas conditions (2) and (3) occurred when the number of nucleotide substitutions was relatively large, as expected. The numbers of excluded sites were relatively small for most parameter sets used in the present study. However, about two-thirds of all codon sites (9846/15,000) were excluded in the case of rN/rS = 5 and b = 0.03 with 128 sequences. Under this parameter set, each codon site was highly polymorphic and neutrality could not be tested mainly because of the occurrence of condition (3). In the modified SG method, however, the occurrence of conditions (2) and (3) was completely avoided, although that of condition (1) was not.
Table 2.
Numbers of codon sites where neutrality could not be tested due to the occurrence of conditions (1) (leftmost), (2) (middle), and (3) (rightmost) by the original and modified (in parentheses) SG methods in the computer simulation
|
rN/rS |
||||||
|---|---|---|---|---|---|---|
| Sequences | b | 0.2 | 0.5 | 1 | 2 | 5 |
| 64 | 0.01 | 255,0,0 | 82,0,0 | 18,0,0 | 1,0,0 | 0,0,0 |
| (255,0,0) | (82,0,0) | (18,0,0) | (1,0,0) | (0,0,0) | ||
| 0.02 | 127,0,0 | 19,0,0 | 0,0,0 | 0,0,0 | 0,10,43 | |
| (127,0,0) | (19,0,0) | (0,0,0) | (0,0,0) | (0,0,0) | ||
| 0.03 | 63,0,0 | 4,0,0 | 0,1,0 | 0,2,0 | 0,12,966 | |
| (63,0,0) | (4,0,0) | (0,0,0) | (0,0,0) | (0,0,0) | ||
| 128 | 0.01 | 114,0,0 | 16,0,0 | 2,0,0 | 0,0,0 | 0,1,1 |
| (114,0,0) | (16,0,0) | (2,0,0) | (0,0,0) | (0,0,0) | ||
| 0.02 | 36,0,0 | 0,0,0 | 0,0,0 | 0,1,0 | 0,6,1649 | |
| (36,0,0) | (0,0,0) | (0,0,0) | (0,0,0) | (0,0,0) | ||
| 0.03 | 5,0,0 | 0,0,0 | 0,0,0 | 0,1,35 | 0,43,9803 | |
| (5,0,0) | (0,0,0) | (0,0,0) | (0,0,0) | (0,0,0) | ||
Table 3 presents the overall efficiencies of the original and modified SG methods, which are defined as the proportions of negatively and positively selected sites inferred among the entire (15,000) codon sites. Note that in the above notation, the overall efficiency is given by x/15,000, which is always equal to or smaller than the conditional efficiency. In both the original and the modified SG methods, the overall efficiencies were similar to the conditional efficiencies for most parameter sets, because the numbers of excluded sites were relatively small. In the original SG method, however, the overall efficiency of inferring positively selected sites (0.32) was about one-third the conditional efficiency (0.92) in the case of rN/rS = 5 and b = 0.03 with 128 sequences. This observation is obviously caused by the fact that about two-thirds of all codon sites were excluded from the computation of the conditional efficiency but included in the computation of the overall efficiency. In the modified SG method, in contrast, the overall efficiency was similar to the conditional efficiency for all parameter sets. As a result, the overall efficiency of the modified method (0.86) became much higher than that of the original method under the parameter set of rN/rS = 5 and b = 0.03 with 128 sequences.
Table 3.
Proportions of negatively and positively selected codon sites inferred among the entire (15,000) codon sites (overall efficiencies) by the original and modified (in parentheses) SG methods in the computer simulation
|
rN/rS |
|||||||
|---|---|---|---|---|---|---|---|
| Sequences | b | Selection | 0.2 | 0.5 | 1 | 2 | 5 |
| 64 | 0.01 | Negative | 0.08 (0.09) | 0.05 (0.06) | 0.02 (0.03) | 0.00 (0.01) | 0.00 (0.00) |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.01 (0.01) | 0.21 (0.17) | ||
| 0.02 | Negative | 0.22 (0.22) | 0.09 (0.09) | 0.02 (0.02) | 0.00 (0.00) | 0.00 (0.00) | |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.05 (0.05) | 0.47 (0.42) | ||
| 0.03 | Negative | 0.33 (0.33) | 0.12 (0.12) | 0.02 (0.02) | 0.00 (0.00) | 0.00 (0.00) | |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.01 (0.01) | 0.08 (0.08) | 0.56 (0.54) | ||
| 128 | 0.01 | Negative | 0.22 (0.23) | 0.10 (0.12) | 0.02 (0.04) | 0.00 (0.01) | 0.00 (0.00) |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.06 (0.05) | 0.58 (0.42) | ||
| 0.02 | Negative | 0.43 (0.43) | 0.15 (0.15) | 0.02 (0.02) | 0.00 (0.00) | 0.00 (0.00) | |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.01 (0.01) | 0.15 (0.14) | 0.75 (0.74) | ||
| 0.03 | Negative | 0.57 (0.57) | 0.21 (0.21) | 0.03 (0.03) | 0.00 (0.00) | 0.00 (0.00) | |
| Positive | 0.00 (0.00) | 0.00 (0.00) | 0.01 (0.02) | 0.21 (0.21) | 0.32 (0.86) | ||
Effect of Incorrect Trees
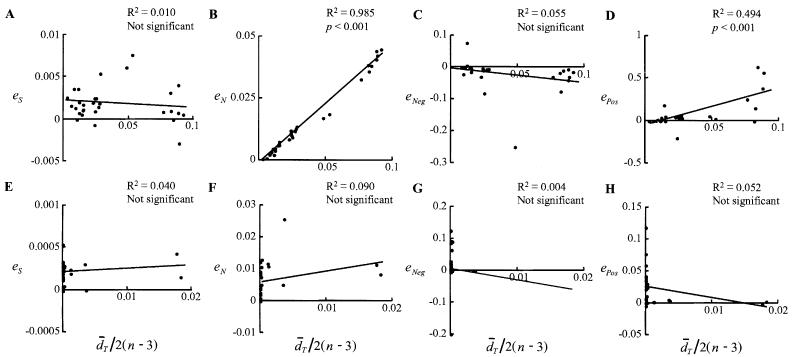
The effect of errors in the phylogenetic tree inferred on detection of natural selection was assessed for the original SG method. When the phylogenetic tree was inferred by the NJ method using the number of synonymous substitutions, d̄S,Inferred and d̄N,Inferred were usually larger than d̄S,True and d̄N,True, respectively, probably because the former values were inflated owing to topological errors. In addition, eN tended to be greater than eS, because only the number of synonymous substitutions was optimized in the inference of tree. When I plotted eS and eN against d̄T/2(n − 3), it was found that eN increased as d̄T increased (p < 0.001) (Fig. 1B), whereas eS did not (Fig. 1A). Consequently, nNeg,Inferred was usually smaller than nNeg,True and nPos,Inferred was larger than nPos,True, and ePos increased as d̄T increased (p < 0.001) (Fig. 1D), whereas eNeg did not show a clear relationship with d̄T (Fig. 1C). Note, however, that the difference between the results obtained by using the true tree and inferred tree was usually negligibly small.
Fig. 1.
The relationship between (A, E) eS, (B, F) eN, (C, G) eNeg, and (D, H) ePos and d̄T/2(n −3) when the phylogenetic tree was inferred by the NJ method using the number of synonymous substitutions (A, B, C, D) and the p-distance (E, F, G, H) in the original SG method in the computer simulation. The R2 value and the result of the test of independence are also included in each panel. “Not significant” indicates that the independence was not rejected at the 5% significance level.
When I inferred the phylogenetic tree by the NJ method using the p-distance, the d̄T values obtained were usually smaller than those obtained by using the number of synonymous substitutions. In addition, none of eS, eN, eNeg, and ePos showed a clear relationship with d̄T/2(n − 3) (Figs. 1E, F, G, and H).
Positively Selected Sites in the E1 and E2 Glycoproteins of HCV
Table 4 presents the codon sites where positive selection was inferred by the original and modified SG methods and by the ML method, and condition (3) occurred in the original SG method in the E1 and E2 glycoproteins of HCV. Condition (2) did not occur in the original (and modified) SG method in the present example. In the original SG method, positive selection was inferred at 17 codon sites and condition (3) occurred at 11 codon sites, all of which were located in the B-cell (BCE) or T-cell (TCE) epitopes. In the modified SG method, positive selection was inferred at similar codon sites as in the original SG method. However, 8 of 11 codon sites where condition (3) occurred in the original method were also inferred as positively selected in the modified method. As a result, a larger number (25) of codon sites were inferred as positively selected in the modified method. In both the original and the modified SG methods, condition (1) occurred at 22 codon sites and negative selection was inferred at about 60% (377 and 378 codon sites by the former and latter methods, respectively) of all codon sites in E1 and E2. The negatively selected sites were evenly distributed throughout E1 and E2 except for HVR1, where positively selected sites predominated, as has been discussed in Suzuki and Gojobori (2001).
Table 4.
Codon sites where positive selection was inferred by the original and modified SG methods and by the ML method, and condition (3) occurred in the original SG method in the E1 and E2 glycoproteins of HCV
| Selection |
||||||
|---|---|---|---|---|---|---|
| Protein | Position | Originala | Modifiedb | ML | Function | Reference(s) |
| E1 | 19 | No | No | Positive | TCE | Lechmann et al. 1996 |
| 28 | Positive | No | No | BCE, TCE | Lechmann et al. 1996; Zibert et al. 1999 | |
| 40 | Positive | No | No | BCE, TCE | Lechmann et al. 1996; Zibert et al. 1999 | |
| 42 | (3)c | No | Positive | BCE, TCE | Lechmann et al. 1996; Zibert et al. 1999 | |
| 44 | Positive | Positive | No | BCE, TCE | Lechmann et al. 1996; Zibert et al. 1999 | |
| 60 | Positive | Positive | No | BCE, TCE | Lechmann et al. 1996; Zibert et al. 1999 | |
| 62 | Positive | No | No | BCE | Zibert et al. 1999 | |
| 65 | Positive | Positive | No | BCE | Zibert et al. 1999 | |
| 108 | Positive | Positive | No | BCE | Zibert et al. 1999 | |
| 123 | Positive | Positive | Positive | BCE, TCE | Lechmann et al. 1996; Zibert et al. 1999 | |
| 139 | No | No | Positive | TCE | Lechmann et al. 1996 | |
| 154 | Positive | Positive | No | TCE | Lechmann et al. 1996 | |
| E2 | 1 | (3) | Positive | Positive | HVR1, BCE | Zibert et al. 1997 |
| 3 | (3) | Positive | Positive | HVR1, BCE | Zibert et al. 1997 | |
| 4 | Positive | Positive | Positive | HVR1, BCE | Zibert et al. 1997 | |
| 5 | No | No | Positive | HVR1, BCE | Zibert et al. 1997 | |
| 8 | (3) | Positive | Positive | HVR1, BCE | Zibert et al. 1997 | |
| 9 | No | Positive | Positive | HVR1, BCE | Zibert et al. 1997 | |
| 12 | (3) | Positive | Positive | HVR1, BCE | Zibert et al. 1997 | |
| 14 | (3) | Positive | Positive | HVR1, BCE | Zibert et al. 1997 | |
| 16 | (3) | No | Positive | HVR1, BCE | Zibert et al. 1997 | |
| 17 | No | No | Positive | HVR1, BCE | Zibert et al. 1997 | |
| 21 | (3) | No | Positive | HVR1, BCE, TCE | Zibert et al. 1997; Gruner et al. 2000 | |
| 22 | (3) | Positive | Positive | HVR1, BCE, TCE | Zibert et al. 1997; Gruner et al. 2000 | |
| 25 | No | No | Positive | HVR1, BCE, TCE | Zibert et al. 1997; Gruner et al. 2000 | |
| 27 | No | No | Positive | HVR1, BCE, TCE | Zibert et al. 1997; Gruner et al. 2000 | |
| 51 | (3) | Positive | Positive | BCE | Zibert et al. 1999 | |
| 61 | No | No | Positive | BCE | Zibert et al. 1999 | |
| 63 | Positive | Positive | Positive | BCE | Zibert et al. 1999 | |
| 81 | Positive | Positive | Positive | BCE | Zibert et al. 1999 | |
| 83 | No | No | Positive | BCE | Zibert et al. 1999 | |
| 92 | No | No | Positive | BCE | Zibert et al. 1999 | |
| 95 | (3) | Positive | Positive | BCE | Zibert et al. 1999 | |
| 97 | Positive | Positive | Positive | BCE | Zibert et al. 1999 | |
| 109 | No | No | Positive | BCE | Zibert et al. 1999 | |
| 118 | Positive | Positive | Positive | BCE | Zibert et al. 1999 | |
| 141 | No | Positive | No | BCE | Zibert et al. 1999 | |
| 145 | Positive | Positive | Positive | BCE | Zibert et al. 1999 | |
| 242 | Positive | Positive | No | BCE, TCE | Zibert et al. 1999; Erickson et al. 2001 | |
| 258 | No | Positive | Positive | BCE | Zibert et al. 1999 | |
| 337 | Positive | Positive | No | BCE | Zibert et al. 1999 | |
| 407 | No | No | Positive | TCE | Erickson et al. 2001 | |
Original SG method.
Modified SG method.
Condition (3) occurred.
By the ML method, 31 sites were inferred to be positively selected (Table 4). The estimated rN/rS values ranged from 1.54 to 10.89, and the χ2 statistics from 3.87 to 132.82. Although evolutionary models assumed in the ML and SG methods were different, many of the positively selected sites inferred by these methods overlapped. Interestingly, all of 11 codon sites where condition (3) occurred in the original SG method were inferred as positively selected by the ML method. In addition, all of 31 positively selected sites were located in the BCE or TCE.
Discussion
In this paper, I developed a modified SG method which avoids the deficiencies of the original SG method mentioned earlier. In the computer simulation, the modified SG method showed a slightly higher conditional efficiency of inferring negatively selected sites but a slightly lower conditional efficiency of inferring positively selected sites than the original SG method. These observations were probably caused by the fact that in the modified SG method ancestral codons were inferred so as to minimize the number of amino acid (=nonsynonymous) substitutions (Nei et al. 1998), whereas in the original SG method the numbers of synonymous and nonsynonymous substitutions were minimized together. Therefore, the modified method may overestimate cS but underestimate cN compared with the original method. At any rate, the inference of positively selected sites by the modified method appears to be a little safer than the original method, because the former method is slightly more conservative than the latter method (Nei and Kumar 2000).
The overall efficiencies were similar to the conditional efficiencies for most parameter sets in both the original and the modified SG methods, because the numbers of codon sites which were excluded from the test of neutrality were relatively small. In the original SG method, however, the proportion of excluded sites became large when codon sites were highly polymorphic, mainly because of the occurrence of condition (3). Consequently, the overall efficiency of inferring positively selected sites in the modified method became much higher than that in the original method. Note that the highly polymorphic codon sites are more likely to be inferred as positively selected than other sites because a substantial number of nonsynonymous substitutions are necessary for producing a high polymorphism at a codon site. Therefore, codon sites which are excluded in the original SG method are highly likely to be positively selected, and the modified SG method may be useful for rescuing those sites.
These predictions were confirmed by the analysis of the E1 and E2 glycoproteins of HCV. In the original SG method, all of the positively selected sites inferred were located in the BCE or TCE, suggesting that host's immune responses are the main driving force of positive selection and these epitopes are neutralization epitopes. Condition (3) occurred at 11 codon sites, which were all located in the BCE or TCE. In particular, 8 of 11 codon sites were located in HVR1, which is known as the major neutralization epitope of HCV. These observations imply that these 11 codon sites are also positively selected. Indeed, in the modified SG method, 8 of 11 codon sites were inferred as positively selected. Since other positively selected sites inferred by the original and modified SG methods were similar to each other, the overall efficiency of inferring positively selected sites for the latter method appeared to be higher than that for the former method.
In the computer simulation, 5% of codon sites were expected to be inferred as negatively or positively selected under the assumption that rN/rS = 1, because the significance level was set at 5% in the test of neutrality. However, the false-positive rate sometimes appeared to be smaller than 5% in Tables 1 and 3 (e.g., 2–3% in the case of rN/rS = 1 and b = 0.01 with 64 sequences). These observations were caused not because the test of neutrality is biased but a relatively large number of nucleotide substitutions are required for obtaining statistically significant results in the original and modified SG methods. For example, if we assume that the probability of occurrence of nonsynonymous substitution is twice as large as that of synonymous substitution, the minimum number of nucleotide substitutions required for inferring negative selection is 3 (cS = 3 and cN = 0), whereas that for inferring positive selection is 9 (cS = 0 and cN = 9). In fact, the false-positive rate increased toward 5% as the number of nucleotide substitutions increased (e.g., 4–5% in the case of rN/rS = 1 and b = 0.03 with 128 sequences).
The effect of errors in the phylogenetic tree inferred by the NJ method using the number of synonymous substitutions on detection of natural selection appeared to be negligibly small for the parameter sets used in the present simulation. However, it may become larger if we analyze many more sequences. This problem may be solved by inferring trees using a distance measure which takes into account both the number of synonymous and the number of nonsynonymous substitutions. Here I used the p-distance, which has been reported to produce reliable topologies, particularly when many sequences with short branches are analyzed (Takahashi and Nei 2000). The d̄T values obtained using the p-distance were usually smaller than those obtained using the number of synonymous substitutions. In addition, none of eS, eN, eNeg, and ePos showed a clear relationship with d̄T/2(n − 3). These observations indicate that the p-distance is preferable to the number of synonymous substitutions for inferring the tree in the SG method.
The results obtained from the analysis of E1 and E2 glycoproteins of HCV by the ML method appeared to be more or less reliable. In addition, the ML method appeared to be more sensitive than the SG methods. Actually, the rN/rS values of codon sites where positive selection was inferred only by the ML method was relatively small compared with those of other positively selected sites (data not shown). It should be noted, however, that we have to be cautious about the results obtained from the ML method, because the codon substitution model may not always hold and the LRT can be biased when the assumption is violated (Zhang 1999). In addition, it is recommended that the ML method is applied only to the codon sites with relatively large numbers of nucleotide substitutions (cS + cN), because the LRT is a large sample test. To obtain rough ideas about the cS + cN value required for producing reliable results by the ML method, I analyzed 218 nucleotide sequences of the human leukocyte antigen (HLA) gene which have been used for evaluating the original SG method and the Yang method (Suzuki and Gojobori 1999; Suzuki and Nei 2001). The amino acid sites of HLA protein can be divided into antigen recognition sites (ARSs) and non-ARSs, and it is known that most of the former sites are positively selected, whereas most of the latter are negatively selected. By the ML method, 33 sites were inferred as positively selected, of which 24 were ARSs and 9 were non-ARSs. Among the nine sites of non-ARSs, three have also been inferred as positively selected by the original SG method but six have not. Interestingly, when the cS + cN values were estimated for these codon sites by the original SG method, 18 ≤ cS + cN ≤ 47 for the former sites, whereas 8 ≤ cS + cN ≤ 16 for the latter, indicating that the latter sites were falsely inferred as positively selected by the ML method due to relatively small values of cS + cN. These results suggest that, roughly speaking, the cS + cN value should be larger than 15 for obtaining reliable results in the ML method. (The cS + cN values for positively selected sites in the E1 and E2 glycoproteins of HCV were larger than 15 [data not shown].) These observations for the ML method, together with those for the original and modified SG methods as discussed above (and for the Yang method [Suzuki and Nei 2001, 2002]), indicate that these methods are useful for detecting overdominant and frequency-dependent selection, but less so for detecting directional selection unless the sequences are derived from subpopulations or different species.
The computer programs for the modified SG method and the ML method presented in this paper are implemented in ADAPTSITE (version 1.3) (http://mep.bio.psu.edu/adaptivevol.html; http://www.cib.nig.ac.jp/dda/yossuzuk/welcome.html).
Acknowledgments
The author thanks Masatoshi Nei for his valuable suggestions and comments. This work was supported by National Institutes of Health Grant GM20293 to Masatoshi Nei.
References
- Choo Q-L, Kuo G, Ralston R, Weiner AJ, Overby LR, Bradley DW, Houghton M. Isolation of a cDNA clone derived from a blood-borne non-A, non-B hepatitis genome. Science. 1989;244:359–362. doi: 10.1126/science.2523562. [DOI] [PubMed] [Google Scholar]
- Erickson AL, Kimura Y, Igarashi S, Eichelberger J, Houghton M, Sidney J, McKinney D, Sette A, Hughes AL, Walker CM. The outcome of hepatitis C virus infection is predicted by escape mutations in epitopes targeted by cytotoxic T lymphocytes. Immunity. 2001;15:883–895. doi: 10.1016/s1074-7613(01)00245-x. [DOI] [PubMed] [Google Scholar]
- Fitch WM. Toward defining the course of evolution: minimum change for a specific tree topology. Syst Zool. 1971;20:406–416. [Google Scholar]
- Goldman N, Yang Z. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol Biol Evol. 1994;11:725–736. doi: 10.1093/oxfordjournals.molbev.a040153. [DOI] [PubMed] [Google Scholar]
- Gruner NH, Gerlach TJ, Jung M-C, Diepolder HM, Schirren CA, Schraut WW, Hoffmann R, Zachoval R, Santantonio T, Cucchiarini M, Cerny A, Pape GR. Association of hepatitis C virus-specific CD8+ T cells with viral clearance in acute hepatitis C. J Infect Dis. 2000;181:1528–1536. doi: 10.1086/315450. [DOI] [PubMed] [Google Scholar]
- Hartigan JA. Minimum mutation fits to a given tree. Biometrics. 1973;29:53–65. [Google Scholar]
- Hijikata M, Kato N, Ootsuyama Y, Nakagawa M, Ohkoshi S, Shimotohno K. Hypervariable regions in the putative glycoprotein of hepatitis C virus. Biochem Biophys Res Commun. 1991;175:220–228. doi: 10.1016/s0006-291x(05)81223-9. [DOI] [PubMed] [Google Scholar]
- Hughes AL, Nei M. Pattern of nucleotide substitution at major histocompatibility complex class I loci reveals overdominant selection. Nature. 1988;335:167–170. doi: 10.1038/335167a0. [DOI] [PubMed] [Google Scholar]
- Hughes AL, Nei M. Nucleotide substitution at major histocompatibility complex class II loci: evidence for overdominant selection. Proc Natl Acad Sci USA. 1989;86:958–962. doi: 10.1073/pnas.86.3.958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jukes TH, Cantor CR. Evolution of protein molecules. In: Munro HN, editor. Mammalian protein metabolism. Academic Press; New York: 1969. pp. 21–32. [Google Scholar]
- Kato N, Ohkoshi S, Shimotohno K. Japanese isolates of the non-A, non-B hepatitis viral genome show sequence variations from the original isolate in the USA. Proc Jpn Acad. 1989;65:219–223. [Google Scholar]
- Kato N, Hijikata M, Ootsuyama Y, Nakagawa M, Ohkoshi S, Sugimura T, Shimotohno K. Molecular cloning of the human hepatitis C virus genome from Japanese patients with non-A, non-B hepatitis. Proc Natl Acad Sci USA. 1990;87:9524–9528. doi: 10.1073/pnas.87.24.9524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M. A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. J Mol Evol. 1980;16:111–120. doi: 10.1007/BF01731581. [DOI] [PubMed] [Google Scholar]
- Lechmann M, Ihlenfeldt HG, Braunschweiger I, Giers G, Jung G, Matz B, Kaiser R, Sauerbruch T, Spengler U. T- and B-cell responses to different hepatitis C virus antigens in patients with chronic hepatitis C infection and in healthy anti-hepatitis C virus-positive blood donors without viremia. Hepatology. 1996;24:790–795. doi: 10.1002/hep.510240406. [DOI] [PubMed] [Google Scholar]
- Muse SV, Gaut BS. A likelihood approach for comparing synonymous and nonsynonymous nucleotide substitution rates, with application to the chloroplast genome. Mol Biol Evol. 1994;11:715–724. doi: 10.1093/oxfordjournals.molbev.a040152. [DOI] [PubMed] [Google Scholar]
- Nei M, Gojobori T. Simple methods for estimating the numbers of synonymous and nonsynonymous substitutions. Mol Biol Evol. 1986;3:418–426. doi: 10.1093/oxfordjournals.molbev.a040410. [DOI] [PubMed] [Google Scholar]
- Nei M, Kumar S. Molecular evolution and phylogenetics. Oxford University Press; Oxford, New York: 2000. [Google Scholar]
- Nei M, Kumar S, Takahashi K. The optimization principle in phylogenetic analysis tends to give incorrect topologies when the number of nucleotides or amino acids used is small. Proc Natl Acad Sci USA. 1998;95:12390–12397. doi: 10.1073/pnas.95.21.12390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson B, Myers G, Howard C, Brettin T, Bukh J, Gaschen B, Gojobori T, Maertens G, Mizokami M, Nainan O, Netesov S, Nishioka K, Shin-i T, Simmonds P, Smith D, Stuyver L, Weiner A. Classification, nomenclature, and database development for hepatitis C virus (HCV) and related viruses: proposals for standardization. Arch Virol. 1998;143:2493–2503. doi: 10.1007/s007050050479. [DOI] [PubMed] [Google Scholar]
- Saitou N, Nei M. The neighbor-joining method: A new method for reconstructing phylogenetic trees. Mol Biol Evol. 1987;4:406–425. doi: 10.1093/oxfordjournals.molbev.a040454. [DOI] [PubMed] [Google Scholar]
- Su C, Nguyen VK, Nei M. Adaptive evolution of variable region genes encoding an unusual type of immunoglobulin in camelids. Mol Biol Evol. 2002;19:205–215. doi: 10.1093/oxfordjournals.molbev.a004073. [DOI] [PubMed] [Google Scholar]
- Suzuki Y. Molecular evolution of pathogenic viruses. Hayama, Japan: 1999. Doctoral dissertation, Department of Genetics, School of Life Science, Graduate University for Advanced Studies. [Google Scholar]
- Suzuki Y, Gojobori T. A method for detecting positive selection at single amino acid sites. Mol Biol Evol. 1999;16:1315–1328. doi: 10.1093/oxfordjournals.molbev.a026042. [DOI] [PubMed] [Google Scholar]
- Suzuki Y, Gojobori T. Positively selected amino acid sites in the entire coding region of hepatitis C virus subtype 1b. Gene. 2001;276:83–87. doi: 10.1016/s0378-1119(01)00640-0. [DOI] [PubMed] [Google Scholar]
- Suzuki Y, Nei M. Reliabilities of parsimony-based and likelihood-based methods for detecting positive selection at single amino acid sites. Mol Biol Evol. 2001;18:2179–2185. doi: 10.1093/oxfordjournals.molbev.a003764. [DOI] [PubMed] [Google Scholar]
- Suzuki Y, Nei M. Simulation study of the reliability and robustness of the statistical methods for detecting positive selection at single amino acid sites. Mol Biol Evol. 2002;19:1865–1869. doi: 10.1093/oxfordjournals.molbev.a004010. [DOI] [PubMed] [Google Scholar]
- Suzuki Y, Gojobori T, Nei M. ADAPTSITE: Detecting natural selection at single amino acid sites. Bioinformatics. 2001;17:660–661. doi: 10.1093/bioinformatics/17.7.660. [DOI] [PubMed] [Google Scholar]
- Takahashi K, Nei M. Efficiencies of fast algorithms of phylogenetic inference under the criteria of maximum parsimony, minimum evolution, and maximum likelihood when a large number of sequences are used. Mol Biol Evol. 2000;17:1251–1258. doi: 10.1093/oxfordjournals.molbev.a026408. [DOI] [PubMed] [Google Scholar]
- Thompson JD, Higgins DG, Gibson TJ. CLUSTAL W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994;22:4673–4680. doi: 10.1093/nar/22.22.4673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner AJ, Brauer MJ, Rosenblatt J, Richman KH, Tung J, Crawford K, Bonino F, Saracco G, Choo Q-L, Houghton M, Han JH. Variable and hypervariable domains are found in the regions of HCV corresponding to the flavivirus envelope and NS1 proteins and the pestivirus envelope glycoproteins. Virology. 1991;180:842–848. doi: 10.1016/0042-6822(91)90104-j. [DOI] [PubMed] [Google Scholar]
- Weiner AJ, Geysen HM, Christopherson C, Hall JE, Mason TJ, Saracco G, Bonino F, Crawford K, Marion CD, Crawford KA, Brunetto M, Barr PJ, Miyamura T, McHutchinson J, Houghton M. Evidence for immune selection of hepatitis C virus (HCV) putative envelope glycoprotein variants: potential role in chronic HCV infections. Proc Natl Acad Sci USA. 1992;89:3468–3472. doi: 10.1073/pnas.89.8.3468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z, Nielsen R, Goldman N, Pedersen AM. Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics. 2000;155:431–449. doi: 10.1093/genetics/155.1.431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J. Performances of likelihood ratio tests of evolutionary hypotheses under inadequate substitution models. Mol Biol Evol. 1999;16:868–875. doi: 10.1093/oxfordjournals.molbev.a026171. [DOI] [PubMed] [Google Scholar]
- Zhang J, Nei M. Accuracies of ancestral amino acid sequences inferred by the parsimony, likelihood, and distance methods. J Mol Evol. 1997;44:S139–S146. doi: 10.1007/pl00000067. [DOI] [PubMed] [Google Scholar]
- Zhang J, Rosenberg HF, Nei M. Positive Darwinian selection after gene duplication in primate ribonuclease genes. Proc Natl Acad Sci USA. 1998;95:3708–3713. doi: 10.1073/pnas.95.7.3708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zibert A, Kraas W, Meisel H, Jung G, Roggendorf M. Epitope mapping of antibodies directed against hypervariable region 1 in acute self-limiting and chronic infections due to hepatitis C virus. J Virol. 1997;71:4123–4127. doi: 10.1128/jvi.71.5.4123-4127.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zibert A, Kraas W, Ross RS, Meisel H, Lechner S, Jung G, Roggendorf M. Immunodominant B-cell domains of hepatitis C virus envelope proteins E1 and E2 identified during early and late time points of infection. J Hepatol. 1999;30:177–184. doi: 10.1016/s0168-8278(99)80059-2. [DOI] [PubMed] [Google Scholar]