Structural parameters affecting the kinetics of RNA hairpin formation

Abstract

There is little experimental knowledge on the sequence dependent rate of hairpin formation in RNA. We have therefore designed RNA sequences that can fold into either of two mutually exclusive hairpins and have determined the ratio of folding of the two conformations, using structure probing. This folding ratio reflects their respective folding rates. Changing one of the two loop sequences from a purine- to a pyrimidine-rich loop did increase its folding rate, which corresponds well with similar observations in DNA hairpins. However, neither changing one of the loops from a regular non-GNRA tetra-loop into a stable GNRA tetra-loop, nor increasing the loop size from 4 to 6 nt did affect the folding rate. The folding kinetics of these RNAs have also been simulated with the program ‘Kinfold’. These simulations were in agreement with the experimental results if the additional stabilization energies for stable tetra-loops were not taken into account. Despite the high stability of the stable tetra-loops, they apparently do not affect folding kinetics of these RNA hairpins. These results show that it is possible to experimentally determine relative folding rates of hairpins and to use these data to improve the computer-assisted simulation of the folding kinetics of stem–loop structures.

INTRODUCTION

RNA chains can fold into complex secondary and tertiary structures, which often correspond to the minimum energy or equilibrium structure. Some RNAs, however, fold into long-lasting non-equilibrium conformations, which are known as metastable structures (1–8). Most of these structures are not biologically active and are thus termed misfolded (9,10). However, in a number of biological systems metastable structures exist that are actually not misfolded, but functionally important. In addition, a single RNA sequence can exhibit two catalytic activities resulting from two different structures (11).

To understand how a folding RNA chain chooses between different alternative structures it is important to know which structural, thermodynamic and kinetic parameters control the folding of the various structural elements. Today, thermodynamic parameters of most of the RNA secondary structural elements are known (12,13), whereas kinetic parameters of RNA folding are scarce (8,14–17). It has been shown that the rate-determining step of hairpin formation is dependent on cancellation of the positive loop energy by the stacking interaction between the first closing base pairs (16,18) and that local hairpin formation is favoured over long-distance structural elements, because of the spatial proximity of the opposing base pairing partners (1,15). Little is known, however, about the effects of the nucleotide sequence and the size of hairpin loops and of the nature of the closing base pairs on folding kinetics. Even less is known about the effects of bulges, internal loops and other secondary structural elements.

Despite this lack of quantitative knowledge, great progress has been made in predicting folding routes of RNA using computer simulations, based on existing thermodynamic parameters and statistical polymer physics (2,4,19–25). These predictions, however, have rarely been verified experimentally. As a result it is still difficult to estimate which of the potential hairpins in a given RNA sequence will fold predominantly and which are kinetically disfavoured. Therefore, the prediction of a correct metastable structure in a given RNA molecule, even if it is suspected to have kinetically favourable metastable hairpins, has not always been straightforward (4,6,26) (J. H. A. Nagel, J. Møller-Jensen, C. Flamm, K. J. Öistämö, J. Besnard, I. L. Hofacker, A. P. Gultyaev, M. H. de Smit, P. K. Schuster, K. Gerdes and C. W. A. Pleij, manuscript submitted).

To determine kinetic parameters experimentally, we have developed an approach in which the kinetic folding ratios of two mutually exclusive hairpins in a given RNA sequence can be measured by structure probing. Although, this approach does not allow direct measurement of the hairpin-folding rate, it enables one to determine the effects of nucleotide substitutions, deletions and insertions. In turn, this allows us to assess, which sequence elements in an RNA chain are involved in the initiation of hairpin formation and to what degree. With these results it is possible to test current theoretical assumptions and to improve the predictive power of the RNA folding simulation programs.

MATERIALS AND METHODS

5′ End ³²P labelling of RNA

The RNA fragments were synthesized by IBA NAPS GmbH. The 5′ end labelling was done in 1× One Phor All plus buffer with 0.95 U of T4 Polynucleotide Kinase (Pharmacia) and incubated for 45 min at 37°C.

Kinetic trapping of RNA fragments

The heating and rapid cooling procedure for the RNAs was done in 50 mM Na cacodylate buffer (pH 7.2). First the sample was heated at 95°C for 2 min and then immediately placed into liquid nitrogen. Subsequently, the sample was slowly melted and used in the probing experiments (27).

The acid denaturation of the RNA was done in 50 mM HCl at 0°C. Renaturation was achieved by adding 50 mM NaOH, 900 mM NaCl and 50 mM Na cacodylate buffer (pH 7.2). The pH was checked after each mixing procedure (27).

Thermodynamic equilibrium samples were obtained from kinetically trapped RNA fragments after an incubation of 30 min at 65°C, followed by slow cooling to 37°C and a final incubation of 2 h at 0°C, prior to structure probing.

Structure probing

Structure probing with RNases T1, T2 and V1 under native conditions was performed in 100 mM NaCl, 10 mM MgCl₂ and 50 mM Na cacodylate buffer (pH 7.2) in the presence of 10 µg tRNA per reaction mixture. The enzyme concentrations used were 1.25 U of RNase T1 (Promega), 0.5 U of RNase T2 (Promega) and 0.001 U of RNase V1 (Estonian Academy of Sciences) in 50 µl with incubation times of 5 and 15 min for the kinetically trapped and thermodynamic equilibrium samples. For the refolding experiments of the kinetically trapped RNAs, the RNA samples were incubated at 0°C for 0, 30, 60 and 120 min followed by a 10 min enzymatic probing incubation at 0°C. The thermodynamic equilibrium sample (∞) was used as a reference sample. Digestion with RNase T1 under denaturing conditions was done in 6 µl of 0.4% (w/v) Na citrate·2H₂O, 0.14% (w/v) citric acid, 8 M urea and 0.4% (w/v) EDTA and 10 µg tRNA was added to 3 µl of sample RNA (³²P 5′ end labelled). The mixture was pre-incubated for 15 min at 55°C. Then 1.5 µl of RNase T1 (1 U) was added to the mixture, which was incubated for a further 20 min at 55°C. The alkaline ladder was made from the tested RNA sequence in a freshly prepared 25 mM Na₂CO₃/NaHCO₃ (1:9) buffer and heated for 2 min at 95°C. All probing mixtures were loaded on a 20% polyacrylamide sequencing gel containing 8 M urea, and detection was by autoradiography and phosphor imaging. The results from four to eight independent experiments were taken to calculate the folding ratios and standard deviation of the two mutually exclusive hairpins.

RESULTS

Design of the experiment

Candidate RNA sequences were designed manually to fold into either of two mutually exclusive hairpins. These two hairpins differ in their so-called ‘nucleation points’ or hairpin starting points by having different closing base pairs or loop sequences (Table 1). In adition, differences beyond the five loop-proximal base pairs were introduced to prevent misfolding, duplex formation and to control the hairpin stability as required. The folding ratio is assumed to depend exclusively on the top of the hairpins, since the subsequent stacking interactions form approximately two orders of magnitude faster than the first closing interaction (16,28,29). Furthermore, the more distal base pairs are unlikely to be nucleation points of hairpin formation due to their unfavourable localization along the chain (14,25,29).

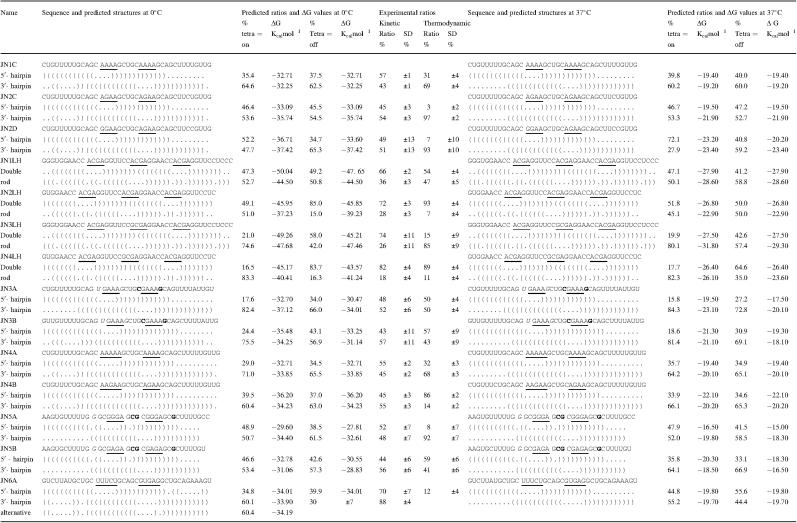
Table 1.

The predicted and experimentally determined folding ratios of the studied RNA sequences

Brackets indicate paired bases, while dots indicate unpaired residues. The underlined residues correspond with the position of the loops. The boldface and bold italic residues indicate the changes within each stem. Tetra = on or tetra = off show the simulated ratios when in- or excluding the stable tetra-loop energies, respectively. SD is the calculated standard deviation and ΔG is the calculated stability of the respective hairpin (RNA-fold).

The computer program ‘Barriers’ (2,19,28,30) was then used to analyse the folding landscape of these candidate sequences (Figure 2B). This enabled us to select those sequences having no additional significant stable hairpins and/or local energy minima in their folding landscape beyond the two desired ones. When necessary, further manual changes were introduced until the sequences met all design criteria.

The selected RNA sequences were synthesized and used in experiments where folding of the two competing hairpins from the single-stranded RNA was detected by secondary structure probing. To trap the RNA in the kinetically favoured conformation, it was denatured either by heat or by acid, followed by rapid cooling or a pH-jump to neutral pH, respectively (see Materials and Methods). Both methods gave identical results, indicating that the trapping procedure does not influence the kinetic competition between the two mutually exclusive hairpins, identical to earlier findings from our group (27).

This kinetically based competitional folding places strict experimental constraints on the design of the RNA sequences. First of all an individual RNA molecule, once folded into one of the two mutually exclusive hairpins should be prevented from refolding during the trapping and detection procedure into the competing, potentially more stable second hairpin (Figure 1A). Otherwise one would detect the thermodynamically most stable hairpin and not necessarily the kinetically favoured one. The absence of this so-called ‘thermodynamic scrambling’ of the hairpins was tested for each RNA fragment with one or both trapping methods by following the refolding for 2–3 h at 0°C. Samples were taken at different time points and probed at 0°C. In none of the designed RNAs, the refolding into the thermodynamically more stable hairpin was complete after the incubation period. This indicated that during the probing time of 5, 10 and 15 min at 0°C, no significant thermodynamic scrambling occurred.

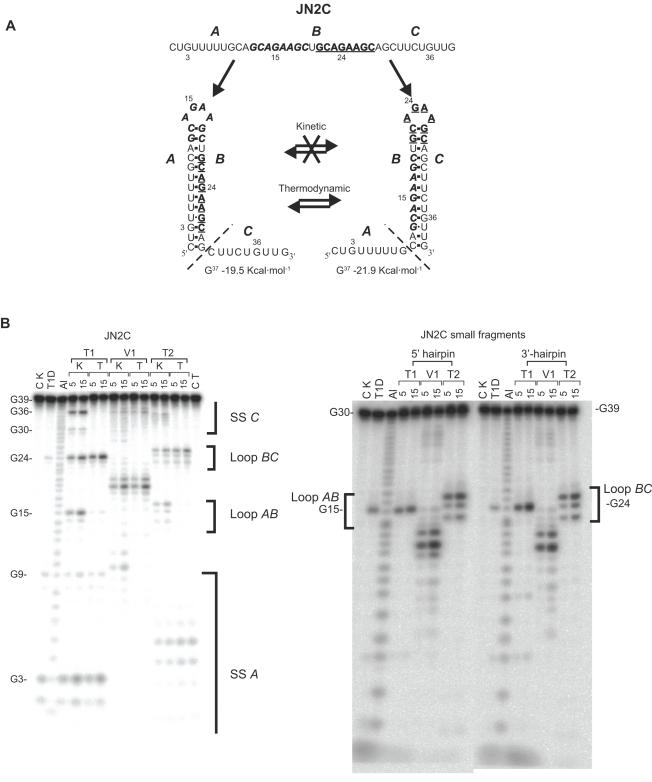
Figure 1.

Enzymatic structure probing of the JN2C and shorter JN2C-derived RNA fragments. (A) Schematic representation of the folding trajectories, in which the A nucleotides can base pair with B, resulting in the boldface/italics loop, or B with C, resulting in the boldface/underlined loop. In the kinetic experiments there should not be an interchange between the two mutually exclusive structures, while in the thermodynamic experiments they should be in equilibrium. The dashed lines delimit the size of the two smaller JN2C-derived 5′ and 3′ end hairpin fragments. ΔG values were calculated using RNA-fold (www.tbi.univie.ac.at/RNA/) (B) Structure probing of JN2C and JN2C-derived fragments. CK is the control lane (without enzyme) for the kinetic probings and CT for the thermodynamic ones. K indicates the kinetic probing experiments and T the thermodynamic ones. Al is alkaline hydrolysis, T1D is digestion with RNase T1 under denaturing conditions, T1, V1 and T2 represent digestions with RNases T1, V1 and T2 under native conditions. Probing times are 5 and 15 min. The brackets indicate the position of the hairpin loops and single-stranded regions and the letters A, B and C indicate their respective positions in (A).

Probing times of 5, 10 and 15 min were used to ensure that the enzyme concentration used would result in only a single cut in each RNA chain probed. This increase in probing time should result into a linear increase in the intensities of the probing bands observed, but should not lead to a significant decrease of the unprobed RNA fraction. For all RNA fragments this was indeed observed.

A further experimental constraint is that the two mutually exclusive hairpins should have distinct non-overlapping probing patterns. This means that the fragment lengths created by the RNases T₁ and T₂ for both the hairpin loops and single-stranded regions, should be unique and localized in a specific region in the separation gel to allow accurate determination of the folding ratios (Figures 1 and 2). This ensures that the measured intensity of a particular band can be directly correlated with its corresponding hairpin. In addition, quantitative differences in the accessibility to the RNases T₁ and T₂ of the individual unpaired nucleotides should be compensated for. This was achieved by comparing the probing efficiencies of the two mutually exclusive hairpins individually, using smaller RNA fragments harbouring only one of the two hairpins (Figure 1A and B). RNase V₁, probing paired nucleotides, was used as a control for the stem regions of the two hairpins.

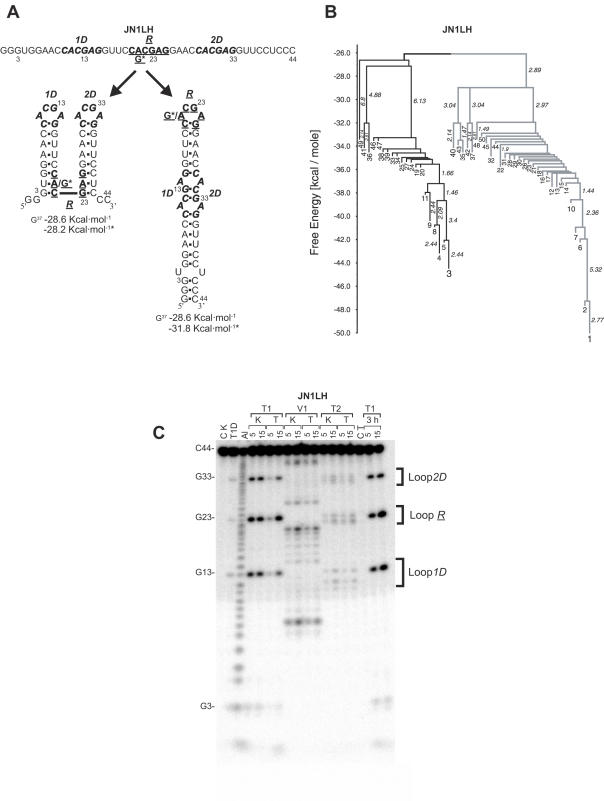
Figure 2.

Enzymatic structure probing and barrier tree of the JN1LH sequence. (A) Schematic representation of the folding trajectories. The loop sequences of the double-hairpin structure are indicated by 1D and 2D, while R represents the loop of the rod-like structure. G* is the substitution of an A residue into a G, giving the stable tetra-loop sequence in the JN3LH RNA. (B) Barrier tree computed for JN1LH at 0°C. The black and grey parts represent the barrier trees of the double-hairpin and rod-like structure, respectively. Free energy values on the left hand axis are given in kcal mol⁻¹. Numbers indicate local minima ordered according to free energies. Numbers written along vertical lines give the free energies to the next higher saddle point. (C) Structure probing of the JN1LH structure. The 3h lanes are the probing patterns of the JN1LH kinetic samples after incubation for 3 h at 0°C. For other symbols see legend to Figure 1B.

Finally, to test and to minimize duplex formation, the concentration of the RNA was varied and/or a 10 to 100-fold excess of tRNA was added prior to both kinetic trapping procedures. No significant changes were observed (data not shown).

Experimental determination of folding ratios

To test the design of the RNA fragments, first identical loops were introduced in the two mutually exclusive hairpins JN1C and JN2C, with the loop sequences GCAAAAGC and GCAGAAGC, respectively (Table 1). The folding kinetics of the two hairpins are expected to be the same, because the loops and the closing base pairs constitute identical nucleation points. The experimental kinetic ratio for the JN1C fragment suggested a slight preference for the 5′ end hairpin (Table 1). However, this is still within experimental error, because the overall reproducibility of the trapping and probing procedure is ∼5–10%.

In the thermodynamic equilibrium experiment the two hairpins were also found in similar amounts, so thermodynamic scrambling during the trapping procedure could not be excluded. With the JN2C fragment the differences in ΔG between the two hairpins was enlarged while maintaining identical loops and closing base pairs. Furthermore, the presence of a G residue in the loop enabled us to include RNase T₁ (specific for unpaired G residues) as a structure probe. The kinetic experiment again yielded equal amounts of the two hairpins, while a clear thermodynamic shift towards the more stable 3′-hairpin was observed in the thermodynamic folding experiment, as expected (Figure 1A; Table 1). These findings strongly support the validity of the experimental approach.

Effects of stable tetra-loops

In RNA so-called stable tetra-loops exist, in which an additional gain in free energy of hairpin formation is obtained by specific stacking and hydrogen bond interactions in the loop (12). The two main classes are the GNRA and YNMG tetra-loops (N can be any nucleotide, R is either A or G, M is either C or A and Y is either C or U) (31). To test the effect of a stable tetra-loop upon hairpin formation, a GCAGAAGC loop was compared against a stable GCGGAAGC (GNRA) tetra-loop (JN2D, Table 1). We expected that the hairpin with the GGAA stable tetra-loop would out-compete the AGAA loop, because it stabilized the first stacking interaction by 3 kcal/mol (13). Surprisingly, however, the hairpins folded in a equal ratio (Table 1). The experimental result indicates that the possibility of forming a GGAA tetra-loop does not accelerate folding of the corresponding hairpin.

Previous computer simulations indicated that the folding ratio of a particular structure correlates directly with its number of nucleation points (2,3). To examine the effects of multiple nucleation points and to test an additional GNRA stable tetra-loop, four more RNA sequences were designed (JN1LH, JN2LH, JN3LH and JN4LH) (Table 1). These four sequences can either fold into a two-hairpin structure without stable tetra-loops or into a single hairpin (rod-like), with (JN3LH and JN4LH) or without (JN1LH and JN2LH) the GCGA stable tetra-loop (Figure 2A).

The kinetic folding experiment of the JN1LH and JN2LH fragments showed a 1:2 folding ratio between the rod-like structure, with one nucleation point and the two-hairpin structure with two nucleation points, as predicted (Figure 2; Table 1). The fact that the folding ratio was identical for both fragments confirmed that these directly reflect folding kinetics. This despite the fact that the thermodynamically most stable conformation, at 37°C, is the rod-like structure in JN1LH, and the two-hairpin one in JN2LH.

Remarkably, the same kinetic folding ratios were experimentally obtained for the JN3LH and JN4LH sequences, in which a GCGA stable tetra-loop was introduced into the rod-like structure. This confirms the results obtained with the JN2D sequence (Table 1), showing that the extra thermodynamic stability of the stable tetra-loops does not influence their folding kinetics.

Effects of stem and loop sequences

Next, we addressed the possible role of several primary and secondary structure elements like closing base pairs, loop sizes, loop sequences and internal loops, on hairpin-folding kinetics. With JN3A and JN3B (GUGAAAGC versus GCGAAAGC) the influence of the close stacking interaction on the kinetic folding was examined. We expected that a U–G closing base pair would form less efficiently than a C–G closing pair, due to its smaller ΔG contribution upon stacking. Similarly, we expected that the change in loop size from four to five bases in JN4A (GCAAAAAGC versus GCAAAAGC) and in JN4B (GCAAGAAGC versus GCAGAAGC) would result in slower folding rates. The kinetic probing experiment, however, showed equal ratios for both the closing base pair and loop size RNA sets (Table 1), indicating that the folding kinetics were unaffected.

The importance of the nucleotide composition of a loop for the rate of hairpin formation has been shown in DNA hairpins (32–34). In DNA folding, pyrimidine-rich loops (T-loops) fold faster than A-rich-loops, because in the latter case single-stranded A stacks have to be disrupted prior to folding. A similar effect is expected for RNA hairpin formation. Therefore, the JN6A sequence was designed, containing a 5′ end hairpin loop with only pyrimidines and a mutually exclusive 3′ end purine-rich hairpin loop (Table 1). The pyrimidine-rich 5′ end hairpin motif was derived from the kinetically favourable 5′ end metastable hairpin I of the hok mRNA (J. H. A. Nagel, J. Møller-Jensen, C. Flamm, K. J. Öistämö, J. Besnard, I. L. Hofacker, A. P. Gultyaev, M. H. de Smit, P. K. Schuster, K. Gerdes and C. W. A. Pleij, manuscript submitted) (35,36). The experimental results show that this pyrimidine-rich loop is indeed the faster folder, as it partially out-competed the purine-rich loop of the 3′-hairpin (Table 1).

The potential kinetic effect of an internal loop on hairpin formation rates was tested with the JN5A and JN5B sequences. In these RNAs the 5′ end hairpin contains a GG mismatch after the first two closing base pairs, while the mutually exclusive 3′ end hairpin forms an uninterrupted stem. The experimentally determined ratio is approximately equal in both the JN5A and JN5B RNA fragments. This was unexpected, because the interrupted base pair zippering in the 5′ hairpin was presumed to slow down its folding. Apparently, zippering through and beyond the internal loop is still faster than disruption of the initial closing interactions.

Folding simulations

To directly compare theoretical predictions and experiments, we extracted predicted folding ratios from folding simulations using the recently developed program ‘Kinfold’ from the Vienna RNA package (www.tbi.univie.ac.at/TBI/software.html). This comparison is important, because thus far, little direct experimental verification existed to justify the currently used kinetic parameters. The Kinfold program performs stochastic simulations of folding and refolding behaviour of RNA sequences [see Refs (2,28) for details]. The program models the process of RNA folding as a Markov Chain at single base pair resolution via a Monte Carlo process, meaning that the smallest change or move set in the simulation is an addition or disruption of a single base pair. To calculate the folding rates between two neighbouring states the Metropolis rule was used. Each simulation for an RNA sequence was started in the open chain conformation (i.e. with no base pairs present) and ran until one of the two stable states was reached. At least 2000 such trajectories were computed for each designed molecule to get an accurate estimate of the folding ratio.

The program ‘Barriers’ (21,28) was used to construct the folding landscape and barrier trees for the Kinfold program, from an energy sorted list of all possible suboptimal conformations generated by the program RNAsubopt (30) (Figure 2B). To aid the calculations, the list of suboptimal conformations was limited to a predefined energy range so that those suboptimal conformations, which contributed <1% to either the folding landscape or the folding ratios were eliminated from the calculation. This is to prevent endless calculations for non-contributing conformations.

The program Barriers identifies all local minima and the energy barriers between them according to a single base pair move set. Thus, the calculated folding funnels are ideally separated by a single ‘saddle point’ (the lowest energy barrier between the two funnels). In our RNA fragments the folding ratios of the two mutually exclusive hairpins can then be calculated, provided that there are only two major nucleation points in the RNA chain, each leading to one of the two possible hairpins (Figure 2B). This turned out to be a difficult condition to fulfil, because the experimentally required high stability of the hairpins demanded relatively long sequences, thereby increasing the risk of creating multiple nucleation points.

The simulations with the ‘Kinfold’ program for our RNA sequences illustrate the difficulties encountered with this type of computer predictions. While the computations and experiments are in excellent agreement for JN2C and JN5B sequences they differ significantly for JN1C, JN4A and JN4B RNAs. This could be due to an additional hairpin observed in the calculations but not in the experiments, which creates an additional nucleation point favouring the 3′ hairpin. Theoretically this could result in the 2:1 ratio in favour of the 3′-hairpin, which was predicted for the JN1C, JN4A and JN4B fragments (Table 1).

The folding simulations initially included the additional energy for the stable tetra-loop as a favourable kinetic parameter. However, on the basis of the experimental results for the JN2D, JN3LH and JN4LH RNAs, containing GNRA tetra-loops, a subsequent simulated folding analysis was done excluding this energy as a folding parameter. This gave folding ratios, which were similar to the experimental results for the JN3LH and JN4LH sequences and improved the predicted ratios for the JN2LH, JN3B and JN5B (Table 1). However, for the JN2D and JN5A RNAs, correct prediction of the folding ratio seemed to require the tetra-loop parameter at 0°C (Table 1). For the JN2D, this could be due to the prediction of an additional hairpin favouring the 3′-hairpin when the stable tetra-loop energy was excluded.

Though, the simulation program does not take the nucleotide content of the loop into account, the predicted JN6A ratios favoured the purine-rich 3′ end loop at 0°C, in contrast with the experimental results. In addition, when the tetra-loop energies were included, it predicted an alternative stable tetra-loop and a G bulge (Table 1).

DISCUSSION

In this paper a set of RNA sequences were designed that enabled us to experimentally determine relative folding rates of two mutually exclusive RNA hairpins, by kinetic trapping and structure probing procedures. The advantage of this combination of techniques is that it is applicable to a large variety of RNA hairpins without the need to modify the RNA with, for instance, fluorescent labels. In addition, it can be used with a variety of buffers and reaction conditions. Although enzymatic structure probing was chosen here, one can in principle use chemical modifications or other detection techniques as well. The methods chosen allowed us to address a number of questions in relation to sequence specific folding kinetics of RNA hairpins, both experimentally and computationally.

The results obtained with the JN1C and 2C sequences show that after kinetic trapping of the RNA, the ratio of the two mutually exclusive hairpins can be accurately determined and that no thermodynamic scrambling or refolding takes place during the detection time of the probing experiment.

The introduction of a stable GNRA tetra-loop in one of the hairpins in the JN2D and JN3LH and JN4LH RNAs was expected to increase the folding rates of those hairpins, because of the extra thermodynamic stability of these loops. However, the experimentally determined equal (JN2D) and 2 to 1 (JN3LH and JN4LH) folding ratios clearly showed that this was not the case. Rather, the JN3LH and JN4LH RNAs showed, together with the JN1LH and JN2LH fragments, that the folding of either the rod-like or double-hairpin structure is instead determined largely by its number of nucleation points (Figure 2; Table 1).

The fact that the GNRA tetra-loops show no kinetic effects suggests that the additional stabilizing interactions in these loops form after the formation of the first stacking interaction of the stem. This is not difficult to imagine. The specific interactions within the stable tetra-loops require a precise positioning and orientation of the bases, which is not necessarily achieved rapidly. Therefore, the decision to zipper the stem or not could therefore be taken while the loop still has the stability of a regular four-membered loop. Although not tested here, the same might hold true for YNMG tetra-loops as well.

In the JN6A RNA fragment the folding of the 5′-hairpin loop with the nucleotide composition CUUUCUG is favoured kinetically over the 3′ end CGUGAGG loop. The likely reason is that the 3′-loop region is less flexible because of the rigid G and A stacks at the start of the folding process, hence the 70/30 ratio observed experimentally. The disruption of single-stranded A and G interactions requires ∼0.5 kcal·mol⁻¹ per stack broken in DNA strands (32). In DNA hairpins, poly(T) loops fold ∼5 times faster than poly(A) loops (32–34,37–39). If purine–purine stacking also slows down the formation of RNA hairpins, this could explain the consensus CUNUNUG loop sequence in the metastable 5′ end structure of the hok mRNA family (38,40), from which the CUUUCUG loop studied here, was derived. If this loop sequence is particularly prone to form a hairpin loop, then this could provide the driving force behind the rapid folding of these metastable 5′ end hairpins.

The JN5A and JN5B RNAs contain a GG mismatch in the 5′ end hairpin stem, which was presumed to favour the regular 3′ end hairpin. However, this was neither observed experimentally, nor predicted at 0°C (Table 1). Apparently, overcoming a GG mismatch in the hairpin does not result in a sufficient delay in the zippering of the remainder of the hairpin to significantly affect the overall folding rate.

The equal folding ratios between the 4 and 5 nt containing loops in the JN4A and JN4B RNAs was not expected either, because in DNA hairpins it was shown that the folding time increased with loop size. This loop size effect stems from the increased risk of misalignment of the loop resulting in formation of a closing base pair that does not allow subsequent zippering into a hairpin (41). Its effect on the folding time was estimated to be L^2.6 (L = loop length), for DNA hairpins (33). In our RNAs this would lead to an expected 30/70 folding ratio in favour of the four-membered loop, exactly as predicted by the Barriers program using a similar exponential (Table 1). However, this exponential factor L^2.6 was determined for DNA loops of 12–30 nt (33).

The equal folding ratio observed in the JN4A and JN4B RNAs can be explained by the energy cost of bending an RNA chain. In DNA hairpins it decreases by 1/L (34), potentially favouring 5 over 4 nt loops. It could thus be that the lack of flexibility of a 4 nt loop counteracts the favourable effect of shorter loop lengths, especially for loops containing A and G residues.

Changing the closing base pair from a C–G to a U–G was expected to disfavour the formation rate of the U–G containing hairpin, because the C–G pair should be a more stable starting interaction and because the formation of the first stacking interaction is believed to be the rate limiting step in the folding of a hairpin (41). Unexpectedly, this was not observed in the JN3A and JN3B RNAs, which showed an approximately equal folding ratio for both hairpins. This seems to suggest that it is the rate of formation of the first closing base pair that is important rather than its thermodynamic stability, presumably because after this initial closing of the loop a subsequent efficient zippering of additional base pairs of the stem takes place. If this is the case then it also provides an alternative explanation for the absence of a kinetic effect of the stable tetra-loops on hairpin formation.

More in line with expectations is that the stability of the closing base pair does play a role. Then it is likely that not the U–G pair but the subsequent G–C pair acts as the closing base pair, forming a six-membered loop instead of a 4 nt one. This 6 nt loop should then fold with the same rate as the four-membered one of the C–G hairpin. Several observations are in favour of this explanation. The first one is that the 4, 5 and 6 nt loops have nearly identical ΔS contributions (www.bioinfo.rpi.edu/~zukerm/rna/energy/), which is one of the barriers that needs to be overcome in hairpin formation (42,43). Second, equal folding ratios were also obtained for the folding of the 5 versus 4 nt loops in JN4A and JN4B. Third, the increased flexibility of the loop could compensate for the negative effects of the two extra nucleotides.

The computer predictions at 0 and 37°C with the Barriers program were in reasonable agreement with the experimentally determined folding ratios when the additional tetra-loop energies were excluded as a folding parameter. This effect was most striking for the JN3B and JN4LH sequences (Table 1). Some of the remaining differences between the simulated and experimentally observed folding ratios could be related to the roughness of computational folding landscapes, making it difficult to calculate the correct folding ratio of the two major competing structures. However, the similarities between the simulated and experimental folding ratios showed the validity of the simulation approach, while indicating that not all thermodynamic parameters exert a kinetic effect. This emphasizes the need to experimentally determine additional kinetic parameters, to allow more realistic kinetic simulation of RNA folding landscapes. For instance, the kinetic effects of pyrimidine- and purine-rich loop sequences shown by the JN6A RNA may be incorporated into the Barriers program.

Thus far, little experimental work has been presented on kinetic folding parameters of RNA hairpins (16), despite growing interest in hairpin formation in DNA (32,34,37–39). The experimental results presented here give a tentative insight in the parameters that determine the folding rate of an RNA hairpin. We also showed that the current folding program ‘Barriers’ is capable of predicting the folding ratios of competing structures in an RNA chain, especially if the stable tetra-loop energies are not included. However, additional kinetic parameters must be included to allow more accurate predictions, such as those relating to hairpin loop size and nucleotide composition. Our experimental results show that GNRA tetra-loops do not affect the folding rate while pyrimidine-rich loops seem to enhance the folding rate, like in DNA. Such effects can be used by nature to intrinsically guide the folding of an RNA chain into its biologically active conformation and to avoid alternative or misfolded structures.