Modified Hudson–Kreitman–Aguadé Test and Two-Dimensional Evaluation of Neutrality Tests

Abstract

There are a number of polymorphism-based statistical tests of neutrality, but most of them focus on either the amount or the pattern of polymorphism. In this article, a new test called the two-dimensional (2D) test is developed. This test evaluates a pair of summary statistics in a two-dimentional field. One statistic should summarize the pattern of polymorphism, while the other could be a measure of the level of polymorphism. For the latter summary statistic, the polymorphism-divergence ratio is used following the idea of the Hudson–Kreitman–Aguadé (HKA) test. To incorporate the HKA test in the 2D test, a summary statistic-based version of the HKA test is developed such that the polymorphism–divergence ratio at a particular region of interest is examined if it is consistent with the average of those in other independent regions.

SINCE the development of the coalescent theory (Kingman 1982; Hudson 1983; Tajima 1983), a number of polymorphism-based statistical tests have been developed to examine a neutral null model (i.e., neutrality tests). With increasing intraspecific variation data in various species, these tests have been ubiquitous tools in molecular population genetic analysis (Kreitman 2000).

Neutrality tests include the following two major categories, although there are other types of tests available such as haplotype tests (Hudson et al. 1994; Fu 1996; Sabeti et al. 2002) (see Innan et al. 2005, for a recent review of haplotype tests). The first category focuses on the amount of polymorphism. Balancing selection increases the level of polymorphism because multiple alleles are likely maintained for a long time (Hudson and Kaplan 1988), while the level of polymorphism is reduced shortly after a fixation of adaptive mutation. This event is called a selective sweep because the fixation of a beneficial allele could sweep out the variation in the surrounding region of the selection target site by the hitchhiking effect (Kaplan et al. 1989). The Hudson–Kreitman–Aguadé (HKA) test (Hudson et al. 1987) focuses on this effect of selection by comparing the levels of polymorphism and divergence from an outgroup (see also Wright and Charlesworth 2004).

The second major category of neutrality tests examines whether the observed frequency spectrum of nucleotide polymorphism is consistent with the neutral expectation. Tajima (1989) has devised a simple method that compares 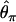and 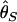, two unbiased estimators of θ, the population mutation rate. 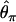is identical to the average number of pairwise nucleotide differences, which can be a direct estimator of θ (Tajima 1983). 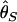is an estimator based on the number of segregating sites, S (Watterson 1975). Tajima's D is defined as 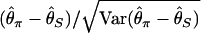, and its expectation under the standard neutral model of a constant-size population is ∼0. Balancing selection creates an excess of alleles in intermediate frequencies so that Tajima's D is likely positive, while Tajima's D tends to be negative in a region shortly after a selective sweep or under the pressure of purifying selection due to an excess of variation in low frequencies. A number of tests similar to Tajima's D have been developed (Fu and Li 1993; Simonsen et al. 1995; Fay and Wu 2000).

Thus, most neutrality tests use either the amount or the allele frequency spectrum of polymorphism. That is, those tests do not use part of the important information, which could result in a loss of power to detect selection. For example, consider a gene that experienced a recent selective sweep so that no polymorphism is observed. The HKA test could work, but the second category of tests cannot be performed when the number of segregating sites is zero. This article introduces a simple algorithm to examine both the amount and the freqeuncy spectrum of polymorphism simultaneously, which is referred to as the two-dimensional (2D) test because it examines a pair of test statistics in a two-dimensional field.

To incorporate the first category of tests into the 2D test, the HKA test is modified. The original HKA test examines the null hypothesis that the ratio of the level of polymorphism to divergence is the same for multiple regions (Hudson et al. 1987). The most common application of the HKA test is to a pair of regions. The test examines whether the ratios of polymorphism to divergence in the two regions are consistent with each other. A possible understanding of the rejection of the neutral hypothesis is that one region might be subject to selection, but it is difficult to determine which one is under selection. The application of the HKA test to more than two regions has a similar problem. Here, the HKA test is modified to test only a particular region of interest using information from other multiple reference regions as a control, which are supposed to be neutral. Therefore, one can test whether the ratio of polymorphism to divergence in a region of interest is consistent with the average of other reference regions. This design of the HKA test may be useful when polymorphism data from multiple regions are becoming available in many species.

MODIFIED HKA TEST: A FOCAL REGION VS. MULTIPLE REFERENCE REGIONS

While the original version of the HKA test uses a contingency table of polymorphism and divergence (Hudson et al. 1987), the modified version of the HKA test uses a summary statistic, r, which is the ratio of the amount of polymorphism to the level of divergence. Suppose we are interested in a particular region, for which polymorphism data of species A and a sequence from outgroup species B are available. Let L_f be the nucleotide length of this focal region. Assume that the sample size of the polymorphism data is n_f. The observed levels of polymorphism and divergence are denoted by p_f and d_f, respectively. There are also polymorphism data of species A and outgroup sequences of species B for m independent reference regions available. We want to know whether the ratio of the level of polymorphism to divergence in the focal region (r_f = p_f/d_f) is consistent with r_ave, the average r of the reference regions. This modified version of the HKA test consists of two steps:

1. The divergence time (T) between species A and B is estimated from the m reference regions.

2. The null distribution of r is obtained conditional on the estimated T, from which the statistical significance of r_f is evaluated.

For step I, a rejection-sampling method (e.g., Tavaré et al. 1997; Pritchard et al. 1999; Beaumont et al. 2002; Marjoram et al. 2003) can be useful, which produces a sample from the posterior distribution of T conditional on r_ave. Following the standard framework of the HKA test (Hudson et al. 1987), it is assumed that the present population of species A and the ancestral population have the same constant diploid effective population size, N, and that the two species split T × 2N generations ago. The population mutation and recombination rates are assumed to be θ = 4Nμ and ρ = 4Nγ, where μ and γ are the mutation and recombination rates per site per generation. It is assumed that θ and ρ are constant across loci.

Let 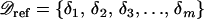be the polymorphism and divergence data for the m independent reference regions. δ_i consists of the sample size (n_i), the nucleotide length (L_i), the level of polymorphism (p_i), and the divergence from an outgroup sequence (d_i) for the ith regions. From 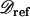, r_ave can be calculated as

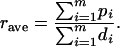(1)

Then, the posterior distribution of T conditional on r_ave is obtained by a rejection-sampling method (e.g., Marjoram et al. 2003), which is implemented basically as follows.

1. Generate a random value of T from its prior distribution.

2. Simulate polymorphism and divergence data for m independent regions using a coalescent simulation (e.g., Hudson 2002). The nucleotide length and sample size for the ith region are L_i and n_i, respectively. Estimates of θ and ρ from the m reference regions may be used in the coalescent simulation.

3. Calculate r_ave using (1) in the simulated data, which is denoted by r′_ave. Accept T if |r_ave − r′_ave| < δ, where δ is a constant; otherwise, discard T and go to step 1.

This process is continued until a sufficient number of accepted values of T are obtained. The choice of δ involves a tradeoff between computational time and accuracy (see below). The prior distribution of T can be determined according to the prior knowledge of the divergence time. One of the possible prior distributions is a uniform distribution from 0 to a sufficiently large value, T_max. T_max is set such that the acceptance probability is nearly zero for T > T_max. When a uniform distribution is used as the prior distribution, the posterior distribution is approximately proportional to the likelihood distribution. Another possible choice would be a normal distribution, which could reduce the computational effort. The mean and variance of the normal distribution could be determined according to the observed distribution of r across the reference regions. For example, T can be roughly estimated as 1/r − 1 for each reference region. Then, the mean and variance of the estimated T may be plugged in the prior distribution. Although this is a biased estimate, it might serve as an efficient prior distribution for T. The posterior distribution would be much narrower than the prior distribution because the acceptance of T is based on r_ave.

The modified HKA test uses this posterior distribution of T to determine the null distribution of r_f in step II. In practice, a coalescent simulation under the standard framework of the HKA test (see above) is performed, in which T is a randomly chosen value from the list of the accepted T in step I. From this simulation, the null distribution of r_f is obtained conditional on r_ave, making it possible to test whether r_f is consistent with the average of the reference regions.

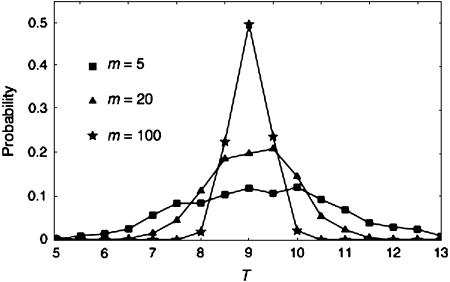
This process of the modified HKA test is demonstrated under a simple condition: all reference regions have the same sample sizes and nucleotide lengths, and the average r in the reference regions is r_ave = 0.1. θ = ρ = 0.01, n = 50, and L = 1 kb are assumed for all reference regions. To investigate the effect of m on the posterior distribution of T, m = 3, 5, 10, 20, 50, and 100 are considered. For step I, the prior distribution of T is set to a uniform distribution from 0 to 30, and the average number of pairwise nucleotide differences, π_i, is used as a measure of the level of polymorphism, p_i. δ is set to 0.01 because preliminary simulations demonstrated that δ = 0.01 is sufficiently small so that δ < 0.01 only slightly improved the accuracy. Polymorphism and divergence are simulated using the “ms” software (Hudson 2002). It is found that the variance of the estimate of T decreases as m increases, making the posterior distribution of T narrower. To visualize this effect, Figure 1 shows the three posterior distributions of T (m = 5, 20, and 100). Almost the same results are obtained for (n, L) = (20, 1 kb), (20, 5 kb), and (50, 1 kb) (results not shown).

Figure 1.—

The posterior distributions of T from m reference regions when r_ave = 0.1. n = 50 and θ = ρ = 0.01 and L = 1 kb are assumed.

The computation time for step I increases with m. However, if m is sufficiently large, the posterior distribution of T can be approximately obtained by a bootstrap method (Efron 1982). That is, choose a random set of m regions with replacement and calculate r_ave, from which an estimate of T is approximately given by 1/r_ave − 1. Although this estimate is biased as mentioned above, the bias is negligible when m is very large. Repeating this process produces an approximate posterior distribution of T in significantly less computational time.

As the null distribution of r_f is conditional on the posterior distribution of T, it is expected that more reliable estimates of T (i.e., narrower posterior distribution of T) could make the test more accurate and powerful. This effect of the posterior distribution of T on the power of the modified HKA test is investigated by coalescent simulations. θ = ρ = 0.01 is assumed for the focal region, as well as for the reference regions. It is also assumed that n and L for the focal region are the same as those for the reference regions. The null distribution of r for the focal region (r_f) for each parameter set is determined as described above. Then, the effect of m on the power to detect selection is investigated for two modes of selection: biallelic symmetric balancing selection and recent selective sweep.

The power is evaluated by simulating a number of patterns of polymorphism under selection models. For balancing selection, the “sarg” software (Nordborg and Innan 2003) is used. The backward mutation rate between two alleles is set to be α = 0.01 and 0.02 (for details, see Nordborg and Innan 2003), which determines the expectation of the age of the alleles. Table 1 summarizes the results, where the power is measured as the number of replications of simulation that reject the null neutral model at the 5% level. As expected, the power to reject the null model increases with increasing m, the number of reference regions. It seems that the power is nearly saturated for large m. The results for the two sample sizes (n = 20 and 50) are similar. The power is higher for the smaller region (1 kb) because the signature of balancing selection does not likely extend far from the target site (Hudson and Kaplan 1988; Schierup et al. 2001; Navarro and Barton 2002; Nordborg and Innan 2003).

TABLE 1.

Power of the modified HKA test with m reference regions

	L = 1 kb						L = 5 kb
Selectiona\m	3	5	10	20	50	100	3	5	10	20	50	100
n = 20
BS (α = 0.01)	4501	5208	5759	6189	6068	6301	1704	2292	2372	2440	2664	2692
BS (α = 0.02)	3751	4500	4958	5311	5122	5472	1459	1944	2050	2118	2261	2331
SW1 (τ = 0)	8798	8937	9029	9103	9151	9136	8168	8204	8339	8471	8547	8441
SW1 (τ = 0.1)	7805	8069	8253	8316	8419	8398	7388	7443	7569	7765	7826	7747
SW1 (τ = 0.2)	6298	6557	6846	6935	7158	7129	6531	6530	6730	6918	6972	6861
SW1 (τ = 0.5)	2383	2521	2651	2559	2702	2612	3968	3905	4016	4321	4288	4148
SW2 (τ = 0)	9967	9970	9977	9980	9984	9978	9996	9994	9995	9997	9997	9998
SW2 (τ = 0.1)	9839	9866	9892	9909	9907	9907	9956	9963	9972	9982	9978	9982
SW2 (τ = 0.2)	9228	9423	9567	9617	9682	9676	9879	9896	9918	9930	9927	9926
SW2 (τ = 0.5)	4219	4500	4732	4742	4966	4878	8818	9010	9169	9286	9313	9292
n = 50
BS (α = 0.01)	4453	5247	5338	5996	6079	6180	1756	1985	2272	2744	2676	2989
BS (α = 0.02)	3727	4455	4572	5223	5248	5395	1487	1789	1935	2355	2277	2549
SW1 (τ = 0)	9070	9219	9338	9324	9357	9378	8192	8376	8552	8692	8678	8730
SW1 (τ = 0.1)	8139	8359	8608	8566	8705	8755	7404	7684	7980	7996	7962	8100
SW1 (τ = 0.2)	6801	7113	7450	7377	7681	7673	6562	6872	7124	7280	7166	7366
SW1 (τ = 0.5)	2790	2880	3101	2911	3134	3096	3898	4182	4320	4556	4380	4642
SW2 (τ = 0)	9975	9973	9983	9980	9984	9987	9994	9994	9994	9994	9992	9998
SW2 (τ = 0.1)	9906	9921	9942	9940	9954	9954	9964	9978	9990	9994	9990	9988
SW2 (τ = 0.2)	9466	9639	9752	9731	9803	9811	9924	9944	9960	9956	9958	9968
SW2 (τ = 0.5)	4762	4915	5370	5119	5474	5539	8926	9206	9348	9478	9434	9474

The power of the modified HKA test given m is shown as the numbers of replications of coalescent simulations that reject the null hypothesis. The total number of replications for each parameter set is 10,000, except that 5000 replications of simulation are performed for n = 50 and L = 5 kb and the numbers are doubled.

^aThe mode of selection with the selection parameter in parentheses. BS, balancing selection with the backward mutation rate at the selection target site (α). SW1 and SW2, selective sweep with 2Ns = 100 and 1000, respectively. τ, the time to the sweep event in units of 2N generations, is in parentheses.

For recent selective sweeps, patterns of polymorphism are simulated by using the “sw” software (Kim and Stephan 2002). The parameters to determine the selection intensity (2Ns) are assumed to be 100 and 1000 (for details, see Kim and Stephan 2002). τ is the time to the completion of the selective sweep in units of 2N generations. The results are similar to those of balancing selection: the power increases with increasing m (Table 1). When 2Ns = 1000, the power is higher for the wider region (5 kb) because the signature of a strong selective sweep extends much longer than that of balancing selection, although the relationship between the power and the region length may be complicated when selection is relatively weak (Kaplan et al. 1989; Braverman et al. 1995; Kim and Stephan 2002; Przeworski 2002).

2D TEST

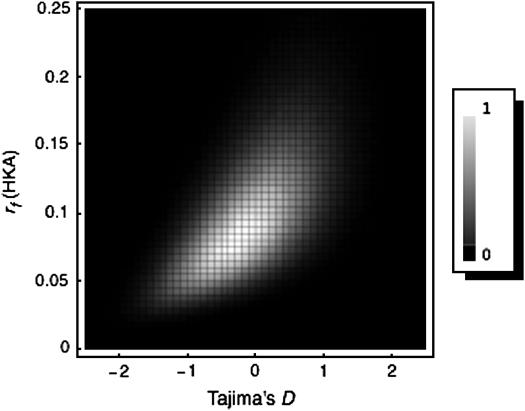
The modified HKA test using a summary statistic r is ready to be incorporated in the 2D test. The 2D test requires another summary statistic, which should use information that the HKA test does not use, such as Tajima's D (Tajima 1989) and Fu and Li's D* (Fu and Li 1993). The basic idea is that a pair of summary statistics is evaluated in a two-dimensional field. As an example, the two-dimensional density distribution of Tajima's D and r (r_f) is considered when θ = ρ = 0.01, n = 50, and L = 1 kb. For reference regions, it is assumed that m = 5, n = 50, and L = 1 kb. Suppose r_ave = 0.1; therefore, the posterior distribution of T is that shown with solid squares in Figure 1. Under the standard HKA model of a constant population size, the two-dimensional density distribution of Tajima's D and r is obtained from 10⁶ replications of a coalescent simulation (Figure 2). In the simulation, the posterior distribution of T is incorporated in the same way as the modified HKA test: in each replication, one of the accepted T is randomly picked up.

Figure 2.—

The two-dimensional density distribution of Tajima's D and r_f. The density is scaled between 0 and 1, where 1 represents ∼8000 counts of 10⁶ replications.

From the two-dimensional distribution of D and r, the 95% confidence region can be determined as follows. The number of replications of simulation is denoted by U. The simulation results (U = 10⁶ pairs of D and r) are binned into two-dimensional grids. Let a and b be the grid sizes for D and r, respectively. For this example, a and b are set to be 0.01 and 0.001. This binned two-dimensional density distribution is denoted by G(x, y), which represents the number of pairs of D and r in the grid x − a/2 < D ≤ x + a/2 and y − b/2 < r ≤ y + b/2.

Then, the 95% confidence region of D and r may be defined as the region with

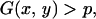(2)

where p is defined such that p satisfies

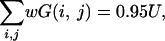(3)

and

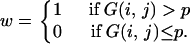(4)

Note that this method produces a somewhat discrete confidence region unless the number of replications of a coalescent simulation is extremely large. Therefore, in practice, it is recommended that G(x, y) is first smoothed, which is denoted by G′(x, y). For example, G′(x, y) could be the average over (2x_s + 1) × (2y_s + 1) neighbor grids:

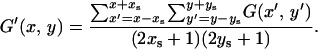(5)

Then, the 95% confidence region may be approximately obtained from (2)–(4) by replacing G(x, y) with G′(x, y). However, this method with a smoothed distribution may sometimes produce a biased confidence region when x_s and y_s are not very small. This bias may be corrected if the shape of the 95% confidence region is determined by G′(x, y) and the bias is adjusted by using G(x, y). That is, the 95% confidence region is approximately given as the region with G′(x, y) > p′, where p′ satisfies

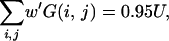(6)

and

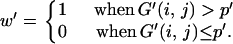(7)

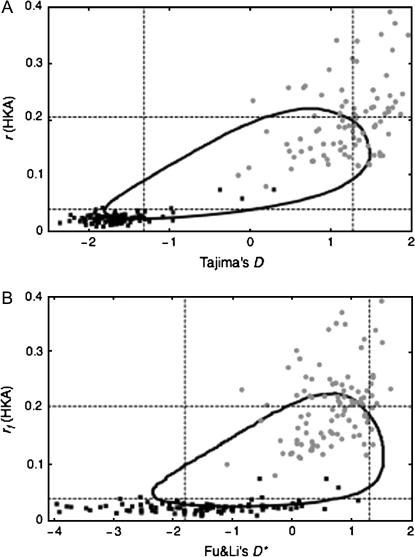
A C-program to determine the 95% confidence region is available on request. This procedure with x_s = y_s = 5 is applied to the distribution in Figure 2, and the obtained 95% confidence region is shown in Figure 3A.

Figure 3.—

The 95% confidence regions of the 2D tests when n = 50, θ = ρ = 0.01, and L = 1 kb. (A) Tajima's D vs. r_f. The 95% confidence intervals of D and r_f are the intervals between the vertical and horizontal dashed lines, respectively. The shaded circles and solid squares represent simulated pairs of D and r_f in a region under balancing selection (α = 0.01) and recent selective sweep (2Ns = 1000 and τ = 0.2), respectively. (B) Fu and Li's D* vs. r_f.

The effect of selection on D and r is also visually demonstrated in Figure 3A. The shaded circles and solid squares represent simulated pairs of D and r in a region under balancing selection (α = 0.01) and after a recent selective sweep (2Ns = 1000 and τ = 0.2), respectively. Most shaded circles are in a region of high D and r, while the solid squares make a cluster in a region of low values of D and r. In addition to Tajima's D, it is possible to use other summary statistics such as Fu and Li's D* (Figure 3B).

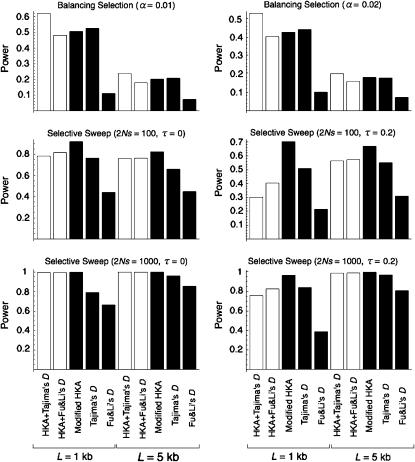
The power of the two 2D tests (r vs. Tajima's D and Fu and Li's D*) is quantitatively evaluated by coalescent simulations as described above. For balancing selection, it is demonstrated that the power of the 2D tests is generally higher than that of the three single tests (modified HKA, Tajima's D, and Fu and Li's D*) (Figure 4) and that the 2D test with r and Tajima's D may be the most powerful. For a selective sweep, the modified HKA test may be the most powerful. The 2D tests are not as powerful as the modified HKA test especially when L is short, probably because the 2D test might share the weakness of Tajima's D and Fu and Li's D* tests, that is, low power when the number of segregating sites is small.

Figure 4.—

Power of the 2D tests (open bars) compared with single tests (solid bars).

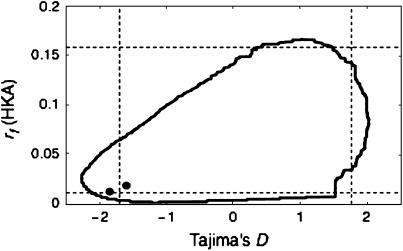
The 2D test with Tajima's D and r is applied to the GD2-A and GD2-B genes in Arabidopsis thaliana. It is considered that these two genes were duplicated recently. Moore and Purugganan (2003) showed that the levels of polymorphism in these duplicated genes are generally lower than those in six single-copy loci, suggesting the fixation processes of duplicated genes might have occurred in a short time, likely by adaptive selection. Here, these six single-copy loci are used as reference regions and the 2D test is applied to each of the duplicated genes. Note that interlocus gene conversion might be active in young duplicated genes, which could elevate the level of polymorphism (Innan 2003). However, because the maximum-parsimony haplotype network of this pair of genes exhibits no evidence for gene conversion (see Figure 3B of Moore and Purugganan 2003), the standard coalescent model for a single-copy gene is employed (see Innan 2003 for a coalescent simulation of duplicated genes). First, the posterior distribution of T is obtained from the six reference genes assuming θ = 0.02, which is roughly in agreement with the average of estimates of θ over the reference genes. It is important to note that the regions of interest (i.e., GD2-A and GD2-B) should not be included in the estimation of θ. The population recombination parameter is assumed to be 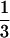× θ according to Hagenblad and Nordborg (2002). Then, the 2D test is performed for the focal regions (L ≈ 500 bp) and the result is shown in Figure 5. The 95% confidence region is smoothed with x_s = y_s = 5. The two observed pairs of D and r are within the 95% confidence region, although they are close to the 95% boundary.

Figure 5.—

Application of the 2D test with Tajima's D and r_f to the GD2-A and GD2-B genes in A. thaliana. The observed values are shown by the two solid circles together with the 95% confidence regions.

Note that the boundary of the 95% confidence region is not as smooth as those in Figure 3 because of the low θL used to determine the 2D null distribution. Finite numbers of polymorphic sites and sampled sequences make the distributions of D and r_f somewhat discrete, and this effect may not be negligible when θL and n are not sufficiently large, suggesting some limitation of the application of the 2D test to data in a short region.

DISCUSSION

The HKA test (Hudson et al. 1987) examines the null hypothesis that the polymorphism–divergence ratio is constant across regions. When neutrality is rejected, however, the test does not determine which region is likely under selection. This article introduces a new design of the HKA test such that it tests whether the polymorphism–divergence ratio in a region of interest (r_f) is consistent with the average over multiple reference regions (r_ave). This design of the modified HKA test may be useful when polymorphism data from multiple regions are becoming available in many species. Coalescent simulations show that the power of the test increases with increasing the number of reference regions (see Table 1).

There are a number of polymorphism-based statistical tests of neutrality, but most of them focus on either the amount or the pattern (e.g., allele frequency spectrum) of polymorphism. Because selection affects both, it may be more powerful to detect selection if information from both is used. This article introduces the 2D test, which evaluates a pair of statistics that summarize the amount and the pattern of polymorphism in a two-dimensional field. Following the original idea of the HKA test (Hudson et al. 1987), the polymorphism–divergence ratio is used for the one that summarizes the amount of polymorphism. There might be several candidates for a statistic that summarizes the pattern of polymorphism such as Tajima's D (Tajima 1989) and Fu and Li's D* (Fu and Li 1993). As shown in Figure 4, the 2D tests are generally more powerful than the commonly used single tests for detecting balancing selection, while the modified HKA may be more powerful than the 2D tests for detecting selective sweeps.

Using the 2D test might be one of the solutions to a multiple-testing problem. Suppose that two statistical tests of neutrality (e.g., the HKA and Tajima's D tests) are applied to a single-polymorphism data set and that one rejects neutrality but the other does not. As these two tests are not independent because they are applied to the same data, it may be difficult to evaluate the joint result of the two tests. For the 2D test, such a problem could be somewhat relaxed although similar problems could arise when more than two tests are used. It may be possible to evaluate more than two summary statistics in a multidimensional field, but the computational effort would be huge.

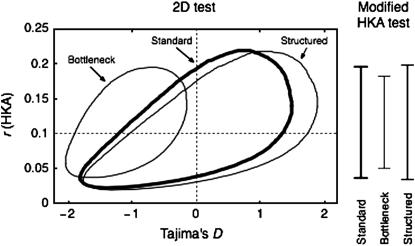
There are many difficulties in testing neutrality from polymorphism data (e.g., Kreitman 2000; Nielsen 2005) and the 2D and modified HKA tests are not exceptions. The most serious one could be that demography also affects the amount and the pattern of polymorphism. In other words, the effects of selection and demography are confounded. To demonstrate the effect of demography, the 95% confidence region of the 2D test is investigated under two demographic models, recent expansion following a bottleneck event and structured population. The demographic parameters are adjusted such that the expectation of r ∼ 0.1. In the bottleneck-expansion model, in which the expectation of Tajima's D is negative, the 95% confidence region shifts left (Figure 6). On the other hand, the 95% confidence region shifts right in the structured population, in which Tajima's D tends to be positive. Demography also plays an important role to determine the variance of the coalescent time. This directly affects the 95% confidence interval of the modified HKA test as shown in Figure 6. In the bottleneck-expansion model, in which the variance of the coalescent time is smaller than that in the standard constant-size population model, the 95% confidence region is narrower, while in the structured population model, the 95% confidence region is (slightly) wider because of large variance of the coalescent time. A similar effect is also seen in the 95% confidence regions of the 2D test (Figure 6).

Figure 6.—

The effect of demography on the 95% confidence region and interval of the 2D and modified HKA tests, respectively.

To evaluate the effect of selection alone, coalescent simulations to determine the null distribution of a test statistic should be carried out under a demographic model that is consistent with the history of the population (e.g., Innan and Stephan 2000), rather than using the standard constant-size population model. Reference regions required by the two tests are useful to obtain information on the demographic history of the population (e.g., Weiss and von Haeseler 1998; Pritchard et al. 2000; Wakeley et al. 2001; Adams and Hudson 2004).

In a similar sense, one of the advantages of the 2D and the modified HKA tests is that the null distribution is determined with θ and ρ, which could be estimated from the reference regions. This strategy works as long as θ and ρ are constant across the genome. It is obvious that more reference regions provide better estimates with low variances and consequently better statistical results. See Wall and Hudson (2001) and Innan et al. (2005) for the effect of the uncertainty about θ and ρ on neutrality tests, especially when these parameters are estimated from the region to which neutrality tests are applied. In practice, however, the mutation and recombination rates might be very difficult to estimate even with large amounts of polymorphism data, because they are not constant across the chromosome (Andolfatto 2001; Daly et al. 2001; Jeffreys et al. 2001; Crawford et al. 2004; McVean et al. 2004). Other independent information could be helpful, such as recombination rate estimates based on physical maps.

Very important caveats must be taken into consideration when applying the 2D and modified HKA tests to data. First, reference regions have to be a random independent sample from the genome. Currently, polymorphism data for multiple regions are being accumulated in several model species such as humans (Hinds et al. 2005; International HapMap Consortium 2005), Drosophila melanogaster (Glinka et al. 2003), and A. thaliana (Nordborg et al. 2005), and the genome projects of their close relatives are underway. Such genomewide polymorphism data are suitable for reference regions. Although there might be ascertainment bias due to nonrandom sampling of investigated individuals and/or regions (especially in genotyping data in humans), simple bias may be corrected as long as the sampling strategy is known (e.g., Nielsen and Signorovitch 2003). The 2D and modified HKA tests work best for such model species for which genomewide data of polymorphism and divergence are available. Once researchers find a region of their special interest, the 2D and modified HKA tests can be readily applied to the region of interest using the available genomewide polymorphism data as the reference regions. The genomewide polymorphism data are also suitable for estimating demographic parameters and mutation and recombination rates, which can be incorporated to determine the null distributions of the two tests.

A more important caveat is the choice of the focal region, which has to be selected without any prior knowledge of polymorphism. That is, the focal region should be chosen on the basis of information independent of polymorphism such as phenotypes. It is not appropriate to choose one region from a multilocus polymorphism data set as the focal region after looking at its pattern of polymorphism. Suppose that in such a multilocus data set, one locus seems unusual in some way (e.g., very high level of polymorphism). If this “unusual” locus is used as the focal region and the rest are used for the reference regions, then it is not surprising that the P-value for the focal region is very low. In other words, this P-value for the focal region is not the rejection probability of neutrality because of the prior knowledge of polymorphism (i.e., ascertainment bias in the choice of the focal region).

Then, can the 2D and modified HKA tests be applied to such a multilocus polymorphism data set? I recommend the following methods:

1. The focal and reference regions are chosen before producing or looking at the polymorphism data. This strategy is fair, but may not agree with the purpose of multilocus polymorphism data, that is, to look for outliers with unusual patterns of polymorphism, which could be candidate regions for selection. In such a case, the second approach should be used.

2. All regions are used as the reference regions, and the P-value is determined for each region. The obtained P-values can be used as a measure of the “unusualness” (but cannot be considered as the rejection probabilities of neutrality as mentioned above). To understand how unusual they are statistically, the q-values (Storey and Tibshirani 2003) could be suitable, which is a modified version of the false discovery rate (Benjamini and Hochberg 1995). The q-value, which can be computed from the obtained list of the P-values, represents the likelihood for a significant test to be false positive; therefore, we can measure the relative responsibilities of selection to the unusualness.