Abstract
Recombination occurs through both homologous crossing over and homologous gene conversion during meiosis. The contribution of recombination relative to mutation is expected to be dramatically reduced in inbreeding organisms. We report coalescent-based estimates of the recombination parameter (ρ) relative to estimates of the mutation parameter (θ) for 18 genes from the highly self-fertilizing grass, wild barley, Hordeum vulgare ssp. spontaneum. Estimates of ρ/θ are much greater than expected, with a mean 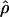 /
/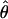 ≈ 1.5, similar to estimates from outcrossing species. We also estimate
≈ 1.5, similar to estimates from outcrossing species. We also estimate 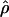 with and without the contribution of gene conversion. Genotyping errors can mimic the effect of gene conversion, upwardly biasing estimates of the role of conversion. Thus we report a novel method for identifying genotyping errors in nucleotide sequence data sets. We show that there is evidence for gene conversion in many large nucleotide sequence data sets including our data that have been purged of all detectable sequencing errors and in data sets from Drosophila melanogaster, D. simulans, and Zea mays. In total, 13 of 27 loci show evidence of gene conversion. For these loci, gene conversion is estimated to contribute an average of twice as much as crossing over to total recombination.
with and without the contribution of gene conversion. Genotyping errors can mimic the effect of gene conversion, upwardly biasing estimates of the role of conversion. Thus we report a novel method for identifying genotyping errors in nucleotide sequence data sets. We show that there is evidence for gene conversion in many large nucleotide sequence data sets including our data that have been purged of all detectable sequencing errors and in data sets from Drosophila melanogaster, D. simulans, and Zea mays. In total, 13 of 27 loci show evidence of gene conversion. For these loci, gene conversion is estimated to contribute an average of twice as much as crossing over to total recombination.
THERE are two sources of genetic diversity, mutation and recombination. Mutation, broadly defined here as novel heritable change in nucleotide state, introduces new variants while recombination reassorts the variants along a chromosome into novel combinations or haplotypes. Recombination can occur through both homologous crossover and homologous (intralocus) gene conversion, processes that occur as part of meiosis in diploid (or higher ploidy) organisms (Wiuf and Hein 2000). Under the Holliday junction model (Holliday 1964), homologous gene conversion is thought to occur when only a short tract of the alternate chromosome (usually a few hundred base pairs) is incorporated during meiotic exchange (e.g., Stahl 1994).
Inbreeding dramatically reduces the role of recombination. Recurrent inbreeding can rapidly increase homozygosity; the recombination process continues to exchange chromosomal segments during gamete formation but with little effective recombination of mutations. Thus the primary impact of inbreeding is expected to be a reduction of the contribution of recombination, relative to mutation, to total genetic diversity.
Under coalescent theory and assuming a standard neutral model, the impact of inbreeding can be measured as a reduction in the ratio of the recombination parameter ρ to the mutation parameter θ, i.e., ρ/θ (where ρ = 4Ner and θ = 4Neμ and where Ne is the effective population size, r is the rate of recombination, and μ is the rate of mutation) (symbols used are listed in Table 1). It is predicted that both ρ and θ are reduced by inbreeding, but the impact on recombination is expected to be much greater (Nordborg 2000). Nordborg (2000) showed that ρ is predicted to be reduced under partial self-fertilization based on the relationship ρs = ρ(1 − s), where s is the selfing rate; θ will be affected as θs = θ/(1 + (s/(2 − s))). As inbreeding approaches maximal values, i.e., 98–99%, the value of ρ is reduced by 40- to 50-fold, while θ is reduced by only 2-fold relative to that expected under outcrossing.
TABLE 1.
Symbols and abbreviations used
| ARG | Ancestral recombination graph |
| f | The relative contribution of gene conversion vs. crossing over, f = ρg/ρc |
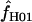 |
A composite-likelihood estimate of f (Hudson 2001) |
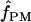 |
A pattern-matching-based estimate of f (cf. Padhukasahasram et al. 2004) |
| h | Observed number of haplotypes |
| l | Locus length |
| L | Tract length |
| LD | Linkage disequilibrium |
| LPAC | The PAC likelihood function (Li and Stephens 2003) |
| PAC | The product of approximate conditionals (Li and Stephens 2003) |
| μ | The per generation rate of mutation |
| n | Number of sampled chromosomes |
| r | The per generation rate of recombination |
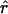 Lamarc Lamarc
|
An estimate of the per generation rate of recombination (Kuhner et al. 2000) |
| Rh | An estimate of the number of recombination events at a locus (Myers and Griffiths 2003) |
| Rl | An estimate of the number of recombination events at a locus (Song et al. 2005) |
| Rm | An estimate of the number of recombination events at a locus (Hudson and Kaplan 1985) |
| Rs | An estimate of the number of recombination events at a locus (Myers and Griffiths 2003) |
| Ru | An estimate of the number of recombination events at a locus (Song et al. 2005) |
| ρ | The population recombination parameter, 4Ner |
| ρc | The population recombination parameter due to crossover |
| ρg | The population recombination parameter due to gene conversion |
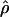 FD02 FD02
|
An approximate-likelihood estimate of ρ (Fearnhead and Donnelly 2002) |
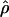 H01 H01
|
A composite-likelihood estimate of ρ (Hudson 2001) |
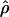 Lamarc Lamarc
|
A full-likelihood estimate of ρ (Kuhner et al. 2002) |
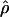 LS03 LS03
|
The PAC-likelihood estimate of ρ (Li and Stephens 2003) |
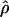 MAF02 MAF02
|
A composite-likelihood estimate of ρ (McVean et al. 2002) |
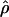 T05 T05
|
A summary statistic-based estimate of ρ (Haddrill et al. 2005) |
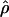 W00 W00
|
A summary statistic-based estimate of ρ (Wall 2000) |
| s | The rate of self-fertilization |
| S | Number of segregating sites |
| Sp | Number of parsimony informative segregating sites |
| T | Tajima's D (Tajima 1989) |
| θ | The population mutation parameter, 4Neμ |
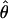 FD02 FD02
|
θ coestimated with ρ (Fearnhead and Donnelly 2002) |
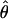 Lamarc Lamarc
|
θ coestimated with ρ (Kuhner et al. 2002) |
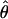 π π |
An estimate of θ based on pairwise differences (Tajima 1983) |
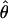 T05 T05
|
θ coestimated with ρ (Haddrill et al. 2005) |
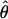 W W
|
An estimate of θ based on the number segregating sites (Watterson 1975) |
The relative roles of gene conversion and crossing over are important because they influence the degree of the association among segregating sites, particularly at the intragenic level. The gene conversion process results in the exchange of small tracts of a chromosome, creating a mosaic sequence. At the population level, gene conversion interrupts linkage disequilibrium (LD, the association among segregating sites) in a very localized manner while long-distance LD remains largely unaffected (Andolfatto and Nordborg 1998). This can result in a reduction in LD among closely linked markers, while flanking markers remain in complete association. Thus the relative role of gene conversion is a topic of considerable practical importance. For example, the density of the mapped polymorphic sites needed for disease association studies in humans and for marker-assisted selection in crops and domesticated animals is dependent on the degree to which extrapolations from larger-scale estimates of LD predict the degree of association between genetic markers and causative mutations (Ptak et al. 2004).
We focus on the impact of recombination in wild barley (Hordeum vulgare ssp. spontaneum), a species with an estimated selfing rate of 98.4% (Brown et al. 1978). We estimate the relative contribution of recombination and mutation (ρ/θ) on the basis of nucleotide sequence-level diversity. We also examine the relative contributions of gene conversion and crossing over to estimated levels of recombination.
There are a number of methods for estimation of the recombination parameter (ρ) from nucleotide sequence polymorphism data. Most methods rely on a standard model of recombination that includes the assumptions that recombination results from homologous crossover events during normal meiosis and that the recombination rate per base pair is constant with the probability of recombination proportional to the distance between sites. For the majority of estimators the population history is assumed to conform to a coalescent model with recombination (Hudson 1990; Griffiths and Marjoram 1996). Many methods assume that samples are drawn from a large and panmictic population of constant size, evolving under neutrality (reviewed in Fearnhead and Donnelly 2002; Stumpf and McVean 2003). The infinite-sites model of mutation is also often assumed (each mutation affects a unique site).
Estimation of the population recombination parameter ρ = 4Ner is challenging. When based on nucleotide sequence polymorphism, the estimated value is always a product of the effective population size and rate of recombination. Methods for estimating ρ from nucleotide sequence include product moment estimators (Hudson 1987; Hey and Wakeley 1997), “composite-likelihood” methods that result from a product of coalescent likelihoods for a series of two-site or three-site configurations (Hudson 2001; Wall 2004), “approximate-likelihood” methods that combine summary statistics from the data with estimated histories with recombination (Wall 2000), and “full-likelihood” methods (Griffiths and Marjoram 1996; Kuhner et al. 2000) that attempt to fit parameter estimates to the estimated underlying coalescent history with recombination (reviewed in Stumpf and McVean 2003).
We also estimate the relative contribution of gene conversion (ρg) and crossing over (ρc) to total recombination (f = ρg/ρc) (Frisse et al. 2001), using a composite-likelihood estimator (Hudson 2001) and a method that matches patterns of nucleotide sites with coalescent simulations of gene conversion (Padhukasahasram et al. 2004). We compare these methods using an empirical data set from 18 loci sequenced from a common sample of 25 wild barley accessions (Morrell et al. 2005) and population genetic data sets from Zea mays (maize), Drosophila melanogaster, D. pseudoobscura, and D. simulans.
METHODS
Sequence data:
Sequence diversity from 18 loci for 25 wild barley individuals from across the species' range has been reported previously (Cummings and Clegg 1998; Lin et al. 2001, 2002; Morrell et al. 2003, 2005). The sequences are fully resolved haplotypes with a minimum quality criterion of a phred score ≥20 for both the forward and the reverse strands. Singleton mutations were confirmed through a second PCR amplification and resequencing of both the forward and the reverse strands. The total data set includes 678 segregating sites, 420 of which are parsimony informative. Five sites (0.74%) have more than two nucleotide states; there are 4 sites with three nucleotide states and a single site with four states. Detailed methods for sequencing and sequence assembly are included in Morrell et al. (2003). Diversity statistics and the levels of LD within and between loci are reported in Morrell et al. (2005). Two abutting portions of the Pepc locus were sequenced separately (Morrell et al. 2003, 2005), but in a combined length of 3173 bp contain only four parsimony-informative segregating sites and are treated here as a single locus, referred to as PepcC.
In addition to data from the wild barley loci, we have analyzed additional nucleotide sequence data sets to assess the relative role and extent of evidence for gene conversion.
Estimates of the role of recombination, particularly the relative role of gene conversion, depend on sampling a relatively large number of segregating sites. To infer the role of gene conversion using the pattern-matching methods of Padhukasahasram et al. (2004) we focus on published nucleotide sequence data sets ≥1000 bp aligned length, with ≥20 sampled chromosomes and ≥20 parsimony-informative segregating sites, at least two detected recombination events (see below), and minimal missing data. Data from seven of the wild barley loci we have sequenced meet these criteria. We also considered sequence data from all of the 98 D. melanogaster loci compiled into a single list by Presgraves (2005). This resulted in inclusion of data from 10 loci from multiple populations of D. melanogaster (Begun and Aquadro 1995; Harr et al. 2002; Zurovcova and Ayala 2002; Riley et al. 2003; Balakirev and Ayala 2004a,b; DuMont et al. 2004), 1 locus from multiple populations of D. pseudoobscura (Schaeffer and Miller 1992), 2 loci from multiple populations of D. simulans (DuMont et al. 2004), 4 loci from cultivated maize (Tenaillon et al. 2001), 1 locus from both maize and its wild progenitor teosinte (Z. mays ssp. mays and ssp. parviglumis) (Bomblies and Doebley 2005), and 3 loci from a separate sample of wild barley (Caldwell et al. 2005). Descriptive statistics for all sampled loci are in Table 2.
TABLE 2.
Descriptive statistics and estimates of nucleotide sequence diversity for a common set of 25 samples at 18 loci in wild barley
| Gene | n | h | Aligned length, bp | Sp |
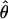 W × 10−3 W × 10−3
|
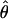 π ×10−3 π ×10−3
|
T | Wall's B | Rm | Rh | Rs | Rl | Ru |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H. vulgare ssp. spontaneum | |||||||||||||
| Adh1 | 25 | 11 | 1362 | 6 | 2.73 (±1.11) | 2.07 | −0.926 | 0.154 | 0 | 0 | 0 | 0 | 0 |
| Adh2 | 25 | 19 | 1980 | 14 | 4.84 (±1.72) | 3.19 | −1.289 | 0.057 | 2 | 2 | 2 | 2 | 2 |
| Adh3 | 25 | 21 | 1873 | 81 | 15.42 (±5.11) | 22.42 | 1.734 | 0.423 | 2 | 2 | 5 | 5 | 6 |
| α-amy1 | 25 | 5 | 856 | 3 | 3.10 (±1.36) | 1.27 | −1.948 | 0.222 | 0 | 0 | 0 | 0 | 0 |
| Cbf3 | 28 | 10 | 1514 | 22 | 4.52 (±1.64) | 4.43 | −0.071 | 0.160 | 2 | 3 | 3 | 3 | 3 |
| Dhn1 | 24 | 16 | 1538 | 37 | 18.70 (±6.36) | 13.18 | −1.161 | 0.056 | 7 | 11 | 11 | 11 | 17 |
| Dhn4 | 24 | 12 | 1072 | 31 | 14.13 (±4.97) | 17.18 | 0.831 | 0.381 | 5 | 6 | 6 | 6 | 8 |
| Dhn5 | 24 | 19 | 1088 | 25 | 11.70 (±4.09) | 10.81 | −0.295 | 0.239 | 3 | 7 | 7 | 7 | 8 |
| Dhn7 | 28 | 19 | 1389 | 50 | 16.72 (±6.21) | 14.01 | −0.622 | 0.185 | 6 | 11 | 11 | 13 | 16 |
| Dhn9 | 25 | 12 | 1011 | 9 | 4.90 (±1.91) | 3.91 | −0.725 | 0.118 | 1 | 1 | 1 | 1 | 1 |
| Faldh | 25 | 11 | 1091 | 17 | 5.67 (±2.12) | 5.71 | −0.405 | 0.333 | 0 | 0 | 0 | 1 | 1 |
| G3pdh | 26 | 13 | 2010 | 45 | 7.93 (±2.64) | 9.90 | 0.823 | 0.536 | 1 | 1 | 1 | 3 | 3 |
| ORF1 | 27 | 17 | 1533 | 22 | 6.16 (±2.16) | 5.18 | −1.129 | 0.196 | 1 | 1 | 1 | 1 | 1 |
| 5′Pepc | 25 | 6 | 2019 | 1 | 0.66 (±0.35) | 0.23 | −1.841 | — | 0 | 0 | 0 | 0 | 0 |
| Pepc | 25 | 8 | 1154 | 3 | 1.15 (±0.61) | 1.14 | −0.023 | — | 0 | 0 | 0 | 0 | 0 |
| Stk | 26 | 15 | 1057 | 20 | 9.29 (±3.27) | 6.77 | −1.019 | 0.111 | 1 | 3 | 3 | 3 | 3 |
| Vrn1 | 19 | 12 | 1262 | 10 | 3.79 (±1.48) | 3.57 | −0.216 | 0.077 | 2 | 2 | 3 | 2 | 3 |
| Waxy | 28 | 22 | 1232 | 25 | 9.12 (±3.12) | 7.86 | −0.521 | 0.238 | 6 | 12 | 12 | 12 | 16 |
| External H. vulgare ssp. spontaneum data | |||||||||||||
| GSP | 33 | 25 | 1802 | 38 | 19.43 (±5.89) | 7.52 | −2.326 | 0.164 | 9 | 9 | 13 | 10 | 13 |
| hina | 33 | 22 | 1475 | 44 | 10.87 (±3.45) | 10.00 | −0.295 | 0.067 | 9 | 10 | 13 | 9 | 13 |
| hinb | 33 | 26 | 3373 | 134 | 14.08 (±4.29) | 9.16 | −1.331 | 0.080 | 6 | 7 | 10 | 7 | 8 |
| D. melanogaster | |||||||||||||
| bagpipe | 27 | 12 | 1402 | 27 | 6.16 (±2.12) | 7.23 | 0.647 | 0.300 | 6 | 7 | 9 | 9 | 10 |
| CG3588 | 44 | 26 | 1332 | 34 | 11.64 (±3.45) | 8.23 | −1.043 | 0.050 | 13 | 13 | 30 | 31 | — |
| Est6 | 50 | 22 | 2332 | 77 | 13.00 (±3.77) | 11.30 | −0.463 | 0.178 | 15 | 15 | 20 | 21 | 31 |
| Idgf1 | 20 | 18 | 1958 | 72 | 11.61 (±4.03) | 14.66 | 1.073 | 0.132 | 15 | 15 | 20 | 23 | 35 |
| Idgf3 | 20 | 17 | 2401 | 48 | 8.33 (±2.95) | 8.76 | 0.209 | 0.275 | 11 | 11 | 16 | 16 | 21 |
| Notch5′ | 50 | 29 | 1480 | 24 | 8.38 (±2.55) | 4.51 | −1.598 | 0.096 | 9 | 13 | 27 | 24 | — |
| polehole | 22 | 18 | 2259 | 40 | 6.69 (±2.31) | 6.69 | −0.001 | 0.212 | 13 | 13 | 20 | 20 | 31 |
| tinman | 29 | 16 | 2428 | 26 | 4.29 (±1.47) | 5.15 | 0.734 | 0.316 | 2 | 2 | 2 | 2 | 2 |
| vermilion | 71 | 36 | 2081 | 68 | 11.35 (±3.00) | 8.84 | −0.757 | 0.047 | 27 | 27 | 60 | 56 | — |
| yEst6 | 22 | 12 | 2332 | 72 | 10.64 (±3.64) | 11.97 | 0.502 | 0.438 | 4 | 4 | 4 | 4 | 6 |
| D. pseudoobscura | |||||||||||||
| Adh | 139 | 118 | 4736 | 217 | 2.66 (±6.14) | 11.72 | −1.845 | 0.0424 | 54 | 61 | 155 | — | — |
| D. simulans | |||||||||||||
| Notch 3′ | 22 | 16 | 1578 | 26 | 5.91 (±2.16) | 6.92 | 0.664 | 0.091 | 9 | 9 | 17 | 17 | 24 |
| Notch 5′ | 22 | 20 | 1411 | 28 | 7.71 (±2.79) | 8.03 | 0.162 | 0.054 | 10 | 10 | 19 | 19 | 27 |
| Z. mays | |||||||||||||
| Adh | 25 | 11 | 1435 | 40 | 11.93 (±4.07) | 12.58 | 0.210 | 0.138 | 8 | 8 | 9 | 9 | 11 |
| Glb1 | 23 | 20 | 1196 | 50 | 25.19 (±8.36) | 19.87 | −0.843 | 0.082 | 14 | 14 | 21 | 21 | 32 |
| Umc128 | 23 | 15 | 1011 | 23 | 15.45 (±5.68) | 19.43 | 0.979 | 0.207 | 5 | 5 | 7 | 7 | 9 |
| Umc230 | 22 | 12 | 1243 | 17 | 17.79 (±6.56) | 12.79 | −1.082 | 0.0333 | 3 | 3 | 4 | 4 | 5 |
| Zfl2 | 29 | 28 | 4205 | 82 | 16.73 (±5.22) | 10.53 | −1.439 | 0.115 | 24 | 26 | 50 | 44 | — |
See Table 1 for symbols used. For 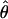 W, standard deviation is shown, based on no recombination.
W, standard deviation is shown, based on no recombination.
Estimating the number of recombination events:
To estimate the number of recombination events in a data set, we employed five estimators that vary in the algorithm they use to detect recombination. The estimators Rm, Rh, Rs, Rl, and Ru were calculated using the programs RecMin (Myers and Griffiths 2003) (to estimate Rm, Rh, and Rs), HapBound (to estimate Rl), and shrub (to estimate Ru) (Song et al. 2005) (see supplemental material at http://www.genetics.org/supplemental/ for links to all software used). The estimators use distinct methods for calculating a minimum number of recombination events for a data set and are related such that Rm ≤ Rh ≤ Rs ≤ Rl ≤ Ru (Song et al. 2005). The Rm estimate is based on the four-gamete test. For any pair of nucleotide sites, only three configurations (represented in binary form as 00, 01, 10) are possible on the basis of unique mutations (Hudson and Kaplan 1985). Producing all four possible gametic combinations requires either recombination or a second mutation of one of the nucleotide sites. When the probability of recurrent mutation is low (i.e., the data are consistent with the infinite-sites model) algorithms can be used to process the results of the four-gamete tests and provide the minimum number of nonoverlapping intervals involved in recombination. Rh is calculated on the basis of the difference (h − S − 1) between the number of observed haplotypes (h) in the sample and the number of segregating sites (S). Rs uses a simplified approximation of the sample history such that any true history of the data would include a larger number of recombination events. Rl and Ru are lower and upper bounds on the minimum number of recombination events required to reconstruct an evolutionary history compatible with the sequence. Ru is computed relative to an ancestral recombination graph (ARG) compatible with the data (Song et al. 2005). The input for each of the estimators is the segregating sites from the nucleotide sequence data set encoded as binary characters. In this study, the minor allele state was represented as 1 and the majority allele as 0. RecMin input can include sites with missing data; thus we have treated as missing the third state at sites with more than two nucleotide states and segregating sites within indels. These sites must be excluded in HapBound and shrub input. Haplotype configurations for 18 wild barley loci for all parsimony-informative sites are presented in Morrell et al. (2005).
Estimating the population recombination rate:
The methods discussed above focus on the number of recombination events observable within a sequenced region. Parameterizing recombination in terms of ρ = 4Ner permits an evaluation of the per base pair input of recombination, in terms of the rearranging of mutations, throughout the coalescent history of the sampled population. Parametric estimates of ρ also provide a useful comparison to estimates of θ = 4Neμ in that they describe the relative importance of recombination and mutation in the history of the organism.
Estimates of ρ for each locus in our wild barley data set were calculated using seven different estimators. This permits a comparison of estimators using a common set of samples across a set of loci with very different numbers of informative mutations and recombination events (Table 2). Thus we briefly examine the utility of estimators across loci and the variance among estimators for each sampled locus.
We used the programs maxhap and LDHat for the composite-likelihood-based estimates 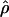 H01 (Hudson 2001) and
H01 (Hudson 2001) and 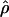 MAF02 (McVean et al. 2002), mss_conv for the summary-statistic-likelihood estimate
MAF02 (McVean et al. 2002), mss_conv for the summary-statistic-likelihood estimate 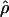 W00 (Wall 2000), rhothetapost for a summary-statistic-based Bayesian estimator with rejection-sampling algorithm for
W00 (Wall 2000), rhothetapost for a summary-statistic-based Bayesian estimator with rejection-sampling algorithm for 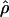 T05 (Haddrill et al. 2005), rholike and sequenceLD for the approximate- or “marginal”-likelihood estimates
T05 (Haddrill et al. 2005), rholike and sequenceLD for the approximate- or “marginal”-likelihood estimates 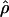 LS03 (Li and Stephens 2003), and
LS03 (Li and Stephens 2003), and 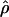 FD02 (Fearnhead and Donnelly 2002) and Lamarc for the full-likelihood estimate
FD02 (Fearnhead and Donnelly 2002) and Lamarc for the full-likelihood estimate 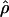 Lamarc (Kuhner et al. 2000, 2002). Because low-frequency mutations necessarily occur in only a minimal number of haplotype configurations, they are less informative as to the extent of recombination. In this study, for methods that apply a frequency filter, only mutations that occurred at least twice in the sample (i.e., those that are “parsimony informative”) are considered. A number of methods permit the use of either an infinite-sites model or a specific nucleotide substitution model. All analyses reported here have assumed an infinite-sites model unless otherwise specified.
Lamarc (Kuhner et al. 2000, 2002). Because low-frequency mutations necessarily occur in only a minimal number of haplotype configurations, they are less informative as to the extent of recombination. In this study, for methods that apply a frequency filter, only mutations that occurred at least twice in the sample (i.e., those that are “parsimony informative”) are considered. A number of methods permit the use of either an infinite-sites model or a specific nucleotide substitution model. All analyses reported here have assumed an infinite-sites model unless otherwise specified.
The composite-likelihood estimator 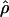 H01 of Hudson (2001) considers the frequency of each of the two-site haplotypes (00, 01, 10, 11) for each pair of sites. The method uses a simulation of the neutral coalescent to identify values of ρ compatible with the observed frequencies for pairs of sites. The composite likelihood is the product of the likelihoods for each ρ-value across pairs of sites. We have used lookup tables where likelihood values have been precalculated (Hudson 2001) (see supplemental material at http://www.genetics.org/supplemental/). The maxhap software, used for composite-likelihood estimation, can estimate
H01 of Hudson (2001) considers the frequency of each of the two-site haplotypes (00, 01, 10, 11) for each pair of sites. The method uses a simulation of the neutral coalescent to identify values of ρ compatible with the observed frequencies for pairs of sites. The composite likelihood is the product of the likelihoods for each ρ-value across pairs of sites. We have used lookup tables where likelihood values have been precalculated (Hudson 2001) (see supplemental material at http://www.genetics.org/supplemental/). The maxhap software, used for composite-likelihood estimation, can estimate 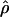 with or without a simultaneous estimate of
with or without a simultaneous estimate of 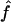 , the relative contribution of gene conversion.
, the relative contribution of gene conversion.
The composite-likelihood method 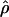 MAF02 of McVean et al. (2002) differs from the Hudson (2001) method in that likelihood tables are generated using the sample size and values of θ that match estimates for the locus being evaluated, rather than a grid of ρ-values for a given sample size. We have generated likelihood tables on the basis of Watterson's (1975) θ-estimate (
MAF02 of McVean et al. (2002) differs from the Hudson (2001) method in that likelihood tables are generated using the sample size and values of θ that match estimates for the locus being evaluated, rather than a grid of ρ-values for a given sample size. We have generated likelihood tables on the basis of Watterson's (1975) θ-estimate (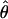 W) for each locus as this approach may improve the accuracy of the composite-likelihood method (McVean et al. 2002).
W) for each locus as this approach may improve the accuracy of the composite-likelihood method (McVean et al. 2002).
The summary statistic method 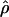 W00 of Wall (2000) uses a simulation of the neutral coalescent process to find a value of ρ that maximizes the proportion of simulations that match the observed number of haplotypes (h) and the number of recombination events (Rm) in a chromosomal segment from a sample of individuals. Inputs into the simulation include the number of segregating sites (S), the length of the region (l), and the number of chromosomes sampled (n). For a diploid, outcrossing organism, n is two times the number of individuals sampled. For wild barley, which is >98% self-fertilizing, the sample more closely approximates a haploid sample, and thus we treat n as the actual number of unique sequences observed at each locus. This number can slightly exceed the 25 individuals sampled due to occasional heterozygous individuals in the sample (Morrell et al. 2005).
W00 of Wall (2000) uses a simulation of the neutral coalescent process to find a value of ρ that maximizes the proportion of simulations that match the observed number of haplotypes (h) and the number of recombination events (Rm) in a chromosomal segment from a sample of individuals. Inputs into the simulation include the number of segregating sites (S), the length of the region (l), and the number of chromosomes sampled (n). For a diploid, outcrossing organism, n is two times the number of individuals sampled. For wild barley, which is >98% self-fertilizing, the sample more closely approximates a haploid sample, and thus we treat n as the actual number of unique sequences observed at each locus. This number can slightly exceed the 25 individuals sampled due to occasional heterozygous individuals in the sample (Morrell et al. 2005).
The summary statistic method 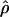 T05 of Thornton (Haddrill et al. 2005; Thornton and Andolfatto 2006) combines the summary of the data used by Wall (2000) and the Rh relationship described above (Myers and Griffiths 2003) with a rejection-sampling algorithm to produce a series of independent, joint estimates of
T05 of Thornton (Haddrill et al. 2005; Thornton and Andolfatto 2006) combines the summary of the data used by Wall (2000) and the Rh relationship described above (Myers and Griffiths 2003) with a rejection-sampling algorithm to produce a series of independent, joint estimates of 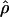 and
and 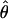 . The method provides a simple means to estimate confidence intervals for
. The method provides a simple means to estimate confidence intervals for 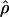 ,
, 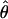 , and
, and 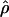 /
/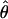 (Haddrill et al. 2005). We plotted the estimated posterior distribution of
(Haddrill et al. 2005). We plotted the estimated posterior distribution of 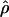 and
and 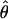 from an initial round of analysis for each locus to assure that posterior estimates were not bounded by the priors. When the distribution of posterior values appeared to be constrained by the priors, priors were adjusted to avoid problems with the boundary and the analysis was rerun. Priors for the second round were the 0.01 and 0.99 percentile values of the estimated posterior distribution from the initial round. Point estimates used to summarize the posterior distributions of
from an initial round of analysis for each locus to assure that posterior estimates were not bounded by the priors. When the distribution of posterior values appeared to be constrained by the priors, priors were adjusted to avoid problems with the boundary and the analysis was rerun. Priors for the second round were the 0.01 and 0.99 percentile values of the estimated posterior distribution from the initial round. Point estimates used to summarize the posterior distributions of 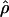 T05 and
T05 and  T05 are the maximum a posteriori estimates and confidence intervals are defined by the 0.025 and 0.975 percentiles.
T05 are the maximum a posteriori estimates and confidence intervals are defined by the 0.025 and 0.975 percentiles.
The approximate-likelihood method 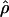 FD02 of Fearnhead and Donnelly (2002) uses a list of observed haplotype configurations [defined by parsimony-informative (nonsingleton) sites (Sp)] with l and n for each locus to produce a joint estimate of
FD02 of Fearnhead and Donnelly (2002) uses a list of observed haplotype configurations [defined by parsimony-informative (nonsingleton) sites (Sp)] with l and n for each locus to produce a joint estimate of 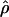 FD02 and
FD02 and 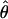 FD02. As with the Wall (2000) method, the value of n we have used is the actual number of unique sequences observed at each locus. For each round of analysis we used 200,000 runs with four driving values (values at which the search is initiated) for both ρ and θ. Driving values and limits on ρ and θ were adjusted after an initial round of analysis, and the estimator was run a second time. The likelihood surface for each value of ρ and θ was calculated on the basis of 251 values of ρ and 3 values of θ.
FD02. As with the Wall (2000) method, the value of n we have used is the actual number of unique sequences observed at each locus. For each round of analysis we used 200,000 runs with four driving values (values at which the search is initiated) for both ρ and θ. Driving values and limits on ρ and θ were adjusted after an initial round of analysis, and the estimator was run a second time. The likelihood surface for each value of ρ and θ was calculated on the basis of 251 values of ρ and 3 values of θ.
The conditional probabilities method 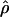 LS03 of Li and Stephens (2003) is based on a model of linkage disequilibrium where the probability of observing a particular set of haplotypes is evaluated across values of ρ. The conditional probabilities represent the probability of observing each haplotype, given all previously observed haplotypes and given a ρ-value. The method of estimation is referred to as “product of approximate conditionals” (PAC) likelihood. Because the order of the observed haplotypes is important, LPAC is averaged over several random orders of the haplotypes (we used the default of 10 random orders). The method does not assume an infinite-sites mutation model. The approximate conditional probabilities consider haplotypes as a unit, differing from the composite-likelihood method in which sites are considered on a pairwise basis.
LS03 of Li and Stephens (2003) is based on a model of linkage disequilibrium where the probability of observing a particular set of haplotypes is evaluated across values of ρ. The conditional probabilities represent the probability of observing each haplotype, given all previously observed haplotypes and given a ρ-value. The method of estimation is referred to as “product of approximate conditionals” (PAC) likelihood. Because the order of the observed haplotypes is important, LPAC is averaged over several random orders of the haplotypes (we used the default of 10 random orders). The method does not assume an infinite-sites mutation model. The approximate conditional probabilities consider haplotypes as a unit, differing from the composite-likelihood method in which sites are considered on a pairwise basis.
Kuhner's full-likelihood method 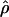 Lamarc implemented in Lamarc (Kuhner et al. 2000, 2002) estimates coalescent histories with recombination compatible with input data and then estimates parameter values compatible with the genealogy. We used as input full-length sequence alignments, treating all samples for each locus as a single population, and estimated
Lamarc implemented in Lamarc (Kuhner et al. 2000, 2002) estimates coalescent histories with recombination compatible with input data and then estimates parameter values compatible with the genealogy. We used as input full-length sequence alignments, treating all samples for each locus as a single population, and estimated 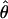 Lamarc and
Lamarc and 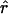 Lamarc, the per generation rate of recombination, for each locus. Program setup and search strategy are similar to that reported in Morrell et al. (2003), including the use of the Felsenstein 1984 nucleotide substitution model (Kishino and Hasegawa 1989; Swofford et al. 1996) (rather than an infinite-sites model) and empirical base frequencies and transition/transversion ratios. Results of an initial analysis using
Lamarc, the per generation rate of recombination, for each locus. Program setup and search strategy are similar to that reported in Morrell et al. (2003), including the use of the Felsenstein 1984 nucleotide substitution model (Kishino and Hasegawa 1989; Swofford et al. 1996) (rather than an infinite-sites model) and empirical base frequencies and transition/transversion ratios. Results of an initial analysis using 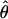 W and
W and 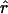 Lamarc = 0.5 were used as starting values of a second round of analysis with 20 initial chains of 1000 and four final chains of 20,000 genealogies with 2000 genealogies discarded per chain. Adaptive heating was used to improve the search of parameter space. Finally, start parameters from the second-round analysis were plugged into a third round of analysis. Results of the third-round analysis are reported.
Lamarc = 0.5 were used as starting values of a second round of analysis with 20 initial chains of 1000 and four final chains of 20,000 genealogies with 2000 genealogies discarded per chain. Adaptive heating was used to improve the search of parameter space. Finally, start parameters from the second-round analysis were plugged into a third round of analysis. Results of the third-round analysis are reported.
Estimating the role of gene conversion:
Estimating gene conversion from nucleotide sequence data is difficult in part because estimation involves four unknowns, θ, ρ, f (the proportion of gene conversion events relative to crossover events), and L (the conversion tract length) (Ptak et al. 2004). Two primary methods of estimating the parameter f have been reported: one method jointly estimates ρ and f using an extension of the composite-likelihood approach (Frisse et al. 2001; Hudson 2001; Wall 2004); a second method matches patterns of nucleotide sites that show evidence of recombination with values of ρ and f using coalescent simulations (Padhukasahasram et al. 2004), referred to here as 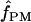 . Previous studies have emphasized that because the distance among sampled loci almost always exceeds likely conversion tract length, the relative roles of gene conversion and crossover can be inferred subtractively from multilocus data (Andolfatto and Nordborg 1998; Ptak et al. 2004; Wall 2004; Plagnol et al. 2006). However, genotyping errors tend to upwardly bias
. Previous studies have emphasized that because the distance among sampled loci almost always exceeds likely conversion tract length, the relative roles of gene conversion and crossover can be inferred subtractively from multilocus data (Andolfatto and Nordborg 1998; Ptak et al. 2004; Wall 2004; Plagnol et al. 2006). However, genotyping errors tend to upwardly bias 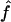 , causing an overestimate of the role of gene conversion (Ptak et al. 2004; Wall 2004), and the issue of typing errors is not remedied by multilocus estimation of f. Thus our focus is on inferring the role of gene conversion within individual loci and, when possible, utilizing data that has been rigorously purged of all detectable genotyping errors.
, causing an overestimate of the role of gene conversion (Ptak et al. 2004; Wall 2004), and the issue of typing errors is not remedied by multilocus estimation of f. Thus our focus is on inferring the role of gene conversion within individual loci and, when possible, utilizing data that has been rigorously purged of all detectable genotyping errors.
The composite-likelihood estimator program maxhap uses a lookup table that permits rapid estimation of ρ and f. However, composite-likelihood estimators can have a high root mean square error (Wall 2004; Smith and Fearnhead 2005). We estimate 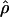 H01 and
H01 and 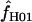 for all sampled loci using maxhap. We also explore the utility of maxhap estimates using coalescent simulations with parameter estimates based on the wild barley empirical data. Specifically, we asked, what is the minimum contribution of gene conversion (or the minimum value of f > 0) that can be detected with the two-site composite-likelihood method with 95% confidence? We then asked, when simulations are generated without any gene conversion, what is the probability of estimating
for all sampled loci using maxhap. We also explore the utility of maxhap estimates using coalescent simulations with parameter estimates based on the wild barley empirical data. Specifically, we asked, what is the minimum contribution of gene conversion (or the minimum value of f > 0) that can be detected with the two-site composite-likelihood method with 95% confidence? We then asked, when simulations are generated without any gene conversion, what is the probability of estimating 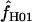 > 0? The simulations were performed across a dense grid of values, with 10,000 replications per grid point with simulation output sent directly to the composite-likelihood estimator software maxhap through the mstoexhap (Thornton 2003) and exhap utilities. Sample size, the length of regions simulated, and parameter values used in the simulation were chosen to reflect mean values from the wild barley empirical data; thus, simulations were based on l = 1500 bp of sequence from n = 25 individuals, with θ = 8 × 10−3/bp, and ρ = 8 × 10−3/bp for simulations with no gene conversion and then with ρ decreased in proportion to increasing values of f, with f from 0.01 to 7 with nine values between 0 and 2 and thereafter increasing by increments of 0.5. For the simulations without gene conversion we used a grid of ρ-values that spanned the range of empirical values estimated from the wild barley loci, i.e., ρ from 0 to 0.032 (including 0.0001, 0.0002, and then increasing from 0.001 by a factor of 2), using tract lengths L = 250 and 500 bp.
> 0? The simulations were performed across a dense grid of values, with 10,000 replications per grid point with simulation output sent directly to the composite-likelihood estimator software maxhap through the mstoexhap (Thornton 2003) and exhap utilities. Sample size, the length of regions simulated, and parameter values used in the simulation were chosen to reflect mean values from the wild barley empirical data; thus, simulations were based on l = 1500 bp of sequence from n = 25 individuals, with θ = 8 × 10−3/bp, and ρ = 8 × 10−3/bp for simulations with no gene conversion and then with ρ decreased in proportion to increasing values of f, with f from 0.01 to 7 with nine values between 0 and 2 and thereafter increasing by increments of 0.5. For the simulations without gene conversion we used a grid of ρ-values that spanned the range of empirical values estimated from the wild barley loci, i.e., ρ from 0 to 0.032 (including 0.0001, 0.0002, and then increasing from 0.001 by a factor of 2), using tract lengths L = 250 and 500 bp.
Padhukasahasram et al. (2004) defined descriptive statistics designed to estimate the role of gene conversion. The first summary statistic is the frequency of “pattern a,” where a set of three parsimony-informative segregating sites designated sites A, B, and C includes external sites (A and C) compatible with the four-gamete test; i.e., three or fewer configurations are present, but where each of the external sites is incompatible with the internal site (A and B, B and C) based on the four-gamete test; that is, all four states are present (Figure 1). Statistics were also defined for evaluating four-site configurations, where we can designate segregating sites A, B, C, and D (Figure 1). For four-site configurations, “pattern b” and “pattern d” were defined. In pattern b, both the outer pair of sites (A and D) and the inner pair of sites (B and C) are incompatible (all four pairwise states are present). In pattern d the outer pair of sites (A and D) and the inner pair of sites (B and C) are compatible pairs, but there is incompatibility between the two outer sites and their corresponding adjacent inner site (A and B, C and D). Both patterns a and d imply that either a gene conversion event or a double recombination has effectively replaced a tract of the chromosome that included the internal site(s).
Figure 1.—
Patterns a, b, and d depend on the absence of all four gametic configurations between sites indicated by brackets, but the presence of four gametes between sites indicated by curved arrows. In patterns a and d, the sites indicated in red have been subject to either double recombination or gene conversion.
The proportions of patterns a, b, and d for the empirical data were considered by comparing them to those observed in coalescent simulations. Simulated data reflecting n, S, and l from the empirical data for each locus were generated using the program ms (Hudson 2002). With S used as a proxy for θ and tract lengths (L) held constant, simulations can explore a grid of ρ- and f-values. Initial values of ρ and f within the simulations were based on estimates from the Hudson (2001) two-site likelihood method described above; values of L = 250 and 500 were used. These values bracket the estimate of L = 352 from D. melanogaster (Hilliker et al. 1994).
Coalescent simulations with proportions of patterns a, b, and d within 20% of that observed in the empirical data were accepted; the proportion of accepted simulations for each set of simulation parameters was then determined for pattern a and for simultaneous acceptance based on both patterns b and d. The product of these two proportions is referred to as the likelihood of the given simulation parameters.
All analyses were performed using single nodes of the Linux cluster at the Bioinformatics Core facility at the University of California, Riverside.
Genotyping errors and gene conversion:
Because triplets and quadruplets in patterns a and d are based on the incompatibility of the internal site or sites with flanking sequence, genotyping errors can generate the same pattern as a conversion event. Base call errors, particularly those arising from the failure to detect heterozygous sites within an individual, can potentially be identified by examining the frequency of each of the haplotypic classes (00, 01, 10, 11) for the site AB and BC comparisons in triplets of sites (see results).
RESULTS
Genotyping errors:
Examination of the triplets of nucleotide sites inferred from our wild barley nucleotide sequence data demonstrated that for some loci, a relatively small number of segregating sites and a relatively small number of individuals from each sequencing panel contributed the majority of pattern a triplets. For each of the outer to inner site comparisons (i.e., sites AB and BC) in a triplet, the rarest of haplotypic classes is the most direct single source of typing error. Samples that are heterozygous at a locus but are incorrectly represented as a single haplotype can result in triplets and quadruplets of sites that mimic the effects of gene conversion or double crossover and thus represent a problematic source of typing error. In a manner analogous to error detection in genetic mapping algorithms (Lincoln and Lander 1992) examination of site frequencies between pairs of sites can identify individual samples and nucleotide sites that lead to the inference of double crossover events. Correcting typing errors can dramatically improve recombination rate estimates (Lincoln and Lander 1992).
For the 18 wild barley loci in Morrell et al. (2005), original sequence traces were available for reexamination. Base calls at each site in each sequence that contributed the rarest gametic class (e.g., 01) for the outer sites in each triplet were reexamined. All sites in the panel had been sequenced with a minimum phred quality of ≥20 for forward and reverse sequence reads. For the vast majority of sites, the base calls from the original data set submitted to GenBank were confirmed and thus the triplet was accepted as valid. For example, all triplets at the Dhn4 locus involve a segregating site at bp 114. The critical two-site haplotype occurs in sample 06 (GenBank no. AY895883). All quadruplets for Dhn4 include bp 992 as the last segregating site in the quadruplet, on the basis of a gametic type again found only in sample 06. Thus in a manner similar to the handling of singleton confirmation in population genetic studies, this sample was reamplified and resequenced using all available primers on both the forward and reverse strands; the original nucleotide states at both of the sites were confirmed, and base calls for sites segregating within the population did not indicate the presence of more than one allele (i.e., there is no evidence that the individual was a heterozygote at this locus).
The targeted examination of base calls (in the original trace files) that contributed the least frequent gametic class for pattern a triplets at other wild barley loci revealed heterozygous individuals that were not previously detected by screening with PolyPhred or by visual inspection. Heterozygous individuals were identified at five loci including samples 04 and 28 at Cbf3, 28 at Dhn1, 12 at Dhn5, 36 at Dhn7, and 12 at Waxy (see Table 3). The phase of mutations was resolved experimentally, using a combination of cloning and allele-specific PCR. Examination of the sequence traces from individuals that were newly detected as heterozygotes at a locus revealed that many of the base calls at segregating sites that differentiate the two parental chromosomes did not show equal amplification of the PCR products from each chromosome. Several sequencing primers produced sequence reads from the PCR product of only one of the two parental chromosomes. Unequal amplification of initial PCR products was also evident; clones of Waxy sample 12 were biased 15:1 for one of the parental haplotypes. The two haplotypes at Waxy sample 12 were ultimately confirmed on the basis of the direct sequencing of the products of allele-specific PCR.
TABLE 3.
The number of heterozygotes detected at wild barley loci and the impact of newly detected heterozygotes on descriptive statistics and parameter estimates
| Gene | Heterozygotes detected | h | Rm |
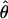 W % change W % change |
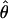 π % change π % change |
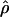 H01% change H01% change |
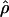 W00% change W00% change |
Pattern a % change | Pattern d % change | GenBank no. of heterozygous sample |
|---|---|---|---|---|---|---|---|---|---|---|
| Cbf3 | 1/3 | 11/10 | 5/2 | −1.9 | 1.1 | −67.3 | −61.6 | — | −1070.3 | AY895833AY895848 |
| Dhn1 | 0/1 | 15/16 | 7/7 | −0.9 | −0.3 | −2.7 | +10.3 | 0.0 | +0.95 | AY895872 |
| Dhn5 | 0/1 | 19/19 | 5/3 | −12.4 | −4.4 | −39.7 | −62.5 | −106.3 | −64.02 | AY349228 |
| Dhn7 | 2/3 | 19/19 | 9/6 | −16.5 | −6.7 | −27.5 | −39.1 | −15.0 | +0.70 | AY895927 |
| Waxy | 2/3 | 22/23 | 6/6 | −1.6 | −0.4 | −13.9 | −1.7 | 0.0 | −0.01 | AY349331 |
Results from the data in Morrell et al. (2005) are presented first followed by revised estimates. Parameter estimates and patterns a and d are expressed as percentage of change in the new data relative to the original estimate. The “—” indicates that the value could not be calculated.
In general, the resolution of heterozygotes reduced the evidence for recombination in the data sets (Table 3). For example, for Dhn7 this resulted in a change from Rm = 9 in the original data set to an Rm = 6 after error checking and experimental resolution of haplotypes. Estimates of θ for the locus were reduced slightly, with a reduction of 16.5% for 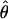 W and 6.7% for
W and 6.7% for 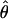 π. Estimates of
π. Estimates of 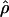 showed a more dramatic decrease with
showed a more dramatic decrease with 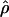 H01 reduced by 27.5% and
H01 reduced by 27.5% and 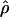 W00 reduced by 39.19%. Experimental resolution of typing errors also tends to reduce the proportions of patterns a, b, and d in the data set (see Table 3). In the extreme case, the original Cbf3 data set had 1.4% of possible triplets in pattern a, but with errors in phasing corrected for three heterozygotes, no pattern a triplets were present.
W00 reduced by 39.19%. Experimental resolution of typing errors also tends to reduce the proportions of patterns a, b, and d in the data set (see Table 3). In the extreme case, the original Cbf3 data set had 1.4% of possible triplets in pattern a, but with errors in phasing corrected for three heterozygotes, no pattern a triplets were present.
Recombination events:
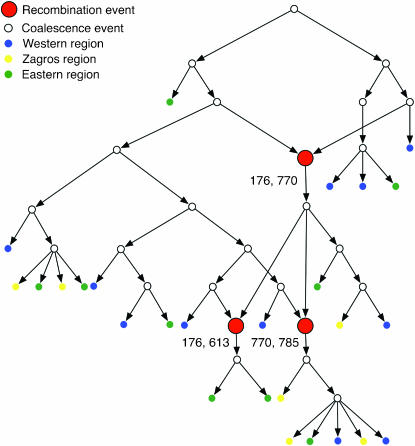
All but four wild barley loci (Adh1, α-Amy1, Faldh, and PepcC) show evidence of recombination on the basis of the four-gamete test (Hudson and Kaplan 1985); i.e., Rm > 0. In loci where recombination was detected, Rm varies from 1 to 7, with the largest number of recombination events evident in Dhn1, Dhn7, and Waxy (Table 2). For the four loci where Rm = 0, the Rh and Rs estimates also did not show any evidence of recombination. Rl and Ru also report no evidence of recombination in loci with Rm = 0 with one exception, the Faldh locus, where Rl and Ru = 1. For loci with Rm > 0, both Rh and Rs ranged from 1 to 12 (Table 2). Values of Rl for wild barley ranged from 0 to 13; Ru had a maximum of 17. In Figure 2, an ARG generated by the Ru estimator depicts the three recombination events inferred at a typical locus (Stk) from the wild barley data set. The Drosophila and Z. mays loci were chosen for inclusion in the study because they were likely to have a sufficient number of recombination events to infer the role of gene conversion. For these loci, Ru-values are as large as 35 in Idgf1 from D. melanogaster and 49 in Zfl2 from Z. mays. For some loci, e.g., vermilion from the D. melanogaster locus, the Rh estimate is larger than the Rs estimate because the RecMin software can make use of more of the polymorphism data by considering sites that are segregating in alignment gaps.
Figure 2.—
An ancestral recombination graph (ARG) for the wild barley locus Stk is shown. Coalescent events are shown as open circles, sampled haplotypes are shown as solid circles, and recombination events are shown as larger red circles. The positions of segregating sites that are on the boundaries of recombination events are shown next to each recombination. Solid colors for haplotypes represent the major portions of the geographic range, or wild barley, previously identified as the Western (blue), Zagros (green), and Eastern (yellow) regions (Morrell et al. 2003).
Estimates of ρ:
Estimated rates of recombination per base pair for each of the wild barley loci are shown in Table 4 and Figure 3. A nonparametric Friedman rank sum test considering the estimation method as the treatment is significant (P = 8 × 10−4), rejecting the null hypothesis that there is no systematic difference in the estimators. The mean value of 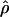 varies almost threefold among the estimators, ranging from 4.33 to 12.48 × 10−3. While the mean estimates from
varies almost threefold among the estimators, ranging from 4.33 to 12.48 × 10−3. While the mean estimates from 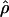 H01,
H01, 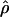 MAF02,
MAF02, 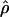 W00,
W00, 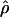 LS03,
LS03, 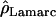 , and
, and 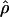 T05 are relatively similar, the much larger average ρ estimate from
T05 are relatively similar, the much larger average ρ estimate from  FD04 results primarily from
FD04 results primarily from 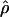 ≥ 24 × 10−3 for three loci, Dhn1, Dhn7, and Waxy. Values of
≥ 24 × 10−3 for three loci, Dhn1, Dhn7, and Waxy. Values of 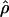 Lamarc,
Lamarc, 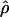 FD04, and
FD04, and 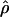 T05 are coestimated along with θ (Figure 3). The values of
T05 are coestimated along with θ (Figure 3). The values of 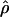 T05 are similar to estimates that were not coestimated, i.e.,
T05 are similar to estimates that were not coestimated, i.e., 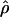 H01,
H01, 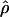 LS03, and
LS03, and 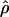 W00. However,
W00. However, 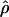 Lamarc and
Lamarc and 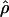 FD04 produce very different estimates of ρ, with much of the difference attributable to
FD04 produce very different estimates of ρ, with much of the difference attributable to 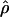 and
and 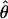 for Dhn1, Dhn7, and Waxy mentioned above (Table 4). While the three loci have
for Dhn1, Dhn7, and Waxy mentioned above (Table 4). While the three loci have 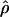 FD04 > 24 × 10−3,
FD04 > 24 × 10−3, 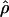 Lamarc estimates are all ≤16 × 10−3, with the largest difference among estimates at Dhn1, where
Lamarc estimates are all ≤16 × 10−3, with the largest difference among estimates at Dhn1, where 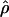 Lamarc = 5.14 × 10−3, but
Lamarc = 5.14 × 10−3, but 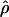 FD04 = 46.55 × 10−3. The estimate of
FD04 = 46.55 × 10−3. The estimate of 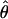 Lamarc for the locus is 38.68 × 10−3 while
Lamarc for the locus is 38.68 × 10−3 while 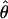 FD04 = 17.88 × 10−3. This difference is consistent with average values of
FD04 = 17.88 × 10−3. This difference is consistent with average values of 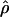 and
and 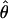 for the two methods (Figure 3). The Lamarc estimator appears to attribute much more of the total diversity to mutation; the average value from
for the two methods (Figure 3). The Lamarc estimator appears to attribute much more of the total diversity to mutation; the average value from 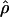 Lamarc is only 35% of
Lamarc is only 35% of 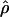 FD04 and
FD04 and 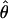 Lamarc is 26% larger than
Lamarc is 26% larger than 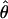 FD04.
FD04.
TABLE 4.
Estimates of 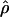 and three coestimated values of
and three coestimated values of 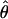 (×10−3) for a common set of 25 samples at 18 loci in wild barley
(×10−3) for a common set of 25 samples at 18 loci in wild barley
| Gene |
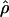 H01 (maxhap) H01 (maxhap) |
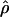 LS03 (rholike) LS03 (rholike) |
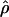 MAF02 (LDhat) MAF02 (LDhat) |
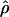 W00 (mss_conv) W00 (mss_conv) |
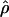 Lamarc (Lamarc) Lamarc (Lamarc) |
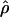 FD02 (sequenceLD) FD02 (sequenceLD) |
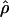 T05 (rhotheta) T05 (rhotheta) |
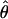 FD02 (sequenceLD) FD02 (sequenceLD) |
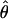 Lamarc (Lamarc) Lamarc (Lamarc) |
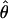 T05 (rhotheta) T05 (rhotheta) |
|---|---|---|---|---|---|---|---|---|---|---|
| Adh1 | 5.51 | 4.04 | 2.79 | 0.00 | 0.04 | 0.74 | 2.02 | 5.15 | 3.68 | 3.29 |
| Adh2 | 6.81 | 4.06 | 2.27 | 6.09 | 1.66 | 5.20 | 9.39 | 4.80 | 8.03 | 4.02 |
| Adh3 | 0.06 | 1.98 | 0.00 | 1.66 | 2.97 | 5.89 | 1.06 | 8.12 | 13.20 | 27.18 |
| α-amy1 | 4.35 | 1.26 | 4.21 | 0.00 | 1.22 | 1.17 | 0.11 | 9.35 | 3.03 | 1.63 |
| Cbf3 | 2.10 | 3.67 | 1.20 | 7.93 | 1.47 | 7.11 | 3.29 | 6.44 | 4.56 | 3.25 |
| Dhn1 | 16.26 | 29.62 | 10.11 | 14.30 | 5.14 | 46.55 | 13.22 | 17.88 | 38.68 | 12.99 |
| Dhn4 | 6.68 | 6.40 | 5.17 | 12.57 | 3.16 | 8.75 | 12.56 | 7.48 | 12.95 | 12.56 |
| Dhn5 | 8.63 | 19.63 | 6.50 | 11.03 | 7.32 | 18.07 | 9.92 | 15.63 | 15.23 | 14.36 |
| Dhn7 | 12.21 | 16.48 | 9.07 | 10.08 | 10.12 | 24.25 | 11.23 | 12.60 | 21.42 | 12.93 |
| Dhn9 | 4.59 | 6.80 | 1.48 | 3.96 | 7.33 | 10.59 | 5.79 | 7.91 | 6.04 | 5.21 |
| Faldh | 3.15 | 3.28 | 1.14 | 0.00 | 4.09 | 7.05 | 0.84 | 7.33 | 5.98 | 6.20 |
| G3pdh | 0.00 | 0.00 | 0.00 | 0.75 | 0.71 | 2.24 | 0.70 | 3.98 | 4.69 | 7.01 |
| ORF1 | 3.01 | 2.00 | 1.15 | 1.30 | 8.03 | 5.86 | 1.70 | 6.52 | 10.76 | 7.88 |
| PepcC | 5.51 | 0.00 | 0.16 | 0.00 | 0.00 | 0.01 | 0.09 | 2.37 | 1.27 | 1.27 |
| Stk | 9.98 | 7.23 | 4.54 | 3.31 | 2.86 | 10.75 | 3.20 | 10.88 | 10.54 | 8.37 |
| Vrn1 | 9.29 | 1.26 | 6.00 | 18.23 | 1.85 | 11.51 | 15.66 | 2.38 | 5.84 | 3.49 |
| Waxy | 36.08 | 42.13 | 34.09 | 34.09 | 15.64 | 46.49 | 33.86 | 9.33 | 11.13 | 7.64 |
| Mean | 7.90 | 8.81 | 5.29 | 7.37 | 4.33 | 12.48 | 7.33 | 8.14 | 10.41 | 8.19 |
The programs used for each estimate are listed below the estimator. The adjacent Pepc regions are combined into a single locus, PepcC for these analyses.
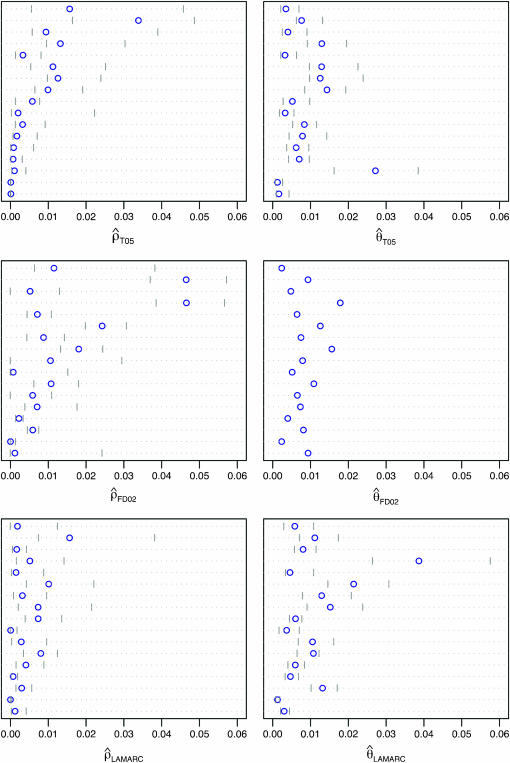
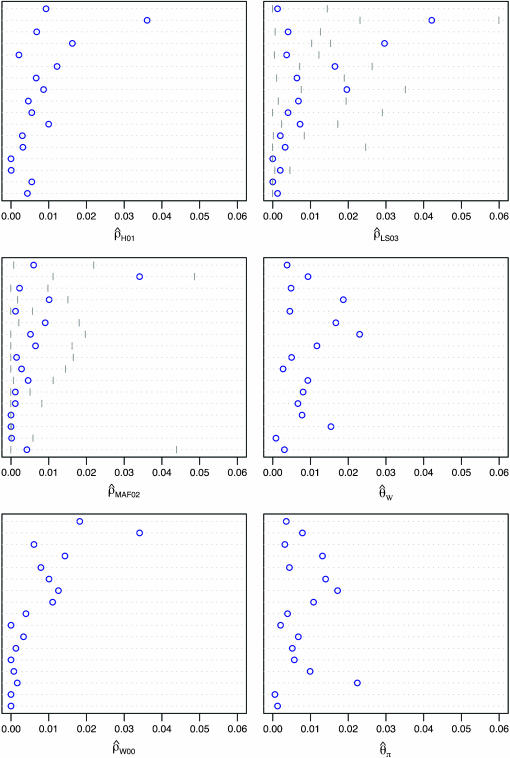
Figure 3.—
Comparison of 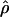 and
and 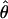 for 17 wild barley loci. (a) The estimators coestimate
for 17 wild barley loci. (a) The estimators coestimate 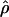 and
and 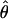 and the values for each locus are paired. (b) Separate estimates of
and the values for each locus are paired. (b) Separate estimates of 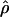 and
and 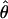 . Point estimates are shown as circles and when 95% confidence intervals could be estimated, they are indicated by gray lines. Loci are presented in the same order as in Figure 4. From top to bottom, the loci are Vrn1, Waxy, Adh2, Dhn1, Cbf3, Dhn7, Dhn4, Dhn5, Dhn9, Adh1, Stk, ORF1, Faldh, G3pdh, Adh3, PepcC, and α-amy1.
. Point estimates are shown as circles and when 95% confidence intervals could be estimated, they are indicated by gray lines. Loci are presented in the same order as in Figure 4. From top to bottom, the loci are Vrn1, Waxy, Adh2, Dhn1, Cbf3, Dhn7, Dhn4, Dhn5, Dhn9, Adh1, Stk, ORF1, Faldh, G3pdh, Adh3, PepcC, and α-amy1.
Despite the differences among estimators, ranks of ρ estimates, analyzed for all seven estimators while considering the locus as the treatment in the Friedman rank sum test, distinguish between the levels of recombination for the 17 loci (P = 2.4 × 10−11). The null hypothesis that all loci have the same 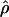 -value is rejected. Within any given estimation method, the estimates of recombination per base pair vary dramatically among loci; for example, the values for
-value is rejected. Within any given estimation method, the estimates of recombination per base pair vary dramatically among loci; for example, the values for 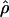 H01 varied from 0 to 36.08 × 10−3/bp (Table 4).
H01 varied from 0 to 36.08 × 10−3/bp (Table 4).
Estimates of ρ/θ:
Four estimates of ρ/θ and the corresponding estimate from Lamarc, 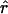 Lamarc, for each of the wild barley loci are shown in Table 5. The mean estimate of
Lamarc, for each of the wild barley loci are shown in Table 5. The mean estimate of 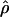 /
/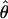 for wild barley varies among estimators from 0.90 to 1.93. Values for
for wild barley varies among estimators from 0.90 to 1.93. Values for 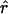 Lamarc for each locus were generally smaller than
Lamarc for each locus were generally smaller than 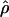 /
/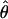 and are dramatically lower for loci with
and are dramatically lower for loci with 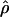 /
/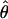 > 1. For example the Waxy locus estimates are
> 1. For example the Waxy locus estimates are 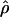 H01/
H01/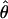 π = 4.59, but
π = 4.59, but 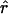 Lamarc = 1.4 even when Lamarc estimates for the locus are reinitiated with higher values of
Lamarc = 1.4 even when Lamarc estimates for the locus are reinitiated with higher values of 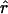 Lamarc and lower values for θ. Estimates of the ratio ρ/θ for wild barley loci follow a relatively narrow range of 0–4 regardless of the estimators of ρ and θ considered (Table 5). The only exceptions are at the PepcC locus, where there are only four informative sites: at PepcC,
Lamarc and lower values for θ. Estimates of the ratio ρ/θ for wild barley loci follow a relatively narrow range of 0–4 regardless of the estimators of ρ and θ considered (Table 5). The only exceptions are at the PepcC locus, where there are only four informative sites: at PepcC, 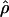 H01/
H01/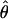 W = 6.6 and
W = 6.6 and 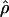 H01/
H01/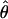 π = 9.8. The
π = 9.8. The 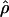 T05/
T05/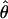 T05 estimator provides a direct means of estimating confidence intervals. Estimates of
T05 estimator provides a direct means of estimating confidence intervals. Estimates of 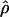 T05/
T05/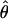 T05 and 95% confidence intervals for the wild barley loci are shown in Figure 4. Estimates of
T05 and 95% confidence intervals for the wild barley loci are shown in Figure 4. Estimates of 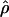 H01/
H01/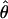 W and
W and 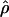 H01/
H01/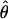 π for sampled Zea and Drosophila loci are in Table S1 (http://www.genetics.org/supplemental/). Estimates of ρ/θ from Zea data are slightly higher than those for wild barley with a mean
π for sampled Zea and Drosophila loci are in Table S1 (http://www.genetics.org/supplemental/). Estimates of ρ/θ from Zea data are slightly higher than those for wild barley with a mean 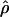 H01/
H01/ 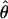 W = 3.5. The D. melanogaster data sets sampled here are generally from multiple populations worldwide, including populations from parts of the species range that were recently colonized. Mean
W = 3.5. The D. melanogaster data sets sampled here are generally from multiple populations worldwide, including populations from parts of the species range that were recently colonized. Mean 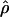 H01/
H01/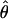 W = 2.5, which is much lower than
W = 2.5, which is much lower than 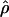 /
/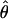 from the apparent core of the range of D. melanogaster in East Africa, where
from the apparent core of the range of D. melanogaster in East Africa, where 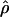 T05/
T05/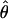 T05 was estimated as 7.6 (Haddrill et al. 2005).
T05 was estimated as 7.6 (Haddrill et al. 2005).
TABLE 5.
Estimates of ρ/θ for wild barley loci including the 95% confidence intervals for 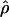 T05/
T05/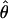 T05 and
T05 and 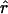 Lamarc
Lamarc
| Gene |
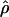 H01/ H01/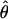 W W
|
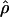 H01/ H01/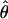 π π
|
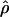 FD02/ FD02/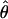 FD02 FD02
|
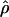 T05/ T05/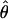 T05 T05
|
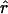 Lamarc Lamarc
|
|---|---|---|---|---|---|
| H. vulgare. ssp. spontaneum | |||||
| Adh1 | 2.019 | 2.661 | 0.143 | 0.504 (0.071, 7.236) | 0.010 (0.000, 0.254) |
| Adh2 | 1.408 | 2.136 | 1.083 | 2.046 (0.778, 10.213) | 0.207 (0.010, 0.374) |
| Adh3 | 0.004 | 0.003 | 0.725 | 0.043 (0.013, 0.173) | 0.225 (0.148, 0.332) |
| α-amy1 | 1.405 | 3.424 | 0.125 | 0.025 (0.006, 0.109) | 0.404 (0.125, 0.938) |
| Cbf3 | 0.464 | 0.475 | 1.104 | 0.775 (0.316, 2.568) | 0.322 (0.083, 0.812) |
| Dhn1 | 0.870 | 1.234 | 2.604 | 1.072 (0.645, 2.454) | 0.133 (0.061, 0.247) |
| Dhn4 | 0.290 | 0.389 | 1.171 | 0.718 (0.305, 1.458) | 0.244 (0.109, 0.463) |
| Dhn5 | 0.737 | 0.798 | 1.156 | 0.679 (0.401, 1.937) | 0.481 (0.231, 0.902) |
| Dhn7 | 0.730 | 0.871 | 1.925 | 0.753 (0.355, 2.065) | 0.472 (0.292, 0.719) |
| Dhn9 | 0.922 | 1.172 | 1.339 | 0.572 (0.216, 2.110) | 1.213 (0.881, 1.754) |
| Faldh | 0.473 | 0.551 | 0.963 | 0.117 (0.018, 1.102) | 0.684 (0.378, 1.030) |
| G3pdh | 0.001 | 0.000 | 0.563 | 0.105 (0.024, 0.480) | 0.151 (0.071, 0.287) |
| ORF1 | 0.375 | 0.582 | 0.898 | 0.194 (0.072, 1.206) | 0.746 (0.539, 1.015) |
| PepcC | 6.588 | 9.765 | 0.004 | 0.038 (0.013, 0.112) | 0.000 (0.000, 0.158) |
| Stk | 1.075 | 1.474 | 0.988 | 0.366 (0.147, 1.290) | 0.271 (0.054, 0.596) |
| Vrn1 | 2.452 | 2.601 | 4.840 | 3.652 (1.059, 14.524) | 0.317 (0.000, 1.145) |
| Waxy | 3.956 | 4.590 | 4.981 | 3.591 (1.596, 6.513) | 1.406 (1.038, 2.196) |
| Mean | 1.398 | 1.925 | 1.448 | 0.897 | 0.461 |
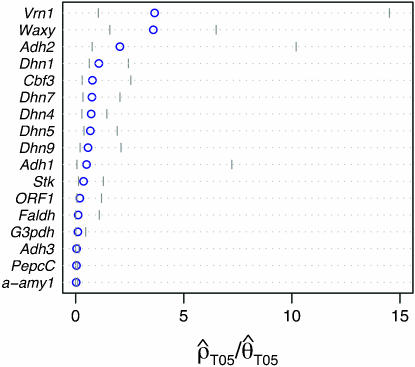
Figure 4.—
Estimates of 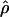 T05/
T05/ 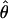 T05 and 95% confidence intervals for all wild barley loci. For each locus, the point of
T05 and 95% confidence intervals for all wild barley loci. For each locus, the point of 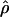 T05/
T05/ 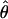 T05 is shown as a circle, and bounds of the upper and lower 95% confidence intervals are indicated by gray vertical lines.
T05 is shown as a circle, and bounds of the upper and lower 95% confidence intervals are indicated by gray vertical lines.
Estimates of f:
On the basis of maxhap estimates, 8 of our 17 wild barley loci show no evidence of gene conversion and return 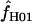 = 0 (Table 6). Among the 10 of our wild barley loci that met our criteria for external data sets (those that include >20 informative sites), 6 have maxhap estimates of
= 0 (Table 6). Among the 10 of our wild barley loci that met our criteria for external data sets (those that include >20 informative sites), 6 have maxhap estimates of 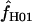 > 0, with estimates ranging from 0 to 59.5 (mean = 18.04 and median = 0.95). The largest two estimates of
> 0, with estimates ranging from 0 to 59.5 (mean = 18.04 and median = 0.95). The largest two estimates of 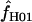 are 59.5 for Dhn5 and 34 for Adh3. Inference of high levels of gene conversion at these loci is perhaps not surprising, as the Dhn5 locus includes a series of repeated sequence motifs (Choi et al. 1999) that may be especially prone to illegitimate recombination, while Adh3 contains a 12-bp segment, delineated by three segregating sites, that shows evidence of either gene conversion or double recombination between deeply divergent haplotypes (see Figure 4 in Lin et al. 2001).
are 59.5 for Dhn5 and 34 for Adh3. Inference of high levels of gene conversion at these loci is perhaps not surprising, as the Dhn5 locus includes a series of repeated sequence motifs (Choi et al. 1999) that may be especially prone to illegitimate recombination, while Adh3 contains a 12-bp segment, delineated by three segregating sites, that shows evidence of either gene conversion or double recombination between deeply divergent haplotypes (see Figure 4 in Lin et al. 2001).
TABLE 6.
Estimates of f based on composite-likelihood and pattern matching, the percentage of decrease in the coestimated 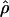 H01, and
H01, and 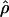 from pattern matching (×10−3)
from pattern matching (×10−3)
| Gene |
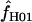 (maxhap) (maxhap) |
% decrease in 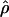 c c
|
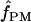 (pattern matching) (pattern matching) |
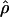 c (pattern matching) c (pattern matching) |
|---|---|---|---|---|
| H. vulgare ssp. spontaneum | ||||
| (loci with Sp > 20, Rm ≥ 2) | ||||
| Adh3 | 34.3 | 95 | — | — |
| Cbf3 | 29.4 | 96 | — | — |
| Dhn1 | 1.3 | 53 | 2 | 2.5 |
| Dhn4 | 0 | — | 1 | 9.4 |
| Dhn5 | 59.5 | 98 | 0 | 18.5 |
| Dhn7 | 1.2 | 57 | 2 | 4.1 |
| Waxy | 0.6 | 39 | 0 | 12.5 |
| (loci with Sp ≤ 20, Rm ≤ 2) | ||||
| Adh1 | 0 | — | — | — |
| Adh2 | 0.7 | 35 | — | — |
| α-amy1 | 0 | — | — | — |
| Dhn9 | 0 | — | — | — |
| Faldh | 0 | — | — | — |
| G3pdh | 0 | — | — | — |
| ORF1 | 0 | — | — | — |
| PepcC | 15.6 | 89 | — | — |
| Stk | 0 | — | — | — |
| Vrn1 | 11.5 | 91 | — | — |
| (external data sets) | ||||
| GSP* | 59.6 | 96 | 2 | 0.7 |
| Hina* | 3.0 | 73 | 2 | 3.4 |
| Hinb* | 57.6 | 95 | — | — |
| D. melanogaster | ||||
| Bagpipe | 0 | — | 2 | 15.6 |
| CG3588 | 50.6 | 98 | 6 | 23.3 |
| Est6 | 1.2 | 50 | 2 | 9.5 |
| Idgf1 | 1.2 | 53 | 1 | 15.3 |
| Idgf3 | 0.9 | 42 | 0 | 10.8 |
| Notch 5′ | 24.5 | 95 | 5 | 21.4 |
| Polehole | 3.2 | 77 | 0 | 29.2 |
| Tinman | 0.5 | 22 | — | — |
| Vermilion | 0.9 | 45 | 0 | 30.3 |
| yEst6 | 1.2 | 42 | 0 | 1.9 |
| D. pseudoobscura | ||||
| Adh | 0 | — | — | — |
| D. simulans | ||||
| Notch 3′ | 29.4 | 97 | 1 | 15.1 |
| Notch 5′ | 29.4 | 98 | 2 | 20.0 |
| Z. mays | ||||
| Adh | 1.3 | 54 | 3 | 3.0 |
| Glb1 | 23.2 | 96 | 0 | 30.8 |
| Umc128 | 0 | — | 0 | 21.6 |
| Umc230 | 7.1 | 94 | 0 | 17.8 |
| Zfl2 | 0 | — | — | — |
Maxhap estimates 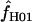 from Z. mays loci range from 0 to 23.2, with
from Z. mays loci range from 0 to 23.2, with 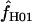 = 0 at two of the five loci. The mean of
= 0 at two of the five loci. The mean of 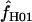 for Z. mays is 6.3 and the median estimate is 1.3. Nine of the 10 D. melanogaster loci show evidence of gene conversion on the basis of maxhap estimates, with
for Z. mays is 6.3 and the median estimate is 1.3. Nine of the 10 D. melanogaster loci show evidence of gene conversion on the basis of maxhap estimates, with 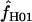 = 0.0–50.6 (mean = 8.4 and median = 1.3). For both portions of the Notch locus from D. simulans,
= 0.0–50.6 (mean = 8.4 and median = 1.3). For both portions of the Notch locus from D. simulans, 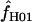 = 29.4. The largest available lookup table for maxhap has n = 100 chromosomes. For the D. pseudoobscura Adh locus 10 samples of 100 of the 139 chromosomes were drawn at random and analyzed with maxhap. In 8 of the 10 samples
= 29.4. The largest available lookup table for maxhap has n = 100 chromosomes. For the D. pseudoobscura Adh locus 10 samples of 100 of the 139 chromosomes were drawn at random and analyzed with maxhap. In 8 of the 10 samples 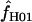 = 0. The remaining two samples return
= 0. The remaining two samples return 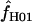 = 6.8 and 25.
= 6.8 and 25.
Maxhap provides an option to return the composite likelihood for each value of 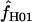 considered. Plotting the output from individual loci demonstrates that for loci with very large values of
considered. Plotting the output from individual loci demonstrates that for loci with very large values of 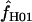 (e.g., Dhn5 with
(e.g., Dhn5 with 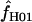 = 59.5) the likelihood value at the maximum-likelihood estimate of
= 59.5) the likelihood value at the maximum-likelihood estimate of 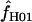 is only very slightly higher than that for much smaller values of
is only very slightly higher than that for much smaller values of 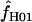 ; i.e., the likelihood surface is almost completely flat and it is difficult to distinguish between the likelihood of small values of
; i.e., the likelihood surface is almost completely flat and it is difficult to distinguish between the likelihood of small values of 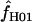 and the very large values returned by maxhap.
and the very large values returned by maxhap.
For our estimates of 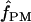 (pattern matching), the proportion of triplets in pattern a was calculated for our 10 wild barley loci that have >20 parsimony-informative sites and Rm ≥ 2; pattern a is not possible in the absence of at least two observed recombination events. Among the 7 loci, 2 have no triplets in pattern a (Table 6). When pattern a triplets are observed, they are always a very small percentage of all possible triplets; e.g., there are 65 pattern a triplets at Dhn4 or 1.4% of all 4495 triplets. Three loci, Dhn1, Dhn4, and Dhn7 have
(pattern matching), the proportion of triplets in pattern a was calculated for our 10 wild barley loci that have >20 parsimony-informative sites and Rm ≥ 2; pattern a is not possible in the absence of at least two observed recombination events. Among the 7 loci, 2 have no triplets in pattern a (Table 6). When pattern a triplets are observed, they are always a very small percentage of all possible triplets; e.g., there are 65 pattern a triplets at Dhn4 or 1.4% of all 4495 triplets. Three loci, Dhn1, Dhn4, and Dhn7 have 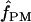 > 0 on the basis of pattern matching, with
> 0 on the basis of pattern matching, with 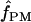 = 2, 1, and 2, respectively. The maxhap estimates for Dhn1 and Dhn7 were
= 2, 1, and 2, respectively. The maxhap estimates for Dhn1 and Dhn7 were 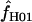 = 1.2 and 1.3, but 0 for Dhn4. Thus pattern matching for wild barley results in a mean
= 1.2 and 1.3, but 0 for Dhn4. Thus pattern matching for wild barley results in a mean 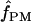 = 1 (median
= 1 (median 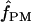 = 1).
= 1).
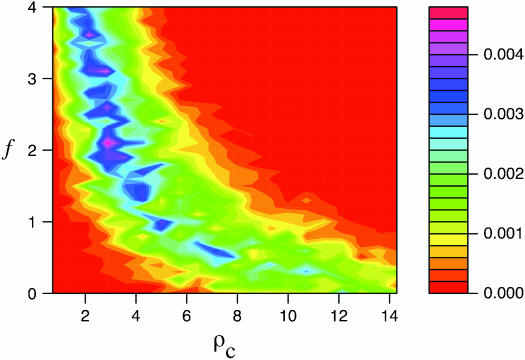
Figure 5 illustrates the results of pattern-matching simulations on a single locus. Simulation input values of ρc and f are plotted relative to a likelihood surface that shows the proportion of coalescent simulations that matched within 20% of the proportion of patterns a and then b and d in the wild barley Dhn7 locus. The locus has 50 parsimony-informative sites and Rm = 6 (Table 2) after the elimination of every detectable genotyping error (Table 3). The best fit to the empirical data is at 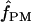 = 2.1 and
= 2.1 and 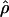 c = 3 × 10−3/bp (for f > 0, ρ-values are for crossover only). For simulations with f = 0, the best fit occurs for ρc = 12 × 10−3/bp (very similar to the ρH01 and ρLS03 estimates of 12 and 14 × 10−3). However, f = 0 simulations provide a much poorer fit to the data than simulations with f ≥ 0.4 (Figure 5). The plot is based on 1000 simulations for each pair of values for ρ and f, where parameter pairs make up a grid of all integer values of ρ (per locus) between 1 and 20 inclusive (plotted values are per base pair × 10−3) and f-values incremented by 0.1 between 0 and 4 inclusive.
c = 3 × 10−3/bp (for f > 0, ρ-values are for crossover only). For simulations with f = 0, the best fit occurs for ρc = 12 × 10−3/bp (very similar to the ρH01 and ρLS03 estimates of 12 and 14 × 10−3). However, f = 0 simulations provide a much poorer fit to the data than simulations with f ≥ 0.4 (Figure 5). The plot is based on 1000 simulations for each pair of values for ρ and f, where parameter pairs make up a grid of all integer values of ρ (per locus) between 1 and 20 inclusive (plotted values are per base pair × 10−3) and f-values incremented by 0.1 between 0 and 4 inclusive.
Figure 5.—
The likelihood surface for the wild barley Dhn7 locus based on the proportions of patterns a, b, and d in coalescent simulations across a dense grid of values of ρ and f. Spectral colors from red toward violet represent increased likelihood of a match between simulation input parameters and the empirical data. The strongest single peak is for 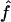 PM = 2.1, and
PM = 2.1, and 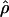 c = 3 × 10−3.
c = 3 × 10−3.
Among the 10 D. melanogaster loci, 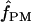 ranged from 0 to 6, with a median value of 1. In D. simulans, the two portions of the Notch locus return estimates of
ranged from 0 to 6, with a median value of 1. In D. simulans, the two portions of the Notch locus return estimates of 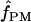 = 1 and 2 (Table 6). Pattern matching for maize loci returns
= 1 and 2 (Table 6). Pattern matching for maize loci returns 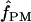 = 0 for three loci and
= 0 for three loci and 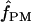 = 3 for the Adh locus. Pattern-matching simulations provided poor fit to the data from the D. melanogaster tinman and the Z. mays Zfl2 loci and D. pseudoobscura Adh, and thus no pattern-matching estimates are reported (Table 6).
= 3 for the Adh locus. Pattern-matching simulations provided poor fit to the data from the D. melanogaster tinman and the Z. mays Zfl2 loci and D. pseudoobscura Adh, and thus no pattern-matching estimates are reported (Table 6).
The accuracy of maxhap estimates of f̂H01:
Simulated data generated with f = 0 and ρ ranging from 0 to 0.032/bp show that almost half of all maxhap estimates 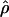 H01 and
H01 and 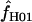 return a point estimate of
return a point estimate of 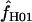 > 0. The variance of
> 0. The variance of 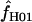 is consistently higher than that of
is consistently higher than that of 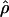 H01. For ρ = 8 × 10−3 (near the mean estimate for wild barley) there is an ∼50% probability of estimating
H01. For ρ = 8 × 10−3 (near the mean estimate for wild barley) there is an ∼50% probability of estimating 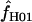 > 0 in simulations with f = 0. In 10,000 simulations each for L = 250 and 500 and with f = 0, median
> 0 in simulations with f = 0. In 10,000 simulations each for L = 250 and 500 and with f = 0, median 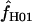 = 5.7 and 7.4. This indicates that in coalescent simulations, single-locus-based estimates of
= 5.7 and 7.4. This indicates that in coalescent simulations, single-locus-based estimates of 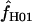 have a large bias and high variance (Wall 2004). Confidence intervals for composite-likelihood estimates of
have a large bias and high variance (Wall 2004). Confidence intervals for composite-likelihood estimates of 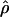 can be estimated using a parametric bootstrap simulation procedure (Hudson 2001; McVean et al. 2002). However, estimating confidence intervals for
can be estimated using a parametric bootstrap simulation procedure (Hudson 2001; McVean et al. 2002). However, estimating confidence intervals for 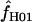 when
when 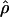 H01 and
H01 and 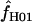 are coestimated is problematic. For simulations based on the loci sampled here, the lower bound of the 95% confidence interval appears to always include 0, and upper bounds can be greater than an order of magnitude larger than the point estimate. Thus, an estimate of
are coestimated is problematic. For simulations based on the loci sampled here, the lower bound of the 95% confidence interval appears to always include 0, and upper bounds can be greater than an order of magnitude larger than the point estimate. Thus, an estimate of 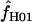 > 0 does not necessarily reflect the presence of gene conversion.
> 0 does not necessarily reflect the presence of gene conversion.
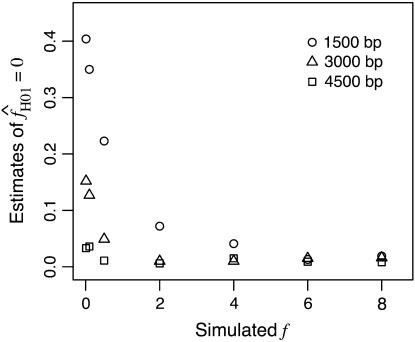
Simulations with f > 0 yielded 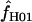 -values that increase dramatically with increasing f in the simulation. For ρ = 8 × 10−3, L = 250, and locus length l = 1500 bp, a simulation input value of f = 5 results in a 97% probability of
-values that increase dramatically with increasing f in the simulation. For ρ = 8 × 10−3, L = 250, and locus length l = 1500 bp, a simulation input value of f = 5 results in a 97% probability of 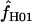 > 0. An increase in the length of the region simulated appears to dramatically improve the potential for rejecting high values of f. For l = 3000 and 4500 bp, the presence of f > 1 can be rejected with >95% probability (Figure 6). For parameter values that reflect the wild barley data (i.e., as above, ρ = 8 × 10−3 and l = 1500 bp) but with a tract length L = 500 a simulation input of f = 5 results in a 92% probability of estimating
> 0. An increase in the length of the region simulated appears to dramatically improve the potential for rejecting high values of f. For l = 3000 and 4500 bp, the presence of f > 1 can be rejected with >95% probability (Figure 6). For parameter values that reflect the wild barley data (i.e., as above, ρ = 8 × 10−3 and l = 1500 bp) but with a tract length L = 500 a simulation input of f = 5 results in a 92% probability of estimating 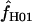 > 0. For 10 of 17 wild barley loci where the maxhap
> 0. For 10 of 17 wild barley loci where the maxhap 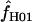 = 0, the haplotype variation observed is not likely to have been generated by high levels of gene conversion (e.g., f > 5).
= 0, the haplotype variation observed is not likely to have been generated by high levels of gene conversion (e.g., f > 5).
Figure 6.—
Coalescent simulations based on mean ρ- and θ-values from the wild barley data, depicting the probability of a composite-likelihood estimate of f = 0 given the input value of f shown along the x-axis. Tract length L = 250 bp is shown with locus lengths l = 1500, 3000, and 4500 bp.
DISCUSSION
We demonstrate that despite a high level of self-fertilization, recombination makes as large a contribution to sequence diversity in wild barley as does mutation (ρ/θ = r/μ ≥ 1). The primary impact of inbreeding is expected to be a dramatic reduction in the effectiveness of recombination. In a coalescent framework, this is realized as a reduction in the effect rate of recombination relative to mutation. For wild barley, 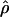 /
/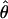 ≈ 1.5, similar to values estimated for outcrossing species (e.g., Balakirev et al. 2003; Balakirev and Ayala 2004b) and is ∼30-fold greater than ρ/θ = 0.05 recently estimated for the self-fertilizing species Arabidopsis thaliana (Nordborg et al. 2005). Published estimates for species-wide samples from the outcrossing species D. melanogaster and maize have means of 1.0 and 1.5 (Balakirev and Ayala 2004b; Wright et al. 2005). However, various published data sets from D. melanogaster, including those considered here, have very different sampling schemes and thus include populations with disparate demographic histories. Recent demographic history in particular can influence estimated rates of recombination (Thornton and Andolfatto 2006). In East African populations of D. melanogaster (putatively the core of the species range) (Lachaise et al. 1988) and in wild Mexican samples of the maize progenitor, teosinte, mean
≈ 1.5, similar to values estimated for outcrossing species (e.g., Balakirev et al. 2003; Balakirev and Ayala 2004b) and is ∼30-fold greater than ρ/θ = 0.05 recently estimated for the self-fertilizing species Arabidopsis thaliana (Nordborg et al. 2005). Published estimates for species-wide samples from the outcrossing species D. melanogaster and maize have means of 1.0 and 1.5 (Balakirev and Ayala 2004b; Wright et al. 2005). However, various published data sets from D. melanogaster, including those considered here, have very different sampling schemes and thus include populations with disparate demographic histories. Recent demographic history in particular can influence estimated rates of recombination (Thornton and Andolfatto 2006). In East African populations of D. melanogaster (putatively the core of the species range) (Lachaise et al. 1988) and in wild Mexican samples of the maize progenitor, teosinte, mean  /
/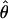 has been estimated as 7.6 and 4.5 (Haddrill et al. 2005; Wright et al. 2005). In A. thaliana, the impact of inbreeding is also confounded by a recent demographic expansion (Nordborg et al. 2005)
has been estimated as 7.6 and 4.5 (Haddrill et al. 2005; Wright et al. 2005). In A. thaliana, the impact of inbreeding is also confounded by a recent demographic expansion (Nordborg et al. 2005)
Why has the high rate of self-fertilization in wild barley not had a more dramatic impact on the relative role of recombination? First, it is important to note that the relative role of recombination and mutation in the wild barley lineage prior to the evolution of self-fertilization is unknown. The species most closely related to H. vulgare ssp. spontaneum is H. bulbosum, which is self incompatible and obligately outcrossing. By comparison to teosinte, and accounting for potential impact of the ancestral mating system, ρ/θ of 5–10 prior to the transition to self-fertilization is plausible. With an average of 98.4% self-fertilization, expected ρs/θs ≈ 0.14–0.28, so observed 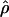 /
/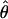 ≈ 5–10 times that expected. A larger ancestral value of ρ/θ leads to a smaller difference in observed and expected values.
≈ 5–10 times that expected. A larger ancestral value of ρ/θ leads to a smaller difference in observed and expected values.
How can we account for the relatively large role of recombination in generating haplotypic diversity in wild barley? One possibility is that the rate of self-fertilization in wild barley has been overestimated. However, this does not seem likely. Brown et al. (1978) reported an average selfing rate of 98.4% (with a 95% confidence interval of 97.3–99.2%). The estimate was based on multiple progeny from each maternal plant and an assay of 22 polymorphic allozyme loci in 26 populations in Israel. The lowest self-fertilization rate estimated in a single population was 90.4%. More xeric sites had a higher self-fertilization rate than mesic sites, with average rates of 99.6 and 97.9%, respectively. A recent study of 12 populations in Jordan that employed microsatellite-based estimates of outcrossing rate reported an average selfing rate of 99.7% (Abdel-Ghani et al. 2004). Reports of observed heterozygosity based on numerous studies of allelic diversity in wild barley are consistent in suggesting very high rates of self-fertilization (cf. Nevo et al. 1979; Volis et al. 2001). Rates of self-fertilization could be as high or higher in other parts of the species range (e.g., Central Asia); populations in Israel and Jordan occur in a region with much higher rainfall than occurs across most of the range of wild barley (Volis et al. 2001, 2002).
A second possible explanation for the relatively large apparent role of recombination in this highly selfing species is that the transition to self-fertilization may have occurred relatively recently (Lin et al. 2002). If self-fertilization evolved recently, perhaps within the last 100,000 years (see discussion in Charlesworth and Vekemans 2005), then many recombination events that occurred before the transition may still be evident in the data (Morrell et al. 2005).
Another possibility is that increased chiasma frequencies may elevate recombination rates within self-fertilizing lineages. Comparisons of inbreeding species and outcrossing relatives have frequently reported higher chiasma frequencies in inbreeders (Grant 1958; reviewed in Charlesworth et al. 1977). The potential compensatory effects of increase in chiasma frequency are limited, however, because the high rate of homozygosity in self-fertilizing species means that most effective recombination follows an outcrossing event (Nordborg 1999). In wild barley the level of heterozygosity is extremely low, <0.5% for highly polymorphic microsatellite loci (Baek et al. 2003) and 3.3% in the present data set after employing our heterozygote detection approach. Also, a phenomenon known as chiasma (or crossover) interference (cf. Malkova et al. 2004) limits the number of additional chiasmata that can occur along an individual chromosome [although some fraction of recombination events appear not to be constrained by interference (Copenhaver et al. 2002)]. Increased chiasma frequency alone is unlikely to compensate for the 5- to 10-fold excess in recombination relative to expectations.
Estimated values of ρ:
Parametric estimates of 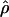 per base pair for wild barley have a mean of 7–8 × 10−3, ∼40 times greater than estimates for A. thaliana (
per base pair for wild barley have a mean of 7–8 × 10−3, ∼40 times greater than estimates for A. thaliana (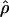 = 2 × 10−4) (Nordborg et al. 2005) and 0.4–0.5 times that of maize (
= 2 × 10−4) (Nordborg et al. 2005) and 0.4–0.5 times that of maize (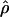 = 16–19 × 10−3) (Tenaillon et al. 2002) and D. melanogaster (
= 16–19 × 10−3) (Tenaillon et al. 2002) and D. melanogaster (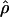 = 12–14 × 10−3) (Haddrill et al. 2005).
= 12–14 × 10−3) (Haddrill et al. 2005).
For several loci, the majority of estimators report 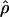 = 0 and it is evident that estimation of recombination in these loci is limited by the number of parsimony-informative sites. Several loci have Rm = 0 (i.e., Adh1, α-Amy1, Faldh, and PepcC) (Table 4), and for these loci, the 95% confidence intervals of many estimators include
= 0 and it is evident that estimation of recombination in these loci is limited by the number of parsimony-informative sites. Several loci have Rm = 0 (i.e., Adh1, α-Amy1, Faldh, and PepcC) (Table 4), and for these loci, the 95% confidence intervals of many estimators include 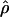 = 0. For the same loci the
= 0. For the same loci the 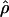 W00 point estimate is always
W00 point estimate is always 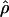 W00 = 0. For most of the same loci,
W00 = 0. For most of the same loci, 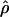 H01 is the largest point estimate of
H01 is the largest point estimate of 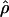 . The
. The 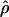 T05 estimate uses a similar summary of the data to that considered in
T05 estimate uses a similar summary of the data to that considered in 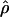 W00 but estimates
W00 but estimates 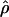 > 0 (although sometimes very small values) for every locus in the data set, including those with Rm = 0.
> 0 (although sometimes very small values) for every locus in the data set, including those with Rm = 0.
A number of studies have reported on the accuracy of 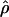 estimators based on coalescent simulations with a known input value of ρ (Kuhner et al. 2000; Wall 2000; Fearnhead and Donnelly 2002; Smith and Fearnhead 2005). Although we cannot estimate the accuracy of the seven estimators we have used on the wild barley empirical data, we can consider the utility of estimators and consistency of
estimators based on coalescent simulations with a known input value of ρ (Kuhner et al. 2000; Wall 2000; Fearnhead and Donnelly 2002; Smith and Fearnhead 2005). Although we cannot estimate the accuracy of the seven estimators we have used on the wild barley empirical data, we can consider the utility of estimators and consistency of 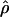 across estimators. As larger numbers of loci are considered, both the difficulty of input file preparation and computational efficiency can be serious limitations.
across estimators. As larger numbers of loci are considered, both the difficulty of input file preparation and computational efficiency can be serious limitations.
Point estimates of ρ from the seven estimators are highly correlated with each other. The most highly correlated measures are from the two composite-likelihood estimators (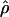 H01 and
H01 and 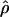 MAF02, Pearson's r2 = 0.95) and the two estimators that are based on summary statistics (
MAF02, Pearson's r2 = 0.95) and the two estimators that are based on summary statistics (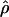 W00 and
W00 and 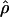 T05, r2 = 0.96). The estimates that are least correlated with those of other estimators are those from
T05, r2 = 0.96). The estimates that are least correlated with those of other estimators are those from 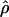 Lamarc (r2 < 0.62 for all pairs involving
Lamarc (r2 < 0.62 for all pairs involving 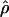 Lamarc). The results of the Friedman test indicate that both the locus and the estimation methods influence the rank of the estimates when the other factor is used as a blocking variable. This indicates that although the estimators differ, the locus rankings of
Lamarc). The results of the Friedman test indicate that both the locus and the estimation methods influence the rank of the estimates when the other factor is used as a blocking variable. This indicates that although the estimators differ, the locus rankings of 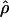 are correlated among the seven methods. Therefore, the estimators concur sufficiently to allow the detection of different recombination rates for the 17 wild barley loci.
are correlated among the seven methods. Therefore, the estimators concur sufficiently to allow the detection of different recombination rates for the 17 wild barley loci.
Among the seven estimators used for our 17 wild barley loci, 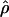 T05 returns the median estimate of
T05 returns the median estimate of 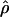 for six loci and
for six loci and 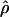 H01 returns the median estimate for three more. No other estimator returns the median estimate more than twice (Table 4). Because one of our principal goals was to estimate the relative role of recombination and mutation, the rhotheta (
H01 returns the median estimate for three more. No other estimator returns the median estimate more than twice (Table 4). Because one of our principal goals was to estimate the relative role of recombination and mutation, the rhotheta (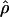 T05) estimator has considerable utility in that it provides a means of estimating
T05) estimator has considerable utility in that it provides a means of estimating 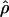 ,
, 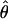 , and
, and 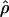 /
/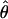 with confidence intervals in a relatively limited amount of computational time with input based on a simple summary of the data. However, for rhotheta computational time increased dramatically for loci with increased numbers of recombination events. The maximum values of Rm and Rh, the two summaries used by rhotheta, were 7 and 12 for our wild barley data. Experimentation with Drosophila and Zea data suggests that the utility of the estimator may be limited for loci with much larger numbers of recombination events (e.g., the Zea Zfl2 locus with Rh = 26).
with confidence intervals in a relatively limited amount of computational time with input based on a simple summary of the data. However, for rhotheta computational time increased dramatically for loci with increased numbers of recombination events. The maximum values of Rm and Rh, the two summaries used by rhotheta, were 7 and 12 for our wild barley data. Experimentation with Drosophila and Zea data suggests that the utility of the estimator may be limited for loci with much larger numbers of recombination events (e.g., the Zea Zfl2 locus with Rh = 26).
The 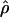 LS03 estimator generally returns ρ estimates only slightly greater than the median of all estimators (Table 4). The rholike software rapidly calculates the
LS03 estimator generally returns ρ estimates only slightly greater than the median of all estimators (Table 4). The rholike software rapidly calculates the 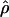 LS03 estimate with confidence intervals. Input file preparation is relatively simple, but for larger empirical studies would have to be automated.
LS03 estimate with confidence intervals. Input file preparation is relatively simple, but for larger empirical studies would have to be automated.
The use of lookup tables for the composite-likelihood estimators 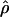 H01 and
H01 and 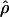 MAF02 allows these estimators to be the most computationally efficient. Also, because data in aligned fasta files can be piped directly into the
MAF02 allows these estimators to be the most computationally efficient. Also, because data in aligned fasta files can be piped directly into the 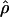 H01 (maxhap) estimation software with no additional data file preparation, the estimator currently provides the most efficient means of estimating ρ for data sets with large numbers of loci. However,
H01 (maxhap) estimation software with no additional data file preparation, the estimator currently provides the most efficient means of estimating ρ for data sets with large numbers of loci. However, 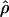 H01 has relatively high root mean squared error (Smith and Fearnhead 2005) and returns the largest values of
H01 has relatively high root mean squared error (Smith and Fearnhead 2005) and returns the largest values of 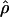 at loci when no recombination events are detected (based on recombination counts Rm–Ru = 0, Table 2), presumably because these loci have a limited number of informative sites.
at loci when no recombination events are detected (based on recombination counts Rm–Ru = 0, Table 2), presumably because these loci have a limited number of informative sites.
Relative to other estimators, Lamarc consistently returns a lower estimate of ρ (Figure 3; Table 4). Estimates of 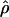 Lamarc do not differ dramatically from other estimates for loci with relatively low values of
Lamarc do not differ dramatically from other estimates for loci with relatively low values of 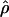 or
or 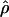 /
/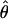 (Figure 3); e.g.,
(Figure 3); e.g., 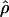 /
/ 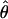 < 1. However, analysis of simulated data sets shows poor performance for Lamarc when
< 1. However, analysis of simulated data sets shows poor performance for Lamarc when 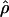 /
/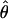 > 1 (Fearnhead and Donnelly 2002). One possible explanation is that in using a nucleotide substitution model, Lamarc is better able to account for the mutation events and attributes a larger proportion of diversity to
> 1 (Fearnhead and Donnelly 2002). One possible explanation is that in using a nucleotide substitution model, Lamarc is better able to account for the mutation events and attributes a larger proportion of diversity to 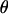 . However, repeat mutations at a single site are quite rare in the wild barley data set with only 0.74% of sites with more than two nucleotide states. Lamarc does return the largest average estimate of θ, but the estimate is not significantly different from the smallest average estimate
. However, repeat mutations at a single site are quite rare in the wild barley data set with only 0.74% of sites with more than two nucleotide states. Lamarc does return the largest average estimate of θ, but the estimate is not significantly different from the smallest average estimate 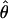 FD02 (one-tailed paired t-test, P = 0.067).
FD02 (one-tailed paired t-test, P = 0.067).
Estimating the role of gene conversion:
Among the wild barley loci, maxhap estimates 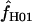 > 0 for nine loci, but only three of these show
> 0 for nine loci, but only three of these show 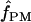 > 0 (on the basis of pattern matching). Several wild barley loci do not include any triplets or quadruplets of sites in pattern a or d. For example, ORF1 and Stk with 22 and 20 parsimony-informative sites do not contain any site configurations consistent with conversion or double crossover, and thus pattern matching is not possible. The number of triplets possible at a locus is (Sp × (Sp − 1) × (Sp − 2))/3!, where Sp indicates parsimony-informative segregating sites. Thus the number of triplets increases exponentially with an increase in the number of informative segregating sites.
> 0 (on the basis of pattern matching). Several wild barley loci do not include any triplets or quadruplets of sites in pattern a or d. For example, ORF1 and Stk with 22 and 20 parsimony-informative sites do not contain any site configurations consistent with conversion or double crossover, and thus pattern matching is not possible. The number of triplets possible at a locus is (Sp × (Sp − 1) × (Sp − 2))/3!, where Sp indicates parsimony-informative segregating sites. Thus the number of triplets increases exponentially with an increase in the number of informative segregating sites.
Pattern-matching simulations result in estimates of 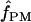 = 1–2 for wild barley loci that show evidence of gene conversion. Because half of coalescent simulations with f = 0 (and ρ set to the mean value for wild barley) result in estimates of
= 1–2 for wild barley loci that show evidence of gene conversion. Because half of coalescent simulations with f = 0 (and ρ set to the mean value for wild barley) result in estimates of 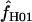 > 0, maxhap estimates cannot be used to accurately identify the presence of gene conversion. However,
> 0, maxhap estimates cannot be used to accurately identify the presence of gene conversion. However, 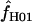 = 0 can be used to rule out high levels of gene conversion at a locus.
= 0 can be used to rule out high levels of gene conversion at a locus.
Much higher rates of gene conversion than we identify on the basis of pattern matching have been reported on the basis of nucleotide sequence data from A. thaliana. Using an ad hoc method, Haubold et al. (2002) reported 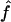 = 9 in sequence data from A. thaliana; two- and three-site likelihood analyses resulted in
= 9 in sequence data from A. thaliana; two- and three-site likelihood analyses resulted in 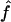 estimates = 14.8 and 16 on the basis of the same data (Wall 2004). Another recent estimate from a large number of A. thaliana loci reported a mean
estimates = 14.8 and 16 on the basis of the same data (Wall 2004). Another recent estimate from a large number of A. thaliana loci reported a mean 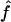 = 5 (Nordborg et al. 2005), although this estimate has recently been revised to
= 5 (Nordborg et al. 2005), although this estimate has recently been revised to 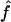 = 1 (Plagnol et al. 2006). For wild barley, if chromosomes were actually subject to five times more gene conversion than crossover, using maxhap, we would mistakenly estimate
= 1 (Plagnol et al. 2006). For wild barley, if chromosomes were actually subject to five times more gene conversion than crossover, using maxhap, we would mistakenly estimate 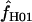 = 0 at 2.4 or 8.3% of loci on the basis of simulations with L = 250- and 500-bp tract lengths. Therefore we can reject f = 5 in wild barley with 98 or 92% confidence depending on the assumed tract length. On the basis of the implications of coalescent simulations and our observation that minor errors in genotyping can dramatically affect
= 0 at 2.4 or 8.3% of loci on the basis of simulations with L = 250- and 500-bp tract lengths. Therefore we can reject f = 5 in wild barley with 98 or 92% confidence depending on the assumed tract length. On the basis of the implications of coalescent simulations and our observation that minor errors in genotyping can dramatically affect 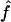 for data sets that have not been rigorously purged of typing errors, it is likely that the role of gene conversion has been overestimated in the literature.
for data sets that have not been rigorously purged of typing errors, it is likely that the role of gene conversion has been overestimated in the literature.
As is evident from the preceding discussion, it is difficult to estimate the relative role of gene conversion from nucleotide sequence data. There are at least four major challenges. The first is that unlike crossing over, which initiates as a point process that extends to the end of the chromosome, gene conversion events involve small tracts of chromosomes and therefore a limited number of segregating sites. Thus evidence for gene conversion is necessarily limited and fragmentary. The second issue is that it is difficult to collect nucleotide sequence data appropriate for estimating the role of gene conversion. In random-mating organisms, direct sequencing of PCR products yields unphased sequence data with little utility for inferring conversion. Experimental phasing of data through cloning of PCR products is expensive and labor intensive and can propagate PCR artifacts such as PCR recombinants that make accurate determination of haplotypes much more difficult (Cronn et al. 2002). The use of inbred lines or inbreeding organisms (with allele-specific PCR and direct sequencing for occasional heterozygotes) makes data collection much more tractable, but there must have been a history of occasional heterozygosity for recombination to have ever been effective. Also, the organism under consideration must have sufficient levels of sequence polymorphism so that at least a single segregating site occurs in conversion tracts likely to be only hundreds of base pairs in length (Hilliker et al. 1994; Frisse et al. 2001; Jeffreys and May 2004). Otherwise gene conversion events will play a limited role in effective recombination. Also the locus sequenced must be of sufficient length to contain perhaps 20 parsimony-informative segregating sites, on the basis of the observation that the observed proportion of pattern a triplets is ≤1% for wild barley loci purged of typing errors and assuming f = 1. The sequenced portion of a chromosome must also be of sufficient length to contain conversion events within its bounds; i.e., in a 1500-bp region, many 500-bp conversion tracts can fall partially out of bounds (Wiuf and Hein 2000). At present, there are relatively few population genetic data sets of sufficient length and sample number to provide information regarding the role of gene conversion within a single locus. The third issue is that genotyping errors, particularly those contributed by undetected heterozygotes, can introduce base calls from one chromosome interstitially with base calls from another; this is especially likely to add a fourth gametic state to a pairwise comparison of sites, resulting in upwardly biased estimates of 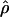 (see Table 3) and
(see Table 3) and 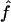 (Ptak et al. 2004). As demonstrated above, examination of the base calls that contribute to inference of double crossover or gene conversion provides a means of eliminating genotyping errors and is particularly effective at identifying heterozygotes that were not detected during sequence assembly. The potential to detect heterozygotes can be considerable, because undetected heterozygotes can contribute the rarest gametic class to multiple, mutually exclusive sets of segregating sites in pattern a. The effects of genotyping or phasing errors on pattern matching vary due to the number of segregating sites that were incorrectly typed (Table 3), with one potential impact being that such a large proportion of sites appear to show evidence of double crossover or gene conversion that it is difficult to find input values for coalescent simulations that provide a good match to the data. Unfortunately, simply increasing sample size does not eliminate the problem. Because of a constant probability of sampling a heterozygote, undetected heterozygotes continue to be a problem with increasing sample size. The fourth issue in estimating f is that it is necessary to account for unknown tract length, and both ρ and θ must be estimated from the data (Ptak et al. 2004). Thus in simulations, the grid of parameter values that must be searched is large and the shape of the likelihood surface could be complex (see Figure 5).
(Ptak et al. 2004). As demonstrated above, examination of the base calls that contribute to inference of double crossover or gene conversion provides a means of eliminating genotyping errors and is particularly effective at identifying heterozygotes that were not detected during sequence assembly. The potential to detect heterozygotes can be considerable, because undetected heterozygotes can contribute the rarest gametic class to multiple, mutually exclusive sets of segregating sites in pattern a. The effects of genotyping or phasing errors on pattern matching vary due to the number of segregating sites that were incorrectly typed (Table 3), with one potential impact being that such a large proportion of sites appear to show evidence of double crossover or gene conversion that it is difficult to find input values for coalescent simulations that provide a good match to the data. Unfortunately, simply increasing sample size does not eliminate the problem. Because of a constant probability of sampling a heterozygote, undetected heterozygotes continue to be a problem with increasing sample size. The fourth issue in estimating f is that it is necessary to account for unknown tract length, and both ρ and θ must be estimated from the data (Ptak et al. 2004). Thus in simulations, the grid of parameter values that must be searched is large and the shape of the likelihood surface could be complex (see Figure 5).
Given these caveats regarding the estimation of the contribution of gene conversion, simulation-based methods can be informative when applied to properly phased, accurate nucleotide sequence data of sufficient length and sample number (Padhukasahasram et al. 2004). When confirmation of base calls is used to corroborate the presence of accurately typed sites in patterns a and d, simulation-based pattern-matching methods permit a likelihood-based assessment of a null hypothesis that the empirical data can be explained without invoking gene conversion. Specifically, are the observed patterns of triplets and quadruplets of sites better explained by a series of proximate recombination events? Our pattern-matching simulations indicate a biologically relevant role for gene conversion in loci from wild barley, Drosophila, and Z. mays. Among data sets from 27 loci that were large enough for pattern matching, 13 return 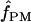 > 0. Across the 27 loci (obviously from a very disparate set of organisms), mean
> 0. Across the 27 loci (obviously from a very disparate set of organisms), mean 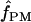 = 1.29 and median
= 1.29 and median 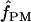 = 1. For loci with
= 1. For loci with 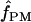 > 0, median
> 0, median 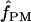 = 2, suggesting that at a subset of loci, gene conversion may have contributed roughly twice as much as crossing over to total recombination.
= 2, suggesting that at a subset of loci, gene conversion may have contributed roughly twice as much as crossing over to total recombination.
In summary, it appears that wild barley has remarkably high levels of genetic diversity, with diversity similar to that observed in outcrossing organisms such as D. melanogaster. Despite high levels of self-fertilization, recombination has been at least as important as mutation in generating allelic diversity in wild barley. There is evidence that gene conversion plays a role in recombination at some loci.
Acknowledgments
We thank J. Lauricha, B. Padhukasahasram, and K. Thornton for suggestions during the analysis and J. Gruber, S. Macdonald, K. Thornton, and D. Wolf for helpful discussion and comments on an earlier version of the manuscript. This work was supported by National Science Foundation grant DEB-0129247.
References
- Abdel-Ghani, A. H., H. K. Parzies, A. Omary and H. H. Geiger, 2004. Estimating the outcrossing rate of barley landraces and wild barley populations collected from ecologically different regions of Jordan. Theor. Appl. Genet. 109: 588–595. [DOI] [PubMed] [Google Scholar]
- Andolfatto, P., and M. Nordborg, 1998. The effect of gene conversion on intralocus associations. Genetics 148: 1397–1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek, H. J., A. Beharav and E. Nevo, 2003. Ecological-genomic diversity of microsatellites in wild barley, Hordeum spontaneum, populations in Jordan. Theor. Appl. Genet. 106: 397–410. [DOI] [PubMed] [Google Scholar]
- Balakirev, E. S., and F. J. Ayala, 2004. a The β-esterase gene cluster of Drosophila melanogaster: is ψEst-6 a pseudogene, a functional gene, or both? Genetica 121: 165–179. [DOI] [PubMed] [Google Scholar]
- Balakirev, E. S., and F. J. Ayala, 2004. b Nucleotide variation in the tinman and bagpipe homeobox genes of Drosophila melanogaster. Genetics 166: 1845–1856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balakirev, E. S., V. R. Chechetkin, V. V. Lobzin and F. J. Ayala, 2003. DNA polymorphism in the β-esterase gene cluster of Drosophila melanogaster. Genetics 164: 533–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Begun, D. J., and C. F. Aquadro, 1995. Molecular variation at the vermilion locus in geographically diverse populations of Drosophila melanogaster and D. simulans. Genetics 140: 1019–1032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bomblies, K., and J. F. Doebley, 2005. Pleiotropic effects of the duplicate maize FLORICAULA/LEAFY genes zfl1 and zfl2 on traits under selection during maize domestication. Genetics 172: 519–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown, A. H. D., D. Zohary and E. Nevo, 1978. Outcrossing rates and heterozygosity in natural populations of Hordeum spontaneum. Heredity 41: 49–62. [Google Scholar]
- Caldwell, K. S., J. R. Russell, P. Langridge and W. Powell, 2005. Extreme population dependent linkage disequilibrium detected in an inbreeding plant species, Hordeum vulgare. Genetics 172: 557–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth, D., and X. Vekemans, 2005. How and when did Arabidopsis thaliana become highly self-fertilising? BioEssays 27: 472–476. [DOI] [PubMed] [Google Scholar]
- Charlesworth, D., B. Charlesworth and C. Strobeck, 1977. Effects of selfing on selection for recombination. Genetics 86: 213–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi, D. W., B. Zhu and T. J. Close, 1999. The barley (Hordeum vulgare L.) dehydrin multigene family: sequences, allele types, chromosome assignments, and expression characteristics of 11 Dhn genes of cv Dicktoo. Theor. Appl. Genet. 98: 1234–1247. [Google Scholar]
- Copenhaver, G. P., E. A. Housworth and F. W. Stahl, 2002. Crossover interference in Arabidopsis. Genetics 160: 1631–1639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cronn, R., M. Cedroni, T. Haselkorn, C. Grover and J. F. Wendel, 2002. PCR-mediated recombination in amplification products derived from polyploid cotton. Theor. Appl. Genet. 104: 482–489. [DOI] [PubMed] [Google Scholar]
- Cummings, M. P., and M. T. Clegg, 1998. Nucleotide sequence diversity at the alcohol dehydrogenase 1 locus in wild barley (Hordeum vulgare spp. spontaneum): an evaluation of the background selection hypothesis. Proc. Natl. Acad. Sci. USA 95: 5637–5642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DuMont, V. B., J. C. Fay, P. P. Calabrese and C. F. Aquadro, 2004. DNA variability and divergence at the notch locus in Drosophila melanogaster and D. simulans: a case of accelerated synonymous site divergence. Genetics 167: 171–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fearnhead, P., and P. Donnelly, 2002. Approximate likelihood methods for estimating local recombination rates. J. R. Stat. Soc. Ser. B Stat. Methodol. 64: 657–680. [Google Scholar]
- Frisse, L., R. R. Hudson, A. Bartoszewicz, J. D. Wall, J. Donfack et al., 2001. Gene conversion and different population histories may explain the contrast between polymorphism and linkage disequilibrium levels. Am. J. Hum. Genet. 69: 831–843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant, V., 1958. The regulation of recombination in plants. Cold Spring Harbor Symp. Quant. Biol. 23: 337–363. [DOI] [PubMed] [Google Scholar]
- Griffiths, R. C., and P. Marjoram, 1996. Ancestral inference from samples of DNA sequences with recombination. J. Comput. Biol. 3: 479–502. [DOI] [PubMed] [Google Scholar]
- Haddrill, P. R., K. R. Thornton, B. Charlesworth and P. Andolfatto, 2005. Multilocus patterns of nucleotide variability and the demographic and selection history of Drosophila melanogaster populations. Genome Res. 15: 790–799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harr, B., M. Kauer and C. Schlotterer, 2002. Hitchhiking mapping: a population-based fine-mapping strategy for adaptive mutations in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 99: 12949–12954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haubold, B., J. Kroymann, A. Ratzka, T. Mitchell-Olds and T. Wiehe, 2002. Recombination and gene conversion in a 170-kb genomic region of Arabidopsis thaliana. Genetics 161: 1269–1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey, J., and J. Wakeley, 1997. A coalescent estimator of the population recombination rate. Genetics 145: 833–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilliker, A. J., G. Harauz, A. G. Reaume, M. Gray, S. H. Clark et al., 1994. Meiotic gene conversion tract length distribution within the rosy locus of Drosophila melanogaster. Genetics 137: 1019–1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holliday, R., 1964. A mechanism for gene conversion in fungi. Genet. Res. 5: 282–287. [DOI] [PubMed] [Google Scholar]
- Hudson, R. R., 1987. Estimating the recombination parameter of a finite population model without selection. Genet. Res. 50: 245–250. [DOI] [PubMed] [Google Scholar]
- Hudson, R. R., 1990. Gene genealogies and the coalescent process. Oxf. Surv. Evol. Biol. 7: 1–44.
- Hudson, R. R., 2001. Two-locus sampling distributions and their application. Genetics 159: 1805–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson, R. R., 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18: 337–338. [DOI] [PubMed] [Google Scholar]
- Hudson, R. R., and N. L. Kaplan, 1985. Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 111: 147–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffreys, A. J., and C. A. May, 2004. Intense and highly localized gene conversion activity in human meiotic crossover hot spots. Nat. Genet. 36: 151–156. [DOI] [PubMed] [Google Scholar]
- Kishino, H., and M. Hasegawa, 1989. Evaluation of the maximum likelihood estimate of the evolutionary tree topologies from DNA sequence data, and the branching order in Hominoidea. J. Mol. Evol. 29: 170–179. [DOI] [PubMed] [Google Scholar]
- Kuhner, M. K., J. Yamato and J. Felsenstein, 2000. Maximum likelihood estimation of recombination rates from population data. Genetics 156: 1393–1401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhner, M. K., P. Beerli, J. Yamato and J. Felsenstein, 2002. Lamarc: Likelihood Analysis with Metropolis Algorithm using Random Coalescence. University of Washington, Seattle.
- Lachaise, D., M. L. Cariou, J. R. David, F. Lemeunier, L. Tsacas et al., 1988. Historical biogeography of the Drosophila melanogaster species subgroup. Evol. Biol. 22: 159–225. [Google Scholar]
- Li, N., and M. Stephens, 2003. Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics 165: 2213–2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, J.-Z., A. H. D. Brown and M. T. Clegg, 2001. Heterogeneous geographic patterns of nucleotide sequence diversity between two alcohol dehydrogenase genes in wild barley (Hordeum vulgare susbpecies spontaneum). Proc. Natl. Acad. Sci. USA 98: 531–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, J.-Z., P. L. Morrell and M. T. Clegg, 2002. The influence of linkage and inbreeding on patterns of nucleotide sequence diversity at duplicate alcohol dehydrogenase loci in wild barley (Hordeum vulgare ssp. spontaneum). Genetics 162: 2007–2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lincoln, S. E., and E. S. Lander, 1992. Systematic detection of errors in genetic linkage data. Genomics 14: 604–610. [DOI] [PubMed] [Google Scholar]
- Malkova, A., J. Swanson, M. German, J. H. McCusker, E. A. Housworth et al., 2004. Gene conversion and crossing over along the 405-kb left arm of Saccharomyces cerevisiae chromosome VII. Genetics 168: 49–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean, G. A. T., P. Awadalla and P. Fearnhead, 2002. A coalescent-based method for detecting and estimating recombination from gene sequences. Genetics 160: 1231–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrell, P. L., K. E. Lundy and M. T. Clegg, 2003. Distinct geographic patterns of genetic diversity are maintained in wild barley (Hordeum vulgare ssp. spontaneum) despite migration. Proc. Natl. Acad. Sci. USA 100: 10812–10817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrell, P. L., D. M. Toleno, K. E. Lundy and M. T. Clegg, 2005. Low levels of linkage disequilibrium in wild barley (Hordeum vulgare ssp. spontaneum) despite high rates of self-fertilization. Proc. Natl. Acad. Sci. USA 102: 2442–2447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers, S. R., and R. C. Griffiths, 2003. Bounds on the minimum number of recombination events in a sample history. Genetics 163: 375–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevo, E., D. Zohary, A. H. D. Brown and M. Haber, 1979. Genetic diversity and environmental associations of wild barley, Hordeum spontaneum, in Israel. Evolution 33: 815–833. [DOI] [PubMed] [Google Scholar]
- Nordborg, M., 1999. The coalescent with partial selfing and balancing selection: an application of structured coalescent processes, pp. 56–76 in Statistics in Molecular Biology and Genetics (IMS Lecture Notes-Monograph Series, Vol. 33), edited by F. Seillier-Moiseiwitsch. Institute of Mathematical Statistics, Hayward, CA.
- Nordborg, M., 2000. Linkage disequilibrium, gene trees and selfing: an ancestral recombination graph with partial self-fertilization. Genetics 154: 923–929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg, M., T. T. Hu, Y. Ishino, J. Jhaveri, C. Toomajian et al., 2005. The pattern of polymorphism in Arabidopsis thaliana. PloS Biol. 3: e196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padhukasahasram, B., P. Marjoram and M. Nordborg, 2004. Estimating the rate of gene conversion on human chromosome 21. Am. J. Hum. Genet. 75: 386–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plagnol, V., B. Padhukasahasram, J. D. Wall, P. Marjoram and M. Nordborg, 2006. Relative influences of crossing over and gene conversion on the pattern of linkage disequilibrium in Arabidopsis thaliana. Genetics 172: 2441–2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Presgraves, D. C., 2005. Recombination enhances protein adaptation in Drosophila melanogaster. Curr. Biol. 15: 1651–1656. [DOI] [PubMed] [Google Scholar]
- Ptak, S. E., K. Voelpel and M. Przeworski, 2004. Insights into recombination from patterns of linkage disequilibrium in humans. Genetics 167: 387–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riley, R. M., W. Jin and G. Gibson, 2003. Contrasting selection pressures on components of the Ras-mediated signal transduction pathway in Drosophila. Mol. Ecol. 12: 1315–1323. [DOI] [PubMed] [Google Scholar]
- Schaeffer, S. W., and E. L. Miller, 1992. Estimates of gene flow in Drosophila pseudoobscura determined from nucleotide sequence analysis of the alcohol dehydrogenase region. Genetics 132: 471–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, N. G., and P. Fearnhead, 2005. A comparison of three estimators of the population-scaled recombination rate: accuracy and robustness. Genetics 171: 2051–2062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song, Y. S., Y. F. Wu and D. Gusfield, 2005. Efficient computation of close lower and upper bounds on the minimum number of recombinations in biological sequence evolution. Bioinformatics 21: I413–I422. [DOI] [PubMed] [Google Scholar]
- Stahl, F. W., 1994. The Holliday junction on its thirtieth anniversary. Genetics 138: 241–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stumpf, M. P. H., and G. A. T. McVean, 2003. Estimating recombination rates from population-genetic data. Nat. Rev. Genet. 4: 959–968. [DOI] [PubMed] [Google Scholar]
- Swofford, D., G. L. Olsen, P. J. Waddell and D. M. Hillis, 1996. Phylogenetic inference, pp. 407–514 in Molecular Systematics, edited by D. M. Hillis, C. Moritz and B. K. Mable. Sinauer Associates, Sunderland, MA.
- Tajima, F., 1983. Evolutionary relationship of DNA sequences in finite populations. Genetics 105: 437–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima, F., 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123: 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenaillon, M. I., M. C. Sawkins, A. D. Long, R. L. Gaut, J. F. Doebley et al., 2001. Patterns of DNA sequence polymorphism along chromosome 1 of maize (Zea mays ssp. mays L.). Proc. Natl. Acad. Sci. USA 98: 9161–9166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenaillon, M. I., M. C. Sawkins, L. K. Anderson, S. M. Stack, J. Doebley et al., 2002. Patterns of diversity and recombination along chromosome 1 of maize (Zea mays ssp. mays L.). Genetics 162: 1401–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton, K., 2003. libsequence: a C++ class library for evolutionary genetic analysis. Bioinformatics 19: 2325–2327. [DOI] [PubMed] [Google Scholar]
- Thornton, K., and P. Andolfatto, 2006. Approximate Bayesian inference reveals evidence for a recent, severe, bottleneck in a Netherlands population of Drosophila melanogaster. Genetics 172: 1607–1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volis, S., S. Mendlinger, Y. Turuspekov, U. Esnazarov, S. Abugalieva et al., 2001. Allozyme variation in Turkmenian populations of wild barley, Hordeum spontaneum Koch. Ann. Bot. 87: 435–446. [Google Scholar]
- Volis, S., S. Mendlinger, Y. Turuspekov and U. Esnazarov, 2002. Phenotypic and allozyme variation in Mediterranean and desert populations of wild barley, Hordeum spontaneum Koch. Evol. Int. J. Org. Evol. 56: 1403–1415. [DOI] [PubMed] [Google Scholar]
- Wall, J. D., 2000. A comparison of estimators of the population recombination rate. Mol. Biol. Evol. 17: 156–163. [DOI] [PubMed] [Google Scholar]
- Wall, J. D., 2004. Estimating recombination rates using three-site likelihoods. Genetics 167: 1461–1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watterson, G. A., 1975. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 7: 188–193. [DOI] [PubMed] [Google Scholar]
- Wiuf, C., and J. Hein, 2000. The coalescent with gene conversion. Genetics 155: 451–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, S. I., I. V. Bi, S. G. Schroeder, M. Yamasaki, J. F. Doebley et al., 2005. The effects of artificial selection on the maize genome. Science 308: 1310–1314. [DOI] [PubMed] [Google Scholar]
- Zurovcova, M., and F. J. Ayala, 2002. Polymorphism patterns in two tightly linked developmental genes, Idgf1 and Idgf3, of Drosophila melanogaster. Genetics 162: 177–188. [DOI] [PMC free article] [PubMed] [Google Scholar]