The protein-folding speed limit: Intrachain diffusion times set by electron-transfer rates in denatured Ru(NH₃)₅(His-33)-Zn-cytochrome c

Abstract

The kinetics of electron transfer from the triplet-excited Zn-porphyrin to a Ru(NH₃)₅(His-33)³⁺ complex have been measured in Zn-substituted ruthenium-modified cytochrome c under denaturing conditions. In the folded protein, the electron-tunneling rate constant is 7.5 × 10⁵ s⁻¹. As the protein is denatured with guanidine hydrochloride, a faster adiabatic electron-transfer reaction appears (4.0 × 10⁶ s⁻¹, [guanidine hydrochloride] = 5.4 M) that is limited by the rate of intrachain diffusion to bring the Zn-porphyrin and Ru complex into contact. The 250-ns contact time for formation of a 15-residue loop in denatured cytochrome c is in accord with a statistical model developed by Camacho and Thirumalai [Camacho, C. J. & Thirumalai, D. (1995) Proc. Natl. Acad. Sci. USA 92, 1277–1281] that predicts that the most probable transient loops formed in denatured proteins are comprised of 10 amino acids. Extrapolation of the cytochrome c contact time to a 10-residue loop sets the folding speed limit at ≈10⁷ s⁻¹.

The formation of tertiary contacts during protein folding is recognized as a pivotal step in the formation of native structure (1–3). Under denaturing conditions, transient loops will form as a result of tertiary contacts between amino acids. After a rapid shift in equilibrium to conditions that favor native structure, hydrophobic tertiary contacts will persist, producing collapsed structures. It is clear that proteins can fold no faster than the rate at which native tertiary contacts are made. Statistical mechanical models suggest that the probability and rate of forming transient tertiary contacts in random polymers are determined largely by two factors: the coefficient for intrachain diffusion and the size of the resultant loop (4–6). The most probable loop formed in a random polypeptide is estimated to be comprised of 10 residues (6).

Experimental investigations of tertiary-contact formation in proteins and polymers have been aimed at determining the upper limit for protein-folding rates (1–3). The 40-μs time scale for methionine (Met-65 and Met-80) binding to the ferroheme in denatured cytochrome c (cyt c) suggested an ≈10⁶ s⁻¹ folding speed limit (2). Subsequent investigations of electron-transfer (ET) quenching of triplet-excited tryptophan by cysteine in synthetic peptides led to a value closer to 10⁷ s⁻¹ (7). This larger value is in line with estimates based on triplet energy transfer in dye-labeled peptides (3).

These experimental determinations of polymer contact times exploit measurements of the rates of reactions with very small intrinsic barriers. ET reactions are well suited to investigations of this type, because the barriers can be minimized by tuning the reaction driving force (8–12). In prior studies, we measured ET kinetics and identified likely tunneling pathways in Zn-cyt c labeled at surface histidine residues with a Ru(NH₃)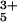 moiety (13–16). The dominant electronic coupling pathway between the redox centers in Ru(NH₃)₅(His-33)-Zn-cyt c [Ru(His-33)-Zn-cyt c] has 15 covalent bonds and 1 H bond between the carbonyl oxygen of Pro-30 and the proton on the N^δ atom of His-18 (Fig. 1; ref. 15). Chemical denaturants will disrupt this pathway, leaving only the 15-residue covalent link between His-33 and the Zn-coordinated His-18 residue. Electron tunneling along this 45-bond covalent pathway will be extremely unfavorable (17, 18). ET from the triplet-excited Zn-porphyrin (*ZnP) to the Ru(His-33)³⁺ complex in the denatured protein, then, will likely be an adiabatic process within an encounter complex formed by intrachain diffusion to bring the two redox complexes into van der Waals contact. Driving-force and temperature dependencies demonstrated that the *ZnP → Ru(His-33)³⁺ ET (7.5 × 10⁵ s⁻¹) is nearly activationless. In the presence of denaturant, then, *ZnP → Ru(His-33)³⁺ ET should be a diffusion-limited process, and the time scale for the reaction will set the speed limit for formation of an ≈15-residue loop in an unfolded polypeptide.

Figure 1.

Peptide backbone of a structural model of Ru(His-33)-Zn-cyt c. A well coupled electron-tunneling pathway from His-33 to the porphyrin is shown in black. The dashed line is a hydrogen-bonded contact between the carbonyl group of Pro-30 and the N^δ of His-18.

Materials and Methods

Guanidine hydrochloride (Gdn⋅HCl, ultrapure grade, Sigma) was used as received. Gdn⋅HCl concentrations were determined by refractive index measurements (19). Zinc-substituted cyt c was prepared from the horse heart protein (Sigma) according to standard procedures (13). Ru modification was accomplished by reaction of the protein with Ru(NH₃)₅(OH₂)²⁺; the derivatized protein was purified by ion-exchange chromatography (13, 20).

Intraprotein ET kinetics were measured by transient absorption spectroscopy by using a Nd-YAG pumped optical parametric oscillator as an excitation source (λ_ex = 580 nm; 10-ns pulse) and a Xe arc lamp as a probe source (λ_obs = 450 nm) (21). The kinetics were fit to single- and double-exponential functions by using a Levenberg–Marquardt nonlinear least-squares algorithm implemented in MATLAB (Mathworks, Natick, MA).

Results and Discussion

Chemical denaturants (e.g., Gdn⋅HCl and urea) destabilize the secondary and tertiary contacts in folded proteins, producing polymers with highly disordered, albeit not necessarily random, conformations. Because of the spectroscopic, photophysical, and redox properties of Zn-porphyrin, we can initiate *ZnP → Ru(His-33)³⁺ ET with a nanosecond laser pulse and monitor the reaction kinetics by transient absorption spectroscopy (λ_obs = 450 nm) (13). In the native (folded) protein, the *ZnP → Ru(His-33)³⁺ ET rate constant is 7.5 × 10⁵ s⁻¹ (13). The addition of Gdn⋅HCl up to a concentration of 1.6 M produces only a modest increase in the observed rate of ET (Fig. 2). This behavior contrasts with that observed in the bimolecular quenching reaction of Zn-cyt c with Ru(NH₃)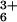 in which modest concentrations of Gdn⋅HCl (≤1.5 M) substantially accelerate ET, presumably because of ionic strength effects (22, 23).

Figure 2.

Relative amplitudes (Upper) and rate constants (Lower) extracted from biexponential fits to the *ZnP decay kinetics in Ru(His-33)-Zn-cyt c plotted as functions of denaturant concentration.

At Gdn⋅HCl concentrations >1.6 M, intramolecular ET kinetics in Ru(His-33)-Zn-cyt c must be fit with biexponential functions. The rate constant for the slower phase is about the same as that found for the native protein. The rate constant for the faster phase increases with increasing denaturant concentration, reaching a maximum at [Gdn⋅HCl] = 2.5 M. The amplitudes of the two phases depend on denaturant concentration as well; the contribution of the slower phase decreases in favor of the faster phase as [Gdn⋅HCl] increases (Fig. 2). At the highest denaturant concentration (5.5 M), the biphasic Ru(His-33)-Zn-cyt c ET kinetics are dominated by a component (83%) with a 250-ns lifetime. The lifetime of the minor component (17%, 610 ns) is shorter than that found in the folded protein. It is not likely that any folded protein is still present in 5.5 M Gdn⋅HCl; the biphasic Ru(His-33)-Zn-cyt c kinetics may be attributable to structural heterogeneity in the unfolded ensemble (24, 25). Clearly, denaturation of Ru(His-33)-Zn-cyt c produces species in which intramolecular ET is faster than the bond-mediated tunneling process in the folded molecule. The likely explanation for this behavior is that intrachain diffusion in the denatured polypeptide brings *ZnP and Ru(NH₃)₅(His-33)³⁺ into close contact before ET (2, 7). This interpretation is consistent with diffusion-controlled quenching of denatured *Zn-cyt c by Ru(NH₃)₆³⁺ (22).

Above 2.5 M [Gdn⋅HCl], the higher ET rate in Ru(His-33)-Zn-cyt c decreases slightly from a maximum value of 5.5 × 10⁶ s⁻¹, perhaps in response to the increased viscosity of concentrated denaturant solutions. To test this proposition, we examined Ru(His-33)-Zn-cyt c ET kinetics in solutions of 5.4 M [Gdn⋅HCl] to which sucrose had been added as a viscometric reagent (Fig. 3). The rate constants of both components of the ZnP triplet decay decrease substantially as the solution viscosity increases, but their amplitudes remain relatively invariant. These observations provide compelling support for the interpretation that intramolecular ET in denatured Ru(His-33)-Zn-cyt c is limited by intrachain diffusion.

Figure 3.

Variation of fast (●) and slow (♦) *ZnP decay-rate constants in denatured Ru(His-33)-Zn-cyt c (8 μM) as functions of the amount of viscometric reagent (sucrose) added (1.5-ml sample volume, [NaP_i] = 100 mM, [Gdn⋅HCl] = 5.4 M).

The time scales of tertiary-contact formation in peptides and proteins have been investigated both experimentally (1–3, 7, 26–28) and theoretically (4–6, 29–31). Szabo et al. (4) used a diffusion model to develop an expression describing the time scale for end-to-end contact formation in polymers. Building on this model, Hagen et al. (2) suggested that the end-to-end contact rate in a polymer will vary as Dn^−3/2 (D is the polymer diffusion constant, and n is the number of residues in the polymer). Thirumalai (6) used a statistical mechanical model for semiflexible polymers to determine the probability of transient loop formation [P(n)] in a random polypeptide. If tertiary-contact formation is diffusion-limited, this model predicts that the contact rate constant varies as DP(n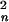)/〈R〉 (〈R〉 is the mean-squared distance between two residues separated by n monomer units) (6). The two models suggest that contact rates will be proportional to the intrachain diffusion constant, but they predict different dependencies on n (Fig. 4). Hagen et al. (2) and Jones et al. (32) measured the rates of Fe-S(Met-80/65) and Fe-N(His-26/33) contact formation (Met, 2.5 × 10⁴ s⁻¹; His, 2.5 × 10³ s⁻¹) after CO dissociation from denatured Fe^II(CO)-cyt c ([Gdn⋅HCl] = 4.6 M, temperature = 40°C). The Fe-N(His-26/33) binding kinetics proved to be less useful for evaluating intrachain diffusion rates than the Fe-S(Met-80/65) binding data. Our measured 250-ns time constant for formation of an ≈15-residue loop (His-18–His-33, [Gdn⋅HCl] = 5.4 M) in Ru(His-33)-Zn-cyt c demonstrates that tertiary-contact formation can occur very rapidly in denatured cyt c. Met ligands can bind to only one face of the heme in denatured cyt c, whereas adiabatic ET reactions of the Zn-cyt c porphyrin should be nearly isotropic. A correction factor is required to compare contact rates measured by ligand binding to those extracted from ET reactions; we have multiplied the Met-80/65 binding rate by a factor of 2 for this purpose. The solid angle for ligand approach to the axial binding site of an iron–porphyrin is likely to be smaller than the 2π steradians of a hemisphere, suggesting that 2 is a lower limit for this correction factor. If the diffusion coefficient is treated as an adjustable parameter (D = 2 × 10⁻⁵ cm²/s), the Camacho–Thirumalai model accords closely with the experimental His-33 and Met-80 contact-formation rate constants (Fig. 4) and predicts that the most probable loop in denatured cyt c will form in ≈65 ns. This value agrees well with measurements of end-to-end contact formation in small (n = 3–19) peptides (3, 7). Taken together, these measurements suggest that a 10-residue polypeptide loop will form in ≈100 ns, which sets the speed limit for protein folding near 10⁷ s⁻¹.

Figure 4.

Rates of tertiary-contact formation in denatured cyt c have been extracted from measurements of ET rates in Ru(His-33)-Zn-cyt c (●, [Gdn⋅HCl] = 5.4 M, temperature = 22°C, 15-residue loop) (this work) and Met-65/80 binding kinetics in Fe^II-cyt c (♦, [Gdn⋅HCl] = 5.6 M, temperature = 40°C, 47 (Met-65) and 62 (Met-80) residue loops) (2). The experimental binding rates have been corrected by a statistical factor of 2, because ligand substitution can proceed only on one side of the heme plane. The solid line was calculated by using the Camacho–Thirumalai model of the loop-size dependence of tertiary-contact rates (6) with a diffusion coefficient of 2 × 10⁻⁵ cm²/s. The dashed line was calculated by using the Szabo model (4) with a diffusion coefficient of 5.4 × 10⁻⁷ cm²/s (2). All other parameters used in the two models were the same as those described by Hagen et al. (2).

Abbreviations

cyt c

cytochrome c

ET

electron transfer

Ru(His-33)-Zn-cyt c

Ru(NH₃)₅(His-33)-Zn-cyt c

*ZnP

triplet-excited Zn-porphyrin

Gdn⋅HCl

guanidine hydrochloride