Estimation of chest-wall-induced diffused wave distortion with the assistance of ultrasound

Abstract

The chest-wall layer underneath breast tissue consists of muscles and bones, which induce distortion in near-infrared diffused waves measured at distant source–detector pairs when reflection geometry is used. A priori information on chest-wall depth obtained from coregistered real-time ultrasound can be used to assist in the removal of distant measurements. We applied Monte Carlo simulation to a simple two-layer model consisting of breast tissue and a chest wall to investigate chest-wall-induced distortion. The Monte Carlo method indicates that, when more than 50% of the received photons travel through the breast tissue layer before being detected, the detected signal may be useful for image reconstruction. The results of phantom experiments obtained from the two-layer model further validate the distortion problem and demonstrate imaging improvement after distant measurements have been filtered out. Clinical examples have shown similar imaging improvements on reconstructed absorption maps. Clinical data obtained from 20 patients with the chest-wall depths of less than 2 cm from the skin surface suggest that the cutoff distances of distorted measurements are largely related to the chest-wall depth and are relatively independent of the optical properties of tissue.

1. Introduction

Optical tomography that uses, diffused light in the near-infrared (NIR) region has great potential to differentiate malignant from benign tissues.^1–6 However, optical tomography alone has not been widely used in clinics, and the fundamental problem of intense light scattering in tissue has to be overcome. Many research groups have investigated the use of a priori lesion structure information obtained from other imaging modalities, such as ultrasound,^5–7 MRI,⁸ and x-ray mammography⁹ to improve the localization of optical tomography. We have developed a hybrid technique by employing NIR optical imaging sensors and a commercial ultrasound transducer on a hand-held probe. The optical sensors are used for imaging tumor angiogenesis, and the ultrasound transducer is used for lesion localization. Preliminary results for a group of biopsy patients have shown that early-stage invasive cancers may have a twofold higher total hemoglobin concentration than fibroadenomas and other benign lesions.^5,6

Three geometries have been used frequently in optical tomography: transmission geometry, ring geometry, and reflection geometry. Transmission geometry¹⁰ is similar to x-ray mammography, in which the breast is compressed between two plates with NIR source fibers distributed on one plate and detector fibers on the opposite plate. Ring geometry² is similar to an x-ray computer tomography configuration, in which the patient is placed in a prone position with the breast inserted into an opening with source and detector fibers deployed over a ring or multiple rings. Reflection geometry^5–7 is similar to conventional ultrasound pulse echo geometry, in which the patient is placed in a supine position with the sources and detectors distributed on a flat probe. We have adopted reflection geometry for NIR measurements. Compared with other geometries, reflection geometry has the advantage of probing reduced breast tissue thickness; therefore lesions closer to the chest wall can be imaged.

Our data from more than 100 patients have shown that more than 30% of breast lesions are located close to the chest wall. When the chest wall is within 1.0 to 2.0 cm from the skin surface, the optical measurements obtained from distant source–detector pairs are distorted. The distortion is caused by the underlying heterogeneous chest wall consisting of mixtures of muscles and bones. As a result, measurements beyond a certain distance have to be removed before imaging. As the depth of the chest wall and average breast tissue absorption and scattering coefficients vary from patient to patient, it is difficult to predict the cutoff source–detector distance. Consequently data processing and image reconstruction have to be done off line for each patient by examination of the data and removal of distant measurements.

On-line image reconstruction is important for providing timely diagnosis information to radiologists, surgeons, and oncologists. Therefore a predetermined cutoff distance based on a priori information on chest-wall depth measured from real-time ultrasound is essential for fast image reconstruction. In this paper we introduce a chest-wall-induced distortion problem from clinical data, and we use a two-layer model consisting of breast and chest-wall tissue to assess the distortion measured at distant source–detector pairs. A Monte Carlo method is used to simulate photon propagation in the two-layer model. By tracing the photons received from the breast tissue layer and from both breast tissue and chest-wall layers, we estimate the cutoff distance. Phantom experiments are performed to confirm the cutoff distance and the improvement in imaging quality. The predicted cutoff distances are compared favorably with clinical results.

2. Methods

A. Monte Carlo Simulation

The Monte Carlo method^11–13 was adopted to simulate light propagation in a layered medium. Briefly, a turbid medium was modeled as having layers with finite thickness (along the z axis) of specified optical properties. In our simulation, 10⁷ photons at each source location were generated. Each photon was incident normally at the surface of the turbid medium and was assigned a unity weight W, which could be compared with the intensity of light. Each calculated step size (s) was

$$s=\frac{-ln(1-\xi )}{{\mu }_t},$$ (1)

where ξ was a random number from 0 to 1, μ_t = μ_a + μ_s was the total interaction coefficient, μ_a was the absorption coefficient of the medium, and μ_s was the scattering coefficient of the medium. After each step, part of the weight ΔW was absorbed by the medium, and the weight of the photon was decreased as

$$\mathrm{\Delta }W=W({\mu }_a/{\mu }_t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}W=W-\mathrm{\Delta }W.$$ (2)

Once the photon was changed in position and its weight was reduced, the photon was scattered following the Henyey–Greenstein function. The scattering angle was related to a random number and to the medium’s anisotropy. When this process was repeated, the weight of this photon was decreased owing to absorption and scattering. Each photon was either absorbed in the medium or detected at a detector position. At the boundary of two layers, the reflection was considered in the model. The photon was either totally reflected back to the same layer or refracted to the next layer, following Snell’s law. The Roulett technique was used to terminate the photon when W ≤ W_th, where W_th was a threshold value. For each detected photon, a weight was obtained that was the survival weight after all the absorption and scattering had been completed. The propagation trace of the detected photon could also be obtained that provided the greatest depth that the photon had reached. Based on the greatest depth of each photon, we separated detected photons into two groups: those photons that had propagated only in the first layer (group 1) and those photons that reached the second layer (group 2). By summing the weights of all detected photons for each group and then dividing by the total weight, we obtained the percentage of the weight for each group as follows:

$$P_1=W_1/W_t(\text{group\hspace{0.17em}}1),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{P}_2=W_2/W_t(\text{group\hspace{0.17em}}2),$$ (3)

where W₁ = ∑_l W_1l and W₂ = ∑_j W_2j, l is the index of received photons in group 1, W_1l is the weight of each received photon in this group, j is the index of received photons in group 2, W_2j is the weight of each received photon in this group, and W_t = W₁ + W₂ is the total weight.

The detected photons that had propagated only through the first layer (group 1) carried the desired breast tissue information, while those that had propagated through the first and second layers (group 2) carried both the desired information on the tissue layer and the undesired information on the chest wall. Because each source–detector pair could receive photons of both groups, a criterion needs to be established on whether this pair should be used or removed for imaging reconstruction.

B. Optical Properties of the Two-Layer Model

Optical properties of breast tissue and chest wall vary from patient to patient; therefore it is essential to choose typical optical properties for the simulation. The optical properties of breast tissue were reported in the literature.^2,4,5,14 For a healthy female, absorption coefficient μ_a is in the range 0.02 to 0.08 cm⁻¹, and the reduced scattering coefficient μ_s′ is in the range 4.0 to 12.0 cm⁻¹. Therefore we have chosen average values of μ_a = 0.04 cm⁻¹ and μ_s′ = 6.0 cm⁻¹ in our Monte Carlo simulation.

The optical properties of the chest wall are not available in the literature. The only available data are on the optical properties of muscles and bones. In Refs. ^15–20 the muscle was reported to have large absorption and medium scattering coefficients, with μ_a in the range 0.12 to 0.25 cm⁻¹ and μ_s′ in the range 3 to 10 cm⁻¹. We chose average values of μ_a = 0.176 cm⁻¹ and μ_s′ = 8.5 cm⁻¹ as representative optical properties of muscle. The bone is a highly absorbing and scattering medium. From the literature,^21,22 the reported optical properties of bone are μ_a = 0.23 cm⁻¹ and μ_s′ = 21.4 cm⁻¹. By assuming a 1:1 ratio of muscle and bone as a typical representation of the chest wall, we chose optical properties of μ_a = 0.2 cm⁻¹ and μ_s′ = 15 cm⁻¹ in the Monte Carlo simulation.

Tissue refractive index n is another important optical property and is assumed to be constant throughout a medium, with a representative value of n = 1.33 for soft tissue. However, the refractive index is intimately tied to the overall reduced scattering coefficient. Although the actual absolute value of a tissue’s refractive index is debatable owing to difficulties in obtaining accurate data, it is widely accepted that these values differ among different types of tissue. The refractive index of chest wall is not available in the literature. However, some related refractive indices of bones and muscles are given in the literature.^23,24 Bone has a high refractive index, n = 1.556; and muscle, n = 1.431. Following a 1:1 muscle–bone ratio, we chose a representative refractive index of chest wall layer as n = 1.5.

C. Phantom Experiments

We conducted a set of phantom experiments to evaluate the chest-wall-induced distortion and the effect of distortion on imaging. The chest-wall phantom was made from silicone material, and the calibrated optical properties were μ_a = 0.2 cm⁻¹ and μ_s′ = 15 cm⁻¹. The thickness of the chest-wall phantom layer was 3.0 cm, and the phantom was placed at the bottom of a tank filled with 0.7% Intralipid. India ink was added to the Intralipid solution to increase the absorption coefficient of the solution. The measured optical properties of the Intralipid solution were μ_a⁷⁸⁰ = 0.033 cm⁻¹, μ_s′⁷⁸⁰ = 6.70 cm⁻¹, μ_a⁸³⁰ = 0.040 cm⁻¹, and μ_s′⁸³⁰ = 6.65 cm⁻¹. The depth of the Intralipid phantom layer was changed to simulate various thicknesses of breast tissue. Three Intralipid layers of 2.0, 1.5, and 1.0-cm depth were used in the experiment. To estimate the imaging distortion caused by the chest-wall phantom we performed an imaging experiment with a phantom target. A target made from a 1 cm × 1 cm × 1 cm cube of silicon material was placed in the Intralipid at a depth of 1.0 cm. The calibrated optical properties of the target were μ_a = 0.1 cm⁻¹ and μ_s′ = 7.0 cm⁻¹.

The frequency domain system used in the phantom and clinical experiments was described in Ref. 7. Briefly, the system consists of 12 pairs of dual-wavelength (780 and 830 nm) laser diodes, which are used as light sources, and their outputs are coupled to a hand-held probe through optical fibers. Eight parallel detection channels coupled to eight photomultiplier tubes are used to detect diffusely scattered light from the tissue. A black probe was used to house optical sources and detectors as well as a commercial ultrasound probe. Because a black probe was used, a semi-infinite absorbing boundary condition was a reasonable approximation for the optical measurements. For a semi-infinite absorbing-boundary geometry, the following set of linear equations was used to relate the calibrated amplitude R_αβ and phase φ_αβ measured at source–detector pair αβ to source–detector separation ρ_αβ (Ref. ⁷):

$$\begin{array}{l}log({\rho }_{\alpha \beta }^{\text{2}}{R}_{\alpha \beta })=-k_i{\rho }_{\alpha \beta },\\ {\phi }_{\alpha \beta }=k_r{\rho }_{\alpha \beta },\end{array}$$ (4)

where k_i and k_r are the real and the imaginary parts, respectively, of the complex wave number of the photon density wave.

The dual-mesh reconstruction algorithm used in optical imaging was described in Ref. 25. Briefly, the total imaging volume was segmented into two regions, target (T) and background (B). The target region contained the heterogeneity, which was estimated from coregistered ultrasound images. Different voxel sizes (a fine grid for the target region and a coarse grid for the background region) were used for target and background. As a result, the total number of voxels with unknown absorption coefficients was reduced significantly. In addition, the total absorption distribution, instead of absorption distribution per se, was reconstructed, and the total was divided by different voxel sizes of target and background regions. Because the absorption changes in the background region were smaller than the lesion region in general, the total distribution was maintained in the same order for both regions, and the inversion was well conditioned for convergence.

D. Clinical Experiments

Clinical examples used in this paper were obtained from Hartford Hospital. The protocol was approved by the Institutional Review Board of Hartford Hospital. Patients who were scheduled for ultrasound-guided biopsies were recruited for the study. During the experiments, ultrasound images and optical measurements were acquired simultaneously at multiple locations, including the lesion region, a normal region of the same breast, and a normal symmetric region of the contralateral breast, before the biopsies were performed. The optical data acquired at normal regions were used for calculating bulk optical properties of normal tissue used in weight matrix computation and for calculating perturbations used for imaging reconstruction. A perturbation is the difference between measurements obtained at the lesion site and at the normal site. The chosen normal side has the best linear fitting result based on the calculations of

$$\begin{array}{l}{E}_{\text{amp}}=\sum _m{\left[\frac{R({\rho }_m)-\overline{R}({\rho }_m)}{\overline{R}({\rho }_m)}\right]}^2,\\ E_{\text{phase}=}{\sum _m\left[\frac{\phi ({\rho }_m)-\overline{\phi }({\rho }_m)}{\overline{\phi }({\rho }_m)}\right]}^2,\end{array}$$

where R(ρ_m) and $\overline{R}({\rho }_m)$ are measured amplitude and fitted amplitude, respectively, obtained at source–detector separation ρ_m, and φ(ρ_m) and $\overline{\phi }({\rho }_m)$ are the measured phase and the fitted phase obtained at ρ_m. Outliers were removed first, before E_ampl and E_phase were calculated.

3. Results

A. Monte Carlo Simulations

We computed the amplitudes received from all source–detector pairs, using the two-layer model and the geometry corresponding to our clinical probe. Two sets of Monte Carlo simulations were performed. The first set of simulations was used to visualize the influence of the second layer on the measured amplitude distribution acquired at all source–detector pairs. The second set of simulation was used to establish a guideline for cutoff distance.

Figure 1 shows simulation results for a one-layer model with breast tissue only [Fig. 1(a)] and the two-layer model with breast tissue and chest-wall layers [Fig. 1(b)]. In both Figs. 1(a) and 1(b) the horizontal axis is the propagation depth in centimeters and the vertical axis is the lateral dimension in centimeters. The gray scale is the absorption intensity. The source is located at the center (0, 0), and the detector is located at (0, 4.5 cm). In Fig. 1(a) the thickness of the tissue layer in the propagation direction is 7 cm, while in Fig. 1(b) the thicknesses of the tissue and of the chest-wall layer are 1.5 and 5.5 cm, respectively. The white line in Fig. 1(b) marks the boundary between the breast tissue and the chest wall layer. To compare the influence of the chest-wall layer we also marked the boundary position with the white line at the same depth in Fig. 1(a). By comparing Figs. 1(a) and 1(b) we can see that the chest-wall layer affects the traces of photons in both spatial and propagation directions. When the chest-wall layer is absent [Fig. 1(a)], the photons can penetrate deeper, to ~7.0 cm, and can be scattered in a much larger spatial extension. When the second layer is present [Fig. 1(b)] the photon penetration depth is ~3.5 cm, and photons are absorbed and scattered quickly in the second layer.

Fig. 1.

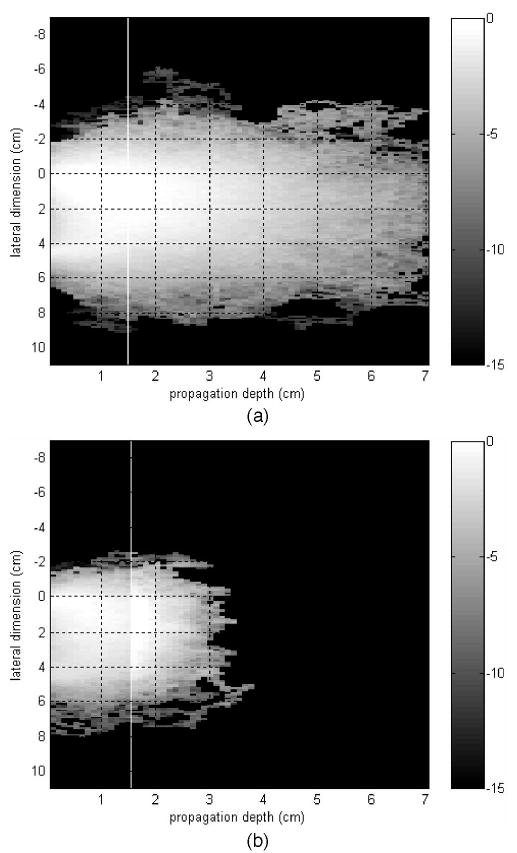
Monte Carlo simulation illustrating detected photon traces of (a) a one-layer model of n = 1.33, μ_a = 0.04 cm⁻¹, and μ_s′ = 6.0 cm⁻¹ with a layer thickness of 7 cm; (b) a two-layer model of the same μ_a and μ_s′ as in (a) for the first layer of 1.5 cm thickness. The second layer’s optical properties were n = 1.5, μ_a = 0.2 cm⁻¹, μ_s′ = 15 cm⁻¹, and 5.5 cm thickness.

Because the received amplitude at distant source–detector pairs is the summation of all photons coming from the tissue layer and the chest wall, it is distorted by the heterogeneous chest-wall layer. We used the percentage weight that we introduced in Subsection 2.B to estimate the influence of the second layer on the amplitude distribution. We made a set of simulations that used the Monte Carlo method to assess the influence of the second layer on the received amplitude distribution. In the simulations the first layer’s optical properties were kept the same as n = 1.33, μ_a1 = 0.04 cm⁻¹, and μ′_s1 = 6.0 cm⁻¹, and the second layer’s optical properties were n = 1.5, μ_a2 = 0.20 cm⁻¹, and μ′_s2 = 15.0 cm⁻¹. Table 1 lists Monte Carlo results obtained from first-layer thicknesses of 1.0, 1.5, and 2.0 cm. If a criterion of P₁ > 50% is used, the cutoff distances for 1.0, 1.5, and 2.0 cm are 3.5 to 4.0 cm, 4.5 to 5.0 cm, and 5.5 to 6.0 cm, respectively.

Table 1.

Computed Percentage of Weight for Tissue Layer Thicknesses of 1.0, 1.5, and 2.0 cm^a

First-Layer Thickness (cm)	Source–Detector Distance (cm)	Layer 1, P1	Layer 2, P2
1.0	3.0	0.65	0.35
	3.5	0.59	0.41
	4.0	0.49	0.51
	4.5	0.40	0.59
1.5	4.0	0.59	0.41
	4.5	0.55	0.45
	5.0	0.43	0.57
	5.5	0.42	0.58
2.0	4.5	0.65	0.35
	5.0	0.62	0.38
	5.5	0.51	0.49
	6.0	0.49	0.51
	6.5	0.42	0.57

^aThe optical properties of two layers were μ_a1 = 0.04 cm⁻¹, μ_s1′ = 6.0 cm⁻¹, μ_a2 = 0.20 cm⁻¹, and μ_s2′ = 15 cm⁻¹.

B. Phantom Experiments

We conducted phantom experiments to validate the simulation results and the image improvement. In the first set of experiments we used a two-layer model without a target to evaluate the chest-wall effect on the optical measurements. Figure 2(a) shows progressive changes of measured amplitude log[ρ²R(ρ)] versus source–detector separation ρ at 780 nm for gradually reduced Intralipid layer thickness l as marked in the figure, and Fig. 2(b) shows the change of the phase versus ρ. When the medium is homogeneous, the measured amplitude and phase demonstrate good linearity, as shown by the open circles. When the first layer is shallower, for example, l = 1.0 cm, the measured amplitude beyond a certain distance is very small and the phase is noisy. The same progressive changes were seen in measurements obtained at 830 nm as well (not shown).

Fig. 2.

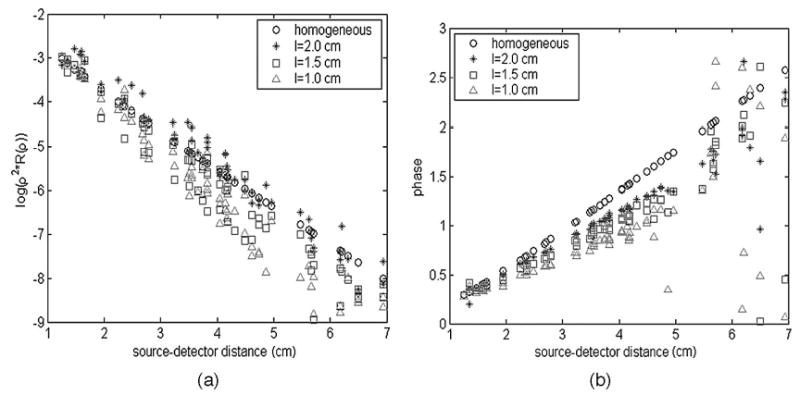
(a) Measured amplitude log[ρ²R(ρ)] versus source–detector distance ρ for gradually reduced Intralipid layer thicknesses l = 2.0, 1.0 cm at 780 nm; (b) the measured phase versus ρ, also at 780 nm.

By filtering our distant source–detector pairs, the imaging quality can be improved. In the second set of experiments, the target was suspended 1.0 cm deep in the Intralipid solution. The thicknesses of the intralipid layers were 1.5 and 2.0 cm. Figure 3 shows the reconstructed absorption maps at the 1.0 cm target layer when the Intralipid layer thickness was 1.5 cm. In these figures the x and y axes correspond to spatial dimensions of the probe. Figure 3(a) is the map with the distant source–detector pairs included, and Fig. 3(b) shows the map with noisy distant source–detector pairs filtered out. We can see that the image quality after filtering has been improved compared with that in Figs. 3(a) and 3(b), particularly the reconstructed value in the target region and correction of the target location. The reconstructed target maximum values before (column 3) and after (column 7) filtering as well as the corresponding percentage errors (columns 4 and 8) from the calibrated value are given in Table 2. In addition, columns 2 and 6 provide the measured target centers before and after filtering, respectively. The target is located approximately at (0, 0, 1.0 cm), within a small experimental error of less than 0.5 cm, and the target location after filtering is close to the true position. The target location offset before filtering is related to the amplitude and phase shifts caused by the second layer and is largely corrected by filtering. By comparing results before and after filtering we can see that the reconstructed values have been improved by at least 40%.

Fig. 3.

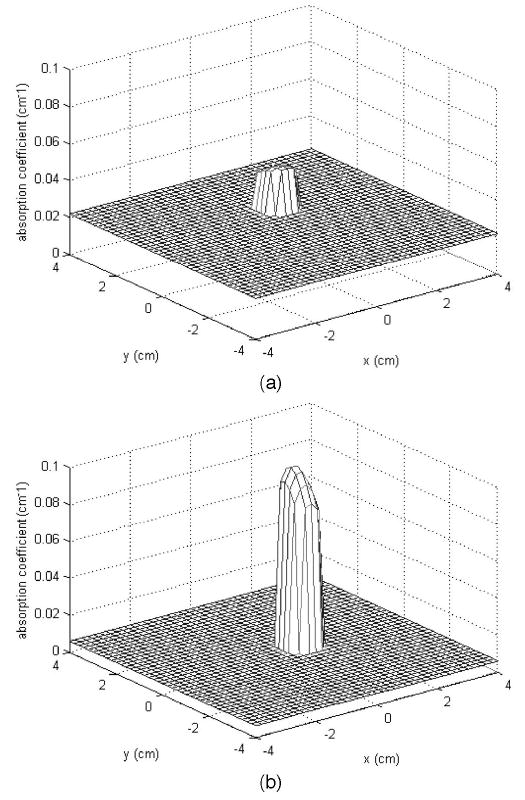
(a) Reconstructed optical absorption map at the target layer without filtering out of distance source–detector pairs; μ_amax⁷⁸⁰ = 0.047 cm⁻¹; error from true value, 53.2%. (b) Reconstructed optical absorption map at the target layer after removal of distant pairs. μ_amax⁷⁸⁰ = 0.089 cm⁻¹; error from true value, 11.4%.

Table 2.

Comparison of Experimental Results Before and After Filtering ^a

	Before Filtering			After Filtering
Intralipid Layer Thickness (cm)	Target Position (cm)b	Reconstructed Maximum Value Measured at 780 nm	Error from the Calibrated Value (%)	Cutoff Distance d (cm)	Target Position (cm)b	Reconstructed Maximum Value Measured at 780 nm	Error from the Calibrated Value
1.5	(0.6, 1.1, 1.0)	0.0468	53.2	5.0	(0.6, 0.1, 1.0)	0.0886	11.4
2.0	(0.6, 1.1, 1.0)	0.0331	66.9	6.0	(−0.3, 0.5, 1.0)	0.1171	17.1

^aColumn 1 lists the Intralipid layer thickness used in the experiments. The reconstructed target’s maximum absorption values and the corresponding percentage errors from the calibrated value before noisy distant pairs have been filtered out and are given in columns 3 and 4. The target was a 1 cm × 1 cm × 1 cm cube centered at approximately (0, 0, 1.0 cm) with calibrated optical properties of μ_a = 0.1 cm⁻¹ and μ_s′ = 7.0 cm⁻¹. The measured center positions before and after filtering are given in columns 2 and 6, respectively.

^bTarget is located approximately at (0, 0, 1.0 cm).

C. Clinical Experiments

Figures 4(a) and 4(c) are ultrasound images obtained from the left breast of a patient who had a suspicious lesion located at the 3 o’clock position on that breast. The biopsy result revealed an intraductal and invasive carcinoma. Figure 4(a) is the ultrasound image obtained at the 9 o’clock normal location used for reference, and Fig. 4(c) is the ultrasound image of the carcinoma obtained at 3 o’clock of the same breast. The chest wall in both Figs. 4(a) and 4(c) was located at approximately 1.3 cm depth as marked by the array of arrows in the figures. Figures 4(b) and 4(d) are the corresponding optical measurements of log[ρ²R(ρ)] versus ρ obtained at 780 nm. At the normal tissue location [Fig. 4(b)] the optical measurements demonstrate good linearity up to ρ = 4.4 cm and are distorted beyond 4.4 cm. At the lesion’s location [Fig. 4(d)] the optical measurements demonstrate some linearity up to 4.4 cm but with perturbations caused by the lesion. The measurements beyond 4.4 cm are distorted similarly, as shown in Fig. 4(b). For comparison, optical measurements obtained from homogeneous Intralipid are shown in Fig. 4(e), and the linearity is quite good within the source–detector distance range that we studied. The measured optical properties of the Intralipid solution were μ_a⁷⁸⁰ = 0.014 cm⁻¹, μ_s′⁷⁸⁰ = 5.8 cm⁻¹, μ_a⁸³⁰ = 0.012 cm⁻¹, and μ_s′⁸³⁰ = 4.4 cm⁻¹.

Fig. 4.

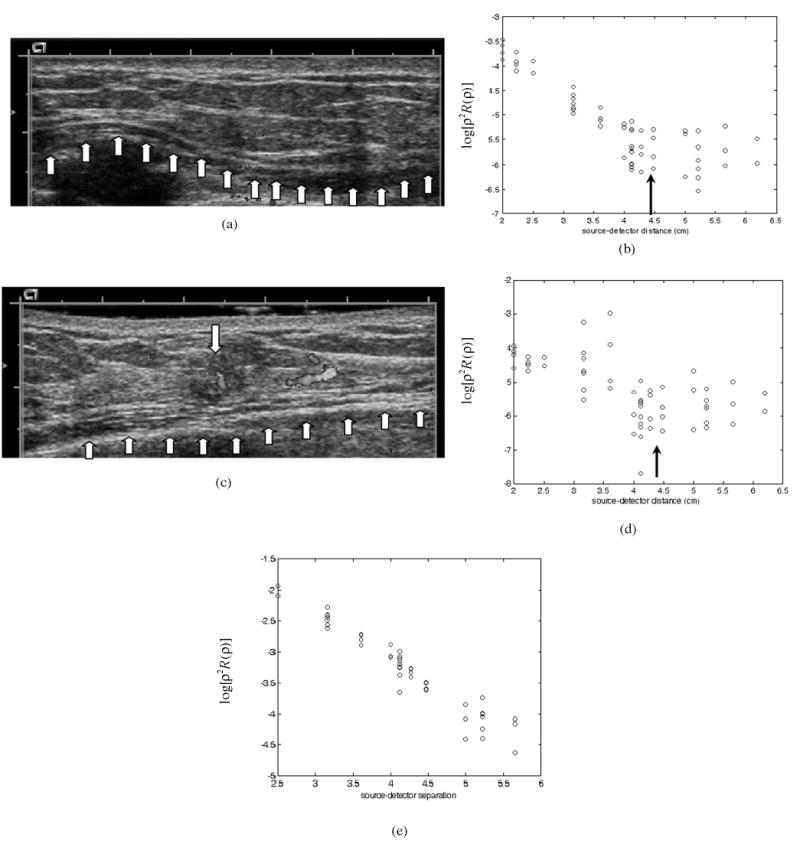
(a) Ultrasound image obtained at the normal side of the breast. (b) Corresponding optical measurements of log[ρ²R(ρ)] versus source–detector separation. (c) Ultrasound image of an intraductal and invasive carcinoma with a Doppler image superimposed on that of the carcinoma. (d) Corresponding optical measurements of log[ρ²R(ρ)] versus source–detector separation. (e) Optical measurements of log[ρ²R(ρ)] versus source–detector separation obtained from Intralipid.

Figures 5(a) and 5(b) are reconstructed optical absorption maps of the carcinoma obtained at 780 and 830 nm after distant source–detector pairs beyond 4.4 cm were filtered out. The first slice is the spatial x–y image 0.5 cm deep from the skin surface, and the last slice is 3.5 cm toward the chest wall. The dimension of each slice is 9 cm by 9 cm, and the spacing between the slices is 0.5 cm. The vertical scale is the absorption coefficient in units of inverse centimeters. The lesion is well resolved in slice #2. The measured maximum absorption coefficients of the carcinoma were μ_a⁷⁸⁰ = 0.21 cm⁻¹ and μ_a⁸³⁰ = 0.24 cm⁻¹ at 780 and 830 nm, respectively, and the measured average values within the FWHM region of the carcinoma were μ_a⁷⁸⁰ = 0.15 cm⁻¹ and μ_a⁸³⁰ = 0.17 cm⁻¹, respectively. Figures 5(c) and (d) are reconstructed absorption maps obtained at 780 and 830 nm, respectively, when the distorted distant measurements at normal and lesion locations were used for imaging. The measured maximum absorption coefficients of the carcinoma were μ_a⁷⁸⁰ = 0.13 cm⁻¹ and μ_a⁸³⁰ = 0.12 cm⁻¹ at 780 and 830 nm, respectively, and the measured average values within the FWHM region of the carcinoma were μ_a⁷⁸⁰ = 0.09 cm⁻¹ and μ_a⁸³⁰ = 0.08 cm⁻¹, respectively. The reconstructed absorption coefficients of the carcinoma have improved by approximately twofold compared with those when no filtering has been applied to the distorted distant measurements.

Fig. 5.

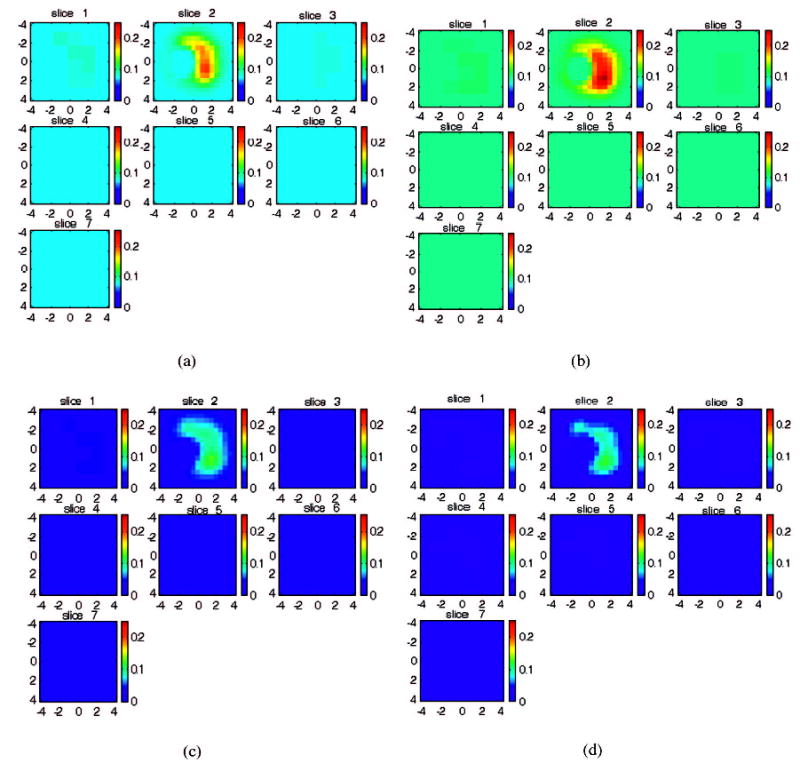
Reconstructed optical absorption maps of the carcinoma with the ultrasound image shown in Fig. 4(c). (a), (b) Optical absorption maps obtained at 780 and 830 nm, respectively, after filtering out of distant measurements beyond 4.4 cm. (c), (d) Optical absorption maps obtained at 780 and 830 nm, respectively, when distant measurements were used for imaging reconstruction. In each figure the first slice is the spatial x–y image 0.5 cm deep from the skin surface, and the last slice is 3.5 cm toward the chest wall. The dimensions of each slice are 9 cm by 9 cm, and the spacing between slices is 0.5 cm. The vertical scale is the absorption coefficient in units of inverse centimeters. The carcinoma is well resolved in slice 2.

During the past year we collected coregistered NIR and ultrasound data from 70 patients at Harford Hospital who had undergone biopsies. A total of 20 patients had chest walls within 2.0 cm as estimated by ultrasound. Table 3 provides chest-wall depths estimated from coregistered ultrasound (column 1), case number (column 2), and measured breast tissue optical absorption and reduced scattering properties at the normal side of the breast at 780 and 830 nm (columns 3 and 4, respectively). The cutoff distance for each patient is given in column 5, and the distance is obtained based on outlier removal and linearity evaluation. The average cutoff distance for the 1.0 cm chest-wall group is 4.1 cm, for the 1.5 cm group is 4.4 cm, and for 1.5 to 2 cm group is 5.79 cm, as is shown for the end of each group’s data. The variation in cutoff distance caused by optical property differences in breast tissue is small, as is desirable for establishing a predetermined criterion for each group. Column 6 lists the predicted cutoff distances based on Monte Carlo simulation. We compared the Monte Carlo results and the clinical results and found that, if weight percentage P₁ from the first layer is more than 50%, the source–detector pair is useful for image reconstruction; otherwise it should be removed.

Table 3.

Clinical Data Obtained from 20 Patients with Chest Wall Located within 2.0 cm Depth^a

		Breast Tissue Properties
Chest-Wall Depth (cm)	Case Number	At 780 nm $\left(\begin{array}{c}{\mu }_a\\ {\mu }_s{}^{\prime }\end{array}\right)({\text{cm}}^{-1})$	At 830 nm $\left(\begin{array}{c}{\mu }_a\\ {\mu }_s{}^{\prime }\end{array}\right)({\text{cm}}^{-1})$	Cutoff Distance from Clinical Experiments (cm)	Cutoff Distance Expected from Monte Carlo Simulation (cm)
1.0	1	0.015 12.74	0.013 13.26	4.0
1.0–2.0 (tilted)b	2	0.041 3.60	0.031 4.28	4.0
1.0	3	0.007 7.79	0.019 6.19	4.0
1–1.5	4	0.060 3.83	0.037 3.23	4.0
1.3	5	0.078 5.37	0.101 4.12	4.4
				Mean: 4.1	3.5–4.0
1.25	6	0.035 4.64	0.036 4.07	4.5
1.5	7	0.048 4.49	0.033 4.83	4.5
1.5	8	0.045 9.63	0.040 10.24	4.25
1.3–1.5 (tilted)	9	0.055 10.41	0.04 11.62	4.5
1.5–2.0 (tilted)	10	0.042 5.41	0.041 4.17	4.5
1.5–2.0 (tilted)	11	0.019 3.99	0.045 2.583	4.0
1.5–2.0 (tilted)	12	0.076 3.52	0.071 3.19	4.0
1.5–1.6	13	0.040 5.68	0.052 7.03	4.5–4.6
				Mean: 4.4	4.5–5.0
1.5–2.0	14	0.035 6.32	0.053 5.91	5.5
1.8–2.0	15	0.028 10.91	0.041 11.56	5.5
1.7–2.2	16	0.022 7.08	0.040 6.75	6.0
1.7–2.0	17	0.026 8.70	0.017 10.67	5.5
2.0	18	0.037 6.62	0.044 6.15	6.0
2.0	19	0.026 9.02	0.031 7.27	6.0
2.0	20	0.017 10.88	0.018 8.53	6.0
				Mean: 5.79	5.5–6.0

^aThe chest-wall depth estimated from coregistered ultrasound is given in column 1. The measured breast tissue’s optical properties at 780 and 830 nm are given in columns 3 and 4, respectively. The cutoff distances of clinical data for different chest-wall thicknesses are given in column 5. The cutoff distances computed from Monte Carlo simulations using a 50% criterion are given in column 6.

^bThe chest wall is not flat and is tilted with respect to the ultrasound transducer.

4. Discussion and Summary

In the research reported in this paper chest-wall-induced diffused wave distortion was estimated by use of a simple two-layer model. The actual measured distant distortion obtained from breast tissue is more complex than the distortion seen in a two-layer model. In some patients the measured distant amplitude profiles consist of many random points, whereas in others, the amplitude profiles deviate considerably from linear curves. However, the filtering approach reported in this paper provides first-order estimation and correction, and it can largely eliminate the image distortion caused by the noisy distant source–detector pairs.

Currently we are working on finite-element-based imaging reconstruction by setting up a suitable boundary condition between breast tissue and chest-wall layers. We are also working on an analytical solution of the layer problem for imaging reconstruction by incorporating the curved amplitude and phase profiles. In addition, different probe sizes and different modulated frequencies will be used for patients with different chest-wall depths identified by ultrasound.

In summary, we have reported the use of a priori information on chest-wall depth obtained from coregistered real-time ultrasound to assist in the removal of distant near-infrared measurements. Clinical data, Monte Carlo simulations, and phantom experiments all suggest that predetermined cutoff distances can be obtained for different chest-wall depths and are relatively independent of tissues’ optical properties. This result indicates that on-line imaging with ultrasound guidance for both lesion location and chest-wall depth is possible.