The relationship between the volume of antimicrobial consumption in human communities and the frequency of resistance

Abstract

The threat to human health posed by antibiotic resistance is of growing concern. Many commensal and pathogenic organisms have developed resistance to well established and newer antibiotics. The major selection pressure driving changes in the frequency of antibiotic resistance is the volume of drug use. However, establishing a quantitative relationship between the frequency of resistance and volume of drug use has proved difficult. Using population genetic methods and epidemiological observations, we report an analysis of the influence of the selective pressure imposed by the volume of drug use on temporal changes in resistance. Analytical expressions are derived to delineate key relationships between resistance and drug consumption. The analyses indicate that the time scale for emergence of resistance under a constant selective pressure is typically much shorter than the decay time after cessation or decline in the volume of drug use and that significant reductions in resistance require equally significant reductions in drug consumption. These results highlight the need for early intervention once resistance is detected.

The increasing frequency with which antimicrobial-resistant microorganisms are recovered from patients in hospital and community settings has been commented on widely in recent years (1–3). Many species and strains of bacteria that are pathogenic to humans have developed resistance to both well established and newer antibiotics. Multiply resistant organisms give special cause for concern because they are responsible for increasing numbers of infections in intensive care units, hospitals in general, and communities (4). A recent example is the emergence of heteroresistant vancomycin resistant Staphylococcus aureus in hospital settings in Japan and the USA after 30 years of use as the drug of choice for the treatment of methicillin-resistant S. aureus and other Gram-positive infections (5). More alarming still is a recent report of the extensive spread of vancomycin-resistant (heteroresistant), methicillin-resistant S. aureus strains in Japanese hospitals (6).

A number of pathogen-specific epidemiological models of drug resistance have been proposed for both community-acquired (7–10) and hospital-acquired infections (11, 12, 14). The major selective pressure driving changes in the frequency of resistance is, in each case, the volume of drug use. Establishing a precise quantitative relationship between the frequency of resistance to a defined antibiotic and the volume of drug use has proved difficult because of the paucity of longitudinal studies that record resistance and drug use patterns (15–23). It is important to do so, however, given the urgent need to develop national and international antibiotic prescribing policies based on precise scientific understanding of key factors, which minimize the rate of evolution and spread of resistant organisms.

In both clinical and community settings, patterns of emergence tend to be similar; typically, a long period of very low-level resistance precedes a phase of rapid increase in frequency and a slow approach to an equilibrium level <100%. The evolution of methicillin-resistant S. aureus strains in the USA and England and Wales are good examples in which, in the former case, resistance frequency was 2% in 1975 and 35% in 1996 whereas, in the latter, the number of hospitals affected by epidemic methicillin-resistant S. aureus has increased from 40 a month in 1993 to >110 in early 1996 (24, 25). The sigmoidal shape of observed longitudinal changes in the frequency of resistance often has been attributed to rising volume of drug consumption over the period of surveillance. In fact, theory predicts such sigmoid patterns are to be expected under a constant selective pressure (=drug consumption). We briefly comment on the underlying population genetics that underpin interpretation of observed epidemiological patterns before turning to detailed analyses of these trends.

Population Genetics.

We consider the case of a single gene as the determinant of resistance with two bacterial genotypes: 𝒮 (sensitive) and ℛ (resistant) (for simplicity we do not include the effect of independently transmissible resistance plasmids). In the absence of antibiotic use, evidence suggests that the sensitive genotype is typically at a fitness advantage where w_𝒮 = 1 ≥ w_ℛ, with the ws representing relative fitness values for each genotype (=strain). Under haploid selection, the frequency of the resistant (p_t) and sensitive (q_t = 1 − p_t) genotypes after t successive generations is determined by

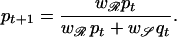1

The selective pressure imposed by antibiotic use can be measured in defined daily doses (DDDs)/1,000 inhabitants or individuals, equivalent to the proportion of the community receiving treatment a (a ≃ prescribing rate × treatment duration). For adults, the equivalence between DDDs and prevalence of antibiotic consumption is good, and a ≃ 0.5 − 1%. For children, however, in whom doses depend on age and consumption is much greater (≃5%), the equivalence is poor. Antibiotic use reduces w_𝒮 from 1 to 1 − a while leaving w_ℛ unchanged (resistance is assumed to be complete). Because a denotes the probability that selection is present, the relevant time scale will be the duration of treatment (typically 10 days for children and less for adults). In the absence of frequency-dependent selection, if p₀ and q₀ are the respective initial frequencies for resistant and sensitive genotypes (typically, p₀ ≪ 1), rearranging Eq. 1 gives p_t+1/q_t+1 = w_ℛp_t/w_𝒮q_t and, hence, (p_t/q_t) = (p₀/q₀)(w_ℛ/(1 − a))^t. Once a exceeds the threshold level a > 1 − w_ℛ, under a constant drug consumption pattern, emergence will be sigmoid in shape, tending to fixation as t → ∞. Furthermore, the time, T_ℛ, for the resistance genotype to increase from initial frequency p₀ to some value p_ℛ is given by

2

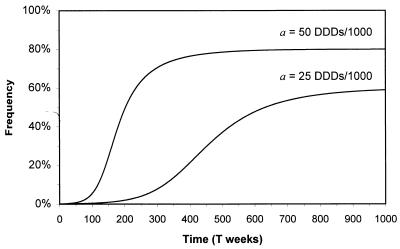
where D is the duration of treatment. A minimal fitness cost relative to the sensitive strain (w_ℛ ≃ 1) implies T_ℛ ∝ 1/a, and, hence, doubling the antibiotic prescribing rate halves the time to reach a given frequency of resistance (which may determine the effective lifespan of the drug). If antimicrobial prescribing is frequency-dependent, i.e., if consumption reduces as resistance increases, an intermediate equilibrium frequency, p̂, is possible. For example, if antibiotic consumption falls off in a nonlinear manner such that w_𝒮(q_t) = 1 − aq_tⁿ (where n is a constant and n < 1 signifies a reluctance to reduce consumption), equilibrium is reached provided w_𝒮(q̂) = w_ℛ or, equivalently, p̂ = 1 − ((1 − w_ℛ)/a)^1/n (Fig. 1).

Figure 1.

Change in the frequency of resistance p_t after frequency-dependent selection in which antibiotic consumption falls as resistance rises (w_𝒮(q_t) = 1 − aq_t, w_ℛ = 0.99, and p₀ = 10⁻³).

Transmission Dynamics.

In a recent paper, a theoretical framework was described addressing the question of how antibiotic consumption influences the carriage rate (i.e., prevalence) of resistant commensal bacteria within the community (10). Many bacterial species exist as commensals in their human hosts, such as Escherichia coli, Haemophilus influenzae, Neisseria meningitidis, Moraxella catarrhalis, Streptococcus pneumoniae, and S. aureus. Such colonization is usually asymptomatic, although acquisition of a more virulent strain or changes in host defenses can lead to symptomatic infection that may require antibiotic treatment. Although epidemiological data are limited at present, it is typically assumed that the frequency of drug resistance in treated infections reflects the resistance pertaining in the commensal population (10).

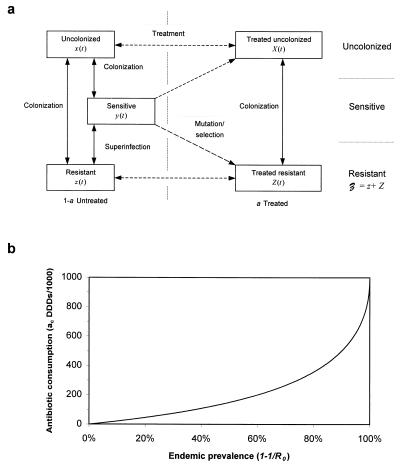
Hosts are colonized by either antibiotic-sensitive or -resistant strains of the normally commensal organism (Fig. 2a). The colonizing potential of the bacteria is measured by the basic reproductive number R₀, which defines the average number of secondary cases of colonized hosts generated when the primary case is introduced in a naive population (26). If R₀ > 1, a directly transmitted commensal will persist in the community with endemic prevalence 1 − 1/R₀ (10). The value of R₀ is determined by the effective contact rate β (defined as the average number of susceptibles that one colonized person passes the bacteria to per unit of time), the average duration of colonization 1/f, (where f is the natural rate of loss of carriage), and the duration hosts remain in the community 1/μ (μ is the death or removal rate of hosts):

3

For infant day-care and adult nursing homes, where there is a rapid turnover of hosts, μ may be comparable with f (typically months), although for adults in the community, f will typically be much greater than μ (typically years).

Figure 2.

(a) Theoretical model of bacterial colonization and antibiotic consumption. Individuals may be uncolonized (x and X), colonized with sensitive bacteria (y), or colonized with resistant bacteria (𝒵 = z + Z), x + X + y + 𝒵 = 1 (10). Antibiotic treatment is independent of colonization, and a proportion a of individuals receive treatment at any time. Treatment either clears sensitive bacteria with a probability 1 − σ or selects for mutations or preexisting resistant strains. (b) Threshold antibiotic consumption, a_c, required for eradication of a commensal with endemic prevalence 1 − 1/R₀. Highly prevalent commensals require sustained antibiotic consumption for eradication.

Antibiotics usually are prescribed in relation to overt morbidity rather than colonization rates. It is assumed that the rate of prescribing is γ per unit of time for an average compliance 1/g time units. The proportion of hosts receiving treatment at any time a is, therefore, a ≃ γ/g. For the purpose of illustration, it is assumed that treatment clears sensitive carriage in the majority of hosts but selects for resistance in a small fraction σ ≪ 1 (so-called acquired resistance), either by mutation of sensitive or expansion of preexisting resistant strains. Resistant organisms are assumed to be unaffected (resistance is complete), and treated hosts therefore remain susceptible to resistant strains. Let y₀(a) denote the endemic prevalence of sensitive carriage as a function of antibiotic consumption. In the absence of antibiotic treatment, y₀(0) = 1 − 1/R₀. Antibiotic treatment reduces both the proportion of susceptible hosts (to 1 − a) and the average duration of carriage for sensitive organisms. In the absence of resistance, the sensitive organism will persist in the community with reduced endemic prevalence y₀(a) = (1 − a) − (1 + δa/(1 − a))/R₀, where δ = (μ + g)/(μ + f) ≫ 1 is the ratio of duration of colonization to duration of treatment. Colonization can be eradicated provided y₀(a) ≤ 0, i.e., if community consumption exceeds some threshold a_𝒮(R₀) ≃ (R₀ − 1)/(R₀ + δ). For example, if 50% of hosts are colonized (R₀ = 2) and δ = 5, then 14% (140 DDDs/1,000) of hosts must be treated to eradicate sensitive carriage (Fig. 2b). Highly prevalent commensals (R₀ large) are difficult to eradicate unless the majority of the population receive treatment. If two commensal species or strains coexist at similar prevalence, the one with the lowest effective transmission rate will be eradicated most easily.

Before the community-wide use of antibiotics, bacterial populations were largely sensitive to the drugs, suggesting that resistance carries some fitness cost [although compensatory genetic changes can be selected for rapidly (27–29)]. This cost may take the form of reductions in transmission or duration of carriage or may arise as a result of superinfection (both resistant and sensitive strains present in the same person), restricting the susceptibility of hosts already colonized, or some combination of the two. The strain with the highest fitness may competitively replace less fit organisms, although mutations and transfer of resistance on mobile elements (e.g., plasmids) can stabilize less-fit resistant strains at very low levels (typically of order σ) (11). Antibiotic use can easily upset the relative fitness ratio between sensitive and resistant strains, resulting in the dominance of resistant strains, and theory shows that superinfection mechanisms may result in coexistence of both types, with resistance at an equilibrium frequency <100% (30).

An original model (10) consisted of five coupled equations describing the five classes (Fig. 2a). If antibiotic consumption is low (a ≪ 1), then the resistantly colonized hosts can be subdivided such that a proportion a is treated and 1 − a untreated. The model then simplifies to the extent that the prevalence of sensitive (y) and resistant (𝒵) carriage are determined by two coupled ordinary differential equations:

4

and

5

where β is the transmission rate between hosts (R₀ = β/(μ + f)), y₀(a) is the prevalence of sensitive colonization before resistance, σ is the probability of acquired resistance during treatment, and ag is the antibiotic prescribing rate. We introduce a superinfection fitness φ that measures the relative invasibility of the different strains. One interpretation of φ is the net probability that a resistantly colonized host will become colonized by sensitive bacteria after contact with other sensitively colonized hosts (negative φ denotes conversion in the opposite direction, i.e., sensitive to resistant). Primes denote parameters for resistant strains, and β′φ′ = βφ.

In the absence of acquired resistance (σ = 0), three equilibrium solutions of equations (Eqs. 4 and 5) are possible; sensitive (y* = y₀(a), 𝒵* = 0), coexisting (y* ≠ 0, 𝒵* ≠ 0), or resistant (y* = 0, 𝒵* = 1 − 1/R₀′). Resistant strains should emerge, provided antibiotic consumption a exceeds a threshold a ≥ a_ℛ [determined by d𝒵/dt ≥ 0 when y* = y₀(a)], whereas sensitive strains should be eradicated, provided a ≥ a_𝒮 (determined by dy/dt ≤ 0 when 𝒵* = 1 − 1/R₀′). Thresholds a_ℛ and a_𝒮 are, respectively,

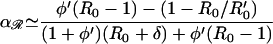and

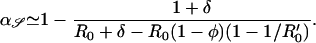6

Endemic coexisting sensitive and resistant strains require only that a_ℛ ≤ a ≤ a_𝒮. Selection of resistance during treatment (σ ≠ 0) results in resistant strains always being present, and, under these circumstances, a_ℛ represents a transmission threshold above which endemic resistance may increase rapidly (Fig. 3a). The existence of two thresholds provides a possible explanation of why in some communities resistance does not persist while in others it may reach either intermediate levels or fixation.

Figure 3.

(a) Endemic resistance as a function of antibiotic consumption ℛ(a). Below the threshold a_ℛ, transmission of resistant strains cannot become established. Above the threshold a_𝒮, sensitive strains are eradicated. Mutation/selection maintains resistant strains below the threshold a_ℛ, although transmission is not possible (σ = 10⁻²). (b) Time taken for resistance to increase from 1–10% (solid line) and fall again after instantaneous reductions in antibiotic consumption of 25, 50, 75 and 100%. Emergence is typically more rapid than decline, highlighting the need for early intervention. Parameters are estimated from the Finland study and are given in Table 1.

To assess the impact of antibiotic consumption on the frequency of resistance, an analytical expression is required relating the two key variables. Setting σ = 0, the following expression can be derived for the endemic frequency (dy/dt = d𝒵/dt = 0) with which colonized hosts harbor resistant organisms, ℛ(a), when a proportion a of the community are receiving treatment:

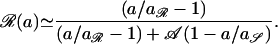7

where 𝒜 = {φR₀(R₀′ − 1) + (R₀ − R₀′)}/{φ′R₀′(R₀ − 1) + (R₀ − R₀′)}. Numerical studies reveal that this approximation is very accurate (Fig. 3a). If 𝒜 ≃ 1, then changes in antibiotic use (Δa) will be accompanied by corresponding changes in the frequency of resistance (Δℛ) such that (Δℛ/ℛ) ≃ a_ℛ/(a − a_ℛ)(Δa/a). When just below the resistance threshold a_ℛ, a small change in consumption may trigger the threshold to be breached, with a concomitant sharp rise in the frequency of resistance. When this occurs, a crucial variable is the time, T_ℛ, for the resistance to change from its low starting prevalence (𝒵₀) to a frequency ℛ. If the sensitive strain is endemic, with prevalence y₀ before the introduction of wide-spread antibiotic use and σ = 0, then Eq. 5 reduces to d𝒵/dt ≃ 𝒵(r − s𝒵), and the time T_ℛ is given by;

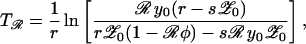8

where r = β′{(1 − 1/R₀′) − y₀[1 + φ′(1 − a)]} and s = β′{1 − (1 − a)(1 − φ)(1 + φ′(1 − a))}. During the early stages of the emergence of resistance 𝒵₀ is of order 1/community size. Once resistance is established, Eq. 8 also can be applied to calculate the time required for a given decrease in drug use (a → {a}′) to reduce resistance to a defined level (ℛ), provided y₀ is replaced by the new endemic value {y₀}′. During the emergence of resistance, resistant strains have a considerable selective advantage (because of antibiotic use). Once resistance approaches endemic levels, reductions in antibiotic selection pressure will give a correspondingly smaller selective advantage for sensitive strains. The implications are that, typically, the emergence of resistance will occur on a faster time scale than its decay after a reduction in antibiotic consumption (Fig. 3b).

Resistance in Communities in Finland and Iceland.

Few epidemiological studies have recorded temporal changes in both the frequency of resistance to a specific drug and the volume of drug consumption in the community. However excellent examples are those of β-lactamase producing strains of M. catarrhalis in Finland and penicillin-resistant pneumococci in Iceland. High quality surveillance data from these two countries provides an opportunity to derive estimates of the key population genetic- and transmission-related parameters.

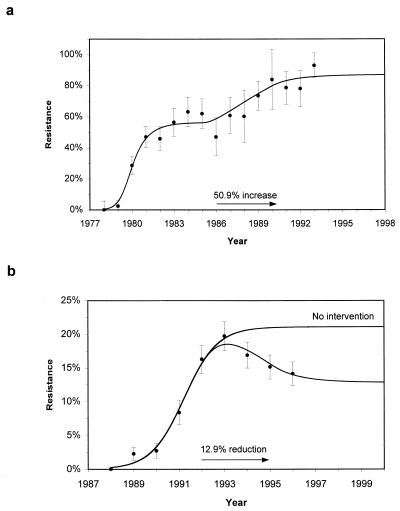
Since 1977, M. catarrhalis resistance to β-lactams has increased rapidly in Europe and the USA, reaching 80–85% (31–33). In Finland, studies show a rapid rise in resistance from 0% (n = 53) in 1978 to 57% (n = 115) in 1983, during which time total β-lactam consumption remained roughly constant at 5.5 DDDs/1,000 individuals (21). Increasing cephalosporin usage during the 1980s led to a 50.9% rise in consumption between 1985 and 1990, accompanied by a further rise in antibiotic resistance (Fig. 4a and Table 1). Penicillin-resistant pneumococci have been reported worldwide (34). During the late 1980s, they were isolated in Iceland (35). After a rapid rise in the frequency of resistance, measures were taken to reduce antibiotic consumption in children from 18.9 DDDs/1,000 children by 12.7% between 1992 and 1995. As a result of this intervention, resistance peaked in 1993 at 19.8% (n = 1296) and has since declined (36) (Fig. 4b and Table 1). Parameter estimation is done by minimizing a weighted least squares estimate by using multidimensional direction set methods (37) and numerical realizations of the full model (10). For the Iceland study, independent estimates of antibiotic consumption (a) and prevalence of colonization (R₀) are available (22), thereby reducing the number of fitted parameters. The 95% confidence intervals are obtained from the parameter values yielding similar fits to the minimum χ² estimates for 6df (Finland) and 4df (Iceland) (37). It is important to note that estimated levels of antibiotic consumption in children differ widely from those of the whole community (Finland) and from established measures using adult doses (Iceland).

Figure 4.

(a) Prediction of a two-step rise in the frequency of β-lactamase-producing isolates of M. catarrhalis from children aged <6 years in Finland. (b) Prediction of a rise and subsequent decline in the frequency of penicillin-resistant pneumococcal isolates carried by children aged <7 years in Iceland. Prompt intervention has substantially reduced the likely endemic level of resistance. All parameters used are given in Table 1. Error bars show 95% confidence intervals for the observed data.

Table 1.

Parameters estimation from both Finland and Iceland data

Parameter	Symbol	Finland	Iceland	Comments
Reproductive number	R0	2.0 (1.9–5.8)	2.1
Duration of carriage	1/f	1.1 (0.8–5.3)	2.6 (0.9–2.9)	Months
Maximum age	1/μ	72	84	Months
Superinfection fitness	φ	0.43 (0.20–0.8)	1 (0.44–1)	ℛ → 𝒮
Transmission fitness	R0′/R0	1.29 (1.20–1.8)	1.44 (1.28–1.56)
Initial resistance	log10 𝒵0	−2.7 (−5.0–−2.3)	−3.1 (−3.8–−2.7)
Treatment rate	γ	1.42 (0.8–3.5)	1.43	Courses/year
Change in consumption	ρ	50.9%	−12.7%
Treatment duration	1/g	10	10	Days
Mutation probability	σ	0	0	Not used
Antibiotic consumption (of children)	a ≃ γ/g	37.7 (4%)	38.0 (4%)	Infant DDDs/1,000 children
Period of study		1978–93	1988–96
χ2 (df)		16.08 (10)	11.134 (5)
Goodness-of-fit P value	P	0.11	0.06

Fitted parameters are shown with 95% confidence intervals. 

DISCUSSION

The majority of antibiotic consumption in developed countries is in response to community-acquired infections. By using a single gene population genetic framework, embedded in a model for the transmission dynamics within a community of people of a commensal bacteria that may induce disease, it has been shown how simple principles explain both the coexistence of resistant and sensitive strains and the sigmoid rise in resistance over time in the presence of a constant rate of antibiotic consumption. Furthermore, the model also helps explain why, in some communities, the frequency of resistance is low to negligible whereas in others it is high. Specifically, there is a critical level of drug consumption required to trigger the emergence of resistance to significant levels. Where detailed longitudinal records of the frequency of resistance and drug use are available, the model of commensal colonization and antibiotic action accurately mirrors observed trends in Finland and Iceland. These epidemiological data sets permit parameter estimation, suggesting that the any fitness cost of resistance (which has been defined in terms of both transmission and superinfection) for β-lactams and penicillin appears to be low. Resistant organisms appear to have an increased reproductive number but reduced superinfection, implying that the presence of sensitively colonized hosts provides a form of herd immunity against resistance.

The model facilitates the derivation of functional relationships between the endemic frequency of resistance and antibiotic consumption and the time taken for resistance to emerge or decay (when drug pressure is relaxed) with defined starting conditions. Two further conclusions emerge from the analyses. First, significant reductions in the frequency of resistance will only result from equally significant changes in antibiotic use patterns. An illustration of this prediction is provided by experience in Iceland with penicillin-resistant pneumococci, where only significant reductions in drug use resulted in a measurable decay in resistance frequency. Second, the decay in resistance after a reduction in prescribing volume will typically occur on a slower time scale than the rise in resistance once the critical threshold drug consumption is crossed. This has been suggested before on the basis of theory (38) but not using a model that has been parameterized via observed patterns of changes in resistance and drug use over time.

Whether increasing antibiotic resistance will eventually lead to associated changes in the clinical outcome for community-acquired infections is uncertain at present (13). This is an area in which research is urgently required. Concomitantly, there is also a need for better surveillance, both in terms of defining more clearly the association between resistance in cases of clinical disease and the frequency of resistance in commensal bacterial populations in human communities and in delineating longitudinal changes in the frequency of resistance and drug consumption (bearing in mind that drug sales do not necessarily accurately reflect consumption patterns by patients). More generally, the principles of population genetics rarely are applied by those directly concerned with the study of antimicrobial resistance, and an obvious need is to meld these techniques with those more commonly used in pharmacoepidemiological studies. Patients have high expectations of antibiotic therapy, which in the past have always been met by the development of new drugs once resistance to older products has raised treatment failure rates to unacceptable levels. Given the observed decline in the rate of development of novel antibiotics, in the future, more attention must be given to the development of prescribing policies designed to maximize the life expectancy of a given compound. It must always be remembered that the strength of the selective pressure (i.e., the rate of drug consumption) is intimately and positively associated with the rate of evolution of resistance, as clearly illustrated by our analyses.

ABBREVIATION

DDDs

defined daily doses