Abstract
We present a method for determining structural properties of the ensemble of folding transition states from protein simulations. This method relies on thermodynamic quantities (free energies as a function of global reaction coordinates, such as the percentage of native contacts) and not on “kinetic” measurements (rates, transmission coefficients, complete trajectories); consequently, it requires fewer computational resources compared with other approaches, making it more suited to large and complex models. We explain the theoretical framework that underlies this method and use it to clarify the connection between the experimentally determined Φ value, a quantity determined by the ratio of rate and stability changes due to point mutations, and the average structure of the transition state ensemble. To determine the accuracy of this thermodynamic approach, we apply it to minimalist protein models and compare these results with the ones obtained by using the standard experimental procedure for determining Φ values. We show that the accuracy of both methods depends sensitively on the amount of frustration. In particular, the results are similar when applied to models with minimal amounts of frustration, characteristic of rapid-folding, single-domain globular proteins.
Keywords: protein folding, Φ values, folding funnels, folding landscapes
Energy landscape theory and the funnel concept have provided a theoretical framework for understanding protein folding (1–7), which is an alternative to the earlier idea that there is a single pathway for the folding event comprising uniquely defined structural intermediates (8, 9). The connection between the landscape theory and real proteins is best established in the context of small fast folding proteins, which fold on millisecond time scales and have a single folding domain; i.e., they are two-state folders with a single, well defined funnel (10). In addition to the theoretical literature describing this theory and its applications (see, for example, the citations above, refs. 5 and 6, and references therein), a new generation of clever experiments [NMR dynamic spectroscopy, protein engineering, laser initiated folding, and ultrafast mixing (see, for example, refs. 11–27)] are providing the temporal and spatial detail needed to extend and elaborate on it.
A central result of this theory is that proteins with funneled landscapes have population dynamics that can be understood as the diffusion of an ensemble of configurations over a low-dimensional free energy surface (1, 3, 4). This energy surface may be constructed by using many different order parameters. The primary requirements are that they distinguish native-like and non-native-like structures and that they group together conformations with similar energies;¶ i.e., the dispersion in energies of states with similar values of these parameters is small. Many simple order parameters that are computationally convenient, like the number of tertiary contacts Q, or experimentally convenient, like the radius of gyration, satisfy these requirements. A successful description of the folding mechanism using only a few of these parameters is possible because the funnel of a protein landscape is deep compared with its energetic ruggedness, which is produced by frustration (1, 2). The rate of local motion on the landscape is set by the reconfigurational diffusion coefficient. Free energy barriers that separate the unfolded and native state ensembles impede this population diffusion and set crossing times that can be determined (for weak frustration) from a Kramer's-like equation.‖ When these crossing times are rate-limiting, the free energy of activation for folding is set by the height of these barriers on the landscape. The structural properties of the transition state ensemble can then be determined by sampling the thermal distribution of states in the dominant free energy barrier rather than by making “kinetic” measurements (e.g., measuring folding rates and transmission coefficients, or simulating complete folding pathways). The elimination of these kinetic measurements allows the folding transition state to be rapidly computed (compared with alternate methods), especially in large and complex systems (31–35) that cannot be studied by other means (29, 36–39).
Some kinetic methods have been used by others to compute Φ values from atomically detailed simulations. In one method (40, 41), strong unfolding biases are put to the native protein by raising the temperature, and the subsequent unfolding trajectory is interpreted as the reverse of a typical folding trajectory. The trajectories found by this method do show interesting correlation with the Φ values of experiments, but the unphysically high temperatures needed to force this transition in a reasonable time introduce large distortions into the landscape, creating difficulties in quantitatively connecting these results with proteins at physiological temperatures.
In this manuscript, we introduce the landscape-based method and validate its use by using a minimalist lattice protein model. By studying several different potentials, we determine the amount of frustration for which this approach can be reliably applied to determine transition state structure.
Methods and Simulations
Spatially localized transition state structure in proteins can be inferred by measuring the effect that point mutations have on the native stability and the folding (unfolding) rate. These effects can be used to compute the Φ value (42), an approximate measure of the protein structure around the site of the mutation:
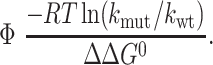 |
1 |
kmut and kwt are the mutant and wild-type folding rates, and ΔΔG0 is the change in total stability of the folded state when the mutation is made.
As we have discussed in the introduction, the crossing rate in minimally frustrated systems can be described via a Kramer's-like equation,
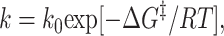 |
2 |
where k0 depends on the reconfigurational diffusion coefficient and the geometric shape of the barrier.** If this prefactor is insensitive to the specific amino acid sequence [this is expected in weakly frustrated systems and has been observed in some simple models (10)], then
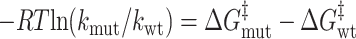 |
3 |
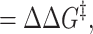 |
and the Φ value is a measure of the ratio of the change in activation free energy of the folding barrier to the change in total stability upon making a particular mutation; i.e.,
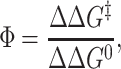 |
4 |
as illustrated in Fig. 1. If the amount of frustration is greatly increased, the folding times become controlled by long lived traps, and the assumption of a single k0 that depends only on the average ruggedness of the landscape breaks down. When such traps are dominant, the ensemble of states in the top of the free energy barrier cannot be associated with transition states anymore.
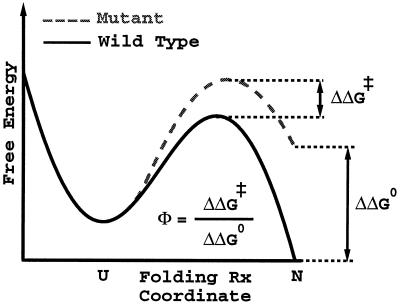
Figure 1.
Approximate schematic of a Φ value, which holds for proteins that are weakly frustrated. The solid curve is a schematic free energy profile for a wild-type protein; the dashed curve is for a suitable mutant. The free energy profile is drawn against a single order parameter for folding. For many small proteins, many simple global structural measures of nativeness may be used for this free energy projection. ΔΔG0 and ΔΔG‡ are, respectively, the change in native state stability and change in activation free energy upon mutation. A Φ value near 1 suggests that the local environment of the mutated residue is native-like in the transition state; a Φ value near 0 suggests that the local environment of the mutated residue is unfolded-like in the transition state. This interpretation of Φ values becomes less valid as the frustration increases.
If the free energy change created by the mutation is related in a simple way to some structural quantity, then the Φ value is a measure of the average difference in that quantity between the unfolded and transition state ensembles, expressed as a fraction of the average unfolded to native difference—it is in this sense that the Φ value tells us the “location” of the barrier via a number that varies between 0 and 1 (44). [But because Φ values only measure relative free energy changes, they cannot be directly interpreted in terms of structure without knowledge of the typical unfolded state structure (27).] Intermediate range Φ values can arise as an average over a heterogeneous transition state ensemble with different amounts of local structure (for experimental support for this, see ref. 45). Comparisons of Φ values from different point mutations at the same sequence position have generally supported the simple interpretation of the Φ value as an indication of local structure (46), although exceptions have been observed in at least one small protein (13).
Unfortunately, an average transition state ensemble structure cannot for most systems be practically determined from simulations by computing changes in folding rates. A 3% error in the folding rate requires >1,000 separate folding simulations, and it is impossible to perform this many simulations except for the simplest models. It will certainly remain an infeasible computation in all atom models for many decades because most protein folding times are in the millisecond time range or greater, and simulations are currently limited to a few tens or hundreds of nanoseconds of real time. As discussed in the introduction, the landscape framework provides an alternate computational method for studying the transition state ensemble. By using a small number of order parameters to define a landscape, we can identify the dominant barrier separating the unfolded and native basins. The change in the folding rate when a mutation is made can then be computed by finding the change in the activation free energy of this barrier; i.e., we assume that the transition states are the thermally occupied states in the free energy barrier region. In systems in which Φ values are accurate probes of the average transition state structure, we show that this method is equally valid as the experimental technique.
To demonstrate the applicability of this computational approach, we use a model that retains only the most essential characteristics of small globular proteins. We represent a protein as a short chain of monomers that are constrained to the vertices of a three-dimensional cubic lattice. The nonbonded interactions between the monomers are contact interactions between neighboring lattice sites with an AB type of potential. These models, pioneered by Lau and Dill (47) and extensively characterized by others (see refs. 5, 6, and 48 for relevant citations), capture many of the general features of real proteins. The particular lattice polymers used in this manuscript are 27 monomers long with compact 3 × 3 × 3 native states. Details of this model and its behavior can be found in refs. 4, 49, and 50.
The landscape theory has shown that energetic frustration can have profound effects on folding dynamics and on the nature of the transition state ensemble. To study these effects, we perform the calculations for the three different sequences shown in Fig. 2. Although these sequences have the same native structure and native energy, they have different levels of frustration, which is reflected in their respective (Tf/Tg) ratios of folding to glass transition temperatures. The first sequence is a Gō-like sequence, which is nearly maximally unfrustrated for a given native structure. In this model, only native interactions are attractive; all others are simply excluded volume interactions. Tf/Tg > 2 in this system. The second system has a three-monomer type AB potential: i.e., there are three types of monomers (A, B, and C), identical monomer types are strongly attractive (energy = −3), and nonidentical monomer types are weakly attractive (energy = −1). We refer to this system as the three-letter code system (3LC). The introduction of attractive non-native interactions increases the frustration. Tf/Tg ≈ 1.6. Of the three systems, this most resembles the frustration level and configurational entropy of small, fast-folding proteins (51). The third system has a two-monomer type AB potential: i.e., the same potential as before, but with only two monomer types. We refer to this as the two-letter code system (2LC). Additional frustration created by the reduction in the number of monomer types reduces the Tf/Tg ratio to ≈1.3. We observe that the amount of frustration in the system can drastically change the nature of folding and the effectiveness of using simple reaction coordinates and equilibrium sampling to probe folding transition state structure.
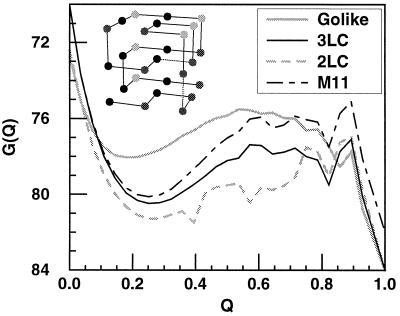
Figure 2.
The free energy profile G(Q) shown at Tf for the three models studied in this paper and one of their mutants. The three models have the same structure but different potentials: a Gō-like potential where every bead is a different type, and only beads adjacent in the native structure are attractive; a 3LC sequence ABABBBCBACBABABACACBACAACAB, where contacts of identical type have energy of −3 units and contacts of different type have energy of −1 units (arbitrary energy units are used to have a folding temperature and glass temperature of order unity); and a 2LC sequence ABABBBBBABBABABAAABBAAAAAAB. The mutant (M11) is from the 3LC system, in which the native interaction between beads 6 and 13 (numbered starting from the lower left corner of the structure shown in the inset) is reduced in energy from −3 to −1. All mutants show two-state behavior. (Inset) The native 3 × 3 × 3 structure for all of the different wild-type and mutant sequences studied in this paper.
We begin by determining Φ values through the standard experimental procedure: namely, by measuring the change in the stability and folding rate created by different mutations. The Φ values for these mutants are computed by using Eq. 1. We then determine the Φ values by using the landscape approach (Eq. 4). In this method, the free energy as a function of a folding order parameter—in this instance, Q, the fraction of native (“tertiary”) contacts formed in a state—is used (rather than changes in the folding rate) to determined the change in activation free energy of different mutations.
Equilibrium constants are not determined by exponential fitting of the relaxation in Q of a population versus time and the use of a two-state approximation as in the experimental manner. Instead, a thermal ensemble at each value of Q is computed from a long trajectory, and changes in free energy are computed by using the well known free energy perturbation method (52), which gives the change in free energy of a system as
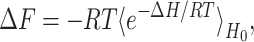 |
5 |
where 〈… 〉H0 is a thermal average of the unperturbed (wild-type) system (indexed by Q). Every equilibrium quantity we need is then rapidly computed from a single wild-type simulation. Representative examples of wild-type and perturbed free energy profiles are shown in Fig. 2.
We produce mutants by weakening one of the native interactions (from an energy of −3 to −1), so the Φ value is measuring the amount of formation of the weakened bond. One could refer to these Φ values as “bond” Φ values instead of “residue” Φ values like those in typical protein experiments. Bond mutations are preferred over residue mutations because they provide a more detailed structural picture of the transition state ensemble. Similar values can be computed by measuring the rate and stability changes of double and single mutants and subtracting the one-body, single-mutant changes from the full double-mutant changes (53). Because residue Φ values are (to lowest order in perturbation theory) an average over bond Φ values, the range of variation of residue Φ values with position is much smaller than the range of variation of bond Φ values with position; consequently, bond Φ values are more useful for comparing various methods of calculation, even though these methods can be used to calculate residue Φ values with equal validity under identical conditions.
Results and Discussion
There are 28 possible bond mutants in our models. The Φ values for these contacts are computed from folding simulations by using Eq. 1 and from equilibrium sampling and free energy perturbation by using Eq. 4. The values computed via the two methods are compared in Fig. 3. To perform the free energy perturbation calculation, we assume that the folding transition state structures are the ensemble of thermally occupied microstates that have a value of Q with the highest free energy between 5/28 and 23/28. (The upper cutoff is used because lattice artifacts can produce sharp free energy peaks above Q = 23/28 that are not actual folding barriers.) Taking the highest free energy point rather than a fixed point allows the transition state to shift along the Q coordinate. To compute changes in stability, we take all states with Q < 16/28 as the unfolded ensemble and Q = 1 as the native state. The comparison of Φ values from the two methods is shown for the different systems with differing levels of frustration.
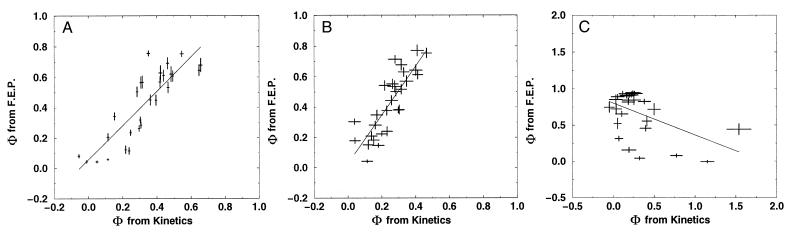
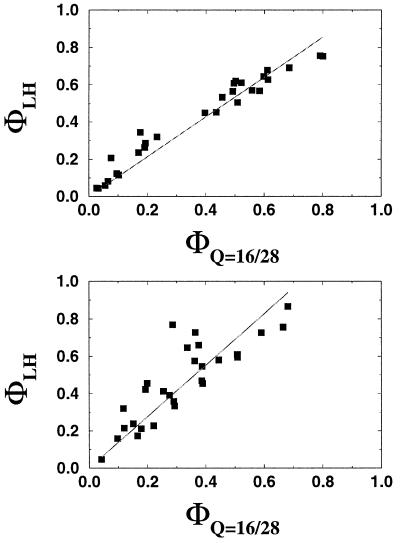
Figure 3.
A comparison of the kinetic and free energy perturbation methods for inferring folding transition state structure. Each panel shows the comparison for a different sequence (and Hamiltonian): A is the Gō-like sequence, B is the 3LC sequence, and C is the 2LC sequence. The Gō-like sequence has the least amount of energetic frustration, and C the most. The native structure and potential for these sequences are shown in Fig. 2. Mutants are made by weakening specific nonbonded interactions between beads that are adjacent in the native structure. The Φ values for these contacts are then computed by the standard experimental procedure (ordinate) and by a free energy perturbation technique (abscissa). Agreement is good (normalized correlations 0.86 and 0.84) for the models in A and B, which have energetic frustration less than or comparable to small, fast-folding globular proteins. Because the Gō sequence in A has no energetic frustration, the heterogeneity of the Φ values is mostly determined by topological factors attributable to a combination of the polymeric nature of the chain and the structure of the native state. More frustrated sequences, such as in C, show no agreement (normalized correlation −0.49) between the two methods and out-of-range Φ values, which suggests that the assumption of a Kramer's type of rate with a fixed rate prefactor is not valid. In the experimental method (ordinate), the folding rate of the wild type (kwt) and the mutant (kmut) as well as the change in native stability under mutation are measured and used to compute a Φ value as Φ −RT ln(kmut/kwt)/ΔΔG0. These Φ values should be similar to the measure of ΔΔG0/ΔΔG‡, the ratio of the change in the folding activation free energy to the change in native stability, when the assumption that folding follows a Kramer's type of equation with a fixed rate prefactor is valid. In the free energy perturbation method, we determine the free energy as a function of a folding reaction coordinate—in this instance, Q, the fraction of formed native nonbonded interactions. The barrier height is defined as the difference in free energy between the highest free energy point along Q between 5/28 and 23/28 and the free energy of states, with Q < 16/28. The Φ value is then computed directly from ΔΔG0/ΔΔG‡ by taking Q < 16/28 as the unfolded conformations. For both methods, the unfolded state is defined as all conformations with Q < 16/28. Error bars show 68% confidence limits calculated from 1,000 bootstrapping simulations.
How well the Φ values computed via the two methods agree depends strongly on the degree of frustration in the system. The sequence with the least amount of frustration (Gō-like) has the best agreement between the two Φ values (normalized correlation coefficient 0.86 and a slope close to 1). The 3LC, a sequence with greater frustration (Tf/Tg ≈ 1.6), shows a slightly larger variation between the two sets of Φ values (normalized correlation 0.84) and a slope around 1.6; namely, the Φ values computed from changes in the free energy barrier seen with Q are consistently overestimated by about a factor of 1.6. The 2LC, the sequence with the greatest amount of frustration (Tf/Tg ≈ 1.3), shows no agreement between the two sets of Φ values (normalized correlation −0.49). Clearly, the effective use of a small number of global order parameters as reaction coordinates depends critically on the degree of frustration. This degree of frustration in real proteins will clearly determine how effective the use of simple order parameters is in interpreting real data or studying more detailed protein models.
Different contacts (bonds) can have different Φ values not only because of energetic heterogeneity but also because of topological factors that arise from a combination of the polymeric nature of the chain and the structure of the native state. In Fig. 4, we compare the Φ values computed for the same structure with two different potentials (Gō-like and 3LC). The strong correlation between these two different sequences indicates the central role of topology in determining the folding mechanism and Φ values as long as the energetic frustration is not too large. However, already for the systems with energetic frustration comparable to the 3LC, the impact of energetic effects is noticeable in the sensitivity of the choice of barrier. Recent theoretical (54, 55) and experimental (56, 57) work supports this idea that much of the transition state ensemble structure in real proteins is determined by the topology of the particular protein under consideration. This agreement is another indication that the amount of energetic frustration in real single-domain fast-folding proteins is similar to or less than the 3LC sequence. A comparison of the Φ values of the Gō-like and 2LC model shows no significant correlation (data not shown).
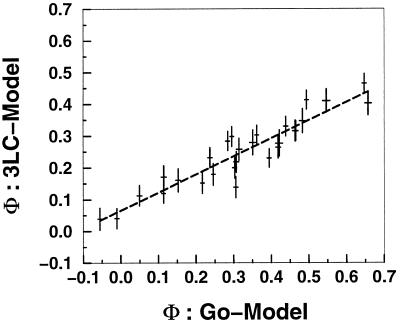
Figure 4.
A comparison of the 28 bond Φ values—produced by mutating a single native interaction, decreasing its energy from −3 to −1—from the model with a Gō-like potential and a 3LC potential. (The sequence and native structure are shown in Fig. 2.) The agreement shows that, for sequences with reduced frustration, the native structure (topology) has a large role in determining the Φ values. Details of the potential interactions may not be as critical. Φ values are determined here from the rates by using Eq. 1.
Fig. 3 also shows that several Φ values for the 2LC sequence computed by the experimental procedure lie well outside the range of 0–1—values for which a simple explanation of Φ values in terms of structural changes becomes problematic. The sudden appearance of these large Φ values indicates that the conventional interpretation is no longer valid for systems with this higher level of frustration. In this regime, the experimental method of using rate changes to infer the transition state structure is not significantly more accurate than using a free energy function of one- or two-order parameters. This suggests that, in large, slow folding proteins—those that might contain a significantly higher level of frustration than in the smaller single domain proteins—Φ values may not be reliable probes of transition state structures as in the smaller, faster folding proteins.
Why does the agreement break down with increasing frustration? Clearly, one or more of the assumptions made are invalid. Either folding cannot be described via a Kramer's-like rate equation in which the prefactor is identical for both mutant and wild-type proteins, or the transition state ensemble cannot accurately be approximated by using simple reaction coordinates such as Q (that are effective in less frustrated models). We have not precisely quantified the level of frustration at which these two assumptions become invalid. The appearance of Φ values outside the range of 0 and 1 and the sudden loss of correlation between the Φ values of the Gō-like and 2LC sequences suggests that the entire description of folding in terms of diffusion along a macroscopic coordinate becomes invalid for sequences with frustration levels comparable to the 2LC.
Although the Φ values computed from changes in folding rates correlate well with Φ values computed from the free energy surface, it is clear that the latter values are generally overestimated. This is visible in the best fit line of the 3LC, where the slope is ≈1.6 instead of near unity (Fig. 3B). This discrepancy can be traced to inaccuracies in the method of computing the change in the free energy barrier height ΔΔG‡: i.e., uncertainties in the choice of barrier location. The actual barrier location appears to be closer to Q = 16/28, as can be seen in Fig. 5—using a fixed location of Q = 16/28 to compute ΔΔG‡ yields slightly more dispersion in the Φ values but a better overall slope. The greater sensitivity of the 3LC to the choice of barrier location is attributable to the larger number of traps in the barrier region, which are off-pathway as compared with the less frustrated Gō-like model. Because the free energy barriers for folding are quite broad, the inclusion of these off-pathway traps and the existence of kinetic effects such as moves that make several steps in Q and a positionally dependent configurational diffusion coefficient can shift the average barrier location by an appreciable amount—from the free energy maximum toward the lower Q end of the barrier near Q = 16/28.
Figure 5.
(Upper) A comparison of the Φ values computed for the Gō-like model from the free energy perturbation formula (based on Eq. 4) by using two different formulas for estimating the activation free energy ΔΔG‡. The abscissa shows the Φ values computed by assuming a fixed transition state location at Q = 16/28; the ordinate shows the Φ values computed by assuming that the activation free energy is equal to the variation between the unfolded free energy minimum and the maximum barrier point. The solid line is a least squares fit constrained to pass through the origin with a slope of 1.07. (Lower) The same plot but shown for the 3LC model. The solid line has a slope of 1.38. These two plots demonstrate that the less frustrated models have less sensitivity of their Φ values to the assumed position of the barrier. The overestimation of the Φ values computed from free energy perturbation in the 3LC model is apparent from the lower panel. Because the top of the free energy barrier is very broad, variations in the reconfigurational diffusion coefficient with Q and the existence of fundamental motions that allow jumps of several units in Q can shift the actual barrier location. In this instance, the actual location is close to Q = 16/28, which is at the lower Q position of the barrier.
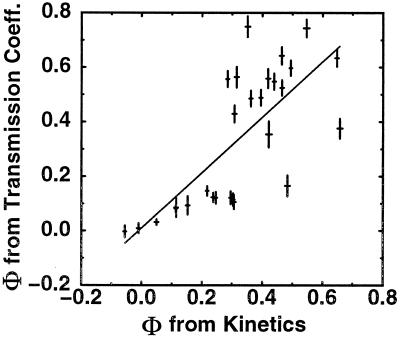
Certainly, there are other methods that can be used to determine transition state structures. Most of these methods eschew the use of simple reaction coordinates like Q in favor of more complicated coordinates, which in principle could better identify the transition state ensemble. For example, in refs. 29 and 30, a transmission coefficient is used to identify putative transition state structures. That is, a transition state structure is identified as one for which approximately half of simulations begun in that state reach the folded state before unfolding. These approaches are much more computationally intensive, and the proposed reaction coordinates cannot be associated with any experimentally accessible measurement. More importantly, these coordinates do not in practice provide more quantitative information than simple coordinates like Q, which can be rapidly computed for any structure. As we have discussed, no single coordinate will determine an exact transition state ensemble, but for sequences with reduced frustration, many coordinates provide reasonable answers. To demonstrate this assertion, we have shown that Φ values computed with our method are similar to the ones obtained with “transmission coefficient” reaction coordinates for the minimally frustrated Gō sequence in Fig. 6. It should be noted that this manuscript uses a slightly different method for locating transition states than ref. 29: we generate a proper thermal ensemble of states with transmission coefficients near 0.5 rather than selecting one transition state from each of several folding simulations.
Figure 6.
A comparison of the Φ values computed by measuring changes in the folding rates and by averaging over the thermally weighted population of conformations with transmission coefficients between 0.4 and 0.6. Comparison is done for the minimally frustrated Gō sequence and structure shown in Fig. 2. The two results have a normalized correlation coefficient of 0.73—agreement is thus of comparable quality to using our method with a single order parameter Q but at a much greater computational cost. Ten-thousand states with Q values in the range 6/28 to 27/28 were sampled in equilibrium at ≈100,000 step intervals. Three-hundred and ninety states from this sample had transmission coefficients between 0.4 and 0.6, defined as the fraction of folding simulations that, when started in a given conformation, find the native conformation before any conformation with Q ≤ 7 (as determined from 100 independent folding simulations). This set of structures was then used as a putative transition state ensemble for computing Φ values via the free energy perturbation equation.
Conclusion
Often it is difficult (or impossible) to use a fully molecular model to interpret experimental measurements of protein properties. For example, to understand the effects that mutations have on the folding rate, and to use this information to determine the structural details of the transition state ensemble, we cannot turn to atomically detailed models. Thus, there is a need for a theoretical/computational framework that is able to determine this structural transition state ensemble without the need for fully kinetic simulations of these models. In addition, such a framework is necessary to relate the effects of local mutations observed experimentally to structural details of the protein. In this paper, we developed a landscape approach to computationally determine these structural details (computing Φ values) without the need for kinetic information, and we tested the assumptions behind this approach on a minimalist protein model.
We showed that the connection between the folding rate (kinetics) and the free energy barrier (thermodynamics) depends strongly on the degree of energetic frustration in the protein. For good folders with sufficiently weak frustration, this connection can be expressed via a Kramer's-like equation, and the folding rates can be clearly described as a diffusive process on a low-dimensional free energy surface constructed by using simple structural measures of native state similarity. For these proteins, interpretation of the experimentally measured Φ values as changes in free energy differences of a simple transition state ensemble is accurate and useful. We also notice that, for minimally frustrated systems, geometric reaction coordinates like the percentage of native contacts Q work effectually and give similar results to those of more complex coordinates. This indicates that many features of the system are insensitive to the microscopic details. Because real proteins need to fold reliably and be robust to slight changes in environment and sequence, their frustration level is usually low enough for this approach to work.
However, the situation changes dramatically when the level of frustration increases. The equivalence of the Φ values determined from simple geometric reaction coordinates and from changes in rates does not hold. In this increased frustration regime, the folding rates are controlled by long lived traps. The folding can no longer be described as diffusion over a free energy barrier observed by using simple parameters measuring structural overlap with the native state. No general theoretical framework will be able to capture the features critical to folding. Instead, many microscopic details are relevant for understanding the folding mechanism and must be modeled precisely, and the conventional experimental interpretation of Φ values in terms of geometrical features breaks down.
Acknowledgments
Work at the University of California at San Diego was supported by the National Science Foundation (Grant MCB-9603839) and by the molecular biophysics training grant program (NIH T32 GN08326) for H.N. Work at The Rockefeller University was funded by the National Science Foundation (Grant DMR-7932803) and the Alfred P. Sloan Foundation.
Abbreviations
- 3LC
three-letter code
- 2LC
two-letter code
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
The accuracy of this method in predicting folding rates is demonstrated in the context of a simple lattice model in ref. 4. Equilibrium sampling with a simple order parameter is used to determine the height of the free energy barrier, and the autocorrelation time in the order parameter is used to estimate the reconfigurational diffusion constant. A Kramer's equation constructed from these two parameters provides an estimate of folding rates around the folding temperature correct to within a factor of order unity. This is expected because, although several recent studies have shown that a large fraction of free energy barrier states are actual microscopic transition states in moderately designed systems (28–30) and nearly all transition states lie in the barrier region, some of the configurations in this region are not real microscopic transition states (due, for example, to topological constraints).
For real proteins, measurements of the rate of intrachain diffusion have put a lower bound on the rate prefactor of ≈10 μs (43), although its exact value is unknown.
These energies are actually free energies averaged over the degrees of freedom not explicitly included in the structure of the landscape: e.g., solvent degrees of freedom (5).
References
- 1.Bryngelson J D, Wolynes P G. Proc Natl Acad Sci USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Leopold P E, Montal M, Onuchic J N. Proc Natl Acad Sci USA. 1992;89:8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bryngelson J D, Onuchic J N, Socci N D, Wolynes P G. Proteins Struct Funct Genet. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 4.Socci N D, Onuchic J N, Wolynes P G. J Chem Phys. 1996;104:5860–5868. [Google Scholar]
- 5.Onuchic J N, Luthey-Schulten Z, Wolynes P G. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 6.Dill K A, Chan H S. Nat Struct Biol. 1997;4:10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 7.Nymeyer H, Garcia A E, Onuchic J N. Proc Natl Acad Sci USA. 1998;95:5921–5928. doi: 10.1073/pnas.95.11.5921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Englander S W, Mayne L. Annu Rev Biophys Biomol Struct. 1992;21:243–265. doi: 10.1146/annurev.bb.21.060192.001331. [DOI] [PubMed] [Google Scholar]
- 9.Kim P S, Baldwin R L. Annu Rev Biochem. 1990;59:631–660. doi: 10.1146/annurev.bi.59.070190.003215. [DOI] [PubMed] [Google Scholar]
- 10.Onuchic J N, Socci N D, Luthey-Schulten Z, Wolynes P G. Fold Des. 1996;1:441–450. doi: 10.1016/S1359-0278(96)00060-0. [DOI] [PubMed] [Google Scholar]
- 11.Fersht A R. Curr Opin Struct Biol. 1997;7:3–9. doi: 10.1016/s0959-440x(97)80002-4. [DOI] [PubMed] [Google Scholar]
- 12.Eaton W A, Munoz V, Thompson P, Chan C K, Hofrichter J. Curr Opin Struct Biol. 1997;7:10–14. doi: 10.1016/s0959-440x(97)80003-6. [DOI] [PubMed] [Google Scholar]
- 13.Burton R E, Huang G S, Daugherty M A, Calderone T L, Oas T G. Nat Struct Biol. 1997;4:305–310. doi: 10.1038/nsb0497-305. [DOI] [PubMed] [Google Scholar]
- 14.Riddle D S, Santiago J V, Bray S T, Doshi N, Grantcharova V, Yi Q, Baker D. Nat Struct Biol. 1997;4:805–809. doi: 10.1038/nsb1097-805. [DOI] [PubMed] [Google Scholar]
- 15.Elove G A, Bhuyan A K, Roder H. Biochemistry. 1994;33:6925–6935. doi: 10.1021/bi00188a023. [DOI] [PubMed] [Google Scholar]
- 16.Jennings P, Wright P. Science. 1993;262:892–896. doi: 10.1126/science.8235610. [DOI] [PubMed] [Google Scholar]
- 17.Plaxco K W, Dobson C M. Curr Opin Struct Biol. 1996;6:630–636. doi: 10.1016/s0959-440x(96)80029-7. [DOI] [PubMed] [Google Scholar]
- 18.Sosnick T R, Mayne L, Englander S W. Proteins Struct Funct Genet. 1996;24:413–426. doi: 10.1002/(SICI)1097-0134(199604)24:4<413::AID-PROT1>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 19.Ballew R M, Sabelko J, Gruebele M. Nat Struct Biol. 1996;3:923–926. doi: 10.1038/nsb1196-923. [DOI] [PubMed] [Google Scholar]
- 20.Phillips C M, Mizutani Y, Hochstrasser R M. Proc Natl Acad Sci USA. 1995;92:7292–7296. doi: 10.1073/pnas.92.16.7292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Williams S, Causgrove T P, Gilmanshin R, Fang K S, Callender R H, Woodruff W H, Dyer R B. Biochemistry. 1996;35:691–697. doi: 10.1021/bi952217p. [DOI] [PubMed] [Google Scholar]
- 22.Matthews C R. Annu Rev Biochem. 1993;62:632–683. doi: 10.1146/annurev.bi.62.070193.003253. [DOI] [PubMed] [Google Scholar]
- 23.Cordes M H J, Davidson A R, Sauer R T. Curr Opin Struct Biol. 1996;6:3–10. doi: 10.1016/s0959-440x(96)80088-1. [DOI] [PubMed] [Google Scholar]
- 24.Raschke T M, Marqusee S. Nat Struct Biol. 1997;4:298–304. doi: 10.1038/nsb0497-298. [DOI] [PubMed] [Google Scholar]
- 25.Lin L, Pinker R J, Forde K, Rose G D, Kallenbach N R. Nat Struct Biol. 1994;1:447–452. doi: 10.1038/nsb0794-447. [DOI] [PubMed] [Google Scholar]
- 26.Pascher T, Chesick J P, Winkler J R, Gray H B. Science. 1996;271:1558–1560. doi: 10.1126/science.271.5255.1558. [DOI] [PubMed] [Google Scholar]
- 27.Villegas V, Martinez J C, Aviles F X, Serrano L. J Mol Biol. 1998;283:1027–1036. doi: 10.1006/jmbi.1998.2158. [DOI] [PubMed] [Google Scholar]
- 28.Socci N D, Nymeyer H, Onuchic J N. Phys D. 1997;107:366–382. [Google Scholar]
- 29.Pande V S, Rokhsar D S. Proc Natl Acad Sci USA. 1998;96:1273–1278. doi: 10.1073/pnas.96.4.1273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Du R, Pande V S, Grosberg A, Yu, Tanaka T, Shakhnovich E S. J Chem Phys. 1998;108:334–350. [Google Scholar]
- 31.Li Z, Scheraga H A. Proc Natl Acad Sci USA. 1984;84:6611–6615. doi: 10.1073/pnas.84.19.6611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Boczko E M, Brooks C L., III Science. 1995;269:393–396. doi: 10.1126/science.7618103. [DOI] [PubMed] [Google Scholar]
- 33.Daggett V, Li A, Itzhaki L S, Otzen D E, Fersht A R. J Mol Biol. 1996;257:430–440. doi: 10.1006/jmbi.1996.0173. [DOI] [PubMed] [Google Scholar]
- 34.Guo Z, Brooks C L, III, Boczko E M. Proc Natl Acad Sci USA. 1997;94:10161–10166. doi: 10.1073/pnas.94.19.10161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sheinerman F B, Brooks C L., III Proc Natl Acad Sci USA. 1998;95:1562–1567. doi: 10.1073/pnas.95.4.1562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vakhter B, Berry R S. J Chem Phys. 1999;110:2195–2201. [Google Scholar]
- 37.Klimov D K, Thirumalai D. J Mol Biol. 1998;282:471–492. doi: 10.1006/jmbi.1998.1997. [DOI] [PubMed] [Google Scholar]
- 38.Elber R, Meller J, Olender R. J Phys Chem B. 1999;103:899–911. [Google Scholar]
- 39.Dellago C, Bolhuis P G, Chandler D. J Chem Phys. 1999;110:6617–6625. [Google Scholar]
- 40.Ladurner A G, Itzhaki L S, Daggett V, Fersht A R. Proc Natl Acad Sci USA. 1998;95:8473–8478. doi: 10.1073/pnas.95.15.8473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lazaridis T, Karplus M. Science. 1997;278:1928–1931. doi: 10.1126/science.278.5345.1928. [DOI] [PubMed] [Google Scholar]
- 42.Matouschek A, Kellis J T, Jr, Serrano L, Fersht A R. Nature (London) 1989;340:122–126. doi: 10.1038/340122a0. [DOI] [PubMed] [Google Scholar]
- 43.Hagen S J, Hofrichter J, Szabo A, Eaton W A. Proc Natl Acad Sci USA. 1996;93:11615–11617. doi: 10.1073/pnas.93.21.11615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mines G A, Pascher T, Lee S C, Winkler J R, Gray H B. Chem Biol. 1996;3:491–497. doi: 10.1016/s1074-5521(96)90097-6. [DOI] [PubMed] [Google Scholar]
- 45.Oliveberg M, Tan Y J, Silow M, Fersht A R. J Mol Biol. 1998;277:933–943. doi: 10.1006/jmbi.1997.1612. [DOI] [PubMed] [Google Scholar]
- 46.Matouschek A, Otzen D K, Itzhaki L S, Jackson S E, Fersht A R. Biochemistry. 1995;34:13656–13662. doi: 10.1021/bi00041a047. [DOI] [PubMed] [Google Scholar]
- 47.Lau D F, Dill K A. Macromolecules. 1989;22:3986–3997. [Google Scholar]
- 48.Shakhnovich E I. Fold Des. 1998;3:R45–R58. [PubMed] [Google Scholar]
- 49.Socci N D, Onuchic J N. J Chem Phys. 1995;103:4732–4744. [Google Scholar]
- 50.Socci N D, Onuchic J N, Wolynes P G. Proteins Struct Funct Genet. 1998;32:136–158. [PubMed] [Google Scholar]
- 51.Onuchic J N, Wolynes P G, Luthey-Schulten Z, Socci N D. Proc Natl Acad Sci USA. 1995;92:3626–3630. doi: 10.1073/pnas.92.8.3626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zwanzig R. J Chem Phys. 1954;22:1420–1426. [Google Scholar]
- 53.Fersht A R, Matouschek A, Serrano L. J Mol Biol. 1992;224:771–782. doi: 10.1016/0022-2836(92)90561-w. [DOI] [PubMed] [Google Scholar]
- 54.Onuchic J N, Nymeyer H, Garcia A E, Chahine J, Socci N D. Adv Protein Chem. 2000;53:87–152. doi: 10.1016/s0065-3233(00)53003-4. [DOI] [PubMed] [Google Scholar]
- 55.Shea J E, Onuchic J N, Brooks C L., III Proc Natl Acad Sci USA. 1999;96:12512–12517. doi: 10.1073/pnas.96.22.12512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Grantcharova V P, Riddle D S, Santiago J V, Baker D. Nat Struct Biol. 1998;5:714–720. doi: 10.1038/1412. [DOI] [PubMed] [Google Scholar]
- 57.Martinez J C, Pisabarro M T, Serrano L. Nat Struct Biol. 1998;5:721–729. doi: 10.1038/1418. [DOI] [PubMed] [Google Scholar]