Restitution of Ca²⁺ Release and Vulnerability to Arrhythmias

Abstract

Ca²⁺ Release Restitution. New information has recently been obtained along two essentially parallel lines of research: investigations into the fundamental mechanisms of Ca²⁺-induced Ca²⁺ release (CICR) in heart cells, and analyses of the factors that control the development of unstable rhythms such as repolariza-tion alternans. These lines of research are starting to converge such that we can begin to understand unstable and potentially arrhythmogenic cardiac dynamics in terms of the underlying mechanisms governing not only membrane depolarization and repolarization but also the complex bidirectional interactions between electrical and Ca²⁺ signaling in heart cells. In this brief review, we discuss the progress that has recently been made in understanding the factors that control the beat-to-beat regulation of cardiac Ca²⁺ release and attempt to place these results within a larger context. In particular, we discuss factors that may contribute to unstable Ca²⁺ release and speculate about how instability in CICR may contribute to the development of arrhythmias under pathological conditions.

Interactions Between Ca²⁺ and Electrical Signaling in Heart Cells

To ensure efficient pumping of blood, the heart employs complex bidirectional interactions between electrical and chemical signaling systems, the latter primarily mediated through changes in intracellular Ca²⁺ concentration ([Ca²⁺]_i). Each time the heart beats, depolarization of the cell membrane leads to a large, transient increase in [Ca²⁺]_i in every cell, and contraction results from Ca²⁺ ions binding to myofilaments. Over the past few decades, numerous experimental studies have provided significant insight into this phenomenon of excitation-contraction coupling, and, specifically, how Ca²⁺ entry through the cell membrane triggers the release of a larger amount of Ca²⁺ from sarcoplasmic reticular (SR) stores, a process known as Ca²⁺-induced Ca²⁺ release (CICR). A major conceptual breakthrough occurred with the discovery that CICR occurs via the recruitment of a number of elementary units of Ca²⁺ release, Ca²⁺ sparks,^1–4 each of which is triggered by increases in [Ca²⁺]_i in the immediate vicinity of the SR release channels responsible for these events. Advances in understanding CICR and regulation of Ca²⁺ sparks have been reviewed recently by several groups.^5–7

Ca²⁺ current flowing through L-type Ca²⁺ channels provides the primary trigger for Ca²⁺ release in heart cells,^8–11 although under certain conditions sarcolemmal Ca²⁺ flux through T-type Ca²⁺ channels¹² or via “reverse mode” operation of the Na⁺-Ca²⁺ exchanger (NCX) may also contribute.¹³ Since both the open probability and the single-channel current of L-type channels depend strongly on voltage, changes in the action potential shape affect excitation-contraction coupling and can modulate CICR in subtle and sometimes surprising ways.^14,15 At the same time, the [Ca²⁺]_i-dependence displayed by several ionic currents results in modulation of the action potential shape by changes in cellular Ca²⁺ transients. Potential sites for this regulation include Ca²⁺-dependent inactivation of the L-type Ca²⁺ current,¹⁶ Ca²⁺-dependent K⁺ and Cl⁻ currents,^17,18 and NCX, which, in “forward mode,” imports three Na⁺ ions for every Ca²⁺ ion expelled and therefore contributes inward, depolarizing current.¹⁹ A larger Ca²⁺ transient on a given beat would be expected to simultaneously lead to increased Ca²⁺-inactivation of L-type Ca²⁺ channels, which would tend to shorten the action potential, and increased Ca²⁺ extrusion via NCX, which, by supplying inward current, would tend to lengthen the action potential. The Ca²⁺ and electrical signaling systems in heart cells therefore influence one another in complicated, intricate ways. Under certain circumstances, it is also possible that mechanical movement of heart myocytes affects membrane potential more directly through stretch-sensitive channels, a process known generally as mechano-electric feedback.²⁰

To relate cardiac excitation-contraction coupling to more general questions of beat-to-beat heart electrical rhythms, one of the key questions is: “Once CICR has been triggered, what determines the size of the Ca²⁺ transient at the next beat?” This deceptively simple question is not as easy to answer as it might seem. After Ca²⁺ is released from the SR, several time, voltage, and/or concentration-dependent processes may play a role in the recovery or restitution of the Ca²⁺ transient. These include recovery of L-type Ca²⁺ channels from both voltage and Ca²⁺-dependent inactivation, refilling of SR Ca²⁺ stores, and recovery of the SR release channels, known as ryanodine receptors (RyRs), from whatever mechanism terminated release. Early studies that investigated recovery of Ca²⁺ transient amplitude, or restitution, had to distinguish between different hypotheses using indirect methods and inferences.^21,22 More recently, technical advances have allowed for more precise experimental control of Ca²⁺ release triggers and for the visualization of local release events. A handful of new studies have examined the recovery of Ca²⁺ release at the local level and have provided important new information.

Local Recovery of CICR from Refractoriness

A few recent studies have been able to gain insight into the mechanisms underlying the local recovery of Ca²⁺ release in ventricular myocytes. For instance, Sobie et al. applied low doses of the RyR agonist ryanodine to rat cells loaded with the Ca²⁺ indicator fluo-3 and observed repeated activations of individual Ca²⁺ spark sites.²³ Spontaneous Ca²⁺ sparks occur stochastically in resting ventricular cells at a low rate of approximately 100 per cell/sec.² This translates to roughly 1 spark/sec when images are acquired with a confocal microscope operating in “line scan” mode, and the scan line spans the length of the cell. Exposure to 50 nM ryanodine caused sequences of Ca²⁺ sparks to originate from a limited number of sites within the cell, as shown in Figure 1A, and spark pairs originating from these sites were analyzed to examine how the delay between sparks influenced the amplitude of the second spark and the probability that a second spark would arise. Representative Ca²⁺ spark pairs taken from the data presented in this study are shown in Figure 1B. The plots show that the amplitude of the second spark, relative to the first, increases with an increase of the delay between sparks. Analysis of numerous Ca²⁺ spark pairs demonstrated that the recovery of Ca²⁺ spark amplitude could be well fit by a single exponential with a time constant of roughly 90 msec, whereas the probability of Ca²⁺ spark triggering followed a more sigmoidal time course that lagged behind the recovery of Ca²⁺ spark amplitude. The two recovery functions obtained in that study²³ are plotted together in Figure 1C.

Figure 1.

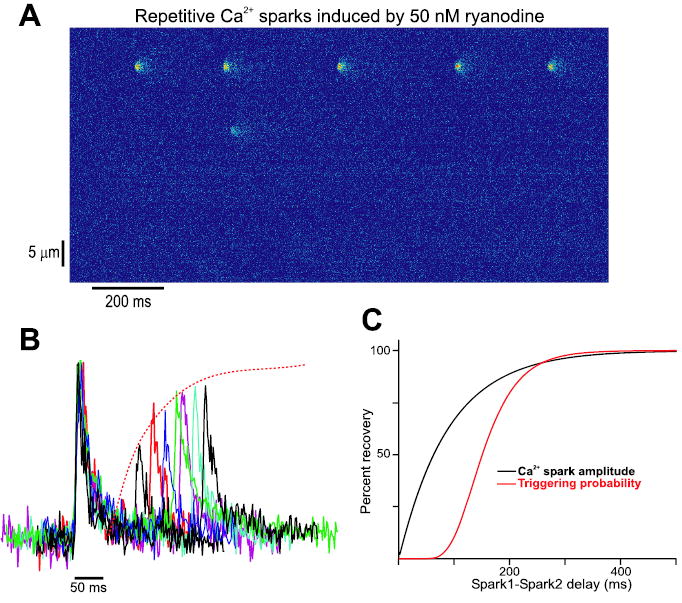
Restitution of Ca²⁺ sparks in rat myocytes. (A) Addition of 50 nM ryanodine to a quiescent rat ventricular myocyte loaded with the Ca²⁺-sensitive dye fluo-3 causes a limited number of Ca²⁺ spark sites to display repetitive activity. Spark pairs derived from repeating sites such as the one near the top of the line scan image displayed can be analyzed to probe the time course of Ca²⁺ spark restitution. (B) Example of Ca²⁺ spark pairs recorded in rat ventricular myocytes after application of 50 nM ryanodine. Individual amplitudes of the initial Ca²⁺ sparks within each pair have been normalized so that spark pairs could be overlaid. Initial Ca²⁺ sparks display very similar time courses. The amplitude of the second spark in each pair, relative to the first, increases with an increase in the delay between sparks. (C) Ca²⁺ spark amplitude and triggering probability recovery functions derived from the analysis of spark pairs. Several potential regulatory factors, discussed in the text, could plausibly account for roughly 90 msec delay (measured at 50% recovery) between the two plots. The results shown have been replotted from the original data discussed in a recent study,²³ with the permission of the authors.

How should the delay between the recoveries of Ca²⁺ spark amplitude and triggering probability be interpreted? Several possibilities exist but are difficult to distinguish, and the current work by us and other groups is aimed at discriminating between various hypotheses. A key factor in the recovery of Ca²⁺ spark amplitude is the refilling of local SR Ca²⁺ stores, which become significantly depleted during Ca²⁺ release, as direct measurements of free [Ca²⁺]_SR have recently shown.^24,25 If Ca²⁺ spark amplitude recovery, to a first approximation, reflects this refilling, the slower recovery of spark triggering probability may indicate that this is controlled by a different mechanism, such as recovery of RyRs from inactivation after dissipation of high local [Ca²⁺]_i. An alternative possibility is that the local refilling of SR stores completely controls Ca²⁺ spark restitution, but the delay occurs because the triggering probability depends on [Ca²⁺]_SR raised to a power greater than 1. Several factors could contribute to this. One is that, in the experiments presented by Sobie et al., the trigger for Ca²⁺ release is a spontaneous opening of a ryanodine-bound channel within the repetitively firing RyR cluster. The amplitude of this trigger increases as the local SR refills, and could increase the probability that a spontaneous RyR opening would activate neighboring RyRs via CICR. Moreover, since planar lipid bilayer studies of RyR gating indicate a sigmoidal dependence of open probability on cytosolic [Ca²⁺],²⁶ this would translate to a nonlinear increase in triggering probability as [Ca²⁺]_SR refills. In addition, the open probability of RyRs depends on [Ca²⁺] in the SR lumen, with RyRs more sensitive to triggering by cytosolic Ca²⁺ when [Ca²⁺]_SR is high.^27,28 If dynamic changes in [Ca²⁺]_SR during and after sparks modulate RyR gating, as has been suggested,^29,30 this factor would add an additional nonlinearity and further contribute to the lag between the two recovery functions. A final possible factor could be that after local [Ca²⁺]_SR returns to its control value, a slow conformational change must occur before the RyRs in the cluster recover their sensitivity to activation by cytosolic Ca²⁺. This could happen if the lumenal dependence of RyR gating depends not on free [Ca²⁺]_SR but instead on interactions of Ca²⁺ with calsequestrin, junction and/or triadin on the lumenal side of the SR membrane. Specifically, it has recently been hypothesized that the higher open probability of RyRs at high [Ca²⁺]_SR is due to the dissociation of calsequestrin, which can inhibit RyRs in its Ca²⁺-free form.³¹ Although the kinetics of these protein-protein interactions have not been well characterized, it is easy to envision a scheme in binding and dissociation reactions such as those proposed contribute to a delay.

Restitution of Cellular Ca²⁺ Transients

No matter which mechanism accounts for the recoveries of Ca²⁺ spark amplitude and triggering probability measured recently by Sobie et al.,²³ the results obtained in this and other recent studies can be helpful for understanding how Ca²⁺ release at the cellular level will recover with time. To a first approximation, the amplitude of a cellular Ca²⁺ transient will be proportional to the product of Ca²⁺ spark amplitude and the probability of Ca²⁺ spark triggering. This probability, in turn, may in general depend on both the recovery from refractoriness of CICR and recovery of the trigger for Ca²⁺ release. Figure 2 displays Ca²⁺ transient recovery functions assessed in four recent studies^23,32–34 on a single set of axes. By comparing the plots and noting the differences in experimental conditions and protocols, insight into the relative importance of different factors may be gained. To avoid potential problems caused by differences between species, in particular expression of the SR/ER Ca²⁺ ATPase (SERCA) responsible for SR refilling after Ca²⁺ release, we have only plotted results obtained in small rodents (rats and mice). These species display robust SERCA function, high SR load even after long periods of quiescence, and Ca²⁺ transients that rely almost entirely on Ca²⁺ release from the SR.⁵

Figure 2.

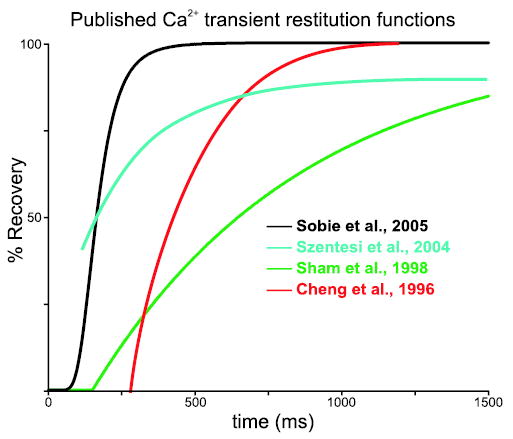
Comparison of Ca²⁺ transient restitution functions measured in different studies. Ca²⁺ transient recovery functions obtained in four recent studies displayed on a single set of axes to allow for easier comparisons. As explained in the text, differences in the experimental conditions and/or protocols used to assess restitution may account for the quantitative differences observed.

Several points of interest can be noted on the composite plot. One is that the recovery of Ca²⁺ transient amplitude assessed by Szentesi et al.³⁴ (cyan line) is slightly slower than the estimate of Sobie et al.²³ (black line). For the latter study we have plotted the product of the Ca²⁺ spark amplitude and triggering probability recoveries, a quantity that should be roughly proportional to the Ca²⁺ transient amplitude recovery. Szentesi et al. loaded mouse ventricular myocytes with the light-sensitive Ca²⁺ buffer DM-nitrophen, then delivered brief flashes of UV light to liberate Ca²⁺ from the buffer and trigger Ca²⁺ release.³⁴ With this technique repeatable triggers for Ca²⁺ release could be given at any interval. Thus, both the Sobie et al. and Szentesi et al. experiments investigated restitution of Ca²⁺ release without any complications due to partial or complete refractoriness of the trigger. The key difference between the two studies is that Sobie et al. measured local restitution of Ca²⁺ sparks whereas Szentesi et al. triggered cell-wide Ca²⁺ transients. The somewhat slower recovery observed in the latter study may therefore reflect slower SR refilling after triggering of global Ca²⁺ transients versus individual Ca²⁺ sparks. This could happen if local refilling after isolated Ca²⁺ sparks depend on both SERCA activity and diffusion of Ca²⁺ from neighboring regions of network SR, which would be predicted based on cellular ultrastructure.

The red plot in Figure 2 is from the study of Cheng et al.,³² who recorded Ca²⁺ transients induced by electrical field stimuli after spontaneous Ca²⁺ waves in Ca²⁺ overloaded cells and plotted, for various subcellular locations, the local Ca²⁺ transient amplitude versus the delay since the wave had passed. The somewhat slower recovery seen by these investigators may reflect refractoriness in the trigger for Ca²⁺ release. In other words, the Ca²⁺ wave could have caused Ca²⁺-dependent inactivation of L-type Ca²⁺ channels, leading to partial refractoriness of these channels at the time of the field stimulus. Finally, the slowest Ca²⁺ transient amplitude recovery was observed by Sham et al.³³ (green line), who delivered paired voltage-clamp depolarizations and recorded the resulting “Ca²⁺ spikes”³⁵ in rat ventricular myocytes. The extremely slow and unphysiological (for rats) recovery recorded in this study could have resulted from the addition of a high concentration (4 mM) of exogenous Ca²⁺ buffer (EGTA) to the cytosol to allow for the recording of “spikes.” This result therefore supports the hypothesis that SR refilling plays a key role in Ca²⁺ transient restitution. In summary, this comparison of several recent studies suggests that (1) refilling of global SR Ca²⁺ content may proceed more slowly after cell-wide transients than local refilling after isolated Ca²⁺ sparks, (2) in healthy cells the recoveries of both Ca²⁺ release and L-type Ca²⁺ current may contribute to Ca²⁺ transient restitution, and (3) recovery of [Ca²⁺]_SR may become an especially important factor when refilling is slowed. Additional experiments, of course, must be performed under carefully controlled conditions to confirm or refute such ideas.

Restitution of Ca²⁺ Transients and Unstable Rhythms

As progress in understanding the molecular mechanisms underlying local and global of Ca²⁺ release recovery continues to be made, one of the key questions will be: what factors determine whether Ca²⁺ release is stable from beat to beat, and under what conditions are regular fluctuations, or Ca²⁺ transient alternans, produced? The answer to this question should provide insight not just into the physiological pathways that control calcium homeostasis in heart cells but also into the factors that predispose the heart to arrhythmias in certain disease states.

Regular, beat-to-beat alternations in the strength of contraction or the characteristics of the ECG, referred to as mechanical and electrical alternans, respectively, have long been associated with lethal arrhythmias and sudden cardiac death.^36,37 More recently, clinical studies have demonstrated that small alternans in the T-wave amplitude, invisible to the naked eye but detectable with signal processing techniques, can identify patients with an increased risk sudden cardiac death in diverse populations.^38–41 Additionally, experiments in an animal model have shown that action potential duration (APD) alternans occur in cells concurrently with T-wave alternans and that spatially discordant APD alternans can immediately precede and facilitate the development of reentrant arrhythmias.⁴² These observations have been given a theoretical grounding by analyses of cellular dynamics based on the APD restitution curve. This literature, which has a long history,⁴³ predicts that restitution properties which allow for the development of alternans in individual cells will encourage the degeneration of ventricular tachycardia into fibrillation in tissue.^44–46 In particular, a region in the restitution curve with a slope greater than unity is thought to be required for stable APD alternans. This prediction has been supported by experimental studies showing that pharmacological agents that “flatten” the APD restitution curve (decrease its slope) can prevent the development of fibrillation in animal models.^47,48

Analyses based on the APD restitution curve are complicated; however, by the fact that this cellular property is not a static function but instead can vary dynamically as circumstances change. Altered “conditions” that can modify the APD restitution curve can be as simple as a change in the pacing rate,⁴⁹ and a few recent studies have highlighted the difficulty of defining a “true” cellular APD restitution curve at a particular instant in time.^50,51 Recent studies have also obtained some counterintuitive results, such as alternans developing at locations or under conditions that would not be expected based on static restitution analyses or vice versa.^52–54 For instance, APD alternans can display “hysteresis” such that the threshold pacing rate is higher when the pacing rate is progressively increased than when it is decreased.⁵⁵ Several of these investigations have pointed to the potential importance of Ca²⁺ cycling in the development of APD alternans. Mechanical and Ca²⁺ transient amplitude alternans have long been known to occur simultaneously with APD alternans;^56–58 however, it has not been clear whether APD alternans leads to Ca²⁺ transient alternans or vice versa. Some of the new, unexpected results recently obtained suggest that Ca²⁺ transient alternans may in fact develop before and cause APD alternans.^52,53,55 This hypothesis has been supported by the observation that Ca²⁺ transient alternans can be produced in isolated cells even when voltage-clamp techniques are used to fix the beat-to-beat voltage waveform.^59–61 Overall, these findings have pointed to the importance of examining the beat-to-beat dynamics of cardiac Ca²⁺ cycling. In particular, there is at present a relative lack of straightforward quantitative predictions regarding which conditions promote and which inhibit Ca²⁺ transient alternans, at least compared with the extensive analyses of APD restitution. Despite the limitations of these analyses that have been noted,^62,63 their relative simplicity leads to a satisfying intuitive understanding and provides a useful framework for considering questions of stability. Analogous analyses of Ca²⁺ dynamics are just beginning to be developed.

Here, we present results from a simple computer model to show how particular nonlinearities in restitution of Ca²⁺ release may contribute to the development of Ca²⁺ transient alternans. These nonlinear relationships have been identified experimentally, but quantitative information is still somewhat lacking, so the model presented should be considered phenomenological and ad hoc. Results from simulations performed with this model are shown in Figure 3.

Figure 3.

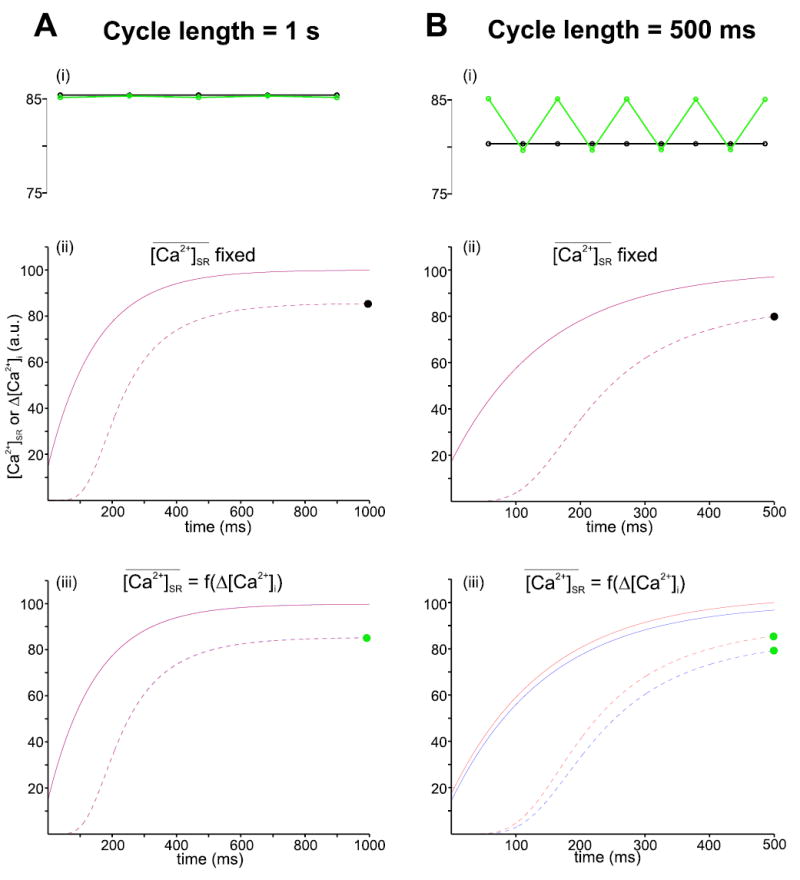
Factors that may contribute to Ca²⁺ transient alternans. Simulations were performed with a simple, phenomenological model to explore the characteristics of Ca²⁺ release restitution that may contribute to rate-dependent Ca²⁺ transient alternans. Ca²⁺ transient amplitude is stable from one beat to the next at a pacing rate of 1 Hz (A), but Ca²⁺ transient alternans may develop, depending on model choices, at a pacing rate of 2 Hz (B). The top plots (i) display the quantity of Ca²⁺ released at each beat (Δ[Ca²⁺]_i) for the last 5 (at 1Hz) or last 9 (at 2 Hz) beats in a sequence of 40 or 80, respectively. The middle (ii) and bottom (iii) plots show how the SR Ca²⁺ content ([Ca²⁺]_SR) and Δ[Ca²⁺]_i recover with time between beats during the next-to-last (blue) and last (red) beats in each sequence. The points on the Ca²⁺ transient recovery curves in (ii) and (iii) corresponding to the amplitude plots in (i) are marked with black and green dots as appropriate. The key features of the model that lead to alternans are a nonlinear dependence of Δ[Ca²⁺]_i on Δ [Ca²⁺]_SR and the dependence of the value toward which [Ca²⁺]_SR increases between beats $(\overline{{[C{a}^{2+}]}_{SR}}]])$ on the quantity just released. Specifically, in the simulations indicated with the green symbols at the top and plotted on the bottom graphs, Δ[Ca²⁺]_i = P_TRIG * [Ca²⁺]_SR and P_TRIG = [Ca²⁺]ⁿ_SR / ([Ca²⁺]ⁿ_SR + K_m ⁿ ) where the exponent n is set at 8 and the SR load that produced 50% release, K_m is equal to 80. Also in these simulations, $\overline{{[C{a}^{2+}]}_{SR}}=-0.52*(\mathrm{\Delta }{[{\text{Ca}}^{2+}]}_{\text{i}}-85)+100$. In the simulations represented with black symbols at the top and displayed in the middle plots, $\overline{{[C{a}^{2+}]}_{SR}}$ does not depend on Δ[Ca²⁺]_i and is equal to 100 after all beats. In additional simulations not shown, P_TRIG was assumed to not depend on [Ca²⁺]_SR but instead to drop to zero immediately after each release and then exponentially rise toward a maximum value of 0.8 with a time constant of 200 msec. Either of these changes to the model abolished alternans at a pacing rate of 2 Hz, confirming that these nonlinear elements are responsible for the instability.

In the model, a fraction of the SR Ca²⁺ content is released into the cytosol at the instant each “beat” occurs, after which [Ca²⁺]_SR follows an exponential time course as it increases from its minimum and approaches a new steady state. The fraction released at a given beat is specified by a term P_TRIG, which varies between 0 and 1 and also increases as the interval since the previous beat increases. In some simulations this factor depends nonlinearly on the SR Ca²⁺ content;^64–66 in others it follows an independent time course. An additional important regulatory factor is the balance between the amount of Ca²⁺ entering the cell versus the amount exiting during each cardiac cycle. The influence of this factor is explored in the model through the parameter $\overline{{[{\text{Ca}}^{2+}]}_{\text{SR}}}$, the steady-state value toward which [Ca²⁺]_SR relaxes during the interval between beats. In some simulations, this is fixed, implying that the Ca²⁺ entry and Ca²⁺ extrusion are exactly in balance. In others, $\overline{{[{\text{Ca}}^{2+}]}_{\text{SR}}}$ is inversely related to the amount of Ca²⁺ released on the previous beat, Δ[Ca²⁺]_i. This reflects the observation that the cell tends to accumulate Ca²⁺ when little SR Ca²⁺ is released, for instance following depletion of [Ca²⁺]_SR. ^67,68 and tends to extrude more Ca²⁺ than the amount entering when Ca²⁺ transients are especially large.⁶⁶ This property of the cell has been referred to as “high feedback gain.”⁶⁰

Figure 3 shows how these nonlinear elements in Ca²⁺ release restitution may interact with changes in pacing rate to promote the development of alternans. Panel A displays simulations performed with a nominal pacing cycle length of 1 second. The top graph (i), which plots Δ[Ca²⁺]_i for the last 5 beats in a sequence of 40, shows that the beat-to-beat Ca²⁺ transient amplitude is extremely stable whether $\overline{{[{\text{Ca}}^{2+}]}_{\text{SR}}}$ is constant (black symbols) or depends on the preceding value of Δ[Ca²⁺]_i (green symbols). Panels (ii) and (iii) in Figure 3A plot the recovery functions corresponding to these two conditions. These graphs show how [Ca²⁺]_SR (solid lines) and Δ[Ca²⁺]_i (dashed lines) evolve as the time since the beat increases for the next-to-last (blue) and last (red) beats in the sequence simulated. These curves are virtually identical from one beat to the next, reflecting the stability observed in the amplitude plot at the top.

When the pacing cycle length is reduced to 500 msec, however, different behavior is observed. When $\overline{{[{\text{Ca}}^{2+}]}_{\text{SR}}}$ is fixed from one beat to the next, implying that Ca²⁺ entry and Ca²⁺ extrusion are exactly balanced, the beat-to-beat Ca²⁺ transient amplitude is stable (black symbols at top and middle curves). However, when $\overline{{[{\text{Ca}}^{2+}]}_{\text{SR}}}$ depends on Δ[Ca²⁺]_i, alternans are produced. This is consistent with the hypothesis of Diaz et al. that increased Ca²⁺ extrusion after large Ca²⁺ transients (high feedback gain) is a factor that promotes instability.⁶⁰ The bottom traces in Figure 3B show that, under these conditions, Ca²⁺ release restitution can no longer be described by a single function. After relatively large beats, [Ca²⁺]_SR increases toward a smaller value before the next beat (blue traces). This leads to a smaller Ca²⁺ transient, which in turn results in [Ca²⁺]_SR increasing toward a larger value before the subsequent beat (red traces). This plot also shows that small differences in the SR Ca²⁺ content from one beat to the next can become amplified by the nonlinear relationship between the SR Ca²⁺ content and the fraction released (see figure legend for details). Indeed, additional simulations (not shown) confirmed that alternans could be abolished if the dependence of P_TRIG on [Ca²⁺ ]_SR were replaced with an independent time-dependent function that did not depend on [Ca²⁺]_SR. Since an infinite number of potential functions could have been chosen in the model, this does not prove that nonlinear gain is critical, but it does suggest that this steep relationship may promote the development of unstable beat-to-beat Ca²⁺ release. The simulations presented with this phenomenological and ad hoc model are simply meant to be illustrative and to suggest that future, more mechanistic analyses may lead to insight into which factors control the stability of Ca²⁺ release. A useful analysis of this type has recently been performed by Shiferaw et al.,⁶⁹ but many more such studies will need to be performed in the future to determine which potentially unstable features of Ca²⁺ cycling are particular to individual mathematical models and which represent general characteristics of cardiac cellular physiology.

The simulations displayed in Figure 3, by calculating individual values of [Ca²⁺]_SR and Δ[Ca²⁺]_i on each beat, implicitly assume that conditions within the cell are identical. However, since CICR release represents the recruitment of individually triggered Ca²⁺ sparks, as mentioned above, this may not always be the case. Experiments have shown that certain pharmacological interventions can promote “subcellular Ca²⁺ transient alternans,” in which different regions of the cell may alternate out-of-phase with one another.⁷⁰ Such subcellular heterogeneities may become especially important in disease states such as heart failure. Structural and/or functional alterations to the EC coupling machinery in HF may promote conditions in which SR Ca²⁺ content and/or CICR efficiency is high in certain locations, due to high local SR load or the local subcellular geometry, but low in others. Such local heterogeneities would be consistent in principle with the decreased synchrony of Ca²⁺ release that has been observed in cells isolated from failing hearts.⁷¹

The future challenge will be to combine quantitative examinations of Ca²⁺ restitution dynamics with analyses of APD to gain a richer understanding of how the electrical and chemical signaling systems of heart cells influence one another. As features that are critical to the development of unstable beat-to-beat rhythms such as alternans are recognized, new targets for therapies may be identified. As mechanistic insight continues to be gained, we may be able to find molecular targets that can be safely modified to prevent rhythm disturbances and reduce the risk of sudden cardiac death in patients while still maintaining adequate heart function.