Femtosecond Stimulated Raman Study of Excited-State Evolution in Bacteriorhodopsin

Abstract

Femtosecond time-resolved stimulated Raman spectroscopy (FSRS) is used to examine the photoisomerization dynamics in the excited state of bacteriorhodopsin. Near-IR stimulated emission is observed in the FSRS probe window that decays with a 400–600-fs time constant. Additionally, dispersive vibrational lines appear at the locations of the ground-state vibrational frequencies and decay with a 260-fs time constant. The dispersive line shapes are caused by a nonlinear effect we term Raman initiated by nonlinear emission (RINE) that generates vibrational coherence on the ground-state surface. Theoretical expressions for the RINE line shapes are developed and used to fit the spectral and temporal evolution of the spectra. The rapid 260-fs decay of the RINE peak intensity, compared to the slower evolution of the stimulated emission, indicates that the excited-state population moves in ∼260 fs to a region on the potential energy surface where the RINE signal is attenuated. This loss of RINE signal is best explained by structural evolution of the excited-state population along multiple low-frequency modes that carry the molecule out of the harmonic photochemically inactive Franck–Condon region and into the photochemically active geometry.

Introduction

Bacteriorhodopsin (bR) is the light-activated proton pump found in the purple membrane of Halobacterium salinarum. Upon absorption of visible light, the all-trans retinal chromophore isomerizes to a 13-cis configuration and initiates a photochemical cycle that transports a proton out of the cell (Figure 1). ^1,2 The excited state of bR decays with a time constant of ∼500 fs, ^3-6 and picosecond resonance Raman studies ^7-10 as well as subsequent time-resolved IR studies ¹¹ have established that J is the ground state 13-cis photoproduct of the isomerization reaction. A number of femtosecond time-resolved studies have probed the details of the excited-state absorption dynamics of bR in the visible and near-IR (NIR). ^3,12 The initially observed excited-state decay was later resolved into two time constants of ∼200–400 fs and 2–4 ps to fit the transient absorption kinetics ^13,14 and three time constants of 100–250 fs, 0.6–0.8 ps, and ∼10 ps to fit the time-resolved fluorescence. ¹⁵ These multiexponential decays may result from multiple protein conformations or intermediates, ¹² the contribution of overlapping transient excited-state absorption and stimulated emission bands, ¹³ as well as the intrinsic temporal complexity of evolution on a multidimensional potential energy surface. ¹⁶

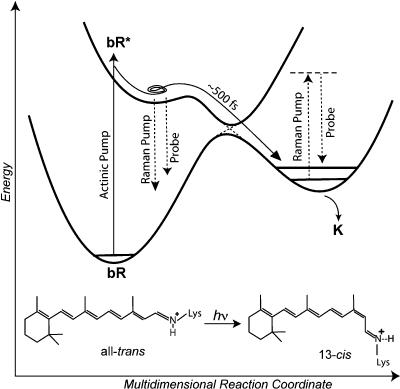
Figure 1.

Schematic diagram of the photoisomerization process of bacteriorhodopsin (bR) and the FSRS experiment. The femtosecond actinic pump pulse initiates the photochemistry, after which a stimulated Raman spectrum is obtained by applying two pulses: the narrow bandwidth Raman pump (∼800 nm) and the femtosecond probe continuum (830–960 nm). At short time delays, the FSRS signal is dominated by nonlinear emission from bR*. At longer time delays, the signal is due to Raman transitions of the photoproduct.

A variety of models for the excited-state structural evolution of the bacteriorhodopsin chromophore have been proposed on the basis of the time-resolved evolution of electronic signatures. The initially proposed model focused on the role of reactive torsional motion along the isomerization coordinate that drives the chromophore away from the Franck–Condon (FC) region and toward an efficient curve crossing back to S₀. ⁶ More recently, a three-state model for the isomerization process has been proposed, which invokes avoided crossings between formally distinct S₀, S₁, and S₂ states producing a small barrier to isomerization in S₁ and efficient photoproduct formation via a nonadiabatic transition to S₀. ¹² This model was put forward to account for the lack of a temporally resolvable dynamic Stokes shift beyond 100 fs in the S₁ absorption and emission spectra ^13,15,17 and the temperature dependence of the fluorescence lifetime. ^18,19 Alternative theoretical studies have supported the idea that isomerization proceeds on a barrierless excited-state potential surface. ^20,21 While the various experimental studies have been relatively consistent in determining the time scales of the excited-state dynamics, electronic absorption spectroscopy is inherently insensitive to the details of the multidimensional structural changes that must occur in the complex isomerization process. In particular, it is difficult to distinguish between motion and relaxation along symmetric bound degrees of freedom, along nontotally symmetric potentially unbound degrees of freedom that project on the overall reaction coordinate, and transitions between potentially distinct electronic surfaces. More precise measures of the structural events that occur on the excited state are needed to resolve these questions.

To obtain time-resolved structural information on ultrafast photochemical processes, we have developed the technique of femtosecond stimulated Raman spectroscopy (FSRS), that enables the rapid collection of high-resolution vibrational spectra with femtosecond time resolution. ^22-25 FSRS spectra are obtained by combining a narrow-bandwidth 800-nm picosecond Raman pump pulse with an ∼15-fs NIR continuum probe pulse to produce stimulated Raman spectra from the pump-induced gain in the probe spectrum. When combined with a sub-50-fs actinic pump pulse, the instrumental frequency resolution limits are uncoupled from the time resolution provided by the actinic pump–probe cross-correlation, allowing the acquisition of spectra with better than 100-fs time resolution and 15-cm⁻¹ frequency resolution. Additionally, FSRS is unaffected by background fluorescence and provides rapid data acquisition. ²³ The FSRS technique has thus far been used to study the ultrafast internal conversion and intramolecular vibrational energy redistribution in β-carotene and diphenyloctatetraene. ^22,24,26 A semiclassical theoretical treatment of the FSRS experiment has appeared, ²⁷ as well as detailed descriptions of the apparatus and method. ²⁵

Here, we use FSRS to examine the excited-state structural dynamics that lead to the primary photoisomerization event in bacteriorhodopsin. The FSRS spectra obtained during the excited-state lifetime of bR are dominated by Raman initiated by nonlinear emission (RINE), a new effect which produces dispersive line shapes at the ground-state frequencies but with intensities that decay with a time constant (∼260 fs) significantly faster than the ∼500-fs excited-state lifetime. The 260-fs decay of the RINE peaks is explained by the multidimensional structural evolution of the excited-state population along low-frequency degrees of freedom that carry the molecule away from the initial harmonic photochemically inactive FC geometry.

Materials and Methods

Bacteriorhodopsin was harvested from Halobacterium salinarum cultures using established techniques. ²⁸ The sample solution was prepared by resuspending a pellet of purple membrane in 5-mM N-2-hydroxyethylpiperazine-N′-2-ethanesulfonic acid (HEPES) (pH 7.4) and sonicating (Heat Systems Ultrasonics #220F, 30 W) for 2 min in 15-s intervals, keeping the solution on ice to prevent warming. Sonication was necessary to reduce scattering from large membrane aggregates. The sample was light-adapted in a Petri dish with a desk lamp while on ice, and adaptation was maintained by constant illumination with a fluorescent bulb. The solution was recirculated through a 0.5-mm path length flow cell at a rate (3 mL/min) sufficient to replenish the illuminated volume between shots. The visible absorption band (OD₅₆₉ = 18/cm) exhibited no changes throughout the experiment.

The laser system for FSRS has been presented in detail elsewhere. ^22,25 Briefly, the three laser pulses needed to perform FSRS are generated from the output of a Titanium:sapphire regenerative amplifier (BMI, Alpha 1000/US). The 500-nm actinic pump pulse (35 fs, 100 nJ) was produced by a noncollinear phase-matched optical parametric amplifier (NOPA), whose output was compressed with an SF10 prism compressor. A grating-based spectral filter ²⁵ generated the 809-nm 3.5-ps Raman pump pulse that was attenuated to 400 nJ/pulse. The Raman pump power was chosen to limit removal of the excited-state population because of excited-state absorption and stimulated emission at the Raman pump wavelength. The excited-state depletion was limited to 28% in the data presented here; however, reducing this depletion further to ∼10% produced no changes in the observed spectra or kinetics. The remainder of the amplifier output was used to produce the probe pulse by continuum generation in a 3-mm-thick sapphire plate, followed by pulse compression in a fused-silica prism compressor. The NIR portion of the continuum is selected by an 850-nm long-pass filter (Kodak #87c) and split into probe and reference beams by a 50:50 beam splitter, producing a 6-nJ probe pulse at the sample point with a spectrum extending from 840 to beyond 960 nm.

The actinic pump, Raman pump, and probe beams, all polarized horizontally, are focused by a 150-mm fl concave mirror and cross at the sample point, after which the probe is spatially selected, collimated, and sent to the spectrograph with the reference beam. The Raman pump/probe overlap and relative delay are optimized to maximize the Raman gain signal from ethanol. As predicted theoretically, the maximum Raman gain is generated when the probe precedes the peak of the Raman pump by ∼1 ps. ²⁹ Two cylindrical lenses focus the probe and reference beams into the spectrograph (ISA HR320, 600 gr/mm), where they are dispersed and detected by a dual photodiode array (Princeton DPDA-1024).

The Raman gain spectrum is calculated as the ratio of the Raman-pump-on probe spectrum divided by the Raman-pump-off probe spectrum after normalization with the reference. The presented time-resolved spectra are the average of 400 alternate 40-ms Raman-pump-on and Raman-pump-off probe exposures, producing a total acquisition time of 40 s per time point. The instrument spectral resolution is ∼8 cm⁻¹, determined primarily by the 120-μm focused width of the probe and reference beams at the spectrograph entrance slit. Time-resolved spectra were collected in random order, with the actinic pump delay set by a computer-controlled translation stage. NIR stimulated emission spectra are obtained simultaneously in the FSRS experiment and are determined by comparing the actinic-pump-on and pump-off spectra in a similar manner. Additionally, the stimulated emission kinetics and excited-state depletion with the Raman-pump on are calculated by comparing the actinic-pump-on/Raman-pump-on probe with the actinic-pump-off/Raman-pump-off probe intensity in regions free from Raman peaks. The photoproduct signals at 0.2 and 10 ps increased linearly with changes in actinic and Raman pump power.

The temporal instrument response was Gaussian in shape, with a full width at half-maximum (fwhm) varying between 60 fs at 941 nm and 73 fs at 860 nm and containing chirp resulting in a ∼15-fs group velocity delay of the 941-nm components relative to 860 nm, as measured by optical Kerr effect cross-correlation. ²⁵ The △t = 0 time delay was initially set by the cross-correlation, but was allowed to vary freely in the fitting of the stimulated emission kinetics.

Difference spectra are produced by subtracting a scaled ground-state spectrum from the FSRS spectrum that contains contributions from the ground state, the excited state, and (at times longer than ∼700 fs) the ground-state photoproduct. For example, the 5-ps difference spectrum presented in Figure 4 is the FSRS spectrum (obtained with the actinic pump on at an actinic pump–probe time delay of 5 ps) minus 0.91 times the ground-state (actinic-pump-off) spectrum. Further analysis of the picosecond time-scale spectra, the details of which will be presented in a separate publication, showed that 9% of the illuminated sample was converted to photoproduct by the actinic pump. ³⁰ When analyzing the shorter time-scale difference spectra, a scaled ground-state spectrum has been subtracted with the scaling factor determined by extrapolating backward from the long-time value of 0.91 using the known quantum yield ^31,32 of 0.6 and the ∼500-fs excited-state decay time determined from the Raman-pump-on stimulated emission kinetics.

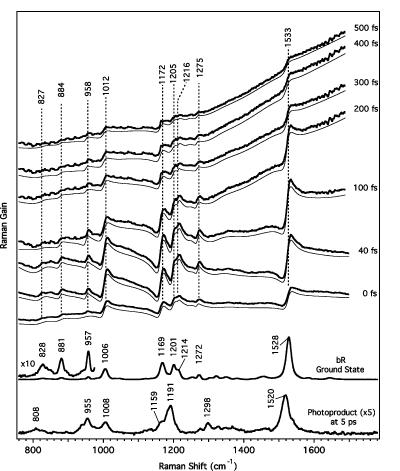
Figure 4.

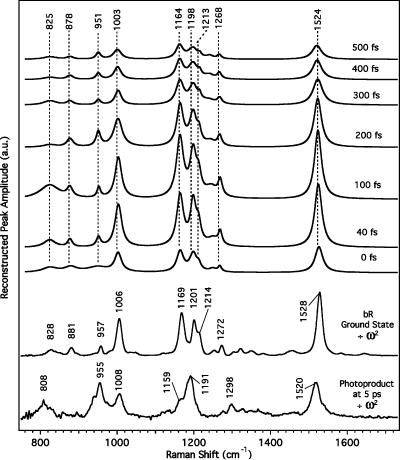
Evolution of bR FSRS spectra from 0 to 500 fs. The sloping baseline is due to the shape of the stimulated emission spectrum in the probe window. Fits to these representative spectra are shown as the thin solid line below each trace and were calculated using the dispersive line shape function described by eq 4 plus a polynomial baseline. The buffer and ground-state spectra have been subtracted, and the spectra vertically offset for clarity. The frequencies label the observed gain maxima.

Theory of Raman Initiated by Nonlinear Emission (RINE)

FSRS line shapes are determined by the imaginary part of the third-order susceptibility of the sample, Imχ⁽³⁾(ω₂ = ω₁ − (ω₁ − ω₂)), which describes the polarization response of the material in response to three optical fields at the Raman pump (ω₁) and probe (ω₂) frequencies. Similarly, the signal generated by traditional Raman transitions produces line shapes that vary with ω₁ and ω₂ according to

$$\mathrm{Im}{\chi }^{\left(3\right)}\left({\omega }_2\right)=\frac{N}{4{\hslash }^3}\frac{{\gamma }_{fg}}{\{{[{\omega }_2-({\omega }_1-{\omega }_{fg})]}^2-{{\gamma }_{fg}}^2\}}\mid {\mathrm{KHD}}_{\mathrm{r}}+{\mathrm{KHD}}_{\mathrm{nr}}{\mid }^2$$ (1)

where the vibrational frequency is ω _fg , N is the concentration of the scattering species and KHD_r and KHD_nr are the resonant and nonresonant terms of the Kramers–Heisenberg–Dirac expression for the Raman excitation profile. ^27,33,34 Equation 1 is a Lorentzian peak centered at ω₂ = ω₁ − ω _fg with vibrational line width 2γ _fg and an intensity determined by the electronic resonance term, $\mid {\mathrm{KHD}}_{\mathrm{r}}+{\mathrm{KHD}}_{\mathrm{nr}}{\mid }^2$ . On resonance, the KHD_r term dominates and the Raman line shape remains positive-definite only when contributions to χ⁽³⁾ from hot luminescence are included. ³³ A typical homogeneously broadened Raman line shape is shown in Figure 2b.

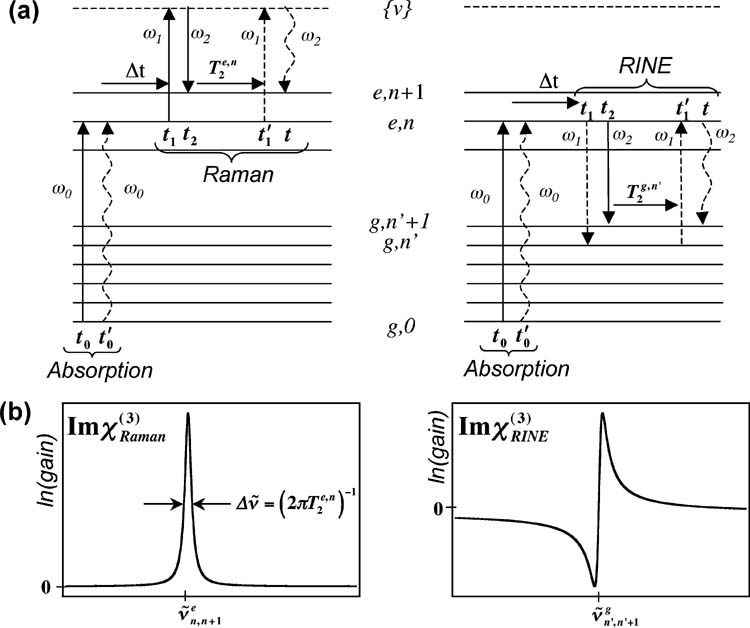
Figure 2.

(a) Wave mixing energy level diagrams describing time-resolved Raman and time-resolved RINE processes. Solid arrows refer to ket dipole couplings and dashed arrows refer to bra dipole couplings. The resulting line shapes are shown in (b).

In a time-resolved experiment, in which the Raman process acts as the probe following electronic excitation by another laser pulse, the Raman signal is given by the same expression, but now, the vibrational resonance, ω _fg , can be with a photochemical product. This process can be described using the density matrix approach and is shown diagrammatically in the wave-mixing energy-level diagram in Figure 2a. Propagation of the density matrix under the influence of the incident electric fields is described by the dipole couplings to the ket (solid arrows) and bra (dashed arrows) sides of the wave function, and the final polarization of the system at time t is symbolized by the final wavy arrow. ³³ The electronic absorption at the actinic pump frequency, ω₀, is treated as a separate process. The Raman transition itself is initiated by sequential dipole couplings of the ket side of the wave function to the Raman pump and probe fields at t ₁ and t ₂. This process generates the vibrational coherent state, $\mid e,n+1\rangle \langle e,n\mid$ , that decays with exponential lifetime $T_2^{e,n}$ and thereby determines the vibrational line width, $\gamma =1∕T_2^{e,n}$ . The Raman transition is completed by a dipole coupling of the bra with the Raman pump at time $t_1^{\prime }$ and decay of the resulting polarization at time t and frequency ω₂.

When the Raman resonance is probed by a coherent stimulated process, additional terms in χ⁽³⁾ can become dominant. Resonant inverse Raman studies have observed dispersive line shapes due to contributions to χ⁽³⁾(ω₁ = ω₁ - ω₂ + ω₂) that have negligible contribution off-resonance. ^35,36 When in resonance with an elecronic transition, the high photon flux of both the Raman pump and probe fields used in FSRS produces observable contributions to the signal that are generally ignored in spontaneous Raman and nonresonant stimulated Raman. Under the electronic resonance conditions of the excited state of bR, the dominant process that generates a signal along the probe wavevector, k ₂, with sharp vibrational features at ω₂ that decay with the excited-state population is a process we term Raman initiated by nonlinear emission, or RINE. In this process, ground-state vibrational coherence is generated by nonlinear emission initiated from the excited-state surface at times t ₁ and t ₂ (Figure 2a). Nonlinear emission is similar to conventional stimulated emission, except that the bra and ket are transferred to the ground electronic state by coupling to two different fields. The ground-state vibrational coherence will decay with time constant $T_2^{g,n^{\prime }}$ ; during this time, the transition is completed by Raman-like dipole couplings on the bra side at $t_1^{\prime }$ and t that produce a population of vibrational state $\mid g,n^{\prime }+1\rangle$ . The RINE signal will travel along the probe wavevector k ₂ and consist of Stokes-shifted vibrational features at the ground-state frequencies.

In traditional Raman scattering and FSRS, dispersive line shapes are not observed because the phase of the final signal at t is necessarily equivalent to that of the probe field, since the vibrational coherence is driven by the mixing of the pump ( $E_1^{\ast }$ ) and probe (E ₂) fields and then upconverted with the pump (E ₁). ²⁷ Importantly, the phase of the pump field couplings at t ₁ and $t_1^{\prime }$ exactly cancel out so that the Raman signal generated at t is in phase with the initial field that drove the vibrational coherence at t ₂. Hence, no interference occurs between the heterodyne detected fields measured at ω₂ along the probe wavevector, k ₂, explaining why spontaneous and stimulated Raman signals generated in this manner have positive-definite line shapes. ^27,33 In the RINE process, however, the Raman-pump fields do not act in quadrature; the pump field at $t_1^{\prime }\left(E_1\right)$ is not simply the complex conjugate of the field at $t_1(-E_1^{\ast })$ . Because of this, the up-converted signal at time t may be out of phase with the probe field acting at time t ₂, giving rise to interference between these two fields and therefore a dispersive line shape in the heterodyne detected signal at ω₂.

The RINE line shape function in the long-time limit approximation can be easily written down using the diagram in Figure 2 and the rules of Lee and Albrecht. ³³ The time-ordered dipole couplings give rise to the RINE third-order susceptibility with the form

$$\begin{array}{c}{\chi }_{\mathrm{RINE}}^{\left(3\right)}=N\sum _{n^{″}}(\langle e,n\mid \mu E_{\mathrm{pu}}\mid g,n^{\prime }\rangle \langle g,n^{\prime }\mid \mu E_{\mathrm{pu}}^{\ast }\mid e,n^{″}\rangle \\ \langle e,n^{″}\mid \mu E_{\mathrm{pr}}\mid g,n^{\prime }+1\rangle \langle g,n^{\prime }+1\mid \mu E_{\mathrm{pr}}^{\ast }\mid e,n\rangle )∕\\ \left[{\hslash }^3({\omega }_{g(n^{\prime },n^{\prime }+1)}-({\omega }_1-{\omega }_2)-i{\gamma }_{g,n^{\prime }})({\omega }_{eg}+{\omega }_{g(n^{\prime },n^{\prime }+1)}-{\omega }_1-i{\Gamma }_{eg})({\omega }_{eg}^{″}-{\omega }_2-i{\Gamma }_{eg})\right]\end{array}$$ (2)

where N is the number density of molecules in the sample, ω _g(n,n+1) is the vibrational frequency in the ground state, ${\gamma }_{g,n^{\prime }}={\left(T_2^{g,n^{\prime }}\right)}^{-1}$ is the homogeneous line width of the vibrational transition in the ground state, ${\omega }_{eg}={\hslash }^{-1}(E_{e,n}-E_{g,n^{\prime }}+1)$ is the energy difference between the initial and final states, ${\omega }_{eg}^{″}={\hslash }^{-1}(E_{e,n^{″}}-E_{g,n^{\prime }+1})$ is the energy difference between the bra and ket states at time t, and Γ _eg is the homogeneous line width of the g←e electronic transition. The sum is over intermediate states $\mid e,n^{″}\rangle$ and indicates that the Raman couplings at times $t_1^{\prime }$ and t need not go through the same excited vibronic state from which the process was initiated. The long-time limit approximation assumes that the intermediate coherences decay exponentially and that the detected signal at ω₂ is integrated over all times, t, where $t>t_1^{\prime }>t_2>t_1$ . This allows the energy denominators, $\hslash ({\omega }_{ij}^{″}-{\omega }_{\mathrm{photon}}-i{\Gamma }_{ij})$ , to represent the Fourier transform of the third-order polarization of the sample. ^27,33

For completeness, we need to include a similar equation for the process in which the time ordering of the first two dipole couplings is reversed

$$\begin{array}{cc}{{\chi }^{\prime }}_{\mathrm{RINE}}^{\left(3\right)}=& N\sum _{n^{″}}(\langle e,n\mid \mu E_{\mathrm{pu}}\mid g,n^{\prime }\rangle \langle g,n^{\prime }\mid \mu E_{\mathrm{pu}}^{\ast }\mid e,n^{″}\rangle \langle e,n^{″}\mid \mu E_{\mathrm{pr}}\mid g,n^{\prime }+1\rangle \langle g,n^{\prime }+1\mid \mu E_{\mathrm{pr}}^{\ast }\mid e,n\rangle )∕\\ & [-{\hslash }^3({\omega }_{g(n^{\prime },n^{\prime }+1)}-({\omega }_1-{\omega }_2)-i{\gamma }_{g,n})({\omega }_{eg}-{\omega }_2+i{\Gamma }_{eg})({\omega }_{eg}^{″}-{\omega }_2+i{\Gamma }_{eg})]\end{array}$$ (3)

The observed line shape will be determined by the sum of eqs 2 and 3

$$\mathrm{Im}{\chi }^{\left(3\right)}\left({\omega }_2\right)=\mathrm{Im}{\chi }_{\mathrm{RINE}}^{\left(3\right)}+\mathrm{Im}{{\chi }^{\prime }}_{\mathrm{RINE}}^{\left(3\right)}=\frac{K_{\mathrm{FC}}}{\{{[{\omega }_2-({\omega }_1-{\omega }_{n,n+1})]}^2+{{\gamma }_{g,n}}^2\}}\cdot \frac{2b}{{(b^2+{{\Gamma }_{eg}}^2)}^2}\cdot \{b{\gamma }_{g,n}-{\Gamma }_{eg}[{\omega }_2-({\omega }_1-{\omega }_{n,n+1})]\}$$ (4)

where b = ω _eg − ω₂ is the electronic resonance term, K _FC subsumes N and all the Franck–Condon factors, transition dipoles, and physical constants, and we have used the approximation that the state $\mid e,n\rangle$ is the dominant term in the sums of eqs 2 and 3. Equation 4 is the product of three factors, the first of which is a simple Lorentzian peak at the ground-state Raman frequency ω₂ = (ω₁ − ω _n,n+1) of width 2γ _g,n . The second factor is similar to a Raman excitation profile term; it is essentially the square of the homogeneously broadened stimulated emission spectrum at ω _eg . The third factor introduces dispersion at the Raman frequency, where the degree of dispersion depends on the relative magnitudes of the electronic and vibrational resonance terms and the vibrational and electronic line widths. A typical RINE line shape is shown in Figure 2b. Equation 4 can be used for empirical spectral fitting, by calculating the value of Imχ⁽³⁾ as a function of ω₂ while varying the vibrational frequency, ω _n,n+1, the amplitude, K _FC, and the line width, γ _g,n of each peak, as well as the electronic resonance terms b and Γ _eg that determine the line shapes of all the peaks. Each vibrational peak in the spectrum will have the same value of b and Γ _eg and different vibrational terms, ω _n,n+1, K _FC, and γ _g,n .

Results

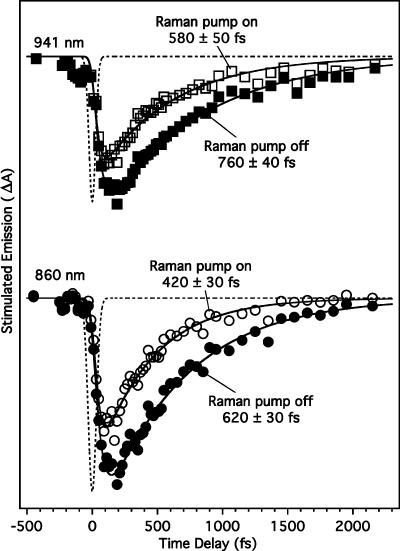
Excited-State Stimulated Emission. The stimulated emission kinetics of bR* presented in Figure 3 reveal the time scale of internal conversion to the ground state. The kinetics are quantified using a nonlinear least-squares fit to a convolution of our 65-fs instrument response with a multiexponential molecular response that includes a short rise time followed by an exponential decay. The results of the fits are summarized in Table 1. With a single-exponential decay and the Raman pump off, the stimulated emission at 941 nm has a 51 ± 9 fs rise time, followed by a 760 ± 40 fs decay. At 860 nm, the stimulated emission has a 52 ± 7 fs rise time and a 620 ± 40 fs decay. With the Raman pump on, the rise time shortens to ∼30 ± 15 fs and the decay times shorten to 580 ± 60 fs at 941 nm and 420 ± 40 fs at 860 nm because of the bR* depletion induced by the Raman pump. ¹² The error estimates are standard deviations determined from the least-squares fit and do not include any contribution from systematic errors associated with the shape and stability of the continuum, which may add an additional ±50 fs to the decay time uncertainty.

Figure 3.

Stimulated emission kinetics of the excited state of bR at 860 and 941 nm. Solid lines are fits to a convolution of the 60–70-fs instrument response (dashed line) with a molecular response exhibiting a ∼30–50-fs rise followed by a single exponential decay, with time constants indicated on each trace.

TABLE 1.

Bacteriorhodopsin Stimulated Emission and RINE Kinetics

signal	amplitude	rise time (fs)	decay time (fs)
stim. emission, 860 nm	−0.0507 ± 0.002	52 ± 7	620 ± 40
stim. emission, 941 nm	−0.0361 ± 0.002	51 ± 9	760 ± 40
stim. em., 860 nm, r. pump on	−0.0366 ± 0.003	30 ± 15	420 ± 40
stim. em., 941 nm, r. pump on	−0.0263 ± 0.002	30 ± 12	580 ± 60
RINE intensity, 1524 cm-1	271 ± 9	16 ± 6	246 ± 9
RINE intensity, 1164–1213 cm-1	455 ± 17	15 ± 5	270 ± 12
RINE intensity, 1003 cm-1	150 ± 3	4 ± 5	264 ± 8

Excited-State FSRS. Figure 4 presents selected FSRS difference spectra with time delays between 0 and 500 fs compared with both a ground-state bR FSRS spectrum and an FSRS spectrum of the photoproduct at Δt = 5 ps. The intensities of the dispersive features are of the same magnitude as the ground-state Raman peaks, despite the fact that the excited-state concentration is only 10–15% of the ground-state concentration. Hence, varying the ground-state subtraction factor by ∼5% produced no observable difference in the resulting spectra. There is no detectable contribution from the unique ground-state photoproduct spectrum until Δt > 700 fs.

The observed spectra consist of a broad, sloping background caused by the Raman pump-induced bleach of the stimulated emission band and sharp features that appear as dispersive lines. These sharp features initiate on the low-frequency side as a negative dip, sharply rise to a positive peak, and then return slowly to baseline, similar to what has been previously observed in resonant inverse Raman. ^35,36 The maxima in the dispersive peaks exhibit no spectral shift over the excited-state lifetime and appear at positions consistently up-shifted by about 3 cm⁻¹ from the ground-state Raman frequencies. The constancy of the dispersive line shape at all time delays indicates that they cannot arise from vibrational coherence generated by the actinic pump. First, the ∼500-cm⁻¹ bandwidth of the actinic pump cannot impulsively excite these high-frequency modes. Second, if the signal depended on vibrational coherence initiated by the actinic pump, then each peak would decay with a separate lifetime depending on the dephasing time of each mode. Instead, as will be shown below, the intensities of all the dispersive features in the spectrum decay with the same time constant. The close correspondence of the dispersive peaks to the ground-state frequencies, the decay of the dispersive lines on roughly the same time scale as the stimulated emission, and the large intensity of the dispersive features all support the assignment of the dispersive features to the RINE process.

The spectra were fit to the sum of a sixth-order polynomial baseline plus twelve RINE peaks with variable peak positions, amplitudes, and widths (Figure 4). In general, all parameters were allowed to vary freely, although at time delays greater than 200 fs, it was necessary to hold Γ _eg , ω _eg − ω₂, and the positions and widths of the small peaks below 1000 cm⁻¹ constant at the average values from 0 to 200 fs to avoid unphysical values. The electronic line width, Γ _eg in eq 4, and resonance, ω _eg − ω₂, terms were determined to be 81 ± 4 and 13 ± 3 cm⁻¹, respectively. However, given the approximations necessary to obtain a tractable line shape function, these values carry little molecular information. More importantly, from the best-fit parameters, it is possible to reconstruct a conventional spectrum allowing us to observe the actual molecular frequencies, amplitudes, and widths of the vibrational resonances. This is accomplished by setting ${\omega }_{eg}\gg {\omega }_2$ in eq 4, which removes the dispersion in the third factor of the equation. The reconstructed Lorentzian spectra from 0 to 500 fs are presented in Figure 5, and the best-fit positions and widths of the major peaks are summarized in Figure 6. Two small, broad peaks around 1300 and 1450 cm⁻¹ tended to broaden to unphysical values to fit small oscillations in the baseline and were left out of the reconstruction. As shown in Figures 5 and 6, the RINE peak positions are initially downshifted ∼3 cm⁻¹ from the ground-state frequencies, consistent with anharmonicity in the bR ground-state potential surface. It is also apparent that the frequencies of the major peaks decrease even further over the excited-state lifetime, for example, the ethylenic shifts from 1526 to 1521 cm⁻¹ between 0 and 600 fs. The narrow peak widths (10–30 cm⁻¹ fwhm) agree with the ground-state spectrum and in many cases are too narrow to be generated by any type of vibrational coherence on the excited-state surface. The line widths tend to increase between 0 and 600 fs, especially for the ethylenic that broadens from 24 to 31 cm⁻¹ and the 1198-cm⁻¹ peak that broadens from 20 to 34 cm⁻¹ between 0 and 600 fs.

Figure 5.

Reconstructed Lorentzian spectra from the fits to the FSRS spectra of bR in Figure 4. Peak amplitudes, positions, and widths are generated from the dispersive line shape function in the nonresonant limit. The FSRS spectra of ground-state bR and the 13-cis photoproduct, presented for comparison, have been divided by a factor of ${\omega }_{\mathrm{vib}}^2$ to remove the vibrational frequency dependence of the Raman scattering. The anomalously large intensity of the 825 cm⁻¹ peak at 100 fs is not significant given the low signal-to-noise ratio of the original data in this region.

Figure 6.

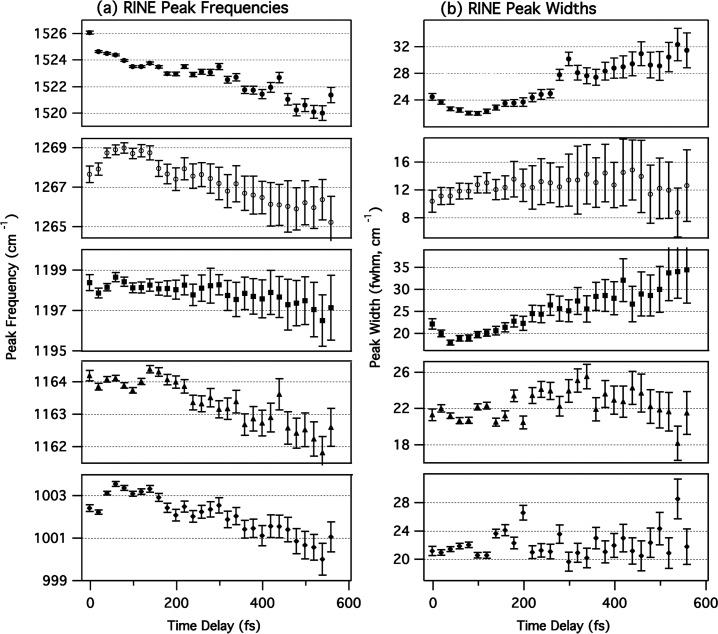
Bacteriorhodopsin RINE peak positions and widths determined using the line shape function from eq 4, where ω _g(n,n+1) is the vibrational frequency and 2γ _g,n is the peak width (Lorentzian fwhm). Errors are 1 standard deviation determined by the nonlinear least-squares fitting procedure. Only the major peaks in the spectra are shown: C=C stretch (), C₁₁–H rock (○), C₁₄–C₁₅ stretch (■), C₁₀–C₁₁ stretch (▲), and methyl rock (◆).

For comparison, we present in Figure 5 stimulated Raman spectra of bR and the photoproduct at 5 ps that have been divided by a factor of ${\omega }_{\mathrm{vib}}^2$ , to correct for the vibrational frequency dependence of Raman intensities. ³⁴ The dominant features in the ground-state bR spectrum are as follows: (1) the ethylenic stretch at 1528 cm⁻¹, which shifts to 1520 cm⁻¹ in the photoproduct because of changes in the conjugation along the polyene backbone; (2) the “fingerprint” peaks at 1169, 1201, and 1214 cm⁻¹ (primarily C–C stretches coupled with CCH rocks) that evolve into an intense peak at 1191 with a small shoulder at 1159 cm⁻¹ in the photoproduct; and (3) the methyl rock at 1006 cm⁻¹, which in the photoproduct is joined by intense hydrogen out-of-plane (HOOP) modes at 808 and 955 cm⁻¹ that gain intensity from the distortion of the 13-cis chromophore in the C₁₄–C₁₅ region. ³⁷ The fingerprint region is a particularly sensitive measure of the configuration of the polyene backbone and has been important in determining that the primary photoreaction of bR is the all-trans to 13-cis isomerization. ^7,37-39 The extreme similarity between the ground-state Raman and reconstructed RINE spectra, particularly in the fingerprint region, support our suggestion that the dispersive line shapes are produced by vibrational coherence on the ground-state bR surface.

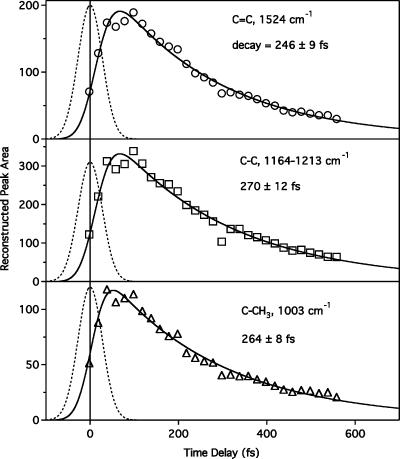
Figure 7 presents an analysis of the time dependence of the reconstructed RINE peak areas of the ethylenic region, the fingerprint region, and the methyl rock region. The growth and decay of the peak areas are described well by a convolution of our 65-fs instrument response with a fast exponential rise and single exponential decay. The <20-fs rise times are faster than for the stimulated emission, but are poorly determined because of limited data points near Δt = 0. The decay times, summarized in Table 1, are 246 ± 9, 270 ± 12, and 264 ± 8 fs for the ethylenic, fingerprint, and methyl rock peaks, respectively. All three decay times are significantly faster than the ∼500-fs stimulated emission kinetics with the Raman pump on (Table 1). These error bars represent a single standard deviation of the least-squares fit. Additional systematic error due to continuum fluctuations has not been included, because baseline fluctuations do not contribute to the RINE peak amplitude.

Figure 7.

Kinetics of the reconstructed RINE peak areas of the C=C peak (1525 cm⁻¹), the C–C fingerprint region (1164–1213 cm⁻¹), and the methyl rock (1003 cm⁻¹). Solid lines are fits to a convolution of the 65-fs instrument response (dashed line) with an exponential molecular response exhibiting a ∼5–15-fs rise time and a single exponential decay with the indicated time constants.

Discussion

The stimulated emission kinetics seen here are in agreement with previous work that observed a <50-fs rise in the NIR stimulated emission signal followed by a ∼500-fs decay. ^{6,14,17,40-42} The slightly longer decay time at 900 nm relative to that at 860 nm is consistent with the wavelength-dependent fluorescence kinetics observed by Du and Fleming ¹⁵ and perhaps indicative of a slow red-shift in the stimulated emission band as suggested by Hochstrasser and co-workers. ¹⁷ With higher SNR emission kinetics, it is possible to separate the ∼500-fs decay into fast (200–300 fs) and slow (0.7–1.1 ps) components, ^13-15 though there are some indications that multiexponential kinetics can be generated by excessive pump pulse intensities. ⁴¹ Our stimulated emission data were not obtained in a manner designed to precisely define the relative amplitudes and time constants of the multiexponential decay. However, with the long time constant fixed at 790 fs, ^12,15 our fast time constant was found to vary from 150 to 460 fs (amplitude of 40–80%), consistent with previous work. ^13-15

The magnitude of the excited-state RINE signals, which depend on both the population of the excited state and the FC overlap of the nonlinear emission, decay significantly more rapidly than the stimulated emission with the Raman pump on. Interestingly, the 250–270-fs decay time of the RINE intensity matches the fast component of the stimulated emission observed by others, which has been ascribed to the 65% of the excited-state population that is “reactive”. ^13-15 It is tempting to argue that the stimulated emission band of the reactive and unreactive populations are different and that the unreactive population does not have the resonance at 800 and 860–950 nm needed to generate the RINE peaks. However, this model would predict a time-dependent stimulated emission spectrum, contrary to the observations of Anfinrud and co-workers. ¹³ The constant shape of the stimulated emission band also allows us to rule out the possibility that the loss of RINE signal is associated with a purely electronic transition, for instance, between the optically active B_u state and a nearby A_g state. However, if the final electronic state in such a process was highly mixed with the B_u state, it might be possible to retain a similar stimulated emission spectrum throughout the excited-state lifetime. ⁴³ Additionally, Ruhman et al. have shown that the efficiency of dumping bR* → bR using a 1070-nm pulse does not change over the lifetime of the excited state. ⁴¹ The decay of our RINE signal thus indicates that the excited-state population has evolved in 260 fs to a new vibronic phase space which we term the “photochemically active region” that does not project into the original harmonic reactant potential energy surface. Moreover, the photochemically active region apparently does not project into any region of the ground-state surface, either of the reactant or of the photoproduct, that can maintain vibrational coherence necessary for the RINE signal.

The observed constancy of the excited-state stimulated emission spectrum ¹³ dictates that the first step in RINE (i.e., the two initial electric field couplings shown in Figure 2 at t ₁ and t ₂) must occur with unchanged efficiency throughout the lifetime of the excited state. Thus, the faster decay of the RINE signal compared to the stimulated emission must be due to a loss in efficiency of the final field couplings, at $t_1^{\prime }$ and t. The most likely scenario that would cause this is a rapid loss of vibrational coherence on the ground-state surface between times t ₂ and $t_1^{\prime }$ . Evolution of the excited state toward the photochemically active region must move the molecule toward a position on the excited-state potential that is vertically displaced from a highly anharmonic portion of the ground-state surface. The transition of the system to a very anharmonic part of the ground-state surface by stimulated emission will lead to very fast vibrational dephasing, which will cause not only a decrease in signal magnitude but also a significant broadening of the vibrational features (for $T_2\approx 100\mathrm{fs},\Delta \tilde{v}\approx 100{\mathrm{cm}}^{-1}$ ), rendering these lines difficult to observe on top of the sloping background. Both of these possibilities require significant movement of the chromophore in the excited state away from the FC region after the fast (<50 fs) initial relaxation. Movement of the excited-state chromophore to a structure that is vertically displaced from an increasingly anharmonic portion of the ground-state surface is further supported by the decreasing frequencies and increasing widths of the RINE peaks over time (Figure 6).

We thus attribute the 260-fs decay of the RINE signal to excited-state intramolecular vibrational energy redistribution (IVR), whereby the initially excited FC active modes relax by coupling with lower-frequency modes that were not coupled to (and excited by) the electronic absorption. Excitation of the lower frequency modes, such as CCC bends, HOOP modes, and torsions, could deform the molecule toward a conical intersection with the ground-state surface. ^21,44-46 However, because the IVR receiving modes are not coupled to the electronic transition (i.e., Δ = 0), this process will have a negligible effect on the stimulated emission spectrum. Significant distortion of the molecular symmetry can occur by the induced torsional motion or by pyramidalization at C₁₄, as has been predicted by theory. ²¹ As described above, a significant twist of the retinal polyene backbone in the excited state may quench the RINE signal by moving the molecule to the photochemically active region that is vertically displaced from a highly anharmonic portion of the ground-state surface, thereby causing rapid decay of the ground-state coherence following nonlinear emission. Our previous FSRS studies of β-carotene have found that, in the excited state, IVR out of the ethylenic mode occurs in ∼450 fs. ²² The somewhat faster 260-fs time constant for IVR observed here is reasonable, considering that this process will be accelerated in bR because of decreased symmetry and the resultant increase in mode-mixing.

A schematic of the excited-state dynamical evolution in bR is shown in Figure 8. Absorption of a photon (step 1) places the chromophore into the FC region, after which the excited-state wave packet rapidly evolves along the phase-space orbit of the displaced (Δ ≠ 0), FC-coupled modes. This evolution is driven primarily by the rapid relaxation along the highly displaced degrees of freedom such as the ethylenic stretch at 1528 cm⁻¹ (22-fs period), the C–C stretches at 1200 cm⁻¹ (28-fs period), and the methyl rock at 1006 cm⁻¹ (33-fs period) to a distribution of geometries centered at the excited-state equilibrium structure (step 2). ¹⁶ This ultrafast intramolecular relaxation occurs at the same time as the inertial dielectric response of the protein, ¹⁴ and together, these processes produce the <30-fs growth of the red-shifted stimulated emission band observed by us and others. ⁴⁷ The multidimensional nature of this initial relaxation, in combination with rapid excited-state IVR, prevents the observation of high-frequency coherent oscillations in the excited state. ⁴⁸ Non-totally symmetric modes, such as HOOP modes and carbon backbone torsions, are not excited by the initial absorption, because they are not FC coupled. Instead, they are excited by IVR from the displaced modes (step 3) in ∼200–300 fs. On this time scale, the protein binding pocket likely contributes to the efficiency and specificity of the isomerization by allowing large-scale chromophore distortion to occur only at or near the C₁₃=C₁₄ bond, as suggested by Schulten and co-workers. ²¹ This focused excitation of nonsymmetric photochemically active modes produces a highly distorted dynamic molecular ensemble that significantly occupies very anharmonic regions of the excited-state potential energy surface. These anharmonic regions are vertically displaced from an equally anharmonic portion of the ground-state surface. The normal-mode mixing that occurs because of the anharmonicity will cause extremely rapid dephasing on the ground-state surface following the nonlinear emission process (step 4), explaining the loss of RINE signal. After the IVR process, the molecule has a direct path from the photochemically active region to the ground-state photoproduct surface via a conical intersection (step 5). The 500–700-fs lifetime measures the time it takes for the molecule to access the particular multidimensional distortion, most likely requiring multiple twists about several double bonds, that efficiently leads to the conical intersection. ⁴⁴

Figure 8.

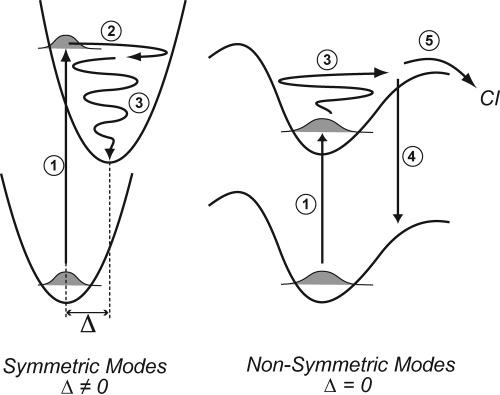
Schematic of the evolution of vibrational excitation and relaxation on the excited-state surface of bR*. The initial absorption of a photon (1) places the molecule into the FC region and excites symmetric FC coupled modes. In <30 fs, the wave packet evolves in the phase space of the displaced double-bond stretch (and other displaced modes on a slower time scale), causing the rapid growth of the red-shifted stimulated emission band (2). IVR from the FC active modes into the nontotally symmetric modes occurs in ∼260 fs (3), driving the molecule into a distorted configuration by exciting torsional and hydrogen wagging modes. In this ”photochemically active region”, the RINE signal is eliminated because of the high degree of anharmonicity in the potential surface of the nonsymmetric modes that prevents long-lived ground-state vibrational coherence following nonlinear emission (4). Finally, the molecule reacts with a 500–700-fs time constant, determined by the time it takes to access the particular combination of multimode trajectories (backbone torsions, HOOPs, etc.) that lead through the conical intersection.

Our data support the general argument that the rate and magnitude of excitation in torsional and out-of-plane vibrational coordinates (e.g., HOOPs) determines the speed, efficiency, and specificity of isomerization in protonated Schiff base retinals. This interpretation is in agreement with the work of Ruhman and co-workers on C₁₃=C₁₄ locked pigments which show a significant increase in excited-state lifetime. ⁴² Such behavior is expected if distortion of the chromophore is required to reach the conical intersection. This interpretation also suggests that the excited state, following initial phase space evolution along displaced modes, is not stationary in structure as has been inferred from the constancy of the stimulated emission spectrum. Instead, delayed low-frequency excitation and evolution along nondisplaced coordinates can produce significant structural changes while maintaining an unchanged emission spectrum during the excited-state lifetime.

In summary, the RINE signal from bR* decays much more quickly than the excited-state population, indicating that significant structural changes occur in the excited state as a result of IVR from the FC active modes (e.g., C=C and C–C stretches) into the dark torsional and HOOP coordinates. Without the protein environment, this IVR causes the excitation of dark modes throughout the chromophore and thereby produces isomerization at several different locations, as observed experimentally. ⁴⁹ However, in the binding pocket of the bR pigment, steric and electrostatic constraints will direct the vibrational excitation to be deposited only into selected torsions and HOOPs of the molecule, thereby causing the very specific isomerization at only the C₁₃=C₁₄ bond. It is interesting to compare the photochemical process of bR with the ultrafast 200-fs-isomerization rhodopsin. The isomerization in rhodopsin occurs much more rapidly and with preserved vibrational coherence of the photoproduct as a result of the direct photoexcitation of important reactive torsional modes and HOOPs. ³ Relative to rhodopsin, the isomerization in bR proceeds more slowly and without observable vibrational coherence, because the chemically reactive modes are indirectly excited by relaxation from the FC active modes.