Relation between native ensembles and experimental structures of proteins

Abstract

Different experimental structures of the same protein or of proteins with high sequence similarity contain many small variations. Here we construct ensembles of “high-sequence similarity Protein Data Bank” (HSP) structures and consider the extent to which such ensembles represent the structural heterogeneity of the native state in solution. We find that different NMR measurements probing structure and dynamics of given proteins in solution, including order parameters, scalar couplings, and residual dipolar couplings, are remarkably well reproduced by their respective high-sequence similarity Protein Data Bank ensembles; moreover, we show that the effects of uncertainties in structure determination are insufficient to explain the results. These results highlight the importance of accounting for native-state protein dynamics in making comparisons with ensemble-averaged experimental data and suggest that even a modest number of structures of a protein determined under different conditions, or with small variations in sequence, capture a representative subset of the true native-state ensemble.

The rapidly growing Protein Data Bank (PDB) (1) is testament to the revolution in structural biology that has occurred over the last 15 years. These newly available protein structures contain a wealth of information that can be used to rationalize and predict the function of proteins. At the same time, however, it has long been realized that native states are best represented as ensembles of similar structures and that the dynamics of proteins are also important for understanding their function (2–5). NMR spectroscopy (4, 6), which can reveal protein dynamics in atomic detail, is thus being applied to characterize protein stability and the effect of mutations (7), the changes upon ligand binding (5, 8, 9), the comparison of homologous proteins (10), and the structure of unfolded states (11).

A number of recent studies have analyzed the extent to which the dynamical information is represented by existing protein structures, with the aim of predicting experimental data on dynamics from single structures, using relatively simple models based on structural properties. The prediction of properties arising from essentially harmonic dynamics, such as x-ray crystallographic B-factors (12) and NMR order parameters for the protein backbone (13), has been reasonably successful using contact-based models or normal mode analysis. However, side-chain order parameters, which depend in many cases on anharmonic dynamics (14, 15), have proved more challenging, because they exhibit only limited correlations with structural properties, such as contact density and the solvent-accessible surface area (16). Improved prediction has been achieved by combining a contact model with the number of rotatable bonds in the side chain (17).

Here we investigate the extent to which the diversity present within different structures of the same protein, or proteins with high sequence identity, in the PDB captures the structural diversity probed by experiments in solution: these different structures arise from the crystallization of mutants, variants from different species, structures of complexes with other biomolecules or drugs, or use of different crystallization conditions. We refer to these structures as “high-sequence similarity PDB” (HSP) ensembles. Because side-chain order parameters, scalar couplings, and residual dipolar couplings (RDCs) report directly on the structural heterogeneity of the native state, it is important to investigate whether these parameters are related to the heterogeneity of HSP ensembles. A recent study by Zoete et al. (18) compared backbone “fluctuations” derived from the different structures of the HIV-1 protease in the PDB with the x-ray B-factors, and multiple crystal structures of T4 lysozyme were analyzed by Matthews and coworkers (19).

We compare the properties of HSP ensembles with experimental NMR data describing the structural heterogeneity present in solution, rather than in the crystalline state. Particularly interesting is the comparison of side-chain dynamics data with HSP ensembles, because the motions of atoms in the amino acid side chains are significantly more complex and varied than those in the polypeptide backbone (15).

Results

NMR Order Parameters from HSP Ensembles.

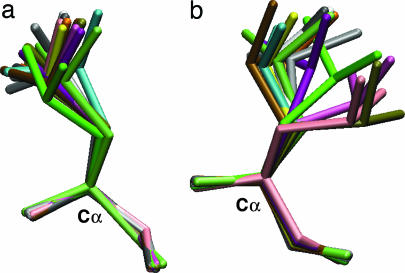
Order parameters of side-chain methyl groups are a sensitive probe of local side-chain motions (6). Specifically, they measure the amplitude of the orientational distribution of the methyl group axis within a reference frame attached to the protein (i.e., excluding overall rotational diffusion of the molecule) on a picosecond to nanosecond time scale (20). One method of generating such a distribution for comparison with experiment is by performing molecular dynamics (MD) simulations (21). By aligning each simulation snapshot with a reference set of coordinates to remove the orientational contribution from molecular diffusion, order parameters may be calculated from the intramolecular variations in orientation. We apply an analogous approach to the HSP ensembles, which are made up of structures with high sequence similarity drawn from the PDB. For example, Fig. 1 shows two Leu side chains taken from such an ensemble for ubiquitin, where the order parameters measure the extent of motion of the C^γ—C^δ bond. A larger-order parameter generally corresponds to more restricted intramolecular motion.

Fig. 1.

Leu side chains from the ubiquitin HSP ensemble with δ-methyl order parameters of 0.7 (L50) (a) and 0.2 (L8) (b).

The idea behind the HSP ensembles is that small differences in sequence or crystal environment act as perturbations that cause the protein to populate alternate minima (5, 18, 22, 23); too many differences in sequence would make the comparison meaningless, because the structure also would diverge (24). In practice, for most of the proteins in the HSP ensembles that we considered, the structural alignments have sequence identity of >98% (see Table 1), corresponding to only one or two point mutations in each case. Because too few structures may not adequately represent the native state heterogeneity, we required at least 10 matches to be found.

Table 1.

Comparison between experimental side-chain order parameters and those calculated from HSP and NMR ensembles

Protein	HSP ensembles				NMR ensembles
	SI,* %	Size, Å	rp†	rmsd, Å	Structure	Size, Å	rp†	rmsd, Å
Cdc42Hs	98.3	13	0.53	0.30	1AJE	20	0.11	0.39
HIV-1 Protease	92.1	330	0.74	0.17	1BVE	28	0.13	0.34
Ubiquitin	99.2	13	0.76	0.18	1D3Z	10	0.57	0.29
Eglin c	99.0	10	0.37	0.30	1EGL	25	0.46	0.31
Calmodulin	99.8	28	0.72	0.20	3CLN	25	0.40	0.27
A-LBP	99.4	14	0.73	0.19
Troponin C	98.9	13	0.69	0.19
Fyn SH3	99.7	12	0.74	0.21
FNfn10					1TTF	36	0.50	0.30
PLCC SH2					2PLE	18	0.36	0.32
M-FABP					1G5W	20	0.41	0.35
Average	98.3		0.66	0.22			0.37	0.32

See ref. 25 for more details on experimental side-chain order parameters.

*Percentage sequence identity in HSP ensemble.

^†Pearson correlation coefficient.

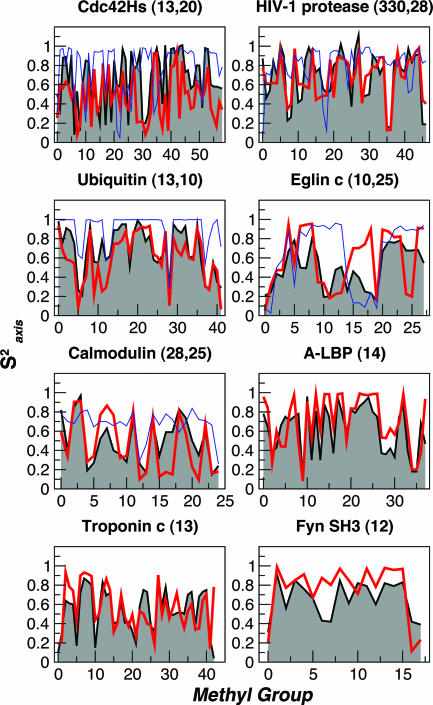
The side-chain order parameters calculated from the HSP ensembles are plotted in Fig. 2, together with experimental values obtained from deuterium relaxation experiments. There is generally a remarkably good agreement between the experimental and calculated data, given the acknowledged difficulty of quantitatively predicting these data (16, 17, 26), especially for the larger-sized ensembles (e.g., HIV-1 protease). Table 1 summarizes the correlation and rms deviation (rmsd) between experimental and calculated data. We favor the rmsd as a measure of similarity, because some proteins tend to have higher correlations simply because of their residue composition (15).

Fig. 2.

Methyl group side-chain order parameters, S_axis², calculated over HSP ensembles (red lines) and NMR ensembles (blue lines) compared with experimental data (shaded black curves). The number of structures in the HSP and NMR ensembles are reported next to the name of the protein. Data for calmodulin and troponin C correspond to the N-terminal lobe only. The methyl group index on the x-axis is obtained by sorting in increasing order of residue number and methyl number (e.g., γ1 < γ2).

We assess the significance of the results by comparing them to a model in which “synthetic” data sets are generated by drawing order parameters for each residue at random from a pool of real experimental data for that residue type. The model accounts for residue identity but not structural context. From a large number of synthetic data sets, we calculate the probability that a rmsd as good as that obtained from the HSP ensemble could be obtained by using this model: for all proteins this probability is <1%, with the exception of Fyn SH3 and Cdc42Hs where it is ≈10%.

Effect of Experimental Uncertainty and Ensemble Size.

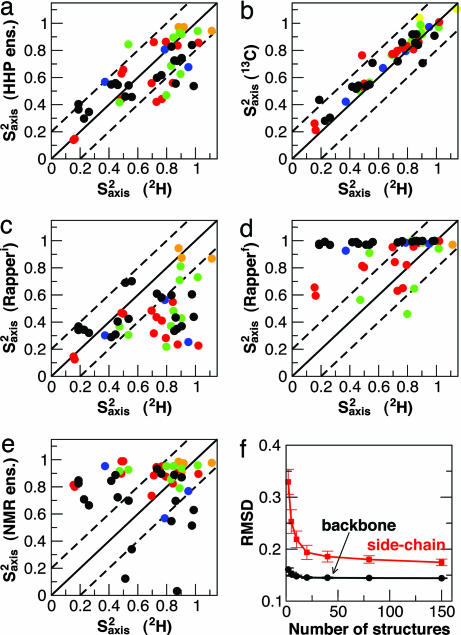
Variations within the HSP ensembles could come from real differences between the structures, as well as from experimental uncertainty. We use HIV-1 protease (which has the largest HSP ensemble) to investigate the origin of these variations, by comparing order parameters calculated for various structural ensembles of this protein (Fig. 3). A good correlation between the full HSP ensemble and experimental deuterium relaxation data is found (Fig. 3a; rmsd 0.17 Å, r_p 0.76); for reference, two different experimental data sets (from carbon and deuterium relaxation) are compared in Fig. 3b (rmsd 0.10 Å, r_p 0.94).

Fig. 3.

Methyl axis order parameters (S_axis²) for HIV-1 protease. (a–e) The following sets of S_axis² are compared with those determined from ²H relaxation experiments. (a) S_axis² calculated from HSP ensembles. (b) A separate set of experimental S_axis² from ¹³C relaxation. (c and d) S_axis² from ensembles of 50 structures generated by the RAPPER algorithm (27) before (c) and after (d) refinement against x-ray data. (e) S_axis² calculated from the NMR ensemble (PDB ID code 1BVE). Solid lines correspond to ideal coincidence of the two data sets; broken lines indicate ±0.2 from this value. Data points are color-coded by methyl type as follows: black, Leu δ1,δ2; red, Val γ1,γ2; green, Ile γ2; blue, Ile δ1; orange, Ala β. (f) rmsd between HSP and experimental order parameters as a function of HSP ensemble size.

Degeneracy in the solution of crystal structures has been shown to give local variations of up to 2.0 Å in the refined solutions of HIV-1 protease x-ray diffraction data (27). This contribution to the order parameters may be quantified by calculating order parameters from the model structures. An ensemble of 50 plausible initial structures, generated by the RAPPER procedure (27), gives order parameters that are generally much lower than experiment (Fig. 3c). Despite this large variation allowed in the initial structures, refinement against the x-ray data produced an ensemble whose order parameters were much higher than experiment (Fig. 3d); therefore, the small degeneracy in solutions underestimates the true variability.

The variability within NMR ensembles is similarly related both to the local density of restraints and to true dynamics (28). We find that side-chain order parameters calculated over the NMR ensemble of HIV-1 protease are poorly correlated with the experimental data (Fig. 3e; rmsd 0.34 Å; r_p 0.13). Similar results are obtained when this same approach is applied to other proteins for which both NMR ensembles with at least 10 members and side-chain order parameters have been determined. The correlations are given in Table 1 and, where there is a corresponding HSP ensemble, are plotted in Fig. 2. Although the correlations vary somewhat from protein to protein, the rmsds from experimental data are consistently better for the HSP ensembles than the NMR ensembles.

The data in Table 1 suggest that larger HSP ensemble sizes tend to give more accurate results. We test this hypothesis by calculating both backbone and side-chain order parameters over randomly selected subensembles of the HIV-1 protease HSP ensemble (Fig. 3f). An increase in the ensemble size indeed improves the agreement with experiment. Furthermore, although there is little improvement for the backbone order parameters beyond 2 structures and almost none beyond 5, a larger number of structures (≈20–40) is necessary to capture the side-chain heterogeneity (Fig. 3f). The limited improvement beyond 40 structures indicates that the approximations inherent in comparing HSP structures will eventually limit the agreement with experiment. Chou et al. (14) have shown that even a small population of a minor rotamer, e.g., <10%, can have a significant effect on the calculated S² value, such that ensembles of 20–40 structures might be needed to get sufficient statistical sampling of such minor conformations. We note that restricting the HSP ensemble to consensus sequence structures (49 for HIV-1 protease) does not appreciably change the agreement with experiment, justifying the inclusion of mutants in the ensembles. Although mutants may shift the equilibrium between two free energy minima, the structure selection criteria for HSP ensembles would tend to find structures within the same basin.

Scalar Couplings and Rotamer Populations.

Side-chain scalar couplings report on the χ₁ dihedral angle and its associated dynamics and provide complementary information to that given by the order parameters. We have back-calculated side-chain scalar couplings from the HSP ensemble of HIV-1 protease, using a recent parameterization of the Karplus equation (14). There is a good correlation with experiment for both NC (r_p = 0.90) and CC (r_p = 0.96) scalar couplings (see Figs. 6 and 7, which are published as supporting information on the PNAS web site). Notably, the scalar couplings for individual structures vary over a wide range for some residues, whereas the mean values are generally close to experiment. To illustrate this point, we note that although the correlation between calculated scalar couplings and experiment for each structure ranges from 0.19 to 0.94 (mean 0.75) for NC couplings, and from 0.28 to 0.97 (mean 0.88) for CC couplings, the correlation obtained for an average over the whole ensemble is as good as that obtained from the best individual structures. This result is in agreement with the earlier finding that the fitting of the parameters in the Karplus equation using individual crystal structures is likely to be inaccurate (14, 29).

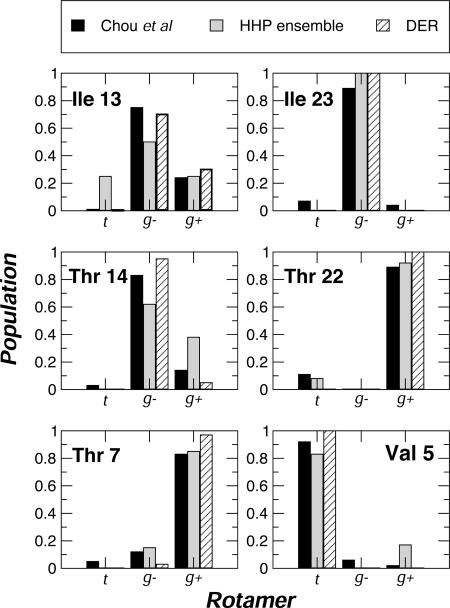
The agreement between experimental scalar couplings and those from the HSP ensemble suggests that the latter may be representative of the dihedral angle distribution in solution. We compared the dihedral angle distributions determined independently from RDCs (14) and the dynamic ensemble refinement (DER) method (30) with those calculated from the HSP ensemble of ubiquitin (Fig. 4): comparable results are obtained by using each method (see Table 2, which is published as supporting information on the PNAS web site, for a complete comparison).

Fig. 4.

χ₁ rotamer populations for representative residues in ubiquitin. Fractional populations calculated from RDCs (solid) (14) and from dynamic ensemble refinement (DER; hatched) (30) are compared. Full results are available in Table 2.

RDCs.

Of the proteins for which RDCs have been measured, hen lysozyme has the largest HSP ensemble (177 structures); the RDCs have been incorporated in a refined structure of the protein (31). We separately fitted each structure in the ensemble to the experimental backbone NH RDCs and also calculated an ensemble average as described (30).

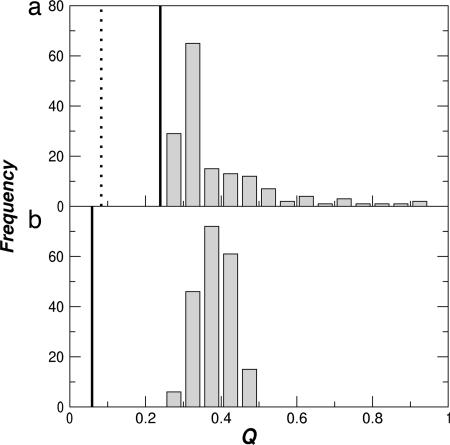
The Q-factor [a goodness-of-fit measure for RDCs (32, 33); low Q indicates better agreement] is plotted for each fit in Fig. 5a. Although the Q-factor for the HSP ensemble (solid line in Fig. 5a) is not as low as that for the structure determined by using dipolar couplings as restraints (broken line in Fig. 5a), it is significantly better than any single experimental structure refined without the couplings. We note that there are a number of remaining outliers that probably indicate real differences between the crystallographic and solution structures (31). Thus, the experimental data can be well reproduced either by a single structure (as for PDB ID code 1E8L) or by an ensemble in which few of the structures are particularly good fits. A similar result was obtained for both backbone and side-chain RDCs in ubiquitin, although with poorer statistics because of the small HSP ensemble (data not shown).

Fig. 5.

Distributions of RDC Q-factors for fits to NH RDCs from hen lysozyme (31). (a) Q factors for fits of individual HSP ensemble members to experimental RDCs. The solid line indicates the fit obtained from an ensemble average and the broken line the fit for the first member of the PDB ID code 1E8L NMR ensemble. (b) Q-factors for fits to structures generated from random normal mode displacements at 300 K to a set of synthetic RDCs derived from the minimum energy structure. Solid lines shows the Q-factors for RDCs ensemble-averaged over this set of structures.

To probe the origin of this effect, we have used a harmonic model, derived from the minimized structure in the EEF1 force field (34). An ensemble of 200 structures at a temperature of 300 K was generated by random superposition of normal modes. As for the HSP ensemble, we find that the ensemble average fit to the data are much better than any individual structure (Fig. 5b); thus, harmonic fluctuations can give rise to significant deviation of individual structures from the RDCs.

Discussion

HSP Ensemble.

We have shown that several types of experimental NMR data related to dynamics and structural heterogeneity in the native state can be reproduced by using ensembles of structures of the same protein (or proteins of high sequence similarity) drawn from the PDB. The heterogeneity of such ensembles is similar to that found by MD simulation [average rmsd of 0.91 Å (backbone), 1.50 Å (side chain), 1.24 Å (all-atom)], although in MD the NMR data are often less accurately reproduced (15, 35).

These results suggest that the HSP ensemble provides a representative sample of the structural fluctuations of a protein under native conditions, although the available structures only constitute a small fraction of the full native ensemble. The HSP analysis can be related to the fluctuation–dissipation theorem, according to which the equilibrium structural fluctuations are equivalent to the changes caused by small perturbations (22). One can consider each structure in the HSP ensemble as subject to a slightly different perturbation, such as a bound ligand, a mutation, or the effect of crystal packing, which favors a particular minimum on the native-state energy surface (5, 18, 23). If the perturbations are sufficiently random, the resulting ensemble will be representative of the full ensemble; for example, if some property of the protein, e.g., a bond vector orientation or a side-chain rotamer, is found in a certain fraction of the native energy minima, then it will be found with the same fraction in a sufficiently large randomly selected subset.

The quantitative comparison that we present between different experimental structures is complicated by many factors, such as differences in the methodology used (x-ray crystallography vs. NMR spectroscopy) and the inherent uncertainties in each structure due to differences in disorder (x-ray) (27, 36) and density of restraints (NMR) (30). Structural uncertainty will tend to obscure the observed correlations: for example, the HIV-1 protease HSP ensemble of high resolution (better than 1.85 Å) structures improves the agreement with experimental NMR data by ≈15% with respect to the HSP ensemble of low resolution (2.6 Å or worse; see Table 3, which is published as supporting information on the PNAS web site). Also, the so-called “model bias” (37) resulting from techniques such as molecular replacement in the solution of x-ray structures may be responsible for the poorer agreement in some of the smaller HSP ensembles. For the consensus sequence HIV-1 protease structures, elimination of structures determined by molecular replacement slightly improves the correlation with experimental order parameters, from 0.72 to 0.75. In certain cases, even single point mutations may have a significant impact on structure. This effect also may contribute to the relatively poor agreement with experiment for Eglin c, because changes in experimental side-chain order parameters upon mutation are relatively large (38). For x-ray structures, crystal packing artifacts also will distort the protein energy landscape to some extent with respect to that in solution.

The above reasons may all contribute to the observed rmsd between experimental and calculated side-chain order parameters and explain why the rmsd does not decrease significantly on increasing the size of the HIV-1 protease HSP ensemble beyond 40 (Fig. 3f). Nonetheless, the fact that the HSP ensembles are close to the experimental data strongly suggests that the differences between crystal structures are largely due to the actual heterogeneity in the native state.

HSP ensembles do not directly include the concept of time. NMR measurements, however, correspond to averaging over the states accessed on a particular time scale, from picoseconds to nanoseconds in the case of order parameters. Agreement of order parameters calculated over HSP ensembles with those from NMR relaxation measurements suggests that each side chain samples most of its conformers on a nanosecond time scale. This observation is in harmony with the finding that order parameters calculated from relaxation measurements (averaged over a picosecond–nanosecond scale) are in most cases similar to those calculated from RDCs and scalar couplings (averaged over a microsecond–millisecond scale) (14).

NMR Order Parameters.

The limited improvement that we found in the agreement with experimental backbone order parameters for more than two HSP structures is consistent with the result that an ensemble size of two is sufficient for the refinement of structures against backbone RDCs (39–41). It should be noted, however, that the accuracy of our backbone order parameter calculations may be adversely affected by the absence of hydrogen atoms in most crystal structures, requiring them to be built with standard geometries. Further, energy minimization during experimental refinement procedures will tend to reduce the vibrational contribution to backbone amide order parameters (42), as was found when ensemble-refined ubiquitin structures were minimized (30).

Our results indicate that an ensemble size of ≈20 is required to represent side-chain heterogeneity (represented by order parameters for side-chain methyl groups), as we have also found independently in the application of the dynamic ensemble refinement method to ubiquitin (30). This result is also expected from the greater complexity of side-chain dynamics (15). Given the redundancy in the PDB, this minimum ensemble size suggests that the present approach may be applicable to several proteins, especially those of particular biological interest for which more structures are likely to be determined. We do not suggest that the native state of a protein comprises ≈20 local minima [e.g., MD simulations (23) and the HIV-1 protease HSP ensemble suggest a much larger number]. Rather, this number seems to provide sufficient heterogeneity to determine order parameters and related quantities that are sensitive to local motions. In principle, sufficiently large HSP ensembles may be used to investigate structural correlations (e.g., covariance of fluctuations; see Fig. 8 and Table 4, which are published as supporting information on the PNAS web site) and could be compared with experiments that probe long-range correlations.

RDCs.

We have found that an ensemble of different experimental structures of the same protein fits backbone RDCs better than any single structure, apart from the one determined by using the couplings as restraints. This result is important given the increasing use of RDCs in structure refinement and structure validation (43), because the quality of a single structure is often assessed by the goodness of fit to the RDC data. In the context of structure refinement, RDC-based backbone restraints are usually imposed on a single copy [although ensemble refinement has also been used (39, 41)], whereas the experimental data represent an ensemble average. A good example of the type of effects resulting from this procedure is provided by the NMR structure of carbonmonoxy hemoglobin, for which the experimental solution structure determined with a single copy was found to be intermediate between two different crystal structures (44).

In many cases, excluding situations such as that of the allosteric hemoglobin, which is known to populate several alternative structures (45), this effect should not result in a significant problem for structure refinement of the backbone, especially if one assumes that the structure remains essentially confined within a single energy minimum and that backbone motions are mainly harmonic in nature. If structures derived from a random superposition of normal mode displacements at 300 K are fitted to a set of synthetic RDCs generated from the minimum (average) structure, the Q-factors range from 0.2 to 0.5 for individual structures Fig. 5b. However, the ensemble fits very well (Q = 0.07) to the data for the minimum structure, except that the dynamics is absorbed into the alignment tensor, scaling it by a factor of ≈0.92; a similar effect was found in an analysis of MD simulations (46). In this case, using ensemble-averaged RDCs as restraints in a single copy refinement would result in an “average” structure. It is unlikely, however, that such refinement will be successful for modeling side-chain motion, which is known to be dominated by anharmonic effects such as the population of multiple rotameric states (15).

Applications of HSP Ensembles.

The results that we discussed so far for HSP ensembles suggest an alternative way to parameterize semiempirical relations such as Karplus equations for scalar couplings. The parameterization of these expressions using a number of experimental structures of different proteins has been complicated by the need to account for the effects of dynamics in solution. Methods for addressing this issue include structure-independent cross-validation approaches (14) or dynamic ensemble refinement-derived structures (29). Alternatively, comprehensive experimental data sets determined for those proteins for which a very large number of structures are already available can be used in an ensemble-averaged fitting procedure, in which the effects of heterogeneity are included and specific packing effects are expected to be reduced.

HSP ensembles also may be useful for drug design calculations. An emerging view is that the bound state of the protein is found within the equilibrium ensemble of the free protein; otherwise, very strong interactions with the drug would be required to offset the cost of adopting such an unfavorable conformation. An increasing amount of experimental evidence, such as the recognition of dissimilar ligands (47) and the enhancement of antibody affinity and specificity by making the unbound state more similar to the bound state (5), supports such a model. The use of “dynamic” pharmacophore models in such calculations has already led to improved results (48); these models have been derived from either MD (48) or several crystal structures chosen in a similar way to the HSP ensembles (49). Hence, HSP ensembles or ensemble-refined experimental structures (30) represent a possible alternative to MD simulations for the purpose of ensemble generation. Conversely, if the bound state corresponds to a different free energy minimum with a different structure, it may not be sampled by this method.

Conclusions

We have studied the properties of ensembles of structures of proteins with high sequence identity in the PDB and found that they provide a representative sampling of the heterogeneity of protein native states, as probed by various NMR measurements. In particular, these HSP ensembles reproduce side-chain order parameters better than ensembles of NMR structures and also fit RDC data better than individual structures, supporting the view that dynamic heterogeneity is an important contribution to such data. Therefore, the assessment of individual structures using ensemble-averaged experimental measurements requires some caution.

The present work indicates that it is important to account for the structural diversity of the native state when comparing predictions from homology modeling or ab initio structure predictions with experimental structures and perhaps even that such a diversity is incorporated into the solutions obtained from these calculations.

Together, our results suggest that the population of closely related structures that form the native state of a protein and often determine its functionality can be sampled not only by probing the dynamics experimentally, but also by using multiple structure determinations of proteins of highly similar sequences.

Methods

Selection of Experimental Data.

HSP ensembles were constructed for a previously compiled set of proteins for which both experimental order parameters and structures are available (25), as well as hen lysozyme.

For each of these proteins, a search for structural homologues in the PDB with >90% sequence identity and ungapped alignment was performed by using the combinatorial extension (CE) algorithm (50). If at least 10 matches were found, those structures were defined as the HSP ensemble for that protein. In crystal structures where several structurally homologous chains were present in the asymmetric unit and were refined independently, each protein was separately entered into the ensemble. For NMR structures only the minimized average structure was used. For HIV-1 protease, the database was constructed from the online HIV protease structure database (51). Tethered dimers, structures with unresolved disordered residues, low-resolution structures, computational models, and structures not submitted to the PDB were excluded. In addition, only structures with <10 mutations relative to the consensus were allowed. A complete list of the structures used is available in Tables 5 and 6, which are published as supporting information on the PNAS web site.

NMR Order Parameter and Dipolar Coupling Calculations.

The HSP ensembles were aligned to the protein studied in the NMR dynamics experiment by least-squares fitting of the corresponding α carbons from the combinatorial extension (CE) alignments (all alignments were ungapped because of the high sequence similarity). Order parameters (20) for each methyl group were calculated as described (15), by using all structures in the HSP ensemble having the same type of residue in that position as the reference protein studied in the NMR dynamics experiments. The calculation of order parameters for the NMR structures was done in the same way as for the HSP ensembles.

RDCs and scalar couplings were calculated from the aligned ensembles of structures as described (30). Normal mode analysis was performed with the CHARMM package (52) and the EEF1 force field (34).

Abbreviations

PDB

Protein Data Bank

HSP

high-sequence similarity PDB

MD

molecular dynamics

RDC

residual dipolar coupling

rmsd

rms deviation.