Coil–globule transition in the denatured state of a small protein

Abstract

Upon transfer from strongly denaturing to native conditions, proteins undergo a collapse that either precedes folding or occurs simultaneously with it. This collapse is similar to the well known coil–globule transition of polymers. Here we employ single-molecule fluorescence methods to fully characterize the equilibrium coil–globule transition in the denatured state of the IgG-binding domain of protein L. By using FRET measurements on freely diffusing individual molecules, we determine the radius of gyration of the protein, which shows a gradual expansion as the concentration of the denaturant, guanidinium hydrochloride, is increased all the way up to 7 M. This expansion is observed also in fluorescence correlation spectroscopy measurements of the hydrodynamic radius of the protein. We analyze the radius of gyration measurements using the theory of the coil–globule transition of Sanchez [Sanchez, I. C. (1979) Macromolecules 12, 980–988], which balances the excluded volume entropy of the chain with the average interresidue interaction energy. In particular, we calculate the solvation energy of the denatured protein, a property that is not readily accessible in other experiments. The dependence of this energy on denaturant concentration is nonlinear, contrasting with the common linear extrapolation method used to describe denaturation energy. Interestingly, a fit to the binding model of chemical denaturation suggests a single denaturant binding site per protein residue. The size of the denatured protein under native conditions can be extrapolated from the data as well, showing that the fully collapsed state of protein is only ≈10% larger than the folded state.

The coil–globule (CG) transition is a hallmark of the physics of polymers in solution. When a polymer molecule is transferred from a good solvent to a bad one, it undergoes a collapse from an expanded coil-like conformation to a contracted, globule-like conformation. This collapse is typically a second-order phase transition and can be accounted well by mean-field theory (1, 2). Proteins are heteropolymers and therefore should exhibit a similar transition. Because proteins also undergo a first-order folding transition to form their native structure, it is of prime interest to deduce the relation between collapse and folding (3). If the CG transition precedes folding significantly, then the final rearrangements of the protein chain to form the native structure occur within a relatively limited configurational space, which might affect the efficiency and speed of the process. The CG transition of proteins is also important for the elucidation of the properties of their denatured states. Chain collapse can have an impact on secondary-structure formation in the denatured protein (4). Determining the energetics of the collapse, which involve changes in the solvation energy of the protein as the solution conditions are varied, might allow us to understand better the role of the denatured state in the folding transition (5).

The occurrence of a collapse preceding protein folding was inferred from kinetic experiments (6–11) and also reported in equilibrium experiments, using small-angle x-ray scattering (SAXS) (12) and single-molecule fluorescence (13, 14). However, the thermodynamics of the CG transition have not been characterized yet. In this work, we use two methods, single-molecule FRET (smFRET) and fluorescence correlation spectroscopy (FCS), to measure the CG transition of a 64-amino acid protein exhibiting two-state folding, the IgG-binding domain of protein L (hereafter denoted simply as protein L) (15). The CG transition is driven by the chemical denaturant guanidinium hydrochloride (GuHCl). We then employ a version of the mean-field theory of Sanchez (16) to obtain a full thermodynamic characterization of the CG transition of a protein, identifying the transition point as well as extracting the average amino acid residue solvation energy as a function of denaturant concentration.

Results and Discussion

Radius of Gyration.

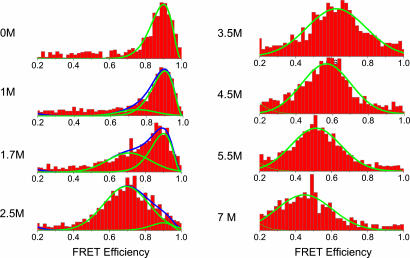
Protein L has been extensively studied in the past using a variety of spectroscopic techniques, which indicated that this protein belongs to the group of two-state folders, lacking any intermediate states on its folding pathway (15, 17). A SAXS experiment on this protein did not detect an expansion of its denatured state as the denaturant concentration was increased up to 5 M (18). However, the small number of points and the relatively large errors inherent in SAXS measurements at high GuHCl concentrations (where the contrast diminishes) might have precluded observation of the expansion reported below. We prepared a mutant of protein L with cysteine residues inserted near the N and C termini and labeled it with donor and acceptor dyes for FRET, using a sequential process. FRET histograms were constructed from fluorescence bursts created by individual molecules freely diffusing in and out of a focused laser beam (13, 19, 20). Sample histograms are shown in Fig. 1. The histogram at 0 M GuHCl shows a peak at E = 0.9 (E is the energy transfer efficiency), which can be assigned to the native protein. As the concentration of GuHCl is increased, a second peak appears, first as a shoulder on the native-state peak and then as a separate peak, gradually shifting to lower and lower E values. This peak can be assigned to the denatured state. A third peak, appearing at E = 0, is a well known artifact, arising either from molecules labeled with the donor only or from molecules in which the acceptor was prematurely photobleached (13, 20) and therefore is not shown. We fitted the native-state distribution by using a beta function, which takes into account the photon noise effect on the FRET efficiency (21). This distribution has three parameters: the overall amplitude, the average FRET efficiency, and the average number of photons per burst. From the 0 M GuHCl we could fix the FRET efficiency at E = 0.9. We also fixed the number of photons at n = 25, so that only the amplitude was fitted. The denatured-state distribution of each histogram was fitted by using a Gaussian function.

Fig. 1.

FRET efficiency histograms of individual protein molecules at increasing concentrations of denaturant (0–7 M GuHCl). The histograms reflect first unfolding of the protein from its folded to its denatured state, followed by further expansion of the denatured state, which is seen as a gradual shift of the denatured-state distribution to lower values of FRET efficiency.

From the relative areas of the denatured and native distributions, we could construct a denaturation curve, which was compared with the bulk denaturation curve based on FRET efficiency. The transition midpoint, C_F, obtained from the histograms was 1.67 ± 0.04 M, which is very similar to C_F extracted from the bulk FRET denaturation curve, 1.64 ± 0.02 M (the two curves are shown in Fig. 5, which is published as supporting information on the PNAS web site). This result confirms the validity of our procedure for separating the two distributions in the histograms. Importantly, a gradual shift of the peak position of denatured-state distribution is seen in Fig. 1, from E = 0.75 at 1 M GuHCl to E = 0.45 at 7 M GuHCl. This shift to a lower FRET efficiency value indicates an expansion of the chain, driven by increased concentrations of the denaturant. The continuous shift of the denatured-state distribution implies a similarly continuous expansion of the denatured protein. This behavior is different from that associated with the folding transition of the protein, which involves coexistence of two populations, folded and denatured. This observation strongly suggests that the expansion/collapse transition is second-order in nature, as is usually observed for the CG transition of flexible polymers (2). The smFRET experiment thus is nicely capable of deciphering the order of a thermodynamic intramolecular transition in a protein.

The denatured-state FRET efficiency distribution does not directly provide the distribution of the end-to-end distance. Recent experiments (22, 23) suggest that the end-to-end distance dynamics for a denatured protein of the size of protein L are on the microsecond time scale, whereas the smFRET data are averaged over millisecond fluorescence bursts. We therefore took the mean E of the denatured-state distribution as an average over the end-to-end distance distribution, P(R_ee), of the protein

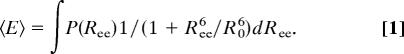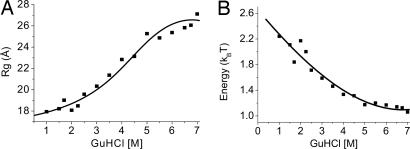
Here R₀ is the Förster radius for energy transfer, taken as 54 ± 3 Å (see details on determination of R₀ in Supporting Text, which is published as supporting information on the PNAS web site). Adopting a particular form for P(R_ee) allows us to calculate the possible 〈E〉 values, then match the experimental values to a particular set of parameters, from which the average mean-squared end-to-end distance, 〈R_ee²〉, and the radius of gyration, R_g, can be obtained. Here, we used the P(R_ee) of a Gaussian chain, and in Fig. 2A we plot the calculated values of R_g = 〈R_ee²〉/6 as a function of the GuHCl concentration. We also used the P(R_ee) of the worm-like chain model (24) for calculating R_g values from the FRET efficiency distributions (data not shown). The R_g values found using the worm-like chain P(R_ee) compare well with values obtained from the Gaussian chain model. The data in Fig. 2A show a strong expansion of R_g from ≈18 Å at 1 M GuHCl to ≈27 Å at 7 M GuHCl. Although work on other proteins already detected chain expansion (12–14), we are not aware of any other example where the expansion continues all the way to 7 M GuHCl. It is clear from the shape of the curve that the full collapse/expansion of the denatured chain is captured in this experiment, from the lowest value in the globule state in 1–2 M GuHCl to essentially the maximal value in the coil state in 6–7 M GuHCl.

Fig. 2.

The CG transition in denatured protein L obtained from smFRET measurements. (A) The radius of gyration of protein L molecules as a function of GuHCl concentration, obtained from the histograms of Fig. 1 (see text), showing a significant expansion of the denatured state as the denaturant concentration increases. The error in the radius of gyration values is estimated to be ≈1.5 Å. The continuous curve is calculated by using the interpolated interresidue interaction energy (see B). (B) Average interresidue interaction energy obtained from the mean-field theory of the CG transition. At each denaturant concentration, Eq. 3 is inverted to find the interaction energy value (see text for more details on the procedure). The continuous line is an interpolation of the data, which is used to generate a continuous representation of the radius of gyration function in A.

Hydrodynamic Radius.

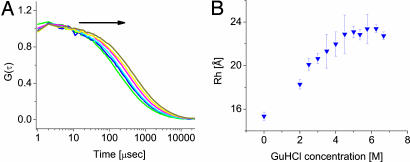
To further confirm the expansion of the denatured state of protein L, we performed FCS measurements on single-labeled molecules of the protein to extract the hydrodynamic radius as a function of GuHCl concentration. Several fluorescence correlation functions are shown in Fig. 3A. To obtain the hydrodynamic radius of the denatured protein from the correlation functions, we fitted them to the following two-component equation (25), which takes into account the coexistence of folded and denatured molecules:

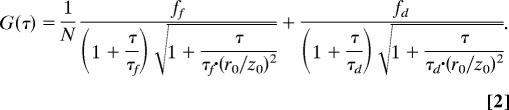G(τ) is the time-correlation function of the fluorescence. f_f and f_d are the fractions of the folded and denatured species, respectively, taken from the denaturation curve of the protein. For the 0 M GuHCl correlation function, f_d was set to 0, whereas for correlation functions at GuHCl concentrations of >3 M, f_f was set to 0. τ_f and τ_d are the diffusion times of the folded and unfolded (denatured) species, respectively. The former is fixed by the measurement at 0 M denaturant, with a correction for the viscosity change in GuHCl solutions. N is the total average number of molecules in the sampling volume, and r₀ and z₀ are the dimensions of the sampling volume in the x–y plane and the z direction, respectively. The hydrodynamic radius of the folded or denatured protein, R_H^f,d, is calculated through the diffusion coefficient of the each species given by D_f,d = r₀²/(4τ_f,d) and the Stokes–Einstein relation D_f,d = k_BT/(6πηR_H^f,d), where k_B is Boltzmann’s constant, T is the absolute temperature, and η is the viscosity of the solvent. The ratio of the sampling volume dimensions, (r₀/z₀)², was calibrated for every GuHCl concentration by using rhodamine 6G. Thus, FCS curves were fitted with only two free parameters (τ_d and N).

Fig. 3.

The CG transition in denatured protein L obtained from FCS experiments. (A) FCS curves at increasing GuHCl concentration. Arrow indicates the direction of increase in denaturant concentration, which shifts the curves to the right. This shift is due to a rise of the diffusion time, caused by expansion of the denatured molecules, as well as an increase of the solvent viscosity. (B) The hydrodynamic radius of denatured protein L molecules as a function of GuHCl concentration, obtained from fits to the curves in A. The expansion is qualitatively similar to that of the radius of gyration in Fig. 2A.

The hydrodynamic radius of denatured protein L as a function of denaturant concentration is shown in Fig. 3B. The points in this figure are averages of measurements on both a single mutant and a double mutant of protein L, which showed very similar trends. At 0 M GuHCl, R_H = 15.3 ± 0.4 Å. We used the freely available program Hydropro (26) to estimate R_H from the protein structure determined by NMR (Protein Data Bank ID code 2PTL, without the unstructured N-terminal tail). This calculation gives 16.3 Å, in close agreement with the measured value. The hydrodynamic radius of the denatured protein shows a clear expansion at least up to 5 M GuHCl. The maximal value of R_H is ≈23 Å. From polymer theory it is expected that for a random coil the ratio between R_H and R_g will be 1.5 (2), although the measured ratio is only ≈1.2. This result could indicate either that at 7 M GuHCl the protein has still not expanded enough to reach random coil dimensions or (more likely) that hydration of the denatured chain, as well as binding of GuHCl molecules to the chain (see below), lead to increased values of R_H. Such deviations from the ideal ratio between the two radii have been observed before for denatured proteins (27). We conclude that the FCS measurement nicely confirms the results of the smFRET experiment. This finding is important, because the FCS measurement does not focus on a single distance as in smFRET and does not rely on any assumptions on the intramolecular dynamics of the unfolded protein.

Theory for the Denatured-State Expansion.

Flory-type mean-field theories of the CG transition treat the density of the polymer as an order parameter, from which changes in the radius of gyration can be readily calculated (1, 2). It is much more difficult to calculate the effect of expansion on the hydrodynamic radius (but see refs. 28 and 29). To quantitatively model the CG transition of protein L, we therefore focus on the radius of gyration, and we particularly adopt the mean-field theory of Sanchez (16). This theory was used by Tanaka and coworkers (30) to fit the first observation of the CG transition in a polymer chain. It also was used by Alonso and Dill (31) in their development of a theory for protein folding. The Sanchez theory models the free energy of a polymer chain as consisting of two opposing terms. The first is the excluded volume entropy, which stems from the self-avoiding property of a real polymer chain. This term resists chain contraction. The second term is the average interresidue interaction, which is in effect the balance of internal attraction between amino acid residues and residue–solvent attractive or repulsive energy. Contrary to other models of the CG transition, this model does not truncate the excluded volume interaction at the secondary or ternary level but takes into account all higher orders, allowing for a better description of the compact globule state. Minimizing the free energy, Sanchez (16) derived the following transcendental equation for the expansion factor (order parameter) α² = R_g²/R_g,0², where R_g,0 is the radius of gyration of a reference state

In this equation, n is the number of amino acid residues in the chain, and φ₀ = R_g,N³/R_g,0³ is the volume fraction of the reference state. [R_g,N is the radius of gyration of the maximally compact state, for which the volume fraction is 1 by definition. In the current context, this value is the radius of gyration of the native state, 16.2 Å (18).] θ/T is the interresidue interaction energy, in k_BT units, which is responsible for the collapse of the chain in a bad solvent. For an infinitely long polymer, the collapse occurs at the θ temperature, i.e., when θ/T = 1, but this rule is not necessarily true for a finite-length polymer.

Solvation Energy of the Denatured State.

In the more common case of temperature-induced CG transition, the relevant variable is T. However, in the case of chemical denaturation, T is constant and θ becomes a function of GuHCl concentration. The interaction energy θ(C)/T is maximal in water, opposing the excluded-volume entropy and contracting the chain to a globular state. As the concentration of GuHCl is increased, the interaction energy decreases, leading to expansion of the chain. By inverting numerically Eq. 3, we can obtain this energy, but to perform this operation we need to know the radius of gyration of the reference state, R_g,0. It is reasonable to associate the reference state with the CG transition point, C_θ, which we define as the point of fastest change in the order parameter α². This point can be simply calculated by using the relation d²(α²)/dC²|_Cθ = 0. We first make a guess for R_g,0 and use it together with Eq. 3 to calculate θ(C)/T. We then recalculate the transition point and iterate the whole calculation several times until we obtain convergence. It is important to note that this calculation leads to an estimate of the energy that is free of any model for the way GuHCl interacts with proteins. The resulting θ(C)/T is shown in Fig. 2B. It decreases by >1 kT in going from 0 to 7 M GuHCl. This change is solely because of an increase in solvation energy of the protein residues in GuHCl solutions. The overall solvation energy for the denatured protein at a particular denaturant concentration can be obtained from n[θ(0) − θ(C)]/T. It is important to remember that this property is one that cannot be readily measured in folding experiments. In principle, the difference between the solvation energies of the denatured and folded states can be equated with the change in folding energy between aqueous and denaturant solutions (32), which is obtained from the denaturation curve of a protein. However, the solvation energy of the denatured state itself is not accessible in standard experiments.

Binding Model.

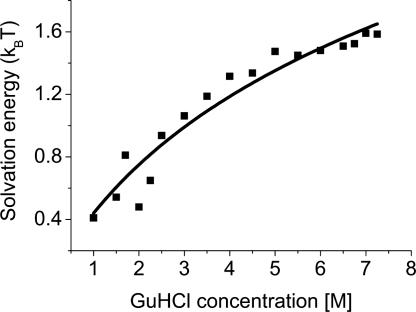
The interaction energy shown in Fig. 2B, or the denatured-state solvation energy that can be calculated from it, are nonlinear in the denaturant concentration. In the common linear extrapolation method, the unfolding energy, which is the difference between the denatured- and folded-state energies, is modeled as a linear function of the denaturant concentration (32). Our finding stands in contrast to this method, or at least puts stringent constraints on the type of models that might lead to a linear dependence. Growing evidence suggests that indeed the interaction of proteins with GuHCl, as well as their unfolding energy in the presence of this denaturant, deviate from linear dependence on concentration, which is not the case for another common denaturant, urea (33).

The effect of chemical denaturants on proteins has been modeled in two different ways. In the first, a chemical denaturant changes the properties of the solvent, indirectly affecting the protein solute. In the second model, the chemical denaturant directly binds to the protein, in particular to its backbone, replacing hydrogen bonds with the solvent and internal hydrogen bonds, thereby promoting unfolding. Both experimental and theoretical results point to the latter model as the more plausible one (33, 34). The energetics of denaturant binding to the protein can be described by the following equation: ΔG₀ − ΔG = blog(1 + KC), where ΔG₀ is the free energy in water, b is the number of binding sites, and K is the binding constant in M⁻¹ [although some authors use the activity concentration scale in relation to the binding model (35), there is no consensus on this issue (36), and we therefore elect to use the molar concentration scale]. As above, the energies are in k_BT units, and all properties are given per amino acid residue. We fitted this binding model to the solvation energies {[θ(0) − θ(C)]/T} obtained from the CG transition model. The result is shown in Fig. 4. From the fit we obtained K = 0.5 ± 0.2 M⁻¹, which agrees nicely with values in the literature (37, 38). Even more interestingly, we found b = 1.1 ± 0.2, which implies that on average there is one binding site for GuHCl per residue, as intuitively expected for denaturant binding to the protein backbone. The important role of the backbone in the solvation of the proteins in denaturant solutions was recently emphasized by Auton and Bolen (32).

Fig. 4.

Fit of the binding model (33) to the solvation energy per residue, [θ(0) − θ(C)]/T. Squares, solvation energy values; line, least-squares fit of a binding isotherm to the data. From the fit (see text), it is concluded that on average, there is one denaturant binding site per amino acid residue of the protein.

CG Transition Point.

The procedure described above to calculate θ(C)/T also provides a value for C_θ, the CG transition point, which is found to be 4.5 M, as well as the radius of gyration at that point,R_g,0, which is 23.3 Å. We are not aware of any previous experiment in which the collapse transition point was determined for any protein. It has been suggested by Thirumalai and Klimov (39), based on simulations of coarse-grained models, that the cooperativity and kinetics of folding of protein sequences are correlated with the relative difference between the collapse point C_θ and the folding point C_F (39), σ = (C_θ − C_F)/C_θ. By using the values obtained in this work (C_θ = 4.5 M, C_F = 1.7 M), we can calculate σ ≈ 0.62. Our experiments pave the way to an experimental exploration of the correlation between σ and folding kinetics, using mutants of protein L with different folding properties.

Unfolded Protein at Native Conditions.

It is of great interest to describe the unfolded state of a protein under native conditions. It is presumably the state of the protein just after its synthesis on the ribosome (if no cotranslational folding occurs), and it is also the state from which many kinetic folding experiments start, after fast dilution of a denaturant. A short extrapolation of the measurement of the radius of gyration (Fig. 2A) to 0 M GuHCl allows us to find that under native conditions, R_g = 17.5 Å. Comparing this number with the radius of gyration of the native states as measured by SAXS, 16.2 Å (18), we find that the unfolded state of protein L under native conditions is highly compact, only ≈10% larger than the folded state. A calculation of R_g of the folded state from the Protein Data Bank coordinates of the protein (ID code 2PTL without the unstructured N-terminal tail) gives a smaller value of 13 Å. If this number is used, the unfolded globular state of protein L is ≈30% larger than the folded state, still rather compact. The R_g of the unfolded state of drkN-SH3 under nondenaturing conditions also was estimated to be 30% larger than that of the folded state (40).

Conclusion.

In this work, we used two different and complementary single-molecule fluorescence methods to show that the denatured state of protein L undergoes an expansion in denaturant solutions, which is akin to the well studied CG transition in polymers. Clearly, the CG transition of protein L is thermodynamically distinct from the folding transitions, with a transition point that lies at a much higher concentration of denaturant than the folding point. It is not possible to infer from the thermodynamic measurement whether the collapse and folding transitions should also be kinetically distinct. In fact, Plaxco et al. (18) provided evidence that in protein L these two transitions are simultaneous, as might be the case in two other proteins, studied by Sosnick and coworkers (41). In any case, it is clear from the present results that the denatured state of protein L continues to change with denaturant concentration well beyond the folding point. This kind of behavior, where an apparent two-state folder shows changes in one of its states, was termed “variable two-state denaturation” by Ferreon and Bolen (42).

We used ideas from polymer theory to obtain the solvation energy of the denatured protein as a function of GuHCl concentration. This quantity is particularly interesting because it cannot be measured in standard folding experiments. Interestingly, the binding model for the effect of chemical denaturants could nicely account for the calculated solvation energy, with a binding constant that matches literature values and, most satisfactorily, a single interaction site for GuHCl per residue, a very sensible result that suggests that the denaturant interacts mostly with the protein backbone. Interaction of the backbone with a large number of GuHCl molecules in a concentrated denaturant solution should lead to a more locally rigid structure than in a low-concentration solution. This assertion is supported by our calculations of the radius of gyration using the worm-like chain model (data not shown). These calculations also generated values for the persistence length of the protein at each denaturant concentration, showing an increase of this length by almost a factor of 3 between aqueous solution and concentrated denaturant solution. Because the persistence length is a measure of local chain rigidity, this finding is another indication for the role of denaturant–protein backbone interaction. Changes in persistence length could perhaps be directly measured by force spectroscopy of denatured proteins or by fitting distance–distribution functions obtained from SAXS experiments (43).

An interesting question is whether the collapse transition of proteins is driven just by average changes in solvent conditions, as is the case in homopolymers, or whether specific interactions within the protein drive and guide this transition. As suggested by Hagen and Eaton (44), as well as Roder and coworkers (45), the observation of exponential kinetics even for the earliest folding phases constitutes evidence for specific, barrier-crossing transitions [although it has been shown that this conclusion might not be universal (46)]. Support for a specific collapse also was provided by the time-dependent SAXS experiment of Kimura et al. (10), who observed a collapsed state of monellin whose overall structure is oblate, similar to that of the native state of the protein. Our equilibrium experiment does not directly bear on this point. As noted above, the smFRET results imply that the CG transition is second order. However, even a second-order transition, although not involving a barrier-crossing event, still needs not be completely random and might be driven by formation of specific structure elements or contacts in the protein. These can be included in the future in a more refined modeling of the interaction energy.

Materials and Methods

Protein Samples and Labeling.

A plasmid containing a histidine-tagged version of protein L was a kind gift of David Baker (University of Washington, Seattle, WA). Donor and acceptor fluorescent probes (Alexa Fluor 488 C₅ maleimide and Alexa Fluor 594 C₅ maleimide, respectively; Molecular Probes) were attached to cysteine residues inserted close to the N and C termini of the protein [at positions 1 and 64, numbers following (15)], by using a sequential process (47). Details on labeling procedures are provided in Supporting Text.

smFRET Experiments.

smFRET measurements were carried out on a home-made confocal microscope (48). Signal detection was performed in a time-stamping mode, i.e., by registering the time lag between consecutive photons arriving at the detectors. Data analysis was performed by using methods similar to those reported by Seidel and coworkers (49). Fluorescence bursts due to passage of individual molecules through the laser beam were identified, and the FRET efficiency E for each burst was calculated, after correction for the donor leakage, by E = 1/(1 + γI_D/I_A), where I_D and I_A are the donor and acceptor intensities, respectively, and γ is a correction factor (γ = 0.7 ± 0.07). Further details on the instrument and data analysis are provided in Supporting Text.

Measured samples of freely diffusing protein contained a protein concentration of 150 pM, guaranteeing a probability of <0.01 for the simultaneous passage of two protein molecules in the ≈1 fl sample volume. All smFRET measurements were conducted at room temperature. All samples contained 50 mM phosphate buffer (pH 7.4) with varying concentration of GuHCl.

FCS.

FCS measurements were performed on the same confocal microscope used for smFRET, but using a 60×, 1.2-NA water-immersion objective (Olympus). A 50-μm pinhole was introduced at the image plane to reject out-of-focus photons. Measurements were conducted on the M1C single mutant labeled with Alexa Fluor 488, as well as on the double mutant, labeled with a single Alexa Fluor 488 dye. The single and double mutants were measured at concentrations of 10 and 20 nM, respectively. The latter sample contained ≈1 mM Tris-(2-carboxyethyl)phosphine (TCEP) to avoid dimerization of the protein. Cross-correlation signals were obtained by splitting the fluorescence into two detectors using a nonpolarizing beam splitter. Data collection and generation of FCS curves were performed by using a hardware correlator (Flex02-12D; Correlator.com).

Abbreviations

CG

coil–globule

FCS

fluorescence correlation spectroscopy

GuHCl

guanidinium hydrochloride

smFRET

single-molecule FRET

SAXS

small-angle x-ray scattering.