Imaging the Migration Pathways for O₂, CO, NO, and Xe Inside Myoglobin

Abstract

Myoglobin (Mb) is perhaps the most studied protein, experimentally and theoretically. Despite the wealth of known details regarding the gas migration processes inside Mb, there exists no fully conclusive picture of these pathways. We address this deficiency by presenting a complete map of all the gas migration pathways inside Mb for small gas ligands (O₂, NO, CO, and Xe). To accomplish this, we introduce a computational approach for studying gas migration, which we call implicit ligand sampling. Rather than simulating actual gas migration events, we infer the location of gas migration pathways based on a free-energy perturbation approach applied to simulations of Mb's dynamical fluctuations at equilibrium in the absence of ligand. The method provides complete three-dimensional maps of the potential of mean force of gas ligand placement anywhere inside a protein-solvent system. From such free-energy maps we identify each gas docking site, the pathways between these sites, to the heme and to the external solution. Our maps match previously known features of these pathways in Mb, but also point to the existence of additional exits from the protein matrix in regions that are not easily probed by experiment. We also compare the pathway maps of Mb for different gas ligands and for different animal species.

INTRODUCTION

Myoglobin (Mb), the first protein to be resolved at the atomic level (1), is a relatively small (∼150 amino acids) globular protein, found mainly in heart and skeletal muscles of numerous animal species (2–4). Its active site, the heme, binds small gas ligands such as molecular oxygen (O₂), carbon monoxide (CO), nitric oxide (NO), and cyanide (CN⁻), making this protein an important participant in the intracellular transport and storage of gases, particularly of O₂. In addition to facilitating the oxygen transport from the cell membrane to the cell's mitochondria, Mb is now believed to also play important roles in oxidative phosphorylation (3) and in the scavenging of NO (5–8).

The heme is buried inside Mb, which protects it from the aqueous environment, and thus is not directly accessible to ligands in solution. Because gas ligands must find their way to the heme by diffusing inside Mb's protein matrix, Mb has long been a prime candidate for the study of gas migration inside proteins. Numerous experiments have investigated this process inside Mb. A popular experimental measurement is the timescale of the geminate recombination of the Mb moiety with its gas ligand (O₂, CO, NO), in which the ligand dissociates from the heme upon flash-photolysis, wanders inside the protein for tens to hundreds of nanoseconds, and then rebinds to the heme (9–15). By measuring the timescale distribution of the recombination process and the rate at which the ligand escapes the molecule instead of rebinding, one gains insight into the internal network of gas migration pathways inside Mb, and into the size of the energy barriers along these pathways.

Early on, Mb was found to bind xenon gas (Xe), and structures of Mb in the presence of bound Xe pointed to cavities between which small gas ligands could potentially hop (16). Early simulations of the gas migration process, although constrained to short timescales and distances from the heme, nevertheless revealed the relevance of the Xe cavities, as well as the importance of the protein's motion in allowing gas ligands to migrate between them (17,18). In the last few years, experiments and simulations have covered considerable new ground. Time-resolved x-ray crystallography of photolyzed Mb-CO geminate complexes provided movies of the evolution of the average CO distribution as a function of time after photolysis (19–23). Long-timescale simulations (>80 ns) of the migration of CO or NO inside Mb reproduced some of these results (24–26), and shed more light on the locations of the ligand-accessible regions inside Mb, as well as on how these regions are connected. The general picture emerging from experiment and simulation is that Mb has, in its interior, several regions (i.e., cavities) favorable for gas molecules to reside. These regions are identified as Xe binding sites observed by x-ray crystallography or as empty space in static x-ray structures. The gas ligands hop from one cavity to another via an unspecified mechanism, but of which it is generally agreed that the protein's thermal fluctuations play a role. The location and properties of the connections between the internal Mb cavities as well as of the exit pathways from Mb have not been fully characterized.

In this work, we address the migration of small gas ligands inside proteins, using Mb in particular, from a proteinwide perspective. To accomplish this, we introduce a computational method, which we call implicit ligand sampling, which computes the potential of mean force (PMF) corresponding to the placement of a given small gas ligand such as O₂, CO, etc., everywhere inside a protein. The PMF that we calculate describes the Gibbs free-energy cost of having a particle located at a given position, integrated over all degrees of freedom of the system, except for the ligand's position, and is the quantity that indicates which areas of the protein are accessible to the ligand and at what free-energy cost. The implicit ligand sampling method for computing a monoatomic or diatomic gas ligand's PMF inside a protein (see Methods) relies on the fact that gas ligands are small and interact weakly with the protein matrix (27). Because of this, we can analyze the protein dynamics in the absence of the ligand and treat the ligand's presence as a weak perturbation, and yet still produce accurate results. This approach may seem surprising, but the absence of ligands in the simulation is in fact beneficial because the protein's migration pathways can now be sampled at every point in space simultaneously—thus generating much better statistics, in most cases, than what would be obtained if one were to follow the trajectory of a single ligand.

When applied to Mb, implicit ligand sampling provides a complete three-dimensional map of the favorable regions and migration pathways for a small gas ligand inside the protein. We devote the rest of the article to describing these pathways. Our maps of the migration pathways inside Mb that are located near the heme match prior experimental and computational evidence for O₂ and CO well. We also convincingly find that Mb has more than one exit to and from the heme binding site, that the network of cavities may have an influence in tuning the different migration properties of various gas ligands, and that general features of the Mb migration pathways are conserved across species.

METHODS

Implicit ligand sampling: theory

Here, we derive an expression for the implicit ligand PMF. The implicit ligand PMF corresponds to the estimated free energy of placing a gas ligand anywhere inside a protein and its immediate environment, calculated from an equilibrium simulation of the protein in the absence of the ligand. To keep the derivation simple, we examine and discuss the case in which the ligand is a point particle. For the general case, however, we must also take into account the ligand's internal degrees of freedom (e.g., for the case of a diatomic molecule, bond length, and orientation). The derivation of the general case is presented separately in the Appendix.

The PMF for the ligand, which, in our case, represents the Gibbs free energy cost of placing the ligand at a specific position r, is directly related to the probability ρ(r) of finding the ligand at that position, and is defined as (28)

(1)

where ρ_o is an arbitrary normalization factor.

At constant temperature (T) and pressure (P), the probability density distribution of the ligand ρ(r) can be expressed as

(2)

where refers to the integration over all degrees of freedom of the protein reference system (which includes the surrounding solvent), and where 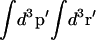is the integration over the ligand's degrees of freedom; 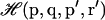is the Hamiltonian for the protein-ligand system, V is the volume enclosing the system, and we define β = (k_BT)⁻¹.

When calculating the PMF of a ligand from a molecular dynamics (MD) simulation, the probability density ρ(r) is usually measured directly from a trajectory of the ligand motion, often with the help of sampling enhancement techniques such as umbrella sampling (28,29) and/or locally enhanced sampling (18). Because a lot of sampling is needed to get an accurate PMF, the ligand is often artificially constrained to a restricted region of space since the thorough exploration of an entire protein by a ligand is not possible during the timescales accessible to MD simulations. Since we are interested in characterizing the PMF for ligand diffusion everywhere inside a protein, and not just along a restricted path, this causes a problem. We overcome this limitation by using an implicit ligand: we treat the ligand as a small perturbation of the lone protein dynamics. A previous study of gas migration inside CpI hydrogenase (27) demonstrated that the pathways taken by O₂ and H₂ inside CpI could be accurately predicted from the protein's equilibrium dynamics in the absence of the ligand. This suggests that the perturbation approach is sensible for case of gas ligands.

We will now derive the PMF of ligand migration by treating the effect of the ligand as a perturbation to a reference ensemble of protein states which contains no ligand. Under the presence of a ligand with no internal degrees of freedom, the Hamiltonian for the protein reference system () will be shifted by an amount equal to the protein-ligand interaction energy ΔE(r) and the ligand's kinetic energy K(p′) (the latter will eventually cancel out and disappear from our formulation). The full Hamiltonian can now be expressed in terms of that of the reference protein as

(3)

Inserting the perturbed Hamiltonian (Eq. 3) into the expression for the ligand probability density (Eq. 2), we get

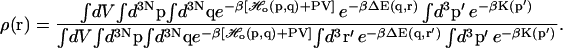(4)

We now wish to express our result in terms of an isobaric-isothermal ensemble (NPT) average over all states of the protein reference ensemble. In the reference protein NPT ensemble, the average of any general observable A(r) is defined as

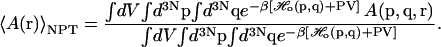(5)

Then, using the definition for the isobaric isothermal ensemble average, the ligand probability distribution (Eq. 2) becomes

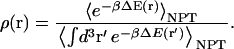(6)

The denominator in Eq. 6 is simply a constant, which we will now refer to as λ. Inserting the ligand probability density (Eq. 6) into our definition for the PMF (Eq. 1), we obtain

(7)

For convenience, we impose that our PMF be zero when the ligand is in vacuum (defined as a region for which ΔE(q, r) = 0 always holds). This condition will be satisfied by setting ρ_o = 1/λ:

(8)

When computing the PMF for a diatomic gas such as O₂, CO, or NO, we must also take into account the internal degrees of freedom of the ligand, in addition to those of its center of mass. In our analysis, we approximate the diatomic bond length to be fixed, and we are only interested in accounting for the ligand's orientational degrees of freedom (which we denote as Ω). For this particular case, and following the more general derivation found in the Appendix, the expression for the PMF becomes (see Eq. 18)

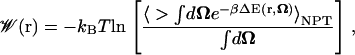(9)

where 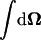is the integration over the unit sphere.

This formulation is equivalent to that used in the one-step free-energy perturbation (FEP) method (e.g., see (30,31)). Traditionally, FEP techniques are used to determine the free-energy difference between two similar states of a system. In that case, it is common to use a series of artificial intermediate states to increase the accuracy of the FEP method. In the present case, since our perturbation is very small, the one-step FEP method already provides good results. We take advantage of this fact by calculating not just one free-energy difference, but a huge number of such differences spatially distributed over the entire protein. This is possible because all that is needed to perform the calculation is a trajectory of the unperturbed protein reference state.

In principle, the analytical form for the implicit ligand PMF (Eq. 8) is exact because the integration is performed over all possible states. In practice, the validity of the implicit ligand PMF is not guaranteed when the thermal average 〈…〉_NPT is replaced by a sum over a finite number of states, such as is the case for MD or Monte Carlo simulations. In this case, only a restricted set of states probable according to the reference energy function 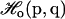is actually sampled. The states that are probable according to the protein-ligand energy function 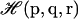, which is what we require, may be undersampled or not sampled at all. If the perturbation introduced by the ligand is small, the two distributions will have significant overlap (see Fig. 1), and the computation of the implicit ligand PMF is possible by simply reweighting the states of the protein reference simulation according to Eq. 9. If the perturbation caused by the ligand is large, then the overlap between the two distributions will be small and the protein states relevant for the protein-ligand system may not be sampled in the reference simulation. As we will see, for the specific case of small gas ligands, the perturbation can, in many cases, be considered to be small enough for the implicit ligand analysis to work.

FIGURE 1.

Schematic diagram showing the probability of occurrence of all the protein states, during a simulation of the protein reference system (solid line), or those desired in order to get a proper PMF for the protein-ligand system (dashed line). The introduction of a ligand inside the protein at a given position perturbs the energies of all the protein states from the reference ensemble, and consequently alters their probability of occurrence.

We now express the implicit ligand PMF (Eq. 9) as an average over a finite number M of protein states taken from a simulation. If we use C different equally probable orientations of the ligand, the final PMF will be given by

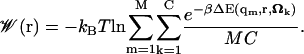(10)

To gain a better understanding of the applicability of the implicit ligand sampling method, we can estimate the maximum error on our free-energy measurements. The PMF calculated by means of Eq. 10, like most other free-energy calculations, suffers from the fact that it can be significantly influenced by rare events. The error caused by the undersampling of rare events may be estimated by calculating the change in PMF that such an event would cause. To do this, we assume conservative values for the frequency and ligand interaction energies of such events. For the frequency, we assume that if a maximally favorable event was not sampled in M states (from the simulation), then such events will on average occur less than once every M + 1 states. We also assume that for this state, the protein-ligand interaction energy will be an optimal value ΔE_min, which is independent of the ligand's internal degrees of freedom. In practice, we choose ΔE_min to be location-independent, and we compute it by measuring the average interaction between the ligand and its environment during a simulation using an explicit copy of the ligand and its environment. Neglecting the effect of allosteric and/or conformational changes whose timescales are greater than those sampled, the maximum lower error due to undersampling (undersampling will always cause the PMF to be overestimated), can thus be estimated as

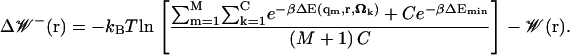(11)

For large values of the number of independent samples M, this becomes

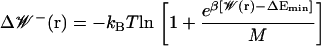(12)

The error estimate provided by Eq. 12 can be used to test the suitability of the implicit ligand analysis to various ligands. If a ligand interacts strongly with the protein (e.g., Cl⁻-protein interaction has been measured to be as strong as ΔE_min = −150 kcal/mol in ClC chloride channels (32)), then the error on Eq. 10 will be gigantic, and the method will fail. Similarly, if the ligand is not very small (e.g., ATP, glycerol, etc.) then the measured PMF will be very large for all simulated reference protein states as compared to ΔE_min, and the error on the PMF will again be huge. For small gas ligands, we have estimated the values of ΔE_min by measuring the average energy during short equilibrium simulations of explicit ligands in a water box. A uniform water box gives excellent statistics and, from our observations and expectations, the very mobile water molecules provide very favorable ligand interaction energies, which in turn will result in an error on the PMF which can be used as a conservative estimate of that inside the protein. We measured the gas-water average interaction energies by placing one copy of the explicit gas ligand in a 30 Å × 30 Å × 30 Å water box. The gas-water system was then simulated under NPT conditions (300 K; 1 atm) for 500 ps, during which the gas-water interaction energies were measured every 1 ps. The interaction energies were found to be converged for the last 450 ps of simulation, over which the interaction energy was averaged. This procedure returned values of ΔE_min = −3.2, −3.7, −4.1, and −5.6 kcal/mol for O₂, CO, NO, and Xe, respectively (with a standard deviation of 0.7–0.8 kcal/mol for all four ligands, and a negligible error). For the case of O₂, this would imply that the lower error on the PMF due to undersampling using 5000 independent snapshots would be <0.1 kcal/mol for a measured PMF of −1, 0.5 for a PMF of 2, and 3.1 for a PMF of 5 kcal/mol, etc. On top of this, there is an additional uncertainty due to the variation in sampling, estimated from the variation in the PMF across different points in space for a 5-ns water box simulation, which we evaluated to be ±0.2 kcal/mol for O₂, ±0.3 kcal/mol for CO and NO, and ±0.8 kcal/mol for Xe (trends in the energy profile over large regions of space can be identified with a much better accuracy than this because the actual error at each point in space acts independently).

Implicit ligand sampling: computational implementation

In practice, we compute the PMF using Eq. 10 for each possible ligand location on a regularly-spaced grid (with a spacing of 1 Å), and for many different ligand orientations. The ligand interaction energy ΔE(q,r) is computed using a Lennard-Jones potential, truncated at 12 Å, using the van der Waals parameters taken from the CHARMM22 force field along with realistic bond lengths (O₂: ε_O = −0.12 kcal/mol, R_min,O/2 = 1.7 Å, l_bond = 1.12 Å; CO: ε_C = –0.11 kcal/mol, R_min,C/2 = 2.1 Å, l_bond = 1.13 Å; and NO: ε_N = – 0.20 kcal/mol, R_min,N/2 = 1.85 Å, l_bond = 1.15 Å). The inclusion of charges in the ligand was found to slow down the computation to intractable levels. An implicit ligand sampling analysis was performed using both explicitly dipolar and uncharged ligands for selected test cases and it was found that the effect of the electrostatic dipoles of NO, CO, and O₂ is negligible. Quantum mechanics calculations have determined partial charges to be <0.025e for all ligands studied in this article, and the solvation energy calculated using the implicit ligand sampling with ligand partial charges of 0.025e varied by <0.05 k_BT from the values in Table 2 for all cases. This also held true for the energies measured for a small number of frames of the Mb dynamics using both dipolar and uncharged models of O₂; the error introduced by the dipole was typically <0.05 k_BT. Because of this, the maps published herein were computed using completely neutral ligands. The ligands' quadrupole moments were not accounted for in this study.

TABLE 2.

Ligand solvation energies

Ligand	ΔGexp	ΔGtheo
Xe	1.04	1.25 ± 0.04
NO	1.53	1.60 ± 0.01
O2	1.78	1.97 ± 0.02
CO	1.94	2.54 ± 0.02

Comparison of the free energies of solvation in units of kcal/mol for different gas molecules measured from experiment and from the implicit ligand PMF analysis. The experimental values of the solvation energy at 20°C are taken from those compiled in Scharlin et al. (53). Theoretical values are obtained by properly averaging the ligand PMF calculated for a 5-ns simulation (5000 frames) of a 40 × 40 × 40 ų water box at 300 K and 1 atm. Quoted errors, which are small because of the huge amount of sampling, represent the statistical variance on the calculated PMF, and do not account for the choice of the force-field parameters for the water and ligands.

The parameter set for Xe (E_N = −0.494 kcal/mol, R_min,N/2 = 2.24 Å) was picked from many choices in the literature, and provided good agreement with Xe solvation and Xe-Mb binding energies. The actual values of the PMF measured for Xe are sensitive to the particular choice of Xe parameters, due to Xe's large size; however, other Xe parameters lead to identical binding site locations and exhibit the same general behavior, but the actual energies measured can differ in magnitude (Xe parameters that use small radii tend to exhibit much smaller barriers between binding sites).

Within each grid cube, we calculated the energies for 2³ (8) equally spaced positions for diatomic ligands (e.g., O₂) and 3³ (27) positions for monoatomic ligands (e.g., Xe), providing much better statistics (i.e., a much narrower distribution of energies for the same averaged value) for each grid cube. For the case of O₂, 50 randomly-chosen orientations of the ligand were evaluated at each location. Furthermore, this was repeated for 5000 trajectory snapshots (sampled at each ps), as we found that this amount of sampling provided a satisfactory accuracy. To speed up the calculation, the interaction between atoms located further than 5.5 Å apart was calculated only once per grid cube, per trajectory snapshot, while the interaction energy below 5.5 Å was calculated for all 2³ or 3³ points inside each grid cube; this approximation was shown to amount to <0.05 k_BT maximum error, while reducing the total computation time for each O₂ PMF map to practical levels. In the end, for each grid point, 50 × 2³ = 400 energy calculations were performed per trajectory snapshot for the diatomic ligands and 27 for monoatomic Xe. The value at each grid point then represents the PMF of having an O₂ molecule located within a 1 ų cube centered at that point.

The implicit ligand sampling algorithm is included and distributed as part of the open source VMD 1.8.4 software package (33) (in VMD's volmap command).

MD protocol and parameters

The dynamic trajectories of the proteins were computed by all-atom molecular dynamics (MD) simulations, using the CHARMM27 force field (34), the NAMD molecular dynamics program (35), and the NAMD-G job submission and automation software (36). Each Mb structure was embedded into a water box and the resulting 20,000–30,000 atom systems were simulated using periodic boundary conditions. Particle-mesh Ewald with a grid resolution of <1 Å was used for long-range electrostatics, and all other nonbonded interactions were calculated using a cutoff of 12 Å. All simulations were carried out at constant temperature of 300 K and constant pressure of 1 atm. Temperature and pressure were controlled using Langevin dynamics with damping constant of 5 ps⁻¹ and a Nose-Hoover Langevin piston with period of 100 fs and decay rate of 50 fs. The integration timesteps were 1 fs, 2 fs, and 4 fs for bonded, nonbonded, and long-range electrostatic interactions, respectively. Every system was initially equilibrated for 1 ns, after which the MD run was extended for 5 ns, with static snapshots taken every 1 ps for analysis. Displacements of the whole structure during the simulations were discounted by using a best-fit alignment on the C_α atoms. The implicit ligand sampling analysis was then performed on these trajectories.

RESULTS

In the following section, we investigate the properties of the gas migration pathways inside Mb, based on the free-energy profiles calculated from our implicit ligand sampling method (see Methods). We show that the computed three-dimensional maps of the PMFs for various ligands in Mb, which we will refer to as implicit ligand PMF maps, match known experimental facts wherever the comparison can be performed. In addition, our method makes predictions that are difficult to measure experimentally, such as the existence and precise locations of additional gas diffusion pathways inside Mb that are situated away from the heme.

Xe binding sites

X-ray crystallization of Mb in the presence of high-pressure Xe gas has been used to locate ligand docking pockets that potentially accommodate small ligands such as O₂, CO, or NO (16,37). For the most part, the location of Xe binding sites matches small static cavities that consist of empty space in the Mb crystal structure. However, the correspondence between empty space and Xe binding sites is not precise, since an empty space search finds many cavities which are not Xe binding sites, provides no criterion for deciding a priori which cavities lodge Xe, and in most cases does not pinpoint a specific location for the trapped Xe. The existence of atomic structures of Mb with and without bound Xe provides an ideal test of our PMF calculation method. Fig. 2 shows the location of Xe binding sites in the sperm whale Mb D122N mutant (PDB accession code No. 1J52), juxtaposed with the locations of minimum free energy computed from implicit ligand sampling on a 5-ns equilibrium simulation of the D122N mutant without Xe (PDB accession code No. 2MBW). In all cases, the experimentally measured locations of the Xe binding site have been successfully pinpointed to well within the 1 Å resolution of the PMF maps, except for the case of Xe3 (within 2 Å), which corresponds to a location occupied during our simulation by two water molecules present in the crystal structure, one of which is actually completely displaced by Xe in the crystal structure under Xe pressure (the binding site was predicted nevertheless based on the fluctuations of the water molecule positions). The free energies of Xe at the binding sites estimated by the implicit ligand sampling method (using the Xe force-field parameters described in Methods) and of the experimentally measured Xe occupancies are shown in Table 1. The exact experimental values differ from the computed ones by 0.5–1.3 kcal/mol, most probably due to our choice of Xe parameters; the relative differences in PMF for the various binding site are nevertheless well reproduced.

FIGURE 2.

Predicted and actual Xe binding sites for the sperm whale Mb D122N mutant (shown in ribbon representation with the heme drawn as licorice). The predictions, shown as red isosurfaces representing the areas where the Xe PMF is <−4.9 kcal/mol (points on this surface have an error of ±0.8 kcal/mol), are based on a 4-ns equilibrium simulation of a Xe-less Mb structure (PDB accession No. 2MBW). The four experimental Xe locations, represented by labeled circles, are taken from a structure of the same protein under 7 atm Xe pressure (1J52) (37).

TABLE 1.

Xenon binding site free energies

Binding site	Theoretical Xe PMF	Experimental Xe PMF
Xe1	−6.4	−5.1
Xe2	−5.2	−4.5
Xe3	−5.1	−4.6
Xe4	−5.5	−4.4

Predicted and experimentally measured free energies for the four Xe binding sites (as labeled in Fig. 2) in the sperm whale Mb D122N mutant, in units of kcal/mol. The theoretical PMF corresponds to the minimum PMF measured in the vicinity of the binding site and the experimental PMF is calculated from the crystal Xe occupancy at the given experimental Xe pressure, using the approximate formula , where P_Xe is the experimental Xe pressure (7 atm), and the Xe occupancy is provided for each Xe binding site in the 1J52 PDB structure.

Experimentally determined Xe binding sites are often used to infer the location of gas diffusion pathways. As we will argue later, the validity of this strategy is limited because the behavior of Xe in proteins is quite different from that of smaller gas molecules such as O₂, NO, and CO, but the results of such an approach are still meaningful. Nevertheless, the prediction of Xe binding sites provides a successful test case for our implicit ligand PMF calculations.

CO migration pathways

Implicit ligand PMF maps for CO inside sperm whale Mb were computed and are shown in Fig. 3 (also see movie in Supplementary Material). The PMF maps clearly show CO-accessible cavities inside Mb, as well as their connectivity and the height of the energy barriers between them. The four Xe binding sites and the distal pocket, all arranged in a loop around the heme, can be clearly identified in the PMF map. Additional cavities near the heme that have been identified as participating in the migration of CO around the heme by simulation (24,25), are also distinctly present in the PMF map. These results also are in good visual agreement with a picosecond-resolution x-ray crystallography movie of the CO migration (19,21). Furthermore, one can observe an energy minimum at the exact location (Xe1 cavity) of a crystallized CO in the L29W Mb mutant (20,38).

FIGURE 3.

Implicit ligand PMF for CO migration inside sperm whale Mb, based on a 5-ns equilibrium simulation of the 1DUK PDB structure, shown from four views looking toward the heme (a–d). The three energy isosurfaces represent PMF values of −1.5 kcal/mol (red), 1 kcal/mol (blue cavities), and 5 kcal/mol (green). The empty white space corresponds to regions of measured PMF above 5 kcal/mol; the zero energy value corresponds to the ligand in vacuum. Practically speaking, the red surfaces show gas docking sites, the inner blue surfaces show the areas inside the protein that are more favorable to CO than the external aqueous solution, and the green surfaces highlight the regions of lowest energy barriers between the various cavities. The low energy barrier exits according to the displayed PMF map are indicated by red lines and circles, and dashed indicators mean that the exits are in the back. The error on points lying on the three PMF isosurfaces are ±0.3, +0.3/−0.4, and +0.3/−3.6 kcal/mol for red, blue, and green, respectively. The Mb's static surface is represented in white-inside-blue-outside color and the heme is displayed with its bound proximal histidine.

In addition to the distal cavity and Xe binding sites, the PMF map for CO migration reveals additional cavities and O₂ pathways that lead outside of Mb (see Fig. 3), suggesting that the distal pocket may not be the only entrance/exit for gas ligands. We find three obvious exit pathways for CO (defined as low barrier CO pathways that reach the solvent but do not necessarily continue into it) in the implicit ligand PMF map of sperm whale Mb: the short distal pathway (gated by His-64), and two separate sets of exits from Mb at the far end away from the heme. In addition, we observe three additional minor exits with higher energy barriers, one of which is a direct connection from Xe2 binding site to the exterior. Unfortunately, there is little direct supporting experimental evidence, since the pathways far away from the heme cannot be seen using time-resolved x-ray experiments monitoring the migration of gas ligands in Mb after their photolysis from the heme. This is because the gas ligand's average density becomes very diffuse by the time it reaches these pathways after photolysis, and also because these extra pathways do not appear to contain strongly attractive docking regions where a significant gas ligand density could be experimentally observed (represented by the lack of red surfaces in the bottom of Fig. 3, a–d).

Geminate rebinding rates of the gas ligand inside Mb are usually interpreted using a four-state model in which the gas ligand can, in turn, be in the external solution, inside the Mb distal pocket, inside a system of internal cavities, or bound to the heme's iron center (e.g., see (39)). Despite experimental evidence pointing to possible ligand escape to the external solution by two separate pathways—directly from the distal pocket and through the secondary cavity network (39)—ligand escape has often been interpreted as occurring solely through the distal pathway (gated by His-64) (13,20). This has resulted into the popular view that Mb has a network of cavities surrounding the heme, linked to the exterior by a single pathway (4).

This view of Mb having only one exit located at the distal pocket, however, besides being at odds with our PMF map, which reveals multiple exit points between the external solution and the interior cavities of Mb for gas ligands, is also at odds with other studies. A simulation of CO escape in Mb has identified a number of alternate exit pathways (18), though an increased CO kinetic energy caused by the methodology used in that study may have influenced this observation. A simulation performed by Bossa et al. (24) also suggests that some of the large cavities inside Mb can be temporarily directly accessible from the external solution. Huang and Boxer (40) have experimentally tested the geminate recombination parameters of Mb against a huge library of ∼1500 single amino-acid Mbs mutants, revealing that many mutations far away from the heme and Xe-binding sites resulted in altered ligand migration behavior, suggesting that there may be multiple access routes for the ligand between the Mb exterior and the Mb internal cavities.

Correlation with point mutations affecting gas ligand migration

Performing random mutagenesis on sperm whale Mb, Huang and Boxer (40) found a number of residues whose substitution by another amino acid led to a substantial change in the geminate recombination rates of Mb and O₂ or CO, after testing roughly half of all possible mutations. These “important” residues are shown in Fig. 4, along with the proposed pathways for O₂ calculated from our implicit ligand PMF analysis. We have classified the residues that affect gas ligand transport into four groups, depending on their placement with respect to our calculated maps. Most residues identified experimentally were also attributed important roles according to our theoretical analysis.

FIGURE 4.

Amino acids whose substitutions significantly affect O₂ or CO migration properties during geminate rebinding in Mb, as determined by Huang and Boxer (40). The heme is drawn with the attached proximal His-93. Residues forming the commonly recognized distal pathway are shown in yellow. The amino acids that are found at the exits from the Mb interior, according to the PMF maps, are shown in red. Small amino acids that line a constriction between cavities, and large amino acids that directly block passages between neighboring ligand-accessible areas, are colored in blue. Residues that were shown to affect ligand migration properties, but do not have any visible influence on the gas pathway according to the PMF maps are colored in green (some of these residues do cap α-helices and may play a structural role). The location of the gas migration pathways is drawn schematically, with light gray and dark gray, respectively, representing likely and highly likely regions for the ligand. Thick dashed lines indicate the exits that go out of the plane of the figure toward the viewer; thin dashed lines correspond to the exits behind the plane. Red arrows have been added to indicate the exits from Mb, dashed arrows represent exits behind the plane. All residues except those lining the distal pocket (yellow) are labeled.

The first group (yellow in Fig. 4) is comprised of amino acids that form the commonly known distal pathway (Leu-29, Phe-33, Phe-43, Phe-46, His-64, and Val-68). The distal pathway is well known from numerous studies of Mb, and our PMF maps also suggest that this pathway is the most favorable and the shortest one for gas ligands to reach (or to escape from) the heme. The residues forming the distal pockets are generally found to be very conserved in Mb, in addition to strongly influencing the recombination kinetics. Indeed, these residues are responsible for coordinating the ligand before and while it binds to the heme, and they are responsible for the binding affinities of various ligands to the heme (41–43). The second group (red in Fig. 4) is comprised of the residues that line putative exits from Mb's interior, as defined by our PMF maps (Arg-45, Thr-67, and Leu-137). Mutation of any of these residues will affect the ability of gas ligands to enter or exit the interior cavity network of Mb. The third group (blue in Fig. 4) is composed of amino acids with a small profile that line a constriction between two cavities and also of bulky amino acids that directly block the passage between two nearby ligand-accessible regions (Trp-14, His-24, Gln-26, Ile-30, Leu-61, Leu-69, Ile-99, Ile-107, Ser-108, Phe-138, and Tyr-146). We expect that mutating such residues would, in general, cause a measurable change on internal migration rates since the cavity network topology would be affected. The fourth group of residues (green in Fig. 4) does not demonstrate a substantial correlation between their location and the PMF map (Lys-16, Ala-19, Lys-34, His-36, Asp-44, Lys-56, Ala-71, Gln-91, Ala-144, and Lys-145). All are found on the periphery of Mb, pointing toward the external solvent, and while some of these residues appear to be structurally important (such as charged surface residues), it is not clear from our results why and how the remaining residues would affect geminate rebinding rates. It is possible that these residues exert their influence indirectly; for example, their presence may be critical for Mb to fold properly.

As pointed out by Huang and Boxer (40), many of the important residues are found far from both the heme and from the distal pathway, which suggests that CO or O₂ may use other pathways in addition to the distal one to enter and exit Mb. Our implicit ligand PMF maps exhibit additional exit pathways which are fully compatible with Huang and Boxer's assessment.

O₂, NO, and CO share similar pathways to and from the binding pocket

We performed the implicit ligand analysis for O₂, NO, CO, and Xe. To check that our ligand parameters could reproduce real-world properties, and thus provide valid conclusions, we first used the implicit ligand method to measure the ligands' solvation energies. We accomplished this by performing the implicit ligand analysis, using O₂, NO, CO, and Xe, on a 5-ns simulated trajectory of a box of water. The PMF at each gridpoint in the entire water box was then properly averaged (i.e., the ligand PMF was converted to and from its associated ligand occupancy probability, which was the quantity used for the averaging) to compute a single free energy of solvation for each ligand in water. Our calculated solvation energies were compared to experimental ones, and the results are listed in Table 2. While the calculated energies are all slightly larger than the experimental ones (by 5–30%), the relative differences between the ligands follow the correct trends and are all respectably close to experiment.

We then computed implicit ligand PMF maps for O₂, NO, CO, and Xe inside sperm whale Mb using the same equilibrium simulation of Mb for each analysis. Any observed variation between the different maps is thus caused solely by the intrinsic properties of the different ligands (which differ here only by their van der Waals parameters), and not by statistical variations since the protein trajectory is identical for each ligand. Generally speaking, the PMF maps for all the ligands have very similar cavity and pathway locations, but different absolute energy values.

Fig. 5, a–c, shows the PMF values at those points on our maps that lie on paths that were computed to minimize the height of the energy barriers for O₂, NO, CO, and Xe between the heme binding site to the three most likely exits identified by our maps. The actual paths taken through Mb are displayed in Fig. 5 d. It must be noted that the PMF values that we quote are the PMFs of having a gas molecule present in a cubic box of 1 Å side length, centered at the grid point where the PMF is measured. The detailed PMF along a path, which is what we show, is defined differently than the PMF of “being in a specify cavity” or of “being in the solvent”, since, in the latter case, the probability of being at every grid point within the specified cavity or in the solvent must be summed and depends on the total size of the given cavity or of the accessible solvent.

FIGURE 5.

PMF profiles experienced by ligands exiting Mb along (a) the distal pathway and (b,c) the two other most favorable exit paths between the heme binding site and the external solution. The path profiles were determined by finding the path, between two predefined endpoints (one at the heme binding site, and one near an Mb exit), that exhibits the smallest energy barriers. The values of the PMF at each point along these paths are then plotted as a function of the ligands' distance from the heme binding site. The procedure is repeated for O₂, NO, CO, and Xe ligands, using the same endpoints for a given exit. The solvation energies of each ligand in water, as given in Table 2, are represented as horizontal dashed lines, and the location of the distal pocket (DP) and Xe binding site Xe4 are indicated. (d) The actual points along the three paths in relation to the Mb PMF maps are plotted in green (for the distal path a), red (path b), and yellow (path c).

For the case of O₂, the energy barrier to enter Mb is very low—only a few k_BT above the computed solvation energy of O₂. Not surprisingly, of all the ligands we have investigated, O₂ has the smallest energy difference between its highest barriers and most attractive cavities. We evaluate the Gibbs free energy difference between the distal pocket's most attractive region and the lowest barrier to be crossed for O₂ to exit through the distal pathway to be ∼6 kcal/mol. This result matches theoretical and experimental measurements of the same barrier energy of 6.4 kcal/mol (44) and 7.5 kcal/mol (39), respectively. This implies that O₂ is the ligand that can enter, exit and move around Mb with the least hindrance of all gases studied, as would suggest Mb's role in storing and transporting O₂.

As compared to O₂, NO exhibits a stronger attraction to the Mb cavities by ∼1 kcal/mol (i.e., all else being equal, NO is approximately seven times more likely than O₂ to be in a given Mb cavity, such as the distal pocket); however, the absolute height of the largest energy barriers between these cavities as well as to the external solution is at approximately the same level as for O₂, which translates into higher relative barriers due to NO's lower solvation energy. Our results suggest that sperm whale Mb would keep NO trapped in its internal cavities, which surround the heme, longer than it keeps O₂. These results are relevant because NO is known to harmfully deactivate cytochrome-c oxidase and recent studies suggest that oxy-Mb plays a role in scavenging stray NO from the cell, which it then deactivates by reaction with its bound O₂ ligand to produce nitrate () (7). It has been suggested (45) that the cavities in Mb could act as hosting stations for NO, and act to increase its chance of collision with heme-bound O₂ by keeping it inside of Mb longer. This latter hypothesis is well supported by our results.

In our modeling, of all the diatomic gas ligands, CO interacts the least favorably with Mb. CO is less attracted to Mb's cavities than O₂ by ∼0.5–1 kcal/mol. CO also experiences significantly higher energy barriers (by ∼3–5 kcal/mol as compared to O₂) between internal cavities as well as to the external solution. CO is toxic for Mb as well as for other proteins which are at the receiving end of Mb's O₂ transport queue, such as respiratory cytochromes and cytochrome oxidase. It appears that Mb is protected from CO by high energy barriers, which would reduce the rate of CO intake (versus O₂ intake), when Mb finds itself at the high concentration end of the intracellular O₂ and CO gradients. Our PMF profiles indicate that whereas the exit through the distal pathway appears to be the most favorable one for O₂ and NO, the variation in absolute energy barriers between the different exits is less pronounced for CO (this conclusion comes with the caveat that the error on large values of the PMF can be important, thus affecting the barriers that we measured for CO). In any case, the increased availability of multiple exits from Mb for CO as compared to O₂ may have a functional role. Notably, the existence of multiple exits lends support for the hypothesis by Radding and Phillips (46) that Mb protects itself from CO poisoning through a kinetic proofreading mechanism by preferentially allowing proportionally more CO than O₂ to exit Mb from the heme through the cavity network, thereby ensuring that only 4–7% (with a relaxation time of ∼180 ns) of photolyzed CO rebinds to the heme, as opposed to 27–42% (with a relaxation time of ∼55 ns) for O₂.

We can compare the PMF profiles of Fig. 5 to the various experimental rates and estimates of equilibrium constants and energy barriers for ligand migration in sperm whale Mb. Despite the variations in methodology and results between studies, our results are generally consistent with other measurements. Olson (47) estimate that the escape barrier height for CO migration between the distal pocket and the solvent to be ∼4 kcal/mol. Our analysis estimates a barrier of 7.5 kcal/mol (with an error of +0.4/−3.6 kcal/mol), which meets the experimental value at the bottom of our error. We expect our high barriers to always be overestimated and believe this to be the case here. Rohlfs et al. (15) have estimated indirect rates for the solvent to distal pocket migration (hereby referred to as k_X→B) and solvent to distal pocket equilibrium constant (K_X→B) for O₂, CO, and NO. The experimental estimates for the equilibrium constants are 0.72 ± 0.25, 0.22 ± 0.12, and 0.07 M⁻¹ for NO, O₂, and CO respectively (the CO value being a very rough estimate with no associated error). The ordering of these occupation probabilities and the reduction by a factor of three as one goes from NO to O₂ to CO matches the sequential reductions in the PMF by ∼1 k_BT PMF in going from NO to O₂ to CO, as seen in the distal pocket (see Fig. 5, b and c). For the k_X→B ligand entrance rates, we expect CO to enter Mb at much slower rates than O₂ and NO. Rohlfs et al. (15) estimate all three rates to be nearly identical—the CO rate, however, having an error of over ±300%. We note here that the experimental results are derivative quantities and thus the errors are large, making it hard to conclude that the agreement is definitive. In principle, it would be possible, through computation, to estimate theoretical effective transport rates for the ligand migration, based on our PMF maps (as opposed to qualitatively inferring trends from the energy profiles).

Banushkina and Meuwly (48) measure a barrier of 7.8 kcal/mol from Xe4 to the distal pocket for the CO migration in wild-type sperm whale myoglobin (and 4.3 kcal/mol for the reverse migration) using umbrella sampling. We estimate these same barriers to be ∼4.5 and 3.5 kcal/mol, respectively. Bossa et al. (25) measure a symmetrical PMF barrier of ∼2.6 kcal/mol from Xe4 to the distal pocket for CO, inferred from a long simulation (in essence, umbrella sampling with a flat umbrella potential) of which ∼3 ns is spent by CO at the barrier. All three methodologies are different and have different strengths, and for this specific case, we lean toward the values provided by Bossa and ourselves as providing the more accurate theoretical results. The implicit ligand sampling analysis is based on a larger amount of independent samples obtained at every point in space (e.g., 5000 ps × 400 conformers per point in space, a 10th of which can be considered independent), as compared to the other methods that use a relatively low number of independent samples per coordinate point at the barrier (e.g., 50–100 ps × 1 conformer per reaction coordinate increment for the umbrella sampling), especially given that the sampling is spread over many values of the reaction coordinate. On the other hand, in implicit ligand sampling, there is little guarantee that large energy barriers will be sampled accurately due to the lacking influence of the ligand, and this results in overestimated energy barriers. However, when a properly conducted umbrella sampling analysis is compared to an implicit ligand sampling analysis and the latter yields a lower final free energy, then the ligand sampling is almost certainly more correct given the much larger number of independent conformations sampled per point. When the implicit ligand approach yields a higher free energy (with a large error), then it is possible that it did not sample the right protein conformations, and the umbrella sampling may be more representative, as could be the case for the Bossa et al. (25) results. One must be aware, however, that both methods do not measure the same quantity. The implicit ligand sampling measures the PMF at every point, whereas umbrella sampling measures the PMF of an area of space delimited by the area explored by the ligand during the simulation, projected onto a predefined reaction coordinate.

While Xe has no relevant biological function, it is frequently used in x-ray crystallography as a probe to identify the locations of cavities which may be involved in gas ligand migration. Furthermore, it has been observed in mammalian Mbs that the amino acids forming the Xe binding sites are much more conserved than other amino acids (4). For this reason, PMF profiles for Xe are relevant because they provide an interpretation for Mb structures obtained under high Xe pressure conditions. Since Xe interacts strongly with Mb and is also very large, its behavior differs from that of small diatomic gases. In our PMF profiles, this translates simply into lower binding energies for Xe in the Mb cavities sites and higher barriers between these cavities as well as to the external solution, as compared to small diatomic gases. Very important, however, is the observation that the location of Xe binding sites correlates very well with the regions of the protein that are most attractive to O₂, NO, and CO. In this respect, the Xe binding sites observed in x-ray crystals do, in fact, truly indicate docking regions for diatomic gas molecules. Gas ligands do not, however, solely diffuse in proteins by means of cavities accessible to Xe, and the presence of such cavities does not automatically imply that diatomic gases must transit through them, nor does their absence indicate that a favorable pathway for gas ligands does not exist. Xe cavities merely indicate the regions in which there is a high probability of finding gas molecules, and more often than not, these cavities will reside along the pathways taken by gas ligands to reach the heme.

Xe's large size and strong interaction with the protein imply that, of all the ligands that we have examined, the Xe PMF is the least accurate. However, the excellent match between predicted and observed Xe binding sites for Mb (see Fig. 2 and Table 1) gives legitimacy to our Xe PMF curves. It must be noted, though, that while the fact that we observe large energy barriers for Xe in Fig. 5, a–c, is to be believed, the actual maximum height of these barriers is inevitably overestimated by a significant amount in our calculations (for reasons detailed in Methods).

We have seen that the PMF profiles of various ligands inside Mb are in qualitative agreement with Mb's function. It remains to be seen whether this agreement is coincidental, or whether Mb's structure and dynamics are finely tuned by evolution to provide ideal energy profiles for different ligands. A full study on the general properties of O₂, NO, CO, and Xe migration in many different proteins needs to be performed before this question can be accurately resolved.

Gas ligand pathways across species

The atomic structure of Mb has been solved for different animal species, and to compare these, we have computed implicit ligand PMF maps for sperm whale (PDB accession codes 1DUK), pig (1MWD), horse (1AZI), Asian elephant (1EMY), yellowfin tuna (1MYT), and sea hare (1MBA), based on 4.6–5.0 ns equilibrium simulations of the above systems. The implicit O₂ PMF maps for sperm whale, pig, tuna, and sea hare Mbs are compared in Fig. 6.

FIGURE 6.

Comparison of the implicit ligand PMF maps in Mbs of different species. The implicit ligand PMF map of O₂ for (a) pig, (b) yellowfin tuna, and (c) sea hare Mbs (red) are compared with that for the sperm whale Mb (blue). The isosurfaces are drawn using a PMF value of 1.8 kcal/mol (points on these contours have an error of +0.2/−0.4 kcal/mol). The sperm whale Mb's heme with the connected proximal histidine is shown along with the protein's external surface (gray).

The similarities between our calculated implicit ligand PMF maps for the various Mbs reflect the evolutionary distance between species. Fig. 6 a highlights the strong similarities between the location of the O₂ migration pathways inside pig and sperm whale Mbs. The implicit ligand PMF maps for horse and the Asian elephant (not shown) demonstrate the same degree of resemblance to sperm whale Mb as is exhibited by pig Mb. As the evolutionary distance between species increases, the migration pathways look more and more different, as we show for the cases of yellowfin tuna (fish) Mb (see Fig. 6 b) and sea hare (mollusk) Mb (see Fig. 6 c), the latter being the least similar to whale Mb in terms of migration pathways.

Despite the obvious differences, the O₂ PMF maps for the Mb of the various species share some common features. First, all three Mbs shown in Fig. 6 appear to be quite “open” to O₂, in that they all display many regions in their interior that are favorable to O₂. This contrasts with what is seen in the example of CpI hydrogenase, which only allows O₂ in a very limited region of its interior (27). Second, all three PMF maps feature a pronounced distal cavity (to the right of the heme in Fig. 6), which is connected to the Mb exterior by a short pathway (out of the page toward the reader in the figure). In all three cases, the Xe binding sites of sperm whale Mb correspond to favorable cavities (the residue lining the Xe binding sites and the distal cavity are, in fact, more conserved than other residues across mammalian species (4)). Finally, all three Mbs exhibit potential exits from the binding pocket other than through the distal pathway, which suggests that gas ligands can enter and leave Mb's interior in many ways for all Mbs.

DISCUSSION

We have described and applied a method to compute the PMF (which is related to the probability of occupation) for the passive migration of small gas ligands inside Mb using a perturbative framework. Our results are important for two reasons. First, they provide a complete and direct determination of all the gas pathways in Mb. This complete picture of gas pathways can be used to determine which residues are involved in gas transport without resorting to per-residue mutations. They also provide a clear interpretation of experimental geminate recombination results, which otherwise involve guesswork and/or numerous years of careful followup experiments in order to be understood correctly. The fact that our observations are direct and detailed means that they have strong predictive power over the effect of residue mutations as well as over the locations of gas pathways and Xe binding sites in any other protein of known structure, irrespective of whether that protein is suitable to be studied by traditional experimental methods such as the monitoring of gas migration events after flash-photolysis. Secondly, they demonstrate unequivocally that short-timescale random thermal motion of the protein matrix and its environment, alone define reproducible and well-defined gas transport pathways inside proteins. In our model, the protein's thermal fluctuations are calculated explicitly without resorting to any assumption besides those inherent in the CHARMM molecular dynamics force field, which was parameterized to empirically reproduce short timescale thermal fluctuations, and thus is particularly valid for the present application.

The implicit ligand sampling method produces results that have very low errors when the PMF values are low (high-probability regions), and large errors when the PMF is very large (inaccessible regions), making it very suitable for the detection of gas migration pathways inside proteins, and to a lesser but still significant extent, for the measurement of all free energy barrier heights along these pathways. The approach works because gas ligands, being small and apolar, interact very weakly with the protein, and thus, do not promote significant conformational changes in the protein. Because of this, there is a strong overlap between the distribution of protein states in the lone protein and protein with ligand ensemble, and the former can thus be used to calculate properties of the latter. Although there is always an amount of uncertainty arising from molecular dynamics simulation, due to short timescale sampling and empirical force-field models, we believe that our specific analysis presents a convincing case despite these caveats.

On the biological side, our results have important ramifications regarding the general mechanism by which gas ligands are transported inside the protein matrix. Numerous hypotheses have been brought forth over the years to describe gas transport inside proteins. The first studies assumed that gas ligand diffused through small permanent channels (16). Other studies have suggested that gas ligands enter proteins directly, as if they were simply a more viscous medium (49). The currently emerging view for many proteins is that, rather than diffusing along permanent channels, gas ligands can migrate through bulky regions of the protein, made possible by the proteins' internal thermal motion (17,18,24,27,50). Our results suggest that this is the case, and furthermore that the pathways taken by the gas ligands are not randomly distributed in the protein, but that they are, in fact, located in well-defined regions that can be identified by examining the protein's thermal fluctuations. The simple fact that we detected pathways that match known data implies that a small ligand can diffuse in and out of Mb solely due to protein's thermal fluctuations at the nanosecond timescale, even though the timescale of the total ligand migration can be much longer.

Cavities inside the protein matrix, such as Mb's xenon binding sites, appear to play a prominent role in accommodating gas ligands inside Mb. Interestingly, such cavities are sometimes barely present in other proteins that still exhibit thermally defined gas ligand pathways that stretch over long distances, such as in CpI hydrogenase (27). Cavities would appear to create favorable docking sites for the ligand, but are not necessary to account for the ligand's mobility as it migrates inside the protein matrix. Our analysis suggests that cavities could perhaps also play a role in the gas ligand selectivity of the protein.

Finally, we wish to mention other systems, besides Mb, where the study of the migration of small gas ligands inside the protein matrix is important. Oxygen sensitivity is a highly relevant issue for hydrogenases, enzymes that produce or break-down hydrogen gas. Their sulfur-metal active sites can usually also bind O₂. Recent developments aim at harnessing the hydrogen-producing power of hydrogenases for biotechnological purposes, but for this to be practical, the sensitivity of hydrogenases to O₂ must be repressed. Buhrke et al. (51) have found that the [NiFe]-hydrogenase of Ralstonia eutropha H16, which is usually resistant to O₂, can be made sensitive to O₂ by a mutation of residues located along a putative channel leading to the active site. This study suggests that the protein matrix of this hydrogenase may play an important role in regulating the access of its active site to O₂ (along with the O₂ sensitivity being regulated by its affinity to the active site and its environment). Another example involves O₂ migration inside cytochrome-c oxidase from Rhodobacter sphaeroides. It was shown (52) that a single point-mutation inside the protein is enough to block O₂ access. There are many examples of proteins which use small gas ligands as a substrate or ligand and in many cases, the gas ligand must reach a buried region of the protein. The above examples demonstrate the relevance of studying gas ligand migration inside proteins and underscore the importance of being able to identify gas migration pathways that are not readily visible in the protein's static structure.

APPENDIX: PMF FOR LIGANDS WITH INTERNAL DEGREES OF FREEDOM

When calculating the implicit ligand PMF for the case of diatomic (or more complex) ligands, we must also take into account the internal degrees of freedom of the ligand, such as its orientation, bond length, etc. In the following derivation, we will treat these generalized degrees of freedom separately from those of the rest of the protein-ligand system. In our notation, r will refer to the ligand's center of mass, p′ will refer to the ligand's momentum degree of freedom, and Ω will denote all of the ligand's remaining generalized coordinates degrees of freedom (i.e., those in addition to its center-of-mass degrees of freedom).

When including the ligand's internal degrees of freedom, the expression for the ligand's probability density (Eq. 2) becomes

(13)

When adding the ligand, the Hamiltonian for the protein reference system () will again be shifted by an amount equal to the protein-ligand interaction energy ΔE(q, r, Ω) and kinetic energy K(p′), but also by the ligand's internal potential energy U(Ω):

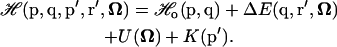(14)

Inserting the perturbed Hamiltonian (Eq. 3) into the expression for the ligand probability density (Eq. 2), we get

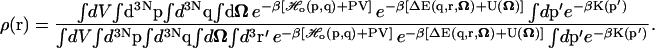(15)

Using the definition for the isobaric isothermal ensemble average (Eq. 5), the ligand probability distribution becomes

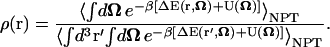(16)

We now insert our expression for the ligand probability density (Eq. 16) into the definition of the PMF (Eq. 1) and, just as we did for Eq. 8, we also impose that our PMF be zero when the ligand is in vacuum (defined when ΔE(q, r, Ω) = 0). We then obtain

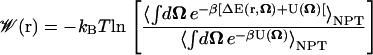(17)

For the case of diatomic ligands, we have chosen to keep the bond lengths fixed, such that the only internal degrees of freedom Ω remaining are those that specify the orientation of the ligand. In this case, the ligand's internal energy U(Ω) is a constant, such that all the terms that contain it in Eq. 17 cancel out. The expression for the PMF (Eq. 17) then takes on the simplified form used in our analysis:

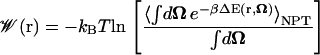(18)