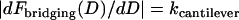The Role of Flexible Tethers in Multiple Ligand-Receptor Bond Formation between Curved Surfaces

Abstract

Ligands mounted to surfaces via extensible tethers are present in nature and represent a growing class of molecules used to engineer adhesion in drug targeting, biosensing, self-assembling nanostructures, and in other biophysical research. Using a continuum approach with geometric and thermodynamic arguments, we derive a number of analytical expressions that relate key properties of single-tethered ligand-receptor interactions to multiple bond formation between curved surfaces. The theoretical predictions are in good agreement with measurements made with the surface forces apparatus. We establish that, when ligated, many tethers commonly used in biophysical research exhibit a discrete binding range that can be accurately measured with force spectroscopy. The distribution of bound ligated tethers is independent of the surfaces' interaction radius, R. The bridging force scales linearly with R, the tether's effective spring constant and grafting density, and with the ligand-receptor bond energy when the surfaces are in direct contact. These results are contrasted to bridging forces that evolve between plane-parallel geometries. Last, we show how our simple analytical reductions can be used to predict adhesive forces for STEALTH liposomes and other targeted and self-assembled nanoparticles.

INTRODUCTION

In this work, we examine the adhesive forces between tethered ligand-receptor architectures. As an example, Fig. 1 shows two surfaces—one anchoring extensible molecular tethers that each bear a ligand that can bind specifically to a dense field of receptors on the opposing surface. Such architectures are biomimetic and are used in targeting liposomes and other bioactive particles toward cell tissues (1,2), in biofunctionalizing surfaces (3,4), and in the self-assembly of colloidal- and nanostructures (i.e., (5,6)).

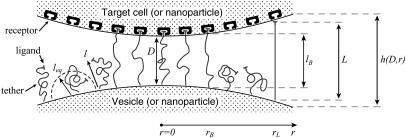
FIGURE 1.

Depiction of two particles (i.e., cells, liposomes, or nanoparticles) bridged by tethered ligand/receptor bonds. The gap height, or surface separation, h(D,r), is a function of the spheres' tip-to-tip distance (D) and the position along the lateral axis (r). The surface curvature limits how many particles may bridge the two surfaces. The relevant interaction area is constrained by the tether extension, or contour length (L), and the corresponding radial distance (r_L). The area containing bound tethers is geometrically limited by the effective binding range of an individual tether (l_B) and the corresponding radial distance (r_B). Ligands tethered to extensible molecules, such as polymers in good solvents, will stochastically sample many distances (l) away from their tether's anchor, which can be much farther away than the tether's time-average or equilibrium extension (l_eq) (16,17). These larger extensions produce the bridging forces that we model in this article.

A wide range of tethers has been utilized in drug targeting and controlled nanoassembly, including the nonimmunogenic poly(ethylene glycol) (PEG) and other synthetic polymers, and biologically harvested materials such as DNA strands, actin filaments, and fibronectin (7–12). Likewise, a wide range of biospecificities has been imparted to many of these tethers and their binding efficacy studied (13–15). What remains debated is the most efficacious structure for engineering adhesion between particles coated with tethered ligands-receptors.

The tethered ligand-receptor architectures that have been studied most are found in targeted STEALTH (ALZA, Mountain View, CA) liposomes. Like the stealth bomber, these drug-carrying vesicles are designed to evade the body's defenses—the immune system—and deliver their payload in a precisely targeted location, such as a cancer cell (1). They are armored by a forest of PEG chains, some of which bear target-specific ligands. These grafted polymer chains stochastically sample many chain conformations, which dramatically increases a tethered ligand's probability of finding its target compared to ligands mounted flush on a surface (16–20). The entropic motion of grafted chains also produces a spring-like force that pulls bridged surfaces together once the tethered ligand and receptor bind (18,19,21). This same entropic motion is responsible for repulsive steric forces as the grafted layer is compressed. The net achievement of these “entropical forests” is a long-range attraction and a shorter-range repulsion between surfaces they bridge. These forces may extend beyond the influence of attractive van der Waals or repulsive electrostatic forces and thus dictate the adhesive properties of surfaces, such as the distance at which bonds form and how strongly a liposome adheres to a target cell.

The tether's tug against the ligand-receptor bond reduces the bond lifetime (22), a phenomenon that has been examined through a variety of kinetic (18,19,21,23), thermodynamic (24–29), and mechanical (30) models. The rupture of single and multiple tethered bonds has also been studied extensively through force microscopy (for a review, see (31)). Unfortunately, it is very difficult to experimentally measure the formation of multiple molecular cross-bridges and to relate the measured adhesive properties to the properties of individual tethered ligand-receptor bonds. The most similar prior works have studied ensembles of grafted tethers using “adhesive dynamics”—a stochastic simulation method that tracks binding probabilities for each molecule and sums the forces on each bond to calculate the net adhesive force between two bridged bodies (32–37).

Here, we seek a continuum model to describe the interaction between individual tethered ligands-receptors and to relate those single-molecule properties to the adhesive strength, range of interaction, and speed of approach between surfaces bridged by many tethered ligands-receptors. This framework allows us to develop scaling laws that are useful for understanding multiple bond formation between tethered ligand-receptor architectures on curved surfaces. We demonstrate the predictive accuracy of our model by comparing it to measurements with the surface forces apparatus (SFA). Last, we illustrate how our analytical solutions can be used to design “smart” biointerfaces for drug targeting, biosensing, and nanoassembly, using STEALTH liposomes as an example.

SINGLE BOND FORMATION: CRITICAL BINDING RANGES

Of fundamental importance to tethered ligand-receptor interactions is the question: at what distance will tethered ligands bind to receptors? Bonds formed when the tether is stretched beyond its equilibrium extension are antagonized by the tether's contractile force and can dissociate if the entropic pull of the tether is sufficiently strong (18,19,22,38). External forces, such as those applied in force microscopy, can also increase the rate of bond dissociation (22,39). However, in contrast to the bulk of experimental work where surfaces are separated, with approaching surfaces the apparent bond strength may appear to decrease with increased surface speed if bond formation is constrained by the time required for tethered ligands to diffuse toward receptors (16,18,19). In the section “Bridging dynamics and surface approach”, we show quantitatively that this is not always an important constraint for modeling the adhesion of liposomes and larger particles, since diffusion of the kinds of small, high affinity ligands tethered by polymers used in drug targeting is often very rapid compared to the timescale of the entire adhesion event. Nonetheless, assuming that tethered ligands and receptors are in chemical equilibrium will reveal some useful scaling relations and provide explicit expressions for the maximum bridging force between surfaces bound by tethered ligands, as well as estimates of the adhesion timescale and fraction of bound tethers.

Moreira et al. (18,19) used a kinetic model to show that in the limit of chemical equilibrium, tethered ligands-receptors have the binding probability

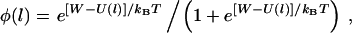(1)

where W is the ligand-receptor bond dissociation energy and 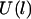is the energy required to stretch a tether a distance l away from its anchor. Fig. 2 plots the probability of bond formation for PEG₂₀₀₀ tethers with various ligand-receptor dissociation energies. Each curve is sigmoidal, with a high probability of bond formation when 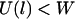and a low probability of binding when 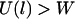. At the inflection point 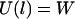, the binding probability is 0.5.

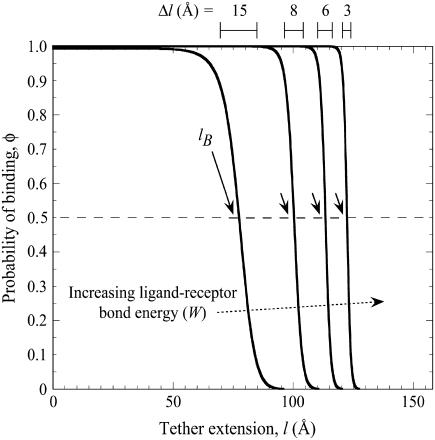
FIGURE 2.

Probability of a single PEG₂₀₀₀ tether binding (Eq. 1) as a function of its extension, l, for various ligand-receptor bond energies (left to right, W = 5, 15, 25, 35 k_BT). Arrows mark each tether's binding range, l_B, defined as the tether extension at which 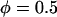, which coincides with each curve's inflection. Bonds form less frequently when the distance between the tether's anchor and the receptor is greater than l_B. This critical binding range becomes greater as the ligand-receptor bond energy increases, as the bond becomes more thermodynamically stable and can more easily resist the entropic pull of the tether. Brackets above the graph designate each curve's Δl, which estimates the range over which φ changes from 1 to 0. The fully extended tether length is L = 159 Å (length of abscissa). As W increases, Δl/L decreases and φ more closely resembles a step function. If the receptor is moving toward the anchored tether, the general shape of the binding probability curves remains, although the inflection point (l_B) will be decreased by an amount that depends on the approach velocity (18,19).

As seen in Fig. 2, the interval in l over which the binding probability changes from 1 to 0, Δl, is a small fraction of the tether length, L. In such cases, there is a sharply defined extension, l_B, below which nearly all tethers bind and beyond which the binding probability is essentially zero. Mathematically,

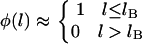(2)

We call this critical extension, l_B, the tether's binding range, corresponding to the inflection of each curve in Fig. 2. For tethers with a harmonic stretching potential, 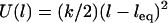, where k is an effective tether spring constant, and so the critical binding range is 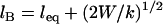and 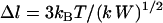(In general, 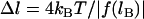, where 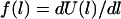is the monotonic stretching force for a single tether, which need not be Hookian. For dilute polymers in good solvents, it follows that 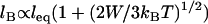. Thus, for freely jointed chains, l_B scales linearly with l_eq, which we have verified with our independent numerical model (R² ≥ 0.996 for all parameters in Table 3). This predicted scaling of l_B with respect to W agrees with reported Monte Carlo calculations of binding probability curves for multivalent ligands with energies totaling 8, 16, and 24 k_BT for a fixed length of end-grafted PEG (N = 64) (40)). Equation 2 also describes well the binding probability of tethered ligands when surfaces approach quickly compared to the bond formation timescale (of the order ∼1 μs for PEG tethers) (16). In that case, the binding probability curve still approximates a step function, but the critical binding range decreases by an amount that depends on the approach speed (18,19). Thus, in settings far from equilibrium, l_B can be interpreted as the maximum effective binding range.

TABLE 3.

Parameters used in calculating numerical results (except where specified)

	Symbol	Value(s)	Units	Reference
Tether (PEG) properties
Molecular weight	PEGx	2000, 3300, 6260	g/mol
Number of mers	N	45, 75, 142*
Length (full extension)	L	159, 262, 497*†	Å
Tether resting extension	leq	42.8, 58.4, 87.9*‡	Å	(16)
Length per mer	a	3.5§	Å
Grafting density	σ	(1.17 ± 0.03) × 105	Tethers/μm2	¶
Ligand-receptor bond energy	W	5–35	kBT
Surface properties
Hamaker constant		3.0 × 10−21	J	(57)
Surface charge densities (grafting surface/receptor surface)		−0.0186/−0.01	C/m2	(94)
Interaction radius	R	0.1–3.0, 1.48 ± 0.05	cm	¶
Slip plane	P	0, 158	Å
Cantilever spring constant	kcantilever	100–300, 236 ± 18	N/m	¶
Environmental properties
Temperature	T	25.0 ± 0.2	°C	¶
pH		7.2 ± 0.1		¶
Ionic concentration		0.50 ± 0.01	mM	¶
Viscosity	μ	8.9 × 10−4	kg m−1s−1	¶
Dielectric constant		78

Values with uncertainties indicate experimentally measured values, which were used in the model when comparing to experimental data.

^*Corresponding to the three polymer molecular weights listed above.

^†L= a × N.

^‡Calculated from Monte Carlo data (16).

^§Coincidentally about the same length as an amino acid in a polypeptide (95).

^¶T. L. Kuhl, S. Zalipsky, and J. Y. Wong, unpublished data.

The question is: do biological tethers (and synthetic tethers) in common use have a sharply defined binding range when interacting with biological receptors? To answer this broad question, we first determine typical bond energies (W) for biospecific interactions. Table 1 compares the bond energies of ligand-receptor pairs commonly used in drug targeting and other biophysical research (13,14). Although this list is not exhaustive, an attempt has been made to represent a variety of molecular classes. With the exception of a single nucleotide bond, all the biospecific interactions listed in Table 1 have a bond energy of W > 5 k_BT and most have W > 15 k_BT. In fact, of the 2276 biological ligand-receptor complexes currently listed in the PDBbind database v.2004 (41,42), we calculate an average bond energy of W = 14.7 k_BT (monomodal with standard deviation 4.9 k_BT). (The bond dissociation equilibrium constant and energy are related by 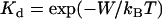(22).) The strongest biological noncovalent interaction is between biotin and avidin (W = 35 k_BT).

TABLE 1.

Some ligands and receptors of interest for drug targeting and other biophysical research

Ligand	Receptor	Bond energy W/kBT*	Dissociation constant Kd (M)*	Ligand MW (D)	Reference
Folic acid	Folate receptor	21–25	10−9 − 10−11	441	(68,69)
Sialyl Lewis X†	L-selectin	18–24	2×10−8 − 4×10−11	120,000	(70–72)
PSGL1	P-selectin	17	5.5 × 10−8	120,000	(72,73)
Adenine (A)	Thymine (T)	2.3	1 × 10−1	135	(74)
RGD peptide	Integrin αIIβ3	14	1 × 10−6	770	(75)
fibrinogen	Integrin αIIβ3	16	1 × 10−7	N/A	(75)
145-2C11 mAb (antibody)	CD3	16	7 × 10−8	N/A	(76,77)
Fluorescein	Anti-fluorescein	19–21	0.75–8.9 × 10−9	380	(78)
Human serum albumin (HSA)	Anti-HSA	14‡	8.3 × 10−7	66,500	(79)
Serine endopeptidases (various)	Protein inhibitor	18–29	1.5 × 10−8 − 2.5 × 10−13	N/A	(77)
“Typical” antibody	“Typical” antigen	18	10−8	>100,000	(22,73)
Biotin	Avidin	35	1.0 × 10−15	244	(80)
Biotin analogues (various)	Streptavidin	5–30	1.0 × 10−2 − 5 × 10−8	214–258	(80,81)

^*When only one of W or K_d was reported, the other was estimated (22).

^†Modified PSGL-1 ligand.

^‡Estimated as W = (rupture force) × (effective rupture length) (22).

To survey characteristic values for tether stiffness, Table 2 compares the lengths (L) and effective spring constants (k) of tethers that have been used in drug targeting, controlled self-assembly, and elsewhere (7). Importantly, a calculation of Δl/L is listed using the characteristic value of W = 15 k_BT that was determined from Table 1. In all cases, Δl is a small fraction of L; thus, tethers listed in Table 2 are expected to exhibit a discrete binding range when bearing “typical” biospecific ligands, such as those listed in Table 1. In some cases, and we expect a binding probability curve much steeper than those shown in Fig. 2, and thus an even more distinct binding range.

TABLE 2.

Some tethers of interest for drug targeting and other biophysical research

Tether	Spring constant, k (mN/m)	Length, L†	Binding interval, Δl (nm)‡	Δl/L	Reference
DNA	10−5 − 10−4	20 μm	70	0.0035	(82)
RNA*	0.1	320 nm	6.1	0.019	(83)
Dextran (polysaccharide)*	5.1	0.4–1.6 μm	0.7	0.0004–0.002	(84)
Xanthan (polysaccharide)*	93	∼1 μm	0.2	0.0002	(85)
Cellulose (carboxylmethylated)*	1–30	0.1–1.2 μm	2	0.001–0.02	(85)
Neutrophil microvilli	0.15–1.3	0.2–1.6 μm	1.2–3.0	0.006–0.002	(86)
Lamellar bodies (lung surfactant complex)	0.0125	8 μm	14	0.0018	(87)
PEG2000	1.0	15.9 nm	3.7	0.23	§
PEG3300	0.57	23.2 nm	4.4	0.19	§
PEG6260	0.27	49.7 nm	7.0	0.14	§
Poly(styrene)	0.1–2	10–1000 nm	1–4	0.04–0.10	§
Poly(vinyl alcohol)*	1.0	50–1000 nm	1.6	0.002–0.03	(88)
Poly(methylacrylic acid)*	1.1	20–120 nm	1.0	0.05–0.005	(89)
Poly(NIPAM)*	1.8	100–1600 nm	1.0	0.0007–0.01	(90)

^*An effective molecular stiffness was estimated from the slope of reported force-distance curves in the low-force regime.

^†“Contour length” or fully-stretched extension.

^‡Estimated for a characteristic value of W = 15 k_BT (cf. Table 1).

^§For comparison, see (38,91–93).

MULTIPLE BOND FORMATION AT CURVED INTERFACES

In the rest of this article, we relate the properties of single tethered ligand-receptor interactions to what may be observed when many such molecules decorate curved surfaces (i.e., Fig. 1). We seek to answer: how many bonds will form at a given surface separation, what will be the bridging force between the two surfaces, and what is the timescale of the adhesion event? Our analysis assumes that anchoring surfaces are nondeformable as the conventional first step in quantifying the interactions of deformable solids.

When tethered ligand-receptor pairs are evenly spread across two opposing curved surfaces, geometry dictates the maximum number of tethers that may bind:

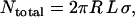(3)

where R is the effective interaction radius of the surfaces, L is the tether's fully extended length or contour length, and σ is the tether surface grafting density. (Although here “grafting density” refers to the areal density of tethers, it can be replaced by the areal density of receptors without complication. Such a substitution would be appropriate if the receptors were the limiting reagent.) (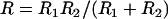 for two interacting spheres with radii R₁ and R₂, respectively. For a sphere interacting with a flat surface, R reduces to the sphere radius. For liposomes (R₁ ∼ 100 nm) targeting a cell (R₂ ∼ 10 μm), the interaction radius is 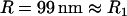.) Equation 3 assumes the surfaces are touching (see Fig. 1). It is exact provided 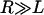, and is still correct to a factor <10 when 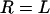. Examples of when Eq. 3 is accurate include the adhesion of two cells (R = 10 μm, L ∼ 1 μm) (Table 2), the binding of a targeted liposome onto a cell surface (R = 38–100 nm, L = 16 nm) (47), and the cross-linking of nanoparticles via adsorbed polymer (R = 100 nm, L = 21 nm) (5). Using Eq. 3, a 100-nm STEALTH liposome with σ = 10⁵ tethers/μm² of PEG₂₀₀₀ (1) may form a maximum of ∼1000 bonds to a cell, whereas the folate-targeted liposomes used by Reddy et al. (R = 50 nm, L = 27 nm, σ ∼ 10³ tethers/μm²) (48) would be expected to form at most ∼10 bonds per liposome. We postulate that in both cases these are enough bonds to render continuum models insightful.

The number of tethers that can form bonds depends not only on the tether-ligand-receptor properties but also on the surface curvature. Tethers near the interaction center will be closest to the receptor surface and thus more likely to form bonds, whereas those away from the center will be more highly stretched and thus less frequently bound. As we have shown that most tethers of interest exhibit a discrete binding range (Eq. 2), we can simplify the analysis considerably. Using geometric arguments, the number of tethers bridging two curved equilibrated surfaces may be readily estimated,

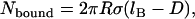(4)

for 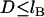and 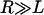. Thus, the number of tethers that can bind depends intimately on l_B. Further, by comparing to the total number of tethers in the interaction area (Eq. 3), the fraction of chains bound is

(5)

Thus, the fraction of bound chains is independent of the size of the interaction area. Although simple in form, Eq. 5 makes a remarkably accurate calculation of compared to our numerical solutions for complimentary surfaces decorated with multiple PEG tethers (identical within ±1% over the entire range, 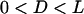for 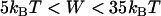). For approaching surfaces, Eqs. 4 and 5 estimate maximum expected values, since l_B decreases with increased approach speed (18,19).

With justification for treating binding ranges of single tethers as discrete when multiple tethers are present, we now develop an analytical solution for the maximum bridging force between two curved, approaching surfaces. Our derivation centers on developing appropriate expressions for the component of the interfacial energy, 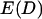, per unit area that develops from multiple tethered ligand-receptor bond formation between two plane-parallel surfaces. As detailed in Appendix A, the many angles at which tethers bind have little effect on the bridging force normal to the plane of interaction. By our definition, individual tethers at equilibrium exhibit significant binding probabilities when 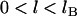. Thus, we set 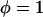(maximum) for 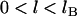, which restricts the validity of the result to 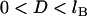. (We will address the possibility of nondiscrete binding ranges in a later section). Last, we assume a constant grafting density, σ. Then for the plane-parallel geometry, the component of the interfacial energy per unit area that arises from the bridging force is

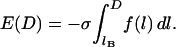(6)

We employ two models for the stretching force, 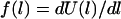. In the first we treat each tether as a Hookian (harmonic) spring. Although ideal springs do not exist in nature, this simplification is useful because spring models are often used to approximate a single molecule's actual mechanical behavior (30,49). (For dilute polymers in good solvents, 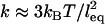and 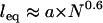(or “Flory radius”; a = mer length, N = number of mers per tether) (38).) For example, single-molecule force spectroscopy has been used to measure effective spring constants for a number of tether molecules (e.g., Table 2). Moreover, because the spring model is one of the simplest models for polymer stretching, it will make the scaling behavior of the bridging force more apparent.

The maximum (or equilibrium) bridging force between two surfaces is calculated using the Derjaguin approximation, which has been shown to be valid for any type of force provided 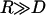(51). For the spring model the result is

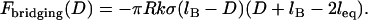(7)

Equation 7 shows that the maximum bridging force for spring-like tethers bridging approaching surfaces scales linearly with the interaction radius (R), tether spring constant (k), and tether grafting density (σ). This scaling behavior for tethered ligand-receptor interactions is also validated in Appendix B without using the Derjaguin approximation. Using Eq. 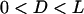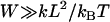7 with our analytical estimate for l_B suggests that the bridging force scales linearly with the ligand-receptor bond energy (W) over the entire regime when , which for freely jointed polymers (i.e., PEG) requires 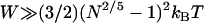, or when 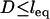requires simply 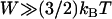for any polymer length. This latter constraint is typically met in drug targeting; thus, we might anticipate 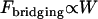when liposomes are attached to target cells.

The second model we employ for the polymer stretching force is the “worm-like chain” (WLC) model, which is known to more accurately describe the stretching potential of many bio- and synthetic polymers at long extension, as it accounts for finite chain length (30). In the WLC model, the force required to stretch a single tether is

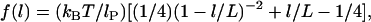(8)

where l_P is the tether's persistence length, which characterizes the chain's resistance to bending stress between adjacent mers. Applying the same assumptions used to derive Eq. 7 except using the WLC model (Eq. 8) estimates the maximum (or equilibrium) bridging force for an entire ensemble of flexible tethers between two curved, approaching surfaces:

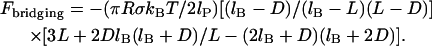(9)

As with the spring model, the WLC model predicts that the bridging force will scale linearly with the interaction radius (R) and tether grafting density (σ), and will vanish as D → l_B. The stiffness of individual chains is manifest in the bridging force as an inverse proportionality to the persistence length (l_P) in Eq. 9.

BRIDGING DYNAMICS AND SURFACE APPROACH

The preceding analysis is useful for calculating the maximum effective binding range of an individual tether (via Eq. 1), the maximum number and fraction of bound tethers (Eqs. 4 and 5), and the maximum bridging force (Eqs. 7 and 9). However, these expressions can represent not just maximal values but exact values when the surface speed is slow enough that tethered ligands and receptors can be assumed to be in a state of chemical equilibrium. Although a detailed kinetic analysis is beyond the scope of this article, identifying the conditions in which tethered ligands and receptors anchored to curved surfaces are expected to be in chemical equilibrium clarifies the applicability of our model and provides useful information about the dynamics of surface approach.

For ligands tethered to immobile surfaces, the average rate of bond formation to opposing receptors depends on the intrinsic kinetics of ligand-receptor bond formation and on the effective diffusion rate of the ligated tether. The distal end of a grafted polymer chain in good solvent has the characteristic diffusion time, 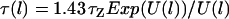(18,19). The chain relaxation time used here is the “Zimm time”, 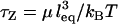, which takes into account hydrodynamic drag of the chain as it moves thermally (38). As an example, a characteristic value for this diffusion time for a single, ligated PEG₂₀₀₀ tether in water opposing a receptor <100Å away is τ_Z ≈ 1 μs. Because this timescale is much longer than that of intrinsic ligand-receptor bond formation (in the nanosecond range), bond formation with ligated PEG—and with less flexible tethers—can be assumed to be diffusion limited. In such cases, surfaces that move slowly compared to the tether diffusion timescale will have equilibrium bond kinetics and equilibrium adhesion forces.

To estimate the surface approach timescale, we note that the adhesion begins near the surface separation D ≈ l_B, where tethers grafted near the contact center are first able to form stable cross-bridges (Fig. 1). These bound tethers begin tugging the surfaces together, bringing more tethers into range until the surfaces are an equilibrium distance apart, D_eq < l_B. The characteristic time for the surfaces to move across this distance is then

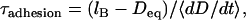(10)

where 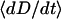is a representative speed of the surfaces' approach. To calculate the approach speed, we use the thin film assumption (52) to write the force balance:

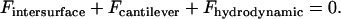(11)

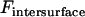is the bridging force plus any nonspecific intersurface forces. 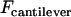is the force of an external cantilever mounting one surface, as would be present in a force microscopy experiment. It has previously been shown that when 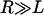, the hydrodynamic force is dominated by the force required to squeeze out fluid from between the two surfaces, viz.

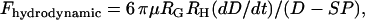(12)

where 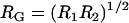and 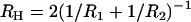are the geometric and hyperbolic radii, respectively, μ is the fluid viscosity, and SP is the distance that the hydrodynamic slip plane extends from the surface (from D = 0) (52). We simplify with 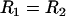so that R_GR_H = R. Then from Eqs. 11 and 12, the approach velocity is

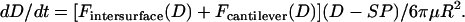(13)

It is insightful to simplify Eq. 13 as follows. First, 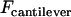is typically much smaller than 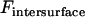during surface movement in force microscopy, and is zero in the context of liposomal targeting in vivo. Second, the bridging force typically dominates over the nonspecific forces except at short distances, and so F_intersurface ≈ F_bridging. With these simplifications, we can use Eqs. 7 and 11 to derive the maximum surface approach speed:

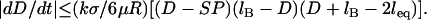(14)

By comparing Eq. 14 to Eq. 10, we can identify the following scaling relation:

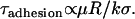(15)

We can use this scaling relation to estimate the minimum adhesive timescale for particles of different sizes, for example. For an SFA experiment that mimics architectures commonly used in drug targeting (1), the adhesion timescale is of the order of 1 s for R ∼ 1 cm. For a self-similar liposomal architecture with R = 50 nm, Eq. 15 estimates 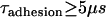. In both cases, 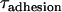is longer than the 1 μs sampling time typical for PEG₂₀₀₀ chains extended below l < 100 Å where surface movement is fastest, and is significantly larger than the polymer's intrinsic relaxation (Zimm) time of 9 ns. This observation substantiates our assumption of chemical equilibrium between PEG-anchored ligands and receptors for the drug targeting applications with which this study is primarily concerned.

METHODS FOR EVALUATING THE ANALYTICAL SOLUTIONS

Independent numerical solutions

To evaluate our analytical reductions, we also calculated more exact expressions for the bridging force as follows. As discussed previously, the bridging force for an ensemble of tethered ligands spread between two curved surfaces depends on the surface geometry and on properties of the ligand, receptor, and tether. Tethers near the interaction center (r = 0) will be less stretched than tethers near the periphery of interaction (see Fig. 1). Thus, the contractile force of a tether, 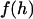, depends on the gap height, h. Because a stretched tether opposes bond formation, the probability that a given tether will bind, 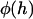, also depends on the gap height. Thus, calculating the total bridging force between two curved surfaces requires an integral over the entire interaction area:

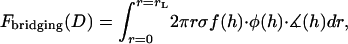(16)

where 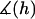is a mathematical operator that accounts for tethers binding to receptors at different angles and r_L is the radius of the interaction area corresponding to a gap height of 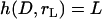(Fig. 1). For two curved surfaces, the gap height is

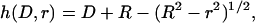(17)

where D is the nominal surface separation (tip to tip), R is the effective interaction radius, and r is the lateral distance from the center of the interaction area (see Fig. 1). To compute this force for PEG tethers, we have interpolated stretching force profiles from Monte Carlo simulations reported elsewhere for various PEG lengths (16). To compute the local binding probability of a single tether, 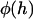, we replace l with the gap height, h, in Eq. 1:

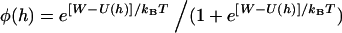(18)

Appendix A provides a detailed derivation of 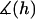for two spherical particles bridged by tethered ligands. In scenarios relevant to drug targeting, 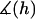ranges between 1 and 1.15, and thus serves as only a small correction to Eq. 16 that we account for in our numerical results.

Experimental measurements

To further validate our model, we compare it to measured adhesive forces between membranes functionalized with tethered ligands and receptors, measured with SFA as reported elsewhere (16, 17; T. L. Kuhl, S. Zalipsky, and J. Y. Wong, unpublished data). The SFA technique is one of the most powerful tools available for determining the force-distance relationship between weakly interacting surfaces. In short, two molecularly smooth mica surfaces were coated with lipid membranes anchoring a known fraction of ligated PEG_x, where the subscript “x” is the average polymer molecular weight. This coating was made using Langmuir Blodgettry, which allowed the tether grafting density to be controlled for each sample. Biotin (to oppose streptavidin receptors) was the chosen ligand because of its typical molecular weight and extensive characterization (cf. Table 1) (54). A dense field of streptavidin receptors (>79% coverage) (55) was presented on the opposing membrane. One surface was mounted on a double cantilever spring; its measured displacement is proportionate to the intersurface force. Simultaneously, the intersurface spacing, D, was controlled and measured with angstrom precision using white-light interferometry (56). For dynamic measurements, a camera recorded the interferogram (52).

In comparing to these experiments, we added to our model nonspecific interactions between biological surfaces as follows: 1), van der Waals attraction between lipid membranes calculated using a nonretarded Hamaker constant typical for membranes (57); 2), electrostatic repulsion calculated numerically by solving the nonlinear Poisson-Boltzmann equation for membranes characteristic in drug targeting research (58); and 3), polymer steric repulsion calculated using Dolan and Edwards theory for grafted polymer mushrooms (59). These three nonspecific forces were added to the specific bridging force (Eqs. 7 or 14) for direct comparison to both static and dynamic measurements with the SFA. For D < l_eq, it was also necessary to add 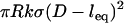so that polymeric compression was not accounted for twice when summing Dolan and Edwards theory to either of Eqs. 7 or 14. The net forces were also used to estimate the ensemble capture distance, D_B ≈ l_B, which is the farthest separation at which two surfaces experience net attraction. In surface force measurements, the capture distance is an artifact of the experiment (the distance at which the slope of the net intersurface force profile equals the spring constant of the cantilever that holds one surface (60). Yet because it is easily quantifiable, D_B serves as a useful third validation of our adhesion model.

Input parameters for the numerical (and analytical) solutions were chosen to match experimental variables (Table 3). Except where noted, all results are a priori estimates, not data fits. The three molecular weights of PEG correspond to lengths that have been commonly used for drug targeting in vivo (47). Likewise, the tether grafting density of ∼10⁵ tethers/μm² is typical for drug targeting (47). This grafting density is also on par with reported expressions of folate receptors on tumor cells (35,61), and only one order of magnitude greater than estimated cell surface densities of integrin receptors (34).

RESULTS AND DISCUSSION

Experimental validation

It is nontrivial to measure bridging forces directly because mechanical instabilities that are present in all force spectroscopy create regions of distances where the surfaces move quickly and equilibrium forces cannot be measured (60). Therefore, to validate our model, we rely on a combination of measurements of static forces, capture distances, and the speed of surface approach.

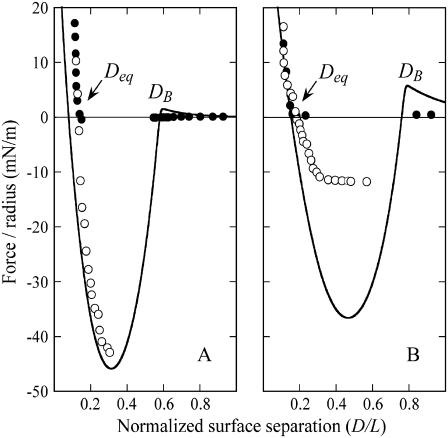
Fig. 3, A and B, compare the measured intersurface forces to those predicted a priori for two tether lengths (PEG₆₂₆₀ and PEG₂₀₀₀, respectively), using the spring model (Eq. 7) for the specific bridging force. The model correctly identifies the capture distances (D_B), adhesive minima, and equilibrium resting positions (D_eq) to within experimental error (±0.1 D/L). From these figures we see that the model predictions are numerically accurate to better than an order of magnitude. It should be emphasized that the solutions shown in Fig. 3 were not “fit” to the experimental data. Instead, these calculations were made a priori using the parameters in Table 3. Further, the predicted force profiles are based on the maximum bridging force expected. With these views, we find that the model agrees remarkably well with the experimental data.

FIGURE 3.

Comparison of a priori predictions of the maximum expected bridging force (lines) and measurements with the SFA for biotin/streptavidin ligand/receptors (W = 35 k_BT) mounted on two tether lengths: (A) PEG₆₂₆₀ and (B) PEG₂₀₀₀ (T. L. Kuhl, S. Zalipsky, and J. Y. Wong, unpublished data). Forces were measured between unperturbed surfaces as they approached (•) and during withdrawal after surfaces had been pressed into adhesive contact (○). Discontinuities in the measured data exist from instabilities in the cantilever spring that support one of the functionalized surfaces. The a priori model correctly identifies the capture distances (D_B) and equilibrium resting positions (D_eq) to within experimental error (±0.1 D/L), and forces to within less than a factor of three.

Differences between the predicted and measured forces arise from two primary sources. First, what is common to both Fig. 3, A and B, is that the long-range steric repulsion is overestimated by the Dolan and Edwards theory. In fact, reliable force laws for grafted polymer mushrooms are only well established for polymer compression (D < l_eq) (59). However, this has little effect on either the capture distances (D_B) or the majority of the force profile because the polymer bridging force dominates when D < D_B.

Second, the measured bridging force for the PEG₂₀₀₀ tethers (Fig. 3 B) is underestimated by about a factor of three. It has been shown that lipid anchors can be the weakest “bond” between membranes bridged by polymers (62). In short, the energy required to extract a phosphatidylethanolamine from a lipid membrane ranges from 10–25 k_BT (62–66), which is significantly less than the biotin-streptavidin bond energy (35 k_BT). Thus, it is likely that the uprooting of lipid anchors—which may also depend on the tether spring constant or kinetics—decreases the bridging force in these experiments. However, this effect is most significant in separating surfaces (62), and does not invalidate our a priori model's general agreement with the SFA data.

The ensemble capture distances (D_B) measured with the SFA were found to agree with our model's predictions, as shown in Table 4. Within experimental error, the ensemble capture distances were also identical to the predicted binding ranges of individual tethers (l_B). However, comparing the predicted capture distances to the predicted binding ranges shows that the two are not numerically equivalent. That is, l_B is a property of a single tether—the inflection point in Fig. 2—whereas D_B is a property of an ensemble and of the measuring method. In fact, using our numerics we estimate the total fraction of bound chains required to pull these surfaces in these experiments together as 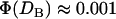(T. L. Kuhl, S. Zalipsky, and J. Y. Wong, unpublished data). In contrast, l_B is defined by 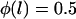. Although the two quantities are not strictly synonymous, our numerical model predicts that D_B is a reasonable estimate of l_B when l_B is discrete (viz. when 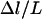is small), and that the same capture distances would be measured for a broad range of cantilever spring constants (1–100 mN/m) and interaction radii (1 μm–10 cm). Consequently, the SFA measurements provide direct evidence of tethers exhibiting discrete binding ranges.

TABLE 4.

Measured and predicted ensemble capture distances and predicted single-tether binding ranges for PEG tethers of different lengths

	Ensemble capture distance (DB)		Single-tether binding range (lB)
Tether	Measured*	Predicted†	Predicted‡
PEG2000	129 ± 10	127	122
PEG3300	176 ± 20	187	181
PEG6260	275 ± 25	294	284

Ligand-receptor was biotin-streptavidin (W = 35 k_BT). The ensemble capture distance is the farthest range at which two surfaces are observed to experience bridging, and hence depends on the measurement method. In contrast, the theoretical binding range of single tethers depends only on the properties of the tether and ligand/receptor.

^*With SFA as reported elsewhere (16).

^†From solving with the independent numerical solution (Eq. 16) (60).

^‡From Eq. 1; i.e., inflection points in Fig. 2.

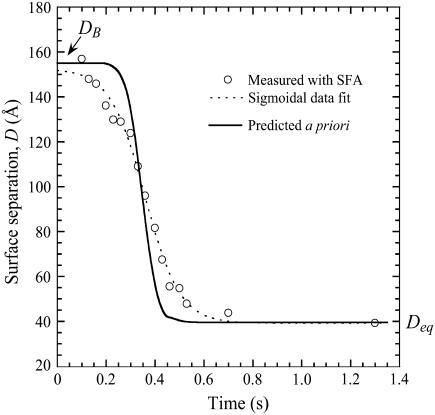
As a third verification, we report the dynamic approach of two surfaces identical to those shown in Fig. 3 B. The results are shown in Fig. 4 along with the prediction based on the dynamic model (Eq. 13). Again, the model's prediction is an a priori estimate, not a data fit. With this view, we find the agreement to be excellent. As predicted by Eq. 13, the surface separation varies sigmoidally with time. By fitting the data to a three-parameter logistical model, we measure τ_adhesion = 0.88 ± 0.06 s, in reasonable agreement with the predicted τ_adhesion = 0.3 s. It was also found numerically that moving the hydrodynamic slip plane to be coincident with the tether's equilibrium extension (SP = l_eq) increased the adhesive timescale by <5% compared to when SP = 0. Thus, although the value of the slip plane affects the equilibrium resting position (D_eq), it should have little effect on the adhesion dynamics in these scenarios.

FIGURE 4.

Dynamic approach of surfaces bound by PEG₂₀₀₀ tethers. The ligand and receptor were biotin and streptavidin (W = 35 k_BT). Measurements with SFA (circles) follow the prediction of Eq. 13 (solid line). Fitting the measured data to a three-parameter logistic model (dashed line) (96) calculates the measured τ_adhesion = 0.88 ± 0.06 s, in reasonable agreement with the a priori model's predicted τ_adhesion = 0.30 s.

Scaling behavior of the bridging force

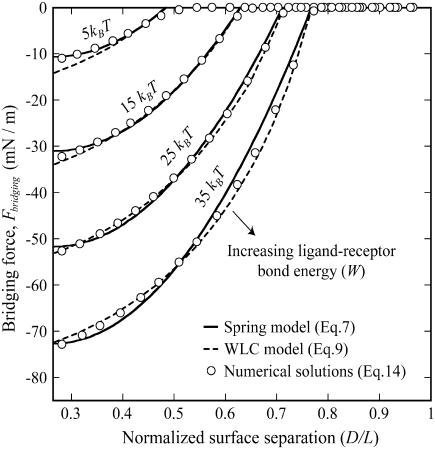
Fig. 5 demonstrates a calculation of the bridging force for PEG₂₀₀₀ tethers. Plotted are both the full numerical solution (Eq. 16) and the two analytical solutions (spring model, Eq. 7; WLC model, Eq. 9). The spring model was fit to the numerical solution by varying only the PEG tether's effective spring constant, k. Reasonable agreement was found for k = 2.6 ± 0.6 mN/m, which is in reasonable agreement with the 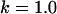mN/m predicted for PEG₂₀₀₀ chains. For high ligand-receptor bond energies (here W ≥ 15 k_BT), the WLC model gives better overall agreement. The latter yields a persistence length of l_P = 5.71 ± 0.01 Å, just longer than the 3.5 Å mer length, and close to the l_P = 4.75 Å determined from fitting Monte Carlo data reported elsewhere for single chains (16). In addition, bridging forces predicted by the numerical solutions scale linearly with the interaction radius, R, as predicted by Eqs. 7 and 9.

FIGURE 5.

Maximum bridging force between approaching surfaces decorated with ligated PEG₂₀₀₀ as a function of the surface separation (normalized as D/L over the range l_eq < D < L, where l_eq is the tether's equilibrium extension and L is the tether's contour length). Ligand-receptor bond energies were (left to right) 5, 15, 25, and 35 k_BT, as marked. The spring model (Eq. 7, solid lines) was fit to exact numerical solutions (Eq. 16, circles) by varying only the tether spring constant, k. Best agreement was found for k = 2.6 ± 0.6 mN/m. For W ≥ 15 k_BT, better agreement was achieved by modeling PEG tethers as worm-like chains (Eq. 9, dashed lines), giving a persistence length of 5.71 ± 0.01 Å. All solutions converge to zero near the critical binding ranges (left to right, l_B = 77, 100, 113, and 122 Å), and reach maximum force at D ≤ l_eq (far left). There the bridging force increases linearly with W, as predicted by the spring model.

Differences in these force profiles stem from differences in mathematical form. For example, the analytical solutions assume that no tethers bind beyond 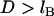(cf. Fig. 2); thus, both slightly underestimate the bridging force at these long extensions. For smaller distances (i.e., D ≈ l_eq), the poorer agreement of the WLC model to the numerical solution with lower bond energies (i.e., W = 5 k_BT) partly arises from assuming all tethers bind in the direction of the surface normal (Appendix A), and it is perhaps an empirical coincidence that the spring model is less sensitive to this simplification, giving differences that are ≤6%. The numerical solutions correctly converge to zero force as 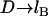, reflecting the distance at which most receptors are beyond the stable binding range of tethers, as predicted by Eqs. 7 and 14. Both the spring model and the numerical solutions reach maximum force at 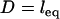, where as predicted the bridging force increases linearly with increased ligand-receptor bond energy, W (R² = 0.9998; note even spacing of vertical intercepts in Fig. 5). Qualitatively, this is because more tethers are able to form stable cross-bridges at larger gap heights near the edge of the interaction area.

It should be noted that the forces plotted in Fig. 5 represent the maximum bridging forces that may be achieved with these molecular architectures, as discussed previously. Kinetic constraints or the uprooting of lipid anchors may create binding probabilities for individual tethers that are functions of time, viz. 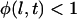for 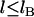, or that are more complicated functions of the tether extension than expressed by Eq. 1. Whereas these effects decrease the magnitude of the bridging force, they are not expected to change its scaling with respect to k, σ, or R, since Moreira et al. have shown that tethered ligands mounted to a movable surface still have discrete, albeit shortened, binding ranges (18,19). Likewise, the scaling of the adhesive timescale (Eq. 15) does not strictly require ligands and receptors to be in chemical equilibrium.

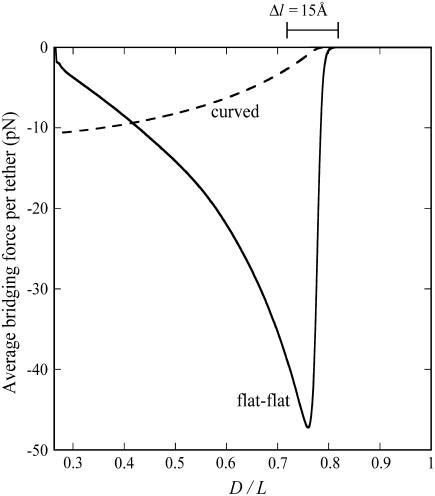
The force profiles shown in Fig. 5 are distinct from what would be observed between two plane-parallel surfaces. As a shortcut, it may be tempting to model the interface as two flat surfaces (hereon “flat-flat”) on the grounds that 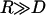in many applications, as discussed. However, at a flat-flat interface, all tethers would have equal probability of binding to receptors. Fig. 6 illustrates how this phenomenological difference creates a qualitatively different force-profile than our model for curved interfaces. As seen in Fig. 6, the bridging force between curved interfaces is zero near l_B and reaches a maximum force at D = l_eq. In contrast, the bridging force between flat-flat interfaces increases sharply at l_B, then vanishes as 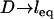. These results are normalized by the number of tethers in the interaction area; hence, they are independent of R. Thus, although correct to an order of magnitude, modeling a curved interface as flat-flat will produce significant error in estimating individual bond forces when ligands are tethered. This finding may be significant for those doing force spectroscopy or flow cytometry. Instead, Eqs. 7 and 9 provide simple yet accurate ways to predict equilibrium or maximum bridging forces while still accounting for the curvature of slowly adhering surfaces.

FIGURE 6.

Effect of surface curvature on the force between two surfaces bridged by tethered ligand-receptors. The tether is PEG₂₀₀₀ with streptavidin-biotin (W = 35 k_BT). The abscissa corresponds to 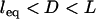. Shown is the average bridging force per tether calculated for two geometries: spherically curved interfaces (i.e., Fig. 1, or equivalently, sphere-flat or cross-cylinder geometries; dashed line) and a plane-parallel, or “flat-flat” interface (solid line). Both are normalized by the number of tethers and therefore are independent of the size of the interaction area (or of the interaction radius for curved interfaces). The presence or absence of curvature at the interface creates phenomenologically different force profiles; i.e., curved interfaces have a bridging force that increases as 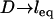and decreases as 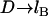(center of bracket), whereas the reverse is true for plane-parallel interfaces.

The model as a predictive tool for drug targeting

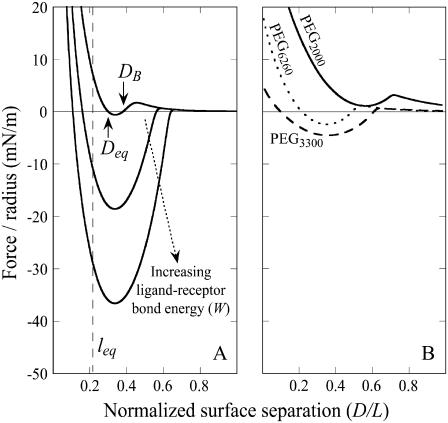
We briefly demonstrate how the analytical solutions we have derived can be used to estimate the adhesive properties of targeted liposomes. Fig. 7 A shows the expected force profile for a “typical” liposome targeted with PEG₂₀₀₀ tethers (1) (parameters in Table 3). As shown in Fig. 7 A, a strong adhesion can be transformed into what is nearly a net repulsion by reducing the ligand-receptor bond energy (W) by <1 order of magnitude. Also, the capture distance (D_B) decreases with W. As before, these forces represent the maximum adhesive forces expected. Anchor removal or impedance from glycocalyx or other membrane-bound molecules may reduce the attractive forces significantly.

FIGURE 7.

Examples of tuning the interaction profile to optimize adhesion for drug targeting or nanoassembly. (A) Choosing ligand-receptors with different bond energies (top to bottom: W = 5, 15, and 25 k_BT). Tethers are PEG₂₀₀₀; all other parameters are from Table 3. Increased bond energy increases the maximum number of bound tethers and hence the net adhesion. Too small of a W will result in an insufficient number of bonds to counteract the repulsive steric and electrostatic forces also present in adhesion. (B) Parameters chosen to simulate folate targeting for a STEALTH liposome. Choosing different lengths for the PEG tether suggests the existence of an optimum tether length for producing the strongest adhesion.

Fig. 7 B shows the predicted interaction profile for a folate-targeted liposome. The folic acid-folate receptor bond energy was fixed at W = 25 k_BT (Table 1), whereas the PEG tether length was varied. Grafting densities were 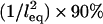to model PEG chains in the slightly overlapping brush regime, which has been shown to be important in minimizing nonspecific adhesion between liposomes and extracellular components (1). The characteristic surface density of folate receptors (2 × 10¹⁶ sites/m²) (67) was on the same order but always less than the density of ligands; thus, this number was used to calculate the number of cross-bridges formed. As before, these are a priori estimates of the maximum adhesive force between such particles. Fig. 7 B suggests there may be an optimum tether length that capitalizes on the synergy between maximizing bond formation and minimizing steric repulsion. Perhaps not coincidentally, the strongest adhesion shown in Fig. 7 B occurs when the PEG tether has a molecular weight of 3400—the same tether some recommend for folate targeting in vitro (48,61).

CONCLUSIONS

We have shown that tethers of practical interest in drug targeting and other biophysical research exhibit a critical binding range. This observation has allowed us to develop analytical predictions for the range, strength, and rate of adhesion between single tethered ligand-receptors and between surfaces they decorate. These metrics were accurately predicted in comparison to measurements made with SFA and with independent numerical predictions. These relations should be useful for optimizing adhesion in drug targeting, biosensing, and nanoassembly, as well as for providing insight into bridging forces involved in biological adhesion.

APPENDIX A: BRIDGING ANGLE INCONSEQUENTIAL TO NORMAL FORCE

Cross-bridges formed at angles away from the surface normal are more highly stretched than bridges formed to a receptor that is directly above the tether's anchor point. Because tethers that are more highly stretched tend to form bonds less frequently, the angle (θ) at which a tether binds affects not only the force that the bond exerts in the normal direction but also the probability of attachment. To correct for these effects, we derive a continuum expression for the angle operator 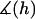in Eq. 16.

If an individual spring-like tether has a contour length, L, much smaller than the particle radius (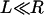), then the gap height, h, will appear constant within each tether's vicinity. A tether can form bonds at an arbitrary angle 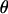away from the surface normal by stretching a distance 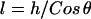. Upon forming a cross-bridge, the normal component of the bridging force is

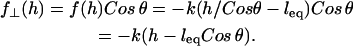(19)

When 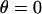, , 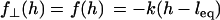which is what we would calculate if we ignored angling effects. By comparing these two quantities, we can estimate the angle operator as

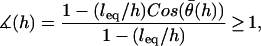(20)

where 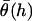is the average angle that tethers bind for a given gap height, h. The angle operator 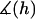is essentially a correction factor to the integrand in Eq. 16. We compute the average binding angle using Boltzmann statistics, viz.

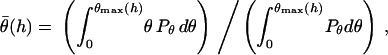(21)

where 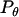is the probability of bond formation at a given angle and 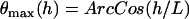is the maximum angle at which bridging can occur. An analytical solution for Eq. 21 exists for tethers with a discrete binding range. A critical binding range (l_B) will correspond to a critical angle (θ_B) beyond which no binding occurs. The average binding angle then approaches

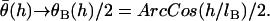(22)

For the ensemble, the error in ignoring angling effects is greatest when the surfaces are in contact (F_bridging underestimated by ∼15% for R ≥ 10 L and ∼25% for R = L.). This error reduces to zero when the surfaces are far apart. This behavior can be explained by noting that when the surface separation is near the binding range (D ≈ l_B), only highly stretched tethers can bind. There 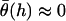and hence 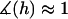(Eq. 20). At closer distances, the error is still small because most of the tethers that are bound are away from the interaction center. It is these highly stretched tethers, which are more numerous, that constitute the bulk of the bridging force (37). Further, anchor diffusion tends to alleviate stresses on cross-bridges by moving anchors nearer receptors (25). Overall, the total bridging force normal to particle interfaces has little dependence on the angles at which tethers bind to receptor surfaces.

APPENDIX B: EXACT ANALYTICAL SOLUTION FOR THE BRIDGING FORCE VALIDATES SCALING BEHAVIOR

To validate the scaling behavior of the bridging force between tethered ligand-receptor architectures (Eq. 7), we have derived an analytical solution for the bridging force (Eq. 16) without using the Derjaguin approximation. As before, we set 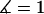, , 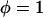and σ constant in the range 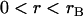, where r_B corresponds to 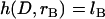. Then Eq. 16 simplifies to

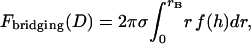(23)

where the gap height, h, is given by Eq. 17. Then for harmonic tethers, Eq. 23 has the exact solution:

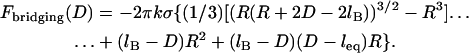(24)

Contrary to how it looks, Eq. 24 is remarkably linear with respect to R over a tremendous range of R values. When 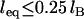, Eq. 24 is linear in R over the range 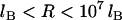. And when 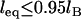, Eq. 24 is linear in R over the range 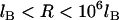. In these regimes, this exact solution is numerically equivalent to the expression for the bridging force for spring-like tethers derived using the Derjaguin approximation (Eq. 7) and exhibits the same scaling behavior.