Climate variability has a stabilizing effect on the coexistence of prairie grasses

Abstract

How expected increases in climate variability will affect species diversity depends on the role of such variability in regulating the coexistence of competing species. Despite theory linking temporal environmental fluctuations with the maintenance of diversity, the importance of climate variability for stabilizing coexistence remains unknown because of a lack of appropriate long-term observations. Here, we analyze three decades of demographic data from a Kansas prairie to demonstrate that interannual climate variability promotes the coexistence of three common grass species. Specifically, we show that (i) the dynamics of the three species satisfy all requirements of “storage effect” theory based on recruitment variability with overlapping generations, (ii) climate variables are correlated with interannual variation in species performance, and (iii) temporal variability increases low-density growth rates, buffering these species against competitive exclusion. Given that environmental fluctuations are ubiquitous in natural systems, our results suggest that coexistence based on the storage effect may be underappreciated and could provide an important alternative to recent neutral theories of diversity. Field evidence for positive effects of variability on coexistence also emphasizes the need to consider changes in both climate means and variances when forecasting the effects of global change on species diversity.

Strong climate variability characterizes ecosystems worldwide, and in many regions this variability is predicted to increase over the next century because of higher frequencies of severe storms and droughts (1, 2). The ecological impacts of increased climate variability are poorly understood (3), especially in comparison with threats posed by increasing mean temperatures (4, 5). This gap in empirical research contrasts sharply with a considerable body of theory examining the effects of environmental fluctuations on the maintenance of species diversity (6–9).

“Storage effect” theory derives the conditions under which climate variability will have stabilizing or destabilizing effects on species coexistence (10). The temporal storage effect described in refs. 6 and 9 requires that three conditions be met. To satisfy condition 1, species must have long lifespans to buffer their populations against unfavorable years. For condition 2, species must differ in their response to climate variation. These species-specific responses to climate cause each species to experience relatively more intraspecific competition during its favorable years and more interspecific competition during its unfavorable years. Condition 3 requires that the effect of competition on each species must be more severe in years favorable for that species than in unfavorable years. When condition 2 is present, intraspecific competition will be more severe than interspecific competition. As a result, climate variability gives species an advantage when they become rare—the signature of stabilizing coexistence mechanisms. The size of this advantage when a species is rare (i.e., the strength of the storage effect) can be quantified by comparing species’ average low-density growth rates in variable vs. constant environments, in the presence of competitors (11, 12). If any of the three conditions does not hold, climate variability can have neutral or negative effects on coexistence.

Despite this well-developed theory and its relevance to climate change questions, the importance of climate variability for maintaining species diversity in natural ecosystems remains unknown. In large part, this uncertainty reflects the scarcity of long-term datasets suitable for testing the prerequisites of the storage effect. Existing empirical studies typically document species-specific responses to the environment for taxa with long-lived life stages, showing the potential for the storage effect to operate (12–16). However, to take the next step and prove that the storage effect is actually helping to stabilize coexistence, evidence for the first two conditions must be combined with the critical third condition: more severe competition in favorable years. In addition, understanding the importance of climate variability in maintaining diversity requires an estimate of the strength of the storage effect relative to other coexistence mechanisms. Better quantifying the strength of stabilizing mechanisms in nature is critical for the evaluation of recent neutral theories of biodiversity, which ignore stabilizing processes altogether (17, 18).

A remarkable dataset from grasslands in western Kansas gave us the opportunity to test all theoretical conditions of the storage effect and quantify its strength. For more than 30 years, starting in the 1930s, all individual plants in permanent quadrats were mapped each year (19). This spatially explicit time-series permits analyses of demographic performance and competitive interactions across three decades of climate variation, including two severe droughts, precisely the information required to quantify the storage effect. Furthermore, because variation in precipitation influences primary production, species composition, and richness in arid to subhumid plant communities, the mixed-grass prairie at the Kansas study site may be particularly sensitive to future increases in precipitation variability (20, 21).

Here, we use the Kansas dataset to (i) test all three theoretical conditions of the storage effect, (ii) evaluate whether climate explains interannual variation in plant performance, and (iii) quantify the strength of the storage effect in stabilizing coexistence. We analyzed the population dynamics of three dominant perennial grasses (Bouteloua curtipendula, Bouteloua hirsuta, and Schizachyrium scoparium) that together comprised >95% of basal vegetative cover on our focal quadrats (Fig. 1). To test the first condition of the storage effect, long-lived life stages, we measured the lifespans of individual plants. We tested conditions 2 and 3 of the storage effect by estimating population growth rates for each species in different years and under varying degrees of competition. These growth rates were projections from a statistical analysis of species-specific survival and colonization, as mediated by neighborhood competition, for each year of the dataset. To assess condition 2, species-specific responses to interannual variation, we compared yearly intrinsic growth rates across species. To test condition 3, more severe competition in high-quality years, we compared the effect of crowding on growth rates in different years. We also used the species-specific estimates of survival and colonization to project low-density growth rates in variable vs. constant environments, quantifying the strength of the storage effect.

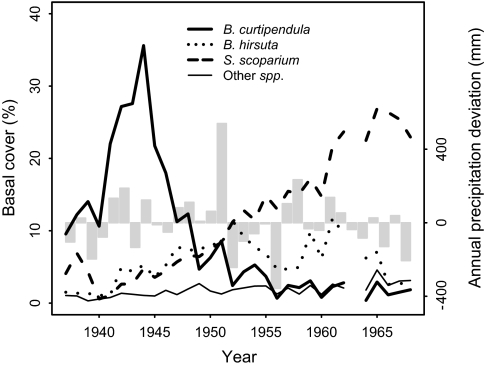
Fig. 1.

Observed basal cover of the little bluestem community at Hays, Kansas, 1937–1968. Shown are means for the perennial grasses B. curtipendula, B. hirsuta, and S. scoparium, along with other species from a group of four 1-m² quadrats located on shallow limestone soils within a livestock exclosure. Abundances were low early in the time series because of the Great Drought of the 1930s. The three focal grasses continue to co-occur in the permanent quadrats, with S. scoparium still the most abundant (P.B.A., unpublished data). The vertical bars show deviation from the mean annual precipitation of 580 mm. This period includes both the wettest water year on record at Hays (1,122 mm in 1951) and the driest (226 mm in 1956).

Results

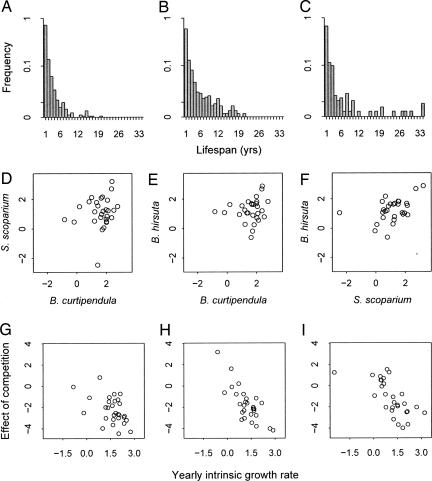
We found strong evidence for long lifespans, the first condition of the storage effect. By tracking individuals across years on the basis of their spatial locations, we found that 27%, 32%, and 40% of B. curtipendula, B. hirsuta, and S. scoparium genets, respectively, lived three or more years. The maximum observed lifespans for these three species were 20, 21, and 34 years, respectively (Fig. 2 A–C).

Fig. 2.

Evidence for the three conditions of the storage effect. (A–C) B. curtipendula (A), B. hirsuta (B), and S. scoparium (C) have the potential for long lifespans, buffering population growth as required by condition 1. (D–F) Comparisons of exponential yearly intrinsic growth rates for each pair of the three species in each of 29 years show considerable scatter (ρ = 0.17, 0.17, and 0.44, respectively), evidence that the species differ in their response to interannual variability (condition 2). (G–I) For B. curtipendula (ρ = −0.49, P = 0.009) (G), B. hirsuta (ρ = –0.78, P < 0.0001) (H), and S. scoparium (ρ = –0.67, P < 0.001) (I), competition had stronger negative effects on growth in years of high intrinsic growth rates (more favorable years), satisfying condition 3. Positive values, indicating that crowding caused relative increases in growth rates, occurred in years of low intrinsic growth rates.

We tested for condition 2 of the storage effect, species-specific responses to climate, by using our statistical model to project the low-density growth rate of each species, in each year, in the absence of competitors. These yearly intrinsic growth rates were weakly correlated for each pair of species (Fig. 2 D–F), but the considerable scatter suggests that the species respond differently to environmental variation. In fact, seasonal temperature and precipitation data explained a considerable portion of the variation in the yearly intrinsic growth rates (Table 1). Stepwise multiple regression selected five climate variables that explained 71% of variation in B. curtipendula’s growth rates. For B. hirsuta, seven variables explained 49% of variation. Climate variables explained only 17% of variation in S. scoparium’s yearly intrinsic growth rates (F = 1.19, df = 4, 24; P = 0.34); however, after removing one outlier (a value more than three standard deviations below S. scoparium’s mean maximum growth rate), a model with six climate variables explained 43% of variation in plant performance (Table 1). Although spring and summer precipitation had consistently positive effects on all three species, the lag effect of previous-year precipitation was negative for B. curtipendula but positive for B. hirsuta and S. scoparium. Similarly, mean annual temperature had a positive effect on B. curtipendula but a negative effect on the other two species. In contrast, fall precipitation had a positive effect on the two Bouteloua species but no effect on S. scoparium. The significant and contrasting climate correlations indicate real differences in species’ responses, satisfying condition 2 of the storage effect.

Table 1.

Correlations between climate and estimated yearly intrinsic growth rates for the three grass species studied

Coefficient	Estimate	SE	t	P
B. curtipendula*
(Intercept)	–5.644	1.624	–3.48	0.0020
PPTOct–Dec	0.006	0.003	2.02	0.0556
PPTApr–Jun	0.003	0.001	3.48	0.0020
PPTJul–Sep	0.005	0.001	4.16	0.0004
Lag 1 PPTApr–Sep	–0.001	0.001	–1.68	0.1075
Mean temperatureannual	0.448	0.110	4.07	0.0005
B. hirsuta†
(Intercept)	–4.300	4.571	–0.94	0.3573
PPTOct–Dec	0.0091	0.0047	1.93	0.0678
PPTApr–Jun	0.0081	0.0034	2.37	0.0274
PPTJul–Sep	0.0114	0.0036	3.13	0.0051
Lag 1 PPTApr–Sep	0.0060	0.0027	2.24	0.0358
Mean temperatureApr–Sep	0.3986	0.2534	1.57	0.1306
Mean temperatureannual	–0.5907	0.2337	–2.53	0.0196
PPTannual lag 1 PPTApr–Sep	–0.000013	0.000005	–2.53	0.0194
S. scoparium‡
(Intercept)	–7.08	4.5200	–1.57	0.1307
PPTApr–Jun	0.0084	0.0033	2.518	0.0200
PPTJul–Sep	0.0112	0.0031	3.603	0.0017
Lag 1 PPTApr–Sep	0.0062	0.0025	2.513	0.0202
Mean temperatureApr–Sep	0.4815	0.2651	1.82	0.0836
Mean temperatureannual	–0.4665	0.2461	–1.90	0.0719
PPTannual lag 1 PPTApr–Sep	–0.00001	0.000004	–2.84	0.0098

Variables were selected by using stepwise regression based on Akaike’s information criterion. PPT, precipitation. Approximately 75% of annual precipitation falls during the April–September growing season. Lag 1, conditions in the previous year.

*R² = 0.71; F = 11.32, df = 5, 23; P < 0.0001.

^†R² = 0.49; F = 2.861, df = 7, 21; P < 0.029.

^‡R² = 0.43; F = 2.66, df = 6, 21; P < 0.044.

Finally, we found evidence for the third condition of the storage effect: more severe effects of competition in more favorable years. For each species, projections of population growth rates across a gradient of crowding showed that neighbors limited growth in favorable years but had weak or even facilitative effects in unfavorable years (Fig. 2 G–I).

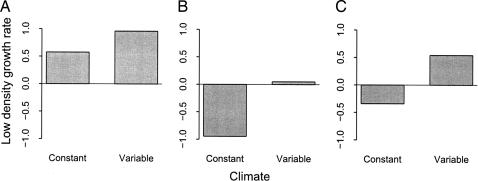
To quantify the strength of the storage effect, we compared species’ simulated average low-density growth rates, in the presence of competitors near their equilibrium abundances, in a variable vs. a constant environment. All three species had much higher long-term average growth rates when rare under the variable environment than under constant mean conditions (Fig. 3 A–C). B. curtipendula’s growth rate was twice as high in the variable environment. Differences in growth rates were even larger for B. hirsuta and S. scoparium, which both had negative growth rates in a constant environment but positive growth rates in a variable one.

Fig. 3.

Estimated long-term low-density growth rates in constant and variable environments. The potential for each species [B. curtipendula (A), B. hirsuta (B), and S. scoparium (C)] to invade a resident community, measured by the species’ long-term low-density exponential growth rate, was much higher in simulations incorporating observed interannual variability in survival and colonization than in simulations based on constant mean survival and colonization.

Discussion

Our results demonstrate that climate variability can play an important role in promoting coexistence. Relative to a constant environment, climate variability greatly increased the ability of all three grass species to recover from low densities. B. curtipendula maintained a positive low-density growth rate in the absence of variability, suggesting that the storage effect is not necessary for its persistence. For this species, climate variability may just provide additional insurance against competitive exclusion. In contrast, the switch from negative growth rates in a constant environment to positive growth rates in a variable environment for B. hirsuta and S. scoparium implies that variability is essential for their long-term persistence.

The dynamics of the three perennial grasses we studied satisfied all of the theoretical prerequisites of the storage effect. We can thus identify the storage effect as the mechanism underlying the stabilizing effects of variability. Like other classical explanations for the maintenance of diversity, the storage effect relies on tradeoffs in species’ responses to a heterogeneous environment. In contrast, recent neutral theories of community structure exclude all stabilizing coexistence mechanisms (17, 18). According to this perspective, species are so similar in their average fitness that competitive exclusion is extremely slow, allowing species to coexist for long periods of time. A primary justification for neutral theory is the relatively scarce empirical evidence for strong stabilizing processes in natural systems (22–25). We suggest that this poor empirical support results not from weaknesses of coexistence theory but rather from a lack of appropriate data and rigorous quantitative analysis. Such analyses will be essential for understanding the relative importance of stabilizing and neutral processes in natural communities.

Storage effect theory is often applied to seed-banking of annual plants, in which species-specific germination cues generate large fluctuations in density in different years. These fluctuations in density can satisfy the second and third conditions of the storage effect, even assuming competitive equivalence among species (7–9). In our model of perennial plants, by contrast, interannual variability in competitive interactions, not fluctuations in abundance, produce the stabilizing effects of variability. Our results illustrate how different components of population dynamics can satisfy the three conditions of the storage effect and also suggest that it can operate in a wider variety of systems than previously thought.

A strong storage effect cannot exist without interannual variability in plant performance. Our analysis indicates that climate played an important role in driving this interannual variability, as shown by significant correlations between yearly intrinsic growth rates and interannual variation in climate. The correlations identified fall precipitation, lagged effects of growing season precipitation, and mean annual temperature as the climate variables that allow for differentiation in species performance.

Could future increases in the variability of these climate drivers lead to stronger stabilizing effects? If so, such effects might partially offset the potentially negative impacts of shifts in climate means. However, this scenario depends on a number of factors. First, past conditions must be representative of future climate. If the observed time-series spans the range of climatic conditions this system will experience in the future, our inference will be stronger than if the future brings more extreme years or extremely long runs of particular kinds of years. Second, our model does not consider effects of changes in species composition, such as the arrival of new competitors, which may affect the relationship between climate and competition. Finally, interactions among climate variables could influence their net effect. Despite these uncertainties, our analysis demonstrates that forecasting future species diversity will require consideration of changes in both climate means and variances.

Materials and Methods

Dataset Description.

Albertson et al. (19, 26) established permanent quadrats in livestock exclosures located in mixed-grass prairie near Hays, Kansas (38.8°N, 99.3°W), where mean annual precipitation is 580 mm, with 75% falling during spring and summer, and mean annual temperature is 12°C. Beginning in the 1930s and ending in 1972, basal cover of all plants in the 1-m² quadrats was mapped at the end of each growing season by using the pantograph technique (27). The original maps were digitized and stored in a geographical information system, with each individual plant represented by a polygon (data and metadata are available at http://knb.ecoinformatics.org/index.jsp).

Storage Effect Condition 1.

We tested for condition 1 of the storage effect, a long-lived life stage, by estimating the longevity of individual genets. We first assigned a unique identification number to each plant (an individual polygon in the geographical information system) present in the first year of data. Plants present in year 2 that overlapped in area with a conspecific from year 1 were then coded as the same genet. If a plant overlapped with multiple “parents,” we assigned it the identification number of the parent that provided the greatest area of overlap. After repeating this process through all years of the dataset, we counted the number of years that each genet survived. These lifespans are conservative because they may be truncated by the beginning or end of the time-series, and because individuals that merged with larger plants were assumed to have died.

Storage Effect Conditions 2 and 3.

To test for storage effect conditions 2 (species-specific responses to climate) and 3 (climate–competition interaction), we first parameterized a statistical model describing plant performance and competitive interactions in each year of the Kansas dataset and then used this model to simulate the performance of each species, as mediated by competition, in different years.

We took a lattice-based approach, transforming the mapped data into grids of 2 × 2-cm cells in which each cell is occupied by one species or bare ground. The statistical model predicts the year-to-year transitions in the states of these cells. These transitions depend on both survival (of occupied cells) and colonization. The central assumption of the model is that cell transitions depend only on the previous state of each cell and the composition of its local neighborhood (28, 29). To limit edge effects, we discarded all focal cells within 10 cm of the quadrat border.

Survival (S) of species i in cell j from time t − 1 to time t is related to the composition of the focal cell’s neighborhood (N) through a logistic regression:

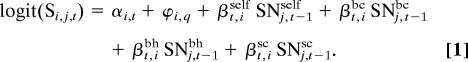The parameter α_i,t is the probability of survival for species i in year t in the absence of any neighboring plants. This intercept is modified by species-specific quadrat effects, ϕ_i,q, that are constant over time but depend on the quadrat (q) in which the cell is located. The β_t,is describe the influence of neighboring plants on the survival of each focal species (i) in each year (t). These regression coefficients are multiplied by the weighted abundances in the local survival neighborhood of SN^self (cells belonging to the same individual plant as the focal cell), SN^bc (cells belonging to nonself plants of B. curtipendula), SN^bh (nonself B. hirsuta), and SN^sc (nonself S. scoparium). We distinguish between cells belonging to the focal plant and conspecific cells belonging to another plant to separate within- and between-plant intraspecific effects on survival.

We defined neighborhoods to include all cells within a 10-cm radius of the focal cell. Because plants close to the focal cell are likely to influence transitions more than will plants far away, we calculated distance-weighted abundances for each species on the basis of a negative exponential function. The value of the exponent was determined through model-fitting (Fig. 4, which is published as supporting information on the PNAS web site).

Colonization (C) of any species i in cell j from time t − 1 to time t is similarly related to the composition of the focal cell’s neighborhood:

δ is the probability of colonization in the absence of any neighboring plants, modified by the quadrat effects, θ. The λs describe the influence of neighboring plants on colonization. For the colonization neighborhoods (CNs), we make no distinction between self and nonself plants, inasmuch as all conspecifics are potential sources of colonists through sexual reproduction or, as is more likely in these grasslands, vegetative growth.

Once we have calculated each species’ probability of survival and colonization in a given cell, we can calculate the overall probability of cell occupancy by each species or bare ground (Table 2, which is published as supporting information on the PNAS web site). For example, the probability that a cell occupied by B. hirsuta will remain occupied in the next time step is equal to the probability that B. hirsuta survives, plus the probability that B. hirsuta dies and then recolonizes the cell.

We parameterized the year- and species-specific survival and colonization functions (Eqs. 1 and 2) by using a hierarchical Bayesian approach and Markov Chain Monte Carlo (MCMC). MCMC sequences converged on the model parameters, minimizing deviations between the predicted probabilities of cell occupancy and the observed states of the cells in each year (see Supporting Methods, Supporting Code, and Fig. 5, which are published as supporting information on the PNAS web site). This approach accommodated the nonlinear model structure and allowed us to estimate both year-specific and average values of the parameters by setting year as a random effect. More formally, the year-specific parameters, which determine survival and colonization for each year of the time series, are random draws from underlying normal distributions that represent the average across-year values of these parameters.

The survival and colonization parameters permit projections of short-term population growth rates from any initial condition, regardless of observed mean abundances. In other words, even if the mean abundance of B. curtipendula was high in 1940, we can extract information about its low-density growth rate from local patches where it was rare. Thus we can initialize a lattice containing any desired abundances of the three species in the model and then use the regression parameters to predict each species’ probability of occurrence in each cell of the lattice at the next time step. The expected abundance of this species in the next time step is the lattice-wide average of its probability of occurrence. Its exponential growth rate is its log expected abundance in the next time step minus its log initial abundance. For all estimations of growth rates described below, we averaged across the spatial variability represented by quadrats by using the mean of the quadrat effects, weighted by the inverse of their standard deviations. In all simulations we used a toroidal lattice to remove edge effects.

To test condition 2 of the storage effect, we estimated the intrinsic growth rate of each species in each year. We initialized lattices with one 10-cm-diameter plant of the focal species in the center of the grid and bare ground everywhere else. We then applied the survival and colonization regressions, choosing parameters for a specific year, to predict the expected abundance of the species at the next time step. Note that we set the probability of colonization of other species to zero, preventing any interspecific competition. Because the initial conditions in these projections were constant, the only source of stochasticity comes from uncertainty associated with the regression parameters. We represented this uncertainty by saving all parameter values from 2,000 iterations of MCMC sequences after convergence was reached. For each simulation of intrinsic growth rate, we used the parameters from one randomly selected MCMC iteration, thus preserving correlations among parameters. We repeated this simulation 250 times for each species in each year. The mean of these realizations is the yearly intrinsic growth rate.

We used similar projections to estimate the effect of competition on growth, the key to the third condition of the storage effect. We created 500 initial lattices, representing a range of total basal cover from 0.5% to 45%. We assigned relative abundances to the three species and bare ground by drawing four random numbers from a uniform distribution and standardizing them to sum to 1. We then applied a set of year-specific regression parameters (drawn directly from the MCMC sequence) to each of these grids to estimate the expected abundances of each species in the next time step, from which we then calculated their realized growth rates. For each year, the effect of competition on a target species’ growth was measured by the relationship between the total cover of the initial grid (higher cover implying greater intra- and interspecific competition) and the target species’ realized growth rate. After a square-root transformation of total cover, we fit a linear regression, the slope of which indicates how combined intra- and interspecific competition (or crowding) affected the target species’ realized growth rate. For each species, we tested for condition 3 by correlating yearly variation in this index of competition with interannual variation in intrinsic growth rates (see condition 2).

To create initial conditions with realistic spatial structure for testing condition 3, we used sequential indicator simulation (30, 31). Indicator simulation is based on a recursive application of indicator kriging, which requires an indicator variogram model for each species; this model is linked to spatial transition probabilities for that species (31). To estimate these variogram functions, we first computed indicator variograms of observed presence/absence data for each species, in each quadrat, in each year. We then inferred the nugget, range, and sill of each variogram model by using a spherical function (32). The relationships between the variogram model parameters and abundance were well described by quadratic functions. To initialize a simulation grid, we first specified cover for each species, then calculated variogram model parameters from the quadratic functions, and finally, used these parameters within indicator simulation and assigned states to all cells in the grid. Maps generated by sequential indicator simulation reproduce (within statistical fluctuations) the specified cover and variogram model for each species (29) and thus constitute realistic initial conditions.

Climate Correlations.

After estimating the yearly intrinsic growth rates, we tested for relationships with interannual variation in climate variables by using multiple linear regressions with stepwise (backward and forward) variable selection based on the Akaike information criterion. The climate variables were precipitation in fall, winter, spring, and summer of the current climate year (September through August); growing season precipitation (spring plus summer) of the previous year; the interaction between total current-year precipitation and the previous year’s growing season precipitation; the coefficient of variation of monthly precipitation in the current growing season; growing season and annual mean temperature of the current year; and the Palmer Drought Severity Index.

Strength of the Storage Effect.

Stable coexistence requires that each species must be able to invade a community composed of its competitors. To test the strength of the storage effect, we therefore compared species’ average low-density growth rates, in the presence of competitors, in a variable vs. a constant environment (11). If the storage effect is stabilizing coexistence, all species should have higher low-density growth rates in the variable compared with the constant environment, meaning that variability increases their potential to increase from low abundance. The magnitude of this difference is the strength of the storage effect.

To estimate these low-density growth rates, we first determined the dynamic equilibrium of each pair of resident species, after removing the focal species, through simulation. In contrast to our projections of short-term population growth rates, in which we calculated expected probabilities at the next time step but did not update states of individual cells, these simulations required updating the state of each cell in the lattice. To maintain realistic spatial structure, we combined information from our survival and colonization regressions with indicator kriging-derived probabilities within sequential indicator simulation (33). At each time step, we chose one cell at random and updated its state based only on the probabilities predicted by the survival and colonization regressions. Once this cell is updated, its new state offers valuable information for updating nearby cells that are potentially part of the same individual plant. For example, depending on the indicator variogram functions, a nearby cell might have a higher probability of taking the same state. Thus, as more cells are assigned new states, we use information about spatial structure to modify the original regression-predicted probabilities for the cells remaining to be updated.

We initialized abundances of each pair of resident species at 10% cover, then conducted 20 runs of 60 time-steps each and used only the last 20 steps of each run to characterize equilibrium abundances. To simulate this equilibrium under a variable environment, at each time step we randomly chose a year and drew the corresponding parameters from the MCMC sequence. To simulate a constant environment, we used the mean regression parameters at every time-step, again drawing their values from the MCMC sequence at each time step.

We then ran a series of simulations quite similar to those used to determine intrinsic growth rates, except instead of initializing the focal species at low abundance in an empty grid, we initialized it at low abundance in a grid populated by the two resident competitors. The initial abundances of the two residents were drawn from their dynamic equilibrium in the appropriate environment type: variable or constant. Next, we used the regression parameters to estimate probabilities of occurrence for the focal species at the next time step and then calculated the species’ population growth rate. We repeated this procedure 500 times, randomly drawing a set of year-specific parameters for each replication of the variable-environment case, or always using the mean parameters for the constant-environment case. Finally, we compared the average exponential growth rate of the focal species with or without interannual variability. We focus on the average rates, not their distributions, because coexistence depends only on the mean value of the low-density growth rate (11).

Key Assumptions.

Our statistical model makes assumptions about the structure of biological processes (survival and colonization) driving changes in cover. To test whether these assumptions influenced our results, we repeated the entire analysis with a purely phenomenological, multinomial regression model. The results of this alternative analysis supported our original conclusions (see Supporting Appendix, which is published as supporting information on the PNAS web site).

Our simulations of growth rates also make an assumption about potential errors. First, we cannot distinguish real interannual variation in performance from noise created by measurement error and parameter uncertainty. Second, although the influence of fine-scale spatial heterogeneity is implicit in the survival and colonization parameters, our projections of growth rates assume a homogeneous environment at the m² scale. We assume that these sources of error have consistent effects in both constant and variable environments and will not bias this critical comparison. Finally, although relative nonlinearity is unlikely to play a strong role in multispecies systems (34), it could make some contribution to the occurrence of higher growth rates in variable than in constant environments.

Abbreviation

MCMC

Markov Chain Monte Carlo.