Quantification of protein half-lives in the budding yeast proteome

Abstract

A complete description of protein metabolism requires knowledge of the rates of protein production and destruction within cells. Using an epitope-tagged strain collection, we measured the half-life of >3,750 proteins in the yeast proteome after inhibition of translation. By integrating our data with previous measurements of protein and mRNA abundance and translation rate, we provide evidence that many proteins partition into one of two regimes for protein metabolism: one optimized for efficient production or a second optimized for regulatory efficiency. Incorporation of protein half-life information into a simple quantitative model for protein production improves our ability to predict steady-state protein abundance values. Analysis of a simple dynamic protein production model reveals a remarkable correlation between transcriptional regulation and protein half-life within some groups of coregulated genes, suggesting that cells coordinate these two processes to achieve uniform effects on protein abundances. Our experimental data and theoretical analysis underscore the importance of an integrative approach to the complex interplay between protein degradation, transcriptional regulation, and other determinants of protein metabolism.

The availability of whole-genome sequences and the advent of microarray technology have made global analyses of mRNA expression mainstream. However, most biological processes are mediated by proteins, which are subject to posttranscriptional regulation that is generally not observable at mRNA levels. A complete understanding of biological systems requires knowledge of protein properties, which is ultimately the goal of proteomics.

Despite tremendous technical advances and effort in proteomics, the chemical heterogeneity of proteins and the large dynamic range of protein abundance make it challenging to establish global proteomic assays. This obstacle has been circumvented in the yeast Saccharomyces cerevisiae with the availability of two collections of yeast strains expressing epitope-tagged fusion proteins, one by using the tandem affinity purification (TAP) tag and a second employing the GFP (1, 2). In an initial study, we analyzed the TAP-tagged strain collection by Western blotting to quantify steady-state levels of protein abundance in actively dividing yeast cells. These data augmented previous efforts to quantify protein abundance by using mass spectrometry and 2D gel electrophoresis and provided a more comprehensive estimate of protein levels in a eukaryotic cell (3, 4).

The availability of high-throughput protein abundance data has facilitated analysis of the relationship between protein abundance and mRNA levels. Although a statistically significant correlation is observed between these parameters, individual genes with similar mRNA levels can produce proteins with very different abundances. This complication makes it difficult to extrapolate from mRNA levels and microarray experiments to protein abundance. Three potential explanations have been proposed to account for the imperfect correlation between mRNA and protein levels: (i) translational regulation; (ii) measurement errors in the data sets; and (iii) differences in protein half-lives (5). Knowledge of protein half-lives is required to understand how mRNA abundances translate into steady-state protein levels.

We report a genomewide study in which we measured half-lives of the proteins in the yeast proteome. This study provides the final piece of information required for the generation of a quantitative model for protein metabolism. We have integrated data from large-scale measurements of mRNA levels, translation rates, protein abundances, and protein half-life measurements to reveal higher-order properties of protein metabolism. Our analysis of a simple dynamic model for protein production reveals a correlation between transcriptional regulation and protein half-life, providing evidence that cells coordinate these two processes to control protein abundance.

Results

Profiling Protein Half-Lives in the Yeast Proteome.

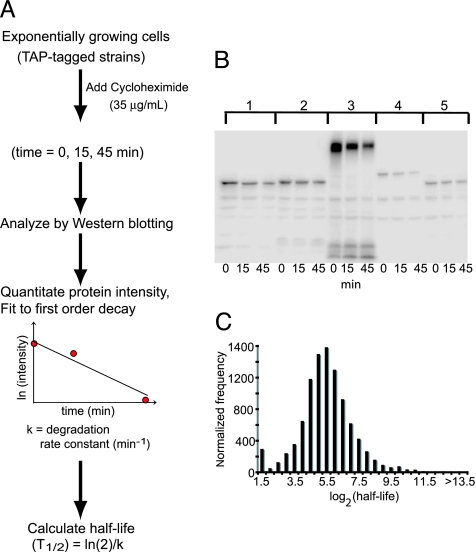
As a first step toward quantifying the influence of protein degradation on protein abundance, we measured the half-life of proteins in the yeast proteome. We started with a collection of ≈4,200 TAP-tagged strains for which a protein product was detected by Western blotting (1). This set includes proteins expressed in exponentially dividing cells grown in standard laboratory conditions. We do not visualize (and therefore cannot obtain half-life information for) proteins expressed in more specialized conditions (e.g., sporulation and alternative nutrient conditions). We monitored the abundance of each TAP-tagged protein by Western blot analysis of cell extracts as a function of time following inhibition of protein synthesis by cycloheximide (Fig. 1A and B).

Fig. 1.

Determination of protein half-life by using the TAP-tagged strains. (A) Schematic diagram of the translation shut-off assay used to determine the half-life of proteins in the yeast proteome. (B) The degradation rate constants of the TAP-tagged proteins were quantified by measuring the relative intensity of each protein by quantitative Western blotting at 0, 15, and 45 min after cycloheximide treatment. The intensity data were fit to a first-order decay function to estimate the degradation rate constant, which then was used to calculate a half-life. The Western blot shows degradation profiles for five representative TAP-tagged proteins. (C) Normalized distribution of the half-lives of the observed yeast proteins. The bins are log₂ increments with the upper boundary indicated.

We measured the half-life of 3,751 proteins and found the distribution of half-lives to be approximately log-normal, with a mean and median half-life of ≈43 min (Fig. 1C). The distribution deviates from log-normal in that we observe an unexpected number of very unstable proteins (161 proteins with a half-life of <4 min), consistent with the idea that degradation may determine the abundance of these proteins.

To estimate the repeatability of our measurements, we chose a random sample of 151 TAP-tagged proteins and independently measured their half-lives twice (Table 1, which is published as supporting information on the PNAS web site). We estimate that our half-life measurements are subject to a multiplicative error term (ε) with σ(ε) = 1.99 (Fig. 6, which is published as supporting information on the PNAS web site), indicating that our half-life measurements are accurate within a factor of 2. This measurement suggests that our data can be used for inferring the general trends in protein degradation when we analyze groups of proteins and focus on major differences between very stable and unstable proteins. It should be stressed, however, that because of the experimental errors in our data, caution should be exercised when interpreting individual measurements quantitatively. More experiments are required before the exact degradation kinetics of individual proteins can be assessed reliably.

One concern with our experimental design is that fusion of the TAP tag to the C terminus might affect protein half-life. To estimate this effect, we measured and compared the half-life of tagged and untagged versions of 24 proteins for which we were able to obtain antibodies. We find that the differences between half-life measurements of tagged and untagged proteins are distributed similarly to the repeat differences (Kolmogorov–Smirnov test, P < 0.57; Table 2, which is published as supporting information on the PNAS web site), suggesting that the effects of the TAP tag on half-life are secondary to other sources of error in the experiments.

To assess the agreement between our half-life measurements and those previously reported in the literature, we compared the two values for 38 yeast proteins. The half-lives reported in the literature come from different measurement techniques, with and without cycloheximide treatment (23 without cycloheximide) and those with no tags or different tags at N- and C-termini of the proteins. We find that the differences between these half-life values are distributed similarly to the repeat differences (Kolmogorov–Smirnov test, P < 0.75; Table 3, which is published as supporting information on the PNAS web site), indicating that the difference between our half-life values and literature data are not different from the inherent variability in our measurements. These comparisons further suggest that, in most cases, the effect of cycloheximide on half-life is secondary to other sources of noise in our experiments.

In summary, we have generated a large-scale collection of protein half-life measurements. We suggest that caution should be exercised when using our data to quantitatively study single-protein dynamics. However, as we shall see below, our measurements are suitable for large-scale quantitative analysis of yeast protein metabolism. Moreover, we can use the data to reliably infer qualitative sets of rapidly or slowly degrading proteins.

Clustering Proteins Based on Protein Metabolism Parameters Correlates with Function and Localization.

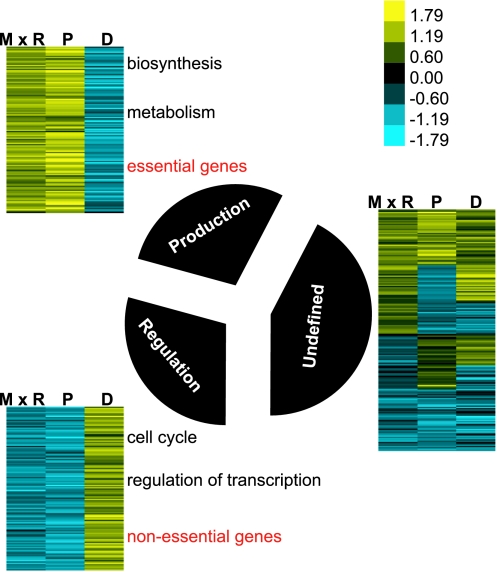
To study the organization of protein metabolism in yeast, we clustered proteins based on similarity in their translation rate (mRNA abundance × ribosome density), protein abundance, and protein degradation rate constant (see Data Sources). We then analyzed the enrichment of protein function and localization in each cluster (see Methods for details) (Fig. 2 and Tables 4–6, which are published as supporting information on the PNAS web site).

Fig. 2.

Clustering genes by similarity in protein metabolism parameters correlates with function and localization. The 3,751 yeast proteins were clustered based on protein production rate [mRNA abundance (M) x ribosome density (R)], protein abundance (P), and degradation rate constant (D). See Data Sources in Methods for details on the data sets used. Clusters with similar profiles were grouped together and graphically visualized by using colors to represent the direction and measure of the attribute (see Supporting Methods for details). A high attribute value is shown in shades of yellow, and a low attribute value is indicated with shades of blue. The black pie slices indicate the relative numbers of proteins belonging to each cluster. Clusters were analyzed for functional enrichment and localization categories. A representative list of significantly enriched GO terms is indicated in black. The entire list of significant GO terms and localization categories obtained in the analysis is described in Tables 4 and 5.

One cluster consists of proteins that appear to be optimized for maximum production and maintenance efficiency. Proteins from this cluster (which we call the “production” cluster) are produced in large quantities and are generally stable. This cluster is enriched in proteins that are involved in protein production, including ribosomal proteins and others involved in protein biosynthesis, and enzymes involved in amino acid metabolism (see Table 5 for P values). In accordance with the functional evidence, this group is enriched in cytoplasmic proteins (P < 1e−14). The metabolism of a second large group of proteins appears to be optimized for regulatory flexibility. Proteins from this cluster (which we call the “regulation” cluster) are rapidly degrading and not abundant. Interestingly, the cluster is enriched in cell cycle proteins and in proteins involved in transcriptional regulation (see Table 5 for P values).

The dominant patterns revealed by clustering suggest that at steady state, during exponential growth, two main regimes control the metabolism of yeast proteins. One regime is optimized for efficient production, and the other is optimized for regulatory flexibility. The production and regulation clusters are much larger than expected by chance (P < 1e⁻⁵⁰).

To further investigate the global effects of function on protein metabolism, we assessed the degree of enrichment of essential proteins in each of the clusters described above. We discovered that the production cluster is enriched in essential genes (hypergeometric P < 1e⁻⁵) and that the regulation cluster is enriched in nonessential genes (hypergeometric P < 1e⁻⁵). We hypothesize that genes in the regulation cluster are important for growth in nonlaboratory conditions and, therefore, contain fewer genes essential for growth in optimal laboratory conditions than expected.

To refine our understanding of the behavior of specific biological functions, we computed the distribution of protein half-lives and other attributes for classes of proteins annotated with particular Gene Ontology (GO) terms (see Methods). This type of analysis provides more resolution than the global cluster analysis and serves as a general resource to characterize the metabolic mode of proteins with particular functions, processes, and localization. As noted above, ribosomal proteins and enzymes are generally stable, and transcription factors and cell cycle proteins are more rapidly degraded than expected by chance. Smaller functional groups with statistically significant distributions of half-lives include proteins involved in the degradation machinery (that are more stable than the average) and cell wall proteins (that are less stable than the average).

To determine whether protein sequence or physical properties of proteins correlates with half-life, we analyzed short and long-lived proteins for enrichment of various physical attributes (see Supporting Methods, which is published as supporting information on the PNAS web site). We observe a significant enrichment of serine density in short-lived proteins and an enrichment of valine density in stable proteins (Fig. 7A, which is published as supporting information on the PNAS web site). The enrichment of serine in short-lived proteins might arise because this amino acid is commonly found in sequences known to target proteins for degradation (e.g., the PEST sequence). However, we do not observe enrichment of threonine, proline, or glutamic acid in unstable proteins. Finally, we find that there is a highly significant negative correlation between protein length and half-life (Fig. 7B; Spearman R = −0.23, P < 3e⁻³⁸); this correlation has been reported in ref. 6, but its mechanistic origins are unclear.

Half-Life and Protein Production Rate Influence Protein Abundance.

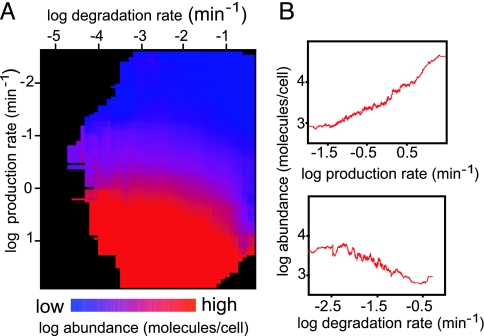
To visualize the influence of protein degradation and protein production on steady-state protein abundance, we plotted the experimentally determined degradation rate constant (this study), protein production rate, and protein abundance measurements for ≈3,700 proteins (see Data Sources in Methods) on a “heat map” (Fig. 3A). The map shows that proteins with similar protein production rates can have very different degradation rate constants, leading to differences in protein abundances. This simple observation underscores the contribution of degradation to steady-state protein abundance. Also, as seen in the 2D plots, which show the moving average of 100 genes, the protein production rate and protein degradation rate constant both influence protein abundance (Fig. 3B).

Fig. 3.

Protein half-life and production rate influence protein abundance. (A) Heat map illustrating the functional relationship between protein production rate (mRNA abundance × ribosome density; y axis), degradation rate constant (x axis), and protein abundance (color-coded). See Data Sources in Methods for details on the data sets used. Each point represents a 2D bin, including all proteins with a degradation rate constant and protein production rate in a defined range. The color of the bin represents the average abundance of the proteins contained within it. Higher values are indicated in shades of red, and lower values in shades of blue. Empty and near-empty bins are colored black. (B) Two-dimensional plot of the relationship between protein abundance and protein production (Upper) or degradation rate constant (Lower). The plots are generated by using a moving average of a window of 100 genes.

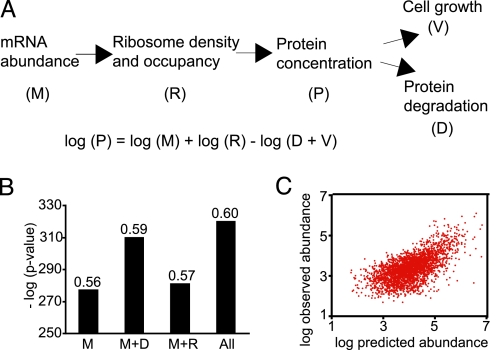
We next wished to test whether different sources of high-throughput information can be used in the context of a unified quantitative model for protein metabolism (see Data Sources). To this end, we used an equation derived from a simplified model of protein metabolism to predict protein abundance from translation rate, mRNA abundance, and protein half-life (Fig. 4A and Methods). We find that the Spearman correlation between the predicted log protein concentration (Fig. 4 B and C) and the experimental measurement was 0.6, better than the correlation of mRNA abundance combined with ribosome density data alone (0.57). Although the increase in correlation is modest, it is highly significant as confirmed by both residual analysis (Methods, P < 1e⁻¹⁸) and correlation increase analysis (P < 1e⁻⁴) (7). These results show that although mRNA abundance plays a major role in determining protein abundance, the incorporation of protein degradation information improves our ability to predict protein abundance. Moreover, the available data, although generated by using strikingly different methods and subject to significant errors, can be integrated in the context of a principled quantitative model, without applying sophisticated normalization (except for multiplicative factors).

Fig. 4.

A simple model for protein metabolism. (A) Schematic of a model for protein metabolism and the corresponding steady-state prediction for protein abundance, where M is absolute mRNA abundance, P is protein concentration, R is the rate of translation per mRNA molecule (approximated by experimental data on ribosome density), D is protein degradation rate constant, and V is growth rate (volume increase factor per unit time). See Data Sources in Methods for details on the data sets used. (B) Correlation between observed and predicted protein abundance. Bar graph shows the P value (y axis) of rejecting the independence hypothesis by using the Spearman test [the Spearman rank correlations (r_s) are indicated on the bars], between observed and predicted protein abundance, when using M, only mRNA abundance; M+D, mRNA abundance and degradation rate constant including growth correction; M+R, mRNA abundance and ribosome density; or all of the parameters described in the steady state protein metabolism equation. (C) Scatter plot showing the relationship between the observed and predicted protein abundances.

Correlation Between Protein Half-Life and Changes in mRNA Levels.

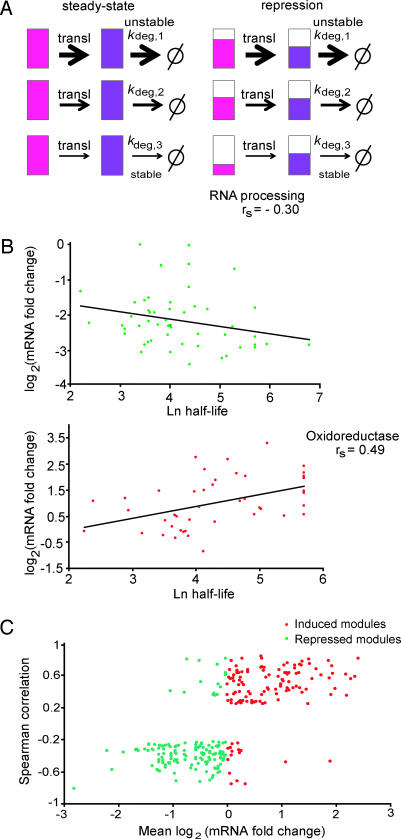
Regulation of protein networks is thought to occur at all levels from transcription to protein degradation. Gene expression studies have revealed that transcriptional networks are organized into transcription modules, consisting of genes that are coexpressed (8, 9). The organization of transcriptional programs into modules facilitates the coordination of large-scale responses of functionally related genes to changes in the environment or to other regulatory needs. However, the half-lives of proteins in a transcriptional module influence the propagation of changes in mRNA to changes in protein abundances. For example, repression of mRNAs coding for stable proteins will take longer to produce changes in protein abundance as compared with similar changes in mRNAs coding for rapidly degrading proteins (Fig. 5A).

Fig. 5.

Correlation between mRNA changes and protein half-life. (A) Model for buffering protein stability differences in regulated transcription modules. Schematic of a transcription module made up of three genes with different protein degradation rate constants shown at steady state (Left) and during the transition to a repressed state (Right). The three coregulated genes produce mRNA (shown in pink) coding for proteins (in purple) of different stabilities as indicated by the different k_deg (1 is least stable, and 3 is the most stable protein). When the genes in the module are transcriptionally repressed (Right) and the cell is aiming to maintain the same relative ratios of protein abundance as in steady state, mRNAs coding for stable proteins will be repressed more than mRNAs coding for unstable ones (indicated by the relative extent of pink filling). The same is true for cases of induction (data not shown). (B) Relationship between fold change in expression and protein half-life in the genes belonging to two transcription modules. The profile of the RNA processing module in osmotic stress (51 genes; ref. 9) (Upper) and the oxidoreductase module (44 genes; ref. 7) in response to DTT (Lower) are shown. The mRNA data come from the time point of maximum mRNA repression (for osmotic stress, 20 min) or activation (for oxidoreductase, 45 min) during time courses after a stress. The lines give the least-square fit to the data points. (C) Global correlation between protein half-life and fold change in gene expression in transcription modules. For 1,200 previously described transcription modules (10), we analyzed 27 different time courses of mRNA expression after a stress (8, 11–14). For each module and each condition, we tested whether the magnitude of transcription induction or repression correlates with the half-life of the protein encoded by the module’s genes. To that end, we calculated the Spearman rank correlation between fold change in gene expression and protein half-life and collected all module-condition pairs for which the correlation was significant (P < 1e⁻³). The scatter plot shows the average fold change in expression (x axis) and Spearman rank correlation (y axis) for significant pairs The plot reflects distinct behaviors for induced (red) and repressed (green) modules, suggesting that, in agreement with our theoretical prediction, in cases where correlation between half-life and expression is observed, it increases the uniformity of the module’s response at the protein level.

If the cell is striving to maintain the relative ratio of protein abundances within a transcriptional module, then genes within the module must be differentially regulated to compensate for differences in protein half-lives. We analyzed the predictions of a dynamic model of protein production to evaluate the nature of such compensatory effects (see Methods). We assumed that transcription temporally changes and that half-life and translation rate are fixed. The model predicts a negative correlation between protein half-life and mRNA log expression fold change in modules that are repressed (meaning more repression of genes encoding stable proteins within the module as compared with those coding for unstable ones) and a positive correlation in induced modules (meaning a stronger induction of genes encoding stable proteins within the module as compared with those coding for unstable proteins) (Fig. 5A and Supporting Methods). The model predicts that transcriptional compensation will be transient and holds as long as the module has not reached the new steady state.

To test the idea that cells buffer differences in half-life by repressing and activating genes coding for stable proteins more strongly than genes coding for rapidly degrading ones, we examined the correlation between half-life and fold repression or activation in two transcriptional modules (Fig. 5B). Genes in the RNA processing module are repressed after osmotic stress, whereas genes in the oxidoreductase module are activated after DTT treatment (8, 14). For both modules, we chose to work with the time point corresponding to peak mRNA repression/activation. In both cases, we observed significant correlation in the predicted direction between log mRNA fold change and half-life.

To more systematically test the theoretical prediction for half-life transcriptional compensation, we examined the behavior of a large set of yeast modules (10) in a series of time-dependent gene expression experiments (Methods). For each transcriptional module in a given condition, we computed the correlation between protein half-life and log-fold expression change. We then plotted the correlation versus the average fold expression change for all module-condition pairs that exhibit significant correlation (Fig. 5C). According to the theory, induced modules (log-fold expression change >0) should exhibit a positive correlation between half-life and fold expression change and repressed modules (log-fold expression change <0) should exhibit a negative correlation. Indeed, the distribution of correlations for cases of induction is significantly different from those of repression (Fig. 5C; Kolmogorov-Smirnov test, P < 1e⁻³²). As expected, this correlation is not observed for every module in every condition. There are many causes for lack of a correlation: (i) requirement for a stoichiometric response may be secondary to other regulatory constraints; (ii) the half-lives of proteins in the module may be regulated; (iii) the half-lives of proteins in the module may be very similar; or (iv) there may be errors in the data sets that obscure a correlation. Nevertheless, the trend we observe implies that the magnitude of transcriptional response can be used to buffer differences in half-lives and generate coherent behavior at the protein level. Our results therefore suggest a highly integrated view of the regulation of functional modules, where regulatory effects on different levels (e.g., transcription and degradation) influence each other to generate a combined cellular response.

Discussion

A complete understanding of protein metabolism requires quantification of the rates of protein production and protein destruction. Although microarray-based approaches have yielded large-scale data sets relevant for the estimation of protein production rates, relatively little is known regarding the rates of protein degradation. Such data are essential to the development of quantitative models of protein metabolism. If successful, such models could be used to understand how changes in mRNA levels propagate to affect changes in protein abundance. For example, changes in the abundance of mRNAs coding for stable proteins will take significant time to propagate to affect changes in protein abundance. Therefore, transient changes in such mRNAs may result in little detectable change in protein abundance. Such an effect of protein half-life complicates the ability to extrapolate from microarray data to changes in the abundance of the corresponding proteins.

In an attempt to fully characterize the parameters from which we can understand the regulation of protein abundance, we combined our half-life measurements with existing measurements of other aspects of protein metabolism (mRNA abundance and translation and protein abundance). Two major issues arise while attempting to perform such integration: (i) the compatibility of different technologies and experimental procedures used to measure each of the parameters and (ii) the numerous sources of experimental artifacts and inaccuracies that we are unable to control. We were surprised by our ability to validate a simple dynamic model governing protein metabolism by using data from multiple sources without applying any sophisticated normalization (except for multiplicative factors). We argue that the integrative quantitative approach holds great promise for the study of complex biological processes, because no single regulatory mechanism can explain such processes faithfully. Future studies might benefit from an approach that integrates transcriptional and protein level data and could enable testing of regulatory hypotheses from the protein metabolism point of view.

We have theoretically demonstrated and validated how tightly coupled transcriptional and degradation-based regulatory mechanisms are by analyzing the transcriptional regulation of groups of coregulated genes. This analysis suggests that transcriptional regulation may be used by cells to buffer the half-life differences among proteins encoded by a group of coregulated genes. We hypothesize that transcriptional control may be easier for evolution to tinker with, standardizing the response of a gene module at the protein level by fine-tuning the transcriptional response. Understanding the changes in protein levels caused by transcriptional changes remains a challenge. One parameter that needs to be studied is the degree of regulation of the half-life of proteins under different conditions. If such regulation is insignificant, then computational prediction of protein abundance by using gene expression profiles and steady-state protein half-lives will be possible. Otherwise, measurement of protein half-lives under the conditions of interest is unavoidable.

Our understanding of regulatory mechanisms is gradually shifting from smaller, qualitative models to larger and more quantitative models. One major obstacle facing attempts to model biological regulatory processes at the systems level is that such processes operate at all stages of a protein’s lifecycle, starting from transcription regulation through to protein degradation. The results and analysis we present here add to an increasing body of evidence that demonstrates the importance of a unified approach to the study of biological regulation. Future studies may benefit from the combination of data on all aspects of regulation, including proteomic as well as transcriptional levels, building our understanding of complex processes from a more realistic standpoint than previously was possible.

Methods

Quantification of Protein Half-Life.

Three parallel cultures (1.7 ml) of each TAP-tagged strain were grown in separate 96-well plates in yeast extract/peptone and dextrose medium to log phase. Cycloheximide, a translation inhibitor, was added to a final concentration of 35 μg/ml to terminate protein synthesis. After cycloheximide treatment, equal numbers of cells were collected at 0, 15, and 45 min, and cell lysates were prepared as described in ref. 1 with minor modifications. The extracts were analyzed by SDS/PAGE and Western blotting. The bands corresponding to TAP-tagged proteins were detected by using chemiluminescence at three exposure times (30 sec, 1 min, and 5 min) by using a CCD camera (FluorChem 8800; Alpha Innotech, San Leandro, CA). Custom software (QuantiAction) was developed and used to quantify the intensity of bands on the Western blots (Supporting Methods).

We assume that protein degradation follows first-order decay kinetics (see Supporting Methods for additional evidence), as described by Eq. 1. The measured protein intensity data (denoted by N in the following equations) was initially log-transformed and then a linear least-squares fit was used to determine the decay rate constant (k). From the decay rate constant, the half-life (T_1/2) was calculated.

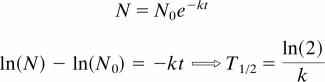Data Sources.

Gene annotations were downloaded from the GO site (www.genomeontology.org, March 2005 version). For each GO term, we assembled the group of genes annotated with the term or with a specialization of it. Data sources are as follows: protein localization (2), absolute mRNA abundance (15, 16) from the combined dataset for ribosome density (17, 18), and absolute protein abundance (1). We analyzed the yeast proteome (Saccharomyces Genome Database version, www.yeastgenome.org, March 2005) to generate statistics on amino acid frequency and protein length. For analysis of transcriptional modules, we used a large compendium of gene expression data as in ref. 10.

A Model Relating Protein Half-Life and Transcriptional Control.

The rate of change in protein concentration can be modeled by using the following differential equation:

where P is the protein concentration, M is the absolute mRNA concentration, R is the rate of translation per mRNA molecule (corresponding to the ribosome density), D is the protein degradation rate constant, and V is the growth rate (volume increase factor per unit time). At steady state, the protein concentration is constant over time, or, mathematically, at t = 0:

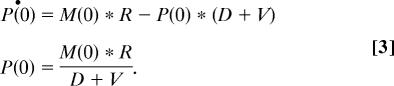To test the compatibility of the various data sources and their adequacy for quantitative modeling, we used experimentally determined data for P, M, R, and D. We set v = 2^{$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$90$}\right.$} because the doubling time is ≈90 min.

We assume that a set of proteins constitutes a functional module and that the goal of a transcriptional program is to regulate the activity of the module at the protein level via regulation of the mRNA levels. For each protein in the module, the degradation rate constant may be different, resulting in different protein level dynamics. At steady state, Eq. 2 defines the relationship between mRNA abundance, translation rate, and degradation rate constant. We analyze the case where all genes in the modules are jointly regulated, such that P(t) = P(0) ∗ π(t) (where π(t) is identical for all genes in the module and represents the joint response profile of the module at the protein level). To generate such a regulated response, the following constraint should hold for all of the proteins in the module at any time (t):

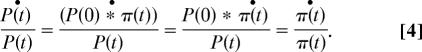Using Eqs. 1 and 2 we derive (see Supporting Methods):

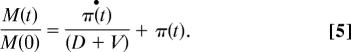According to Eq. 5, parameter D weakens the magnitude of the transcription response: Smaller D values (more stable proteins) will require stronger induction at the mRNA level when π^•(t) > 0, and stronger repression at the mRNA level when π^•(t) < 0. This simple model predicts a positive correlation between the degradation rate constant and log-fold expression change in the case of modules containing transcriptionally repressed genes and a negative correlation in the case of induced modules. The model also shows that upon convergence to a new steady state, π^•(t) = 0, the mRNA expression fold change equals the protein fold change, π(t), predicting that the correlation is a transient property. Although the model is clearly an oversimplification, it does provide insight into the interplay between different mechanisms of regulation.

Supporting Information.

Detailed methods appear in Supporting Methods. The complete data set appears as a Data Set, which is published as supporting information on the PNAS web site. Additional supporting information can be found in Fig. 8 and Tables 7–9, which are published as supporting information on the PNAS web site.

Abbreviations:

GO

Gene Ontology

TAP

tandem affinity purification.