Simulation of polymer translocation through protein channels

Abstract

A modeling algorithm is presented to compute simultaneously polymer conformations and ionic current, as single polymer molecules undergo translocation through protein channels. The method is based on a combination of Langevin dynamics for coarse-grained models of polymers and the Poisson–Nernst–Planck formalism for ionic current. For the illustrative example of ssDNA passing through the α-hemolysin pore, vivid details of conformational fluctuations of the polymer inside the vestibule and β-barrel compartments of the protein pore, and their consequent effects on the translocation time and extent of blocked ionic current are presented. In addition to yielding insights into several experimentally reported puzzles, our simulations offer experimental strategies to sequence polymers more efficiently.

Translocation of polymers through biological channels is very complex involving many machineries and is a fundamental step in many life processes. Although several essential features of translocation are richly documented in systems such as mRNP complex through nuclear pores (1–3), a simple system has only recently been identified for following the single-file passage of one isolated polymer through one channel (4–11). In this system, the channel is constituted by self-assembling heptamers of the Staphylococcus aureus α-hemolysin (αHL) protein. The channel is assembled in a phospholipid bilayer, which offers a physical barrier, and the channel has an opening diameter of ≈1.4 nm at the narrowest constriction (12). A single-stranded polynucleotide, such as poly(deoxyadenylate) and poly(deoxycytidylate), is pulled through the channel by an externally applied voltage gradient across the channel in a solution of a strong electrolyte. The idea is that the ionic current through the channel caused by the passage of small ions of the electrolyte is blocked to a certain extent during the event of translocation of the polymer. It has been hoped that the extent and duration of the current blockade are unique signatures of the identity of the polymer, both in terms of the polymer's chemical characteristics and physical length.

Even this simplest setup, where identical molecules undergo translocation, has generated several puzzling results. The distribution, P(τ), of the duration τ of blockade of ionic current I_b is very broad and appears to exhibit at least two peaks. In addition, there are several levels of ionic current blockade I_b for the same molecule. It is standard practice in experimental investigations to combine the histograms of τ and I_b (8). The resultant scatter plots always yield two groups of data even for monodisperse homopolymers.

To gain insight into these puzzles, we have developed the following simulation. It is complementary to a flurry of theoretical activity (13–21), based on entropic barrier dynamics (22), all of which lead to a generic P(τ) unlike in experiments. Although it is indeed desirable to perform the computation ab initio, the size of the system to be simulated is forbiddingly large to enable such a computation. Therefore we restrict ourselves to generating a minimal model of polymer translocation through the αHL channel, and our goal is to discover the most basic concepts relevant to a molecular understanding of the experimental results. Our minimal model incorporates enough chemical details of the polymer and channel to evaluate the potential roles played by secondary structures of the polymer, orientation of the chain (3′ versus 5′ end), binding sites inside the lumen of the channel, etc. In addition to resolving the above puzzles, the details emerging from our simulations are so vivid that additional experimental protocols can be formulated to substantially narrow down P(τ), and thus enable a much faster sequencing scheme.

The key result of our simulations is that conformational entropy of the polymer plays a dominant role in dictating τ and P(τ). The breadth of P(τ) can be directly attributed to the entropic trap arising from the vestibule of the αHL pore. P(τ) can be made dramatically sharper, sufficient to facilitate sequencing of polymers, by deleting the vestibule or dragging the polymer in a direction normal to the pore axis.

Simulation Method

The system consists of essentially four parts: the heptameric αHL pore, a ssDNA molecule undergoing translocation, a phospholipid membrane barrier carrying the pore, and an electrolyte solution permeating through the pore. The protein pore, αHL, is represented by a united atom model where the residues of the pore are replaced by beads. The coordinates of the residues are extracted from the Protein Data Bank. There can be many choices for the description of beads in terms of their sizes and shapes. In this article we present results for the simplest choice of the beads. In the present united atom model, each residue is replaced by a spherical bead and the diameter of each bead is 3 Å. A bead is assigned −1, 0, or +1 charge according to the ionization of the residue. All aspartic acid residues, glutamic acid residues, and C-terminal groups are deprotonated; arginine, lysine, histidine, and N-terminal groups are protonated. The rest of the residues are electrically neutral. In view of experimental contexts (23), the protein pore is not allowed to move.

Further, the protein pore is treated as a rigid structure with a dielectric constant of 2 surrounded by a solution of dielectric constant 80. The protein pore is embedded in a 48-Å-thick membrane of dielectric constant 2. The membrane surfaces are hard walls. The protein pore is the only space to allow passage of the polymer from the donor compartment to the recipient compartment. The symmetric axis of the pore is positioned along the x axis, as shown in Fig. 1a, which gives the geometry of the pore. The vestibule of the pore is submerged in the donor compartment. The β-barrel of the protein begins at x = 0 and extends up to x = 48 Å.

Fig. 1.

United atom model. (a) The end and side views of αHL. The diameters at the center and mouth of the vestibule are 46 and 30 Å, respectively. (b) The internal wall of the nanotube is made of spherical beads on a curved hexagonal lattice. The interaction between polymer and tube is taken as the Lennard–Jones potential of Eq. 5 with ε = 0.2 kcal/mol and σ = 2.75 Å. (c) United atom representation of single-stranded poly(dC).

We have used the side-chain incorporated model to represent a single-stranded polynucleotide (20), because of its simplicity, fast computational speed, and past success. Each nucleotide is made up of three subunits (phosphate, sugar, and base), and each subunit is taken as a bead. The bead representing the phosphate moiety carries one negative charge. To distinguish the chain directionality in terms of 3′ versus 5′ ends, we deliberately tilt the side chain (base) at a 65^° angle as shown in Fig. 1c. The chain backbone is freely jointed in view of the fact that the persistence length of ssDNA has been measured in high salt concentrations to be roughly the length of 1–2 nt (24–26). Although the three subunits are of different sizes and masses, the results presented below are for the model of all subunits having equal size and mass. The diameter of these beads is taken to be 2.5 Å, and the equilibrium “bond length” between these “atoms” is 2.5 Å. The mass of a nucleotide is distributed equally into the three subunits. For example, in the case of poly(dC), each subunit carries 96 Da.

Polymer conformations are evolved by using the velocity Verlet algorithm (27) to follow the dynamics of the ith bead,

where r⃗_i, m, and ζ are the position vector, mass, and friction coefficient, respectively, of the ith bead.F⃗ (t) is the random force from the solvent bath acting on the ith bead and is stipulated to satisfy the fluctuation–dissipation theorem,

where t is the time and δ is the usual delta function. U in Eq. 1 is the total potential energy acting on the ith bead and consists of four contributions.

These correspond, respectively, to bond stretch, short range, screened Couloumb, and electric potential given by

Here, l is the bond length, l₀ (= 2.5 Å) is the equilibrium bond length, r is the distance between interacting beads, Z_i is the electric charge on the ith bead, ε₀ is the permittivity of the vacuum, and V is electric potential. The values of the parameters are: k = 171 kcal/mol·Å², ε_LJ = 0.5 kcal/mol, and σ = 2.5 Å, κ⁻¹ = 3 Å for 1 M KCl. The dielectric constant ε is inhomogeneous. ε is 2 inside beads and the membrane and is 80 everywhere else.

The ionic current I(t) at time t, because of the passage of electrolyte ions accompanying the polymer transport, is computed by using the Poisson–Nernst–Planck (PNP) formalism (28–30). Taking advantage of the fact that small ions relax much faster than a large polyelectrolyte molecule and that the concentration of electrolyte in the pertinent experiments is very high in comparison with monomer concentration, we assume that at every time step of the Langevin dynamics simulation of the polymer, the electrolyte ions have relaxed to the steady state so that the polymer chain is taken only as a fixed charge distribution ρ_p (r, t) at this time.

With this assumption, the self-consistent coupled PNP equations for the local charge density C_i(r, t) of the ith ionic species and the electric potential V(r, t) for a given polymer conformation at t are

Here ρ_f(r) is the local charge density arising from fixed charges in the system, such as the charged beads of the protein pore. As already mentioned, ε(r) is set to 2 for the beads of polymer and pore and for the membrane. It is 80 everywhere else. In addition, the externally applied voltage gradient is accounted for by fixing the electrostatic potential at the boundaries in the x direction. The box for the ionic current calculations is located at −100 Å < X < 75 Å, −50 Å < Y < 50 Å, and −50 Å < Z < 50 Å. We set V = 0 at X = −100 Å and V = V₀ at X = 75 Å.

Eqs. 8 and 9 are solved by successive overrelaxation method with a grid spacing of 1 Å, following ref. 29. First, we start with V(X) because of the externally applied electrostatic potential gradient across the membrane of dielectric constant of 2 and uniform concentrations (C₊ and C₋) of cations and anions of the dissolved electrolyte.

Then, the coordinates of beads of the pore and polymer are read in. Next, using the successive overrelaxation method, V, C₊, and C₋ are computed iteratively until they converge within the tolerance levels of ΔV = 10⁻⁸ V and ΔC_± = 10⁻⁷ M. In our simulations we have considered 1 M of KCl as the electrolyte. Because C_± is very high in comparison with the counterions from the polymer, the latter are ignored. From the convergent values of C_± and V at each time unit of the Langevin simulation, the ionic current at this time t is given by

with

In evaluating the ionic current, we have taken J_± at X = 48 Å and A at this exit point is 441 Ų. The integral in Eq. 10 is over the cross section of the pore at the exit point. D₊ and D₋ are taken to be 1.96 × 10⁻⁵ cm²·s⁻¹ and 2.03 × 10⁻⁵ cm²·s⁻¹, respectively, for K⁺ and Cl⁻ ions. The magnitude of the applied voltage is V₀ = 120 mV.

The simulation is carried out as follows. First, a single polymer chain is equilibrated in the absence of pore and externally applied voltage gradient, by considering only the connectivity, Lennard–Jones forces, and Debye–Hückel forces among various beads of the chain. Separately the electrostatic potential for the protein pore is computed for 1 M KCl solution in the steady state with a given value of V₀ (120 mV) and in the absence of the polymer. The potential along the central axis of the channel is given as dotted numerical data in Fig. 2. The different gradients (slopes of the curve) at different parts of the trajectory are readily conspicuous in Fig. 2. Because we are interested here in the details of the actual translocation event, and not in the way the polymer arrives at the channel entrance, we have extended the range of the potential gradient inside the vestibule to the donor compartment. In addition, we have ignored the finer details of the potential gradient and replaced the actual potential gradient by the approximated gradient consisting of three parts, namely, up to the β-barrel, inside the β-barrel, and outside the β-barrel in the recipient compartment.

Fig. 2.

PNP and approximated V(X) across the protein pore.

Next, the equilibrated polymer is inserted in the donor compartment such that the center of mass of the chain is at X = −100 Å in front of the mouth of the pore. The polymer is dragged toward the pore by the electrical potential gradient across the membrane. For each time unit of the Langevin dynamics simulation, the coordinates of the polymer beads are stored, and the ionic current at this time is computed. When any one monomer of the polymer enters the mouth of the pore (at X = −50 Å) a clock for measuring the translocation time starts. As the polymer progressively invades the lumen of the pore, the ionic current is calculated at each time unit. This is how the ionic current traces given below are constructed. It is to be noted that ∇V entering the Langevin equation for the polymer bead is the original value of the protein pore in the absence of the polymer. When the last bead of the polymer exits the outer edge of the pore (at X = 48 Å), the clock stops with a reading of the translocation time τ. By repeating the above sequence of simulations thousands of times we construct the histogram of τ, and for each of the entries of the histogram, we have a trace of ionic current as the polymer traverses through the pore.

Results

First, we give results on chain conformations, ionic current, and translocation time τ as the polymer transits through the channel in typical simulations. Then we present distribution functions of blocked current and τ, based on thousands of simulations. Fig. 3A represents a typical simulation result for the model chain of single-stranded poly(dC) with n = 45 nt undergoing translocation through αHL under a potential difference of 120 mV in 1 M KCl solution. One unit of simulation time is arbitrarily taken to be 0.15 μs, by matching the peak values of τ in our simulations and the experiments of refs. 8 and 9, and by noting that the average translocation velocity is constant in the long polymer and high voltage gradient limits (9).

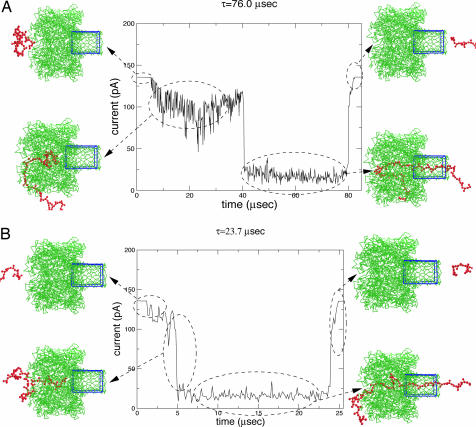
Fig. 3.

Typical ionic current traces. (A) Long τ. (B) Short τ.

There are several key features evident from the typical trajectory of Fig. 3A: (i) The open pore current of ≈135 pA is very close to the experimental value. (ii) The polymer enters the mouth of the vestibule not necessarily as a single file. The presence of polymer monomers at the mouth of the vestibule is sufficient to provoke a response in the ionic current by providing a spatial blockade to the flow of electrolyte ions. (iii) As time progresses the chain gets into the vestibule. Because of its large volume, the vestibule acts as an entropic trap and the chain segments linger in this cavity for some definite time duration. At this stage, the ionic current is I_b1 (≈100 pA). The fluctuations in I around its mean value reflect the dynamics of the polymer rattling inside the vestibule. (iv) One end of the chain eventually enters the β-barrel. At this time, I(t) is reduced precipitously to the blocked current level I_b2. The average value of I_b2 is 17 pA. This very low value reflects the reduction in the cross-sectional area of β-barrel for flow of electrolyte ions by the presence of polymer segments. The fluctuations in I_b2 is solely caused by the dynamics of the polymer. The ionic current is about I_b2 until the last monomer exits the end of the β-barrel. τ is the duration of all of the above events. (v) When the chain has completed its translocation, the ionic current returns to the open pore current after leaving a distinct signature for the presence of some monomers in the back of the exit location, perturbing the flow of electrolyte ions.

It is to be noted from Fig. 3A that the chain spends a significant amount of time inside the vestibule before entering the β-barrel. Although such trajectories are quite common, there are also more prevalent trajectories where the dwell time inside the vestibule is short as illustrated in Fig. 3B. The essential features of Fig. 3B are the same five features discussed for Fig. 3A, except that the time spent inside the vestibule is shorter. As seen from the chain conformations presented in Fig. 3B, the shorter duration inside the vestibule is caused by the initial chain orientation in line with the axis of the channel and the chain entering the vestibule mouth essentially as a single file.

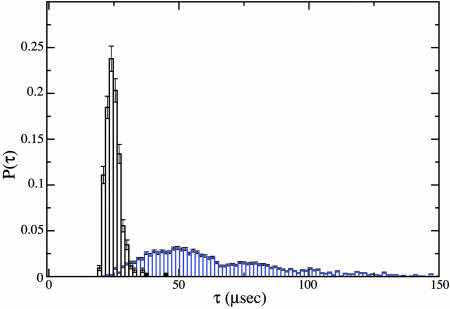
Vivid details such as those in Fig. 3 are available for each of the thousands of simulations that were performed, based on which we have constructed histograms for τ and I_b. The normalized probability P(τ) based on 4,000 simulations is plotted against τ in Fig. 4for n = 45, V₀ = 120 mV, and 1 M KCl. The error bars are estimated from the square root of counts per bin before normalizing the histogram. It is evident that the distribution of τ is very broad, and two dominant peaks at 50 and 75 μs may be identified. This result is in agreement with our earlier report of two peaks based on a smaller number of simulations with shorter (n = 15) chains (20). Now we are in a position to go back to the trajectories of the chains and study them for various events taking different translocation times. Indeed, an example of the trajectory taking 76 μs is Fig. 3A, where the vestibule plays the role of an entropic trap, delaying the translocation process. In contrast, by stochasticity associated with chain end orientation and thermal noise from the background, the chain end can enter the β-barrel sooner by essentially avoiding the vestibule's entropic trap. This is the case with Fig. 3B where τ (= 23.7 μs) is much shorter, and this event belongs to the dominant peak in the histogram. We validate this mechanism for the occurrence of two peaks, by performing further simulations on nanotubes where we have cut out the vestibule part of the channel (see below). Now, only one peak is seen, suggesting the significant role of the vestibule as an entropic trap. However, the two peaks have recently been attributed (31, 32) to different orientations (3′ and 5′ ends) of the polymer entering the β-barrel first. Yet analysis of our simulation data shows that there is no significant discrimination between the 3′ and 5′ ends entering the β-barrel first in terms of translocation time. This finding argues for more work, in terms of both experiments (without the vestibule) and simulations (with explicit solvent molecules).

Fig. 4.

Histogram of τ for αHL (n = 45, V₀ = 120 mV).

As already noted, there are two levels of blocked ionic current during the translocation event. For the event corresponding to Fig. 3A, the normalized histogram P(I_b) of blocked current I_b within the duration of τ, given in Fig. 5A, exhibits two separate distributions. The average values of these two peaks represent whether the blockade corresponds to the vestibule (weak blockade) or the β-barrel (strong blockade). The widths of the peaks correspond to the accompanying polymer dynamics. It must be remarked that the occurrence of two populations of blocked ionic current has nothing to do with the actual value of τ. The histogram of Fig. 5A corresponds to τ = 76 μs. For the case of τ = 23.7 μs corresponding to Fig. 3B, the histogram of I_b is given in Fig. 5B. Here again, there are two distributions representing polymer dynamics inside the vestibule and the β-barrel. However, the weight of I_b population relating to the vestibule is weaker for the faster translocation events. These results emphasize the need to interpret the scatter plots of ref. 8 differently by having to go into individual events instead of clumping them all together.

Fig. 5.

Histogram of I_b. A and B correspond, respectively, to Fig. 3 A and B.

The intervention by the vestibule of αHL as an entropic trap for the translocation of the polymer leads to the breadth of P(τ). To further validate this observation, we have repeated our simulations by replacing the αHL channel by a cylindrical tube of diameter 18 Å and length 98 Å, as illustrated in Fig. 1b. The tube is inserted inside the membrane of dielectric constant 2, and the membrane thickness is the same as the tube length.

A typical trajectory of polymer translocation through the cylindrical tube is given in Fig. 6for n = 45, V₀ = 120 mV, and 1 M KCl. Fig. 6 also exhibits all of the features described for Fig. 3, except the part corresponding to the role of the vestibule, where the weaker blockade is prominently absent. Based on 1,000 simulations, the histogram P(τ) is given in Fig. 7, where the results of Fig. 4 are included for comparison. It is clear that P(τ) is very sharply peaked, and there is only one peak for the nanotube. Our simulations thus suggest that it is preferable to have a nanotube or just the β-barrel for sequencing purposes instead of αHL.

Fig. 6.

Typical ionic current trace for a nanotube.

Fig. 7.

Comparison of P(τ) between αHL and nanotube.

Sequencing Protocol

As already mentioned, there is a perturbation in the ionic current through the channel, as soon as a monomer is eclipsing the pathway for small ions in front of the channel (see Figs. 3 and 6). This finding suggests a novel experimental setup for sequencing polymers by using measurements of ionic current through channels. The strategy is illustrated in Fig. 8A, where the circle represents the mouth of the pore through which electrolyte ions pass and create the measured ionic current under an applied voltage gradient. The pore can be either αHL or a nanotube with prescribed diameters. Then a polymer is dragged across the front of the pore in the direction of the arrow in Fig. 8A. The physical size of the monomer at the pore front excludes small ions to pass by and consequently reduces the magnitude of the ionic current. When monomers with different sizes are dragged normal to the ion flow, different levels of ionic current are registered. When a polymer with eight dC units is dragged at the speed of 1.0 Å/μs near the pore entrance, in the normal direction to the current flow, the time dependence of ionic current is given in Fig. 8 B and C. The saw-tooth nature of the trace is caused by the periodicity arising from the monomer entering the aperture, then generating maximum eclipse, and then exiting the aperture. If an octomer of dA is simulated under identical conditions (where the diameter of the side-chain bead is 5 Å instead of 2.5 Å for dC and the bond length connecting the side-chain to the backbone is 3.75 Å), the ionic trace is as given in Fig. 8 B and C. In these particular simulations, the pore diameter and length are taken as 14 and 50 Å, respectively, to detect the identity of only one monomer. Depending on the size of the aperture, signals corresponding to dimers, trimers, etc., can be generated. In the present illustration of the concept, we now drag octomers with different sequences containing dA and dC. Depending on which monomer sequence is being dragged, the ionic current will toggle back and forth between the values corresponding to pure dA and dC values. There is only one unique ionic current trace for a given sequence, as illustrated by two distinctly different traces for two sequences. Although the differences in the ionic current from our simulations are rather small, the current experimental status (33) is able to discern such small differences. The strategy emerging from our simulations will enable the precise sequencing of polymers by several orders of magnitude faster than the currently available techniques.

Fig. 8.

Proposed experiment. (A) Strategy. (B and C) The ionic current traces for two homopolymers (B) and two heteropolymers (C) (sequence given in Inset). Each polymer has eight bases.

Conclusions

Our simulations using coarse-grained models of the polymer and the channel with appropriate accounting of dielectric heterogeneity reproduce all of the essential features observed experimentally with αHL. The vestibule is found to play a significant role by providing an entropic trap and thereby slowing down the process. Another observation is that there is no direct correlation between translocation time and blocked current. For each value of τ, there are two dominant values of blocked current. Finally, an experimental setup is proposed that would enable precise sequencing of polymers by several orders of magnitude faster than current techniques.

In summary, our combination of Langevin dynamics simulations of polymer dynamics with the PNP formalism for ionic current, in the general premise of united atom description, offers a computational platform for discovering generic physical principles behind polymer translocation through biological channels.

Abbreviations

αHL

α-hemolysin

PNP

Poisson–Nernst–Planck