Skip to main content
NCBI home page
Genome Research logoLink to Genome Research
. 2002 Jan;12(1):165–176. doi: 10.1101/gr.182601

Finding Genes in the C2C12 Osteogenic Pathway by k-Nearest-Neighbor Classification of Expression Data

Joachim Theilhaber 1,4, Timothy Connolly 1, Sergio Roman-Roman 2, Steven Bushnell 1, Amanda Jackson 3, Kathy Call 1, Teresa Garcia 2, Roland Baron 2
PMCID: PMC155256  PMID: 11779842

Abstract

A supervised classification scheme for analyzing microarray expression data, based on the k-nearest-neighbor method coupled to noise-reduction filters, has been used to find genes involved in the osteogenic pathway of the mouse C2C12 cell line studied here as a model for in vivo osteogenesis. The scheme uses as input a training set embodying expert biological knowledge, and provides internal estimates of its own misclassification errors, which furthermore enables systematic optimization of the classifier parameters. On the basis of the C2C12-generated expression data set with 34,130 expression profiles across 2 time courses, each comprised of 6 points, and a training set containing known members of the osteogenic, myoblastic, and adipocytic pathways, 176 new genes in addition to 28 originally in the training set are selected as relevant to osteogenesis. For this selection, the estimated sensitivity is 42% and the posterior false-positive rate (fraction of candidates that are spurious) is 12%. The corresponding sensitivity and false-positive rate for detection of myoblastic genes are 9% and 31%, respectively, and only 4% and ∼100%, respectively, for adipocytic genes, in accordance with an experimental design that predominantly stimulated the osteogenic pathway. Validation of this selection is provided by examining expression of the genes in an independent biological assay involving mouse calvaria (skull bone) primary cell cultures, in which a large fraction of the 176 genes are seen to be strongly regulated, as well as by case-by-case analysis of the genes on the basis of expert domain knowledge. The methodology should be generalizable to any situation in which enough a priori biological knowledge exists to define a training set.

[Online supplementary material available at www.genome.org]

In recent years, much use has been made of clustering methods in the analysis of some of the large gene expression data sets generated by microarrays (Eisen et al. 1998; Wen et al. 1998; Alon et al. 1999; Ben-Dor et al. 1999; Tamayo et al. 1999; Alizadeh et al. 2000; Ross et al. 2000). Such unsupervised methods of data organization are very well suited to situations in which there is little a priori knowledge regarding the expected behavior of gene expression in the given biological system. However, clustering methods also suffer from the fact that they are in part qualitative exploratory tools, ideally suited for visualization, but not as well adapted for precisely defining class boundaries between groups of genes, nor for estimating error rates in classification.

In this study, we present an alternative approach for classifying genes based on a well-known supervised learning method, the so-called k-nearest-neighbor (kNN) method (Duda and Hart 1973; Fukunaga 1990). This method is applied to finding genes in the differentiation pathways of a well-characterized system, the pluripotent mouse C2C12 cell line (Katagiri 1994), with a focus on the genes involved in the osteogenic pathway. The premise of the method is that one first constructs a training set. This training set is a collection of genes that is a subset of the data set under investigation, and for which precise class memberships can be assigned. The definition and choice of the training set classes is determined by the biological context and by the types of questions being asked of the data; in the present case, each class represents a different differentiation pathway. Once the training set has been defined, the remaining genes in the data set can be classified, that is, assigned to one of the classes in the training set. In the kNN method, this is done by a voting scheme in which the class memberships of the k-nearest-neighbors in an expression space to a given gene are used to establish its assigned classification. The nearest neighbors are picked only from the training set, and k is a fixed parameter, typically in the range from 1 to 10 (for the final classification results presented here, k = 2 was found to be optimal).

The classifier used here has been called GENNC (gene expression nearest neighbor classifier). The implementation of GENNC departs from a simple application of the kNN method in that it also includes two important filtering steps that suppress noisy data, and which precede the kNN classification proper.

Because it incorporates some measure of the truth beforehand, in the form of the training set, GENNC has the desirable feature that allows one to estimate its error rates. As a consequence, optimization of the classifier parameters is possible, and in particular, one can maximize sensitivity at a given, fixed level of selectivity. This state of affairs removes much of the arbitrariness that is often present when one is selecting genes using unsupervised methods, although one should remain aware that the results are critically dependent on the quality and relevance of the training set.

Below, we first present the GENNC classifier applied to finding genes in the osteogenic differentiation pathway of the mouse C2C12 cell line, a pathway of direct relevance to disease processes such as osteoporosis. Starting from a data set of 34,130 expression profiles, and by use of an optimized set of classifier parameters, GENNC classifies 176 genes into the C2C12 bone pathway. Biological validation of this selection is then provided by analyzing expression in an independent biological assay consisting of a primary cell culture derived from mouse calvaria (skull bone) tissue.

Related Work

Supervised learning schemes have been applied only relatively recently to the analysis of gene expression. These include the work of Golub et al. (1999), the SPLASH algorithm (Califano et al. 2000), and classification by so-called support vector machines (Brown et al. 2000). The algorithms described by Golub or in connection with SPLASH have been used for a somewhat different task than the one considered here, that of classifying and predicting cell types rather than genes. Furthermore, whereas the support vector machines have been used, as has been GENNC, for the classification of genes, the problems considered are different; for instance, the classification of Saccharomyces Cerevisiae genes into five broad functional classes. Because of these differences, a direct comparison of the methods is not straightforward, and was not attempted here, where, instead, we focused on a self-contained presentation.

Biological System and Experiment Design

In vivo, undifferentiated mesenchymal stem cells (MSC) have the ability to differentiate into chondrocytes, myocytes, adipocytes, and osteoblasts (Taylor and Jones 1979; Grigoriadis et al. 1988; Yamaguchi and Kahn 1991; for review, see Triffitt 1996; Karsenty 1999), and thus represent a valuable model for the study of gene regulation associated with these mutually exclusive differentiation pathways. In particular, several members of the transforming growth factor-β (TGF-β) superfamily have been shown to play regulatory roles in osteoblast differentiation and maturation. Thus, bone morphogenic protein 2 (BMP-2) was initially characterized by its ability to induce new bone formation when implanted into muscular tissues. In vitro, BMP-2 has been reported to stimulate osteoblastic maturation and has the ability to induce or accelerate the appearance of osteoblastic markers in both undifferentiated nonosteogenic cells and committed osteoblast precursors (Groeneveld and Burger 2000).

In the study presented here, we used the GENNC classifier on a specific in vitro system, the well-characterized mouse C2C12 cell line, which captures important aspects of the general MSC differentiation program outlined above. The mouse C2C12 cells are an established progenitor cell line that was initially derived from parental C2 myoblasts isolated from regenerating muscle of adult mouse (Yaffe and Saxel 1977; Blau 1983). Exposure of these pluripotent cells to a low-mitogen medium (2%–5% serum conditions) induces a program of muscle differentiation coupled with terminal withdrawal from the cell cycle and fusion of cells in multinucleate myotubes (Halevy et al. 1995). On the other hand, treatment of the C2C12 cells with recombinant BMP-2 blocks myotube formation and induces osteogenic differentiation instead (Katagiri 1994). Exposure of C2C12 cells to long-chain fatty acids or thiazolidinediones also blocks myotube formation, but now leads to the expression of a typical adipocytic differentiation program (Teboul et al. 1995; Grimaldi et al. 1997). Finally, treatment by TGF-β1 shares with the BMP-2 treatment the ability to repress the myoblastic pathway, but fails to induce osteoblastic differentiation (Katagiri 1994), and thus maintains the C2C12 cells in a undifferentiated state.

The present experimental study focused on the osteogenic pathway of the C2C12 cell line, and thus explored only a subset of the possible differentiation events described above. C2C12 cells were grown for 4 d under three distinct medium conditions (see Methods) as follows BMP-2 (1 μg/mL), TGF-β1 (2.5 ng/mL), and an all-solvent control (HCl 10 mM), these assays promoting either joint osteoblastic induction and myoblastic repression (under BMP-2), or pure myoblastic repression (under TGF-β1). Total RNA samples were obtained at six time points (4 h, 8 h, 1 d, 2 d, 3 d, and 4 d) under each treatment, and the resulting cRNA samples were then hybridized to the Affymetrix 35K murine chip set. For each Affymetrix qualifier (a “qualifier” refers to the set of features which together measure the abundance of transcripts containing a given RNA sequence), ratios for expression in each of the treated samples relative to the solvent control were computed. The assembly of the expression data (see Methods) resulted, on a qualifier-by-qualifier basis, in 34,130 expression profiles, each consisting of 12 points (6 points for the BMP-2 time course, 6 points for the TGFβ1 time course) with the treated-to-solvent-sample expression ratios given at each point.

RESULTS

Construction of the Training Set

To analyze the C2C12 expression data using GENNC, a training set containing genes from all three potential C2C12 differentiation pathways (osteoblastic, myoblastic, and adipocytic), as well as classes of genes defining negative controls, was constructed. The training set contained 481 qualifiers mapping into 241 distinct genes, and subdivided into 5 classes labeled Bone, Muscle, Adipocyte, Tubulin, and Hsp (Supplementary Table 1, available as an online assignment at www.genome.org). Each of the Bone, Muscle, and Adipocyte classes was meant to represent, at least partially, an entire pathway of differentiation into the corresponding cell type, whereas the Tubulin and Hsp embody negative controls.

The Bone class (Supplementary Table 1a, available as an online assignment at www.genome.org) contains 83 qualifiers mapping into 28 genes. The list contains genes for growth factors (BMP-2, BMP-4), gene regulatory proteins and transcription factors (Id, Id-2, Id-3, Osf2/Cbfa1, Hox-8), bone-specific collagens (Type I α1 and α2 chains, Type III α1 chain, and Type V α1 and α2 chains), cell-surface proteins (PTH/PTHrP receptor, CD44), as well as for several extracellular matrix (ECM) proteins constitutive of bone. Note that the selection strives to provide coverage of the commitment and differentiation process from start to finish, and it is in this sense that the Bone class can be said to represent the entire pathway.

The Muscle class (Supplementary Table 1b, available as an online assignment at www.genome.org ) contains 121 qualifiers mapping into 32 genes chosen on the basis of their specificity to skeletal, cardiac, or smooth muscle. It includes multiple components of the motor proteins (myosin, tropomyosin, and troponins T, I, and C), associated structural proteins (dystrophin, dystrobrevin, and DRP2), as well as transcription factors of the myogenic family (MyoD, myogenin, myf-5, herculin/myf-6, and MRF4) and proteins involved in metabolism (CAIII and creatine kinase).

The Adipocyte class (Supplementary Table 1c, available as an online assignment at www.genome.org) consists of 48 qualifiers mapping into 19 genes. These include receptors specific to adipocytes (RXR-α, PPAR-γ, and leptin receptor), transcription factors (C/EBP α and C/EBP δ) as well as metabolic proteins (PEPCK and LPL) and ECM proteins (collagen VI).

The selection criteria for the Tubulin and Hsp (heat shock proteins) classes were looser and nonexhaustive, as the aim was chiefly to provide negative controls for the nearest-neighbor classification scheme. A total of 110 qualifiers (53 genes) were selected for the Tubulin class and 122 qualifiers (84 genes) for the Hsp class, with the overall number adjusted to be roughly equal to the number of qualifiers present in the combined Bone, Muscle, and Adipocyte classes. Below, we refer to the training set members as markers of their corresponding classes. Qualifiers that are not in the training set are referred to as blank qualifiers.

χ2 Diagnostic and Filtering of the Data Set

A first step in the analysis was to reduce the large number of profiles in the C2C12 time courses to a more manageable number by retaining only those with the most significant variation of expression in treated samples relative to the control samples. To do this, all profiles were ranked according to a χ2 statistic defined as the sum of squares of the difference in expression between the treated and control samples, each term in the sum being divided by an estimate of the variance in the measurement at that point (Theilhaber et al. 2001; see equation 1, Methods). The statistic not only gives importance to profiles with a few, very large, and/or very small ratios, but also to profiles with more moderate but more persistent ratios not equal to 1. Although other filtering methods can be used, such as requiring expression ratios above a certain threshold at a certain number of points, an advantage of the χ2 statistic over such pass-fail criteria is that it provides a continuous rather than binary ranking of all profiles.

χ2 Diagnostic

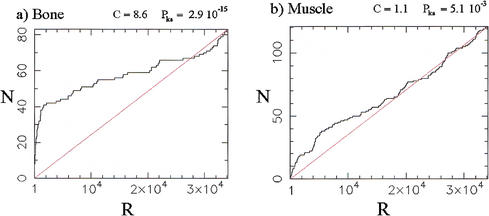
The continuous ranking provided by the χ2 statistic can be used as a diagnostic for the global amount of regulation in each of the classes defined in the training set. For instance, Figure 1a shows the cumulative distribution of the 83 Bone markers relative to the χ2 ranking of all 34,130 qualifiers in the data set. In the figure, the rank is indicated on the abcissa, with significance decreasing left to right, and the ordinate indicating the number of Bone markers that have rank lower than or equal to the rank indicated on the abcissa. The steep leftward rise of the cumulative distribution occurs because a large number of the Bone markers have highly regulated expression profiles. Thus, the over-representation of the Bone markers among the profiles with the greatest variation is such that 50% of the Bone markers (42 qualifiers) are found in the top 5.8% of the profiles in the ranked list (1995 qualifiers). This over-representation (enrichment) of markers can be quantified by a profile concentration C (Methods), which is equal to 0.5 divided by the population cumulative distribution function, computed at the sample median. For the Bone markers, CBone = 0.5/0.058 = 8.6.

Figure 1.

Figure 1

Open in a new tab

Distribution of the 83 Bone and 121 Muscle markers (= training set members) in the population of 34,130 profiles ranked according to the χ2 statistic. A rank R of 1 denotes the most variable (significant) profile, a rank of 34,130 the least variable (least significant) profile. N is the cumulative number of markers found with rank below or equal to the rank R indicated on the abcissa. C denotes the profile concentration (see text and equation 3, in Methods) and Pks is the companion P value (Kolmogorov-Smirnov test). The straight lines indicate the distributions expected if markers were sampled at random in the global population. (a) Bone markers; (b) Muscle markers.

The statistical significance of the distribution of Bone markers can be further quantified by assigning a P value Pks obtained by use of the Kolmogorov-Smirnov test (Keeping 1995) against the reference distribution that would be obtained from a random sample of the population. For the data presented in Figure 1a, one finds PInline graphic = 2.9 × 10−15, a high level of significance confirming the visual impression of pronounced skewness (note that C and Pks are not redundant quantities, as one can have C ∼ 1 alongside Pks << 1).

The distribution of Muscle markers in the global χ2 ranking (Fig. 1b), with CMuscle = 1.1 only, is much less concentrated near the top than for the Bone markers. Nonetheless, the distribution is still significantly different from random, as quantified by PInline graphic = 5.1 × 10−3 and as visible in the figure. Finally, the distribution of Adipocyte markers (figure not shown) is essentially uniform, with CAdipo = 1 and PInline graphic = 0.78.

The profile concentrations and P values Pks for the Bone, Muscle, and Adipocyte markers quantify the global responses along each of the three pathways of the C2C12 cell line subjected to the treatments with BMP-2 and TGF-β1, and, hence, can be thought of as diagnostics for ascertaining whether or not significant response is occurring along a given pathway. 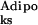Thus, the P values obtained above are consistent with the phenotype of the C2C12 premyoblasts, which can be induced into the osteoblastic pathway upon BMP-2 treatment (PInline graphic, PInline graphic << 1), but do not spontaneously express the adipocytic phenotype (PInline graphic ∼ 1).

χ2 Filtering of the Data

With profiles ranked according to the χ2 statistic, one can proceed with data reduction through profile elimination, a step we will refer to as the χ2 filter. Here, the first Nχ2 = 2500 qualifiers were selected from the ranked list, a number determined heuristically to insure that relative to the training set, about half of the Bone markers were retained. Overall, 109 markers are retained from the total of 484 initially present in the training set, leaving 2391 blank qualifiers to be classified. Note that 22% of the training set markers are retained by filtering the overall data set to 7.3% of its original size, resulting in a threefold relative enrichment of the marker population. In filtering out the noisiest profiles, we are nonetheless also losing 78% of the training set; this is a necessary cost when dealing with microarray data, in which typical signal-to-noise ratios are low (for Affymetrix chips, the median signal-to-noise ratio is only about 3) (Theilhaber et al. 2001). It should also be emphasized that the initial choice of Nχ2 is arbitrary, and is validated a posteriori by whether an acceptable error rate obtains in the nearest-neighbor classification. A method for the systematic optimization of Nχ2 is discussed below, in which it is found that the original heuristic choice of 2500 is, in fact, very close to optimal.

Principal Component Analysis

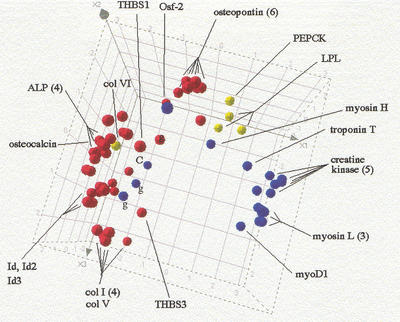
The data set reduced to Nχ2 = 2500 qualifiers was then transformed by generating for each fold change, a new value R' = Sym(R), in which the Sym function equally emphasizes up- and down-regulation and is linear in R and 1/R as R → ∞ and R → 0, respectively (equation 4, Methods). Each profile was then normalized according to a standard procedure (Späth 1980), by subtracting from each value the mean and by dividing by the standard deviation of all components in the profile. Further restricting the data set to just the 109 training set members present, a principal component analysis (PCA) was performed (Ripley 1996). The profiles of the 44 Bone, 20 Muscle, and 5 Adipocyte markers present, projected onto the space defined by the first three principal components, are shown in Figure 2, in which they are labeled red, blue, and yellow, respectively.

Figure 2.

Figure 2

Open in a new tab

Principal component representation for the training set. The profiles of the 44 Bone, 20 Muscle, and 5 Adipocyte training set qualifiers present in the C2C12 reduced data set (Nχ2 = 2500) are projected onto the space defined by their first three principal components. (Bone) Red; (Muscle) blue; (Adipocyte) yellow. (ALP) Alkaline phosphatase; (col) collagen; (THBS) thrombospondin; (myosin H and L) myosin heavy and light chains, respectively; (g) gamma-actin; (c) creatine kinase. Numbers in parenthesis indicate multiplicity of qualifiers mapping to the same gene.

Figure 2 shows that, notwithstanding a few exceptions, the markers of the different pathways are clearly segregated in expression space. The exceptions are col VI, an Adipocyte marker, which is positioned deep in the Bone cluster, and four Muscle markers (3 qualifiers for γ-actin, labeled g, and one for creatine kinase, labeled C), which are positioned at the boundary of the Bone cluster. Note, that as would be expected, in most cases all qualifiers mapping into the same gene are very close to each other in expression space, reflecting the fact that they are measuring the abundance of a unique transcript. This is the case for the six osteopontin, the four alkaline phosphatase (ALP), the three myosin light chain (myosin L) qualifiers, and so on. On the other hand, the presence of a single qualifier for creatine kinase (c) deep in the Bone cluster and remote from the five other tightly grouped creatine kinase qualifiers, suggests an annotation error, or that perhaps the chip features are registering a spurious signal due to cross-hybridization. Conversely, the consistent positioning of the three γ-actin qualifiers (g) at the border of the Bone cluster indicates that their location is not an artefact and their regulation is more Bone-like than Muscle-like (we did not attempt to manually edit out these apparently misclassified instances from the training set).

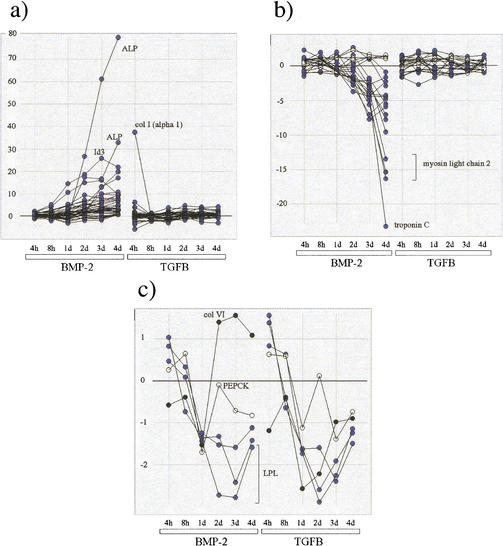
The connection between the representation afforded by Figure 2 and the actual expression profiles is made through Figure 3a, b, and c, which show the profiles superposed for each of the Bone, Muscle, and Adipocyte classes. Thus, the overall signature of the Bone markers is seen to be one of strong up-regulation during the time course with BMP-2 treatment (Fig. 3a), that of the Muscle markers is strong down-regulation during the same time course (Fig. 3b), and for the Adipocyte markers (Fig. 3c), moderate down-regulation during both BMP-2 and TGF-β1 time courses. These observations are in agreement with the expected C2C12 phenotypic response to BMP-2 and TGF-β1 treatments.

Figure 3.

Figure 3

Open in a new tab

Comparison of expression profiles for the Bone, Muscle, and Adipocyte training set qualifiers present in the C2C12 reduced data set (Nχ2 = 2500). (a) Superposition of profiles for the 44 Bone markers (15 distinct genes); (ALP) alkaline phosphatase; [col I (α 1)] type I collagen chain. (b) superposition of profiles for the 20 Muscle markers (nine genes). (○) γ Actin. (c) Superposition of profiles for the five Adipocyte markers (three genes); (col VI) type VI collagen; (PEPCK) phosphoenolpyruvate carboxykinase; (LPL) lipoprotein lipase. All expression ratios have been transformed according to the Sym(R) function (see text and equation 4, Methods).

If, in addition, the positions of the 19 Tubulin and 21 Hsp markers present are imported into Figure 2 (Supplementary Fig. 1, available as an on-line assignment at www.genome.org), it is found that these markers do not cluster with any of the classes examined previously, but rather uniformly fill the spaces between the clusters. This confirms their role as negative controls, delineating the regions of expression space bordering on the Bone, Muscle, or Adipocyte clusters.

The kNN Classification Method

The classification of the 2391 blank qualifiers in the reduced data set (Nχ2 = 2500) was accomplished by GENNC. The classification method embodied in GENNC is the so-called kNN method (Duda and Hart 1973; Fukunaga 1990; Ripley 1996), which we have modified by preliminary noise-filtering steps. As with many other classifiers, the starting point is a data representation in an m-dimensional space of points (Duda and Hart 1973), in which m is the number of values in each expression profile (m = 12 in the present case). This representation is obtained by mapping each profile into a single, m-dimensional point, whose coordinates are given by the values (intensities or expression ratios) defining the original profile. Under this transformation, the distance between two profiles can then be defined precisely as the geometrical (Euclidean) distance between the two corresponding points in dimensions.

GENNC proceeds in three steps. The first step, the χ2 filtering of the data, was already described above, and is fully specified by the parameter Nχ2, the number of ranked profiles to be passed by the filter. The second step, called correlation filtering, eliminates from further consideration all qualifiers that do not have significant correlation with any of the members of the training set, the goal being to exclude qualifiers that do not belong to any of the classes represented in the training set (Ripley 1996), or for which the data is noisy and inconsistent. The third step, called assignment, which is applied to all the qualifiers that passed the first two steps, uses the kNN method proper for establishing classification.

The correlation filter is applied as follows. For each blank qualifier, the Pearson correlation coefficients between its profile, and the profiles of all of the markers in the training set are calculated, and the maximum rmax is recorded. A P value is then assigned to the qualifier by performing a randomization test on rmax (see Methods). Finally, the filter is implemented by excluding all qualifiers for which P > P0, in which the threshold P0 is an adjustable parameter (the optimal choice of P0 is discussed below). Note that all qualifiers excluded by either the χ2 or by the correlation filter are assigned the default classification None.

Each qualifier that passes the filtering steps is then submitted to the assignment step, which uses the so-called voting form of the kNN method (Fukunaga 1990) to assign a classification. A fixed number k is chosen (typically in the range of from 1 to 10). For each qualifier, its k-nearest-neighbors in the training set are then examined. The class that is most frequently represented among these k-nearest-neighbors is then assigned to the qualifier. In case of a tie between two or more classes, the qualifier is assigned the default classification None (in effect, it is not classified), a conservative assignment reducing the number of false positives potentially occurring at class boundaries in expression space.

It should be mentioned that whereas the temporal nature of the data is not explicitly taken into account by the kNN method (which depends only on a distance metric in which time ordering is irrelevant), temporal dependency is still implied, insofar as the training set members have characteristic expression profiles over time and induce classification of genes with similar expression profiles.

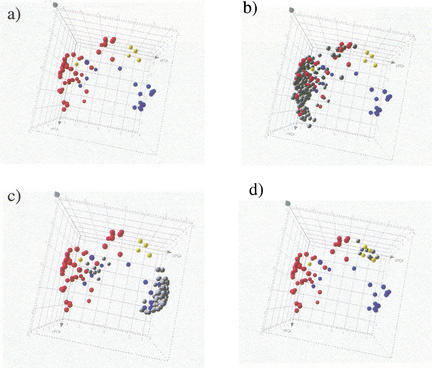
In Figure 4, a–d, we illustrate in a three-dimensional representation the class assignments that obtain when the χ2-filtered data set (Nχ2 = 2500, 109 markers present) is classified with P0 = 0.01 and k = 2. Note that whereas Figure 4, a–d use the same three-dimensional representation as in Figure 2, on the basis of a PCA restricted to the 109 training set markers, the actual classification is done in the full m = 12-dimensional expression space. For the given value of P0, only 896 blank qualifiers pass the correlation filter, the others being assigned the classification None and removed from further consideration. Figure 4a (identical to Fig. 2, but without labels) shows the training set markers alone, composed of 44 Bone, 20 Muscle, and 5 Adipocyte markers, labeled red, blue, and yellow, respectively. Figure 4b shows the set of 201 new qualifiers (176 genes) that get assigned the class Bone, Figure 4c shows the 102 new qualifiers (85 genes) assigned the class Muscle, and finally, Figure 4d shows the 8 new qualifiers (8 genes) assigned the class Adipocyte. In addition, and not shown in the figures, are 109 new qualifiers (89 genes) assigned the class Tubulin (based on the 19 Tubulin markers), and 137 new qualifiers (126 genes) assigned the class Hsp (based on the 21 Hsp markers). Finally, for a total of 33,092 blank qualifiers, classification was not assigned (class None), either because the qualifier did not pass the filtering steps, or because a tied vote occurred during the assignment step. Note that the assignment of a large number of qualifiers to the three classes Tubulin, Hsp, and None results in a conservative clustering of the remaining assignments, Bone, Muscle, and Adipocyte, thereby reducing the number of false positives. Table 1 lists the breakdown of class assignments (an alternative representation of the classification process just described above, using a “heat map,” is shown in Supplementary Fig. 2, available as an online assignment at www.genome.org).

Figure 4.

Figure 4

Open in a new tab

The kNN classification process represented in PCA space, the input (colored) and output (grey) classes for Bone, Muscle, and Adipocyte, using the same principal component coordinates as in Fig. 2. GENNC with parameters Nχ2 = 2500, P0 = 0.01, and k = 2 was applied to the C2C12 data set. (a) Training set qualifiers only, with Bone labeled red (44), Muscle labeled blue (20), and Adipocyte labeled yellow (5). (b) A total of 201 blank qualifiers are assigned to Bone. (c) a total of 102 blank qualifiers are assigned to Muscle. (d) A total of eight blank qualifiers are assigned to Adipocyte.

Table 1.

Gene Classification Results

Class Number of qualifiers Number of genes S FPu
Bone 201 176 0.42 0.12
Muscle 102 85 0.09 0.31
Adipocyte 8 8 0.04 ∼1
Tubulin 109 89 0.04 0.39
Hsp 137 126 0.14 0.42
None 33,092
Total 33,649
Open in a new tab

Overall classification results for the C2C12 data set with classifier parameters Nχ2 = 2500, P0 = 0.01 and k = 2. For each class, the number of assigned qualifiers and the corresponding number of genes are indicated. S denotes the estimated sensitivity and FPu the estimated false-positive rate for the detection of the members of the indicated class. The initial data set contains 34,130 qualifiers, of which 481 are already in the training set. Of the remaining 33,649 unclassified qualifiers (total indicated at bottom of table), 557 (1.7%) are assigned by GENNC to one of the five classes Bone, Muscle, Adiopocyte, Tubulin or Hsp, with classification declined for the remaining 33,092 qualifiers (classification None). 

Optimization of Classifier Parameters

The method for optimizing the classifier parameters Nχ2, P0, and k is based on an analysis of the misclassification error rates as a function of these parameters. To estimate error rates, we combine two estimates, one accounting for misclassifications of qualifiers belonging to the classes present in the training set, and the other accounting for misclassification of qualifiers from other classes not explicitly represented in the training set.

To estimate the error arising from the classes present in the training set, we use the training set itself in an explicit leave-one-out cross-validation (LCV) (Ripley 1996). By this method, one removes a single instance at a time from the training set, and then observes how it is classified by the remaining training set instances, thereby simulating the classification of independent test data with a training set of very nearly the same size as the original one. For a given class, we estimate the detection sensitivity S by the number, under LCV, of correctly classified instances of that class divided by the total number of instances in the class. We also estimate a posterior false-positive rate FPcv for the detection of a given class, with FPcv defined as the probability that an instance already classified, say, as Bone, is not actually in the Bone class; FPcv measures the contamination of a list of putative class members by false positives and is a direct measure of the quality of the (FPcv is equal to 1 minus the so-called “purity” of the candidate list (Cowan, 1998, p. 49); it has also been called the “false-discovery rate” (Tusher et al., 2001)). We estimate FPcv for a given class by the fraction of all instances assigned under LCV to that class that actually belong to other classes in the training set.

The false-positive rate FPcv, on the basis of LCV alone, is an incomplete error estimate because it does not account for misclassification into the classes represented in the training set of qualifiers from (unknown) classes with no representatives in the training set (Ripley 1996). For a given class, we estimated the effect of these qualifiers by introducing an additional contribution to the false-positive rate, proportional to the Correlation Filter threshold P0 and to the total number of blank qualifiers (see Methods). The combination of this term with FPcv yields an upper bound, denoted by FPu, to the total false-positive rate.

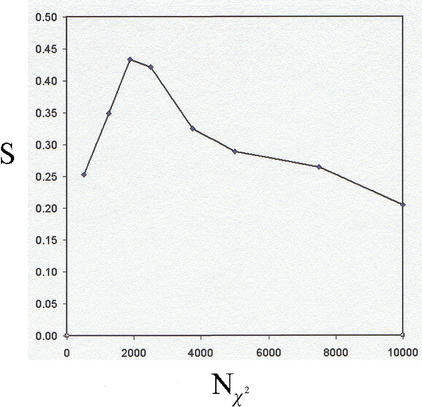
We first conducted a systematic investigation of the dependence of S and FPu for Bone on the number of nearest-neighbors, for k in the range of 1 to 10, and for fixed Nχ2 = 2500 and P0 = 0.01 (an initial, heuristic choice). Although the sensitivity was approximately constant for all values of k (S ≈ 0.4), the false-positive rate was lowest for k = 2 (FPu = 0.12), and we fixed k = 2 in what follows (so that class assignments occur only when both nearest neighbors belong to the same class). The choice of Nχ2 could then be optimized to insure maximum sensitivity at the given level of selectivity. We thus investigated the variation of the sensitivity for a constant false-positive rate FPu = 0.12, maintained by continuously adjusting P0, whereas Nχ2 was allowed to vary. The dependence of the sensitivity on Nχ2 for the detection of Bone markers is shown in Figure 5 for the range 500 ≤ Nχ2 ≤ 10,000.The distinguishing feature of Figure 5 is that it has a maximum of S* = 0.44 at N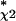Inline graphic = 2,000, which represents an optimal balance between the stringency of the two filtering steps and the accuracy of the nearest-neighbor classifier. The existence of the maximum in Figure 5 is a central result; it shows that it is possible to optimize the classifier parameters according to a quantitative criterion, and to estimate the classification error rates at that optimum.

Figure 5.

Figure 5

Open in a new tab

Dependence, for the detection of Bone qualifiers, of the sensitivity S on the χ2 filtering step parameter Nχ2 (number of qualifiers passed after χ2 ranking). For a given Nχ2, the reduced C2C12 data set is classified by GENNC with fixed k = 2, and with the Correlation Filter threshold P0 adjusted to maintain a false-positive rate FPu = 0.12. The maximum sensitivity occurs for N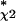Inline graphic = 2,000, S* = 0.44

Biological Cross-Validation of Assigned Genes

We focus on the selection of genes (Table 1) brought on by the classifier parameters Nχ2 = 2500, P0 = 0.01, and k = 2 with resulting sensitivity for detection of Bone markers S = 0.42 (± 0.05) and false-positive rate FPu = 0.12. This choice was initially made on heuristic grounds, but it is very close close to the optimal value N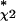Inline graphic ≈ 2,000. (S* = 0.44) determined by Figure 5. Table 1 also lists estimated sensitivities for the four other classes represented in the training set. The sensitivity and false-positive rate for detection of myoblastic genes are 0.09 and 0.31, respectively, for detection of Hsp genes 0.14 and 0.42, respectively, and the sensitivities for the detection of Adipocyte and Tubulin genes are very low, S = 0.04. These results are in accordance with the experiment design, which predominantly stimulated the osteogenic pathway. The fact that the optimal sensitivity for detecting osteogenic genes is still considerably less than 1 (less than one chance in two of detecting a known Bone marker), is a reflection of the cost of detecting genes against a noisy background while maintaining an acceptably low false-positive rate.

Although the error model and internal cross-validation procedures described above are guides for parameter optimization of the classifier, they are no substitute for biological cross-validation of the results. To that end, we examined expression data from a biological assay completely independent of the C2C12 cell line. Primary calvaria (skull bone) cells derived from 2-day-old mouse pups were extracted and cultured in differentiation medium for 21 d. RNA samples were prepared from cells harvested at day 0, 2, 7, 14, and 21 (T. Garcia, S. Roman-Roman, A. Jackson, J. Theilhaber, T. Connolly, S. Spinella-Jaegle, S. Kawai, B. Courtois, S. Bushnell, M. Auberval, et al., in prep.). This widely studied experimental model (Rodan and Noda 1991) realizes, in a biologically more realistic setting, the osteoblast differentiation processes induced in the C2C12 myoblastic cell line by BMP-2. Thus, many of the genes classified on the basis of the C2C12 experiments as belonging to the Bone or Muscle pathways, should also be strongly regulated during the temporal progression of the calvaria primary cells.

As with the C2C12 samples, all calvaria samples were hybridized in duplicate to the complete Affymetrix 35K mouse chip set, and a single, composite data set containing all of the expression data was assembled, resulting in 34,130 expression profiles of 5 time-points each. All expression values were expressed as ratios, relative to the first time point. The 34,130 expression profiles were then ranked according to the χ2 statistic, thereby giving highest rank to profiles with the greatest variation across the five time points. It should be emphasized that the χ2 statistic does not distinguish between up- or down-regulation, nor between early or late induction or repression, but is rather a global measure of variation during the time course.

Validation of Bone Class Members

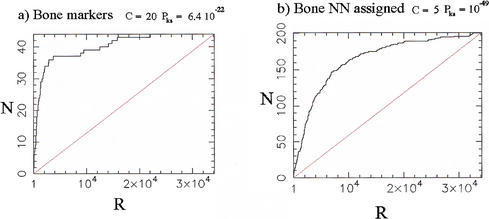
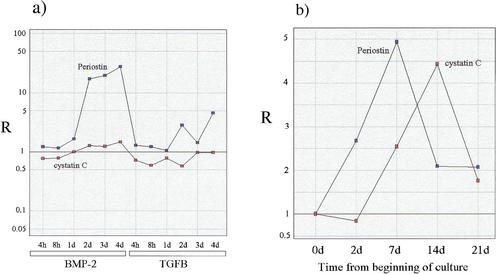
The distribution relative to the global χ2 ranking of the calvaria profiles, of the 44 Bone markers in the training set that were present after χ2 filtering of the C2C12 data (Nχ2 = 2500), is shown in Figure 6a. The over-representation of these markers in the set of strongly regulated profiles is evident in the figure and statistically highly significant (C = 20, Prs = 6.4 × 10−22), however, these results were to be expected on the basis of the original choice of the markers as osteogenic, and can be said to only confirm the soundness of the choice. On the other hand, the distribution in the calvaria data of the 201 qualifiers classified as Bone by GENNC, (Fig. 6b) is also strongly nonuniform and statistically significant (C = 5.0, Pks = 10−49) and was not expected a priori. In other words, a large fraction of the genes selected as relevant to osteogenesis solely on the basis of the nearest-neighbor classification, are found to be strongly regulated in the independent calvaria experiments. A more specific comparison of expression profiles is shown in Figure 7 for Cystatin C, an inhibitor of cysteine protease shown recently be expressed by osteoblasts and to inhibit bone resorption in vitro (Lerner et al. 1997; Candeliere et al. 1999) and periostin (also known as Osf-2) a 90-kD protein that is selectively expressed in osteoblasts and functions as a homophilic adhesion molecules in bone formation (Takeshita et al. 1993). It is of interest to note that whereas periostin was selected by GENNC on the basis of a very strongly regulated profile in the C2C12 time courses, cystatin C was selected on the basis of a much more muted expression profile (Fig.7, cf. a and b); nonetheless, both genes display strong induction during the calvaria time course.

Figure 6.

Figure 6

Open in a new tab

Distribution in the χ2 statistic of the Bone markers and of qualifiers assigned to Bone by GENNC using the C2C12 data set, relative to the expression data from the calvaria primary cell cultures. In each figure, a rank R of 1 denotes the most variable (significant) profile, a rank of 34,130 the least variable (least significant) profile. N indicates the cumulative number of markers found with rank below or equal to the rank R indicated on the abcissa. C denotes the profile concentration of the qualifiers (see text and equation 3 in Methods) and Pks the companion P value. The straight lines indicate the distributions expected if markers are positioned at random in the global population. (a) Distribution of the 44 Bone markers (from the training set); (b) distribution of the 201 qualifiers assigned to Bone by nearest-neighbor classification (Nχ2 = 2500, k = 2, and P0 = 0.01).

Figure 7.

Figure 7

Open in a new tab

Expression profiles for periostin (Osf-2) and cystatin C. (a) Ratios of expression in the treated to expression in the control samples for the two C2C12 time courses under treatment with BMP-2 and TGFB; (b) ratios of expression relative to the first time point for the time course generated by the calvaria primary cell culture.

For the 176 genes assigned to Bone by the nearest-neighbor classifier, a functional assignment based on annotation could be readily found for 78 (Supplementary Table 2, available as an online assignment at www.genome.org), the remaining 98 genes corresponding to currently unannotated Affymetrix qualifier sequence. The potential relevance of the 78 annotated genes in the differentiation and maturation process and in the function of osteoblasts is highlighted by the fact that 19 of the 78 genes have been shown to play revelant roles in bone biology. Eight genes encode for matrix proteins, including α2 collagen type VI, osteonectin, CACP/megakaryocyte stimulating factor precursor, the small leucine-rich proteoglycans (SLRPs), biglycan, and fibromodulin, and the cell-surface heparan sulfate proteoglycans syndecan-1, N-syndecan, and glypican. Fibromodulin and biglycan are known to be expressed at sites of cartilage and bone formation and interstitial tissue deposition (Wilda et al. 2000) and importantly, targeted disruption of the biglycan gene has been reported to lead to an osteoporosis-like phenotype in mice (Xu et al. 1998). CACP is mutated in camptodactyly-arthropathy-coxa vara-pericarditis syndrome (Marcelino et al. 1999). Controlled expression of syndecans by cells of the osteoblast lineage has been suggested recently to play an important role in the regulation of osteoblastic proliferation and differentiation (Birch and Skerry 1999). Two genes encode for proteins involved in adhesion and cell-cell contact, periostin (already mentioned above) and connexin 43. Periostin, previously called osteoblast-specific-factor-2 (Osf-2), plays a role in the recruitment and attachment of osteoblast precursors in the periosteum (Horiuchi et al. 1999), and enhancement of connexin 43 expression has been shown to increase both proliferation and differentiation of osteoblasts (Gramsch et al. 2001). Three genes encode for transcription factor-related proteins, the homeobox transcription factor Prx2, the AP-1 family member fra-1, and Smad6. The role of Smad6 in osteoblast and chondroblast differentiation has been investigated recently by Fuji et al. (1999). Interestingly, Prx-1 has been shown to function in cooperation with Prx-2 to maintain cell fates within the craniofacial mesenchyme (Lu et al. 1999), and mice overexpressing fra-1 display an increased bone formation and osteosclerosis (Jochum et al. 2000). Four genes encode secreted proteins including TGF-β1, FISP-12/CTGF, BMP-1, and cystatin C (already mentioned above). The role of TGF-β1 in bone biology has been described largely (for review, see Centrella et al. 1994). FISP-12 is capable of stimulating the proliferation and differentiation of osteoblasts in addition to chondrocytes and endothelial cells (Nishida et al. 2000). The metalloproteinase BMP-1 has been suggested recently to influence matrix maturation during skeletogenesis (Reynolds 2000). Concerning the cysteine proteinase inhibitor cystatin C, it has been reported that this protein is produced by osteoblasts and inhibits bone resorption (Lerner et al. 1997; Candeliere et al. 1999). Our method also classified the prostaglandin E receptor and gluthatione peroxidase genes. Prostaglandin E2 has been reported to have multiple actions in the osteoblast, such as growth promotion and cell differentiation, and different Prostaglandin E receptor subtypes have been reported to be expressed in osteoblastic cells (Suda 1996). Finally, it has been suggested that the expression of selenoproteins, like glutathione peroxidases, in osteoblasts may represent a new system of osteoblast antioxidative defense that may be relevant for the protection against hydrogen peroxide produced by osteoclasts during bone remodeling (Dreher 1998). The relevance to bone biology of the other 59 annotated genes need to be studied further, but their expression association with bone-relevant genes suggests that they might play a role in the osteoblast function. Note, however, the existence of at least two obvious false positives (myosin heavy chain and myosin regulatory light chain), consistent with the finite false-positive rate of the classification, FPu = 0.12.

DISCUSSION

In connection with an experimental study of osteogenesis, we presented a new method for analyzing large-scale gene expression data, and for extracting sets of genes relevant to given classes of biological processes. This method, embodied in the computer program GENNC, is based on a supervised learning approach, the kNN method, coupled to a set of noise-reduction algorithms. A central feature of the method is that it provides error estimates (sensitivity and false-positive rates), which allow for optimization of the classifier and which remove much of the arbitrariness of selection that is often present when one uses unsupervised methods.

GENNC was used to find genes in the osteogenic pathway of the C2C12 cells, and, in addition to 28 genes in the training set, classified a group of 176 genes (selected from an inititial data set containing 34,130 expression profiles) as belonging to the bone pathway. The estimated sensitivity was ∼42% (±5%), at a false-positive rate (fraction of spurious assignments) of 12% (±2%). As a means of biological cross-validation, the expression of these genes was then analyzed in an independent, primary cell culture derived from mouse calvaria. Both a global, statistical analysis of the expression profiles of the genes in the calvaria, as well as a case-by-case, expert analysis of some of the candidates judged most interesting on the basis of annotation, supported the overall validity of the assignment (although ultimate validation of osteogenic relevance must necessarily come from more experimentation).

It should be noted that the experimental design focused on the effects of treatment and time, but did not explore the intrinsic biological variation between cell cultures; such a study would have been possible only if we had replicated all cell cultures at least once, which we did not. Although this situation may lead to spurious results, for instance, if one of the cell cultures displayed atypical behavior during its time course, we believe that we have two controlling factors; first, the existence of an externally determined set of relevant genes (the training set) gives global indications of success or failure in stimulating a given pathway; second, we have validated the selection of genes on the basis of the C2C12 data by examining their regulation in an independent biological assay (the calvaria primary cell culture). Of course, pending more available resources, biological replicates would have been a welcome addition to the experimental design.

Some additional comments can be made regarding the significance of the class assignments. First, the error estimates are only as good as the training set that is provided as input to the model; if, as is likely, the training set contains an over-representation of high expressor genes, estimates of sensitivity will tend to be overly optimistic. Second, the assignment of genes to a given class is based on coregulation with the markers of that class, but does not carry information about causal relationships within the class. Thus, assignment to a functional class is not a guarantee that a gene plays a central role in that class; the nature of that role can only be answered by additional domain knowledge or by additional, focused experiments.

Because the concept of the training set is very flexible, the approach embodied by GENNC provides a way to identify gene targets associated with any set of physiologic or patho-physiologic events in which some expert knowledge is available beforehand to define an appropriate training set. Examples of training sets other than the one considered here might be entire metabolic pathways, or again, sets of oncogenes and tumor suppressors, perhaps divided into broad classes according to known association in different types of tumors.

Work in progress on the GENNC classifier includes technical improvements such as developing methods for editing the training set (Ripley 1996). However, it should be emphasized that the biological quality of the training set is essential for the relevance of the final results, and thus, is at least as important as any algorithmic detail of the method.

METHODS

Cell Cultures and Chip Hybridizations

Total RNA samples were obtained from three C2C12 cell cultures (BMP-2 treated, 1 μg/mL, TGF-β-treated, 2.5 ng/ml, and solvent-treated control, HCl 10 mM) by use of the RNAplus kit provided by Quantum, harvesting from each culture at six time points (4 h, 8 h, 1 d, 2 d, 3 d, and 4 d). For every resulting sample, labeled cRNA probes were then generated by reverse transcription followed by in vitro transcription (IVT) incorporating biotin labeling as part of the standard Affymetrix protocol. For each sample, the probes were then hybridized to the complete series of Affymetrix 35K mouse chips (Mu19KsubA, Mu19KsubB, Mu19KsubC, Mu11KsubA, and Mu11KsubB), with two identical chips (replicates) used for every type. Because of constraints on the timing of chip supply, replicate hybridizations did not always correspond to probe prepared from a unique IVT. After hybridization and staining, the chips were scanned by laser. The final data set consisted of a total of 180 scan files, each obtained by use of the Affymetrix GeneChip software, which, for each qualifier in the file, assigns an intensity that is a measure of the corresponding transcript abundance. The output files were further post-processed into a format, which, for each intensity, adds an estimate of the standard deviation of the noise (Theilhaber et al. 2001).

Data Assembly

A total of 120 scan files obtained from the BMP-2 and TGF-β1-treated samples (and post-processed as mentioned above), arranged in order of the BMP-2 time course (6 time points, each in replicate, across 5 chips) and the TGF-β1 time course (6 time points, each in replicate, across 5 chips) were concatenated together into a single file with replicates forming adjacent columns, and with the qualifiers of all 5 chips forming the rows. A similar concatenation was performed on the files obtained from the solvent-treated cell cultures. Replicate data were then combined by computing the average of the replicate intensities. The estimate of the standard deviation of the noise was also propagated. The final step in the data assembly consisted of obtaining for each qualifier the expression ratios of treated to solvent samples for all points in the time courses, which were obtained using both intensity and noise data through a Bayesian estimation algorithm (Theilhaber et al. 2001).

Mathematical Details

χ2 Statistic and Expression Ratios

For a given qualifier, consider a double profile consisting of treated and control expression levels (intensities) for different sampling points, i = 1,2,…,m. The χ2 statistic d2 quantifying the overall change in the profile is defined as

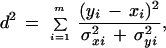graphic file with name M9.gif 1

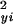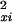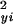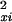in which yi, i = 1,2,…,m are the intensities for the treated samples, xi, i = 1,2,…,m the intensities for the control samples, and in which σInline graphic and σInline graphic are estimates of the variance of the noise present in the measurements of yi and xi, respectively. The variances σInline graphic and σInline graphic include both the effects of chip-to-chip variation and cross-hybridization, and are part of an underlying noise mode (Theilhaber et al. 2001). The ratios Ri ∼ yi/xi are separately estimated by use of a Bayesian estimation scheme (Theilhaber et al. 2001). All intensities are given by the average difference measure of abundance, which is computed by the Affymetrix GeneChip (Lockhart et al. 1996) software algorithm. The average difference is a trimmed mean of the 20 paired differences of intensities, between the 20 perfect match and the 20 mismatch features representing a given qualifier on the chip.

The noise model underlying the variances used in equation 1 has been presented in Theilhaber et al. (2001). Briefly, for a given intensity measurement , the estimated variance σ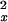Inline graphic noise is written as the sum of two terms,

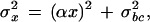graphic file with name M15.gif 2

in which α = 0.25 is a coefficient of variation, derived from a set of Affymetrix-specific development experiments, and in which σ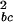Inline graphic. is an intensity-independent variance unique to a given scan, and which simultaneously accounts for background and cross-hybridization effects.

In the specific application to the C2C12 data, m = 12 is the total number of points in each expression profile. The six values of yi for i = 1,2,…6, are given by the six intensities (estimates of abundance) obtained from the BMP-2-treated cell culture, at the sampling times 4 h, 8 h, , 4 d. The corresponding six values of xi, i = 1,2,…,6, are the six intensities obtained from the solvent control cell culture, at the corresponding time points. The six values of yi for i = 6,7,…,12, are given by the six intensities obtained from the TGF-βl-treated cell culture, again at the sampling times 4 h, 8 h, , 4 d, and the corresponding values of xi, for i = 6,7,…,12 are the same, in order, as the ones used for i = 1,2,…,6.

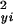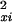If, in equation 1, all intensity observations yi and xi were independent, and the noise model and its estimates of variance σInline graphic and σInline graphic were exact, then the sampling distribution of d2 under the assumption of no significant difference between the profiles in xi and yi would be χ2 with m degrees of freedom. 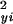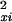In the present situation, these assumptions are not valid, because there is time dependence between successive observations, and the variances σInline graphic and σInline graphic are meant to be approximations only (Theilhaber et al. 2001), so that d2 cannot be used directly in a significance test on the basis of a χ2 distribution. Nonetheless, d2 is very useful as a ranking statistic, and it is used to filter profiles as a pre-processing step for the nearest-neighbor classifier, as described in the main text. The rank threshold for accepting profiles is then determined, not from an absolute significance test, but so as to optimize sensitivity of detection of a given class.

Concentration Measure

The over-representation among most highly regulated profiles of the members of a test data set in a globally ranked data set can be quantified by a concentration measure Cp, defined by

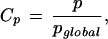graphic file with name M21.gif 3

in which p is a fixed percentile in the test data set (starting from the top of the ranked list), and in which pglobal is the percentile in the global data set of the element with percentile p in the test data set. The choice of p depends on whether one wishes to emphasize the top of the test data distribution (p → 0) or the entire test data distribution (p → 1). In this study, we set p = 0.5, and define C ≡ C0.5.

The Sym Transformation

By the Sym transformation, up or down fold-changes are symmetrically transformed into values R' by the formula

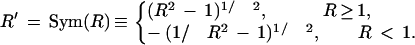graphic file with name M22.gif 4

Although a logarithmic transformation can also be used to perform a symmetric transformation, the Sym transformation has the advantage of not squashing the dynamic range for large or small fold changes.

Randomization Test For Correlation Coefficients

In the Correlation Filter, for each qualifier that is to be classified, the Pearson correlation coefficients between its profile (called the query profile) and all of the markers in the training set are calculated, and the maximum rmax of all of these values is then recorded. To assign a statistical significance to this value, a randomization test is then performed (Sprent 1998); this is done by randomly permuting the values in the query profile Nper times, each time recomputing the Pearson correlation coefficients with all of the training set markers, and recording the resulting maximum, r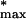Inline graphic. The histogram of r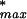Inline graphic is then the basis for defining a P value , which is defined as the fraction of times, out of the Nper randomized samplings, for which r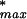Inline graphic > rmax. The parameter Nper specifying the number of random permutations is adjustable, but is determined chiefly by the necessity to adequately sample a large subset of all possible permutations, and should also satisfy Nper >> 1/Pmin, in which Pmin is the smallest P value one wishes to resolve. In this study, we have used Nper = 10,000.

Estimate of Error Rates By Cross-validation

To estimate the effect of the background qualifiers (unknown qualifiers not belonging to any of the classes represented in the training set) on the false-positive rate for classification into a specific class (say for Bone), we make two approximations. We first note that when the Correlation Filter is applied to a total of N0 instances ( the number of blank qualifiers after χ2 Filtering), at a given P value threshold P0, we expect about P0 · N0 spurious instances to be accepted. As a second approximation, we assume a worst-case scenario under the Assignment step, in which all of the spurious instances are classified into Bone.

Let the actual number of blank qualifiers classified into Bone by GENNC be NB. We can estimate an upper bound NFPU for the total number NFP of false positives,

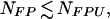graphic file with name M26.gif 5

by adding the expected number of misclassifications from the known classes to those from the background qualifiers, which reside in classes unknown to the training set,

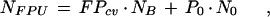graphic file with name M27.gif 6

in which FPcv is obtained by the LCV procedure (Ripley 1996). Note that according to equation 6, NFPU will necessarily be larger than NB as P0 → 1 (because N0 ≥ NB, since the NB Bone-classified qualifiers are chosen from the N0 blank qualifiers), reflecting the crude nature of the estimate. When this occurs, we simply set NFPU = NB. In turn, by dividing equation 6 by NB, an upper bound FPu on the total false-positive rate FP for selecting bone markers can be derived,

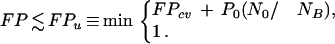graphic file with name M28.gif 7

In equation 7 both FPcv and NB are numerically determined, and given in the GENNC output, N0 is the number of blank qualifiers after χ2 filtering, and P0 is the significance threshold for the Correlation Filter, specified as input by the user.

Acknowledgments

The authors thank Dr. Anatoly Ulyanov and Dr. Michael Rosenberg for providing essential annotation information, as well as for their scientific comments regarding this work.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Footnotes

E-MAIL joachim.theilhaber@aventis.com; FAX (617) 374-8808.

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.182601.

REFERENCES

  1. Alizadeh A, Eisen MB, Davis RE, Ma C, Lossos IS, Rosenwald A, Boldrick JC, Sabet H, Tarn T, Yu X, et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature. 2000;403:503–512. doi: 10.1038/35000501. [DOI] [PubMed] [Google Scholar]
  2. Alon U, Notterman DA, Gish K, Ybarra S, Mack D, Levine AJ. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc Natl Acad Sci. 1999;96:6745–6750. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ben-Dor A, Shamir R, Yakhini Z. Clustering expression patterns. J Computat Biol. 1999;6:281–297. doi: 10.1089/106652799318274. [DOI] [PubMed] [Google Scholar]
  4. Birch, M.A. and Skerry, T.M. Differential regulation of syndecan expression by osteosarcoma cell lines in response to cytokines but not osteotropic hormones. Bone 24: 571–578. [DOI] [PubMed]
  5. Blau HM, Chiu CP, Webster C. Cytoplasmic activation of human nuclear genes in stable heterocaryons. Cell. 1983;32:1171–1180. doi: 10.1016/0092-8674(83)90300-8. [DOI] [PubMed] [Google Scholar]
  6. Brown MPS, Grundy WN, Lin D, Cristiani N, Sugnet CW, Furey TS, Ares M, Jr, Haussler D. Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc Natl Acad Sci. 2000;97:262–267. doi: 10.1073/pnas.97.1.262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Califano A, Stolovitzky G, Tu Y. Analysis of gene expression microarrays for phenotype classification. In: Altman R, editor. Proceedings of the eighth international conference on intelligent systems for molecular biology. Menlo Park, California: AAAI Press; 2000. pp. 75–85. [PubMed] [Google Scholar]
  8. Candeliere GA, Rao Y, Floh A, Sandler SD, Aubin JE. cDNA fingerprinting of osteoprogenitor cells to isolate differentiation stage-specific genes. Nucleic Acids Res. 1999;27:1079–1083. doi: 10.1093/nar/27.4.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Centrella M, Horowitz MC, Wozney JM, McCarthy TL. Transforming growth factor-β gene family members and bone. Endocr Rev. 1994;15:27–39. doi: 10.1210/edrv-15-1-27. [DOI] [PubMed] [Google Scholar]
  10. Cowan G. Statistical Data Analysis. Oxford, U.K: Clarendon Press; 1998. Statistical Tests; pp. 48–50. [Google Scholar]
  11. Dreher I, Schutze N, Baur A, Hesse K, Schneider D, Kohrle J, Jakob F. Selenoproteins are expressed in fetal human osteoblast-like cells. Biochem Biophys Res Commun. 1998;245:101–107. doi: 10.1006/bbrc.1998.8393. [DOI] [PubMed] [Google Scholar]
  12. Duda RO, Hart PE. Pattern Classification and Scene Analysis. New York: John-Wiley; 1973. Nonparametric Techniques. pp. 98–105. [Google Scholar]
  13. Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fuji M, Takeda K, Imamura T, Aoki H, Sampath TK, Enomoto S, Kawabata M, Kato M, Ichijo H, Miyazono K. Roles of bone morphogenetic protein type I receptors and Smad proteins in osteoblast and chondroblast differentiation. Mol Biol Cell. 1999;10:3801–3813. doi: 10.1091/mbc.10.11.3801. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fukunaga K. Introduction to statistical pattern recognition. 2nd ed. New York: Academic Press; 1990. Nonparametric Classification and Error Estimation; pp. 303–322. [Google Scholar]
  16. Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh M L, Downing JR, Caligiuri MA, et al. Molecular classification of cancer: Class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–538. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
  17. Gramsch B, Gabriel HD, Wiemann M, Grummer R, Winterhager E, Bingmann D, Schirrmacher K. Enhancement of vonnexin 43 rxpression increases proliferation and differentiation of an osteoblast-like vell line. J Bone Miner Res Exp Cell Res. 2001;264:397–407. doi: 10.1006/excr.2000.5145. [DOI] [PubMed] [Google Scholar]
  18. Grigoriadis AE, Heersche JN, Aubin J. Differentiation of muscle, fat, cartilage and bone from progenitor cells present in a bone-derived clonal cell population; effect of dexamethasone. J Cell Biol. 1988;106:2139–2151. doi: 10.1083/jcb.106.6.2139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Grimaldi PA, Teboul L, Inadera H, Gaillard D, Amri EZ. Trans-differentiation of myoblasts to adipoblasts: Triggering effects of fatty acids and thiazolidinediones. Prostaglandins Leukot Essent Fatty Acids. 1997;1:71–75. doi: 10.1016/s0952-3278(97)90495-6. [DOI] [PubMed] [Google Scholar]
  20. Groeneveld EH, Burger EH. Bone morphogenetic proteins in human bone regeneration. Eur J Endocrinol. 2000;142:9–21. doi: 10.1530/eje.0.1420009. [DOI] [PubMed] [Google Scholar]
  21. Halevy O, Novitch BG, Spicer DB, Skapek SX, Rhee J, Hannon GJ, Beach D, Lassar AB. Correlation of terminal cell cycle arrest of skeletal muscle with induction of p21 by MyoD. Science. 1995;267:1018–1021. doi: 10.1126/science.7863327. [DOI] [PubMed] [Google Scholar]
  22. Horiuchi K, Amizuka N, Takeshita S, Takamatsu H, Katsuura M, Ozawa H, Toyama Y, Bonewald LF, Kudo A. Identification and characterization of a novel protein, periostin, with restricted expression to periosteum and periodontal ligament and increased expression by transforming growth factor β. J Bone Miner Res. 1999;14:1239–1249. doi: 10.1359/jbmr.1999.14.7.1239. [DOI] [PubMed] [Google Scholar]
  23. Jochum W, David JP, Elliott C, Wutz A, Plenk H, Jr, Matsuo K, Wagner EF. Increased bone formation and osteosclerosis in mice overexpressing the transcription factor Fra-1. Nat Med. 2000;6:980–984. doi: 10.1038/79676. [DOI] [PubMed] [Google Scholar]
  24. Karsenty G. The genetic transformation of bone biology. Genes & Dev. 1999;13:3037–3051. doi: 10.1101/gad.13.23.3037. [DOI] [PubMed] [Google Scholar]
  25. Katagiri T, Yamaguchi A, Komaki M, Abe E, Takahashi N, Ikeda T, Rosen V, Wozney JM, Fujisawa-Sehara A, Suda T. Bone morphogenetic protein-2 converts the differentiation pathway of C2C12 myoblasts into the osteoblast lineage. J Cell Biol. 1994;127:1755. doi: 10.1083/jcb.127.6.1755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Keeping ES. Intoduction to statistical inference. New York: Dover; 1995. Non-parametirc Statistical Tests; pp. 256–260. [Google Scholar]
  27. Lerner UH, Johansson L, Ranjso M, Rosenquist JB, Reinholt FP, Grubb A. Cystatin C, an inhibitor of bone resorption produced by osteoblasts. Acta Physiol Scand. 1997;161:81–92. doi: 10.1046/j.1365-201X.1997.d01-1933.x. [DOI] [PubMed] [Google Scholar]
  28. Lockhart DJ, Dong H, Byrne MC, Follettie MT, Gallo MV, Chee MS, Mittmann M, Wang C, Kobayashi M, Horton H, et al. Expression monitoring by hybridization to high-density oligonucleotide arrays. Nat Biotechnol. 1996;14:1675–1680. doi: 10.1038/nbt1296-1675. [DOI] [PubMed] [Google Scholar]
  29. Lu MF, Cheng HT, Kern MJ, Potter SS, Tran B, Diekwisch TG, Martin JF. Prx-1 functions cooperatively with another paired-related homeobox gene, prx-2, to maintain cell fates within the craniofacial mesenchyme. Development. 1999;126:495–504. doi: 10.1242/dev.126.3.495. [DOI] [PubMed] [Google Scholar]
  30. Marcelino J, Carpten JD, Suwairi WM, Gutierrez OM, Schwartz S, Robbins C, Sood R, Makalowska I, Baxevanis A, Johnstone B, et al. CACP, encoding a secreted proteoglycan, is mutated in camptodactyly-arthropathy-coxa vara-pericarditis syndrome. Nat Genet. 1999;23:319–322. doi: 10.1038/15496. [DOI] [PubMed] [Google Scholar]
  31. Nishida T, Nakanishi T, Asano M, Shimo T, Takigawa M. Effects of CTGF/Hcs24, a hypertrophic chondrocyte-specific gene product, on the proliferation and differentiation of osteoblastic cells in vitro. J Cell Physiol. 2000;184:197–206. doi: 10.1002/1097-4652(200008)184:2<197::AID-JCP7>3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
  32. Reynolds SD, Zhang D, Puzas JE, O'Keefe RJ, Rosier RN, Reynolds PR. Cloning of the chick BMP1/Tolloid cDNA and expression in skeletal tissues. Gene. 2000;248:233–243. doi: 10.1016/s0378-1119(00)00114-1. [DOI] [PubMed] [Google Scholar]
  33. Ripley BD. Pattern recognition and neural networks. Cambridge, UK: University Press; 1996. [Google Scholar]
  34. Rodan GA, Noda M. Gene expression in osteoblastic cells. Crit Rev Euk Gene Expr. 1991;1:85–98. [PubMed] [Google Scholar]
  35. Ross DT. Systematic variation in gene expression patterns in human cancer cell lines. Nat Genet. 2000;24:227–244. doi: 10.1038/73432. [DOI] [PubMed] [Google Scholar]
  36. Späth H. Cluster analysis algorithms. New York: John Wiley; 1980. p. 20. [Google Scholar]
  37. Sprent P. Data driven statistical methods. London, UK: Chapman and Hall; 1998. Correlation and Concordance; pp. 225–231. [Google Scholar]
  38. Suda M, Tanaka K, Natsui K, Usui T, Tanaka I, Fukushima M, Shigeno C, Konishi J, Narumiya S, Ichikawa A, et al. Prostaglandin E receptor subtypes in mouse osteoblastic cell line. Endocrinology. 1996;137:1698–1705. doi: 10.1210/endo.137.5.8612504. [DOI] [PubMed] [Google Scholar]
  39. Takeshita S, Kikuno R, Tezuka K, Amann E. Osteoblast-specific factor 2: Cloning of a putative bone adhesion protein with homology with the insect protein fasciclin I. Biochem J. 1993;294:271–278. doi: 10.1042/bj2940271. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Tamayo P, Slonim D, Mesirov J, Zgu Q, Kitareewan S, Dmitrovsky E, Lander ES, Golub TR. Interpreting patterns of gene expression with self-organizing maps: Methods and applications to homeopoietic differentiation. Proc Natl Acad Sci. 1999;96:2907–2912. doi: 10.1073/pnas.96.6.2907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Taylor SM, Jones PA. Multiple new phenotypes induced in 10T1/2 and 3T3 cells treated with 5-azacytidine. Cell. 1979;17:771–779. doi: 10.1016/0092-8674(79)90317-9. [DOI] [PubMed] [Google Scholar]
  42. Teboul L, Gaillard D, Staccini L, Inadera H, Amri EZ, Grimaldi PA. Thiazolidinediones and fatty acids convert myogenic cells into adipose-like cells. J Biol Chem. 1995;270:28183–28187. doi: 10.1074/jbc.270.47.28183. [DOI] [PubMed] [Google Scholar]
  43. Theilhaber J, Bushnell S, Jackson A, Fuchs R. Bayesian estimation of fold-changes in the analysis of gene expression: the PFOLD algorithm. J Comp Biol. 2001;8:585–614. doi: 10.1089/106652701753307502. [DOI] [PubMed] [Google Scholar]
  44. Triffitt JT. Principles of bone biology. San Diego, CA: Academic Press; 1996. The stem cell of the osteoblast; pp. 39–50. [Google Scholar]
  45. Tusher VG, Tibshirani R, Chu G. Significance analysis of microarrays applied to the ionizing radiation response. Proc Natl Acad Sci. 2001;98:5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wen X, Furhman S, Michaels GS, Carr DB, Smith S, Barker JL, Somogyi R. Large-scale temporal gene expression mapping of central nervous system development. Proc Natl Acad Sci. 1998;95:334–339. doi: 10.1073/pnas.95.1.334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wilda M, Bachner D, Just W, Geerkens C, Kraus P, Vogel W, Hameister H. A comparison of the expression pattern of five genes of the family of small leucine-rich proteoglycans during mouse development. J Bone Miner Res. 2000;15:2187–2196. doi: 10.1359/jbmr.2000.15.11.2187. [DOI] [PubMed] [Google Scholar]
  48. Xu T, Bianco P, Fisher LW, Longenecker G, Smith E, Goldstein S, Bonadio J, Boskey A, Heegaard AM, Sommer B, et al. Targeted disruption of the biglycan gene leads to an osteoporosis-like phenotype in mice. Nat Genet. 1998;20:78–82. doi: 10.1038/1746. [DOI] [PubMed] [Google Scholar]
  49. Yaffe D, Saxel O. Serial passaging and differentiation of myogenic cells isolated from dystrophic mouse muscle. Nature. 1977;270:725–727. doi: 10.1038/270725a0. [DOI] [PubMed] [Google Scholar]
  50. Yamaguchi A, Kahn AJ. Clonal osteogenic cell lines express myogenic and adipogenic developmental potential. Calcif Tissue Int. 1991;49:221–225. doi: 10.1007/BF02556122. [DOI] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES